1. Introduction

In recent years, mobile devices have been ubiquitous in our daily lives, thanks to their high capacity to perform various tasks such as speech recognition, image conversion, and virus scanning [1, 2]. Nevertheless, those tasks require high processing and storage capabilities that make them difficult to be performed by mobile devices [3]. Therefore, cloud computing and fog computing technologies have been recently employed as robust resource providers to allocate storage capacities and computing power to these devices assisting them in processing resource-intensive tasks. In essence, tasks from mobile devices are offloaded to a cloud server for processing and the feedback is then sent back to the devices [4]. However, the cloud servers may be situated far from the mobile devices, potentially resulting in delayed responses due to the long time taken to receive tasks from mobile users and send responses back to them.

Hence, mobile edge computing (MEC) emerges as a robust solution to address these shortcomings. By utilizing multiple servers situated at the network edge, MEC facilitates the offloading of users’ tasks from mobile devices to the nearest server [5]. Nevertheless, the static nature of the MEC servers restricts their ability to adapt to the varying needs of mobile devices. Also, natural disasters and climate change may affect the MEC network and offload tasks. In response to these shortcomings, unmanned aerial vehicles (UAVs) have been recently integrated with the MEC servers to present a novel system, known as UAV-assisted MEC. This integration aims to enhance the quality of services (QoS) provided to users. In this system, the MEC servers are mounted on the UAVs, offering two distinct advantages: (I) reducing the transmission distance between the server and mobile users through the mobility of UAVs and (II) presenting improved line-of-sight links for the mobile users by flying the UAVs at a high altitude [6].

In [6], the integration of multiple UAVs, as opposed to a single UAV, into the MEC system was explored to expedite the collection and processing of mobile tasks. This integration aimed to minimize the total energy consumption compared to utilizing a single UAV. However, this approach poses two significant issues: optimizing UAV deployment and task scheduling, which need to be carefully addressed to minimize overall energy consumption effectively. To tackle these issues, the authors in [6] introduced a novel greedy method for scheduling mobile tasks for UAVs and employed population-based differential evolution (DE) to optimize UAV deployment. It is essential to note that task scheduling heavily relies on UAV deployment. Hence, tackling the deployment optimization problem carefully is crucial for achieving better task scheduling and ultimately minimizing overall energy consumption. In essence, the task scheduling problem comprises two main parts: offloading decision and resource allocation. The offloading decision determines whether a task should be executed locally on mobile devices or transmitted to a UAV for remote processing. Meanwhile, resource allocation determines the resources that are required to complete this task efficiently.

The algorithm proposed in [6] demonstrates remarkable outcomes in facilitating UAV deployment and scheduling tasks for the multi-UAV-enabled MEC system with a dual-layer framework: upper layer optimization, driven by DE, for deployment optimization, and lower layer optimization handles task scheduling. Despite its effectiveness, this algorithm still warrants further improvement and refinement, particularly in the upper layer optimization, to better deploy UAVs and perform task scheduling, thus efficiently minimizing the total energy consumption in the MEC system. Therefore, in this paper, we propose a novel optimization technique, namely, IToGBOTaS, IToGNDOTaS, IToDETaS, and IToSWOTaS, aimed at achieving more accurate UAV deployment and task scheduling with the ultimate goal of minimizing the total energy consumption. These techniques are based on a dual-layer framework: lower layer optimization based on the greedy algorithm and improved upper layer optimization. In the lower layer optimization, we employ the greedy algorithm presented in [6] as it has proven its effectiveness and efficiency in tackling this problem. Meanwhile, the upper layer optimization is improved in this research with a two-step approach. The first step discards the random selection used to replace stop points in the original layer and relies on sequential replacement. This sequential approach ensures that solutions in the current deployment are replaced with new solutions generated from the same individual in the updated deployment. This strategy preserves the essential exploration and exploitation behaviors of the metaheuristic algorithms, thus guarding against a reduction in solution diversity that may lead to falling into local minima. The second step is based on employing a variety of metaheuristic algorithms, such as gradient-based optimization (GBO), generalized normal distribution optimization (GNDO), and spider wasp optimization (SWO), to assess their efficiency in obtaining the optimal deployment of UAVs.

The efficacy of these newly proposed optimization techniques is evaluated using nine instances with a number of mobile tasks ranging between 100 and 900. This comprehensive assessment aims to validate the stability and performance of the algorithms. To validate the effectiveness of the proposed models, both IToDETaS and IToGBOTaS are initially compared against the highly performing algorithm, ToDETaS [6], across several performance metrics. This includes metrics such as best fitness, worst fitness, average fitness, standard deviation, Friedman mean rank (Frk), Wilcoxon rank sum (WRS) test, and multiple comparison test. This thorough comparison highlights the effectiveness of our proposed algorithms. The results proved the effectiveness of IToGBOTaS for all performance indicators for all used instances, except for the instance with 900 tasks that could be better solved by the IToDETaS technique. Furthermore, to show the effectiveness of the proposed algorithms, they are compared against other several metaheuristic algorithms, such as the sine-cosine algorithm (SCA), the whale optimization algorithm (WOA), the equilibrium optimizer (EO), and the crested porcupine optimizer (CPO), under the same dual-layer design. The results show that the performance of IToGBOTaS and IToSWOTaS is competitive and outperforms all other compared algorithms.

The rest of this paper is organized as follows: Section 2 presents the related work; Section 3 presents the problem formulation; Section 4 presents the standard metaheuristic algorithms used in this study; in Section 5, our proposed algorithms for task scheduling and deployment optimization in multi-UAV-enabled MEC systems are explained; the experiment settings are provided in Section 6; the experimental results are provided in Section 7; Section 8 presents managerial implications; and the conclusion and future work are given in Section 9.

2. Related Work

Several studies in the literature proposed various approaches to tackle task scheduling in MEC systems. In [7], Zhang et al. proposed an energy-efficient offloading (EEO) technique in MEC systems to minimize energy costs. They formulated the offloading decision as an optimization problem and developed the EEO mechanism to minimize the total energy consumption. In [8], Chen et al. presented a study to jointly address task scheduling and UAV deployment in the MEC system. Similar to [6], they divided the optimization problem into two layers: the lower layer for task scheduling and the upper layer for optimizing UAV deployment by integrating both particle swarm optimization and genetic algorithms. Zhang et al. [9] utilized a game-theoretic method to optimize the offloading decision and resource allocation problems. In [10], the genetic algorithm was employed to optimize task scheduling in UAV-enabled MEC systems.

In addition, several other algorithms, especially metaheuristic algorithms due to their high effectiveness in solving several NP-hard optimization problems [11–13], were proposed in the literature for optimizing task scheduling, including the deep reinforcement learning algorithm [14], gray wolf optimizer (GWO) [15], particle swarm optimization [16–18], Nutcracker optimization algorithm [19], GBO [19], genetic algorithm [20], trees social relations algorithm [21], snake optimizer [22], Q-learning-based hybrid algorithm [23], and deep reinforcement learning approach [24].

The UAV deployment is essential; it must consider the UAV’s trajectory from the beginning to the endpoint while considering safety and shorter distances to save consumed energy. Several papers in the literature have been proposed for addressing the trajectory optimization problem for single and multi-UAVs, including those reviewed in the remainder of this section. For a single UAV-enabled MEC, the authors in [25] designed a framework to maximize the computation rate in a UAV-enabled MEC system by optimizing its trajectory and communication resources simultaneously. This problem was classified as a nonconvex optimization problem and is a highly challenging task. Hence, they presented two-stage and three-stage alternate techniques to solve this problem. In [26], the authors designed an optimization problem for the joint optimization of UAV trajectory, resource allocation, and offloading decisions with the purpose of minimizing task delay and energy consumption.

Huang et al. [27] introduced an encoding strategy aimed at capturing the solutions for optimization of UAV deployment in a way that avoids various drawbacks, including mixed variables and extreme dimensionality. This strategy was combined with the DE algorithm to suggest a new variation, VIPS, which was evaluated across seven instances. In addition, comparative analysis against various optimization approaches demonstrates the superiority of the encoding scheme. In [28], leveraging the same encoding methodology, three different metaheuristic optimization algorithms, including the flower pollination algorithm (FPA), the SCA, and the salp swarm algorithm (SSA), were applied to optimize the UAV trajectory with the aim of minimizing total energy consumption. These algorithms were developed to regulate the number and positions of stop points over the drone deployment. Extensive evaluations across diverse scenarios highlighted SCA’s remarkable performance, surpassing other algorithms consistently. Similarly, Zhang [29] enhanced the backtracking search algorithm (BSA) by utilizing the same encoding technique to solve this problem, which was enhanced with opposition-based learning and a population updating technique, called BSADP. To demonstrate the effectiveness of the proposed BSADP, it was tested on multiple cases and the obtained results compared to the rival algorithms.

Asim et al. [8] devised a GA-based trajectory planning technique, integrating variable population size, to minimize energy consumption in multi-UAV-aided MEC systems. Their approach involved two stages: initially, employed GA with variable population size to determine the near-optimal stop point deployment for UAVs, followed by utilizing the multichrome genetic algorithm to find out the interrelation among UAVs and HPs, the near-optimal stop points order for UAVs, and the UAV’s near-optimal number. Furthermore, in [9], an iterative optimization method coupled with a double-loop structure is proposed to jointly optimize the partial computation offloading, CPU allocation, user association, power and spectrum resources, and UAVs’ trajectory, aiming to minimize total energy consumption and improve computation efficiency in MEC systems. Huang et al. [30] presented a trajectory planning algorithm that consists of three stages to reduce UAVs’ overall energy usage in the multi-UAV-enabled MEC system. Initially, the DE method was paired with a variable population-based encoding strategy to update the number and placements of stop points at the same time. Subsequently, the k-means clustering algorithm was used to split the given stop points into groups proportional to the number of UAVs, with each group including stop points visited by the same UAV. Finally, a low-complexity greedy technique was used to identify the order of stop points in each cluster, resulting in the trajectory of each UAV. There are several other approaches proposed recently for optimizing task scheduling problems in MEC systems [31–33].

3. Problem Formulation

In the multi-UAV-assisted MEC system, a significant number of mobile users M = {1, 2 … .m} are served by N UAVs acting as flying edge clouds. In this system, each task can be executed either locally (i.e., on its mobile device) or on UAVs. Therefore, each task could be executed on (N + 1) execution patterns. Those execution patterns are denoted as Q = {0, 1, 2, …, N}. For more illustration, k = 0| k ∈ Q refers to executing the task on the local device, while k > 0 indicates executing the tasks on the kth UAV. In addition, N UAVs use frequency division multiple access with an equal bandwidth to serve all mobile devices. In this study, as described in [6], each ith mobile user is represented in 3-D coordinates (x_i, y_i.0) and assigned a task T_i. This task is represented as T_i = (C_i,  D_i), where C_i stands for the total number of CPU cycles required to execute this task and D_i stands for the input data size. All those parameters are given a priori. All UAVs are first prepared with directional antennas of constant bandwidth. In this study, the altitude of the flying UAVs is constant and symbolized as H, and the location of the jth UAV is represented in 3-D coordinates (X_j, Y_j, H). It worth mentioning that X_j, Y_j, N are considered decision variables that need to be optimized for reaching the best coordinates and UAVs that could achieve better deployment. To manage the task execution on various patterns, according to [6], a binary matrix a of (M × (N + 1)) cells is defined and initialized with 0. If the task T_i is processed in pattern k, a_i, q = 1; otherwise, a_i, q = 0. In addition, for the resource allocation, a matrix f is defined, where f_i,q stands for the resources assigned to the task T_i in pattern q. In the multi-UAV-assisted MEC system, as discussed in [6], three models are employed to estimate the energy consumed by both UAVs and local devices for completing m tasks. Those models are discussed in detail in the rest of this section.

4. Metaheuristic Algorithms: Overview

5. Proposed Algorithms: IToDETaS, IToGBOTaS, and IToGNDOTaS

The task scheduling problem in the multi-UAV-enabled MEC system is primarily dependent on the deployment of UAVs, where a task could be executed on the UAV only if this task exists within this UAV’s coverage area. From that, the deployment of multiple UAVs has to be accurately optimized to deploy them in a form that aids in covering all mobile tasks as effectively as possible to minimize total energy consumption. In addition, the deployment of UAVs cannot be considered unless the tasks are accurately scheduled. Therefore, both the deployment of UAVs and task scheduling in the multi-UAV-assisted MEC system have to be accurately addressed to minimize total energy consumption.

In [6], two optimization layers, upper and lower, were proposed to optimize those two problems, where the upper layer is responsible for optimizing the deployment and the lower layer is responsible for optimizing the task scheduling problem. The upper layer used the DE algorithm in conjunction with an effective encoding scheme to optimize the deployment, while task scheduling was solved in the lower layer based on an effective greedy algorithm. However, in [6], the new deployment generated by DE is randomly inserted one by one in the previous deployment and that might reduce the probability of reaching better outcomes because each individual in the population tries to improve its previous solution, and hence, replacing the new solution with a random solution might leave the bad solution of this individual in the population, negatively affecting the whole deployment. Therefore, we found that the solution obtained by one individual might be more effective if it is inserted in place of its original position in the previous deployment. In our research conducted in this paper, we extensively focus on how to effectively optimize the deployment of UAVs for better task scheduling with the purpose of minimizing total energy consumption in multi-UAV-enabled MEC systems. This optimization was based on two steps: The first is based on replacing the old solution of an individual in the current deployment with its newly generated solution to aid in diversifying the stop points, thereby aiding in covering the area of mobile users more effectively. The second step is based on adapting new metaheuristic-based algorithms for effectively finding the stop points of each UAV. In addition, the task scheduling of mobile tasks is addressed in our proposed algorithms using lower layer optimization based on a novel greedy algorithm, which is discussed in detail in [6]. In brief, the proposed algorithms for joint optimization of both task scheduling and deployment of UAVs are based on the following steps: encoding mechanism, initialization, improved upper layer optimization based on GBO, SWO, DE, and GNDO, and pseudocode of the proposed algorithms.

5.1. Solution Encoding Mechanism

In [6], a new solution encoding method was designed in an effective manner to minimize the total number of decision variables, thereby aiding the optimization techniques in achieving better outcomes when applied to this problem. In a more general sense, assuming that we try to adapt the population-based GBO algorithm for tackling the deployment optimization problem and make each solution in the population suitable for a single deployment, the number of dimensions significantly increases because each deployment is composed of N stop points, and each stop point i involves two dimensions (X_i, Y_i) in the deployment. Hence, in this case, the total number of dimensions in each solution is N∗2, thereby minimizing the efficiency and effectiveness of the optimization techniques and significantly consuming storage and computing resources. Therefore, in [6], a new solution encoding mechanism was presented to process this challenge. This mechanism proposes that each individual is responsible for a stop point, and all individuals are responsible for the whole deployment, as depicted in Figure 1. As a result, the total dimension for each individual is a constant of 2, thereby saving the computer resources and improving the effectiveness and efficiency of the optimization algorithms. Also, the number of UAVs needs to be optimized because increasing or decreasing them unreasonably might consume a huge amount of energy. To achieve that under the traditional encoding scheme, the individuals must be of variable length and that is hard to achieve with the metaheuristic and evolutionary algorithms. As an alternative, this new encoding scheme enables the removal of some UAVs without looking at the dimensions of each individual. In brief, this encoding scheme has the following merits:

• •

  Simple.

• •

  Fixing the number of dimensions for each individual.

• •

  Enabling the removal and addition of new UAVs to the population easily.

• •

  Affecting effectively and efficiently the performance of metaheuristic and evolutionary algorithms.

5.3. Improved Upper Layer Optimization: GBO, DE, and GNDO

In this layer, the number and stop points of UAVs are estimated to optimize the deployment of UAVs, thereby scheduling mobile tasks more accurately and minimizing overall energy consumption. According to the solution encoding scheme, the number of UAVs is equal to the population size. Hence, to optimize the number of UAVs, we only need to minimize N in a form that could minimize the overall energy consumption, taking into consideration that all tasks have not been processed in real time but could be executed under the delay constraints discussed in C₇ and C₈. Based on that, in [6], the authors suggested that the number of UAVs should be minimized as much as possible. The population size in our proposed algorithms is set to N = m/n_max, and the elimination operator discussed in [6] was applied to remove the individuals from Pp that has the lowest distance with the remaining individuals.

After adjusting the number of UAVs, we need to search for the optimal deployment of UAVs, which could minimize the total energy consumption while at the same time distributing UAVs in a manner that aids in processing all mobile tasks. Therefore, in this study, we use a newly proposed metaheuristic algorithm, namely, GBO, to tackle this problem. The GBO, SWO, DE, or GNDO algorithms are employed to update Pp to generate a new population Ppⁿ. This new population is thereafter used to replace the individuals in Pp. In [6], each individual in Ppⁿ replaces a randomly selected individual from Pp to generate a new deployment Ppⁿ¹. However, randomly selecting an individual from Pp to be replaced might contradict the nature of metaheuristic techniques, which propose that each individual seeks to search for a solution better than its current solution. Hence, replacing the ith solution in Pp with the ith solution in Ppⁿ might be more effective because that will preserve the characteristics of each individual in the population; hence, the exploration and exploitation operators of metaheuristic algorithms are not negatively affected within the optimization process. After generating Ppⁿ¹, we check that it still satisfies the constraint C2. If that, the offloading decision aⁿ and resource allocation fⁿ is computed. If {N, Ppⁿ¹,  aⁿ,  fⁿ} is able to execute more mobile tasks while satisfying the delay constraint than {N, Pp,  a,  f}, then the former replaces the latter. However, if both {N, Ppⁿ¹,  aⁿ,  fⁿ} and {N, Pp,  a,  f} could execute the same number of tasks and the energy consumption under the former is lower than that under the latter, then the former replaces the latter.

$$ ()

where NC_n represents the number of completed tasks under the new deployment Ppⁿ¹, NC_o represents the number of completed tasks under the current deployment Pp, E({N, Ppⁿ¹, aⁿ, fⁿ}) stands for the energy consumed under {N, Ppⁿ¹, aⁿ, fⁿ}, and E({N, Pp, a, f}) stands for the energy consumed under {N, Pp, a, f}. Finally, the lower layer optimization based on the greedy algorithm discussed in [6] was integrated with the upper layer optimization based on the newly proposed GBO to propose a new optimization technique for optimizing both the task scheduling and deployment of UAVs. This technique is called ToGBOTaS. However, as mentioned before, the original upper layer optimization used randomization selection to replace the current solution and that might affect the performance of metaheuristic algorithms, so an improved variant of this layer is presented in this study based on replacing the solution of the current individual in Ppⁿ¹ with the solution of the same individual in Ppⁿ. This improvement is added to ToGBOTaS to present a new variant known as IToGBOTaS. The pseudocode of this algorithm is described in Algorithm 5.

Algorithm 5: Pseudocode of IToGBOTaS.
•  

  Input: N and t_max;

•  

  Output: $$

• 1.

   Pp = Initialize N individuals, $$ using Algorithm 4

• 2.

   Compute a and f according to Pp under the greedy algorithm

• 3.

   Evaluate the overall energy consumption under {N, Pp, a, f}

• 4.

   $$ and $$

• 5.

   t = 1; %% Function evaluation counter

• 6.

   F = 0 %%A flag to determine if the algorithm could not achieve a feasible solution for a number of consecutive function evaluations

• 7.

   Inf = 0%% Number of consecutive times the algorithm could not achieve a feasible solution

• 8.

   while (t < t_max)

• 9.

    while (F = = 0 && {N, Pp, a, f}is feasible)

• 10.

     Apply the elimination operator discussed above

• 11.

    end

• 12.

    %% Generate new population using GBO

• 13.

    for each $$

• 14.

     //GSR strategy.

• 15.

     Applying (31) to generate the new solution $$

• 16.

     //LEO Strategy

• 17.

     Applying (34) to generate the new solution $$

• 18.

     t = t + 1

• 19.

    End

• 20.

    $$

• 21.

    %% Evaluation

• 22.

    fori = 1 : N

• 23.

     %% Creating new deployment Ppⁿ¹

• 24.

     Ppⁿ¹ = Pp

• 25.

     $$

• 26.

     Compute aⁿ and fⁿ according to Ppⁿ¹ under the greedy algorithm

• 27.

     Evaluate the overall energy consumption under {N, Ppⁿ¹, aⁿ, fⁿ}

• 28.

     Pp = Applying (53) to compare Ppⁿ¹ with Pp

• 29.

     $$

• 30.

      $$

• 31.

     End

• 32.

     $$

• 33.

      $$

• 34.

     End

• 35.

     if {N, P, a, f} is infeasible

• 36.

      Inf = Inf + 1

• 37.

      if Inf > 1000

• 38.

       $$

• 39.

       Break;

• 40.

      end

• 41.

     end

• 42.

     if {N, P, a, f} is infeasible && F = = 0

• 43.

      Inf = 0

• 44.

      Break;

• 45.

     end

• 46.

     t = t + 1

• 47.

    End

• 48.

   End

This algorithm receives the maximum number of UAVs, N, and the maximum function evaluation, t_max. Then, it starts with creating a population of N UAVs and initializes it using Algorithm 4. This population is thereafter employed with the greedy algorithm described in [6] to compute the offloading decision a and resource allocation f. Both a and f are employed with the initialized population Pp and the population size N to compute the total energy consumption in the multi-UAV-enabled MEC system. This initialized population Pp is considered as the best-so-far deployment $$ and the worst-so-far deployment $$, which are later updated within the optimization process. In addition, this algorithm uses two factors, F and Inf: the first factor is used to determine if the algorithm is inability to reach a feasible solution within a consecutive number of function evaluations, and the second factor is used to determine the number of consecutive times within which it could not achieve a feasible solution. Afterward, the optimization process is started to update the initial population Pp to search for a better deployment for UAVs, which could aid in achieving better task scheduling, thereby minimizing the overall energy consumption. Broadly speaking, Lines 9–11 employ the elimination operator to remove some UAVs that are crowded with the remaining UAVs to minimize the energy consumed by them, which might negatively affect the performance of the UAV-enabled MEC system. Lines 13–20 update Pp using the updating schemes of GBO to generate a new population Ppⁿ. Afterward, this new population is evaluated according to the following steps:

• •

  Step 1: Set Pp to Ppⁿ¹, then the ith stop point in Ppⁿ is used to replace the same stop point in Ppⁿ¹.

• •

  Step 2: Ppⁿ¹ is used with the greedy algorithm to compute a and f, which are then employed to compute the overall energy consumption in the system.

• •

  Step 3: Applying (54) to compare Ppⁿ¹ and Ppⁿ

• •

  Step 4: Update $$ and $$

• •

  Step 5: If the number of consecutive infeasible solutions exceeds 1000, then $$.

• •

  Repeat Steps 1–5 to observe the performance of all UAVs in Ppⁿ.

Finally, the optimization process of IToGBOTaS is repeated until the maximum number of function evaluations are met, and then the best-so-far solution is returned $$. The GNDO, SWO, and DE algorithms were used to replace the search engine GBO in IToGBOTaS to propose three additional optimization techniques, namely, IToDETaS, IToSWOSTaS, and IToGNDOTaS, to observe their performance for optimizing the task scheduling and deployment of UAVs in the UAV-enabled MEC system. Figure 2 depicts a generic flowchart demonstrating how the upper layer optimization under four algorithms collaborates with the lower layer optimization under the greedy algorithm in the proposed algorithms.

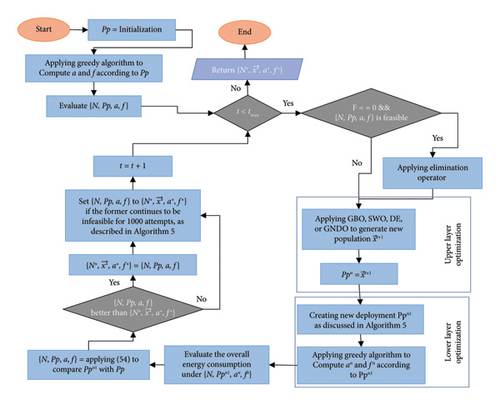
6. Experimental Settings

All algorithms in this study are executed 25 independent times, and the obtained outcomes are analyzed using several performance metrics, such as average EC (AEC), average completed task (ACT), Frk, p value returned by the WRS test, and multiple comparison test based on Frk. In addition, the computational cost consumed by each algorithm for completing its task is estimated to show the speedup of each algorithm. The same maximum number of function evaluations, which is 3000, was set for all algorithms to ensure a fair comparison. Also, all algorithms are implemented using MATLAB R2019a on the same device.

7. Results and Discussion

This study assesses the performance of the proposed algorithms using nine instances with a number of mobile users ranging between 100 and 1500. In addition, those algorithms are compared to a recently published task scheduling technique known as ToDETaS [6] and several recently published metaheuristic algorithms as search engines to search for the best deployment for UAV, including the CPO [45], EO [46], SCA [47], and WOA [48]. The controlling parameters of all algorithms, including the proposed and compared algorithms, are set as recommended in the cited papers. This section first compares the proposed algorithms (IToGBOTaS and IToDETaS) to ToDETaS and ToGBOTaS to expose the effect of our improvement on the original upper layer optimization. Afterward, those proposed algorithms are extensively compared to several metaheuristic algorithms as search engines without adding our improvement to show their effectiveness. Finally, our improvement is assessed on all metaheuristic algorithms to show whether it could achieve better outcomes or not.

7.1. Comparison Between the Proposed Algorithms and ToDETaS

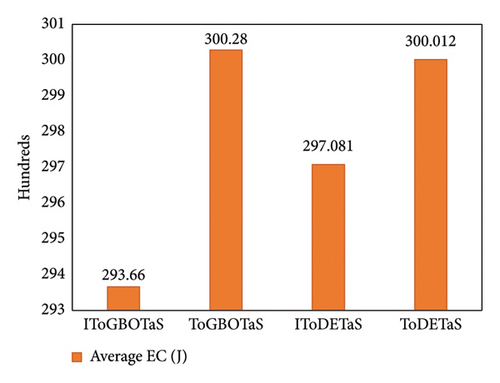
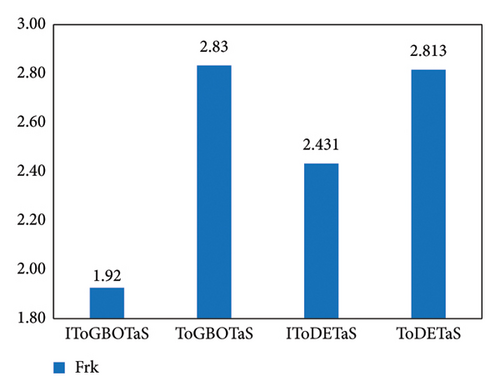
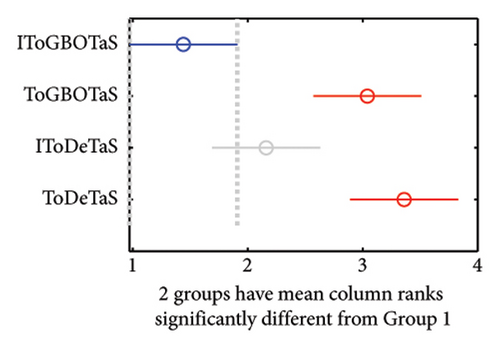
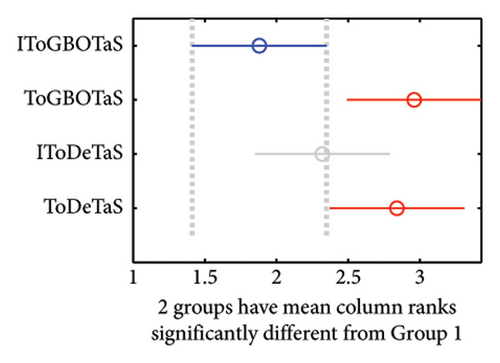
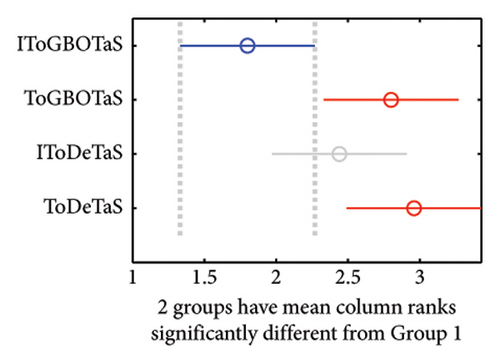
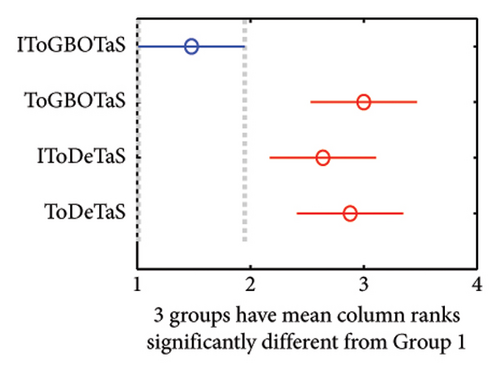
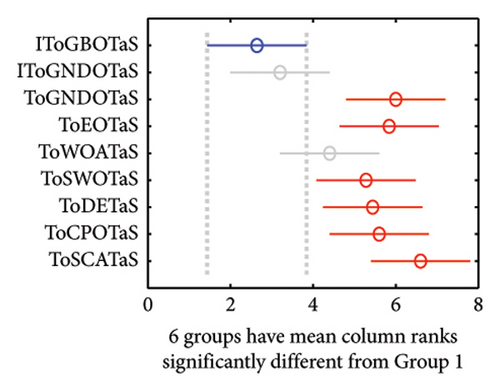
The proposed algorithms, IToGBOTaS, ToGBOTaS, and IToDETaS, are executed 25 independent times on each instance, and the obtained outcomes are reported in Table 1. This table shows that IToDETaS is better than all algorithms for only one instance with 900 mobile users, and IToGBOTaS is the best for the other instances in terms of all considered performance metrics. Those results reveal the effectiveness of our improvement to ToDETaS, which enables it to achieve better outcomes when applied to search for the best deployment for UAVs that could schedule the tasks more accurately and minimize the overall energy consumption. To highlight the overall performance of algorithms, Figures 3 and 4 show the average of AEC values and the average of Frk values reported in Table 2 for each algorithm. Those figures show the effectiveness of IToGBOTaS over all compared algorithms, where it could achieve an average AEC value of 29,365.77 and an average Frk of 1.92, IToDETaS is the second best, and ToGBOTaS is the worst. To show the difference between the outcomes of IToGBOTaS and those of the other algorithms, both the WRS test and the multiple comparison test are employed. The results of the WRS test are shown in Table 3, which reveals that IToGBOTaS is significantly different from ToDETaS for all instances, from ToGBOTaS for seven instances, and from IToDETaS for four instances. The results of the multiple comparison test are shown in Figure 5 for some instances. This figure shows that the means of IToGBOTaS are significantly different from those of ToGBOTaS and ToDETaS for all depicted instances, and are slightly different from those of IToDETaS for three instances and significantly different for the other instances.

Table 2. Comparison between the proposed algorithms and ToDETaS.

	IToGBOTaS			ToGBOTaS			IToDETaS			ToDETaS
	AEC	CT	Frk	AEC	CT	Frk	AEC	CT	Frk	AEC	CT	Frk
100	5467.194	100	1.44	6026.806	100	3.04	5547.242	100	2.16	6106.855	100	3.36
200	11,698.652	200	1.88	12,058.732	200	2.96	11,978.587	200	2.32	11,938.864	200	2.84
300	17,739.386	300	1.80	18,099.681	300	2.80	17,820.134	300	2.44	18,379.305	300	2.96
400	23,030.334	400	1.72	23,830.741	400	2.76	23,950.400	400	2.92	23,670.814	400	2.60
500	27,394.586	500	1.48	29,033.679	500	3.00	28,793.588	500	2.64	28,793.945	500	2.88
600	34,182.666	600	2.20	34,582.930	600	2.80	34,503.353	600	2.28	34,543.058	600	2.72
700	41,178.541	700	2.20	41,418.776	700	2.40	41,578.494	700	2.48	41,938.290	700	2.92
800	48,044.770	800	1.96	49,244.350	800	2.84	48,844.941	800	2.56	49,284.434	800	2.64
900	55,555.869	900	2.64	55,955.351	900	2.88	54,356.447	900	2.08	55,355.565	900	2.40

• Note: Bold values represent the best and most competitive results.

Table 3. Comparison between IToGBOTaS, ToDETaS, ToGBOTaS, and IToDETaS under the WRS test.

	100	200	300	400	500	600	700	800
ToGBOTaS	2.7771E − 05	3.5681E − 04	1.3733E − 02	6.8504E − 04	3.5302E − 06	1.0034E − 02	7.4151E − 01	3.6093E − 03
IToDETaS	2.2156E − 01	4.6140E − 03	1.3517E − 01	2.0352E − 03	3.5836E − 05	4.8486E − 01	4.3768E − 01	9.8635E − 03
ToDETaS	5.1234E − 06	1.6708E − 03	4.2399E − 05	8.3203E − 03	2.7771E − 05	1.9360E − 02	3.7738E − 02	9.8635E − 03

• Note: Bold text highlights the p value less than 0.05, indicating the number of cases in which the proposed IToGBOTaS could produce different outcomes significantly.

7.2. Comparison With Six Rival Metaheuristic Optimizers Under Random Selection

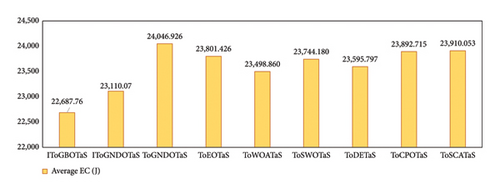
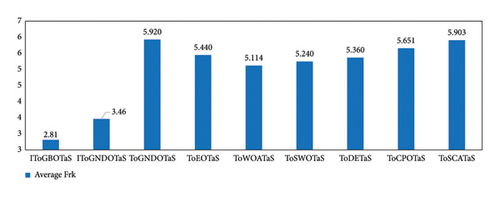
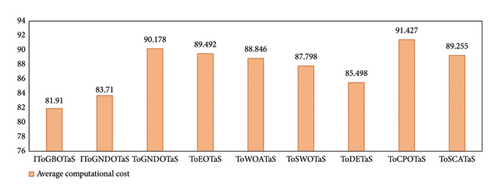
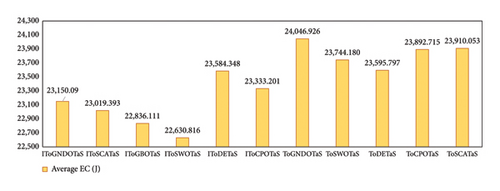
This section presents the results of an extensive comparison between the proposed algorithms, IToGBOTaS and IToGNDOTaS, and six rival optimizers based on the original upper layer optimization. Each algorithm is executed 25 times independently on each instance, and the results, which are represented in AEC, CR, and Frk, are shown in Table 4. This table reveals that all algorithms could execute all mobile tasks, but IToGBOTaS outperforms all algorithms in terms of AEC for six out of seven mobile tasks, and IToGNDOTaS could outperform the remaining tasks. To better clarify the results in this table, Figure 6 is presented to report the average AEC obtained by each algorithm on all observed instances. This figure shows that IToGBOTaS is the best with an average value of 22,687, followed by IToGNDOTaS as the second best with a value of 23,110, and ToGNDOTaS is the worst with a value of 24,046. Also, Figure 7 affirms that IToGBOTaS is the best-performing algorithm because it could achieve a better average value for the Frk metric. To show off the efficiency of each algorithm, the average computational cost on the observed instances is computed and reported in Figure 8, which shows that IToGNDOTaS and IToGBOTaS are slightly better than all compared algorithms.

Table 4. Comparison between the proposed algorithms and six rival optimizers under random selection.

m		IToGBOTaS	IToGNDOTaS	ToGNDOTaS	ToEOTaS	ToWOATaS	ToSWOTaS	ToDETaS	ToCPOTaS	ToSCATaS
100	AEC	5387.214	5507.129	6026.884	5747.005	5827.122	5866.985	5866.941	5946.946	5627.190
	CT	100	100	100	100	100	100	100	100	100
	Frk	2.68	3.44	6.08	4.84	5.76	5.32	5.76	5.88	5.24
200	AEC	11,498.809	11,578.832	12,178.594	11,818.994	12,018.899	11,818.934	12,258.679	12,018.736	12,218.707
	CT	200	200	200	200	200	200	200	200	200
	FR	2.48	3.08	5.80	5.08	5.76	4.68	6.16	5.52	6.44
300	AEC	17,699.408	17,579.791	18,459.395	17,900.059	18,259.400	18,539.276	18,179.598	18,259.626	18,339.529
	CT	300	300	300	300	300	300	300	300	300
	FR	2.72	3.08	6.28	4.72	5.12	5.72	5.80	5.84	5.72
400	AEC	22,631.164	22,790.801	24,350.102	23,990.514	23,510.953	24,110.127	23,510.885	24,509.823	24,030.452
	CT	400	400	400	400	400	400	400	400	400
	FR	3.00	2.88	6.16	5.72	4.52	5.48	4.84	6.40	6.00
500	AEC	27,475.040	28,033.968	28,674.194	29,393.524	29,113.721	28,833.737	28,953.416	29,273.404	29,233.91
	CT	500	500	500	500	500	500	500	500	500
	FR	2.76	3.44	5	6	5.76	5.04	5.24	5.68	6.08
600	AEC	33,463.769	33,823.206	35,582.353	35,582.100	34,503.040	34,902.238	35,222.190	35,382.294	35,742.41
	CT	600	600	600	600	600	600	600	600	600
	FR	2.64	3.2	6	5.84	4.4	5.28	5.44	5.6	6.6
700	AEC	40,708.515	42,456.769	43,056.960	42,177.787	41,258.883	42,137.964	41,178.870	41,858.179	42,178.17
	CT	700	700	700	700	700	700	700	700	700
	FR	3.70	5.08	6.12	5.88	4.48	5.16	4.28	4.64	5.24

• Note: Bold values represent the best and most competitive results.

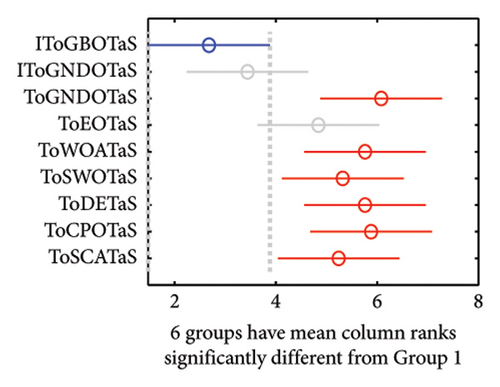
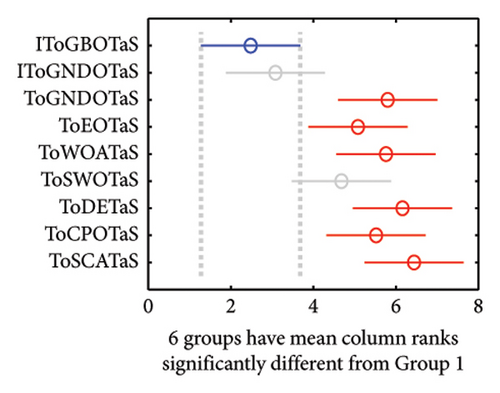
In addition, the WRS test and the multiple comparison test are used to show the difference between the outcomes of IToGBOTaS and those of the other algorithms. Table 5 shows the results of the WRS test, which reveals that IToGBOTaS is significantly different from all compared algorithms, with the exception of IToGNDOTaS, which could achieve outcomes slightly comparable to IToGBOTaS. Figure 9 shows the results of the multiple comparison test for some instances. This figure illustrates that the means of IToGBOTaS are significantly different from all algorithms except for IToGNDOTaS.

Table 5. Comparison between IToGBOTaS and rival optimizers with random selection under the WRS test.

	100	200	300	400	500	600	700
IToGNDOTaS	3.22E − 01	2.14E − 01	5.35E − 01	6.14E − 01	9.91E − 02	1.30E − 01	1.21E − 01
ToGNDOTaS	2.66E − 06	2.20E − 06	1.13E − 04	1.67E − 04	1.28E − 03	1.43E − 04	3.19E − 03
ToEOTaS	2.65E − 04	1.97E − 05	8.32E − 03	7.35E − 04	1.81E − 04	1.43E − 04	3.61E − 02
ToWOATaS	1.38E − 05	3.90E − 05	1.95E − 04	2.09E − 02	3.02E − 05	5.53E − 03	1.94E − 02
ToSWOTaS	6.42E − 05	1.55E − 04	5.94E − 04	6.85E − 04	4.13E − 04	5.14E − 04	4.16E − 02
ToDETaS	2.00E − 06	6.75E − 06	1.43E − 04	1.53E − 02	4.45E − 04	3.57E − 04	4.48E − 02
ToCPOTaS	8.10E − 06	3.53E − 06	9.72E − 04	4.24E − 05	5.44E − 05	1.81E − 04	3.82E − 02
ToSCATaS	2.32E − 03	2.00E − 06	3.57E − 04	6.85E − 04	7.39E − 06	3.02E − 05	2.78E − 02

• Note: Bold text highlights the p value less than 0.05, indicating the number of cases in which the proposed IToGBOTaS could produce different outcomes significantly.

7.3. Comparison With Six Rival Optimizers Under Improved Upper Layer Optimization

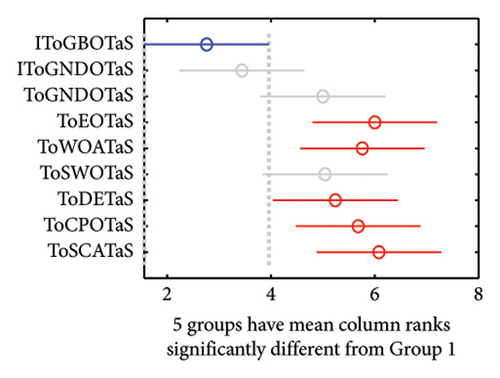
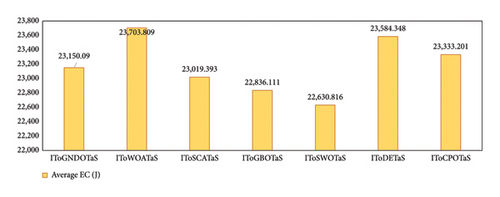
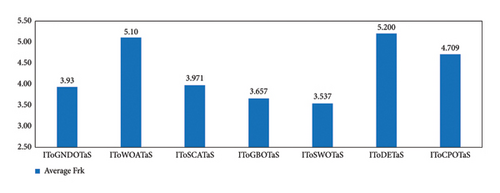
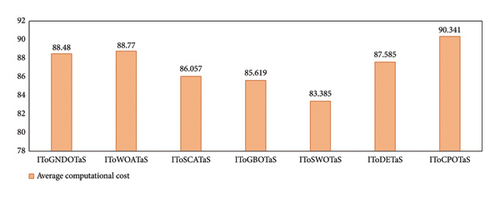
This section gives the findings of a thorough comparison between the proposed algorithms and six competing optimizers based on the improved upper layer optimization. Each algorithm is conducted 25 times independently on each instance, and the results are displayed in Table 6 as AEC, CR, and Frk. This table shows that all algorithms can complete all mobile tasks. However, IToSWOTaS surpasses all algorithms in terms of AEC for four of the seven mobile tasks, IToGBOTaS could outperform in two instances (200 and 700), and IToGNDOTaS could outperform in only one instance. To help comprehend the results in this table easily, Figure 10 is presented to show the average AEC obtained by each approach on all observed instances. This figure reveals that IToSWOTaS is the best with an average value of 22,630, IToGBOTaS is the second best with a value of 22,860, and ToWOATaS is the worst with a value of 23,703. Furthermore, Figure 11 shows that IToSWOTaS is the best-performing algorithm since it can reach a better value for the Frk measure. To demonstrate each algorithm’s efficiency, the average computational cost on the observed instances is computed and reported in Figure 12, which demonstrates that IToSWOTaS and IToGBOTaS outperform all compared algorithms somewhat.

Table 6. Comparison between the proposed algorithms and six rival optimizers under improved upper layer optimization.

m		IToGNDOTaS	IToWOATaS	IToSCATaS	IToEOTaS	IToGBOTaS	IToSWOTaS	IToDETaS	IToCPOTaS
100	AEC	5507.138	5427.318	5507.157	6146.903	5706.954	5427.251	5577.123	5587.143
	CT	100	100	100	100	100	100	100	100
	FR	3.68	4.72	3.96	6.36	3.88	3.48	6	3.92
200	AEC	11,618.793	11,858.712	11,658.982	—	11,538.914	11,738.790	11,698.913	11,978.589
	CT	200	200	200	199.88	200	200	200	200
	FR	3.88	5.16	4.12	5.48	3.36	4.12	4.88	5
300	AEC	17,340.200	18,059.472	17,580.117	—	17,739.431	17,499.963	17,900.035	18,259.288
	CT	300	300	300	299.96	300	300	300	300
	FR	3	4.8	4.12	5.68	3.72	3.72	5.24	5.72
400	AEC	22,391.353	23,670.305	22,871.411	—	22,790.780	22,311.567	23,390.946	22,991.165
	CT	400	400	400	399.96	400	400	400	400
	FR	3.52	5.4	4.28	6.44	3.72	3.48	4.68	4.68
500	AEC	28,313.837	29,472.506	27,794.751	—	27,993.897	27,435.025	28,553.980	28,274.382
	CT	500	500	500	499.92	500	500	500	500
	FR	3.84	5.76	3.72	5.92	4.04	3.2	5.16	4.36
600	AEC	34,661.623	35,221.240	33,944.466	35,222.710	33,423.877	32,944.484	34,822.468	34,303.435
	CT	600	600	600	600	600	600	600	600
	FR	5.12	5.16	3.76	5.00	3.52	3.08	5.44	4.92
700	AEC	42,217.690	42,217.107	41,778.866	—	40,658.925	41,058.631	41,578.494	41,938.406
	CT	700	700	700	699.96	700	700	700	700
	FR	4.68	4.72	3.84	6.36	3.36	3.68	3.75	4.36

• Note: Bold values represent the best and most competitive results. “—” represents infeasible solutions.

7.4. Comparison Between Improved and Original Upper Layer Optimization

In this section, we showcase the superiority of the improved upper layer optimization over the original one when it is applied to metaheuristic algorithms for solving the deployment of UAVs in the MEC system. The average AEC obtained by several metaheuristic algorithms under both improved and original upper layer optimization on seven tasks is computed and reported in Figure 13. Inspecting this figure shows that the improved method with all metaheuristic algorithms, except for IToDETaS, could fulfill better outcomes than the original upper layer optimization with the same algorithms. Also, this figure shows that IToSWOTaS is the best with an average AEC of 22,630, followed by IToGBOTaS and IToSCATaS with values of 22,836 and 23,019 as the second and third best algorithms, and ToGNDOTaS is the worst algorithm with a value of 24,046. From all the previous experiments, we can draw the following conclusions:

• •

  The improved upper layer optimization is better than the original one since it could improve the performance of all used metaheuristic algorithms when applied to optimize the deployment of UAVs.

• •

  Also, both IToGBOTaS and IToSWOTaS are the most effective algorithms for optimizing the deployment of UAVs in the multi-UAV-enabled MEC system.

• •

  ToGNDOTaS is the worst-performing algorithm.

8. Managerial Implications

Those questions needed a response to achieve two purposes: The first is to ensure that all tasks have been completed, and the second is to minimize the overall energy consumption in this system. Therefore, several algorithms, such as ToDeTaS, have been recently presented to address those issues. Those algorithms suffered from low-quality final results, so the proposed IToGBOTaS and IToSWOTaS are presented to better optimize the deployments of multiple UAVs, leading to better scheduling and low energy consumption. The better UAVs are deployed, the better IoT tasks are scheduled. Those algorithms suffered from low-quality final results, so the proposed IToGBOTaS and IToSWOTaS are presented to better optimize the deployments of multiple UAVs, leading to better scheduling and low energy consumption. The better UAVs are deployed, the better IoT tasks are scheduled. Smart agriculture, smart vehicles, smart cities, and smart pollution control are some of the most popular IoT applications in the world. For those applications supported by the multi-UAV-enabled MEC system, the proposed IToSWOTaS could be used for better deploying various UAVs and accurately scheduling the received tasks to various UAVs, thereby minimizing energy consumption and lowering response time. In brief, the better the deployment, the faster the IoT tasks are received and the lower the energy consumption. The better the scheduling of various tasks, the lower the response latency.

9. Conclusion and Future Work

Recently, an optimization technique based on two optimization layers: Upper layer optimization and lower layer optimization have been proposed for optimizing task scheduling and deployments of UAVs in the multi-UAV-assisted MEC system. The lower layer was responsible for optimizing task scheduling, while the upper layer was in charge of optimizing UAV deployment to improve mobile user coverage and task scheduling, hence reducing overall energy usage. However, the upper layer optimization needs further improvement to aid in attaining better deployments. Therefore, in this paper, this layer is improved based on two folds: The first fold is based on avoiding the random selection of the solutions to be replaced and relying on the sequential selection. This will preserve the exploration and exploitation characteristics of each individual within the whole optimization process, thereby aiding in achieving better outcomes. The second fold is adapting some of the recently published metaheuristic algorithms, such as SWO, GNDO, and GBO for optimizing the deployments of UAVs. Both improved upper layer and lower layer optimization help present new more effective optimization techniques, namely, IToGBOTaS, IToGNDOTaS, and IToSWOTaS. Those techniques are tested using nine instances with a variety of mobile tasks ranging from 100 to 1500 to determine their stability and then compared to different optimization techniques to determine their effectiveness. First, various experiments were carried out to compare IToDETaS and IToGBOTaS to the very effective method, namely, ToDETaS. This comparison used a lot of statistical information to determine the superiority and difference between their outcomes. The results of this comparison demonstrated the success of IToGBOTaS for all performance indicators across all used instances, except for one instance with 900 tasks that could be completed more efficiently by IToDETaS. Second, to demonstrate the usefulness of the proposed algorithms, they are compared to several metaheuristic algorithms that are adapted using the same two layers. The results of this comparison demonstrate that the performance of IToGBOTaS and IToSWOTaS is slightly competitive and better than all the other compared algorithms. Although these algorithms have shown superior performance for numerous IoT tasks, they still have some drawbacks that need further improvement in future work. For example, their performance is a little degraded as the number of mobile users increases. Hence, for large-scale instances, they might not be better than, but competitive with, the latest ToDETaS. Also, relying on a dual-layer framework to address both deployment optimization and task scheduling makes the proposed algorithms more complicated and hard to grasp. Therefore, our future work includes presenting an alternative to the dual-layer framework for optimizing both task scheduling and deployment optimization more simply and straightforwardly. In addition, we will adapt the metaheuristic algorithms for better scheduling IoT tasks in a reasonable amount of time. Finally, there are several other optimization problems for UAVs, such as 3-D routing planning for UAVs, UAV-assisted IoT data collection systems, and lost target search with UAVs, which we will try to solve using some of the latest metaheuristic algorithms.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Mohamed Abdel-Basset: conceptualization, methodology, investigation, resources, supervision, visualization, writing–original draft, review, and editing.

Reda Mohamed: conceptualization, methodology, investigation, writing–original draft, review, and editing.

Amira Salam: conceptualization, methodology, writing–original draft.

Karam M. Sallam: investigation, methodology, software, validation, writing–review and editing.

Ibrahim M. Hezam: validation, investigation, resources, writing–review and editing.

Ibrahim Radwan: validation, investigation, writing–review and editing.

Funding

This research was supported by the Researchers Supporting Project (RSP2024R389), from King Saud University, Riyadh, Saudi Arabia.