In the field of artificial intelligence, facial expression recognition (FER) in natural scenes is a challenging topic. In recent years, vision transformer (ViT) models have been applied to FER tasks. The direct use of the original ViT structure consumes a lot of computational resources and longer training time. To overcome these problems, we propose a FER method based on octonion orthogonal feature extraction and octonion ViT. First, to reduce feature redundancy, we propose an orthogonal feature decomposition method to map the extracted features onto seven orthogonal sub-features. Then, an octonion orthogonal representation method is introduced to correlate the orthogonal features, maintain the intrinsic dependencies between different orthogonal features, and enhance the model’s ability to extract features. Finally, an octonion ViT is presented, which reduces the number of parameters to one-eighth of ViT while improving the accuracy of FER. Experimental results on three commonly used facial expression datasets show that the proposed method outperforms several state-of-the-art models with a significant reduction in the number of parameters.

1. Introduction

With the rapid development of AI and computer vision, automatic facial expression recognition (FER) systems are now widely applied in various fields such as healthcare, transportation, education, and smart home technology. In the medical field, FER technology can help doctors monitor the emotional state of patients in real time, issue timely alerts to ensure the health of patients, and record long-term emotional state to assist in the control of disease [1]. In addition, in the field of classroom monitoring, FER system can be used to improve the quality of online class teaching, real-time monitoring of the emotional state of students and learning enthusiasm, to help teachers adjust the teaching strategy to improve students’ learning engagement [2]. In summary, FER technology has important significance and potential application research value in different fields.

The domain of FER has witnessed remarkable advances and transformations in recent decades. From the early stages, when it faced many challenges, to the current increase of deep learning and computer-based techniques, researchers are constantly exploring new methods and applications for FER. Datasets acquired under controlled laboratory conditions such as CK + [3] and JAFFE [4] have provided an important foundation for the development of the field, but at the same time, researchers are aware of the limitations of facial expression datasets acquired in a laboratory setting. Facial expressions captured in controlled laboratory settings often lack the diversity and complexity observed in real-life scenarios. This has led to a shift in research focus toward utilizing large-scale datasets gathered from natural scenes, including AffectNet [5], FERPlus [6], and RAF-DB [7]. However, FER in natural scenes faces many challenges, including complex backgrounds, head pose changes, and facial occlusion. These factors not only affect the quality of the dataset but also make it difficult to train expression classification networks.

With the emergence of deep learning techniques, most expression recognition methods have adopted convolutional neural networks (CNNs) [8] as their foundation, leading to significant advancements in this field. However, these CNN-based methods often lack robustness and are susceptible to common problems in natural scene datasets. CNNs achieve local-to-global image feature extraction by superimposing convolutional layers, but the approach is computationally intensive and prone to gradient vanishing problems, making it difficult for the network to converge. In contrast, the transformer [9] network transforms feature images into sequences of visual features and uses a global self-attention mechanism to model the contextual relationships between the sequences. The approach is not limited by local interactions, allowing the network to learn the relationships among feature sequences with more powerful feature extraction capabilities from the global perspective.

In 2021, Dosovitskiy [10] proposed the ViT, which has had a substantial impact on image recognition. Following its introduction, vision transformer (ViT) is widely applied in a variety of computer vision domains, such as the realm of expression recognition. Although there have been many research attempts to apply ViT to expression recognition tasks, the direct use of the original ViT structure tends to consume a lot of computational resources [11] and the performance needs to be further improved.

To solve the problem that the FER method based on ViT consumes a lot of computing resources, this paper proposes a FER method based on octonion orthogonal feature extraction and octonion ViT. This model improves the performance of FER in natural scenes and significantly reduces the number of parameters. The specific contributions of this paper are as follows:

1.
We propose an orthogonal feature decomposition method to map extracted features to seven orthogonal sub-features to reduce feature redundancy.
2.
We propose an octonion orthogonal representation to preserve the intrinsic relationship between different orthogonal features.
3.
We propose to extend ViT to octonion field and build an octonion ViT module, which can capture rich local features while reducing the number of parameters to approximately one-eighth of ViT.
4.
Experimental results on three commonly used facial expression datasets show that the proposed method outperforms several state-of-the-art models with a significant reduction in the number of parameters.

2. Related Work

Early traditional face expression recognition methods achieved decent results on smaller-scale datasets, but, in the era of big data, dealing with massive facial expression data, these methods often demand significant time and computational resources to train the final network model. Additionally, enhancing the final recognition accuracy can be challenging. Recently, the accuracy and robustness of face expression recognition have been significantly improved with the advancement of deep learning algorithms. Compared to traditional methods, deep learning algorithm is capable of learning more abstract and advanced feature representations automatically, leading to better capture of the nuances of expression. In addition, deep learning algorithms can handle large-scale data, making them better able to cope with real-world face expression recognition problems.

Many researches have successively proposed expression recognition methods based on deep network models, especially the CNN. This network extracts local features of an image through operations such as convolution, thus realizing the recognition of expressions. For example, the direct application of CNN to FER tasks first appeared in 2012, when Rifaiet al. [12] first proposed to use CNN models to extract emotional feature from the pixels of a facial expression image, and then these emotional features are directly outputted as seven basic types of target expressions at the network output. Yu and Zhang [13] proposed an FER method for integrating multiple deep neural networks by adaptively assigning different weights to each network so that the integrated networks can complement each other. A single CNN is not good at extracting visual features from facial images, and some work has combined feature extraction algorithms with CNNs to achieve better results. Alphonse and Dharma [14] in 2017 proposed the enhanced Gabor filter to extract expression features from images and used discriminant analysis to extracted features for classification, which achieved a 35.40% recognition accuracy on the outdoor conditional dataset SFEW. Zadeh et al. [15] used the Gabor filter for feature extraction and input the feature images into the CNN for classification, with a shorter training time and higher accuracy.

Mainstream deep learning methods typically center on directly extracting deep features through CNNs. However, the filters in CNNs work mainly through local neighborhood operations. It can lead to the relationship among local and global features being overlooked. In contrast, transformer model is the sequential model based on the attention mechanism, which was originally utilized in the field of natural language processing. Recently, the transformer has also been applied to various computer vision tasks, including image classification, object detection, and facial recognition. In contrast to CNN, transformer employs the self-attention mechanism to establish attention-weighted relationships among image sequences, which better captures the global dependencies between features, leading to a more comprehensive understanding of the overall image information. However, since transformer lack a priori knowledge of features, they usually require richer datasets and longer training times, and these methods consume a lot of computational resources and need further improvement.

Some current works construct the hybrid model of CNN and transformer and use the feature maps processed by CNN as the input of transformer, which achieves good results. Ma et al. [16] first proposed the application of convolutional ViT to expression recognition, i.e., transforming face images into visual vocabulary sequences for expression recognition from a global point of view and summarizing the global and local facial information by attentional selective fusion (ASF) module, which guides the main stem to extract the required information. The experimental results demonstrate that the ViT has a much better classification result in the expression recognition task. Zhao et al. [11] proposed an innovative FER framework rooted in geometric guidance, leveraging graphical convolutional networks and transformers. This approach aims to discern emotions conveyed in video form. The POSTER [17] method achieved the SOTA performance of the FER algorithm at that time by integrating face key points and image features using the two-stream pyramid cross-fusion transformer network. Mao et al. [18] proposed the POSTER++ algorithm, which improves POSTER from three aspects: cross-fusion, two-stream, and multiscale feature extraction.

In recent years, there has been increasing interest in neural networks that utilize multidimensional number field values. Several works [19–21] have demonstrated that quaternion theory can effectively uncover the intrinsic relationships among various components and significantly decrease the number of parameters. Gaudet and Maida [22] and Zhou et al. [19] used quaternion operations to process multichannel images, which can consider the spatial dependence between channels during feature extraction. Octonions, as another form of generalization of quaternions and complex numbers, have been widely used in mathematical physics, especially in electrodynamics, electromagnetism, and quantum physics [23–25], and have great potential in the field of neural networks. The aim of this study is to develop a method that combines octonion with ViT to reduce the number of model parameters and improve the accuracy of expression recognition.

3. Methods

3.1. The Proposed Framework

The architecture of the proposed model in this paper is illustrated in Figure 1. The model mainly consists of three parts: octonion orthogonal feature decomposition module, octonion orthogonal representation module, and octonion ViT module.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The architecture of the proposed method.

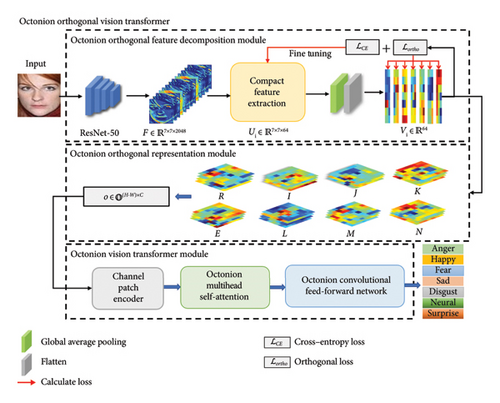
The original image is first fed into the octonion orthogonal feature decomposition module, and seven groups of orthogonal sub-features are obtained using the ResNet-50 model that adds orthogonal loss for fine-tuning. Then, the seven sets of orthogonal sub-features are constructed into an octonion matrix using the octonion orthogonal representation module. Finally, the inputs are fed into the octonion ViT module to process these octonion features and output the final FER results.

3.2. Octonion Orthogonal Feature Decomposition Module

Many FER-related tasks extract features from a pretrained backbone network. The pretrained model captures generic image features such as edges, textures, shapes, etc., which are useful in many image-related tasks. When performing face expression recognition tasks, these generic features can be used as a base to adapt to specific expression recognition tasks by adding additional layers (e.g., fully connected layers) on top to achieve higher accuracy. In this paper, the ResNet-50 model introduced in the subsection is chosen as the pretrained backbone network.

To reduce feature redundancy between features extracted from the pretraining skeleton, from the perspective of strengthening the difference between the features and enriching the diversity of the features, this paper proposes an orthogonality feature extraction method. Firstly, the expression feature tensor F is extracted from the original image by using the pretrained ResNet-50. Then, the dimension of the feature tensor F is reduced using compact feature extraction to obtain the feature mapping U_i. Next, the global average pooling and flattening operation is applied to each U_i to obtain the feature vector V_i. Then, the orthogonal loss L_ortho is calculated to ensure the independence of the feature vectors. Finally, the combined loss function L is formed by combining the cross-entropy loss L_CrossEntropy and the orthogonal loss L_ortho. The octonion orthogonal feature decomposition module is fine-tuned by minimizing the combined loss function L. The specific process is as follows.

Expression Feature Extraction: Feature extraction using the model pretrained on the MS-Celeb1M dataset can take advantage of the model’s face feature representation learned from large-scale and diverse datasets, which helps to capture rich and generic features in the original images, which in turn could be used for subsequent expression recognition tasks. Therefore, the emotion feature tensor is first extracted from the original image by the pretrained ResNet-50 model.

Compact Feature Extraction: At the end of the ResNet-50 network, seven separate 1 × 1 convolutional layers are added. The purpose of these convolutional layers is to reduce the dimensionality of the feature F by linear transformations while retaining important information. Each convolutional layer outputs a feature mapping , where i takes on values from 1 to 7, indicating seven different feature mappings.

Global Average Pooling and Softmax Operation: Applying global average pooling to each U_i, this operation computes the average of each channel in the feature mapping, thus reducing the 7 × 7 × 64 tensor to a 1 × 1 × 64 tensor, which is reduced to the feature vector . The values of these feature vectors are then converted by Softmax operations into the form of probability distributions that are used to express the classification.

Orthogonal Loss: Orthogonal loss L_ortho is introduced to ensure that the intermediate feature vectors U_i and V_i are orthogonal, i.e., they are mathematically independent. This helps the model to capture more diverse features, reduce redundancy, and improve feature representation.

The vector dot product V_i·V_j should ideally be zero if V_i and V_j are perfectly orthogonal. The L2 norm

is the Euclidean length of the vector V_i, and the calculation formula is as follows:

()

where n denotes the number of vectors and n equals 64 in this paper. V_i1, V_i2, …, V_in denote the elements of vector V_i.

The orthogonal loss is calculated as the summation of the ratios between the dot product of all pairs of vectors and the L2 norms of those vectors. Mathematically, it is expressed as

()

where the notation ‖·‖₂ is the L2 norm, |·| is the absolute value operator, and n denotes the number of vectors. L_ortho denotes the absolute value of the cosine of the angle between the vectors V_i and V_j. The ratio is 0 when V_i and V_j are perfectly orthogonal (i.e., the angle is 90 degrees). When V_i and V_j are perfectly congruent or inverted, the ratio is 1. The smaller the value of L_ortho, the more orthogonal the set of vectors is (i.e., the closer the angle between the vectors is to 90 degrees). If all the vectors are perfectly orthogonal, then the value of L_ortho will be zero. If there is a large cosine of the angle between the vectors (i.e., there is a large projection between the vectors), then the value of L_ortho will be larger.

Fine Tuning: The improved backbone network is fine-tuned by integrating both the conventional cross-entropy loss L_CrossEntropy and orthogonal loss L_ortho. The combined loss function is formulated as follows:

()

where the cross-entropy loss function is calculated as follows:

()

where n represents the number of samples, y represents the true label, and

represents the prediction probability.

In the combined loss function, L_CrossEntropy quantifies the disparity from the model prediction to the actual label. The hyperparameter λ is used to adjust the relative impact of the cross-entropy loss and the orthogonal loss within the total loss function. By adjusting λ, the importance of orthogonality in model training can be controlled. The combined loss function improves generalization ability and model interpretability by simultaneously optimizing classification accuracy and feature orthogonality so that the model learns more robust and less redundant feature representations while maintaining high classification performance. The seven orthogonal feature vectors U_i obtained from the backbone network after fine-tuning will be input into the octonion orthogonal representation module.

3.3. Octonion Orthogonal Representation Module

The octonion orthogonal representation module is devised to preserve the inherent relationship among distinct orthogonal features. In detail, seven orthogonal features

are allocated to each of the seven imaginary parts in octonion matrix. In addition, to ensure a balanced distribution of the seven orthogonal sub-features, the averaged features of these sub-features are assigned to the real part of the octonion feature matrix. Therefore, the octonion orthogonal representation is be formulated as follows:

()

where O(x) represents the octonion feature matrix, x represents the seven orthogonal sub-features. Ave(x) represents the orthogonal average feature and F₁(x), F₂(x), F₃(x), F₄(x), F₅(x), F₆(x), F₇(x) represent seven mutually orthogonal features.

The primary goal of the proposed octonion orthogonal representation module is to establish correlations among orthogonal features, thereby enhancing the efficiency of information extraction. Finally, the resulting octonion orthogonal matrix O is input into the octonion ViT module to classify facial expressions.

3.4. Octonion ViT Module

The general structure of the octonion ViT follows the ViT architecture, replacing the original ViT operations with octonion operations, including an octonion fully connected layer with an octonion convolutional layer, and introduces several key enhancements in critical modules. These improvements encompass the channel patch encoder, the octonion multihead self-attention (O-MHSA) module, and an octonion convolutional feed-forward network (OC-FFN) module. The complete architecture is illustrated in Figure 2, where hyperparameters N, M, and L denote the number of individual modules.

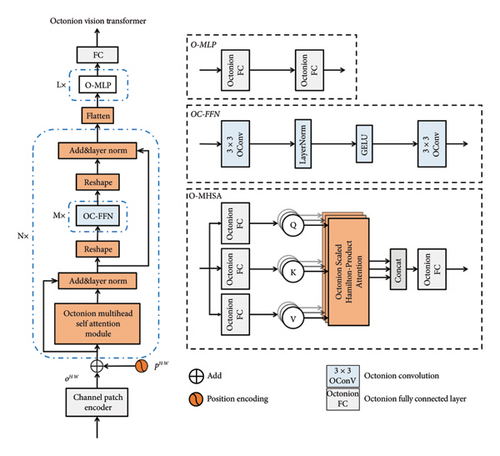
3.4.1. Channel Patch Encoder

The channel patch encoder is distinguished from the patch encoder of ViT by dividing the feature map into multiple patches along channel dimensions, and the exact computational procedure for the channel patch encoder module is as follows.

For the input o ∈ O^H×W×C, its dimension is H × W × C. Reshape o into 2D patches o^′ ∈ O^(H·W)×C, each with dimension C, denoted as o^′ ∈ O^(H·W)×C:

()

where C represents the number of channels, and H and W represent the height and width of the feature map.

The o^′ is encoded into C sequences of length H·W, denoted as o^″ ∈ O^H·W:

()

To preserve the positional information of the channels, the 1D position embedding p^H·W ∈ O^H·W is generated and added to o^″:

()

where o^‴, o^″, p^H·W are all octonion elements.

The final output sequence o^‴ is fed into the O-MHSA module for further processing.

3.4.2. O-MHSA

O-MHSA module is generated by octonion operation. The specific structure is shown in Figure 3.

Compared with the ordinary operation of ViT, the octonion operation handles one-eighth of the parameters. The octonion operation mainly involves two components: the octonion convolutional layer OConv(·) and the octonion fully connected layer OFC(·). The fully connected layer can be viewed as the specialized 1D convolutional layer. OConv(·) and OFC(·) comply with the octonion multiplication rule and the convolution of an octonion matrix O with an octonion kernel g can be expressed as

()

where ⊗ is the Hamilton product.

The detailed computational steps for the O-MHSA module are as follows. In O-MHSA, we first convert the sequence of octonions o^‴ into an octonion query Q, an octonion key K, and an octonion value V using three separate OFC(·), as shown in the following equation:

()

The self-attention is then computed by replacing the scaled dot product in ViT with the Hamilton product, as shown in the following equation:

()

The CompoSoftmax operation applies a Softmax activation operation to each component of the octonions. Subsequently, the self-attention output is linked and projected to an octonion matrix by OFC(·) as depicted in equation (12):

()

where Concat(·) denotes the concatenation operation.

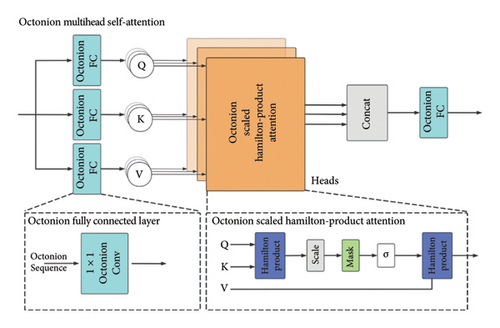
Ultimately, the octonion feature extracted by the O-MHSA module is forwarded to the OC-FFN module for further processing.

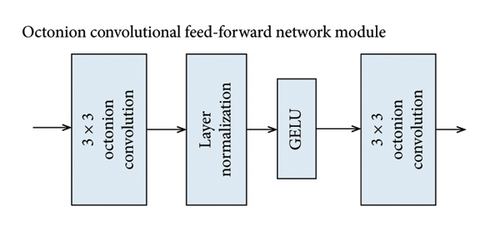
3.4.3. OC-FFN

To enhance the capability of capturing localized features, the octonion convolution operation is integrated into the OC-FFN module.

In the octonion ViT module, the octonion features are normalized by layer normalization before entering the OC-FFN module. The specific structure of the octonion convolutional feedforward network is shown in Figure 4. The OC-FFN module consists of octonion convolution, layer normalization, and GELU activation function. This design aims to fully utilize the properties of octonions to improve the expressiveness and performance of the network for data with complex structures and high-dimensional features.

The specific computational procedure of the OC-FFN is as follows:

()

where LayerNorm denotes the process of layer normalization, OConv(·) refers to the 3 × 3 octonion convolution operation, and X and X_out are used to represent the inputs and outputs of the OC-FFN module, respectively. GELU stands for the activation operation.

During the classification phase, the octonion matrix X_out is reconstructed and then processed through an Add layer and a LayerNorm layer. The octonion features are then flattened into the one-dimensional vector, which is further processed by the octonion multilayer perceptron (O-MLP) and the fully connected layer to finalize the classification.

4. Experimental Results

4.1. Experimental Detail and Environment Setup

The network model is implemented using the deep learning library PyTorch and the programming language Python. The hardware configuration includes an NVIDIA GeForce GTX 3090 GPU. Specific details of the deep learning service architecture are provided in Table 1. The model is uniformly trained using the Adam Optimizer. The batch size is set to 12, the initial learning rate in the network model is set to 0.00001, the weight decay parameter is set to 0.0001, and the learning batch is set to 200. During the experiments, the hyperparameters of the model are configured as follows: M = 2 for the number of OC-FFN modules, L = 2 for the number of O-MLP modules, and N = 4 for the number of Encoder modules.

Table 1. Configuration information of the deep learning server.

Hardware and software equipment	Model and specification
Graphics card	NVIDIA GeForce GTX 3090 GPU
VRAM	24G
Internal storage	80G
Python	3.8
CUDA	11.3
Pytorch	1.10

4.2. Accuracy Comparison With Other SOTA Methods

Table 2 lists the accuracies of the model proposed in this paper and the FER methods in the last 3 years on the RAF-DB dataset. The RAF-DB dataset contains seven basic expressions, and as with the other methods, the experiments evaluate the effectiveness of the network by recognizing the seven basic emotions. The experimental results show that the proposed model has the highest recognition rate on the RAF-DB dataset, reaching 90.43%.

Table 2. Accuracy comparison with other SOTA methods on RAF-DB.

Methods	Accuracy (%)
SPWFA-SE [26]	86.31
VTFF [27]	88.14
RCL-Net [28]	88.20
PACVT [29]	88.21
EfficientFace [30]	88.36
MA-Net [31]	88.40
Meta-Face2Exp [32]	88.54
DAN [33]	89.70
EAC [34]	90.35
Our method	90.43

Comparison with other FER methods on the SFEW 2.0 dataset is shown in Table 3. On the SFEW 2.0 dataset, our method achieved a FER accuracy of 62.28% for the seven expression categories. It is 3.39% higher than AHA [35] and 0.12% higher than the accuracy of the FDRL [39] method. In comparison with previous methods, the proposed model shows better generalization ability on the dataset.

Table 3. Accuracy comparison with other SOTA methods on SFEW 2.0.

Methods	Accuracy (%)
AHA [35]	58.89
MA-Net [31]	59.40
LDLVA [36]	59.90
CS-GResNet [37]	60.55
APVit [38]	61.92
FDRL [39]	62.16
Our method	62.28

Table 4 lists the test results of the model proposed in this paper and the FER methods from the last 3 years on the AffectNet dataset. Comparisons are made with many SOTA facial expression methods, including DAN [33], TransFER [41], DACL [40], EAC [34], APViT [38], POSTER [17], DDAMFN [42], POSTER++ [18], and S2D [43]. TransFER [41] designed a multiattention dropping (MAD) algorithm to eliminate the attentional map, pushing the model to extract from other than the most discriminative each facial part to extract comprehensive local information. POSTER++ [18] improves POSTER in terms of cross-fusion, two-stream, and multiscale feature extraction. The experimental results show that the proposed model achieves a 67.74% accuracy on the AffectNet dataset, which is 2.05% higher than that of DAN [33] and 1.51% higher than that of TransFER [41]. It is also 0.25% higher than the POSTER++ [18] model.

Table 4. Accuracy comparison with other SOTA methods on AffectNet.

Methods	Accuracy (%)
DACL [40]	65.20
EAC [34]	65.32
DAN [33]	65.69
TransFER [41]	66.23
APViT [38]	66.91
DDAMFN [42]	67.03
POSTER [17]	67.31
POSTER++ [18]	67.49
S2D [43]	67.62
Our method	67.74

4.3. Visual Analysis

Accuracy is not entirely convincing in categorization tasks, especially in the face of categorization imbalance and without explicitly showing the performance of each category. The problem of category imbalance in FER can be explored by means of confusion matrices, which demonstrate the differences in categorization between different expressions. Figure 5 shows the corresponding confusion matrices plotted on the three datasets using the proposed model, which helps to evaluate the performance of the model.

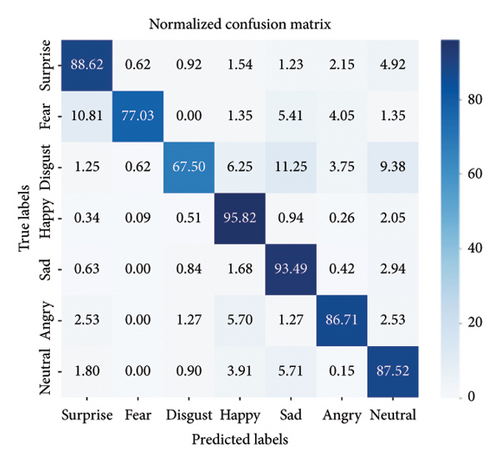
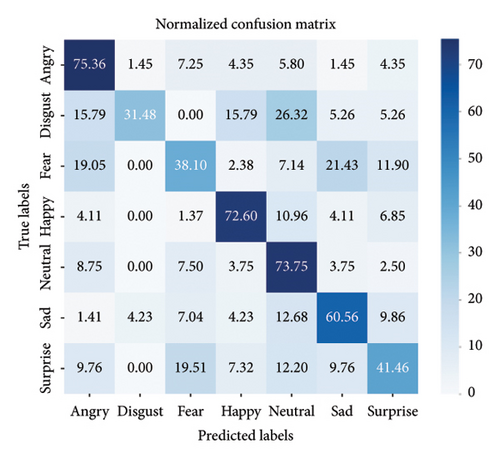
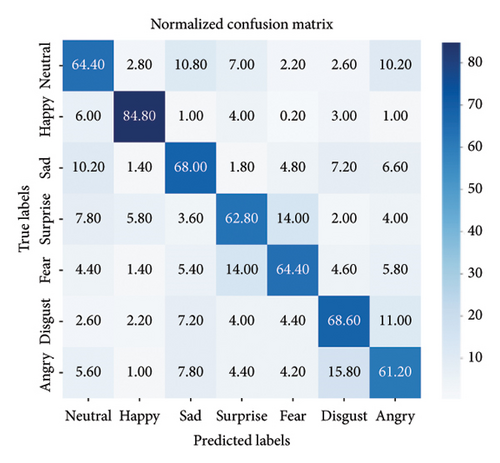
The results of the confusion matrix show that, in general, our method not only achieves the highest performance in the “happy” expression category but also confounds some of the expression categories. The RAF-DB confusion matrix shows that the model’s accuracy performance is high in the categories of “happy,” surprise, “sad,” and “neutral.” On the SFEW 2.0 dataset, the proposed model had difficulty recognizing the “fear” and “disgust” categories. The “fear” category is easily confused with “angry” and “sad,” while “disgust” is easily confused with “neutral.” This confusion may be caused by the lack of data on “fear” and “disgust” in the training set. For the AffectNet dataset, the performance of our method on the “angry” category was relatively low often confused with the “disgust” category, and there was a recognition of “fear” as “surprise.” The root cause of this confusion may be due to the shared and overlapping signals used to convey these facial expressions, which results in some expressions being perceived as very similar, making it more difficult to accurately distinguish between them.

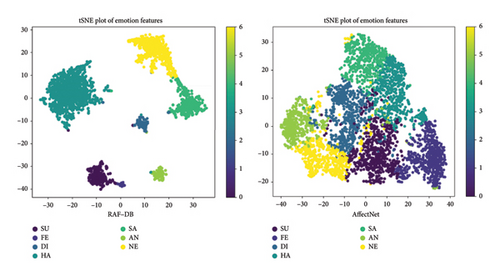
This article demonstrates the high-dimensional features of our method using the t-SNE method, as shown in Figure 6. The t-SNE visualization of the RAF-DB dataset exhibits clear clustering effects and significant cross-group segregation. The distance between points of different colors is relatively far, while points of the same color are tightly clustered in low-dimensional space. This indicates that they have similar features in high-dimensional space, with a tight distribution of features. This further demonstrates the state-of-the-art capability of our method in performing facial expression classification tasks. From the results on the AffectNet dataset, it can be seen that the distance between the points of each color is relatively close, which is due to its large sample size and imbalanced distribution between samples. However, the method presented in this article also demonstrates competitive performance.

4.4. Analysis of Model Parameter Quantity

Smaller models have lower memory and computational power requirements and are critical for applications with high real-time requirements. Such models are often able to complete training faster, which is especially beneficial when dealing with large datasets or when time is of the essence. In addition, models with fewer parameters are less likely to overfit the training data, and when the model becomes too complex, there is a tendency to memorize training examples rather than learn generic patterns. In contrast, simpler models are more likely to capture the underlying structure of the data and successfully generalize to new, unforeseen examples.

Table 5 compares the model size of our method with that of different methods and also compares their performance on the AffectNet and RAF-DB datasets. The proposed model uses 6.69 and 10.08 M of parameters and FLOPs, respectively, which corresponds to a much lower parameter size and computational complexity than the other models, and achieves excellent FER performance on the AffectNet and RAF-DB datasets, with accuracies of 90.43% and 67.74%.

Table 5. Params comparison with other SOTA methods.

Methods	Params	FLOPs	Accuracy (%)
Methods	Params	FLOPs	RAF-DB	AffectNet
ViT [10]	21.59M	21.58M	74.76	51.14
RAN-ResNet18 [44]	11.19M	14.55G	86.90	59.50
SCN [45]	11.18M	1.82G	87.03	60.23
VTFF [27]	51.8M	—	88.14	61.85
MA-Net [31]	50.54M	3.65G	88.40	64.53
PSR [46]	20.24M	—	88.98	63.77
DMUE [47]	78.4M	—	89.42	63.11
DAN [33]	19.72M	2.23G	89.70	65.69
Our method	6.69M	10.08M	90.43	67.74

To facilitate comparison with the traditional ViT model, a real-valued ViT^∗ model is constructed with the same structure as the Octonion-ViT^∗ model. The input vectors for both models are of size (512, 49). The notation ∗ indicates specific hyperparameter settings (N = 1, M = 2, L = 1) in the octonion-ViT^∗ model, chosen to enable intuitive comparisons in the table.

Table 6 provides a detailed comparison of the specific layer parameters between the two models. Both the octonion convolution layer and the octonion dense layer have their parameters reduced to 1/8 of the ViT model, while the quantity of parameters in the O-MHSA layer is increased compared to that of the regular multihead self-attention layer. The impact is minimal due to the low parameter count of this operation. Overall, the octonion ViT module significantly reduces the model’s parameter count, achieving a reduction of approximately 87.5% compared to the real-valued ViT model.

Table 6. Parameter of octonion-ViT^∗ and corresponding ViT^∗.

Octonion-ViT^∗			ViT^∗
Layer	Name	Params	Name	Params
1	Input layer	0	Input layer	0
2	Channel patch encoder	26,976	Channel patch encoder	26,976
3	Layer normalization	96	Layer normalization	96
4	O-MHSA	1344	MHSA	480
5	Add	0	Add	0
6	Layer normalization	96	Layer normalization	96
7	Reshape	0	Reshape	0
8	Octonion convolutional layer	5280	Convolutional layer	41,568
9	Layer normalization	192	Layer normalization	192
10	Activation	0	Activation	0
11	Octonion convolutional layer	10,464	Convolutional layer	83,040
12	Octonion convolutional layer	5232	Convolutional layer	41,184
13	Layer normalization	96	Layer normalization	96
14	Activation	0	Activation	0
15	Octonion convolutional layer	2640	Convolutional layer	19,008
16	Reshape	0	Reshape	0
17	Add	0	Add	0
18	Layer normalization	96	Layer normalization	96
19	Flatten	0	Flatten	0
20	Dropout	0	Dropout	0
21	Octonion dense layer	6,293,504	Dense layer	50,333,696
22	Dropout	0	Dropout	0
23	Octonion dense layer	263,168	Dense layer	2,098,176
24	Dropout	0	Dropout	0
25	Dense	7175	Dense	7175
	Total parameters	6,616,359	Total parameters	53,651,879

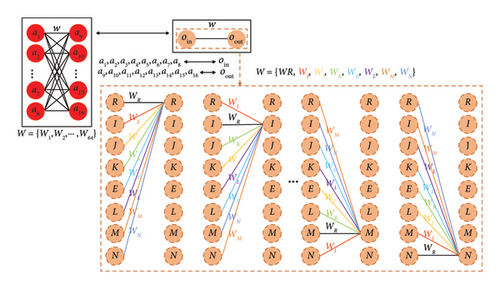
The principle of the low parameter numbers of the octonion ViT module can be explained in terms of the octonion algebra. The principle is shown in Figure 7. For the dense layer with 1024 hidden units and 1024 input values, the real-valued model would have parameters of 10,242 = 1M. In order to maintain an equal number of input and output nodes (1024), the equivalent octonion model would have 128 octonionic inputs and 128 octonionic hidden units. As a result, the count of parameters in the octonion ViT module would be 128² × 8 = 0.125M, which is approximately 87.5% less.

4.5. Ablation Study

In order to validate the effectiveness of each module in the proposed model, we conducted ablation experiment of the RAF-DB dataset for the octonion module, ViT module, and orthogonal feature module, and the accuracy and parameters of the comparison models are illustrated in Table 7.

Table 7. Ablation experimental results on RAF-DB.

Methods	Accuracy (%)	Params	FLOPs
Octonion-ViT	76.01	6.69M	10.08M
Ortho-CNN	88.23	23.90M	4.15G
Ortho-ViT	88.38	21.59M	21.58M
Our method	90.43	6.69M	10.08M

First, the orthogonal feature module was removed from the proposed model and octonion-ViT was constructed to compare. From the experimental results, the orthogonal feature module improves the accuracy of the model by 14.42%. In addition, the ViT model was removed from the proposed model and the Ortho-CNN model was constructed for comparison, and the results of the experiment showed that the ViT module in the proposed model improved the accuracy by 2.2%, and the number of parameters was reduced by 17.21M. At the same time, the computational complexity is significantly reduced from 4.15G to 10.08M. Finally, the octonion module was removed from the proposed model and Ortho-ViT was constructed for comparison. After removing the octonion module, the accuracy is reduced by 2.05%, and the number of parameters and the computational complexity are increased to 21.59M and 21.58M, respectively. This demonstrates that octonion module can effectively represent high-dimensional data, enhancing the expressiveness and performance of the model. The experimental results prove the effectiveness of each module in the proposed model.

5. Conclusion

In this paper, we introduce an FER method based on octonion orthogonal feature extraction and octonion ViT. The octonion orthogonal feature decomposition module, octonion orthogonal feature representation module, and octonion ViT module proposed in this method further improve the accuracy of FER in natural scenes and keep the number of parameters low. The experimental results and analysis show that the accuracy of the proposed model on SFEW 2.0, AffectNet, and RAF-DB are 62.28%, 67.74%, and 90.43%, respectively, and the number of parameters remains at 6.69M. The ablation experiments of each module are carried out to verify the effectiveness of each module of the model. Compared with other models, the proposed model shows superior performance in the natural FER task.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the General Project for Education of National Social Science Fund, Study on the Mechanism of Emotional Engagement and its Intervention in Primary and Secondary School Teachers’ online Training (Grant Number: BCA230278).

Open Research

Data Availability Statement

The data used to support the findings of this study are included within the article.

References

1 Li B., Mehta S., Aneja D. et al., A Facial Affect Analysis System for Autism Spectrum Disorder, 2019 IEEE International Conference on Image Processing (ICIP), 2019, 4549–4553, https://doi.org/10.1109/ICIP.2019.8803604.
10.1109/ICIP.2019.8803604
Google Scholar
2 Whitehill J., Serpell Z., Lin Y., Foster A., and Movellan J. R., The Faces of Engagement: Automatic Recognition of Student Engagement From Facial Expressions, IEEE Transactions on Affective Computing. (2014) 5, no. 1, 86–98, https://doi.org/10.1109/TAFFC.2014.2316163, 2-s2.0-84903626001.
10.1109/TAFFC.2014.2316163
Web of Science® Google Scholar
3 Lucey P., Cohn J., Kanade T., Saragih J., Ambadar Z., and Matthews I., The Extended Cohn-Kanade Dataset (CK+): A Complete Dataset for Action Unit and Emotion-Specified Expression, 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Workshops, 2010, 94–101, https://doi.org/10.1109/CVPRW.2010.5543262, 2-s2.0-77956509035.
10.1109/CVPRW.2010.5543262
Google Scholar
4 Lyons M., Akamatsu S., Kamachi M., and Gyoba J., Coding Facial Expressions With Gabor Wavelets, Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition, 1998, 200–205, https://doi.org/10.1109/AFGR.1998.670949, 2-s2.0-84857444525.
10.1109/AFGR.1998.670949
Google Scholar
5 Mollahosseini A., Hasani B., and Mahoor M., AffectNet: A Database for Facial Expression, Valence, and Arousal Computing in the Wild, IEEE Transactions on Affective Computing. (2019) 10, 2019, no. 1, 18–31, https://doi.org/10.1109/TAFFC.2017.2740923, 2-s2.0-85028454548.
10.1109/TAFFC.2017.2740923
Web of Science® Google Scholar
6 Barsoum E., Zhang C., Ferrer C., and Zhang Z., Training Deep Networks for Facial Expression Recognition With Crowd-Sourced Label Distribution, Proceedings of the 18th ACM International Conference on Multimodal Interaction, 2016, 279–283, https://doi.org/10.1145/2993148.2993165, 2-s2.0-85016568635.
10.1145/2993148.2993165
Google Scholar
7 Li S., Deng W., and Du J., Reliable Crowdsourcing and Deep Locality Preserving Learning for Expression Recognition in the Wild, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2017, 2584–2593, https://doi.org/10.1109/CVPR.2017.277, 2-s2.0-85044307466.
10.1109/CVPR.2017.277
Google Scholar
8 Zaman K., Zhaoyun S., Shah B. et al., A Novel Driver Emotion Recognition System Based on Deep Ensemble Classification, Complex and Intelligent Systems. (2023) 9, no. 6, 6927–6952, https://doi.org/10.1007/s40747-023-01100-9.
10.1007/s40747-023-01100-9
Google Scholar
9 Vaswani A., Shazeer N., Parmar N. et al., Attention Is All You Need, 2017, https://doi.org/10.48550/arXiv.1706.03762.
10.48550/arXiv.1706.03762
Google Scholar
10 Dosovitskiy A., Beyer L., Kolesnikov A. et al., An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale, Proceedings of the International Conference on Learning Representations (ICLR), 2021, 1–22, https://doi.org/10.48550/arXiv.2010.11929.
10.48550/arXiv.2010.11929
Google Scholar
11 Zhao R., Liu T., Huang Z., Lun D., and Lam K., Spatial-Temporal Graphs Plus Transformers for Geometry-Guided Facial Expression Recognition, IEEE Transactions on Affective Computing. (2023) 14, no. 4, 2751–2767, https://doi.org/10.1109/TAFFC.2022.3181736.
10.1109/TAFFC.2022.3181736
Google Scholar
12 Rifai S., Bengio Y., Courville A., Vincent P., and Mirza M., Disentangling Factors of Variation for Facial Expression Recognition, Lecture Notes in Computer Science, Proceedings of the European Conference on Computer Vision (ECCV), 2012, 808–822, https://doi.org/10.1007/978-3-642-33783-3_58, 2-s2.0-84867843700.
10.1007/978-3-642-33783-3_58
Google Scholar
13 Yu Z. and Zhang C., Image Based Static Facial Expression Recognition With Multiple Deep Network Learning, Proceedings of the 2015 ACM on International Conference on Multimodal Interaction, 2015, 435–442, https://doi.org/10.1145/2818346.2830595, 2-s2.0-84959297432.
10.1145/2818346.2830595
Google Scholar
14 Alphonse A. and Dharma D., Enhanced Gabor (E-Gabor), Hypersphere-Based Normalization and Pearson General Kernel-Based Discriminant Analysis for Dimension Reduction and Classification of Facial Emotions, Expert Systems with Applications. (2017) 90, 127–145, https://doi.org/10.1016/j.eswa.2017.08.013, 2-s2.0-85027501922.
10.1016/j.eswa.2017.08.013
Web of Science® Google Scholar
15 Zadeh M., Imani M., and Majidi B., Fast Facial Emotion Recognition Using Convolutional Neural Networks and Gabor Filters, Proceedings of the 5th Conference on Knowledge Based Engineering and Innovation (KBEI), 2019, 577–581, https://doi.org/10.1109/KBEI.2019.8734943, 2-s2.0-85068328741.
10.1109/KBEI.2019.8734943
Google Scholar
16 Ma F., Sun B., and Li S., Robust Facial Expression Recognition With Convolutional Visual Transformers, 2021, https://doi.org/10.48550/arXiv.2103.16854.
10.48550/arXiv.2103.16854
Google Scholar
17 Zheng C., Mendieta M., and Chen C., Poster: A Pyramid Cross-Fusion Transformer Network for Facial Expression Recognition, Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCVW), 2023, 3138–3147, https://doi.org/10.1109/ICCVW60793.2023.00339.
10.1109/ICCVW60793.2023.00339
Google Scholar
18 Mao J., Xu R., Yin X., Chang Y., and Nie B., Poster V2: A Simpler and Stronger Facial Expression Recognition Network, 2023, https://doi.org/10.48550/arXiv.2301.12149.
10.48550/arXiv.2301.12149
Google Scholar
19 Zhou Y., Jin L., Liu H., and Song E., Color Facial Expression Recognition by Quaternion Convolutional Neural Network With Gabor Attention, IEEE Transactions on Cognitive and Developmental Systems. (2021) 13, no. 4, 969–983, https://doi.org/10.1109/TCDS.2020.3041642.
10.1109/TCDS.2020.3041642
Google Scholar
20 Zhou Y., Jin L., Ma G., and Xu X., Quaternion Capsule Neural Network With Region Attention for Facial Expression Recognition in Color Images, IEEE Transactions on Emerging Topics in Computational Intelligence. (2022) 6, no. 4, 893–912, https://doi.org/10.1109/TETCI.2021.3120513.
10.1109/TETCI.2021.3120513
Google Scholar
21 Zhou Y., Guo L., and Jin L., Quaternion Orthogonal Transformer for Facial Expression Recognition in the Wild, Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2023, 1–5, https://doi.org/10.1109/ICASSP49357.2023.10096851.
10.1109/ICASSP49357.2023.10096851
Google Scholar
22 Gaudet C. and Maida A., Deep Quaternion Networks, Proceedings of the International Joint Conference on Neural Networks (IJCNN), 2018, 1–8, https://doi.org/10.1109/IJCNN.2018.8489651, 2-s2.0-85056554293.
10.1109/IJCNN.2018.8489651
Google Scholar
23 Kaplan A., Quaternions and Octonions in Mechanics, Revista de la Unión Matemática Argentina. (2008) 49, no. 2, 45–53.
Google Scholar
24 Chanyal B., Bisht P., and Negi O., Generalized Split-Octonion Electrodynamics, International Journal of Theoretical Physics. (2011) 50, no. 6, 1919–1926, https://doi.org/10.1007/s10773-011-0706-1, 2-s2.0-79954631949.
10.1007/s10773-011-0706-1
CAS Web of Science® Google Scholar
25 Dray T. and Manogue C., The Geometry of the Octonions, 2015, https://doi.org/10.1142/8456.
10.1142/8456
Google Scholar
26 Li Y., Lu G., Li J., Zhang Z., and Zhang D., Facial Expression Recognition in the Wild Using Multi-Level Features and Attention Mechanisms, IEEE Transactions on Affective Computing. (2023) 14, no. 1, 451–462, https://doi.org/10.1109/TAFFC.2020.3031602.
10.1109/TAFFC.2020.3031602
Google Scholar
27 Ma F., Sun B., and Li S., Facial Expression Recognition With Visual Transformers and Attentional Selective Fusion, IEEE Transactions on Affective Computing. (2023) 14, no. 2, 1236–1248, https://doi.org/10.1109/TAFFC.2021.3122146.
10.1109/TAFFC.2021.3122146
Web of Science® Google Scholar
28 Zeng D., Lin Z., Yan X., Liu Y., Wang F., and Tang B., Face2exp: Combating Data Biases for Facial Expression Recognition, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022, 20259–20268, https://doi.org/10.1109/CVPR52688.2022.01965.
10.1109/CVPR52688.2022.01965
Google Scholar
29 Liu C., Hirota K., and Dai Y., Patch Attention Convolutional Vision Transformer for Facial Expression Recognition With Occlusion, Information Sciences. (2023) 619, 781–794, https://doi.org/10.1016/j.ins.2022.11.068.
10.1016/j.ins.2022.11.068
Web of Science® Google Scholar
30 Zhao Z., Liu Q., and Zhou F., Robust Lightweight Facial Expression Recognition Network With Label Distribution Training, Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 3510–3519, https://doi.org/10.1609/aaai.v35i4.16465.
10.1609/aaai.v35i4.16465
Google Scholar
31 Zhao Z., Liu Q., and Wang S., Learning Deep Global Multi-Scale and Local Attention Features for Facial Expression Recognition in the Wild, IEEE Transactions on Image Processing. (2021) 30, 6544–6556, https://doi.org/10.1109/TIP.2021.3093397.
10.1109/TIP.2021.3093397
PubMed Web of Science® Google Scholar
32 Liao J., Lin Y., Ma T., He S., Liu X., and He G., Facial Expression Recognition Methods in the Wild Based on Fusion Feature of Attention Mechanism and LBP, Sensors. (2023) 23, no. 9, https://doi.org/10.3390/s23094204.
10.3390/s23094204
Google Scholar
33 Wen Z., Lin W., Wang T., and Xu G., Distract Your Attention: Multi-Head Cross Attention Network for Facial Expression Recognition, Biomimetics. (2023) 8, no. 2, https://doi.org/10.3390/biomimetics8020199.
10.3390/biomimetics8020199
Google Scholar
34 Zhang Y., Wang C., Ling X., and Deng W., Learn from All: Erasing Attention Consistency for Noisy Label Facial Expression Recognition, Proceedings of the European Conference on Computer Vision (ECCV), 2022, 418–434, https://doi.org/10.1007/978-3-031-19809-0_24.
10.1007/978-3-031-19809-0_24
Google Scholar
35 Weng J., Yang Y., Tan Z., and Lei Z., Attentive Hybrid Feature With Two Step Fusion for Facial Expression Recognition, Proceedings of the 25th International Conference on Pattern Recognition (ICPR), 2020, 6410–6416, https://doi.org/10.1109/ICPR48806.2021.9412554.
10.1109/ICPR48806.2021.9412554
Google Scholar
36 Le N., Nguyen K., Tran Q., Tjiputra E., Le B., and Nguyen A., Uncertainty-aware Label Distribution Learning for Facial Expression Recognition, Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), 2023, 6077–6086, https://doi.org/10.1109/WACV56688.2023.00603.
10.1109/WACV56688.2023.00603
Google Scholar
37 Jiang S., Xu X., Liu F., Xing X., and Wang L., CS-GresNet: A Simple and Highly Efficient Network for Facial Expression Recognition, Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2022, 2599–2603, https://doi.org/10.1109/ICASSP43922.2022.9747322.
10.1109/ICASSP43922.2022.9747322
Google Scholar
38 Xue F., Wang Q., Tan Z., Ma Z., and Guo G., Vision Transformer With Attentive Pooling for Robust Facial Expression Recognition, IEEE Transactions on Affective Computing. (2023) 14, no. 4, 3244–3256, https://doi.org/10.1109/TAFFC.2022.3226473.
10.1109/TAFFC.2022.3226473
Google Scholar
39 Ruan D., Yan Y., Lai S., Chai Z., Shen C., and Wang H., Feature Decomposition and Reconstruction Learning for Effective Facial Expression Recognition, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021, 7656–7665, https://doi.org/10.1109/CVPR46437.2021.00757.
10.1109/CVPR46437.2021.00757
Google Scholar
40 Farzaneh A. and Qi X., Facial Expression Recognition in the Wild via Deep Attentive Center Loss, Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), 2021, 2401–2410, https://doi.org/10.1109/WACV48630.2021.00245.
10.1109/WACV48630.2021.00245
Google Scholar
41 Xue F., Wang Q., and Guo G., Transfer: Learning Relation-Aware Facial Expression Representations With Transformers, Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021, 3581–3590, https://doi.org/10.1109/ICCV48922.2021.00358.
10.1109/ICCV48922.2021.00358
Google Scholar
42 Zhang S., Zhang Y., Zhang Y., Wang Y., and Song Z., A Dual-Direction Attention Mixed Feature Network for Facial Expression Recognition, Electronics. (2023) 12, no. 17, https://doi.org/10.3390/electronics12173595.
10.3390/electronics12173595
PubMed Google Scholar
43 Chen Y., Li J., Shan S., Wang M., and Hong R., From Static to Dynamic: Adapting Landmark-Aware Image Models for Facial Expression Recognition in Videos, 2023, https://doi.org/10.48550/arXiv.2312.05447.
10.48550/arXiv.2312.05447
Google Scholar
44 Wang K., Peng X., Yang J., Meng D., and Qiao Y., Region Attention Networks for Pose and Occlusion Robust Facial Expression Recognition, IEEE Transactions on Image Processing. (2020) 29, 4057–4069, https://doi.org/10.1109/TIP.2019.2956143.
10.1109/TIP.2019.2956143
Web of Science® Google Scholar
45 Wang K., Peng X., Yang J., Lu S., and Qiao Y., Suppressing Uncertainties for Large-Scale Facial Expression Recognition, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020, 6896–6905, https://doi.org/10.1109/CVPR42600.2020.00693.
10.1109/CVPR42600.2020.00693
Google Scholar
46 Vo T., Lee G., Yang H., and Kim S., Pyramid With Super Resolution for in the Wild Facial Expression Recognition, IEEE Access. (2020) 8, 131988–132001, https://doi.org/10.1109/ACCESS.2020.3010018.
10.1109/ACCESS.2020.3010018
Web of Science® Google Scholar
47 She J., Hu Y., Shi H., Wang J., Shen Q., and Mei T., Dive Into Ambiguity: Latent Distribution Mining and Pairwise Uncertainty Estimation for Facial Expression Recognition, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021, 6244–6253, https://doi.org/10.1109/CVPR46437.2021.00618.
10.1109/CVPR46437.2021.00618
Google Scholar

All articles

Facial Expression Recognition Method Based on Octonion Orthogonal Feature Extraction and Octonion Vision Transformer

Abstract

1. Introduction

2. Related Work

3. Methods

3.1. The Proposed Framework

3.2. Octonion Orthogonal Feature Decomposition Module

3.3. Octonion Orthogonal Representation Module

3.4. Octonion ViT Module

3.4.1. Channel Patch Encoder

3.4.2. O-MHSA

3.4.3. OC-FFN

4. Experimental Results

4.1. Experimental Detail and Environment Setup

4.2. Accuracy Comparison With Other SOTA Methods

4.3. Visual Analysis

4.4. Analysis of Model Parameter Quantity

4.5. Ablation Study

5. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley