International Journal of Intelligent Systems
Volume 2025, Issue 1 5054424
Research Article
Open Access

MCOA: A Multistrategy Collaborative Enhanced Crayfish Optimization Algorithm for Engineering Design and UAV Path Planning

Yaning Xiao, 

Yaning Xiao

School of Automation and Intelligent Manufacturing , Southern University of Science and Technology , Shenzhen , 518055 , China , sustc.edu.cn

Search for more papers by this author
Hao Cui, 

Hao Cui

College of Mechanical and Electrical Engineering , Northeast Forestry University , Harbin , 150040 , China , nefu.edu.cn

Search for more papers by this author
Ruba Abu Khurma, 

Corresponding Author

Ruba Abu Khurma

Information Technology Department , Al-Huson University College , Al-Balqa Applied University , Irbid , 19117 , Jordan , bau.edu.jo

Search for more papers by this author
Abdelazim G. Hussien, 

Abdelazim G. Hussien

Department of Computer and Information Science , Linköping University , Linköping , 58183 , Sweden , liu.se

Faculty of Science , Fayoum University , Faiyum , 63514 , Egypt , fayoum.edu.eg

Search for more papers by this author
Pedro A. Castillo, 

Pedro A. Castillo

Department of Computer Engineering, Automatics and Robotics , University of Granada , Granada , 18071 , Spain , ugr.es

Search for more papers by this author
First published: 10 June 2025
https://doi.org/10.1155/int/5054424
Academic Editor: Said El Kafhali

Abstract

The crayfish optimization algorithm (COA) is a recent bionic optimization technique that mimics the summer sheltering, foraging, and competitive behaviors of crayfish. Although COA has outperformed some classical metaheuristic (MH) algorithms in preliminary studies, it still manifests the shortcomings of falling into local optimal stagnation, slow convergence speed, and exploration–exploitation imbalance in addressing intractable optimization problems. To alleviate these limitations, this study introduces a novel modified crayfish optimization algorithm with multiple search strategies, abbreviated as MCOA. First, specular reflection learning is implemented in the initial iterations to enrich population diversity and broaden the search scope. Then, the location update equation in the exploration procedure of COA is supplanted by the expanded exploration strategy adopted from Aquila optimizer (AO), endowing the proposed algorithm with a more efficient exploration power. Subsequently, the motion characteristics inherent to Lévy flight are embedded into local exploitation to aid the search agent in converging more efficiently toward the global optimum. Finally, a vertical crossover operator is meticulously designed to prevent trapping in local optima and to balance exploration and exploitation more robustly. The proposed MCOA is compared against twelve advanced optimization algorithms and nine similar improved variants on the IEEE CEC2005, CEC2019, and CEC2022 test sets. The experimental results demonstrate the reliable optimization capability of MCOA, which separately achieves the minimum Friedman average ranking values of 1.1304, 1.7000, and 1.3333 on the three test benchmarks. In most test cases, MCOA can outperform other comparison methods regarding solution accuracy, convergence speed, and stability. The practicality of MCOA has been further corroborated through its application to seven engineering design issues and unmanned aerial vehicle (UAV) path planning tasks in complex three-dimensional environments. Our findings underscore the competitive edge and potential of MCOA for real-world engineering applications. The source code for MCOA can be accessed at https://doi.org/10.24433/CO.5400731.v1.

1. Introduction

Optimization pertains to determining the optimal solution for a given problem under certain constraints [1]. Concomitant with the technological revolution and advancements driven by artificial intelligence, optimization problems are emerging in various research domains, rendering the question of how to address these problems efficiently a subject of ardent discourse among scholars [2, 3]. Currently, existing optimization techniques can be classified into traditional methods and metaheuristic (MH) algorithms [4]. Traditional methods primarily utilize specific mathematical rules, such as gradient descent, quasi-Newton techniques, and Levenberg–Marquardt [5]. These methods necessitate gradient information and invariably produce the same solution once an input is given, so they are only suitable for solving some small-scale optimization problems at a theoretical level [6]. Nevertheless, the complexity of real-world engineering optimization problems is escalating, manifesting nondifferentiable, discontinuous, and nonlinear characteristics [7]. This results in traditional methods being almost powerless when confronted with such challenges. As research deepens, a gradient-free, problem-independent, and efficient stochastic optimization technique, namely, the MH algorithm, has garnered prominent attention, which is capable of finding optimal or near-optimal solutions for highly complicated nonlinear optimization problems within a rational time frame [8]. Besides, the MH algorithm possesses the advantages of simple structure, good adaptability, and robust local optimum avoidance [9]. Consequently, they are regarded as an ideal alternative to traditional methods and are becoming increasingly prevalent in scientific and engineering applications.

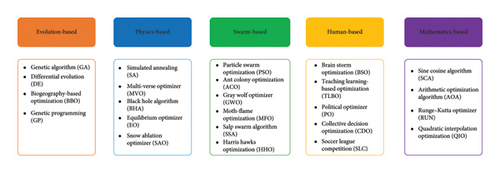
MH algorithms are inspired by natural phenomena, physical laws, or collective behaviors, and they can be grouped into five main categories [10]: evolutionary, physical, swarm-based, human-based, and mathematics-based algorithms, as shown in Figure 1. Evolutionary algorithms, like genetic algorithm (GA) [11], have a protracted development history and focus on natural selection and genetics. Physics-based algorithms derive their inspiration from chemical reaction processes and physical phenomena such as magnetism, attraction, and gravity. One well-known instance is simulated annealing (SA) [12], inspired by the principles of metallurgical annealing, which directs the convergence of the initial solution toward the global optimum according to the temperature distribution. The third category relates to the collective behaviors of birds, insects, animals, and other natural organisms referred to as swarm-based algorithms. Particle swarm optimization (PSO) [13] is a famous swarm-based optimization paradigm, which iteratively updates candidate solutions by emulating the foraging behavior observed in bird flocks. These algorithms are highly successful due to their ability to balance exploration and exploitation, allowing for efficient search across complex solution spaces. They are adaptable to various problem types, computationally efficient, and robust against local optima, making them reliable for diverse optimization tasks. Additionally, their self-organizing nature enhances their ability to handle distributed and dynamic environments. Human-based algorithms, including brain storm optimization (BSO) [14], are inspired by human social behavior, and mathematics-based algorithms, like sine cosine algorithm (SCA) [15], leverage mathematical principles for optimization.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Categories of MH algorithms.
In this study, we highlight a novel swarm-based crayfish optimization algorithm (COA) [16], which mimics the shelter-seeking, foraging, and competitive behaviors of crayfish in nature. COA offers the benefits of simple structure, high flexibility, and excellent operability. Therefore, since its inception, COA has received widespread attention and application from scholars in various fields. To enhance the accuracy and robustness of listening strategy evaluation, Cheng [17] proposed an automatic evaluation method using COA to optimize the deep confidence network. Cuk et al. [18] applied COA to fine-tune the architecture and training parameters of a long short-term memory network for Parkinson’s disease detection, achieving an accuracy of 87.4187%. Shikoun [19] designed a binary variant called BinCOA based on COA for feature selection. Chauhan et al. [20] employed COA to optimize the regularization and kernel parameters of a support vector machine for accurate prediction of friction during the wear of Ti-6Al-4V alloys under different lubrication conditions. Although COA has exhibited decent performance in addressing engineering optimization problems, this paper insists on proposing a brand-new variant of COA, mainly driven by three motivations:
  • 1.

    COA encompasses two exploitation phases, undermining its exploration capability. In the early iterations, COA maintains a high propensity to exploit, allowing for rapid convergence. Nonetheless, in later iterations, the exploration performance of COA is relatively feeble, making it susceptible to becoming trapped in local optima, thereby yielding suboptimal results. Consequently, there is a need to improve COA by adopting multiple strategies to establish a better exploration–exploitation balance and enhance stability so that it can cope with higher complexity and high-dimensional engineering optimization challenges.

  • 2.

    As the dimensionality and nonlinear constraints escalate, MH algorithms manifest a prevalent tendency of sluggish convergence and unsatisfactory solution accuracy for engineering optimization. While introducing a search operator can somewhat enhance the algorithm’s performance, it may indirectly impair its search capability in other facets. Therefore, multiple strategies can be adopted to synergistically reinforce the performance of MH algorithms from different aspects to confront complex optimization problems.

  • 3.

    According to the no free lunch (NFL) theorem [21], no single algorithm can guarantee the optimal solution for all optimization problems. Continuous development and enhancement of MH algorithms are necessary to provide more effective solutions for engineering optimization problems.

To address the aforementioned issues, this study propounds a modified crayfish optimization algorithm (MCOA) that incorporates multiple strategies as described in motivations (1) and (2): implementing complementary search mechanisms to balance exploration–exploitation capabilities and combining diverse algorithmic techniques to enhance performance across different optimization aspects. First, specular reflection learning is incorporated during the early iteration stage to enrich population diversity and expand the search range. Then, the mathematical model of the extended exploration behavior from Aquila optimizer (AO) is used to replace the location update equation in the exploration procedure of COA, which endows the algorithm with more powerful exploration capability and faster convergence speed. Next, in the exploitation phase, step sizes derived from the Lévy probability distribution are introduced to augment the algorithm’s local search efficiency in the neighborhood. Finally, the vertical crossover operator is employed in later iterations to de-perturb two random dimensional variables of the search individual to help escape from local optima and create a reasonable trade-off between exploration and exploitation. These strategies work in tandem to boost the overall optimization performance of COA and compensate for its weaknesses of premature convergence and suboptimal solution accuracy in engineering optimization. To assess the effectiveness of the presented method, MCOA is comprehensively compared against twelve state-of-the-art MH algorithms and nine similar improved variants on 23 benchmark functions, the CEC2019 test set, and the CEC2022 test set. Furthermore, MCOA is applied in constrained engineering design and unmanned aerial vehicle (UAV) path planning to evaluate its practicability in real-world engineering scenarios. The main contributions are summarized as follows:
  • •

    We propose MCOA that integrates four improvement strategies: specular reflection learning for broader search, expanded exploration mechanism for enhanced global exploration, Lévy flight for efficient local search, and vertical crossover operator that helps stagnant individuals escape local optima.

  • •

    The performance of MCOA is comprehensively evaluated on 23 benchmark functions and the CEC2019/2022 test sets, comparing it with state-of-the-art MH algorithms across different dimensions (D = 50, 100, 500, 1000) to demonstrate its scalability.

  • •

    The applicability of MCOA is validated through seven constrained engineering design problems and UAV path planning cases, with experimental results confirming its superior convergence accuracy and stability even when facing highly complex optimization challenges.

The structure of this paper is as follows. Section 2 presents a literature review. Section 3 outlines the mathematical model of COA and the principles of the four improvement strategies. In Section 4, a detailed description of the proposed MCOA is provided, and its time complexity is analyzed. Section 5 compares the numerical optimization performance of MCOA with various well-established optimizers. MCOA is applied to address engineering design and UAV path planning problems in Section 6. Section 7 concludes this study.

2. Literature Review

Exploration and exploitation are indispensable components of MH algorithms. Exploration aims to comprehensively search the problem domain to uncover superior candidate solutions, while exploitation executes local searches within identified promising regions to converge toward the global optimum. Maintaining an appropriate balance between exploitation and exploration is crucial for an optimizer, as it directly determines its optimization performance. Notwithstanding the excellent flexibility and viability exhibited by MH algorithms in addressing optimization projects, due to the increasing complexity of emerging challenges in various fields, MH algorithms are inevitably susceptible to deficiencies such as sluggish convergence speed, suboptimal solution accuracy, and the propensity to become trapped in local optima [22]. The same is true for COA. Therefore, further enhancements to the original algorithm’s search performance are requisite. Wang et al. [23] proposed an improved multistrategy COA (IMCOA), which integrates the cave candidate strategy, fitness–distance balance competition strategy, optimal nondominance search strategy, and food covariance learning strategy. Compared to eight other algorithms, IMCOA can provide more reliable numerical results when solving three engineering design benchmarks. Zhong et al. [24] designed a hybrid remora crayfish optimization algorithm (HRCOA) for continuous optimization. HRCOA introduces exploitation operators from the remora optimizer to strengthen the exploitation behavior while reducing the complexity of the summer resort operator. On the CEC2020 and CEC2022 benchmark functions, as well as wireless sensor network coverage problems, HRCOA demonstrates superior convergence speed and accuracy over competing methods. To address the limitations of premature and insufficient exploitation capability, Maiti et al. [25] hybridized differential evolution (DE) with COA to develop the HCOADE algorithm. Through extensive experiments involving 34 benchmark functions and six engineering design problems, HCOADE exhibits robust global optimization performance with faster convergence. Wei et al. [26] presented a multistrategy fusion COA algorithm, namely JLSCOA, based on the subtraction averaging strategy, the sparrow search position update operator, and Lévy flight, which is applied to tune the parameters of the terminal sliding mode controller. Compared with the original COA, experimental results indicate that JLSCOA achieves the optimal value in 83% of scenarios. Elhosseny et al. [27] introduced an adaptive dynamic crayfish algorithm (AD-COA-L) with the local escape operator and lens opposition–based learning, successfully improving the stability in dealing with complex optimization challenges.

In this study, four strategies are adopted to augment the optimization performance of the original COA from multiple aspects, namely, specular reflection learning, expanded exploration strategy, Lévy flight, and vertical crossover operator. These strategies have been leveraged in many studies on MH algorithms, yielding substantial effects. For instance, El-Hameed et al. [28] incorporated specular reflection learning into the hunger games search to balance exploration and exploitation, thus enabling more accurate and stable gain regulation of proportional–integral–derivative (PID) controllers for load frequency control systems. Similarly, Adegboye et al. [29] proposed a modified gray wolf optimizer (CMWGWO) that employs specular reflection learning to enhance population diversity, allowing the algorithm to discover higher-quality inverse candidate solutions. As its name reveals, the expanded exploration operator focuses on boosting exploration and accelerating convergence. Consequently, Ma et al. [30] embedded the exploration mechanism into the position update formulation of GWO to design a hybrid Aquila gray wolf optimizer (AGWO), which can explore the search domain of complex high-dimensional problems more thoroughly. Wang et al. [31] proposed an enhanced hybrid Aquila optimizer and marine predator algorithm (EHAOMPA), which merges the exploration strengths of AO with the exploitation mechanisms of MPA, resulting in better numerical optimization performance for combinatorial problems. Lévy flight is a random walk with step sizes that follow a heavy-tailed distribution, allowing for occasional large jumps. This strategy enhances search efficiency by enabling the algorithm to explore distant regions of the solution space, thus improving convergence toward global optima. In [32], Lévy flight is utilized to guide the search agent through extensive exploration in the problem domain to quickly locate the target solution, alleviating the premature convergence of the artificial hummingbird algorithm. Additionally, He et al. [33] adopted Lévy flight to substitute the random step size of search individuals, endowing the butterfly optimization algorithm with superior local optima avoidance. The final strategy, vertical crossover operator, addresses the critical issue of search stagnation. In the enhanced rime optimization algorithm (CCRIME) developed by Zhu et al. [34], implementing the vertical crossover operation during the latter exploration phases promotes information exchange across diverse dimensions, significantly augmenting the algorithm’s local optima avoidance while boosting convergence accuracy. To address stagnation in search agents and sustain their exploration behavior, Chen et al. [35] suggested an improved shuffled frog leaping algorithm with a vertical crossover operator (HVSFLA), which showcases great potential in medical image segmentation.

This study proposes a multistrategy fusion COA (MCOA) to overcome the inherent limitations of traditional COA, providing more robust and adaptable solutions for complex optimization challenges. Distinguishing itself from existing literature, MCOA undergoes comprehensive evaluation through a wider spectrum of comparative algorithms, including both standard and improved variants. Our benchmarks incorporate 23 classical functions, 10 CEC2019 functions, and 12 CEC2022 functions, enabling performance assessment across diverse numerical optimization scenarios. Furthermore, MCOA is applied to solve multiple real-world constrained engineering design problems and UAV path planning tasks. The broader range of benchmark functions and real-world applications highlight the significant progress MCOA has made in the optimization field, demonstrating its superior performance and versatility.

3. Preliminaries

3.1. COA

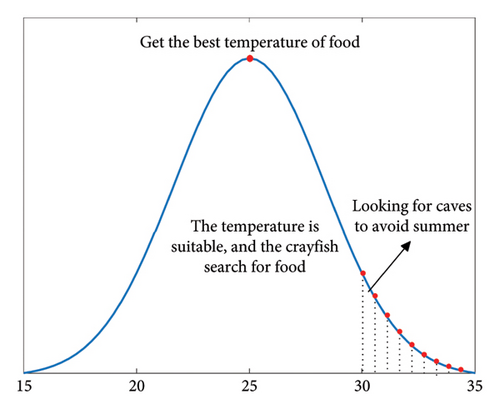
COA is a cutting-edge swarm intelligence optimization technique that mimics the summer sheltering, foraging, and competition behaviors of crayfish. As a eurythermal aquatic organism, the ideal temperature range for crayfish growth is between 15°C and 30°C, with the most favorable survival temperature being 25°C. Crayfish habitually dig burrows to evade predators and escape the summer heat. These burrows serve as shelters against natural enemies, prevent desiccation, and provide suitable conditions for hatching. During foraging, crayfish typically use their claws to seize and tear apart larger food items before transferring them to their second and third legs for further manipulation. When dealing with small food, crayfish directly capture and bite using their second and third walking feet. Based on these biological traits, the mathematical model of COA is developed, which consists of initialization, temperature definition, summering phase (exploration), competition phase (exploitation), and foraging phase (exploitation).

3.1.1. Initialization

Firstly, as with other population-based MH algorithms, the initialization of COA involves setting the positions of all search agents. Assuming the population size is N and the dimension space is D, the initialization step of COA can be expressed using the following equation:
()
where denotes the initial population position, represents the position of each crayfish, i.e., a solution of the problem, and xi,j indicates the jth dimensional decision variable of the ith individual, and its value is calculated as
()
where LBj and UBj represent the upper and lower boundary values of the jth dimension, respectively, and rand denotes a random number in the interval 0-1.

3.1.2. Temperature Definition

Temperature fluctuations directly affect the behavior of crayfish, transitioning them to different stages. The value of temperature can be obtained from the following equation:
()
where Temp represents the current ambient temperature. COA regulates the temperature to vary in the range of 20°C to 35°C. When the temperature surpasses 30°C, crayfish will choose cool places to avoid the summer heat. Notably, crayfish exhibit a pronounced foraging tendency within the temperature range of 20°C and 30°C, with 25°C being optimal. The food intake of crayfish is closely associated with temperature and can be approximated to the normal distribution, defined mathematically as follows:
()
where μ indicates the most suitable temperature for crayfish. C1 and σ are utilized to control the crayfish intake at different temperatures. Figure 2 illustrates the relationship between temperature and crayfish intake.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Correlation between temperature and crayfish intake.

3.1.3. Summer Resort Phase

When the temperature (Temp) exceeds 30°C, crayfish will hide in their caves to avoid the heat. The position of the cave is modeled below:
()
where denotes the current position of the cave, refers to the best solution obtained so far, and is the optimal location for the current population.
The competition among crayfish for caves is a stochastic event. If the value of rand is less than 0.5, this implies that no other crayfish are competing for the cave, and the crayfish will immediately move toward the cave for summer refuge. In this scenario, the position update formula is as follows:
()
where represents the current position of the ith individual and is the position of the ith individual at the next iteration t. C2 decreases linearly from 2 to 0 over the iterations, as given in the following equation:
()
where Tmax is the maximum iteration number.

3.1.4. Competition Phase

In the case of Temp > 30°C and rand ≥ 0.5, it signifies that other different crayfish individuals may also be interested in the same cave. They will fiercely compete for the cave, and this behavior is simulated as shown in the following equation:
()
where r represents the index value of a random individual in the population, calculated as follows:
()
where round(·) indicates rounding to the nearest integer.

3.1.5. Foraging Phase

When Temp ≤ 30°C, crayfish proceed to the foraging phase and steadily advance toward food sources. Here, the location of the food is determined as
()
The mathematical expression for the food size Q is given as follows:
()
where C3 stands for the food coefficient fixed to 3, Fitnessi denotes the fitness value of the ith search agent, and Fitnessfood denotes the fitness value of the food position.
Crayfish determine the food size according to the size of the largest food. If Q > (C3 + 1)/2, it signifies that the food is too large. Then, the crayfish will use its first claw to shred the food. It can be described as follows:
()
After the food is torn and made smaller, the crayfish will alternately pick up the food with the second and third paws and eat it. To model this alternation process, an ensemble of sine and cosine functions is employed as follows:
()
where p represents the food intake, which can be calculated using equation (4).
For Q ≤ (C3 + 1)/2, the crayfish merely has to approach the food and consume it directly, which is simulated in the following equation:
()

The pseudocode for COA is outlined in Algorithm 1.

    Algorithm 1: Crayfish optimization algorithm (COA).
  •  

    Input: Maximum iteration number Tmax, population size N, dimension size D, current iteration t = 1

  • 1.

     Initialize the position of each crayfish using equation (2)

  • 2.

     Evaluate the fitness value of all crayfish individuals to gain ,

  • 3.

     Whilet ≤ Tmaxdo

  • 4.

      Calculate the current temperature value Temp using equation (3)

  • 5.

      Fordo

  • 6.

       IfTemp > 30then

  • 7.

        Calculate the location of the cave according to equation (5)

  • 8.

        Ifrand < 0.5then

  • 9.

         Update the current position of the crayfish using equation (6)

  • 10.

        Else

  • 11.

         Update the current position of the crayfish using equation (8)

  • 12.

        End If

  • 13.

       Else

  • 14.

        Define the food intake p and food size Q using equations (4) and (11), respectively

  • 15.

        If Q > (C3 + 1)/2then

  • 16.

         Update the current position of the crayfish using equation (13)

  • 17.

        Else

  • 18.

         Update the current position of the crayfish using equation (14)

  • 19.

        End If

  • 20.

       End If

  • 21.

      End For

  • 22.

     Calculate the fitness value of each individual

  • 23.

     Update ,

  • 24.

     t = t + 1

  • 25.

    End While

  •  

    Return: Global optimal solution

3.2. Specular Reflection Learning

Opposition-based learning (OBL) serves as a robust search mechanism that concurrently evaluates the fitness values of the current solution alongside its opposite solution. This approach then filters out the superior candidate solution for inclusion in subsequent iterations [36]. Drawing inspiration from the concept of specular reflection, Zhang [37] introduced a specular reflection learning strategy by combining OBL with the specular reflection law. Unlike the one-to-one corresponding relationship between a solution and its opposite solution in OBL, specular reflection learning entails a correspondence between one solution and one neighborhood of its opposite solution.

As illustrated in Figure 3(a), specular reflection is a well-known optical phenomenon in physics. When light travels to a smooth plane mirror, a portion of it will be reflected back. In this figure, AO represents the incident light, while OB represents the reflected light. The angle between AO and the normal line is referred to as the angle of incidence, denoted as α. Likewise, the angle between OB and normal is the angle of reflection, denoted as β. Note that the angles α and β are equal. Figure 3(b) illustrates the conceptual model of specular reflection learning. The upper and lower boundaries of the search domain are up and low, respectively. O = (X0, 0) is the midpoint of [low, up]. The projection of any incident light point on the x-axis is defined as the location of a candidate solution. And the projection of any reflected light point on the x-axis signifies the opposite solution. Suppose Xi(a, 0) is a random variable within [low, up] and its corresponding opposite point is located at (b, 0). According to the law of specular reflection, the following geometric relation equation is obtained:
()
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Schematic illustration of specular reflection learning. (a) Specular reflection in physics. (b) Specular reflection learning model.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Schematic illustration of specular reflection learning. (a) Specular reflection in physics. (b) Specular reflection learning model.
As mentioned before, α is equal to β. Then, equation (15) can be transformed into
()
Let B0 = λsA0, and then b can be computed as follows:
()
where λs denotes the scale factor assigned by
()
where r1 and r2 are two random numbers between 0 and 1. φ represents the elasticity coefficient and Q indicates the neighborhood radius, both of which are in the range 0-1.
Finally, the opposite solution generated by specular reflection learning can be expressed as
()

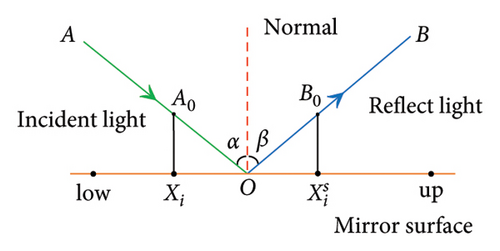
The initial positions of the population are generated using a randomized distribution mode. However, if the initial solution is distant from the global optimum or situated in the opposite direction, it may result in prolonged convergence time or even stagnation of the algorithm. In the early iterations, specular reflection learning facilitates a broader bidirectional simultaneous exploration of the solution space and increases the probability of finding the optimal solution.

3.3. Expanded Exploration Strategy

The expanded exploration strategy models the behavior of Aquila soaring at high altitudes to extensively explore the search space for potential prey locations [38]. Upon identifying the optimal hunting area, Aquila will swoop vertically toward it, as visualized in Figure 4. The mathematical model for this strategy is as follows:
()
()
where is the current position of the ith search agent, is the position of the ith search agent at the next iteration t + 1, is the best solution obtained so far, is the average position of the population, and rand is a random number in the interval 0-1.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Expanded exploration strategy of AO.

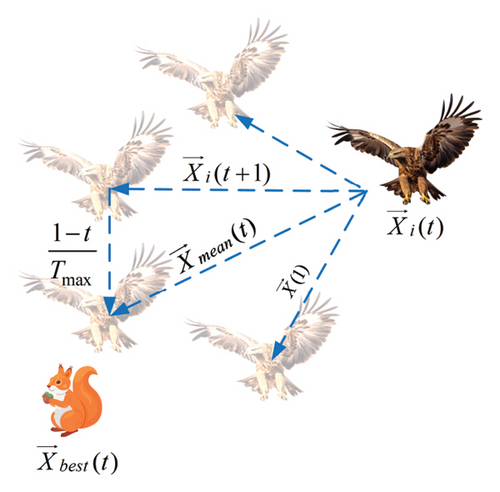
In COA, search agents in early iterations use equation (6) to conduct global exploration to identify areas where the global optimum may be present. This stage simulates the behavior of crayfish moving toward the cave for the summer resort, where the current position is updated based on and . However, due to the limited spatial information as well as insufficient population diversity, this approach cannot swiftly guide the algorithm into the correct search domain. Hence, the exploration capability of COA still needs to be strengthened. On the other hand, the exploration procedure of AO directly incorporates the global optimal position , allowing individuals to execute Aquila’s fast flight and predation maneuvers in the search space with faster convergence and better exploration competence. Considering the above, we hope to take advantage of the expanded exploration strategy (equation (20)) to replace the original position update formula (equation (6)), thus bringing a more stable exploration–exploitation balance and faster convergence speed to the algorithm.

3.4. Lévy Flight

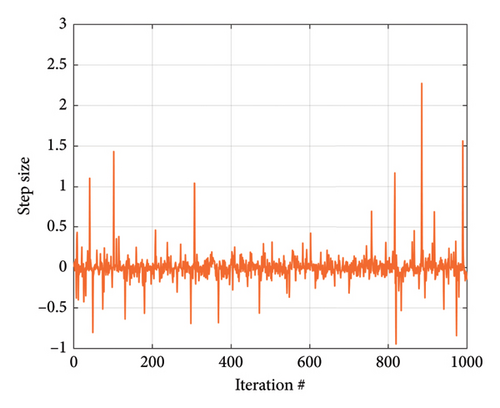
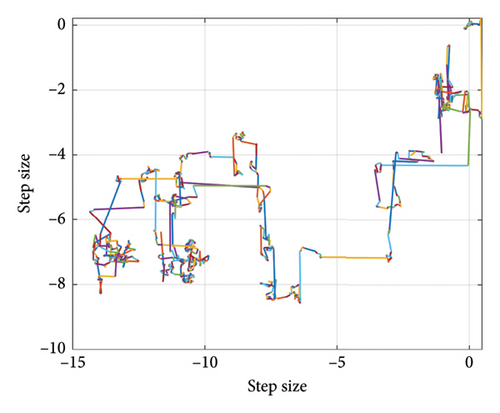
Lévy flight is a non-Gaussian stochastic walk method with step sizes taken from the Lévy probability distribution [39]. Figure 5 visualizes the distribution and 2D path of Lévy flight. Initially, the particle undergoes local movement, frequently taking numerous short-distance steps, and then occasionally embarks on a large step and commences a new cycle.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Distribution and 2D trajectory of Lévy flight over 1000 consecutive steps. (a) Lévy distribution. (b) Flight trajectory.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Distribution and 2D trajectory of Lévy flight over 1000 consecutive steps. (a) Lévy distribution. (b) Flight trajectory.
In COA, when Q ≤ (C3 + 1)/2, the crayfish uses equation (14) for equal-step convergence in the search space, which is not efficient and prone to premature convergence. Here, the characteristic of Lévy flight is utilized to replace the random number rand in order to guide the crayfish in a more efficient search for potential food resources. The new Lévy flight–based position update formula is as follows:
()
where αF represents the scale factor, which will be demonstrated to take the value of 0.06 in Section 5. LF stands for Lévy flight step:
()
where U and V are two random numbers derived from the normal distribution as follows:
()
with
()
where Γ(·) represents the standard Gamma function and β is a fixed value equal to 1.5.

3.5. Vertical Crossover Operator

Indeed, the primary reason why most MH algorithms converge to a local optimum is that some dimensions of the population may be stagnant [40]. The vertical crossover operator was first introduced in the crisscross optimization algorithm (CSO) [41]. This operator facilitates the exchange of useful information between different dimensions of the same search agent, specifically to eliminate local minima in the stagnant dimension by swapping good information with other “normal” dimensions. In this study, the vertical crossover is implemented to perform a dimensional crossover between any two stochastic dimensions of the crayfish individual location at the later stages of the search to generate a new trial individual, as follows:
()
where is the offspring of and . If the newly generated candidate solution is better than the current solution , will replace as the parent of MCOA for the next iteration, as shown in the following equation:
()

Here, F(·) indicates the fitness function. By using the vertical crossover strategy to perturb the position of the search agent, the algorithm’s local optima avoidance ability is enhanced, thereby further boosting convergence accuracy.

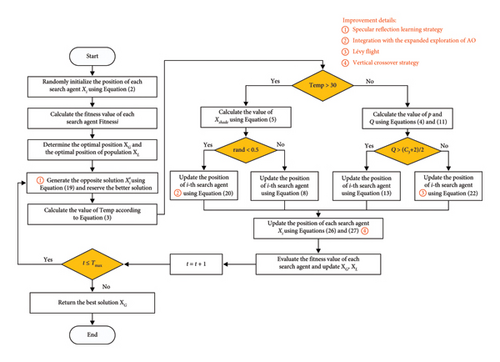
4. Proposed MCOA Algorithm

4.1. Detailed Implementation Steps for MCOA

To overcome the shortcomings demonstrated by the original COA when faced with complex optimization tasks, such as premature convergence, sluggish convergence speed, and low solution accuracy, this study proposes a modified variant with multiple enhancement strategies named MCOA:
  • 1.

    Specular reflection learning is introduced in the early iterations to enrich the population diversity and expand the search area.

  • 2.

    The expanded exploration strategy of AO is integrated with COA to replace its original position update formula, which endows the proposed method with better exploration capability and faster convergence speed.

  • 3.

    The Lévy flight step is embedded into the exploitation phase to improve the search efficiency in the neighborhood domain.

  • 4.

    The vertical crossover operator is applied in later iterations to randomly cross-perturb individual dimensions to further improve the solution accuracy.

After all these, MCOA is expected to yield comprehensively enhanced global optimization performance in terms of solution quality, stability, and local optima avoidance. The steps of MCOA are outlined below:
  •  

    Initialization

  •  

    Step 1: Parameter setting: Maximum number of iterations Tmax, population size N, variable dimension D, and search range [LB, UB]. Fix the number of current iterations t = 1.

  •  

    Step 2: Initialize the position of each search agent in the search space using equation (2).

  •  

    Step 3: Evaluate the fitness value for each search agent Fitnessi(i = 1, 2, …, N) and record the optimal solution obtained so far and the optimal location for the whole population .

  •  

    Iteration

  •  

    Step 4: While t ≤ Tmax, perform specular reflection learning based on equation (19) to generate the corresponding opposite candidate solution for each individual and retain the superior one of both into the subsequent procedure.

  •  

    Step 5: Calculate the ambient temperature value Temp using equation (3) to determine which position update strategy needs to be adopted in the following.

  •  

    Step 6: If Temp > 30 and rand < 0.5, MCOA enters the exploration phase. The location of each search individual is updated using equation (20). Note that here and are equivalent, i.e., the current optimal solution.

  •  

    Step 7: If Temp > 30 and rand ≥ 0.5, MCOA executes the competition exploitation strategy by updating the location of each search individual via equation (8).

  •  

    Step 8: When Temp ≤ 30, MCOA performs the foraging exploitation strategy. Define the food intake p and food size Q using equations (4) and (11). In case Q > (C3 + 1)/2, update the location of each search individual using equations (12) and (13). Instead, update the location of each search individual using equation (22).

  •  

    Step 9: Perform the vertical crossover operator to update the location of the population using equation (26).

  •  

    Step 10: The fitness values of all search agents are reevaluated to update and .

  •  

    Output

  •  

    Step 11: Set t = t + 1; if t is greater than the maximum iteration termination criterion, output the global optimal solution ; otherwise, return to Step 4.

Figure 6 illustrates the flowchart of the proposed MCOA, while Algorithm 2 provides the pseudocode outlining the MCOA procedure.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Flowchart of MCOA.
    Algorithm 2: Modified crayfish optimization algorithm with multistrategy (MCOA).
  •  

    Input: Maximum iteration number Tmax, population size N, dimension size D, current iteration t = 1

  • 1.

     Initialize the position of each search agent using equation (2)

  • 2.

     Evaluate the fitness value of all search agents to gain ,

  • 3.

     Whilet ≤ Tmaxdo

  • 4.

      Perform the specular reflection learning to generate according to equation (19), and retain the better one of and into the next generation //Specular reflection learning

  • 5.

      Calculate the value of Temp using equation (3)

  • 6.

      Fordo

  • 7.

       IfTemp > 30then

  • 8.

        Calculate the value of using equation (5)

  • 9.

        Ifrand < 0.5then

  • 10.

         Update the current position of the search agent using equation (20) //Expanded exploration

  • 11.

        Else

  • 12.

         Update the current position of the search agent using equation (8)

  • 13.

        End If

  • 14.

       Else

  • 15.

        Define the food intake p and food size Q using equations (4) and (11), respectively

  • 16.

        IfQ > (C3 + 1)/2then

  • 17.

         Update the current position of the search agent using equation (13)

  • 18.

        Else

  • 19.

         Update the current position of the search agent using equation (22) //Lévy flight

  • 20.

        End If

  • 21.

       End If

  • 22.

      End For

  • 23.

      Perform the vertical crossover operator to update each search agent according to equations (26) and (27) //Vertical crossover strategy

  • 24.

      Evaluate the fitness value of all search agents

  • 25.

      Update ,

  • 26.

      t = t + 1

  • 27.

     End While

  •  

    Return: Global optimal solution

4.2. Computational Complexity Analysis

The computational complexity of MCOA is determined by three main components: initialization, fitness evaluation, and position updating. The locations of all search individuals are randomly distributed in the search space during the initialization process with a computational complexity of O(N × D), where N is the population size and D is the problem dimension. In each iteration, the fitness values of all search agents’ positions are evaluated to obtain the current optimal solution as well as population optimal position , which needs to consume the computational complexity of O(N × Tmax), where Tmax is the maximum number of iterations. The computational complexity of updating the positions of all search individuals during the exploration and exploitation phases is O(N × D × Tmax). Moreover, the introduction of specular reflection learning and the vertical crossover operator to improve the optimization performance incurs an additional computational complexity of O(N × D × Tmax) + O(N × D × Tmax). Therefore, the total computational complexity of MCOA is: O(MCOA) = O(initialization) + O(fitness evaluation) + O(position update) = O(N × D) + O(N × Tmax) + O(3 × N × D × Tmax) = O(N × (D + Tmax + 3DTmax)).

5. Numerical Optimization Experiments

In this section, a set of numerical simulation studies are performed on the three IEEE CEC test suites: CEC 2005, CEC 2019, and CEC 2022 to thoroughly validate the effectiveness of MCOA. The implementation platform consists of hardware including an Intel(R) Core (TM) i7-13700F 2.10 GHz CPU with 32 GB RAM and MATLAB R2023b software running on Windows 10 operating system.

5.1. Benchmark Suites and Performance Indices

The CEC2005 suite comprises 23 classical functions [6] categorized as unimodal (F1∼F7, testing exploitation capability), multimodal (F8∼F13, assessing exploration and escape from local optima), and fixed-dimension multimodal (F14∼F23, evaluating stability). Functions F1∼F13 feature adjustable dimensions for testing scalability.

The CEC2019 test suite [42] contains 10 challenging functions designed for complex numerical optimization problems. In addition, this paper employs the popular CEC2022 test suite [43] to further demonstrate the superiority of MCOA. This test set includes not only unimodal (CEC2022-01) and multimodal functions (CEC2022-02∼CEC2022-05) but also hybrid functions (CEC2022-06∼CEC2022-08) as well as composition functions (CEC2022-09∼CEC2022-12). These functions are nonlinear, nonconvex, nonderivable, and closely resembling realistic optimization problems and can provide a comprehensive assessment of an algorithm’s tracking capability. Detailed descriptions of all benchmark functions appear in Tables A.1–A.5 (Appendix A Benchmark function description).

Performance evaluation employs two measures: mean fitness value (Mean) and standard deviation (Std), with statistical significance determined through the Wilcoxon rank-sum test [44] (significance level 0.05, where “+” indicates MCOA outperforms the comparison algorithm, “−” indicates underperformance, and “=” signifies no significant difference) and the Friedman ranking test [45] revealing each algorithm’s overall ranking (“Mean rank”) across all benchmarks.

5.2. Comparison With Different State-of-the-Art MH Algorithms on 23 Classical Functions

This subsection employs 12 advanced MH algorithms for comparison experiments with MCOA, namely, the original COA, AO [38], dandelion optimizer (DO) [46], snake optimizer (SO) [47], arithmetic optimization algorithm (AOA) [48], artificial rabbit optimization (ARO) [49], tunicate swarm algorithm (TSA) [50], slime mould algorithm (SMA) [51], wild horse optimizer (WHO) [52], liver cancer algorithm (LCA) [53], rime optimization algorithm (RIME) [54], and sand cat swarm optimization (SCSO) [55]. The maximum number of iterations Tmax and the population size N for each optimization method are fixed at 500 and 30, and other core parameters remain the same as those in the original literature, see Table 1. To avoid accidental errors as much as possible, all algorithms are implemented independently 30 times on each benchmark function.

Table 1. Parameter settings for different comparison methods.
Algorithm Year Parameter value
AO 2021 ω = 0.005; R = 10; α = 0.1; δ = 0.1; g1 ∈ [−1, 1]; g2 = [2, 0]
DO 2022 α ∈ [0, 1]; k ∈ [0, 1]
SO 2022 c1 = 0.5; c2 = 0.05; c3 = 2
AOA 2021 α = 5; μ = 0.499
ARO 2022 —
TSA 2020 Pmin = 1; Pmax = 4
SMA 2020 z = 0.03
COA 2023 C1 = 0.2; C3 = 3; μ = 25; σ = 3
WHO 2021 PC = 0.13; PS = 0.2; Crossover = Mean
LCA 2023 f = 1
RIME 2023 w = 5
SCSO 2022 rG = [2, 0]; SM = 2

5.2.1. Parameter Sensitivity Analysis

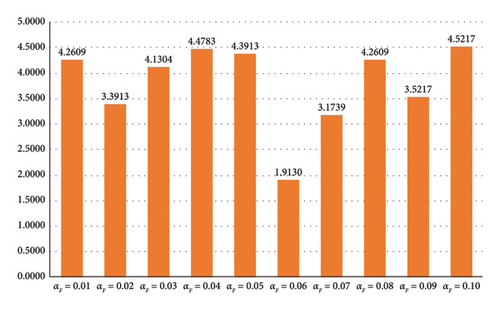
In Section 3.4, the addition of the Lévy flight strategy to the foraging phase of COA aims to enhance the search efficiency in locating potential food sources. The scale factor αF critically influences this improvement. If the value of αF is larger, the search agent will depend more on the optimal solution when updating its current position, and the algorithm is prone to premature convergence. Instead, a smaller αF value weakens the influence of Lévy flight on the guided foraging mechanism, leading to a decrease in the algorithm’s search capability and convergence accuracy. Based on the literature [32], the experimental range for αF is set between 0.01 and 0.1, with a value selected at each interval of 0.01. For each specified parameter value of αF, the results obtained by MCOA after 30 independent runs are shown in Table 2. With αF = 0.06, MCOA provides the most satisfactory solutions on 14 out of 23 test functions (60.87%), outperforming other values. For unimodal functions, MCOA performs consistently across different αF values on F1∼F4. The gap between the optimal solutions derived from different settings is also not particularly large on F5∼F7. The main reason is unimodal functions have fewer local solutions, which interfere less with the MCOA. For multimodal and fixed-dimension multimodal functions, a larger value of αF increases the step size of the Lévy operator, thus helping the proposed method to explore the search space more efficiently when facing complex optimization problems, especially on F8,  F12,  and F20. Figure 7 illustrates the Friedman mean rankings obtained by MCOA with different values of αF. MCOA exhibits the most desirable overall optimization performance when αF is 0.06, as it obtains the smallest ranking value of 1.9130. This indicates that this parameter value can balance exploration and exploitation favorably. Consequently, in the following sequence of experiments, taking αF = 0.06 is beneficial in avoiding local optimal solutions without affecting the sensitivity of the Lévy flight strategy and the algorithm’s convergence accuracy.

Table 2. Experimental results for different values of the scale factor αF in MCOA.
Function Metric αF = 0.01 αF = 0.02 αF = 0.03 αF = 0.04 αF = 0.05 αF = 0.06 αF = 0.07 αF = 0.08 αF = 0.09 αF = 0.1
F1 Mean 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F2 Mean 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F3 Mean 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F4 Mean 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F5 Mean 1.2213E − 08 1.5859E − 06 9.3781E − 06 3.7685E − 06 2.5762E − 06 5.6298E − 08 1.2641E − 06 5.4132E − 06 8.3174E − 05 4.2134E − 05
Std 1.7049E − 08 2.1616E − 06 9.9527E − 06 3.8543E − 06 3.2459E − 06 7.9445E − 08 1.7644E − 06 6.0916E − 06 9.5472E − 05 5.6217E − 05
Rank 1 4 8 6 5 2 3 7 10 9
  
F6 Mean 1.0933E − 21 1.5183E − 21 3.5111E − 21 1.5761E − 21 1.0039E − 19 3.3497E − 22 1.1515E − 19 5.4588E − 19 2.9277E − 22 3.0059E − 22
Std 4.7362E − 21 4.8629E − 21 1.6669E − 20 6.6035E − 21 4.6720E − 19 8.4095E − 22 5.7749E − 19 2.9868E − 18 6.2975E − 22 8.0293E − 22
Rank 4 5 7 6 8 3 9 10 1 2
  
F7 Mean 3.7337E − 05 3.6381E − 05 4.4903E − 05 4.6794E − 05 5.0800E − 05 3.2531E − 05 2.9116E − 05 3.8652E − 05 4.0749E − 05 5.5205E − 05
Std 3.5815E − 05 4.1921E − 05 4.6964E − 05 4.2886E − 05 4.2928E − 05 2.7696E − 05 2.5914E − 05 2.6853E − 05 2.7816E − 05 7.1512E − 05
Rank 4 3 7 8 9 2 1 5 6 10
  
F8 Mean −11772.32968 −11761.48907 −11787.84561 −11812.18143 −11742.52688 −11853.70331 −11784.61259 −11803.85376 −11739.794 −11761.69685
Std 4.5979E + 02 3.2519E + 02 5.2271E + 02 3.9870E + 02 3.9325E + 02 3.0227E + 02 4.2833E + 02 4.8630E + 02 4.5192E + 02 3.1348E + 02
Rank 6 8 4 2 9 1 5 3 10 7
  
F9 Mean 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F10 Mean 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F11 Mean 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1
  
F12 Mean 1.6944E − 20 6.7606E − 22 4.8048E − 23 5.6620E − 22 4.1700E − 22 2.4595E − 23 1.7602E − 21 4.8386E − 22 3.7241E − 23 3.8594E − 22
Std 9.2709E − 20 2.7795E − 21 1.2321E − 22 2.3222E − 21 1.9451E − 21 1.0630E − 22 9.0052E − 21 2.0371E − 21 1.4032E − 22 1.8951E − 21
Rank 10 8 3 7 5 1 9 6 2 4
  
F13 Mean 1.9120E − 21 4.8487E − 21 2.0410E − 17 2.5589E − 20 9.3884E − 22 2.3875E − 21 1.0154E − 21 1.9242E − 21 2.1038E − 20 1.0790E − 14
Std 8.5397E − 21 2.4178E − 20 1.1632E − 20 7.2840E − 20 2.4112E − 21 1.1178E − 16 3.2054E − 21 6.4821E − 21 8.2858E − 20 5.9102E − 14
Rank 3 6 9 8 1 5 2 4 7 10
  
F14 Mean 1.3917E + 00 9.9800E − 01 1.3871E + 00 1.3917E + 00 1.5885E + 00 1.3917E + 00 1.1948E + 00 1.3917E + 00 9.9800E − 01 1.1948E + 00
Std 1.4982E + 00 0 2.1311E + 00 1.4982E + 00 1.8019E + 00 1.4982E + 00 1.0782E + 00 1.4982E + 00 0 1.0782E + 00
Rank 9 1 5 8 10 5 3 5 1 3
  
F15 Mean 3.1278E − 04 3.1264E − 04 3.1472E − 04 3.1509E − 04 3.2881E − 04 3.0982E − 04 3.1116E − 04 3.1855E − 04 3.1267E − 04 3.8859E − 04
Std 1.5063E − 05 9.8728E − 06 1.2612E − 05 1.5755E − 05 9.7831E − 05 6.4028E − 06 8.5334E − 06 2.4872E − 05 1.4389E − 05 2.3911E − 04
Rank 5 3 6 7 9 1 2 8 4 10
  
F16 Mean −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316
Std 1.1005E − 10 5.7139E − 11 2.5934E − 11 4.2697E − 11 3.2594E − 11 4.5518E − 11 8.4454E − 11 5.5814E − 11 6.9643E − 11 7.5303E − 11
Rank 10 6 1 3 2 4 9 5 7 8
  
F17 Mean 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979
Std 1.5403E − 05 3.7291E − 06 8.0940E − 06 9.6520E − 06 8.8392E − 06 4.8362E − 06 2.1947E − 06 2.4870E − 05 7.9734E − 06 7.0392E − 06
Rank 9 2 6 8 7 3 1 10 5 4
  
F18 Mean 3.0000 3.9000 3.0000 3.9000 3.0000 3.0000 3.0000 3.9000 3.0000 3.0000
Std 9.2199E − 16 4.9295E + 00 9.9643E − 16 4.9295E + 00 1.0464E − 15 1.1337E − 16 1.1095E − 15 4.9295E + 00 1.0784E − 15 1.2506E − 15
Rank 2 8 3 8 4 1 6 8 5 7
  
F19 Mean −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628
Std 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15 2.7101E − 15
Rank 1 1 1 1 1 1 1 1 1 1
  
F20 Mean −3.3101 −3.3061 −3.2982 −3.3101 −3.3022 −3.3220 −3.3141 −3.3180 −3.3022 −3.3220
Std 3.6278E − 02 4.1107E − 02 4.8370E − 02 3.6278E − 02 4.5066E − 02 7.5540E − 13 3.0164E − 02 2.1707E − 02 4.5066E − 02 2.5036E − 11
Rank 5 7 10 6 9 1 4 3 8 2
  
F21 Mean −10.1532 −10.1532 −10.1532 −10.1532 −10.1532 −10.1532 −10.1532 −10.1532 −10.1532 −10.1532
Std 7.1207E − 15 7.2269E − 15 7.1740E − 15 7.2269E − 15 7.1740E − 15 7.1207E − 15 7.1740E − 15 7.2269E − 15 7.0670E − 15 7.2269E − 15
Rank 2 7 4 7 4 2 4 7 1 7
  
F22 Mean −10.4029 −10.4029 −10.4029 −10.4029 −10.4029 −10.4029 −10.4029 −10.4029 −10.4029 −10.4029
Std 1.8915E − 10 9.3299E − 16 1.0940E − 15 1.1893E − 15 1.1893E − 15 1.0431E − 15 9.8958E − 16 9.3299E − 16 1.0940E − 15 2.4629E − 11
Rank 10 1 5 7 7 4 3 1 5 9
  
F23 Mean −10.5364 −10.5364 −10.5364 −10.5364 −10.5364 −10.5364 −10.5364 −10.5364 −10.5364 −10.5364
Std 3.9729E − 09 1.8067E − 15 1.9792E − 15 1.8949E − 15 1.8949E − 15 1.8067E − 15 1.8949E − 15 1.9515E − 15 1.8067E − 15 1.8949E − 15
Rank 10 1 9 4 4 1 4 8 1 4
  • Note: The best results obtained are highlighted in bold.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Friedman mean rankings obtained by MCOA with different values of αF.

5.2.2. Qualitative Analysis

This subsection presents a qualitative analysis to visualize the optimization dynamics of the proposed algorithm throughout the iterative process. Four unimodal, four multimodal, and two fixed-dimension multimodal benchmark functions are selected for testing. As shown in Figure 8, the first column depicts the topological structure of each function in two-dimensional space. The second to sixth columns, respectively, display: (1) convergence curves, (2) search trajectories in the first dimension, (3) average fitness values, (4) search history of the first two agents, and (5) trends in exploration and exploitation percentages.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Qualitative analysis results of MCOA for unimodal, multimodal, and fixed-dimension multimodal functions.

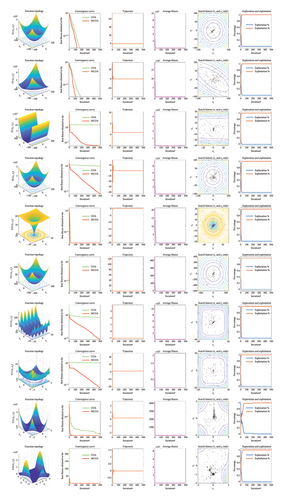
The convergence curves demonstrate how each algorithm progresses toward the optimal solution. Compared to COA, MCOA converges faster and achieves the desired convergence accuracy with fewer iterations in most test cases. On F1 and F3, both COA and MCOA converge to the global optimal point (0), but the latter requires fewer iterations. On F5 and F6, MCOA demonstrates stronger exploitation capabilities and achieves much higher convergence accuracy, thanks to its enhanced search mechanism guided by the Lévy flight strategy. For multimodal and fixed-dimension multimodal functions, both algorithms exhibit similar convergence accuracy and speed on F10,  F11, and F18. However, on F12,  F13,  and F15, MCOA clearly has better local optimal avoidance, and the curve gradually decreases toward the global optimal solution.

The iteration trajectory can be approximated from the third column in Figure 8. In the early stages of iterations, the curves show large oscillations, indicating that the algorithm favors exploration at this stage. In the medium and late iterations, the curves gradually flatten out, which implies that exploitation is utilized to ensure that MCOA converges to a higher level of accuracy.

The average fitness value represents the average target optimal value of all dimensions in each iteration and is used to characterize the evolutionary tendency of the whole population. All the curves exhibit a significant decrease over iterations, suggesting that MCOA can quickly steer the population closer to the global optimum.

The search history illustrates the locations where the search agent has explored in its quest to find the global optimum during the optimization process. The red dot marks the best solution found within the given iteration limit. Many search agents are centered around the optimal solution, suggesting that MCOA is more inclined to exploit promising solutions. Additionally, the dispersion and traversal of search agents across the search space validate the excellent search breadth of MCOA.

Finally, the last column shows how MCOA balances exploration and exploitation based on a dimension-wise diversity model [56]. In the initial iteration stage, MCOA exhibits a high level of exploration to thoroughly explore the search space and locate promising regions. As iterations progress, the percentage of exploitation gradually increases, ensuring accuracy of the final solution. Throughout this procedure, MCOA achieves a smooth transition from exploration to exploitation. This figure also captures the switching time points between these two key components for MCOA.

5.2.3. Ablation Analysis of Multiple Improvement Strategies

In this subsection, an ablation analysis experiment is designed to verify the effectiveness of each improvement strategy. Table 3 outlines the 10 derivative variants of MCOA, where 1 indicates activation of the corresponding strategy, while 0 indicates its absence. COA, MCOA, and other different MCOA derivatives are tested simultaneously on 23 benchmark problems, and the results are shown in Table 4.

Table 3. MCOA-derived algorithms with different improvement strategies.
Strategy MCOA-1 MCOA-2 MCOA-3 MCOA-4 MCOA-5 MCOA-6 MCOA-7 MCOA-8 MCOA-9 MCOA-10 MCOA
Specular reflection learning 1 0 0 0 1 1 1 0 0 0 1
Expanded exploration 0 1 0 0 1 0 0 1 1 0 1
Lévy flight 0 0 1 0 0 1 0 1 0 1 1
Vertical crossover operator 0 0 0 1 0 0 1 0 1 1 1
Table 4. Experimental results for ablation analysis of improvement strategies on 23 benchmark functions.
Function Metric COA MCOA-1 MCOA-2 MCOA-3 MCOA-4 MCOA-5 MCOA-6 MCOA-7 MCOA-8 MCOA-9 MCOA-10 MCOA
F1 Mean 0 0 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F2 Mean 0 0 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F3 Mean 0 0 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F4 Mean 0 0 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F5 Mean 2.8339E + 00 2.8229E + 00 9.4824E − 01 2.6837E + 00 2.5733E + 00 1.6028E − 03 2.6606E + 00 2.8015E + 00 1.8943E + 00 1.2088E − 03 2.6158E + 00 6.5468E − 10
Std 8.6474E + 00 8.6137E + 00 5.1048E + 00 8.1899E + 00 7.8531E + 00 8.0295E − 03 8.1201E + 00 8.5493E + 00 7.1088E + 00 5.4444E − 03 7.9825E + 00 3.3974E − 09
Rank 12 11 4 9 6 3 8 10 5 2 7 1
  
F6 Mean 4.9581E − 01 3.6394E − 01 9.2552E − 04 4.6614E − 01 4.4874E − 08 2.7375E − 05 3.9998E − 01 2.9657E − 18 5.8338E − 04 3.0936E − 08 3.6069E − 08 1.1042E − 21
Std 3.5948E − 01 2.7476E − 01 1.8400E − 03 2.8322E − 01 5.9490E − 08 2.2632E − 05 2.7702E − 01 1.5185E − 17 9.9238E − 04 4.9425E − 08 2.8818E − 08 5.3596E − 21
Rank 12 9 8 11 5 6 10 2 7 3 4 1
  
F7 Mean 8.1905E − 05 1.1367E − 04 6.3096E − 05 6.8164E − 05 4.1200E − 05 5.3659E − 05 7.8830E − 05 3.6702E − 05 7.9099E − 05 4.4214E − 05 3.6104E − 05 3.5231E − 05
Std 8.4466E − 05 1.0435E − 04 5.8071E − 05 6.8581E − 05 4.3879E − 05 4.6726E − 05 7.1452E − 05 3.2258E − 05 1.1355E − 04 3.5477E − 05 3.4912E − 05 3.0745E − 05
Rank 11 12 7 8 4 6 9 3 10 5 2 1
  
F8 Mean −5242.7189 −8686.5444 −8329.8712 −8106.5679 −11587.9782 −8213.3889 −8658.6230 −11691.5067 −5573.7303 −11508.0893 −11714.0076 −11829.1962
Std 6.8306E + 02 6.7034E + 02 1.3453E + 03 1.3844E + 03 4.8453E + 02 2.8154E + 03 6.9393E + 02 3.9648E + 02 1.5700E + 03 5.0753E + 02 4.0317E + 02 3.8003E + 02
Rank 12 6 8 10 4 9 7 3 11 5 2 1
  
F9 Mean 0 0 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F10 Mean 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16 8.8818E − 16
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F11 Mean 0 0 0 0 0 0 0 0 0 0 0 0
Std 0 0 0 0 0 0 0 0 0 0 0 0
Rank 1 1 1 1 1 1 1 1 1 1 1 1
  
F12 Mean 1.4950E − 02 1.3070E − 02 4.9624E − 05 1.4443E − 02 1.9757E − 09 2.1801E − 06 1.2297E − 02 8.1146E − 21 5.8363E − 05 1.3261E − 09 1.7528E − 09 4.4560E − 22
Std 1.3620E − 02 7.5554E − 03 1.2902E − 04 1.1037E − 02 2.1721E − 09 2.3345E − 06 9.2124E − 03 3.1105E − 20 8.9406E − 05 2.3415E − 09 2.0703E − 09 1.5576E − 21
Rank 12 10 7 11 5 6 9 2 8 3 4 1
  
F13 Mean 2.5461E + 00 2.6629E + 00 1.1824E − 03 2.2444E + 00 9.8869E − 02 1.8785E + 00 2.1944E + 00 2.8123E − 07 3.0870E − 03 8.0494E − 09 3.7913E − 05 1.4575E − 21
Std 6.9273E − 01 6.5553E − 01 2.0458E − 03 2.8428E − 01 5.4153E − 01 1.4538E + 00 2.4985E − 01 4.0820E − 07 1.4676E − 02 1.5178E − 08 3.4548E − 05 6.1017E − 21
Rank 11 12 5 10 7 8 9 3 6 2 4 1
  
F14 Mean 5.4081E + 00 2.6649E + 00 2.8500E + 00 3.4750E + 00 9.9800E − 01 2.7697E + 00 2.8928E + 00 1.1948E + 00 3.6212E + 00 2.1653E + 00 1.6159E + 00 9.9800E − 01
Std 4.9117E + 00 3.2382E + 00 3.4574E + 00 4.1251E + 00 1.7001E − 16 2.7369E + 00 3.4534E + 00 1.0782E + 00 4.0354E + 00 3.5616E + 00 2.4347E + 00 0
Rank 12 6 8 10 2 7 9 3 11 5 4 1
  
F15 Mean 3.2644E − 03 4.4858E − 04 3.9398E − 04 1.2984E − 03 4.7506E − 04 3.9651E − 04 4.2208E − 04 3.3332E − 04 4.3627E − 04 3.1380E − 04 4.7124E − 04 3.1322E − 04
Std 6.8257E − 03 1.9829E − 04 1.9152E − 04 3.6113E − 03 2.4168E − 04 2.5464E − 04 1.3001E − 04 5.3566E − 05 2.9654E − 04 1.7453E − 05 2.0537E − 04 8.6955E − 06
Rank 12 8 4 11 10 5 6 3 7 2 9 1
  
F16 Mean −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316 −1.0316
Std 1.3592E − 10 9.7968E − 12 8.7392E − 12 7.4590E − 15 7.8949E − 12 2.4479E − 11 1.6049E − 15 9.4566E − 16 1.6421E − 15 2.1587E − 15 7.6919E − 16 6.2532E − 16
Rank 12 10 9 7 8 11 4 3 5 6 2 1
  
F17 Mean 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979 0.3979
Std 1.2830E − 05 8.3105E − 06 3.1170E − 06 4.1011E − 05 9.7162E − 09 6.6459E − 09 5.3952E − 08 7.1487E − 08 1.1628E − 05 1.1803E − 09 3.1557E − 09 1.4768E − 09
Rank 11 9 8 12 5 4 6 7 10 1 3 2
  
F18 Mean 3.9000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000
Std 4.9295E + 00 5.0484E − 06 1.9001E − 05 5.6397E − 11 2.4269E − 11 1.2397E − 15 1.2259E − 15 2.9733E − 16 4.9479E − 16 9.3201E − 12 1.0464E − 11 5.0835E − 16
Rank 12 10 11 9 8 5 4 1 2 6 7 3
  
F19 Mean −3.8625 −3.8628 −3.8628 −3.8370 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628 −3.8628
Std 1.4390E − 03 1.1418E − 12 5.0657E − 09 1.4113E − 01 6.0842E − 13 2.7101E − 15 2.7101E − 15 2.7101E − 15 9.4576E − 09 3.8424E − 09 2.7101E − 15 2.7101E − 15
Rank 11 7 9 12 6 1 1 1 10 8 1 1
  
F20 Mean −3.2565 −3.2903 −3.2900 −3.2785 −3.2774 −3.2863 −3.2943 −3.3101 −3.3180 −3.2982 −3.3220 −3.3220
Std 7.7179E − 02 5.3481E − 02 5.3297E − 02 6.5862E − 02 5.7641E − 02 5.5415E − 02 5.1147E − 02 3.6278E − 02 2.1707E − 02 4.8370E − 02 4.1485E − 09 4.4621E − 09
Rank 12 7 8 10 11 9 6 4 3 5 1 2
  
F21 Mean −7.2776 −9.4735 −8.7936 −7.4343 −9.1336 −8.6237 −9.9833 −10.1532 −10.1532 −9.4735 −9.8133 −10.1532
Std 2.7974E + 00 1.7626E + 00 2.2929E + 00 2.5868E + 00 2.0741E + 00 2.3761E + 00 9.3076E − 01 6.8855E − 12 7.2269E − 15 1.7626E + 00 1.2934E + 00 7.1207E − 15
Rank 12 7 9 11 8 10 4 3 2 6 5 1
  
F22 Mean −7.1337 −9.4176 −10.0485 −7.4907 −10.2258 −9.8714 −9.6826 −10.4029 −10.4029 −10.4029 −10.0500 −10.4029
Std 3.2066E + 00 2.0430E + 00 1.3485E + 00 2.8020E + 00 9.7043E − 01 1.6218E + 00 1.8342E + 00 4.4101E − 09 7.4927E − 05 9.3299E − 16 1.3433E + 00 3.2986E − 16
Rank 12 10 7 11 5 8 9 3 4 2 6 1
  
F23 Mean −7.5558 −10.3561 −10.1758 −7.7540 −10.5364 −10.5364 −10.5364 −10.5364 −10.3561 −10.5364 −10.5364 −10.5364
Std 3.1046E + 00 9.8735E − 01 1.3720E + 00 3.1145E + 00 1.6546E − 09 2.0600E − 15 1.5055E − 08 8.8723E − 10 9.8734E − 01 5.9927E − 08 3.4279E − 09 1.8949E − 15
Rank 12 8 10 11 4 2 6 3 9 7 5 1
  
Mean rank 8.4783 6.4783 5.6087 7.3913 4.5652 4.6522 4.9565 2.6522 5.0870 3.2609 3.1739 1.1739
Final ranking 12 10 9 11 5 6 7 2 8 4 3 1
  • Note: The best results obtained are highlighted in bold.

As shown in Table 4, MCOA achieves the best overall performance with a Friedman mean ranking of 1.1739, significantly outperforming all variant algorithms and the original COA. When examining individual strategies, their effectiveness can be quantitatively ranked from highest to lowest impact: vertical crossover operator (MCOA-4, rank 5.5652), expanded exploration strategy (MCOA-2, rank 5.6087), specular reflection learning (MCOA-1, rank 6.4783), and Lévy flight (MCOA-3, rank 7.3913).

The vertical crossover operator demonstrates exceptional local exploitation capability, evidenced by MCOA-9’s superior performance on unimodal functions F5,  F6,  and F7, where precise local search is critical. For multimodal functions, the expanded exploration strategy (MCOA-2) yields the best results among single-strategy variants, showing significantly lower mean values compared to COA, particularly on functions F8 (−8329.8712 vs. −5242.7189) and F13(1.1824E-03 vs. 2.5461E + 00). This confirms its effectiveness in overcoming COA’s exploration deficiencies while preserving exploitation strength.

Furthermore, the synergistic integration of these strategies in MCOA produces remarkably consistent performance, achieving optimal results on 18 of 23 benchmark functions with minimal standard deviations, particularly on complex multimodal functions. For instance, on F8, the mean value of MCOA is −11829.1962, while the mean value of COA is −5242.7189, representing a 125.6% improvement. The combination of specular reflection learning and vertical crossover operator (MCOA-7) proves particularly effective for navigating local optima traps, as evidenced by its second-place overall ranking (2.6522), demonstrating how complementary strategies enhance both exploration and exploitation phases. Specular reflection learning and expanded exploration strategy enhance exploration, whereas Lévy flight and vertical crossover operator focus on strengthening exploitation, synergistically leading MCOA toward the optimal solution.

5.2.4. Quantitative Analysis

In this subsection, we quantitatively evaluate the numerical optimization performance of MCOA against twelve established MH algorithms: AO, DO, SO, AOA, ARO, TSA, SMA, COA, WHO, LCA, RIME, and SCSO. The statistical results are presented in Table 5.

Table 5. Numerical results of MCOA and comparison algorithms on 23 benchmark functions.
Function Metric MCOA AO DO SO AOA ARO TSA SMA COA WHO LCA RIME SCSO
F1 Mean 0 1.2014E − 101 1.1698E − 05 1.4548E − 94 3.9390E − 35 3.8009E − 65 6.6645E − 195 0 0 2.2857E − 44 2.0725E − 01 1.9599E + 00 2.1307E − 110
Std 0 6.5804E − 101 6.4523E − 06 3.4672E − 94 2.1575E − 34 2.0495E − 64 0 0 0 6.4927E − 44 2.4941E − 01 8.2185E − 01 1.1671E − 109
p value — 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 NaN NaN 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 6 11 7 10 8 4 1 1 9 12 13 5
  
F2 Mean 0 1.2580E − 52 1.5150E − 03 5.1539E − 43 0 5.5376E − 36 4.3975E − 100 0 0 9.4366E − 24 1.7163E − 01 1.7947E + 00 4.9236E − 61
Std 0 6.8904E − 52 7.7126E − 04 1.2954E − 42 0 1.2643E − 35 1.9856E − 99 0 0 5.0227E − 23 1.9407E − 01 1.4158E + 00 9.4981E − 61
p value — 1.2118E − 12 1.2118E − 12 1.2118E − 12 NaN 1.2118E − 12 1.2118E − 12 NaN NaN 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 7 11 8 1 9 5 1 1 10 12 13 6
  
F3 Mean 0 2.7322E − 99 2.4004E + 01 2.7757E − 56 1.0008E − 02 5.9800E − 49 2.9285E − 182 0 0 1.9650E − 21 3.8052E + 01 1.3895E + 03 5.6172E − 111
Std 0 1.4965E − 98 1.8300E + 01 1.5105E − 55 1.5955E − 02 3.2090E − 48 0 0 0 1.0762E − 20 3.8905E + 01 4.0077E + 02 2.6073E − 110
p value — 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 NaN NaN 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 6 11 7 10 8 4 1 1 9 12 13 5
  
F4 Mean 0 1.0076E − 53 9.2019E − 01 9.8256E − 41 2.6076E − 02 3.6544E − 27 1.1759E − 91 0 0 2.6781E − 16 8.3346E − 02 7.1134E + 00 6.0476E − 59
Std 0 5.5085E − 53 6.8201E − 01 1.6184E − 40 2.0631E − 02 1.6360E − 26 3.7854E − 91 0 0 1.3583E − 15 5.5805E − 02 2.5478E + 00 2.1111E − 58
p value — 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 NaN NaN 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 6 12 7 10 8 4 1 1 9 11 13 5
  
F5 Mean 1.5982E − 07 8.0245E − 04 1.2713E + 01 8.1014E + 00 9.5104E + 00 1.1935E + 00 9.5724E + 00 3.7068E + 00 8.9767E + 00 1.2470E + 01 5.5234E − 01 1.1965E + 02 9.6259E + 00
Std 5.4520E − 07 1.7527E − 03 2.0941E + 01 1.2851E + 01 1.3642E + 01 4.9565E + 00 1.3770E + 01 9.2134E + 00 1.2927E + 01 2.1930E + 01 1.7195E + 00 3.1563E + 02 1.3846E + 01
p value — 1.7072E − 04 1.2710E − 11 1.7072E − 04 1.6025E − 09 1.7072E − 04 1.7072E − 04 3.8303E − 03 3.8303E − 03 1.7072E − 04 1.2710E − 11 1.2710E − 11 1.7072E − 04
Rank 1 2 12 6 8 4 9 5 7 11 3 13 10
  
F6 Mean 1.1124E − 22 1.1238E − 04 1.7637E − 05 1.0880E + 00 3.1760E + 00 4.3183E − 03 6.1029E + 00 3.3753E − 03 3.4253E − 01 1.4773E − 02 1.9287E − 01 2.4266E + 00 2.5319E + 00
Std 2.1677E − 22 3.3118E − 04 7.9050E − 06 8.8946E − 01 2.3486E − 01 2.0796E − 03 9.6084E − 01 1.8976E − 03 2.6772E − 01 5.0520E − 02 3.4373E − 01 1.1534E + 00 4.7022E − 01
pvalue — 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11
Rank 1 3 2 9 12 5 13 4 8 6 7 10 11
  
F7 Mean 4.6440E − 05 9.5864E − 05 2.1025E − 02 2.6626E − 04 8.0932E − 05 6.6734E − 04 6.4010E − 05 1.2063E − 04 8.1337E − 05 1.2373E − 03 7.3769E − 04 4.0334E − 02 1.5063E − 04
Std 4.5346E − 05 1.1056E − 04 8.5499E − 03 1.6645E − 04 6.2971E − 05 4.2719E − 04 4.6300E − 05 1.0443E − 04 8.1403E − 05 1.1608E − 03 4.9856E − 04 1.3855E − 02 1.6752E − 04
p value — 6.1452E − 02 3.0199E − 11 1.4110E − 09 7.2884E − 03 2.3715E − 10 7.7272E − 02 8.1200E − 04 4.5146E − 02 3.0199E − 11 4.5043E − 11 3.0199E − 11 3.5638E − 04
Rank 1 5 12 8 3 9 2 6 4 11 10 13 7
  
F8 Mean −11853.5931 −7551.7382 −7639.7174 −12494.4857 −5302.6190 −10042.2968 −3368.2420 −12569.1358 −8360.2620 −8819.3101 −8649.1994 −9970.0736 −4599.6274
Std 3.2266E + 02 3.7125E + 03 7.6321E + 02 1.1531E + 02 4.8120E + 02 5.0598E + 02 4.2519E + 02 2.4943E − 01 4.7041E + 02 5.3122E + 02 4.5318E + 03 4.8474E + 02 1.0661E + 03
p value — 2.0681E − 02 3.0199E − 11 7.3803E − 10 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 8.7663E − 01 3.0199E − 11 3.0199E − 11
Rank 3 10 9 2 11 4 13 1 8 6 7 5 12
  
F9 Mean 0 0 2.4217E + 01 2.8386E + 00 0 0 2.0511E + 01 0 0 9.6122E − 12 1.7250E + 01 6.7690E + 01 0
Std 0 0 2.1331E + 01 8.0596E + 00 0 0 4.7975E + 01 0 0 3.6709E − 11 6.5699E + 01 1.4776E + 01 0
p value — NaN 1.2118E − 12 1.7016E − 08 NaN NaN 8.8658E − 07 NaN NaN 1.6080E − 01 1.2118E − 12 1.2118E − 12 NaN
Rank 1 1 12 9 1 1 11 1 1 8 10 13 1
  
F10 Mean 8.8818E − 16 8.8818E − 16 6.3064E − 04 2.1238E − 01 8.8818E − 16 8.8818E − 16 4.5593E − 15 8.8818E − 16 8.8818E − 16 1.9540E − 15 1.2623E − 01 1.9719E + 00 8.8818E − 16
Std 0 0 2.2418E − 04 6.5405E − 01 0 0 6.4863E − 16 0 0 1.6559E − 15 1.5477E − 01 5.5281E − 01 0
p value — NaN 1.2118E − 12 1.2003E − 13 NaN NaN 2.7085E − 14 NaN NaN 1.3055E − 03 1.2118E − 12 1.2118E − 12 NaN
Rank 1 1 10 12 1 1 9 1 1 8 11 13 1
  
F11 Mean 0 0 1.7566E − 02 9.7614E − 02 2.0686E − 01 0 2.1866E − 03 0 0 0 2.5235E − 01 9.7313E − 01 0
Std 0 0 1.5164E − 02 2.1233E − 01 1.7253E − 01 0 4.6871E − 03 0 0 0 2.9673E − 01 5.8124E − 02 0
p value — NaN 1.2118E − 12 2.7880E − 03 1.2118E − 12 NaN 1.1035E − 02 NaN NaN NaN 1.2118E − 12 1.2118E − 12 NaN
Rank 1 1 9 10 11 1 8 1 1 1 12 13 1
  
F12 Mean 5.5182E − 22 5.3309E − 06 4.1188E − 02 6.6459E − 02 5.0828E − 01 5.3152E − 04 1.0151E + 00 2.4929E − 03 1.3537E − 02 1.3919E − 02 2.4905E − 03 3.1475E + 00 2.1259E − 01
Std 2.4183E − 21 1.1174E − 05 1.5607E − 01 1.4895E − 01 5.5470E − 02 1.1914E − 03 2.9093E − 01 3.0834E − 03 1.0987E − 02 3.5814E − 02 5.3829E − 03 1.5219E + 00 9.1213E − 02
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11
Rank 1 2 8 9 11 3 12 5 6 7 4 13 10
  
F13 Mean 7.2674E − 19 3.7313E − 05 1.4965E − 03 5.6600E − 01 2.8558E + 00 6.1432E − 03 2.6254E + 00 5.1881E − 03 2.3028E + 00 8.2866E − 02 1.3434E − 02 2.8794E − 01 2.8650E + 00
Std 3.9609E − 18 7.7594E − 05 3.7935E − 03 9.2016E − 01 1.0236E − 01 1.6917E − 02 2.2479E − 01 6.3860E − 03 3.1519E − 01 1.6488E − 01 1.5913E − 02 1.9597E − 01 6.5642E − 02
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E − 11
Rank 1 2 3 9 12 5 11 4 10 7 6 8 13
  
F14 Mean 9.9800E − 01 2.6972E + 00 9.9800E − 01 9.9800E − 01 1.0065E + 01 9.9800E − 01 1.0742E + 01 9.9800E − 01 5.0974E + 00 1.6252E + 00 1.1330E + 01 9.9800E − 01 3.8790E + 00
Std 0 3.2838E + 00 1.4277E − 15 1.9755E − 06 3.7068E + 00 4.1233E − 17 5.2001E + 00 1.4114E − 12 4.9969E + 00 1.2032E + 00 2.9788E + 01 2.9483E − 12 3.9294E + 00
p value — 1.2118E − 12 1.1575E − 12 1.2177E − 07 1.2118E − 12 3.3371E − 01 1.2118E − 12 1.2118E − 12 1.2098E − 12 3.1296E − 04 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 8 3 6 11 2 12 4 10 7 13 5 9
  
F15 Mean 3.1838E − 04 4.9982E − 04 1.8442E − 03 5.7538E − 04 1.4003E − 02 3.2466E − 04 4.6376E − 03 5.7419E − 04 2.5654E − 03 1.3941E − 03 1.2771E − 02 4.4301E − 03 7.7314E − 04
Std 1.8035E − 05 1.2567E − 04 5.0410E − 03 2.9943E − 04 2.5025E − 02 3.6114E − 05 8.1702E − 03 2.8266E − 04 6.0362E − 03 3.6145E − 03 3.0340E − 02 7.5764E − 03 4.7210E − 04
p value — 1.2057E − 10 5.6073E − 05 1.2023E − 08 6.0658E − 11 6.6273E − 04 1.0702E − 09 8.3520E − 08 2.3768E − 07 3.1565E − 05 3.0199E − 11 7.3891E − 11 2.1544E − 10
Rank 1 3 8 5 13 2 11 4 9 7 12 10 6
  
F16 Mean −1.0316 −1.0313 −1.0316 −1.0316 −1.0316 −1.0316 −1.0263 −1.0316 −1.0316 −1.0316 −0.8394 −1.0316 −1.0307
Std 4.9651E − 16 3.9153E − 04 1.0345E − 12 5.4546E − 16 1.2736E − 07 9.7461E − 11 1.1985E − 02 7.3076E − 10 1.3065E − 15 5.5319E − 16 1.6454E − 01 1.5929E − 07 2.4211E − 03
p value — 1.7895E − 11 3.5769E − 01 6.0025E − 01 1.7895E − 11 5.0829E − 01 1.7895E − 11 1.3120E − 06 3.7211E − 01 7.8859E − 05 1.7895E − 11 6.6730E − 11 1.7895E − 11
Rank 1 10 5 2 8 6 12 7 4 3 13 9 11
  
F17 Mean 0.3979 0.3981 0.3979 0.3979 0.4077 0.3979 0.3993 0.3979 0.3979 0.3979 0.9020 0.3979 0.4130
Std 2.6258E − 15 3.0193E − 04 5.8965E − 11 1.3093E − 06 6.6929E − 03 4.4884E − 06 1.3987E − 03 1.3815E − 07 2.0909E − 09 0 1.1421E + 00 3.5878E − 07 2.0886E − 02
p value — 4.5043E − 11 3.0199E − 11 4.1040E − 11 3.0199E − 11 3.1602E − 12 3.3384E − 11 9.0632E − 08 3.0199E − 11 1.2118E − 12 3.0199E − 11 1.2477E − 04 3.0199E − 11
Rank 2 9 3 7 11 8 10 5 4 1 13 6 12
  
F18 Mean 3.0000 3.0315 3.0000 7.5000 7.5005 3.0000 7.5007 3.0000 3.0000 3.0000 19.5239 3.0000 3.0010
Std 1.1125E − 15 3.3959E − 02 1.6494E − 08 1.0234E + 01 1.0234E + 01 1.3576E − 15 1.0236E + 01 9.6637E − 12 9.2370E − 12 1.6306E − 15 1.0812E + 01 1.3147E − 06 2.3255E − 03
p value — 1.7546E − 11 1.7546E − 11 5.7130E − 08 1.7546E − 11 3.7853E − 02 1.7546E − 11 1.7546E − 11 1.7546E − 11 7.6974E − 04 1.7546E − 11 1.7546E − 11 1.7546E − 11
Rank 1 9 6 10 11 2 12 5 4 3 13 7 8
  
F19 Mean −3.8628 −3.8565 −3.8628 −3.8628 −3.8521 −3.8628 −3.8586 −3.8628 −3.8628 −3.8628 −3.2444 −3.8628 −3.8498
Std 2.4101E − 15 4.6038E − 03 3.1119E − 07 2.5391E − 15 4.9238E − 03 2.4338E − 15 3.8757E − 03 6.6070E − 07 1.4640E − 12 2.6962E − 15 3.8246E − 01 5.8676E − 07 8.1185E − 03
p value — 1.2118E − 12 1.2118E − 12 1.2819E − 04 1.2118E − 12 1.7918E − 07 1.2118E − 12 1.2118E − 12 1.2118E − 12 3.3371E − 01 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 10 6 3 11 2 9 8 5 4 13 7 12
  
F20 Mean −3.3180 −3.1614 −3.2744 −3.3101 −3.0548 −3.3022 −3.1557 −3.2543 −3.2744 −3.2863 −1.7718 −3.2705 −2.5672
Std 2.1707E − 02 1.0313E − 01 5.9242E − 02 3.6278E − 02 8.7518E − 02 4.5066E − 02 1.7686E − 01 6.0203E − 02 6.6992E − 02 5.5415E − 02 5.7144E − 01 5.9930E − 02 4.6047E − 01
p value — 3.4939E − 10 2.7875E − 09 5.5310E − 03 1.2676E − 11 2.1547E − 06 8.2776E − 10 6.2217E − 10 8.2703E − 09 4.0485E − 01 1.2676E − 11 1.9262E − 09 1.2676E − 11
Rank 1 9 5 2 11 3 10 8 6 4 13 7 12
  
F21 Mean −10.1532 −10.1458 −6.8968 −10.0293 −3.5438 −10.1505 −6.6362 −10.1528 −6.7781 −7.9737 −4.8880 −8.3036 −3.2110
Std 7.2269E − 15 1.0302E − 02 3.4191E + 00 2.5029E − 01 1.1557E + 00 1.2640E − 02 1.4262E + 00 2.1748E − 04 2.9086E + 00 2.9988E + 00 1.2337E + 00 2.7217E + 00 2.1989E + 00
p value — 1.2118E − 12 1.2118E − 12 1.1680E − 12 1.2118E − 12 1.2009E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 5.0090E − 09 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 4 8 5 12 3 10 2 9 7 11 6 13
  
F22 Mean −10.4029 −10.3955 −6.5803 −10.3717 −3.4513 −9.9577 −5.6700 −10.4027 −7.6337 −8.4904 −5.0128 −9.3472 −3.7030
Std 9.8958E − 16 1.0012E − 02 3.7393E + 00 1.2710E − 01 1.1586E + 00 1.6944E + 00 2.4093E + 00 2.4446E − 04 3.0825E + 00 3.0370E + 00 9.3867E − 01 2.1455E + 00 1.9874E + 00
p value — 1.0149E − 11 1.0149E − 11 3.8609E − 08 1.0149E − 11 1.0045E − 11 1.0149E − 11 1.0149E − 11 1.0149E − 11 1.3184E − 03 1.0149E − 11 1.0149E − 11 1.0149E − 11
Rank 1 3 9 4 13 5 10 2 8 7 11 6 12
  
F23 Mean −10.5364 −10.5225 −5.9477 −10.4759 −3.9802 −10.1326 −6.0682 −10.5361 −8.0181 −8.3159 −4.5777 −9.7278 −4.1211
Std 1.8067E − 15 2.2253E − 02 3.9028E + 00 1.9642E − 01 1.6526E + 00 1.5454E + 00 2.6659E + 00 2.2169E − 04 2.9789E + 00 3.4865E + 00 1.4196E + 00 2.1065E + 00 1.4776E + 00
p value — 1.2118E − 12 1.2118E − 12 3.9038E − 12 1.2118E − 12 1.2068E − 12 1.2118E − 12 1.2118E − 12 1.2118E − 12 1.5405E − 04 1.2118E − 12 1.2118E − 12 1.2118E − 12
Rank 1 3 10 4 13 5 9 2 8 7 11 6 12
  
+/−/= — 19/1/3 22/1/0 22/1/0 20/0/3 18/2/3 22/1/0 16/0/7 15/1/7 19/1/3 22/1/0 23/0/0 20/0/3
Mean rank 1.1304 5.2174 8.0435 6.5652 9.3478 4.5217 9.1304 3.4348 5.0870 6.6087 10.4348 9.6522 8.4348
Final ranking 1 5 8 6 11 3 10 2 4 7 13 12 9
  • Note: The best results obtained are highlighted in bold.

For unimodal functions, SMA, COA, and our proposed MCOA converge to the global optimal value (0) on F1∼F4, sharing the top ranking among all methods. AOA also achieves the global optimal solution on F2. These functions are still relatively easy to solve, and the advantage of MCOA still cannot be effectively emphasized. However, on F5∼F7, MCOA significantly outperforms the other comparison algorithms. On F5 and F6, MCOA achieves solution orders of magnitude better than COA and is substantially closer to the theoretical optimum. These results on unimodal functions, which contain only one global optimum, highlight MCOA’s exceptional exploitation capability in thoroughly searching the solution space. This enhanced performance stems from the integration of the Lévy flight strategy in equation (14), which strengthens local search, while the innovative vertical crossover operator ensures precise convergence.

For multimodal functions, MCOA obtains the most optimal results in terms of the average fitness value and the standard deviation on F9∼F13. Especially on F12 and F13, the convergence accuracy of MCOA is significantly improved over AO and COA owing to the powerful exploration mechanism of AO. It is worth noting that on F9 and F10, MCOA, AO, AOA, ARO, SMA, COA, and SCSO show consistent searchability, all providing desirable solutions. On F11, MCOA performs the same as AO, ARO, SMA, COA, WHO, and SCSO, and they rank tied for first. On F8, MCOA is slightly inferior to SMA and SO and ranks third among all methods. However, it can be noticed that the convergence accuracy of MCOA is still significantly enhanced compared with that of COA. Synthesizing these results, MCOA demonstrates strong exploration and local optimum avoidance abilities in solving multimodal functions. The expanded exploration mechanism of AO compensates for the lack of exploration capability, and the specular reflection learning strategy enables the search agent to perform bidirectional searches in the iterations, thus increasing the probability of locating the global optimum.

For fixed-dimension multimodal functions, MCOA ranks first on 9 out of 10 functions. On F17, the standard deviation of MCOA turns out to be slightly worse than that of WHO, thus ranking second. The underperformance of COA on F21∼F23, with solutions far from theoretical optimal values, indicates insufficient balance between exploration and exploitation in the original algorithm. MCOA, on the other hand, establishes a robust balance between exploration and exploitation and therefore can better address fixed-dimension multimodal functions.

The third to last row in Table 5 reports the p values of the Wilcoxon rank-sum test. It can be observed that MCOA outperforms AO on 19 problems, DO on 22, SO on 22, AOA on 20, ARO on 18, TSA on 22, SMA on 16, COA on 15, WHO on 19, LCA on 22, RIME on all 23, and SCSO on 20 problems. Furthermore, the last two rows in Table 5 present the Friedman mean ranking as well as the final ranking of different algorithms on 23 benchmark functions. MCOA attains the best mean ranking value of 1.1304. These comprehensive quantitative results show that the proposed technique has good potential for numerical optimization on the CEC2005 test set.

5.2.5. Convergence Analysis

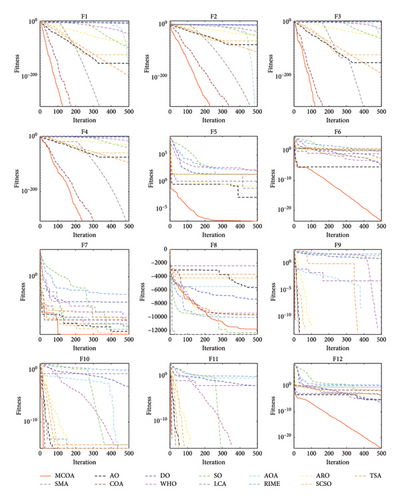
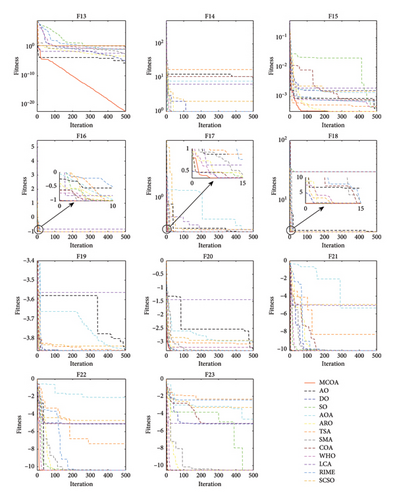
Figure 9 presents the convergence curves of MCOA compared with other algorithms across all 23 benchmark functions. The results demonstrate that MCOA can continuously converge to the optimal solution within 500 iterations in most test cases. For unimodal functions, while MCOA, COA, and SMA all reach the optimal value (0) on F1∼F4, MCOA requires notably fewer iterations, indicating superior convergence speed. This acceleration can be attributed primarily to the Lévy flight operator, which enhances the exploitation phase and guides the algorithm more efficiently toward the global optimum. For the more challenging F5 and F6, the convergence curves of MCOA exhibit steady decay with continuously improving solution accuracy. In contrast, the other comparison algorithms stagnate earlier. On F7, MCOA is slightly inferior in the initial iterations but eventually obtains better convergence results than other optimizers. For multimodal functions, MCOA rapidly identifies promising regions during early iterations and intensively exploits these neighborhoods to enhance convergence accuracy. On F9∼F11, MCOA provides desirable high-quality solutions with minimal iterations. MCOA inherits the superior exploration capability of AO due to the fusion of the position update mode of expanded exploration. On F12 and F13, the exploration performance of MCOA and AO in the early iterations is almost similar, but the former demonstrates superior local optima avoidance, ensuring better convergence accuracy. On F8, MCOA performs slightly worse than SO and SMA, ranking third in the test. For fixed-dimension multimodal functions, MCOA also maintains good convergence speed and accuracy. It can be found that MCOA rapidly transitions from exploration to exploitation in the initial iteration, effectively circumventing local optima. Particularly on F14,  F15,  F22, and F23, COA visibly falls into local optima due to imbalance between exploration and exploitation—a problem that MCOA successfully overcomes. The above experimental results indicate that the four improvement steps adopted in this paper strengthen the algorithm’s exploitation and exploration, allowing it to converge more rapidly to higher accuracy and avoid local stagnation in the optimization process. In summary, MCOA achieves highly competitive convergence performance compared to other state-of-the-art MH algorithms.

Details are in the caption following the image
Figure 9 (a)
Open in figure viewerPowerPoint
Convergence curves of MCOA and comparison algorithms on 23 benchmark functions.
Details are in the caption following the image
Figure 9 (b)
Open in figure viewerPowerPoint
Convergence curves of MCOA and comparison algorithms on 23 benchmark functions.

5.2.6. Boxplot Behavior Analysis

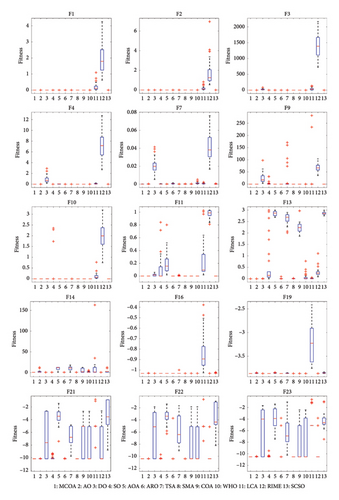
Figure 10 presents the boxplot of MCOA and comparison algorithms on partial benchmark functions. In these boxplots, the center line represents the median value, while the upper and lower whisker edges indicate maximum and minimum values, respectively, with outliers denoted by plus signs (“+”). From the results, MCOA shows good data consistency on unimodal functions F1,  F2,  F3, F4, and F7. Notably, on F7, both AO and COA generate outliers, while MCOA does not. Since multimodal and fixed-dimension multimodal functions have local minima, this is a stability check for the optimizer. MCOA presents a few outliers on F13, but the other algorithms are not as satisfactory, with obvious outliers for SO, and the medians of TSA and COA are far from the theoretical optimum (0). In other test cases, the boxplots of MCOA are more centralized than comparison algorithms in terms of maximum, minimum, and median values. These boxplot analyses confirm that the integration of multiple search strategies significantly improves the robustness of COA.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Boxplots of MCOA and comparison algorithms on partial benchmark functions.

5.2.7. Scalability Analysis

The problem dimension represents the number of independent decision variables to be considered in the optimization problem. As problem dimension increases, many algorithms suffer from dimensional catastrophe, experiencing significant degradation in convergence accuracy. To assess dimensional robustness, we extend the dimension (D) of 13 benchmark functions (F1∼F13) from 30 to 50, 100, 500, and 1000, respectively, with other parameter settings remaining unchanged. The detailed experimental results are presented in Tables 6, 7, 8, and 9.

Table 6. Numerical results of MCOA and comparison algorithms on 13 variable dimension functions (D = 50).
Function Metric MCOA AO DO SO AOA ARO TSA SMA COA WHO LCA RIME SCSO
F1 Mean 0 7.7349E − 104 2.2841E − 03 3.7615E − 88 2.5430E − 04 2.3024E − 64 1.8368E − 185 0 0 9.0793E − 40 1.8894E − 01 1.9083E + 01 6.7692E − 117
Std 0 4.2358E − 103 1.0956E − 03 1.4491E − 87 8.9585E − 04 9.3060E − 64 0 0 0 2.8325E − 39 2.4430E − 01 5.0240E + 00 3.3274E − 116
  
F2 Mean 0 4.2901E − 50 2.1083E − 02 3.4499E − 39 2.4315E − 186 3.7916E − 35 1.1161E − 95 0 0 1.1617E − 22 2.5103E − 01 9.6854E + 00 2.3729E − 59
Std 0 1.7196E − 49 5.1066E − 03 5.2408E − 39 0 1.1433E − 34 2.5455E − 95 0 0 2.2054E − 22 1.6048E − 01 3.5615E + 00 1.1698E − 58
  
F3 Mean 0 1.5405E − 104 1.1544E + 03 2.0839E − 52 7.7499E − 02 5.5181E − 46 1.8650E − 174 0 0 3.8369E − 20 1.4141E + 02 1.4235E + 04 1.5770E − 110
Std 0 8.4251E − 104 6.3811E + 02 9.0553E − 52 6.4032E − 02 2.4178E − 45 0 0 0 1.1419E − 19 1.6365E + 02 2.6278E + 03 7.3573E − 110
  
F4 Mean 0 2.2620E − 56 1.5925E + 01 2.2015E − 38 5.5102E − 02 5.5789E − 25 1.7409E − 87 0 0 5.3149E − 15 9.0639E − 02 3.2034E + 01 1.2047E − 57
Std 0 1.2098E − 55 6.8298E + 00 4.7433E − 38 9.7968E − 03 2.1152E − 24 8.7894E − 87 0 0 1.2580E − 14 6.1348E − 02 5.4084E + 00 4.7629E − 57
  
F5 Mean 6.5146E − 08 2.2281E − 03 2.6482E + 01 9.0498E + 00 1.6269E + 01 1.3554E − 01 1.6186E + 01 4.4411E + 00 1.5860E + 01 1.6144E + 01 1.0536E + 00 6.9548E + 02 1.6306E + 01
Std 1.6391E − 07 6.9299E − 03 1.8210E + 01 1.7317E + 01 2.3323E + 01 2.7514E − 01 2.3282E + 01 1.2213E + 01 2.2818E + 01 2.3371E + 01 3.1476E + 00 1.0962E + 03 2.3454E + 01
  
F6 Mean 4.6773E − 17 3.3897E − 04 1.0637E − 03 5.2073E + 00 7.2754E + 00 5.5860E − 02 1.1075E + 01 3.6408E − 02 2.4550E + 00 5.1673E − 01 2.6528E − 01 1.8307E + 01 4.8530E + 00
Std 2.3449E − 16 8.4400E − 04 3.9624E − 04 4.7520E + 00 3.6447E − 01 5.6515E − 02 8.0492E − 01 2.7966E − 02 6.7714E − 01 5.1087E − 01 3.8861E − 01 4.5393E + 00 8.6371E − 01
  
F7 Mean 5.5914E − 05 1.1463E − 04 5.2070E − 02 2.1473E − 04 7.0890E − 05 6.9430E − 04 7.6761E − 05 2.0777E − 04 6.8026E − 05 1.2825E − 03 1.0858E − 03 1.4042E − 01 1.4376E − 04
Std 4.1994E − 05 1.0774E − 04 2.1278E − 02 2.4099E − 04 7.3905E − 05 4.9112E − 04 6.1382E − 05 1.8227E − 04 8.9522E − 05 1.0268E − 03 9.5761E − 04 3.5595E − 02 1.7278E − 04
  
F8 Mean −2.0854E + 04 −9.7195E + 03 −1.1501E + 04 −1.7331E + 04 −6.7910E + 03 −1.4599E + 04 −4.5282E + 03 −2.0948E + 04 −1.2938E + 04 −1.3485E + 04 −1.6320E + 04 −1.5286E + 04 −8.1440E + 03
Std 1.2508E + 02 6.0323E + 03 8.9620E + 02 1.6049E + 03 4.8902E + 02 7.3064E + 02 7.1793E + 02 1.3306E + 00 8.0954E + 02 7.1133E + 02 6.8184E + 03 7.0800E + 02 1.4347E + 03
  
F9 Mean 0 0 6.4524E + 01 1.0405E + 01 0 0 1.9914E + 01 0 0 1.8948E − 15 1.3293E + 01 1.3930E + 02 0
Std 0 0 4.4011E + 01 1.8069E + 01 0 0 7.5242E + 01 0 0 1.0378E − 14 7.1894E + 01 3.4050E + 01 0
  
F10 Mean 8.8818E − 16 8.8818E − 16 7.9761E − 03 4.4409E − 15 8.8818E − 16 8.8818E − 16 4.7962E − 15 8.8818E − 16 8.8818E − 16 1.1250E − 15 7.7834E − 02 3.4887E + 00 8.8818E − 16
Std 0 0 2.5504E − 03 0 0 0 1.0840E − 15 0 0 9.0135E − 16 6.5108E − 02 6.5645E − 01 0
  
F11 Mean 0 0 1.2615E − 02 0 1.2803E + 00 0 1.2716E − 03 0 0 0 3.4969E − 01 1.1670E + 00 0
Std 0 0 9.2954E − 03 0 7.1519E − 01 0 3.9465E − 03 0 0 0 3.1320E − 01 3.9062E − 02 0
  
F12 Mean 2.3110E − 16 7.1745E − 06 5.6873E − 01 1.8121E − 02 7.3251E − 01 1.8136E − 03 1.0910E + 00 8.7114E − 03 5.9790E − 02 3.8242E − 02 1.0904E − 03 1.2911E + 01 2.5462E − 01
Std 9.2021E − 16 1.6101E − 05 8.9093E − 01 3.3598E − 02 3.3961E − 02 2.2797E − 03 1.8066E − 01 1.4214E − 02 3.0410E − 02 6.6049E − 02 1.8913E − 03 4.5507E + 00 7.1510E − 02
  
F13 Mean 1.8847E − 16 2.4919E − 05 1.1670E + 00 9.4552E − 01 4.8593E + 00 3.8725E − 02 4.6255E + 00 2.0973E − 02 4.4649E + 00 6.3355E − 01 1.5807E − 02 2.1164E + 01 4.8952E + 00
Std 8.9931E − 16 3.2048E − 05 6.0269E + 00 1.4892E + 00 1.1625E − 01 4.8008E − 02 3.1825E − 01 2.5517E − 02 3.4891E − 01 3.8080E − 01 2.5403E − 02 2.5321E + 01 5.1733E − 02
  • Note: The best results obtained are highlighted in bold.
Table 7. Numerical results of MCOA and comparison algorithms on 13 variable dimension functions (D = 100).
Function Metric MCOA AO DO SO AOA ARO TSA SMA COA WHO LCA RIME SCSO
F1 Mean 0 1.0280E − 100 7.9950E − 01 2.0383E − 81 2.3447E − 02 1.0462E − 58 3.8389E − 176 0 0 1.1250E − 34 4.2667E − 01 3.8142E + 02 7.5297E − 113
Std 0 5.6305E − 100 2.9849E − 01 7.3667E − 81 9.3871E − 03 3.6205E − 58 0 0 0 5.4149E − 34 6.6864E − 01 7.6212E + 01 4.1007E − 112
  
F2 Mean 0 3.6125E − 50 4.6184E − 01 1.2834E − 35 3.5570E − 57 5.4971E − 34 1.0145E − 90 0 0 7.9306E + 00 6.0802E − 01 8.1899E + 01 7.8695E − 59
Std 0 1.4726E − 49 6.9436E − 02 1.1444E − 35 1.9051E − 56 1.4422E − 33 1.5057E − 90 0 0 4.3437E + 01 4.8738E − 01 1.6426E + 01 2.5259E − 58
  
F3 Mean 0 1.8293E − 103 2.8873E + 04 8.9938E − 28 2.8475E + 03 2.2876E − 45 1.1240E − 166 0 0 7.7615E − 16 1.2417E + 03 9.7591E + 04 9.6461E − 109
Std 0 1.0012E − 102 9.5236E + 03 4.9261E − 27 1.5593E + 04 1.0221E − 44 0 0 0 2.6433E − 15 1.2857E + 03 1.4764E + 04 5.2613E − 108
  
F4 Mean 0 2.8275E − 51 5.7611E + 01 1.3116E − 36 9.1657E − 02 1.2094E − 24 2.7756E − 84 0 0 2.6653E − 13 8.5062E − 02 6.1159E + 01 3.3397E − 56
Std 0 1.5476E − 50 8.4975E + 00 2.1253E − 36 1.4551E − 02 5.3540E − 24 3.2852E − 84 0 0 4.6102E − 13 5.2885E − 02 6.1479E + 00 1.6400E − 55
  
F5 Mean 1.1789E − 06 7.3024E − 02 3.2959E + 02 9.8905E + 01 9.8909E + 01 8.0408E − 01 9.8354E + 01 4.9957E + 01 9.7746E + 01 9.7699E + 01 4.6839E + 00 1.0046E + 05 9.8921E + 01
Std 9.4324E − 07 9.8156E − 02 4.5907E + 01 5.0650E − 02 2.5919E − 02 2.5957E − 01 4.4047E − 01 6.8409E + 01 2.9123E − 01 2.7783E − 01 5.4918E + 00 6.0071E + 04 2.0762E − 02
  
F6 Mean 1.3574E − 13 3.4756E − 04 1.2750E + 00 1.2831E + 01 1.8019E + 01 4.5997E − 01 2.4394E + 01 9.0584E − 01 1.0097E + 01 5.6031E + 00 7.2485E − 01 3.6689E + 02 1.2577E + 01
Std 3.9085E − 13 7.2419E − 04 5.1230E − 01 1.0975E + 01 6.2769E − 01 2.5261E − 01 4.3691E − 01 9.5606E − 01 1.4159E + 00 1.3568E + 00 1.3895E + 00 6.5292E + 01 2.2131E + 00
  
F7 Mean 4.7761E − 05 1.2987E − 04 2.6727E − 01 1.7911E − 04 8.6091E − 05 6.2538E − 04 9.1754E − 05 1.9109E − 04 9.6381E − 05 3.7210E − 03 1.0868E − 03 1.0376E + 00 2.4695E − 04
Std 3.8300E − 05 8.7567E − 05 7.3757E − 02 1.1022E − 04 9.3700E − 05 4.7611E − 04 8.7116E − 05 1.9036E − 04 7.7564E − 05 1.0246E − 02 8.7126E − 04 2.7361E − 01 3.6582E − 04
  
F8 Mean −3.7145E + 04 −1.0295E + 04 −2.1089E + 04 −4.1359E + 04 −1.0143E + 04 −2.2948E + 04 −6.1434E + 03 −4.1891E + 04 −2.1248E + 04 −2.1739E + 04 −2.6082E + 04 −2.6405E + 04 −1.8223E + 04
Std 5.8996E + 03 2.2147E + 03 1.9093E + 03 1.0173E + 03 7.4680E + 02 9.8218E + 02 7.3868E + 02 8.1244E + 00 2.7163E + 03 1.6436E + 03 3.1647E + 03 1.2346E + 03 2.6373E + 03
  
F9 Mean 0 0 1.9800E + 02 2.2757E + 01 0 0 5.6857E − 01 0 0 0 2.9308E + 01 4.6844E + 02 0
Std 0 0 1.1546E + 02 4.0890E + 01 0 0 5.7831E − 01 0 0 0 1.5914E + 02 5.8863E + 01 0
  
F10 Mean 8.8818E − 16 8.8818E − 16 9.9230E − 01 4.4409E − 15 2.6718E − 04 8.8818E − 16 5.7436E − 15 8.8818E − 16 8.8818E − 16 1.3619E − 15 9.7450E − 02 6.4514E + 00 8.8818E − 16
Std 0 0 6.4943E − 01 0 8.2538E − 04 0 1.7413E − 15 0 0 1.2283E − 15 1.3268E − 01 1.1928E + 00 0
  
F11 Mean 0 0 4.3361E − 01 0 5.9488E + 02 0 1.0693E − 03 0 0 0 3.6712E − 01 4.4507E + 00 0
Std 0 0 1.1933E − 01 0 1.4759E + 02 0 3.3703E − 03 0 0 0 2.9811E − 01 6.9416E − 01 0
  
F12 Mean 5.1195E − 14 9.2978E − 07 4.3135E + 00 1.5198E − 01 9.0474E − 01 6.9506E − 03 1.2246E + 00 1.7697E − 02 2.2540E − 01 8.2441E − 02 5.8482E − 04 3.6685E + 02 3.3567E − 01
Std 1.2882E − 13 1.6679E − 06 1.8361E + 00 3.5096E − 01 2.2806E − 02 3.8724E − 03 7.8149E − 02 4.6295E − 02 5.2620E − 02 3.6325E − 02 1.2302E − 03 7.9056E + 02 9.9947E − 02
  
F13 Mean 1.7144E − 11 4.9527E − 05 9.1214E + 01 1.4810E + 00 9.9663E + 00 2.5081E − 01 9.7899E + 00 4.3329E − 01 9.5430E + 00 4.8490E + 00 3.1294E − 02 5.4596E + 03 9.9077E + 00
Std 9.1529E − 11 1.2352E − 04 2.1356E + 01 2.9277E + 00 5.7282E − 02 1.8847E − 01 7.8983E − 02 8.3778E − 01 2.9732E − 01 1.0141E + 00 4.1138E − 02 5.8103E + 03 4.9238E − 02
  • Note: The best results obtained are highlighted in bold.
Table 8. Numerical results of MCOA and comparison algorithms on 13 variable dimension functions (D = 500).
Function Metric MCOA AO DO SO AOA ARO TSA SMA COA WHO LCA RIME SCSO
F1 Mean 0 2.3744E − 101 8.1243E + 03 8.4588E − 71 6.3288E − 01 2.4095E − 56 2.9656E − 162 0 0 1.9023E − 30 1.5815E + 00 1.6775E + 05 2.3021E − 110
Std 0 1.3005E − 100 1.5910E + 03 3.2087E − 70 3.7477E − 02 1.0544E − 55 2.2228E − 162 0 0 5.2800E − 30 2.1952E + 00 1.1056E + 04 1.0652E − 109
  
F2 Mean 0 9.3901E − 54 6.8703E + 01 1.0861E − 31 1.1772E − 03 8.8065E − 31 8.1518E − 83 0 0 5.9576E + 02 3.6523E + 00 7.7462E + 126 3.1856E − 57
Std 0 5.1432E − 53 7.1143E + 00 1.1724E − 31 1.4740E − 03 4.1447E − 30 3.8002E − 83 0 0 6.1850E + 02 2.3513E + 00 4.2427E + 127 1.2001E − 56
  
F3 Mean 0 3.1524E − 98 1.5436E + 06 3.4130E − 05 3.8224E + 01 3.5641E − 40 9.8772E − 154 0 0 6.2555E − 09 1.8917E + 05 2.6453E + 06 2.6823E − 101
Std 0 1.7263E − 97 2.2355E + 05 1.8694E − 04 2.2731E + 01 1.0371E − 39 4.3541E − 153 0 0 2.5091E − 08 3.1723E + 05 2.3395E + 05 1.3565E − 100
  
F4 Mean 0 1.1188E − 54 9.4454E + 01 1.0073E − 33 1.7824E − 01 1.0994E − 22 1.4261E − 72 0 0 4.6768E − 10 6.5452E − 02 9.3386E + 01 8.5877E − 56
Std 0 5.6234E − 54 1.0581E + 00 1.4463E − 33 1.7090E − 02 2.1659E − 22 5.4324E − 72 0 0 9.4550E − 10 4.4775E − 02 1.3180E + 00 2.0815E − 55
  
F5 Mean 1.2293E − 03 8.8272E − 03 2.7993E + 06 3.4978E + 01 5.0067E + 01 4.9994E − 01 4.9795E + 01 4.4006E + 00 4.9791E + 01 4.9805E + 01 2.9965E + 00 2.9534E + 07 4.9891E + 01
Std 5.9729E − 04 2.9949E − 02 9.2405E + 06 1.2647E + 02 1.5222E + 02 2.2133E + 00 1.5194E + 02 1.7868E + 01 1.5193E + 02 1.5197E + 02 1.0833E + 01 9.1780E + 07 1.5223E + 02
  
F6 Mean 8.0148E − 06 9.6038E − 04 8.5352E + 03 7.7803E + 01 1.1570E + 02 4.9114E + 00 1.2475E + 02 3.0361E + 01 9.6308E + 01 1.0190E + 02 3.8864E + 00 1.6333E + 05 6.7263E + 01
Std 4.2639E − 05 1.6115E − 03 1.9899E + 03 5.5978E + 01 1.5632E + 00 2.6064E + 00 1.6187E − 07 3.4732E + 01 3.7897E + 00 1.7087E + 01 5.7391E + 00 1.2908E + 04 1.3626E + 01
  
F7 Mean 4.6361E − 05 9.2061E − 05 1.1322E + 02 1.5806E − 04 8.2912E − 05 6.6465E − 04 9.6236E − 05 4.2955E − 04 8.3841E − 05 2.3331E − 03 1.8407E − 03 2.0583E + 03 2.0571E − 04
Std 4.0052E − 05 8.2948E − 05 6.3092E + 01 1.3657E − 04 7.2410E − 05 3.7044E − 04 8.1436E − 05 4.7865E − 04 8.7382E − 05 2.8136E − 03 1.4878E − 03 2.9274E + 02 1.9281E − 04
  
F8 Mean −9.1981E + 04 −3.9134E + 04 −7.1601E + 04 −2.0759E + 05 −2.2898E + 04 −5.9284E + 04 −1.3928E + 04 −2.0937E + 05 −6.3220E + 04 −5.8392E + 04 −1.8771E + 05 −8.0364E + 04 −6.7276E + 04
Std 1.0236E + 04 1.2275E + 04 4.4140E + 03 5.4426E + 03 1.5879E + 03 2.8486E + 03 2.1406E + 03 2.5433E + 02 7.0133E + 03 6.9569E + 03 2.9000E + 04 3.3878E + 03 2.8645E + 04
  
F9 Mean 0 0 2.3689E + 03 1.0380E − 01 6.7740E − 06 0 5.6790E − 01 0 0 9.2678E − 11 1.7992E + 00 5.4725E + 03 0
Std 0 0 6.2821E + 02 5.6853E − 01 7.7056E − 06 0 6.3274E − 01 0 0 5.0762E − 10 3.3375E + 00 1.6879E + 02 0
  
F10 Mean 8.8818E − 16 8.8818E − 16 6.7017E + 00 5.3883E − 15 7.9296E − 03 8.8818E − 16 6.9278E − 15 8.8818E − 16 8.8818E − 16 1.9540E − 15 1.2997E − 01 2.0334E + 01 8.8818E − 16
Std 0 0 5.5563E − 01 1.5979E − 15 3.7008E − 04 0 1.6559E − 15 0 0 2.3137E − 15 2.0514E − 01 1.1825E − 01 0
  
F11 Mean 0 0 7.4133E + 01 0 9.9981E + 03 0 3.2886E − 04 0 0 0 3.7696E − 01 1.4915E + 03 0
Std 0 0 1.5202E + 01 0 2.8089E + 03 0 1.8012E − 03 0 0 0 3.6867E − 01 1.0662E + 02 0
  
F12 Mean 5.7937E − 07 1.6036E − 05 1.2025E + 07 7.3927E − 02 1.0818E + 00 1.3846E − 02 1.1987E + 00 6.6236E − 03 7.3447E − 01 8.1462E − 01 3.1149E − 04 3.6313E + 08 2.7103E − 01
Std 1.1181E − 06 5.7879E − 05 9.8827E + 06 1.7681E − 01 1.3998E − 02 4.9426E − 03 1.1450E − 02 1.6565E − 02 4.9539E − 02 2.8525E − 01 4.5977E − 04 9.4372E + 07 1.1045E − 01
  
F13 Mean 2.5584E − 04 7.2447E − 01 4.9499E + 07 6.1562E + 00 5.0199E + 01 3.2535E + 00 4.9781E + 01 3.2755E + 00 4.9827E + 01 5.5996E + 01 1.1724E − 01 1.0275E + 09 4.9921E + 01
Std 3.3881E − 04 3.9553E + 00 4.0576E + 07 1.2724E + 01 2.9298E − 02 2.2001E + 00 4.4677E − 02 5.2037E + 00 8.9446E − 02 6.2152E + 00 1.7994E − 01 2.3270E + 08 5.0976E − 02
  • Note: The best results obtained are highlighted in bold.
Table 9. Numerical results of MCOA and comparison algorithms on 13 variable dimension functions (D = 1000).
Function Metric MCOA AO DO SO AOA ARO TSA SMA COA WHO LCA RIME SCSO
F1 Mean 0 2.9856E − 114 6.9734E + 04 4.0431E − 68 1.7139E + 00 5.9681E − 52 1.6650E − 158 0 0 1.9864E − 28 6.2498E + 00 9.1920E + 05 8.1506E − 111
Std 0 1.2213E − 113 1.3863E + 04 8.1175E − 68 7.7934E − 02 3.2656E − 51 1.0787E − 158 0 0 8.0535E − 28 9.6729E + 00 3.6115E + 04 2.4952E − 110
  
F2 Mean 0 2.3557E − 61 Inf 3.2339E − 19 1.2806E − 02 6.1098E − 30 9.9162E − 82 0 0 2.0554E + 03 5.1278E + 00 2.6852E + 03 4.1971E − 57
Std 0 1.2903E − 60 NaN 1.7713E − 18 6.1394E − 03 1.8666E − 29 2.5170E − 82 0 0 1.2702E + 03 2.7949E + 00 8.8150E + 01 1.0828E − 56
  
F3 Mean 0 1.2666E − 99 5.9197E + 06 2.6098E − 09 1.2807E + 02 1.0508E − 36 3.3140E − 149 0 0 5.7899E − 07 9.7056E + 05 1.0094E + 07 2.5537E − 99
Std 0 5.2244E − 99 7.9554E + 05 1.4294E − 08 5.1991E + 01 4.7374E − 36 9.0341E − 149 0 0 2.2652E − 06 1.0762E + 06 8.4913E + 05 1.3983E − 98
  
F4 Mean 0 1.2448E − 52 9.7598E + 01 7.4351E − 33 2.0877E − 01 4.3472E − 21 7.3046E + 01 0 0 1.6475E − 09 7.8676E − 02 9.7218E + 01 8.9408E − 55
Std 0 6.7095E − 52 6.1092E − 01 1.0810E − 32 1.1437E − 02 8.3507E − 21 4.4802E + 01 0 0 3.7722E − 09 6.0081E − 02 5.9586E − 01 3.0806E − 54
  
F5 Mean 9.9478E − 03 8.6190E − 01 3.4927E + 07 6.6595E + 01 6.6814E + 01 6.9687E + 00 1.3623E + 02 9.8887E + 02 6.6510E + 01 4.8785E + 02 1.9824E + 00 2.0434E + 08 6.6596E + 01
Std 4.8714E − 02 4.5925E + 00 1.3344E + 08 2.5344E + 02 2.5347E + 02 3.5182E + 01 2.3791E + 02 0 2.5311E + 02 2.4902E + 03 8.4931E + 00 7.7791E + 08 2.5344E + 02
  
F6 Mean 7.7946E − 03 1.1170E − 03 7.2787E + 04 1.0647E + 02 2.4278E + 02 9.9086E + 00 2.4975E + 02 3.2849E + 01 2.1427E + 02 2.2599E + 02 5.9813E + 00 9.1347E + 05 1.3999E + 02
Std 4.0913E − 02 1.4630E − 03 1.0785E + 04 1.0651E + 02 1.2542E + 00 5.1747E + 00 1.7640E − 07 4.9734E + 01 3.4013E + 00 2.2909E + 01 1.1349E + 01 5.3172E + 04 2.6253E + 01
  
F7 Mean 5.0377E − 05 6.9669E − 05 5.0945E + 03 2.3111E − 04 1.2346E − 04 7.5169E − 04 9.6673E − 05 4.5623E − 04 8.0742E − 05 3.0568E − 03 3.7797E − 03 3.6246E + 04 2.1985E − 04
Std 3.9966E − 05 5.2334E − 05 2.0012E + 03 1.8875E − 04 1.2029E − 04 5.4362E − 04 8.8095E − 05 3.9299E − 04 7.8869E − 05 5.2683E − 03 4.1201E − 03 3.7503E + 03 2.4883E − 04
  
F8 Mean −1.8649E + 05 −6.3931E + 04 −1.1067E + 05 −4.1467E + 05 −3.2143E + 04 −8.4126E + 04 −1.8174E + 04 −4.1883E + 05 −9.2424E + 04 −8.5749E + 04 −3.7138E + 05 −1.1547E + 05 −1.0885E + 05
Std 2.3285E + 04 1.9424E + 04 7.5454E + 03 7.4849E + 03 2.0424E + 03 3.4652E + 03 2.2270E + 03 2.4606E + 02 1.0548E + 04 8.2143E + 03 5.9020E + 04 4.5758E + 03 2.8701E + 04
  
F9 Mean 0 0 5.3688E + 03 0 6.1114E − 05 0 3.3166E − 01 0 0 0 4.1184E + 00 1.3083E + 04 0
Std 0 0 5.1535E + 02 0 1.1845E − 05 0 4.7706E − 01 0 0 0 6.8399E + 00 2.1376E + 02 0
  
F10 Mean 8.8818E − 16 8.8818E − 16 1.0178E + 01 5.6251E − 15 9.2845E − 03 8.8818E − 16 7.7568E − 15 8.8818E − 16 8.8818E − 16 1.9540E − 15 1.0204E − 01 2.0707E + 01 8.8818E − 16
Std 0 0 5.7536E − 01 1.7034E − 15 2.6316E − 04 0 9.0135E − 16 0 0 1.6559E − 15 8.8998E − 02 3.9470E − 02 0
  
F11 Mean 0 0 6.6670E + 02 0 2.8268E + 04 0 9.5962E − 04 0 0 0 3.5079E − 01 8.1906E + 03 0
Std 0 0 1.0499E + 02 0 4.6720E + 02 0 3.9108E − 03 0 0 0 2.7062E − 01 4.0529E + 02 0
  
F12 Mean 9.8660E − 07 4.6628E − 03 1.2437E + 09 1.3509E − 01 1.1135E + 00 1.2893E − 02 1.1892E + 00 7.7567E − 03 9.0452E − 01 1.0110E + 00 3.6746E − 04 4.9373E + 09 3.3791E − 01
Std 1.9961E − 06 8.9320E − 03 4.3081E + 08 3.5732E − 01 5.6980E − 03 6.2962E − 03 4.4934E − 03 1.7256E − 02 4.0259E − 02 3.9321E − 01 7.0352E − 04 6.9890E + 08 1.0353E − 01
  
F13 Mean 7.7431E − 04 1.0156E + 01 1.8911E + 09 2.3274E + 01 1.0050E + 02 4.3517E + 00 9.9737E + 01 2.6675E + 00 9.9841E + 01 1.1425E + 02 1.5162E − 01 1.0663E + 10 9.9953E + 01
Std 1.2910E − 03 2.6512E + 01 6.1879E + 08 3.9863E + 01 5.0436E − 02 3.4150E + 00 4.7262E − 02 4.7089E + 00 2.3647E − 02 1.2634E + 01 2.6270E − 01 1.2335E + 09 4.3439E − 02
  • Note: The best results obtained are highlighted in bold.

Based on the data in Tables 6, 7, 8, and 9, MCOA achieves the optimal performance on 12 out of 13 50-dimensional problems (92.31%), substantially outperforming SMA (61.54%), COA (53.85%), AO (23.08%), ARO (23.08%), SCSO (23.08%), AOA (15.38%), SO (7.69%), and WHO (7.69%). For 100-dimensional problems, MCOA provides the best mean fitness and standard deviation results on 12 out of 13 (92.31%), higher than SMA (61.54%), COA (53.85%), AO (23.08%), ARO (23.08%), SCSO (23.08%), WHO (15.38%), SO (7.69%), and AOA (7.69%). For 500-dimensional problems, MCOA performs best on 12 out of 13 (92.31%), higher than SMA (61.54%), COA (53.85%), AO (23.08%), ARO (23.08%), SCSO (23.08%), SO (7.69%), and WHO (7.69%). Besides, in the extreme case of 1000 dimensions, MCOA shows the optimal performance on 11 out of 13 (84.62%), higher than SMA (61.54%), COA (53.85%), AO (30.77%), ARO (23.08%), SCSO (23.08%), SO (15.38%), and WHO (15.38%).

Regardless of the dimension extension, MCOA consistently delivers superior quality solutions on F5, F7, F12, and F13. SMA also performs very competitively, consistently ranking first on F8, ahead of MCOA. COA performs the same as MCOA on F1, F2,  F3,  F4,  F9,  F10, and F11, but the gap between them is still evident in other cases. Overall, MCOA provides reliable results with good convergence accuracy, even in the face of high-dimensional optimization tasks. Figure 11 illustrates the Friedman mean ranking of MCOA on the different dimensional benchmark functions. MCOA outperforms competitor algorithms by obtaining the ranking values of 1.0769, 1.1538, 1.2308, and 1.3077 for each dimension, respectively. This is because the specular reflection learning and vertical crossover strategy strengthen the exploration and exploitation of the proposed MCOA so that search agents can more effectively leverage the solution information to converge toward the global optimum in the complex search space.

Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
Friedman mean ranking of MCOA and comparison algorithms on 13 50-, 100-, 500-, and 1000-dimensional CEC2005 functions.

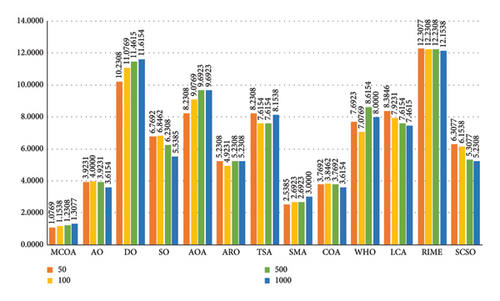
5.3. Comparison With Some Improved Peers on CEC2019 Functions

To further validate the superiority of the suggested optimizer, nine newly proposed improved MH algorithms are selected for comparison with MCOA on the CEC2019 test suite. These algorithms include simplified Aquila optimizer (IAO) [57], dynamic arithmetic optimization algorithm (DAOA) [58], weighted chimp optimization algorithm (WChOA) [59], dynamic multipopulation cooperative sand cat optimizer (DMSCSO) [60], enhanced hybrid arithmetic optimization algorithm (CSOAOA) [61], memetic Harris hawks optimization (EESHHO) [62], hybrid slime arithmetic optimization algorithm (RCLSMAOA) [63], improved hybrid Aquila optimizer and African vulture optimization algorithm (IHAOAVOA) [64], and multistrategy assisted chaotic coot-inspired optimization algorithm (COBHCOOT) [65], and their parameter settings are also consistent with the original literature, as shown in Table 10. All experimental algorithms run independently 30 times on each benchmark problem, and the statistical results obtained are reported in Table 11.

Table 10. Parameter settings for nine similar enhanced algorithms.
Algorithm Year Parameter value
IAO 2022 U = 0.00565; D1 = 10; ω = 0.005
DAOA 2022 α = 25; μ = 0.001
WChOA 2021 f = [2.5, 0]; M = Gauss chaptic value
DMSCSO 2023 G1 ∈ [−1, 1]; SM = 2; rG = [2, 0]
CSOAOA 2022 α = 5; μ = 0.499; δ ∈ [0.001, 0.01]
EESHHO 2021 sp ∈ (−1, 1); E0 ∈ (−1, 1)
RCLSMAOA 2023 z = 0.03; α = 5; μ = 0.499
IHAOAVOA 2022 L1 = 0.8; L2 = 0.2; w = 2.5; P2 = 0.4; P3 = 0.6; U = 0.00565; r = 10; ω = 0.005; k = 12000
COBHCOOT 2022 a ∈ [2, 0]; obllimit = 40
Table 11. Numerical results of MCOA and similar improved algorithms on CEC2019 functions.
Function Metrics MCOA IAO DAOA WChOA DMSCSO CSOAOA EESHHO RCLSMAOA IHAOAVOA COBHCOOT
CEC2019-01 Mean 4.4645E + 04 8.6003E + 04 1.1227E + 12 4.5689E + 05 4.1756E + 04 1.4226E + 09 4.6614E + 04 7.3761E + 09 4.6430E + 04 1.4625E + 07
Std 2.7046E + 03 2.0261E + 04 2.1436E + 12 2.5437E + 05 2.5833E + 03 2.5628E + 09 3.1545E + 03 3.7828E + 10 3.7448E + 03 5.0265E + 07
p value — 3.0199E − 11 1.4440E − 11 3.0199E − 11 1.1747E − 04 3.0199E − 11 1.3832E − 02 3.0199E − 11 6.5671E − 02 6.3560E-05
Rank 2 5 10 6 1 8 4 9 3 7
  
CEC2019-02 Mean 1.7343E + 01 1.7640E + 01 6.9013E + 02 1.7889E + 01 1.7343E + 01 1.7344E + 01 1.7343E + 01 1.7512E + 01 1.7343E + 01 1.7343E + 01
Std 4.0077E − 08 9.7073E − 02 2.7209E + 03 2.2181E − 01 3.0682E − 07 1.8588E − 03 5.6026E − 06 5.1845E − 01 9.5813E − 09 1.8464E-04
p value — 3.0199E − 11 2.3657E − 12 3.0199E − 11 5.4941E − 11 1.1674E − 05 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.0199E-11
Rank 2 8 10 9 3 6 4 7 1 5
  
CEC2019-03 Mean 1.2702E + 01 1.2704E + 01 1.2705E + 01 1.2706E + 01 1.2702E + 01 1.2702E + 01 1.2702E + 01 1.2705E + 01 1.2702E + 01 1.2702E + 01
Std 4.3564E − 12 6.6964E − 04 1.7414E − 03 5.1011E − 03 2.3179E − 12 6.2840E − 07 7.0348E − 08 1.4654E − 03 5.4143E − 10 4.6303E-09
p value — 2.5627E − 11 2.5562E − 11 2.5627E − 11 2.2605E − 02 5.1731E − 11 3.0799E − 02 2.5627E − 11 9.6986E − 03 2.5627E-11
Rank 2 7 9 10 1 6 5 8 3 4
  
CEC2019-04 Mean 3.6020E + 01 4.8204E + 03 2.9110E + 04 3.0950E + 04 1.0100E + 02 1.7584E + 02 5.8143E + 01 4.7296E + 03 1.2886E + 02 5.2437E + 01
Std 9.5968E + 00 1.5501E + 03 9.4946E + 03 9.5882E + 03 4.8510E + 01 1.8824E + 02 2.2925E + 01 1.0807E + 04 6.4910E + 01 3.0560E + 01
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 1.6132E − 10 2.0338E − 09 6.2828E − 06 5.0114E − 01 7.3803E − 10 2.7548E-03
Rank 1 8 9 10 4 6 3 7 5 2
  
CEC2019-05 Mean 1.1825E + 00 2.6168E + 00 7.7139E + 00 6.9314E + 00 1.1899E + 00 1.3907E + 00 1.3239E + 00 1.6896E + 00 1.4996E + 00 1.2925E + 00
Std 4.3591E − 02 3.1224E − 01 1.6181E + 00 8.8225E − 01 7.3195E − 02 3.7221E − 01 2.2619E − 01 1.1900E + 00 4.1011E − 01 1.4050E-01
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 7.0617E − 01 2.4994E − 03 1.1711E − 02 5.9706E − 05 2.1327E − 05 5.3221E-03
Rank 1 8 10 9 2 5 4 7 6 3
  
CEC2019-06 Mean 3.8593E + 00 1.1202E + 01 1.3773E + 01 1.2803E + 01 7.8885E + 00 4.6271E + 00 5.3835E + 00 8.7879E + 00 5.8631E + 00 1.0023E + 01
Std 1.0623E + 00 8.1330E − 01 7.3718E − 01 9.9492E − 01 1.4751E + 00 1.4992E + 00 5.7356E − 01 2.5150E + 00 1.2656E + 00 8.5608E-01
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 7.0881E − 08 8.7710E − 02 2.1540E − 06 8.3520E − 08 1.0233E − 01 3.0199E-11
Rank 1 8 10 9 5 2 3 6 4 7
  
CEC2019-07 Mean 4.5066E + 01 9.9622E + 02 1.7216E + 03 1.7468E + 03 2.3900E + 02 3.0158E + 01 1.6830E + 02 4.1793E + 02 3.3148E + 02 3.8035E + 02
Std 9.1662E + 01 1.8935E + 02 3.4996E + 02 2.7445E + 02 2.3317E + 02 7.2375E + 01 1.2917E + 02 3.1005E + 02 2.1905E + 02 1.6057E + 02
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 6.7650E − 05 3.8710E − 01 5.9706E − 05 3.6459E − 08 4.6856E − 08 9.7555E-10
Rank 2 8 9 10 4 1 3 7 5 6
  
CEC2019-08 Mean 4.7709E + 00 6.2775E + 00 7.4997E + 00 7.3817E + 00 4.4828E + 00 4.1402E + 00 5.2424E + 00 5.7837E + 00 5.5821E + 00 4.8103E + 00
Std 5.1785E − 01 4.0403E − 01 2.5622E − 01 3.8089E − 01 7.0073E − 01 4.2836E − 01 6.9350E − 01 8.1236E − 01 4.5325E − 01 8.3155E-01
p value — 4.0772E − 11 3.0199E − 11 3.0199E − 11 1.2235E − 01 3.1573E − 05 4.9818E − 04 4.4440E − 07 1.7294E − 07 8.3026E-01
Rank 3 8 10 9 2 1 5 7 6 4
  
CEC2019-09 Mean 2.7336E + 00 2.8929E + 02 6.4479E + 03 2.0028E + 03 3.8763E + 00 4.3604E + 00 3.6699E + 00 2.4067E + 02 4.2157E + 00 3.0458E + 00
Std 1.5881E − 01 1.5901E + 02 1.5525E + 03 4.1383E + 02 9.6176E − 01 1.2740E + 00 6.4502E − 01 9.3156E + 02 7.6410E − 01 5.3561E-01
p value — 3.0199E − 11 3.0123E − 11 3.0199E − 11 6.0104E − 08 1.2870E − 09 1.3111E − 08 1.6955E − 02 3.0199E − 11 8.6844E-03
Rank 1 8 10 9 4 6 3 7 5 2
  
CEC2019-10 Mean 1.9003E + 01 2.0393E + 01 2.0854E + 01 2.0786E + 01 1.9404E + 01 1.7428E + 01 1.9998E + 01 2.0259E + 01 1.9991E + 01 1.9038E + 01
Std 3.9762E + 00 3.7995E − 01 1.1840E − 01 1.0789E − 01 2.1881E + 00 6.1841E + 00 2.6367E − 02 2.2395E − 01 9.3851E − 02 5.0702E + 00
p value — 6.5277E − 08 3.0199E − 11 3.0199E − 11 1.7290E − 06 8.8830E − 01 1.8682E − 05 4.9752E − 11 6.5486E − 04 7.1186E-09
Rank 2 8 10 9 4 1 6 7 5 3
  
+/−/= — 10/0/0 10/0/0 10/0/0 8/2/0 7/3/0 10/0/0 9/1/0 8/2/0 9/1/0
Mean rank 1.7000 7.6000 9.7000 9.0000 3.0000 4.2000 4.0000 7.2000 4.3000 4.3000
Final ranking 1 8 10 9 2 4 3 7 5 5
  • Note: The best results obtained are highlighted in bold.

Table 11 demonstrates the superior performance of MCOA on the CEC2019 benchmark suite. MCOA achieves optimal convergence accuracy on 4 out of 10 functions (CEC2019-04, CEC2019-05, CEC2019-06, and CEC2019-09), while ranking second on CEC2019-01, CEC2019-02, CEC2019-03, CEC2019-07, and CEC2019-10, and third on CEC2019-08. Among competitors, DMSCSO, CSOAOA, and IHAOAVOA also deliver notable performance on selected benchmark functions. The Wilcoxon rank-sum test results, expressed as (+/−/=), reveal MCOA’s statistical dominance: it outperforms IAO, DAOA, WChOA, and EESHHO on all 10 problems (10/0/0), RCLSMAOA and COBHCOOT on nine problems (9/1/0), DMSCSO and IHAOAVOA on eight problems (8/2/0), and CSOAOA on seven problems (7/3/0). The Friedman test results show that MCOA receives the best average ranking of 1.7000, followed by DMSCSO and EESHHO. These experimental results demonstrate that MCOA can provide high-quality solutions even for complex numerical optimization challenges.

Figure 12 illustrates the convergence characteristics of MCOA, IAO, DAOA, WChOA, DMSCSO, CSOAOA, EESHHO, RCLSMAOA, IHAOAVOA, and COBHCOOT on the CEC2019 function. On CEC2019-01∼CEC2019-03, MCOA can quickly locate the desired region in the early iteration and then perform the exploration-to-exploitation transition for the precise search of the specified space. For CEC2019-04, CEC2019-06, and CEC2019-08, the convergence curves of MCOA exhibit distinctive step-like patterns, and the convergence accuracy continuously improves with the increase of iteration number, and it finally achieves the highest convergence accuracy among all comparison methods, which proves its excellent global exploration and local optimal avoidance capabilities.

Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
Convergence curves of MCOA and similar improved algorithms on CEC2019 functions.

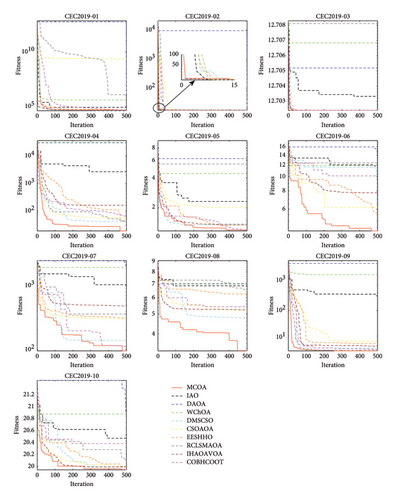
The stability analysis through boxplots in Figure 13 reveals that MCOA generates no outliers on CEC2019-01, CEC2019-02, and CEC2019-09, indicating excellent robustness. On CEC2019-05, the overall distribution of mean, maximum, and minimum values for MCOA is more concentrated than comparison algorithms. For CEC2019-03, CEC2019-04, CEC2019-07, and CEC2019-10, like the other methods, MCOA inevitably produced some outliers (+), which demonstrates that there is room for further improvement in the stability of MCOA. Generally, MCOA obtains more valuable interpretations and narrower box plots than other improved algorithms on most test functions.

Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
Boxplots of MCOA and similar improved algorithms on CEC2019 functions.

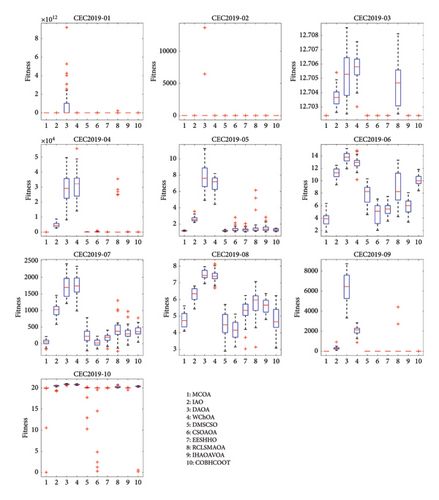
Table 12 presents the average computation time for 30 runs of each algorithm on the CEC2019 functions. It can be found that DAOA requires the least computational consumption, whereas our proposed MCOA is ranked fourth to last. Due to the introduction of several improvement strategies in MCOA, the optimization performance is improved at the expense of additional computational costs. On the whole, by taking some computational time in exchange for superior convergence accuracy, robustness, and local optimum avoidance, MCOA is acceptable, which coincides with the NFL theorem.

Table 12. Average runtime of MCOA and different improved algorithms on CEC2019 functions (unit: s).
Function MCOA IAO DAOA WChOA DMSCSO CSOAOA EESHHO RCLSMAOA IHAOAVOA COBHCOOT
CEC2019-01 0.8974 0.4329 0.1967 0.7003 0.6507 0.3770 0.1986 0.8030 0.4326 0.4496
CEC2019-02 0.2837 0.1141 0.0533 0.5789 0.4388 0.0998 0.0591 0.3290 0.1612 0.1652
CEC2019-03 0.1900 0.0923 0.0524 0.5861 0.4743 0.0842 0.0529 0.2825 0.1206 0.1232
CEC2019-04 0.2540 0.1095 0.0541 0.3653 0.2839 0.1021 0.0524 0.2599 0.1361 0.1302
CEC2019-05 0.1861 0.0943 0.0459 0.3674 0.2912 0.0981 0.0523 0.2624 0.1332 0.1108
CEC2019-06 1.4323 0.9400 0.4843 0.8326 1.4418 1.4073 0.4832 3.0530 1.5969 1.0859
CEC2019-07 0.1729 0.0911 0.0522 0.3501 0.2985 0.1124 0.0559 0.2813 0.1332 0.1029
CEC2019-08 0.1734 0.0889 0.0424 0.3551 0.2994 0.1008 0.0566 0.2802 0.1261 0.0987
CEC2019-09 0.1650 0.0802 0.0422 0.3620 0.2829 0.0907 0.0493 0.2403 0.1158 0.0989
CEC2019-10 0.1808 0.0808 0.0411 0.3346 0.2977 0.1026 0.0534 0.2702 0.1362 0.1051
  
Total runtime 3.9356 2.1242 1.0647 4.8323 4.7591 2.5751 1.1134 6.0618 3.0919 2.4705
  • Note: The best results obtained are highlighted in bold.

5.4. Comparison With Some Improved Peers on CEC2022 Functions

The IEEE CEC2022 test set contains 12 benchmark functions: unimodal, multimodal, hybrid, and composition. The search domains of these functions are more challenging and closer to real-world optimization problems than the previous benchmark problems. In the following, we will apply MCOA and the nine improved methods mentioned above to solve the CEC2022 benchmark functions. Table 13 summarizes the statistical results of each algorithm derived from 30 independent runs on the CEC2022 benchmark suite.

Table 13. Numerical results of MCOA and similar improved algorithms on CEC2022 functions.
Function Metrics MCOA IAO DAOA WChOA DMSCSO CSOAOA EESHHO RCLSMAOA IHAOAVOA COBHCOOT
CEC2022-01 Mean 5.4619E + 02 7.0153E + 03 2.0583E + 05 1.9711E + 04 5.6561E + 03 1.4213E + 03 5.8385E + 02 2.1356E + 03 4.7250E + 02 3.1160E + 02
Std 7.2414E + 02 4.7663E + 03 7.3674E + 05 3.3409E + 04 1.8002E + 03 8.4268E + 02 5.1018E + 02 1.0036E + 04 1.7303E + 02 1.2314E + 01
p value — 4.1191E − 01 3.0199E − 11 8.9934E − 11 7.3891E − 11 8.1527E − 11 3.0199E − 11 5.5727E − 10 3.0199E − 11 3.0199E − 11
Rank 3 8 10 9 7 5 4 6 2 1
  
CEC2022-02 Mean 4.0130E + 02 5.3125E + 02 4.1833E + 03 3.4114E + 03 4.1537E + 02 4.0510E + 02 4.2019E + 02 5.4172E + 02 4.1817E + 02 4.1190E + 02
Std 2.3691E + 00 8.0177E + 01 1.7246E + 03 1.4140E + 03 2.4052E + 01 1.7000E + 01 2.8388E + 01 4.9292E + 02 2.5833E + 01 1.9692E + 01
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 1.1747E − 04 5.2978E − 01 2.3885E − 04 8.8910E − 10 2.2539E − 04 1.4918E − 06
Rank 1 7 10 9 4 2 6 8 5 3
  
CEC2022-03 Mean 6.0161E + 02 6.3367E + 02 7.0167E + 02 6.8098E + 02 6.0519E + 02 6.0195E + 02 6.0835E + 02 6.0577E + 02 6.2682E + 02 6.0182E + 02
Std 7.3082E − 01 7.1698E + 00 1.7149E + 01 5.7724E + 00 3.5932E + 00 8.8014E + 00 7.8021E + 00 1.9555E + 01 1.2272E + 01 2.0253E + 00
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 2.3768E − 07 7.1186E − 09 2.5974E − 05 1.9963E − 05 3.0199E − 11 3.3285E − 01
Rank 1 8 10 9 4 3 6 5 7 2
  
CEC2022-04 Mean 8.1427E + 02 8.5159E + 02 9.2108E + 02 8.7534E + 02 8.2176E + 02 8.2446E + 02 8.2507E + 02 8.3266E + 02 8.2892E + 02 8.1350E + 02
Std 6.2931E + 00 7.2841E + 00 1.1218E + 01 7.1431E + 00 7.1065E + 00 7.2637E + 00 7.6197E + 00 1.7502E + 01 8.4220E + 00 5.1197E + 00
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 9.7917E − 05 5.8587E − 06 2.3168E − 06 6.0459E − 07 2.6015E − 08 7.5059E − 01
Rank 2 8 10 9 3 4 5 7 6 1
  
CEC2022-05 Mean 9.0003E + 02 1.1683E + 03 4.3285E + 03 2.0272E + 03 9.5169E + 02 1.1206E + 03 1.1514E + 03 1.2284E + 03 1.2971E + 03 9.0081E + 02
Std 1.0158E − 01 1.8490E + 02 1.0461E + 03 1.9073E + 02 4.1089E + 01 1.6228E + 02 1.5989E + 02 8.7634E + 02 1.7137E + 02 1.0143E + 00
p value — 3.0199E − 11 2.9991E − 11 3.0199E − 11 3.3384E − 11 3.0199E − 11 3.0199E − 11 3.6897E − 11 3.0199E − 11 9.7555E − 10
Rank 1 6 10 9 3 4 5 7 8 2
  
CEC2022-06 Mean 2.7432E + 03 9.5348E + 06 1.7124E + 09 6.1105E + 08 4.1618E + 03 3.2472E + 03 3.5592E + 03 8.9260E + 06 3.7268E + 03 5.8353E + 03
Std 7.6254E + 02 8.7967E + 06 1.2258E + 09 4.4254E + 08 2.1189E + 03 1.3498E + 03 1.9222E + 03 3.8615E + 07 1.6828E + 03 6.4003E + 03
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 6.7869E − 02 5.0114E − 01 6.1001E − 01 2.7548E − 03 5.5546E − 02 5.5611E − 04
Rank 1 8 10 9 5 2 3 7 4 6
  
CEC2022-07 Mean 2.2174E + 03 2.0814E + 03 2.2618E + 03 2.2528E + 03 2.0329E + 03 2.0222E + 03 2.0269E + 03 2.0362E + 03 2.0580E + 03 2.0299E + 03
Std 5.0147E + 00 1.2905E + 01 5.8495E + 01 7.1837E + 01 1.0226E + 01 1.4310E + 01 1.6216E + 01 2.2348E + 01 3.0551E + 01 9.8930E + 00
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 6.5277E − 08 1.1536E − 02 1.0576E − 03 2.8790E − 06 4.1997E − 10 6.5261E − 07
Rank 1 8 10 9 5 2 3 6 7 4
  
CEC2022-08 Mean 2.2181E + 03 2.2410E + 03 4.7021E + 03 4.1903E + 03 2.2223E + 03 2.2185E + 03 2.2202E + 03 2.2534E + 03 2.2264E + 03 2.2249E + 03
Std 2.7113E + 00 5.9518E + 00 5.3602E + 03 8.3183E + 03 3.3018E + 00 6.1266E + 00 5.3535E + 00 5.1941E + 01 3.7604E + 00 5.2226E + 00
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 5.2650E − 05 1.6238E − 01 9.3519E − 01 6.7220E − 10 2.3715E − 10 1.4733E − 07
Rank 1 7 10 9 4 2 3 8 6 5
  
CEC2022-09 Mean 2.5293E + 03 2.6600E + 03 3.1096E + 03 3.2560E + 03 2.5379E + 03 2.5314E + 03 2.5348E + 03 2.5954E + 03 2.5406E + 03 2.5293E + 03
Std 4.0855E − 02 3.8420E + 01 2.4863E + 02 2.4635E + 02 2.8251E + 01 3.4716E + 00 1.1247E + 01 1.0729E + 02 1.3815E + 01 3.2935E − 02
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 3.1830E − 01 1.7666E − 03 3.0339E − 03 3.0199E − 11 1.5638E − 02 5.0120E − 03
Rank 2 8 9 10 5 3 4 7 6 1
  
CEC2022-10 Mean 2.5037E + 03 2.5713E + 03 3.5873E + 03 3.8978E + 03 2.5384E + 03 2.5507E + 03 2.5711E + 03 2.6300E + 03 2.5638E + 03 2.5379E + 03
Std 1.8250E + 01 8.1884E + 01 8.5524E + 02 8.4885E + 02 5.8853E + 01 6.3005E + 01 6.3079E + 01 1.9545E + 02 6.4392E + 01 5.4042E + 01
p value — 7.0430E − 07 4.1997E − 10 1.7769E − 10 2.3885E − 04 2.2658E − 03 4.1178E − 06 1.4918E − 06 1.1567E − 07 8.3026E − 01
Rank 1 7 9 10 3 4 6 8 5 2
  
CEC2022-11 Mean 2.6003E + 03 2.8478E + 03 4.7517E + 03 4.4270E + 03 2.6659E + 03 2.6354E + 03 2.7828E + 03 2.8801E + 03 2.7056E + 03 2.6788E + 03
Std 1.8480E − 01 8.6038E + 01 7.5824E + 02 3.5935E + 02 1.0495E + 02 1.0284E + 02 1.9962E + 02 6.1461E + 02 1.8242E + 02 1.5665E + 02
p value — 6.0104E − 08 3.0199E − 11 3.0199E − 11 2.9727E − 01 2.5721E − 07 6.8432E − 01 2.6243E − 03 8.5000E − 02 3.9648E − 08
Rank 1 7 10 9 3 2 6 8 5 4
  
CEC2022-12 Mean 2.8622E + 03 2.8739E + 03 3.1984E + 03 3.2648E + 03 2.8684E + 03 2.8673E + 03 2.8773E + 03 2.8766E + 03 2.8718E + 03 2.8641E + 03
Std 1.2103E + 00 2.5682E + 00 1.2713E + 02 1.4063E + 02 6.5321E + 00 6.5020E + 00 1.5807E + 01 1.9451E + 01 1.0634E + 01 1.5020E + 00
p value — 3.0199E − 11 3.0199E − 11 3.0199E − 11 1.4643E − 10 3.5201E − 07 3.0199E − 11 9.9186E − 11 1.8567E − 09 1.6062E − 06
Rank 1 6 9 10 4 3 8 7 5 2
  
+/−/= — 11/1/0 12/0/0 12/0/0 9/3/0 9/3/0 9/3/0 12/0/0 11/1/0 10/2/0
Mean rank 1.3333 7.3333 9.7500 9.2500 4.1667 3.0000 4.9167 7.0000 5.5000 2.7500
Final ranking 1 8 10 9 4 3 5 7 6 2
  • Note: The best results obtained are highlighted in bold.

As can be seen in Table 13, MCOA achieves the optimal results on 9 out of 12 CEC2022 functions, including CEC2022-02, CEC2022-03, CEC2022-05, CEC2022-06, CEC2022-07, CEC2022-08, CEC2022-10, CEC2022-11, and CEC2022-12, whereas COBHCOOT provides the best performance on the remaining functions. In most multimodal, hybrid, and composite test cases, the convergence accuracy and stability of MCOA are more reliable than those of other comparison algorithms. On CEC2022-04 and CEC2022-09, MCOA is slightly behind COBHCOOT in second place, but the outcomes of both are still very close. This demonstrates that the expanded exploration strategy, specular reflection learning, and vertical crossover operator comprehensively enhance the exploration and local optimal avoidance ability of MCOA. From a statistical standpoint, MCOA significantly outperforms IAO on 11 problems, DAOA on 12 problems, WChOA on 12 problems, DMSCSO on 9 problems, CSOAOA on 9 problems, EESHHO on 9 problems, RCLSMAOA on 12 problems, IHAOAVOA on 11 problems, and COBHCOOT on 10 issues. The Friedman test results show that MCOA receives the best average ranking of 1.3333, followed by COBHCOOT and CSOAOA. MCOA can satisfactorily address highly intricate numerical optimization challenges.

Figure 14 shows the convergence curves of MCOA and competing algorithms on CEC2022 functions. MCOA can fulfill a smooth transition between exploration and exploitation in the initial stage of iteration on most test functions, and the final convergence accuracy is effectively guaranteed. These features are particularly demonstrated on CEC2022-03 and CEC2022-04. In contrast, algorithms such as DAOA and WChOA often exhibit poor solution accuracy due to their weak local optimal avoidance, which makes it difficult to explore the complex search domain in depth. These convergence patterns reaffirm the competitive advantage of MCOA in both convergence speed and accuracy.

Details are in the caption following the image
Figure 14
Open in figure viewerPowerPoint
Convergence curves of MCOA and similar improved algorithms on CEC2022 functions.

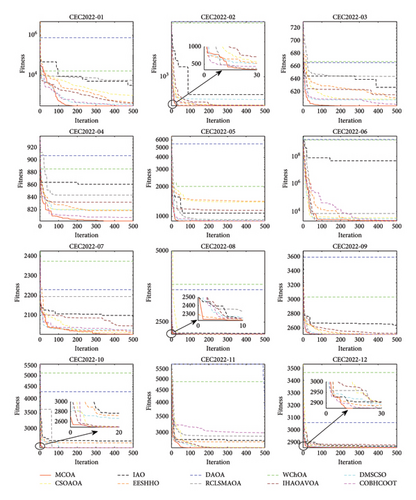
Figure 15 illustrates the boxplots of different algorithms on the IEEE CEC2022 test suite. MCOA generates no outliers on CEC2022-01, CEC2022-06, CEC2022-11, and CEC2022-12, and the data results are highly consistent. For the remaining test problems, MCOA also yields a few outliers, but compared to peer algorithms, its boxplots are narrower and the median, maximum, and minimum values are more concentrated. Compared to the CEC2019 experimental results, the performance of MCOA on the CEC2022 benchmark set is more impressive. Consequently, our proposed method can be expected to maintain good robustness even when confronted with more difficult numerical optimization issues.

Details are in the caption following the image
Figure 15
Open in figure viewerPowerPoint
Boxplots of MCOA and similar improved algorithms on CEC2022 functions.

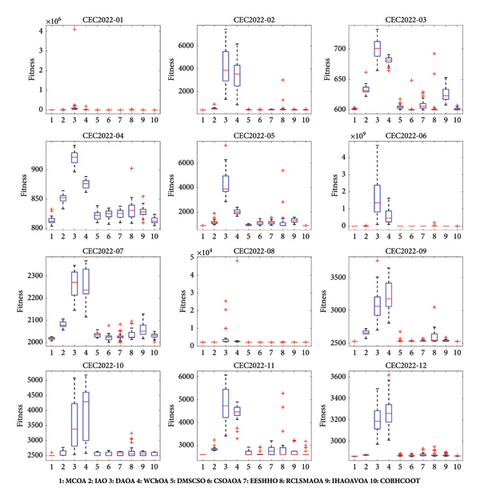
Table 14 presents the average computation time for each algorithm on the CEC2022 functions. The algorithms rank as follows in terms of computational efficiency: DAOA < EESHHO < IAO < COBHCOOT < CSOAOA < IHAOAVOA < MCOA < DSMSCSO < RCLSMAOA < WChOA. There is no doubt that DAOA wins by virtue of requiring the least amount of runtime, but its numerical optimization performance still needs to improve. Taking the above statistical results together, the advantages and limitations of MCOA are acceptable. While consuming slightly more computational time, MCOA provides high-quality and reliable solutions. With the continued advancement of cloud computing, distributed computing, and big data technologies, the computational requirements of MCOA have become increasingly feasible, making it particularly well-suited for intelligent optimization applications where high accuracy is paramount.

Table 14. Average runtime of MCOA and different improved algorithms on CEC2022 functions (unit: s).
Function MCOA IAO DAOA WChOA DMSCSO CSOAOA EESHHO RCLSMAOA IHAOAVOA COBHCOOT
CEC2022-01 0.5126 0.3261 0.1456 1.2956 0.6575 0.2535 0.2172 0.7032 0.3562 0.3320
CEC2022-02 0.2629 0.1038 0.0432 0.4081 0.3114 0.1143 0.0584 0.2750 0.1585 0.1559
CEC2022-03 0.2690 0.1183 0.0518 0.3819 0.3332 0.1617 0.0723 0.3462 0.1798 0.1729
CEC2022-04 0.2405 0.1185 0.0493 0.4124 0.3100 0.1072 0.0506 0.2833 0.1664 0.1535
CEC2022-05 0.1910 0.0893 0.0396 0.3535 0.2896 0.1129 0.0556 0.3051 0.1563 0.1431
CEC2022-06 0.2255 0.1171 0.0488 0.4670 0.3720 0.1213 0.0637 0.3093 0.1664 0.1550
CEC2022-07 0.2801 0.1454 0.0687 0.4384 0.3977 0.2183 0.0927 0.5195 0.2310 0.1682
CEC2022-08 0.3301 0.1670 0.0760 0.4213 0.4280 0.2447 0.1048 0.5867 0.2875 0.1980
CEC2022-09 0.2780 0.1385 0.0634 0.4319 0.3816 0.1862 0.0880 0.4773 0.2243 0.1732
CEC2022-10 0.2588 0.1281 0.0628 0.4172 0.3797 0.1696 0.0781 0.3995 0.1948 0.1471
CEC2022-11 0.3448 0.1660 0.0808 0.4845 0.4766 0.2719 0.1098 0.5704 0.2817 0.2020
CEC2022-12 0.3580 0.1895 0.0950 0.5000 0.5089 0.3042 0.1219 0.6051 0.2879 0.2033
  
Total runtime 3.5513 1.8076 0.8251 6.0119 4.8463 2.2658 1.1130 5.3807 2.6907 2.2042
  • Note: The best results obtained are highlighted in bold.

5.5. Summary of CEC Benchmark Experiments

In this section, we comprehensively validate the effectiveness of MCOA on 23 classic functions, the CEC2019 benchmark set, and the CEC2022 benchmark set. The numerical optimization performance of our proposed method is compared with 12 recently proposed MH algorithms and nine improved variants. The main findings are as follows:
  • •

    When the scale factor αF = 0.06, the Lévy flight strategy can more sufficiently strengthen the local search efficiency of MCOA and help circumvent local optima.

  • •

    For the 23 classic benchmark functions, MCOA provides the optimal solutions on 21 of them. As dimensionality increases, MCOA performs best on 12 out of 13 variable-dimensional benchmark functions in 50 dimensions, 12 out of 13 in 100 dimensions, 12 out of 13 in 500 dimensions, and 11 out of 13 in 1000 dimensions. On the CEC2019 test set, MCOA achieves the best convergence accuracy on 4 out of 10 functions. And on the CEC2022 test set, MCOA obtains the optimal average fitness results on 9 out of 12 functions.

  • •

    Compared to the original COA, the Wilcoxon rank-sum test and the Friedman ranking test suggest that MCOA exhibits significant enhancements in both exploration and exploitation capabilities. Through convergence curves and boxplot analysis, we confirm that MCOA possesses better convergence patterns and robustness than state-of-the-art improved methods such as DAOA, WChOA, DMSCSO, CSOAOA, EESHHO, RCLSMAOA, IHAOAVOA, and COBHCOOT.

The reasons behind these results can be understood from the ablation analysis in Section 5.2.3. Each improvement strategy enhances the algorithm’s search capabilities to some extent. The specular reflection learning enriches population diversity, the expanded exploration strategy boosts exploration trends, and the Lévy flight and vertical crossover operator enable MCOA to achieve more efficient local exploration and better local optima avoidance. The collaborative operation of these strategies achieves a more robust exploration–exploitation balance. Of course, according to the NFL theorem, no single algorithm can solve all optimization problems. Therefore, there is still room for improvement in the numerical results of MCOA on certain functions. However, in terms of overall performance, the proposed method significantly outperforms the comparison algorithms.

6. MCOA for Real-World Optimization Challenges

In this section, we evaluate the applicability of the proposed MCOA in solving two types of real-world optimization challenges: constrained engineering design and UAV path planning under complex terrain.

Constrained engineering design problems represent significant optimization challenges characterized by multiple design variables subject to various constraints. These problems require finding optimal designs that minimize objectives like cost or weight while meeting performance requirements and physical limitations. The complexity arises from nonlinear objective functions, intricate constraint interactions, and discontinuous search spaces. Our selected engineering design cases span mechanical and structural engineering domains. Traditional gradient-based methods often struggle with these problems due to their vulnerability to local optima and sensitivity to initial conditions.

UAV path planning involves determining optimal flight trajectories while balancing multiple conflicting objectives under various constraints. This task is particularly challenging due to several factors: UAVs must navigate three-dimensional environments while minimizing energy usage, flight time, and risk; they must avoid various obstacles including buildings, terrain features, and restricted airspace; they are constrained by physical limitations such as turning radius, climb rate, and velocity bounds; and they must account for environmental uncertainties like wind conditions. By applying MCOA to these complex path planning scenarios, we aim to demonstrate its ability to effectively balance exploration and exploitation while producing safe, efficient flight paths, thereby validating the algorithm’s practical effectiveness in solving real-world optimization challenges.

6.1. Constrained Engineering Design Cases

The mathematical model of a constrained minimization design problem is described below:
()
where is the solution for a particular problem, m represents the number of equality constraints, and l denotes the number of inequality constraints. To convert the constrained optimization problem into an unconstrained optimization problem for feasible solutions, the penalty function method [66] is used. This method linearly weights the nonlinear constraints and the cost function as follows:
()
where ω1 and ω2 represent the weight coefficients for inequality constraints and equality constraints, respectively.

The maximum iterations and population size for each algorithm are fixed at 500 and 30, respectively, with other parameter settings aligning with the numerical experiments. Seven nonlinear engineering design cases with constraints are to be settled, including tension/compression spring design, three-bar truss design, I-beam design, welded beam design, tubular column design, cantilever beam design, and piston lever design. The optimal outcomes derived from 30 independent runs for each scenario are documented in the subsequent subsections.

6.1.1. Case 1: Tension/Compression Spring Design

The objective of this design optimization case is to minimize the weight of a tension/compression spring while adhering to constraints related to the outer diameter, deflection, shear stress, and surge frequency, as illustrated in Figure 16. This problem contains three decision variables to be optimized, namely: wire diameter d(z1), average coil diameter D(z2), and the number of active coils N(z3), which are mathematically described in Appendix B.1.

Details are in the caption following the image
Figure 16
Open in figure viewerPowerPoint
Tension/compression spring design.

Twelve well-regarded MH algorithms (AO, DO, SO, AOA, ARO, TSA, SMA, COA, WHO, LCA, RIME, and SCSO), as well as nine latest enhanced optimizers (IAO, DAOA, WChOA, DMSCSO, CSOAOA, EESHHO, RCLSMAOA, IHAOAVOA, and COBHCOOT), are employed in parallel with MCOA to solve this case. The optimal solution and corresponding fitness values are summarized in Table 15. Notably, the proposed MCOA gets the first place, followed by WHO and SCSO. When d, D, and N are set to 0.05167105, 0.35628458, and 11.31440584, respectively, the tension/compression spring attains the minimum weight .

Table 15. Results of tension/compression spring design optimization.
Algorithm Variables Minimum weight Ranking
d(z1) D(z2) N(z3)
MCOA 0.05167105 0.35628458 11.31440584 0.01266524 1
AO 0.05000000 0.31595975 15.00000000 0.01342829 22
DO 0.05133183 0.34818407 11.80739683 0.01266759 9
SO 0.05186491 0.36096301 11.04435110 0.01266580 4
AOA 0.05000000 0.31049611 15.00000000 0.01319608 20
ARO 0.05157676 0.35400927 11.45355090 0.01266950 10
TSA 0.05000000 0.31532124 14.40123918 0.01292915 19
SMA 0.05137080 0.34910910 11.74939627 0.01266711 8
COA 0.05147564 0.35151492 11.61113327 0.01267773 13
WHO 0.05161011 0.35482133 11.40101877 0.01266535 2
LCA 0.05122637 0.34566146 11.97493341 0.01267617 12
RIME 0.05135404 0.34827829 11.82414583 0.01269737 16
SCSO 0.05178942 0.35913701 11.14855524 0.01266544 3
IAO 0.05035335 0.32531706 13.53811473 0.01281628 18
DAOA 0.05000000 0.31066615 15.00000000 0.01320331 21
WChOA 0.05196913 0.36349280 10.90257816 0.01266669 7
DMSCSO 0.05143710 0.35068643 11.65155381 0.01266642 6
CSOAOA 0.05142417 0.35028906 11.69044107 0.01268173 15
EESHHO 0.05246541 0.37568373 10.25791202 0.01267608 11
RCLSMAOA 0.05348341 0.40144043 9.07920539 0.01272237 17
IHAOAVOA 0.05189182 0.36161528 11.00751058 0.01266598 5
COBHCOOT 0.16751103 0.78491026 14.60163778 0.01267903 14
  • Note: The best results obtained are highlighted in bold.

6.1.2. Case 2: Three-Bar Truss Design

The three-bar truss design problem is a representative optimization challenge in civil engineering, aiming to determine the optimal cross-sectional areas A1(z1) and A2(z2) under stress constraints, with the objective of minimizing the weight of the truss. Figure 17 illustrates the geometric structure of the three-bar truss and its three design variables. The mathematical formulation is provided in Appendix B.2.

Details are in the caption following the image
Figure 17
Open in figure viewerPowerPoint
Three-bar truss design.

Table 16 reports the optimal variable values and minimum weight obtained by each algorithm. MCOA, WHO, and CSOAOA are tied for first place among all the methods since they achieve the same minimum weight of 263.89584338. This result underscores the significant potential of MCOA in addressing this design challenge.

Table 16. Results of three-bar truss design optimization.
Algorithm Variables Minimum weight Ranking
A1(z1) A2(z2)
MCOA 0.78867718 0.40824250 263.89584338 1
AO 0.79295948 0.39673649 263.95646038 20
DO 0.78871402 0.40813840 263.89585293 8
SO 0.78868121 0.40823111 263.89584340 4
AOA 0.79417556 0.39322975 263.94974417 19
ARO 0.78866861 0.40826675 263.89584347 5
TSA 0.78276042 0.42544590 263.94267196 18
SMA 0.79283189 0.39895776 264.14249804 21
COA 0.78808321 0.40992669 263.89626240 13
WHO 0.78867512 0.40824833 263.89584338 1
LCA 0.78894134 0.40750072 263.89638119 14
RIME 0.78944190 0.40609388 263.89727480 15
SCSO 0.78914618 0.40691768 263.89601349 11
IAO 0.78833875 0.40921561 263.89743149 16
DAOA 0.79556463 0.40033693 265.05335225 22
WChOA 0.79398989 0.39341972 263.91622699 17
DMSCSO 0.78877971 0.40795259 263.89585141 7
CSOAOA 0.78867513 0.40824829 263.89584338 1
EESHHO 0.78873817 0.40807003 263.89584630 6
RCLSMAOA 0.78854867 0.40860612 263.89585514 9
IHAOAVOA 0.78846959 0.40882998 263.89587445 10
COBHCOOT 0.78923502 0.40666828 263.89621512 12
  • Note: The best results obtained are highlighted in bold.

6.1.3. Case 3: I-Shaped Beam Design

This design problem aims to keep the vertical deflection of an I-shaped beam as low as possible without violating the conditions of the horizontal load (Q) and design load (P) acting at the midpoint of the span. As illustrated in Figure 18, flange width b(z1), section height h(z2), web thickness tw(z3), and flange thickness tf(z4) are the four critical design variables that need to be estimated in this case. The vertical deflection of the I-shaped beam is calculated using the formula PL3/(48EI), where L represents the length of the beam equal to 5200 cm and E denotes the elastic modulus of 523.104 kN/cm2. Mathematically, the design of an I-shaped beam is represented in Appendix B.3.

Details are in the caption following the image
Figure 18
Open in figure viewerPowerPoint
I-shaped beam design.

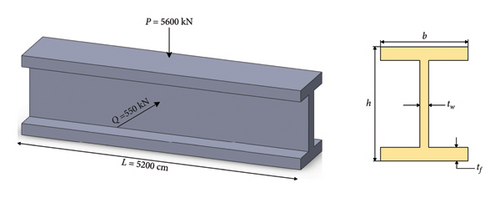
Table 17 shows the numerical results of I-shaped beam design optimization. MCOA and IHAOAVOA yield the same optimal weight , jointly ranking first among all the optimization methods. Hence, it is reasonable to conclude that MCOA is well-suited for effectively resolving this problem.

Table 17. Results of I-shaped beam design optimization.
Algorithm Variables Minimum fitness Ranking
b (z1) h (z2) tw (z3) tf (z4)
MCOA 80.00000000 50.00000000 0.90000000 2.32179226 0.0130741189 1
AO 80.00000000 50.00000000 0.90000000 2.32173276 0.0130744025 11
DO 80.00000000 50.00000000 0.90000000 2.32179221 0.0130741191 3
SO 80.00000000 50.00000000 0.90000000 2.32178743 0.0130741419 8
AOA 80.00000000 50.00000000 0.90000000 2.32063163 0.0130796529 20
ARO 79.99956079 49.98710956 0.90003420 2.32234738 0.0130746747 13
TSA 80.00000000 50.00000000 0.90000000 2.32166970 0.0130747031 14
SMA 80.00000000 49.99998053 0.90000000 2.32179304 0.0130741199 5
COA 80.00000000 49.99996196 0.90000010 2.32179378 0.0130741206 6
WHO 80.00000000 50.00000000 0.90000000 2.32146225 0.0130756919 16
LCA 80.00000000 50.00000000 0.90000000 2.32178183 0.0130741686 9
RIME 80.00000000 50.00000000 0.90000000 2.32177680 0.0130741926 10
SCSO 80.00000000 49.75404110 0.90000000 2.33348132 0.0130776237 18
IAO 80.00000000 50.00000000 0.90000000 2.32035321 0.0130809812 21
DAOA 80.00000000 50.00000000 0.90000000 2.31982154 0.0130835184 22
WChOA 80.00000000 50.00000000 0.90000000 2.32179216 0.0130741194 4
DMSCSO 79.99888209 49.96502190 0.90000266 2.32345566 0.0130749661 15
CSOAOA 80.00000000 50.00000000 0.90000000 2.32114115 0.0130772228 17
EESHHO 80.00000000 50.00000000 0.90017691 2.32165611 0.0130745521 12
RCLSMAOA 80.00000000 49.98296942 0.90166652 2.32131856 0.0130784250 19
IHAOAVOA 80.00000000 50.00000000 0.90000000 2.32179226 0.0130741189 1
COBHCOOT 80.00000000 40.97785551 1.48603832 1.82250020 0.0130741217 7
  • Note: The best results obtained are highlighted in bold.

6.1.4. Case 4: Welded Beam Design

The purpose of the welded beam design challenge is to minimize the fabrication cost of a welded beam subject to the constraints on shear stress τ, buckling load Pc, bending stress θ, and end deflection δ. As depicted in Figure 19, four design variables require optimization: the weld width h(z1), the length of clamped beam l(z2), the height of beam t(z3), and the thickness of beam b(z4). Its mathematical model is presented in Appendix B.4.

Details are in the caption following the image
Figure 19
Open in figure viewerPowerPoint
Welded beam design.

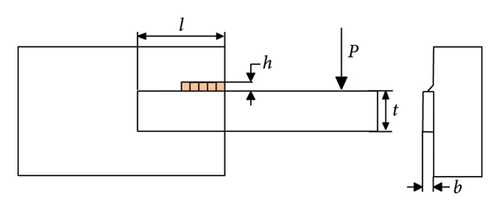
Table 18 presents the optimal solutions and the corresponding fitness values achieved by different algorithms for the welded beam design. According to the tabulated data, the proposed method provides a better outcome than the remaining competitor algorithms. The minimum fabrication cost of MCOA is 1.69276826 when the values of h, l, t, and b are fixed to 0.20572964, 3.23491931, 9.03662391, and 0.20572964, respectively. MCOA demonstrates a more pronounced advantage in welded beam design.

Table 18. Results of welded beam design optimization.
Algorithm Variables Minimum cost Ranking
h(z1) l(z2) t(z3) b(z4)
MCOA 0.20572964 3.23491931 9.03662391 0.20572964 1.69276826 1
AO 0.21243450 3.19396666 8.87672213 0.21627365 1.74729423 16
DO 0.20571591 3.23535159 9.03662766 0.20573020 1.69281177 3
SO 0.20575334 3.23467548 9.03611122 0.20575358 1.69286179 5
AOA 0.16808434 3.74244228 10.00000000 0.20157933 1.83746280 21
ARO 0.20573974 3.23491504 9.03648462 0.20574048 1.69283996 4
TSA 0.18457418 3.64640566 9.21662122 0.20659936 1.75379380 17
SMA 0.20565051 3.23681869 9.03671035 0.20572983 1.69292674 6
COA 0.20564335 3.23768156 9.03931468 0.20572985 1.69347815 7
WHO 0.20614114 3.23881826 9.02655447 0.20619428 1.69566604 12
LCA 0.20533297 3.24533696 9.03755601 0.20573492 1.69380127 9
RIME 0.19731885 3.42042334 9.03068700 0.20600764 1.70630471 14
SCSO 0.22165273 3.07754403 8.69532968 0.22690525 1.78806280 19
IAO 0.19909152 3.38305446 9.05196850 0.21222536 1.75471456 18
DAOA 0.13140212 6.04504374 9.32653815 0.23795146 2.25549059 22
WChOA 0.17532672 4.05852977 9.63981107 0.20290428 1.83714935 20
DMSCSO 0.20546452 3.23373175 9.05164428 0.20565482 1.69421763 11
CSOAOA 0.20572841 3.23494311 9.03664859 0.20572952 1.69277299 2
EESHHO 0.20527672 3.24579385 9.03318141 0.20588647 1.69416970 10
RCLSMAOA 0.19012164 3.66191333 9.00989425 0.20695213 1.73061646 15
IHAOAVOA 0.20335892 3.28334933 9.03899708 0.20571780 1.69616360 13
COBHCOOT 0.16686851 8.18455175 6.74641513 0.37202703 1.69375249 8
  • Note: The best results obtained are highlighted in bold.

6.1.5. Case 5: Tubular Column Design

The tubular column optimization involves designing a uniform column with a tubular cross section to support an axial load P at minimum cost, as depicted in Figure 20. The column is constructed from a material with the elastic modulus of E = 0.85 × 106 kgf/cm2 and the yield stress of σy = 500 kgf/cm2. In this problem, two optimal parameters need to be identified: the column’s mean diameter d(z1) and tube thickness t(z2). The mathematical model for this case can be found in Appendix B.5.

Details are in the caption following the image
Figure 20
Open in figure viewerPowerPoint
Tubular column design.

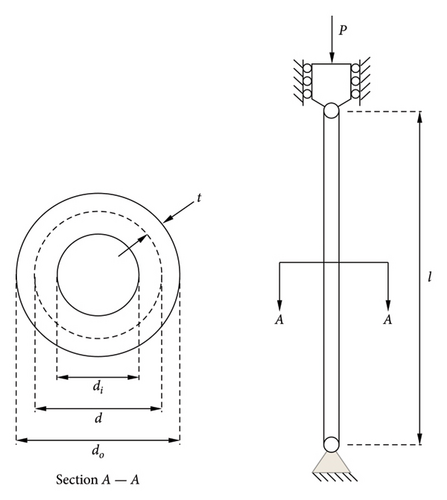
Table 19 presents a comparison of the optimal decision variables and the minimum cost acquired through MCOA and various optimization methodologies for this design scenario. MCOA, ARO, WHO, and CSOAOA are all ranked first, with a minimum fitness value of 26.48636147, proving the suggested optimizer’s favorable competition in solving the tubular column design. On the other hand, there are still some gaps between other comparison methods and MCOA regarding solution accuracy.

Table 19. Results of tubular column design optimization.
Algorithm Variables Minimum cost Ranking
d(z1) t(z2)
MCOA 5.45218074 0.29162643 26.48636147 1
AO 5.44347115 0.29343537 26.54055044 20
DO 5.45218124 0.29162643 26.48636369 7
SO 5.45226239 0.29162743 26.48681171 12
AOA 5.53203767 0.29428059 27.01819425 21
ARO 5.45218074 0.29162643 26.48636147 1
TSA 5.44987539 0.29237177 26.51497022 19
SMA 5.45218741 0.29162625 26.48638448 9
COA 5.45219635 0.29162571 26.48639886 10
WHO 5.45218074 0.29162643 26.48636147 1
LCA 5.45240618 0.29163330 26.48782385 13
RIME 5.45635450 0.29142165 26.49568712 15
SCSO 5.46033217 0.29119111 26.50266612 17
IAO 5.44688475 0.29255452 26.51017508 18
DAOA 5.21392106 0.35658628 28.64812652 22
WChOA 5.44954872 0.29204599 26.49598222 16
DMSCSO 5.45218072 0.29162643 26.48636153 5
CSOAOA 5.45218074 0.29162643 26.48636147 1
EESHHO 5.45218252 0.29162633 26.48636504 8
RCLSMAOA 5.44963078 0.29203288 26.49568114 14
IHAOAVOA 5.45218035 0.29162650 26.48636347 6
COBHCOOT 4.95225730 0.47328918 26.48645977 11
  • Note: The best results obtained are highlighted in bold.

6.1.6. Case 6: Cantilever Beam Design

This structural design case focuses on optimizing the total weight of a cantilever beam. The cantilever beam comprises five hollow elements with a square cross section, rigidly supported at the first element, whereas a given vertical force is applied at the fifth element, as illustrated in Figure 21. The width of each beam element zi(i = 1, 2, …, 5) represents a design variable, and the thickness is held constant. The mathematical definition of this problem is outlined in Append B.6.

Details are in the caption following the image
Figure 21
Open in figure viewerPowerPoint
Cantilever beam design.

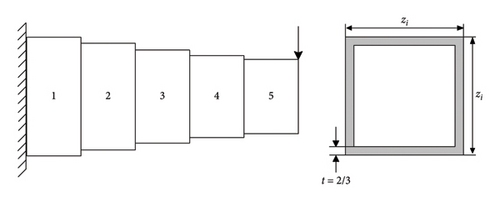
The values of the optimized decision variables and the minimum weight for each algorithm are recorded in Table 20. From the results, MCOA outperforms all other competitors as it reveals a minimum weight of 1.33995767. Thus, MCOA performs an excellent optimization effect in addressing this engineering issue.

Table 20. Results of cantilever beam design optimization.
Algorithm Variables Minimum weight Ranking
z1 z2 z3 z4 z5
MCOA 6.01738279 5.31234147 4.48996478 3.50367197 2.15031959 1.33995767 1
AO 6.14811254 5.42142456 4.33757745 3.39423369 2.20855305 1.34221784 16
DO 6.01762482 5.30410695 4.52306027 3.50375732 2.12663244 1.34005134 9
SO 6.01972060 5.30356939 4.49369427 3.50737041 2.14943104 1.33996423 3
AOA 8.52009058 8.42615912 3.76122853 2.88700239 2.21182768 1.61031364 22
ARO 6.03756468 5.30432522 4.49047601 3.48947675 2.15208679 1.33997320 4
TSA 5.87753978 5.37888456 4.59208953 3.55140060 2.09503293 1.34128472 15
SMA 6.05850070 5.28268294 4.47962105 3.50631853 2.14800134 1.34004777 8
COA 6.00520946 5.32041324 4.48771156 3.49455178 2.16609664 1.33997652 5
WHO 6.02081916 5.31398285 4.48273285 3.50121199 2.15499432 1.33996145 2
LCA 6.02735882 5.29169389 4.50381919 3.49978367 2.15145657 1.33998460 7
RIME 5.74255302 5.48713349 4.77903079 3.37354957 2.17885297 1.34541388 17
SCSO 6.00614912 6.12385869 3.70253473 4.21419281 2.23571179 1.39042470 20
IAO 6.05733849 5.36905293 4.23904778 3.37690985 2.79266084 1.36250462 19
DAOA 8.86752494 4.47381323 3.71699050 5.22980815 2.47384114 1.54514742 21
WChOA 6.48005691 5.03920848 4.39817327 4.05385796 1.84866637 1.36156569 18
DMSCSO 5.95853366 5.20753982 4.56652756 3.50006980 2.25821669 1.34103138 13
CSOAOA 5.98703556 5.30867170 4.57331357 3.45516758 2.15370757 1.34022071 10
EESHHO 5.95126828 5.28559554 4.48479298 3.55423371 2.20328082 1.34030029 11
RCLSMAOA 6.00475844 5.28040681 4.37282991 3.63757109 2.19711311 1.34114319 14
IHAOAVOA 6.00811900 5.22698247 4.54671389 3.49683956 2.20094645 1.34032713 12
COBHCOOT 3.96524768 16.03706041 71.10635175 25.30585626 21.97619575 1.33997974 6
  • Note: The best results obtained are highlighted in bold.

6.1.7. Case 7: Piston Lever Design

The last test case pertains to the design of a piston lever, wherein the ultimate target is to locate the optimal values of four design variables H(z1), B(z2), D(z3), X(z4) for different piston components so as to minimize the amount of oil required to lift the piston lever from 0° to 45°, as can be seen in Figure 22. This problem is mathematically formulated in Appendix B.7.

Details are in the caption following the image
Figure 22
Open in figure viewerPowerPoint
Piston lever design.

Table 21 summarizes the minimum cost and the four corresponding variables of MCOA and other comparative optimization methods. The tabulated data highlight MCOA as the most effective optimizer for tackling the piston lever design case, as it reveals the best design with the minimum cost . Based on these results, MCOA provides a superior solution for the piston lever design.

Table 21. Results of piston lever design optimization.
Algorithm Variables Minimum cost Ranking
H (z1) B (z2) D (z3) X (z4)
MCOA 0.05000000 2.04151359 4.08302718 120.00000000 8.41269832 1
AO 0.05000000 2.05385971 4.08495418 120.00000000 8.46947284 17
DO 0.05000000 2.04151401 4.08302754 120.00000000 8.41270148 4
SO 0.05000000 2.04206436 4.08361374 119.97886535 8.41731392 13
AOA 0.05000125 2.04157994 4.08313277 119.99853952 8.41340882 9
ARO 0.05004260 2.04156710 4.08308405 119.99666220 8.41354659 10
TSA 0.06142367 2.04851934 4.09004933 120.00000000 8.57681980 19
SMA 0.05000000 2.04151486 4.08302743 120.00000000 8.41270438 6
COA 0.05000191 2.04156497 4.08309059 120.00000000 8.41318056 8
WHO 0.05018272 2.04169729 4.08338120 120.00000000 8.41659517 12
LCA 0.05000000 2.04266768 4.08310044 120.00000000 8.41756041 14
RIME 0.05000000 2.04372194 4.08587671 120.00000000 8.43318265 16
SCSO 0.05000000 2.04508593 4.08338038 119.97515883 8.42829689 15
IAO 0.05000000 2.06943426 4.12557716 117.66672171 8.70414342 21
DAOA 0.05000000 2.25549892 4.49825596 98.24966930 11.27862081 22
WChOA 0.05000000 2.07931091 4.09393916 119.31009538 8.60864330 20
DMSCSO 0.05000061 2.04151404 4.08302808 119.99998870 8.41270958 7
CSOAOA 0.05000001 2.04151447 4.08302764 119.99999009 8.41270382 5
EESHHO 0.05000000 2.04151359 4.08302718 120.00000000 8.41269833 2
RCLSMAOA 0.05000000 2.08176791 4.08327557 119.94346366 8.57289798 18
IHAOAVOA 0.05000000 2.04151362 4.08302723 119.99999849 8.41269867 3
COBHCOOT 427.65773392 177.54973049 53.27476217 118.19214246 8.41493494 11
  • Note: The best results obtained are highlighted in bold.

6.2. UAV Path Planning in Complex Terrain

The main objective of UAV path planning is to find an optimal path from the start position to the goal position with the lowest cost, no collision, and satisfying various metrics, including threat constraints, energy consumption, and path lengths. This can be regarded as a typical nondeterministic polynomial-time hard (NP-hard) optimization problem. Figure 23 illustrates the principal model of UAV path planning, where the hexagon and star represent the start and target points, respectively, and the circles represent the obstacles and threat regions to be averted. Connect the start and target points with an S-T line and divide the S-T line segment into k equal parts with k + 1 vertical lines (L1, L2, …, Lk, Lk+1). One discrete point is taken at each vertical component Lk to form a set of discrete point sets P = {Start, L1(x(1), y(1)), L2(x(2), y(2)), …, Lk(x(k), y(k)), Lk+1(x(k + 1), y(k + 1)), Target}, which are then joined to create a path.

Details are in the caption following the image
Figure 23
Open in figure viewerPowerPoint
Schematic diagram of UAV path planning.

Traditional path planning methods such as A∗, Dijkstra, and rapidly exploring random tree frequently suffer from high time cost, slow convergence speed, and susceptibility to local optima, limiting their efficacy in solving path design problems with higher precision and flexibility requirements. Yet, the emergence of MH algorithms provides scholars with a brand-new idea. MH algorithm has good adaptive ability and strong global search performance, so generating effective paths in complex three-dimensional environments is possible [67]. This part employs MCOA and other comparison algorithms to address the UAV path planning problem and further investigate their competitiveness in complex optimization tasks.

6.2.1. Environment Model

In the test case, the flight scenario entails a mountainous environment characterized by intricate terrain features. The function simulation method [68] is used to restore the three-dimensional terrain, as represented in the following equation:
()
where (x, y) denotes the coordinates of the terrain point projected onto the horizontal plane, while z denotes the coordinate height. The coefficients a, b, c, d, e, f, and g are constants used to control the topographic characteristics.
To increase the challenge and realism of the environment, the obstacle zones encountered in flight are simulated using a peak model as follows:
()
where hj denotes the height of the jth peak. (xj, yj) represents the center coordinate of the jth peak. aj and bj indicate the slope of the jth peak in the x- and y-axis directions, respectively.

In practical operations, the UAV must avoid no-fly zones, enemy radars, and surface-to-air missiles, among other potential threats. For simplicity, we use a cylinder of radius r to construct threat areas for the UAV to evade. We design two test cases. In the first test case, the flight area is 200 × 200 × 10 km. The second test case involves a more challenging scenario, with a larger flight area of 300 × 300 × 10 km. Based on the data specified in Table 22, the final three-dimensional environmental model for path planning incorporates terrain, mountains, and threat zones, as illustrated in Figure 24.

Table 22. Parameter settings for peaks and threat zones.
No. Peak Center coordinate (km) Altitude (km) X slope Y slope Threat area Center coordinate (km) Radius (km)
Case 1 Peak 1 (50, 80) 2 20 20 Threat 1 (40, 100) 20
Peak 2 (70, 160) 4 30 20 Threat 2 (90, 120) 20
Peak 3 (120, 40) 4 30 20 Threat 3 (120, 60) 20
Peak 4 (160, 80) 8 20 20      
Peak 5 (140, 140) 6 20 20      
  
Case 2 Peak 1 (60, 50) 4 25 25 Threat 1 (40, 120) 20
Peak 2 (60, 250) 7 30 25 Threat 2 (140, 50) 20
Peak 3 (80, 160) 5 18 20 Threat 3 (160, 250) 20
Peak 4 (150, 150) 8 45 50 Threat 4 (260, 150) 20
Peak 5 (220, 80) 4 35 40      
Peak 6 (240, 230) 6 20 30      
Details are in the caption following the image
Figure 24 (a)
Open in figure viewerPowerPoint
Three-dimensional environment model. (a) Case 1: 200 × 200 × 10 km. (b) Case 2: 300 × 300 × 10 km.
Details are in the caption following the image
Figure 24 (b)
Open in figure viewerPowerPoint
Three-dimensional environment model. (a) Case 1: 200 × 200 × 10 km. (b) Case 2: 300 × 300 × 10 km.

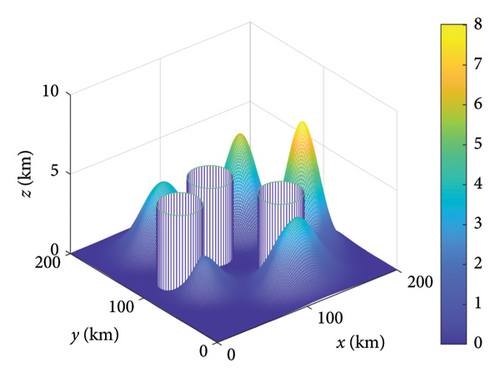
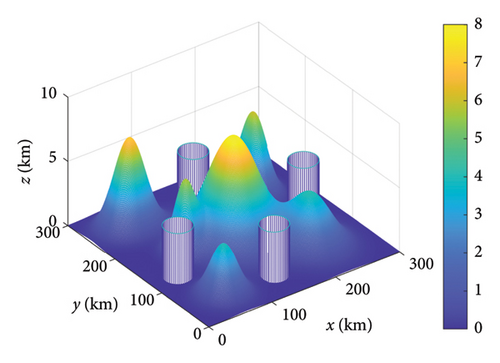
6.2.2. Cost Function

In the UAV flight process, shorter paths can save fuel and time. Suppose there are n waypoints in a complete flight route, and define the distance between the ith waypoint and the (i + 1)th waypoint as Li. The path cost can be calculated as
()
where (xi, yi, zi) indicates the coordinate of the ith waypoint.
Height cost is also a critical metric for UAV flight. Flight height is closely related to the probability of collision between the UAV and obstacles or the ground and should not be subject to large fluctuations. To enable safe and stable operation of the UAV, the height cost can be mathematically depicted as follows:
()
In addition, the turning angle cost function constrains the maneuverability of the UAV. Since UAVs are susceptible to air resistance while turning, the smaller the turning angle is, the more air resistance the UAV suffers, resulting in greater energy loss. During the flight, the turning angle of the UAV should be less than or equal to its maximum turning angle. Let the maximum turning angle be τ, the current turning angle be θ, and ai represent the vector of the ith road segment. The cost function for the turning angle fturn is provided in the following equation:
()
Finally, combining the abovementioned path constraint, height constraint, and turning angle constraint, the global cost function for the UAV path planning problem is as follows:
()
where ωi ≥ 0(i = 1, 2, 3) and the sum of the weights ωi equals to 1.

6.2.3. Experimental Results and Discussion

Case 1: Set the start coordinate position of the experimental flight as (0, 0, 0.5) and the target position as (200, 200, 1), with the number of path nodes n = 2. Case 2: Set the start coordinate position of the experimental flight as (0, 0, 1) and the target position as (300, 300, 3), with the number of path nodes n = 3. The maximum turning angle is 60°, and the weights ωi in the cost function are set to 0.4, 0.4, and 0.2, respectively. For MCOA and other comparison optimization methods, each algorithm operates independently for 30 runs with a population size of 30 and a maximum iteration number of 100. The generated paths are smoothed using a cubic B-spline curve [69].

6.2.3.1. Analysis of Case 1

The results presented in Table 23 reveal that MCOA provides the best path planning solution in complex 3D environments. The mean value obtained by MCOA is 134.6067, representing a 10.83% reduction compared to the original COA algorithm. Additionally, MCOA exhibits the smallest standard deviation, indicating superior robustness. Regarding optimal path cost, the proposed method achieves a value of 126.6594, ranking first among all algorithms, followed by COBHCOOT and IHAOAVOA.

Table 23. Numerical results of different algorithms for path planning in Case 1.
Algorithm Mean Std Best Ranking
MCOA 134.6067 4.4420 126.6594 1
AO 143.4890 5.2160 136.2224 14
DO 153.7499 6.3422 144.4809 18
SO 154.1237 4.7674 146.0373 19
AOA 156.2093 7.9677 146.2621 20
ARO 140.5590 4.8006 132.8115 9
TSA 158.4664 8.8239 147.3131 21
SMA 145.1958 5.7585 135.4345 15
COA 150.9587 7.0876 139.2673 17
WHO 142.8026 5.6703 133.7797 13
LCA 158.7778 9.4366 144.6035 22
RIME 141.3434 5.7546 132.7490 12
SCSO 140.0591 5.7840 132.3410 8
IAO 140.9311 6.6127 131.6480 10
DAOA 145.4497 7.7425 135.1069 16
WChOA 141.1081 6.8013 131.1581 11
DMSCSO 138.0222 5.6192 128.4782 5
CSOAOA 137.9742 6.5247 127.0370 4
EESHHO 138.1802 4.7706 130.7490 6
RCLSMAOA 138.2561 6.8645 129.0225 7
IHAOAVOA 136.2638 5.6735 127.5238 2
COBHCOOT 136.5773 5.9118 126.7358 3
  • Note: The best results obtained are highlighted in bold.

Figure 25 visualizes the performance of all algorithms in Case 1. The convergence curve in Figure 25(a) demonstrates that MCOA has a fast convergence speed and can locate the region where the global optimum may exist through less than 10 iterations. Enhanced by the specular reflection learning and vertical crossover operator, MCOA effectively escapes local optima and achieves the highest convergence accuracy. While DMSCSO and CSOAOA also show competitive convergence speeds, MCOA’s overall search performance is superior. The 3D view in Figure 25(b), X-Y plane top view in Figure 25(c), and side view in Figure 25(d) illustrate that MCOA successfully avoids all obstacles and threat areas while generating the shortest path. The algorithm’s ability to navigate efficiently through complex terrain demonstrates its superior decision-making capabilities in high-dimensional search spaces.

Details are in the caption following the image
Figure 25 (a)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 1. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.
Details are in the caption following the image
Figure 25 (b)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 1. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.
Details are in the caption following the image
Figure 25 (c)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 1. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.
Details are in the caption following the image
Figure 25 (d)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 1. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.

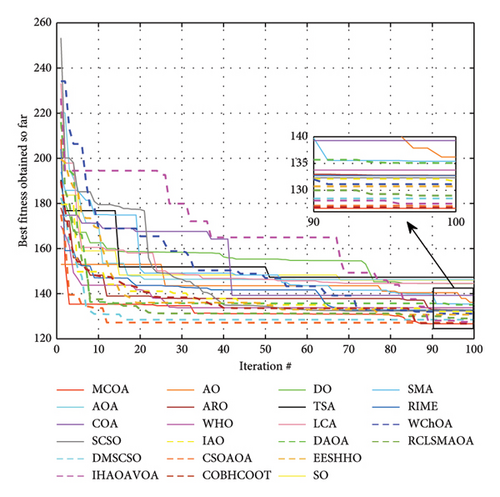
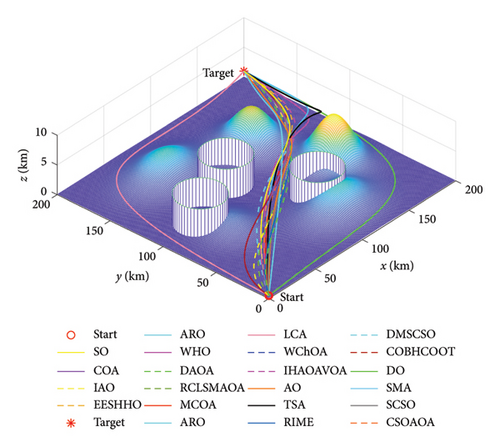
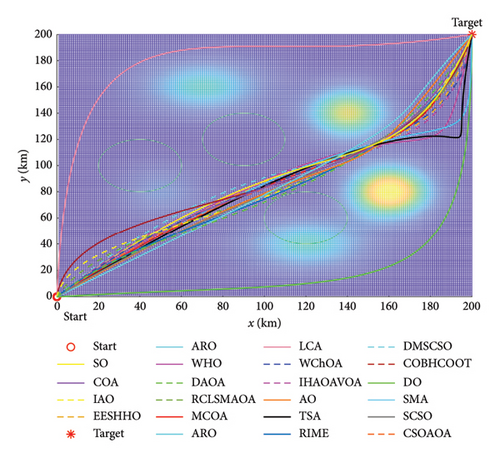
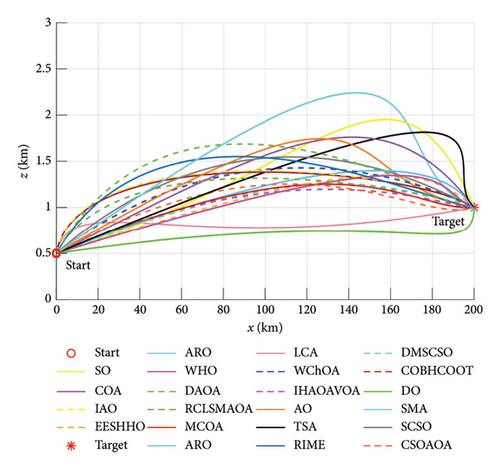
6.2.3.2. Analysis of Case 2

Table 24 presents the numerical results for the more challenging Case 2 scenario, which features longer distances and additional threat constraints. MCOA continues to demonstrate superior performance with a mean value of 236.9840, which represents a 7.61% improvement over the original COA algorithm (256.5099). Despite the increased problem complexity, MCOA maintains competitive robustness with a standard deviation of 14.3125. In terms of optimal path cost, MCOA again ranks first with a value of 217.3903, followed by IHAOAVOA (218.3255) and CSOAOA (218.4870). This consistent top-ranking performance across both test cases with different complexity levels confirms the effectiveness and adaptability of MCOA.

Table 24. Numerical results of different algorithms for path planning in Case 2.
Algorithm Mean Std Best Ranking
MCOA 236.9840 14.3125 217.3903 1
AO 262.9066 16.4338 241.1270 19
DO 256.1609 16.4581 234.7058 12
SO 256.4368 18.4539 229.1236 10
AOA 259.0532 16.4648 240.8990 18
ARO 247.4527 14.8282 225.5775 6
TSA 289.6658 16.7635 267.1326 22
SMA 259.4073 14.3959 239.0314 16
COA 256.5099 13.4672 235.4826 14
WHO 259.9700 17.2747 236.7984 15
LCA 275.3463 16.1519 253.4875 20
RIME 258.3066 12.5638 234.7642 13
SCSO 262.7354 14.9530 239.6591 17
IAO 250.6219 15.8789 227.2110 7
DAOA 252.2951 16.0523 228.7370 9
WChOA 274.3636 15.2650 254.6457 21
DMSCSO 247.3743 12.0350 223.6382 5
CSOAOA 239.8799 16.1351 218.4870 3
EESHHO 254.0341 16.8257 230.4508 11
RCLSMAOA 256.1495 16.8055 228.0506 8
IHAOAVOA 240.7347 12.2784 218.3255 2
COBHCOOT 242.4634 15.1290 221.9067 4
  • Note: The best results obtained are highlighted in bold.

The convergence curve in Figure 26(a) reveals that MCOA maintains its advantage in convergence speed even in this more challenging environment, reaching near-optimal solutions within approximately 60 iterations. While several algorithms show similar early convergence patterns, MCOA ultimately achieves superior final solutions through its enhanced balance between exploration and exploitation. The 3D visualization in Figure 26(b) clearly demonstrates that MCOA can efficiently navigate through complex terrain, avoiding all potential threats to cross the extended distance. The top view in Figure 26(c) and side view in Figure 26(d) further confirm MCOA’s ability to generate smooth, obstacle-avoiding paths that satisfy all constraints while minimizing the total path cost.

Details are in the caption following the image
Figure 26 (a)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 2. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.
Details are in the caption following the image
Figure 26 (b)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 2. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.
Details are in the caption following the image
Figure 26 (c)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 2. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.
Details are in the caption following the image
Figure 26 (d)
Open in figure viewerPowerPoint
Visual analysis of MCOA and other comparison algorithms for path planning in Case 2. (a) Convergence curve. (b) Path trajectories in 3D view. (c) Top view of path trajectories in X-Y plane. (d) Side view of path trajectories in the X-Z plane.

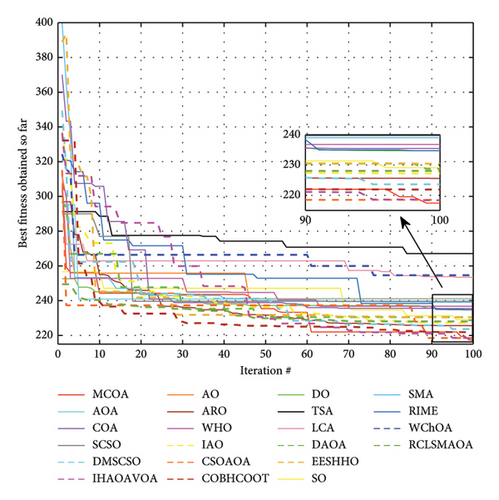
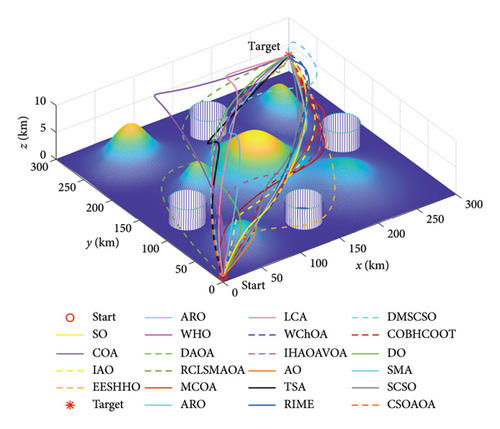
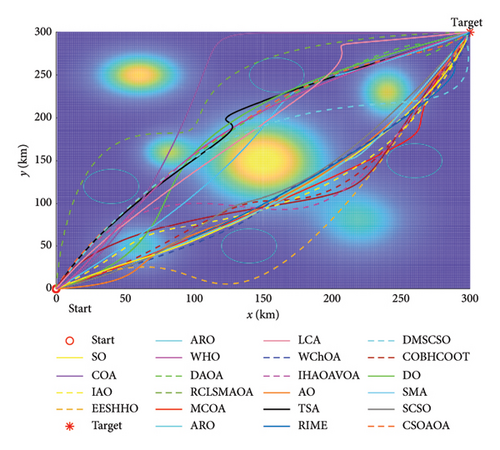
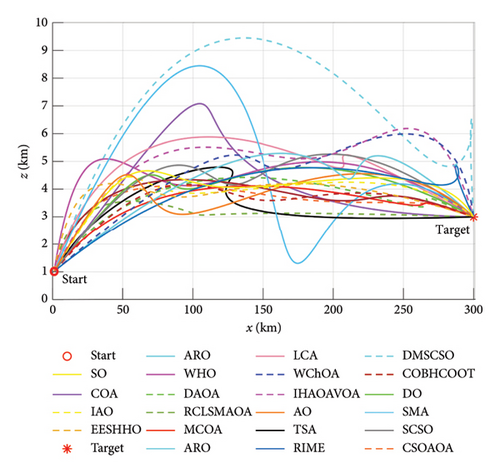
Specular reflection learning enhances population diversity, expanding the search space. The expanded exploration strategy boosts global search capabilities and accelerates convergence. Lévy flight increases local search efficiency, and the vertical crossover operator helps escape local optima. These strategies work synergistically to provide MCOA with superior exploration–exploitation balance, enabling it to outperform other algorithms in solving constrained engineering problems and UAV path planning, demonstrating its robustness and adaptability in complex optimization challenges.

7. Conclusion

This paper presents a multistrategy MCOA designed to address the limitations of the original algorithm, such as premature convergence, slow convergence speed, and an imbalance between exploration and exploitation. The proposed MCOA incorporates four innovative strategies: specular reflection learning, expanded exploration strategy, Lévy flight, and vertical crossover operator. The integration of these strategies creates several advantages. Specular reflection learning increases population diversity and establishes a strong foundation for global search in the early iterations, while the extended exploration model extracted from AO significantly enhances exploration capabilities. Additionally, Lévy flight characteristics replace the random step size in the exploitation phase for more efficient convergence toward the global optimum, and the vertical crossover operator effectively mitigates search stagnation, preventing the algorithm from being trapped in local optima. These enhancements enable MCOA to maintain robust optimization performance across a wide range of benchmark functions and practical engineering problems, including the CEC2005, CEC2019, and CEC2022 test suites, as well as seven constrained engineering design tasks and UAV path planning cases in a complex three-dimensional environment. The experimental results confirm that MCOA outperforms twelve state-of-the-art MH algorithms and nine recent variants in terms of solution precision, local optima avoidance, convergence speed, and scalability across different spatial scales. Notably, the vertical crossover operator has the most significant impact on improving optimization performance, and the optimal scale factor αF for Lévy flight is found to be 0.06. The findings from engineering design problems and UAV path planning further demonstrate MCOA’s competitive edge in real-world applications.

However, while MCOA shows promising results, there are areas for improvement. The incorporation of multiple strategies leads to higher time costs, which may limit its suitability for specific real-time applications. Future work could focus on reducing these time costs by restructuring MCOA in parallel. Additionally, an adaptive dynamic adjustment strategy for the scale factor αF can be developed based on the number of iterations, allowing MCOA to exhibit superior performance in more comprehensive benchmark functions and more challenging engineering scenarios. Moreover, MCOA has the potential to be applied to a broader range of emerging optimization problems, such as parameter identification of photovoltaic models, image segmentation, battery health state estimation, manufacturing schedule, and hyperparameter tuning of neural networks.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Yaning Xiao: software, methodology, conceptualization, writing – original draft, and writing – review and editing. Hao Cui: investigation, validation, writing – review and editing, and formal analysis. Ruba Abu Khurma: methodology, conceptualization, and writing – original draft. Abdelazim G. Hussien: methodology and writing – review and editing. Pedro A. Castillo: writing – original draft and funding.

Funding

This work was supported by the Ministerio Español de Ciencia e Innovación under project numbers PID2020-115570GB-C22 MCIN/AEI/10.13039/501100011033 and PID2023-147409NB-C21 MICIU/AEI/10.13039/501100011033, the C-ING-027-UGR23 Project, and the Cátedra de Empresa Tecnología Para las Personas (UGR-Fujitsu).

Supporting Information

Supporting Information consists of two parts: Appendix A “Benchmark function description” and Appendix B “Case study on engineering optimization.” In Appendix A, detailed descriptions are provided for unimodal benchmark functions, multimodal benchmark functions, fixed-dimension multimodal benchmark functions, the IEEE CEC2019 test suite, and the IEEE CEC2022 test suite. In Appendix B, mathematical models for constrained engineering optimization design cases are provided.

Data Availability Statement

All data used to support the findings of this study are included in this published article.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.