International Journal of Intelligent Systems

Volume 2025, Issue 1 4810561

Research Article

Open Access

Graph Learning of Semantic Relations (GLSR) for Cooperative Multiagent Reinforcement Learning

Pengting Duan,

Pengting Duan

orcid.org/0009-0007-4624-750X

School of Software , Northwestern Polytechnical University , Xi’an , 710072 , China , nwpu.edu.cn

North Automatic Control Technology Institute , Taiyuan , 030006 , China

Search for more papers by this author

Chao Wen,

Chao Wen

orcid.org/0000-0002-6894-8207

Institute of Big Data Science and Technology , Shanxi University , Taiyuan , 030006 , China , sxu.edu.cn

Search for more papers by this author

Baoping Wang,

Corresponding Author

Baoping Wang

[email protected]

orcid.org/0000-0001-6404-9354

School of Software , Northwestern Polytechnical University , Xi’an , 710072 , China , nwpu.edu.cn

Search for more papers by this author

Zhenni Wang,

Zhenni Wang

orcid.org/0009-0005-6187-1760

School of Software , Northwestern Polytechnical University , Xi’an , 710072 , China , nwpu.edu.cn

Search for more papers by this author

Zhifang Wei,

Zhifang Wei

orcid.org/0000-0001-8065-1038

Institute of Big Data Science and Technology , Shanxi University , Taiyuan , 030006 , China , sxu.edu.cn

Search for more papers by this author

Pengting Duan,

Pengting Duan

orcid.org/0009-0007-4624-750X

School of Software , Northwestern Polytechnical University , Xi’an , 710072 , China , nwpu.edu.cn

North Automatic Control Technology Institute , Taiyuan , 030006 , China

Search for more papers by this author

Chao Wen,

Chao Wen

orcid.org/0000-0002-6894-8207

Institute of Big Data Science and Technology , Shanxi University , Taiyuan , 030006 , China , sxu.edu.cn

Search for more papers by this author

Baoping Wang,

Corresponding Author

Baoping Wang

[email protected]

orcid.org/0000-0001-6404-9354

School of Software , Northwestern Polytechnical University , Xi’an , 710072 , China , nwpu.edu.cn

Search for more papers by this author

Zhenni Wang,

Zhenni Wang

orcid.org/0009-0005-6187-1760

School of Software , Northwestern Polytechnical University , Xi’an , 710072 , China , nwpu.edu.cn

Search for more papers by this author

Zhifang Wei,

Zhifang Wei

orcid.org/0000-0001-8065-1038

Institute of Big Data Science and Technology , Shanxi University , Taiyuan , 030006 , China , sxu.edu.cn

Search for more papers by this author

First published: 19 May 2025

https://doi.org/10.1155/int/4810561

Academic Editor: Mohamadreza (Mohammad) Khosravi

Share a link

Email
Wechat
Bluesky

Abstract

Prominent achievements of multiagent reinforcement learning (MARL) have been recognized in the last few years, but effective cooperation among agents remains a challenge. Traditional methods neglect the modeling of action semantic relations in the learning process of joint action latent representations. In other words, the uncertain semantic relations might hinder the learning of sophisticated cooperative relationships among actions, which may lead to homogeneous behaviors across all agents and their limited exploration efficiency. Our aim is to learn the structure of the action semantic space to improve the cooperation-aware representation for policy optimization of MARL. To achieve this, a scheme called graph learning of semantic relations (GLSR) is proposed, where action semantic embeddings and joint action representations are learned in a collaborative way. GLSR incorporates an action semantic encoder for capturing semantic relations in the action semantic space. By leveraging the cross-attention mechanism with action semantic embeddings, GLSR prompts the action semantic relations to guide mining the cooperation-aware joint action representations, implicitly facilitating agent cooperation in the joint policy space for more diverse behaviors of cooperative agents. The experimental results on challenging tasks demonstrate that GLSR attains state-of-the-art outcomes and shows robust performance in multiagent cooperative tasks.

1. Introduction

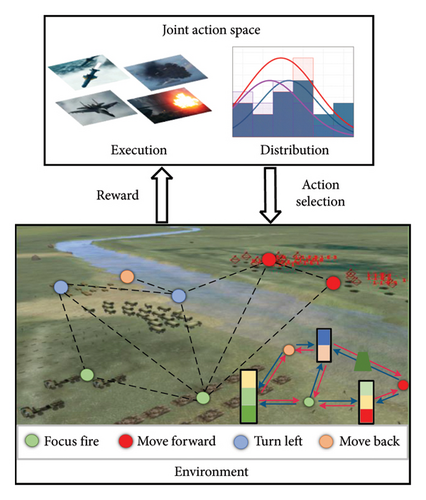
Cooperative multiagent reinforcement learning (MARL) has been widely applied in numerous fields, including autonomous driving [1], intelligent community services [2], traffic control [3], and intelligent UAV systems [4–7]. One of the examples is in the interactive warfare simulation system, as depicted in Figure 1. In the digital twin battlefield, the agents seek to explore diverse policies on large-scale missions training to enhance professional competence in real-world scenarios. To maximize a shared goal, multiple agents make iterative interactions in a common space, continually refining their policies by absorbing useful information and acquiring transferable skills from each other [8]. As the number of agents increases, the dimensions of joint action of multiagent systems (MAS) that interact with each other grow exponentially. From the viewpoint of an individual agent, the behavior selection strategies employed by other agents disrupt the stability of the environment. These defects prevent MARL algorithms from scaling to more agents [9].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Interactive warfare simulation system in military.

To solve the poor convergence of independent policy gradient–based methods [10] in the aforementioned MAS, a plethora of trust region optimization algorithms, such as MAPPO [11] and HATRPO/HAPPO [12], have received notable successes by learning the monotonic policy updating scheme. One of significant aims in MAS is to address the reasonable credit assignment; value function decomposition–based methods [13, 14] decompose the global value function into a combination of local value functions according to the individual global max (IGM) principle [15], which simplifies the policy exploration and ensures that both the global and individual values are strictly monotonic. Policy gradient methods like MADDPG [16], COMA [17], and HAPPO [12] also have made efforts to encourage agent discriminability from the rest in reward distribution. As a general and feasible approach for credit assignment, the multiagent advantage decomposition [12] has promoted individualized policy exploration in cooperative MARL. The multiagent advantage decomposition as well as the value decomposition [18, 19] explicitly models the individual contributions of cooperative agents rather than the topological structure of cooperation space in MARL. The lack of learning with effective cooperation relation modeling may impede agents from diverse policy exploration in complex scenarios. SOG [20] and RODE [21] have been presented to fill out the gap. However, these methods follow a hierarchical learning framework and require manual parameter fine-tuning for joint action space decomposition through action clustering, which may largely limit their applications. Therefore, the research on automatic modeling of cooperative action relation is still insufficient in MARL, where the uncertain semantic relations may hinder the learning of sophisticated cooperative relationships among actions.

A natural solution to mitigating the uncertainty is to design auxiliary objectives to learn cooperative action representations and enrich the MARL exploration process. Hence, the effective understanding of semantic information related to task goals in complex scenarios is crucial for efficient cooperation. Different from attention-based learning for the importance distribution of each agent’s allies or GNN-based relationship learning [22], we concentrate on the graph modeling of structure information in action semantic space in order to diversify exploration for global optimal solutions in large-scale application scenarios with heterogeneous agents. The action semantic space can be established by the semantic embeddings of the heterogeneous actions and the structure of the space can be modeled by the correlation among the embeddings. The semantic embeddings capture the potential cooperation between heterogeneous actions, which is crucial for cooperation-aware modeling of multiagent interaction. This is distinguished from the specific priority setting [23] and interactive communication mechanism [24]. In addition, less attention has been paid to the collaboration between semantic encoding and cooperation-aware action representation for policy optimization.

In this paper, we propose a method named GLSR, i.e., graph learning of semantic relations, for cooperative MARL. The rich semantic dependencies among heterogeneous actions are encoded into action semantic embeddings by capturing the correlations. In a collaborative manner, the action semantics is encoded through graph modeling, while the cooperation-aware action representation is learned for policy optimization. The cooperative information among agent actions can be mined with correlation-aware action semantics, which is also enhanced by the backpropagation of joint action reward information. Each agent employs trust-region policy optimization theory and a cross-attention mechanism [25] to realize the behavior prediction, which can prevent the abrupt degradation in the joint action space. GLSR makes a first endeavor to develop a collaborative learning framework for both the semantic relation graph network and the multiagent actor-critic network.

The contribution of our paper is summarized as follows:

•
We propose graph learning of semantic relationships for cooperative MARL and introduce an innovative collaborative framework of action semantic relation encoding and latent representation learning for policy optimization.
•
We design a reasonable action semantic encoder from the perspective of graph learning. The correlation-aware action semantics provides guidance to the learning process of cooperation-aware latent representations through a semantic-guided actor network.
•
GLSR outperformed the state-of-the-art methods on the challenging StarCraft II Multiagent Challenge (SMAC) benchmark, especially in the superhard map scenarios requiring complex cooperative demands.

2. Related Work

2.1. MARL

MARL extents signal-agent RL and has attracted great attention for functioning well in more dynamic and complex tasks within the framework of Markov Games [26]. The policy of each agent can be independently optimized by directly adopting decentralized learning [27], but it may suffer from nonstability and poor convergence issues of joint policy [28]. MARL algorithms tend to optimize the agents’ action space by learning a joint policy, which can get rid of the instability in MAS [29]. To effectively overcome the problems of lazy agents and spurious rewards in the sharing reward mechanism [30], VDN [13] adopts a simple summation to generate the global value function without additional state information. QMIX [14] generates the weights of the mixing network through independent hypernetworks and limits the weights to positive values to ensure the monotonic constraints. By leveraging a more reliable decomposition technique induced by IGM, QTRAN [15] optimizes individual agent actions and relaxes the monotonicity restriction. However, the monotonicity constraint of these algorithms is a sufficient and unnecessary condition for the joint policy optimization, which may be limited to solving the “credit assignment” problem under completely equivalent cooperative relationships in cooperative tasks with monotonic benefits. To get rid of such limitation, multiagent advantage decomposition assumption [12] holds in general for Markov games, which provides a powerful credit assignment way in MARL. Based on the effective reward criterion, it is interesting to pay close attention to the modeling of cooperative actions and its contribution to performance from agents with interactive actions for dealing with complex scenarios.

2.2. Semantic Modeling for Cooperative MARL

A large number of MARL methods have been devised for cooperative scenarios, where the cooperation modeling under a sharing team reward plays an important role in improving convergence. The prevalent Centralized Training Decentralized Execution (CTDE) algorithms with Actor Critic (AC) network architecture [16, 17] have been developed through the combination of policy gradient with value function decomposition, such as MADDPG [16], MAPPO [11], HAPPO [12], etc. MADDPG stores the latent collective information like agent state transitions and rewards in a replay buffer during the training process to facilitate experience sharing among all agents. MAPPO and HAPPO handle agent interactions by exploiting the others′ observations and actions, which are also committed to modeling task-level semantics for cooperative exploration with strategies such as advantage function decomposition and shared network parameters [31, 32]. From the perspective of implicit semantic communication between agents, interactions among agents with independent action representation have been investigated for cooperative modeling [33–36]. Furthermore, the effects of conflicting policy gradients among agents can be mitigated according to the trust region policy optimization theory, which induces a robust optimization framework with the monotonic improvement guarantee in various scenarios [37, 38]. The effectiveness of semantic feature has been proved to learn inherent structure and generalized relationship in link prediction [39], which facilitates the global task understanding. The semantic consistency inherent in state embedding has been exploited to efficiently capture the memory similar to the current state, which improves policy exploration [40]. However, the latent representation is guided by immutable prior knowledge of relation and the latent representation learning for policy optimization is lack of the collaboration with the dynamic semantic encoding, which inevitably results in the overfitting to specific teammates [41] and frequently suffers from suboptimal convergence traps in complex cooperative scenarios.

2.3. Collaborative Learning

It is significant for MARL to endow agents with the semantic knowledge to infer the actions of other agents, particularly in cooperative tasks. Effective relation modeling enables agents to efficiently cooperate for policy exploration. In addition to revealing the hidden relationship between actions and other agents′ policies, high-level modeling guided by semantic knowledge can be utilized to learn the potential representation of agent policy [42, 43]. However, the computation loads increase significantly with the number of agents, which seriously limits the applications in a large-scale heterogeneous MARL. To overcome this, a hierarchical collaborative learning framework has been investigated by decomposing joint action spaces into specific action spaces or role-related action spaces through clustering [21]. Different from the partition of action space for each agent based on manual construction of role and subtask, graph modeling has been adopted to efficiently construct the edge set of all agents with the joint actions of each agent pair [44]. In order to diversify policy exploration, evolutionary algorithms have been incorporated into MARL through the crossover of policy representations and random parameter perturbations [45–47]. However, these methods primarily focus on learning action latent representation with respect to roles and environmental observations, lacking effective modeling of structure information in action semantic space. It has been demonstrated that the dependency between latent representation and semantics can be well captured by constructing a latent embedding space [48, 49]. The semantic correlations can be explicitly encoded into interdependent relation-aware embeddings by graph neural networks [45]. Owing to the great potentiality of relation representation learning, graph neural networks are promising to model action semantic relation in the MARL scenario. We make our first attempt on semantic relation encoding with collaboratively learning latent action representation for policy optimization.

3. GLSR for MARL

The overall illustration of the network architecture of the proposed GLSR is given in Figure 2. In the action semantic encoding module, the action semantic embeddings are learned in action co-occurrence semantic space through a graph autoencoder with an action relation graph. In the semantic-guided actor network, each agent’s optimal action is decoded from the cooperation-aware joint action representation, the learning of which is guided by the action semantic embeddings. The agents can only access their preceding observations encoded by the critic network before taking actions, which can be ensured by the masked cross-attention blocks. The semantic embeddings and the cooperation-aware action representations are learned in a collaborative way rather than in a two-stage procedure. In the collaborative framework, cooperative relation information can be incorporated into correlation-aware action semantic embeddings, which is also reinforced by the backpropagation of joint action reward information. The essential modules of GLSR will be described in detail.

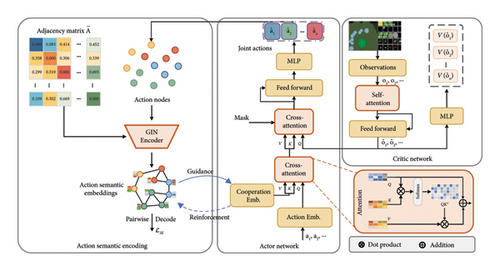
3.1. Problem Formulation

Fully cooperative MAS are generally modeled as Markov games [46] based on shared rewards, consisting of a tuple

describes the set of all possible states, which is a generalization used to represent the environment.

and

denote the joint action and observation space, respectively.

is the reward function,

is the observation function, and γ ∈ [0, 1) is the discount factor to encourage agents to focus more on immediate rewards.

is set of agents. For arbitrary disjoint, ordered subsets of agents i_1:m = {i₁, …, i_m},

. At each time step, agent

in the global state s^t receives an observation

. After that, a joint observation

is created using the collection of these observations. Based on the current state, the agents select specific action

according to the joint policy π to interact with the environment iteratively. The goal of agents is to find the optimal joint policy π^∗ to maximize the expectation of accumulating rewards, i.e.,

()

where

denotes the marginal observation distribution and R(O^t, A^t) is the reward value returned by the environment after executing action A^t, which is a shared reward function for all agents.

3.2. Action Semantic Encoding

The structure modeling of action semantic space is effective understanding of semantic relation information related to task goals, which is crucial for efficient cooperation. Action co-occurrence provides fundamental semantic relation information for the learning of intricate cooperative relationships among actions. In this section, we focus on the graph modeling of action co-occurrence semantic space so as to learn cooperation-aware action latent representations and enrich the MARL exploration process.

Inspired by the efficient sample utilization using the parallel training frameworks [11, 50], GLSR incorporate action statistics into multithread training framework to improve sample utilization. In addition to the interaction with the observations, the action latent presentations are embedded with cooperative relationship through interaction with action semantic embeddings. Specifically, an action relation graph

is firstly constructed based on statistics of action co-occurrence, where the node set V corresponding to the actions set, with the edge set E standing for the corresponding collection of action pairs. Since the similar semantic embeddings should be shared by the actions with strong co-occurrence, the adjacency matrix

is used to store the edge-related weights, standing for the conditional probability of co-occurrence (cooperation) of action pairs. The symmetric adjacency matrix

can be formulated as follows:

()

where Pr(l_j|l_i) represents the conditional probability of action j given action i and the elements along the diagonal of

are zeros. The dimension of

is k × k with k standing for the total number of action types, and it is constructed by the sampled actions in the replay buffer. The dimension of

is determined by action space of agents, and it grows with the number of action types rather than the number of agents. This indicates the proposed action semantic encoding has good scalability. Although the adjacency matrix can be constructed in other alternative ways like a learnable form, we focus on its co-occurrence relationship based form which is embedded in the following collaborative learning framework for cooperation-aware representation and joint policy updating. We leave the research on other forms in the future work.

To integrate the structure information of co-occurrence semantic space into action semantic embeddings, a graph autoencoder is adopted for action semantic encoding network with parameter φ. The graph isomorphism network (GIN) [47]-based encoder is employed for graph learning with the input of an action relation graph. The GIN-based encoder grasps the action cooperation from the semantic relation in the co-occurrence semantic space. The node features output by A GIN layer can be obtained as

()

where

denotes matrix of action nodes, f_φ stands for a two-layer MLP with each linear layer followed by batch normalization and LeakyReLU function, and ϵ is the learnable weight of the remained information of the original node. H⁽⁰⁾ is initialized according to the standard normal distribution instead of one-hot vectors. After encoding,

is regarded as the output action semantic embeddings

, for learning action latent representation in the semantic relation guided actor-critic network.

The GIN encodes the actions with cooperative relationships to adjacent locations in the co-occurrence semantic space by deterministically integrating the correlations among actions into an adjacency matrix. Since GIN is not able to increase the independence among the noncooperative actions only by neighborhood aggregation, it is difficult for the noncooperative action embeddings to pull apart from each other. Consequently, a pairwise decoder in the graph autoencoder is employed to parse the pairwise relationship between learned action semantic embeddings. The topological constraint on action semantic space is imposed with the function of the decoder adopted as follows:

()

where sim(e_i, e_j) stands for the cosine similarity calculation of e_i and e_j, and

. GLSR provides cooperation-aware action semantic representation by capturing the structure of action semantic space rather than simply adopting prior knowledge of uncertain action semantic relations.

3.3. Semantic-Guided Actor Network

In the semantic-guided actor network, the action sequence of preceding agents is initially passed to the decoder, where is an arbitrary symbol indicating the start of decoding. The action correlations are incorporated into the cooperation-aware action representation learning. Meanwhile, the actor network propagates joint action reward information based on the cooperation-aware representation to the action semantic encoder.

Given action of k th category

, a learnable mapping

from original joint action space

to cooperation-aware joint action representation space

is adopted. Furthermore, the action semantic embeddings E from the action semantic encoder are employed to construct semantic specific learnable mapping ϑ_k, which can be obtained as

()

where e_k represents the action semantic embedding corresponding to the k th category action l_k, obtained from the k th row of E.

To realize this mapping, we first obtain the action embedding by mapping each a_i from the original joint action space:

()

where W_a and b_a are learnable parameters, ς is the GELU activation, and the embedded action

of each agent can be optimized to facilitate the following interaction with cooperation embeddings.

Instead of the self-attention mechanism that only extracts correlations between actions [26], the cross-attention mechanism is then employed to learn the cooperation-aware joint action representation with the guidance of the action semantics. Concretely, we exploit an additional projection of a linear layer to obtain the cooperation embeddings:

()

where W_e and b_e are learnable parameters, which make e_k the same dimension as

. Successively, the cross-attention block followed by a two-layer MLP with residual connections is employed to incorporate the action semantics into the enhanced action latent representation. The cooperation relationships among actions of agents can be enhanced through the interaction between

and

, which results in

()

where W^Q, W^K, and W^V are learnable parameters, the attention ξ_i,k is computed to estimate the importance of each action semantics, which benefits the suppression of weakly correlated action semantic information. Another cross-attention mechanism is incorporated in the last decoding block for the interaction between the enhanced action latent representation and encoded observation

from the critic network, generating cooperation-aware action representation:

()

where the attention η_i,j is computed by adopting sequence mask operation on i th observation to achieve the action sequence updating for j th agent wherein i < j. To prevent gradient vanishing with increasing depth, the last decoding block employs an MLP (implemented as a two-layer perceptron with GELU activation) combined with skipping connections to output the joint action representations

. Note that the linear layers scale proportionally with the feature dimension rather than the number of agents. Then, the representations are passed into an MLP, which generates the probability distribution of i_m th agent’s action}, namely, the policy

, that guarantees monotonic performance improvement during training [26]. In the inference stage, action of i_m-th agent is generated in a sequential manner, while during the training stage, the output of all actions can be computed in parallel simply because

have already been collected and stored in the replay buffer. As a result, the joint policy π_ϑ = (a₁, …, a_n) of agents can be obtained simultaneously. The parallel training architecture of semantic-guided decoding block with attention mechanism as the kernel effectively mitigated the limitations inherent in sequential update paradigms, thus have far less time complexity. The cooperation-aware representations are processed by the actor network to construct the following clipping PPO objective [11] for actor network training:

()

where

is the joint advantage function constructed by the advantage decomposition theorem [12]. Using the output

of the critic network, generalized advantage estimation (GAE) [48] is adopted to facilitate multiagent credit assignment.

3.4. Critic Network

The sequence of observations (o₁, …, o_n) is encoded by the critic network with parameters ϕ through several encoding blocks, and output the latent representations, which encode observations into latent representations. To avoid gradient vanishing and network degradation with increasing depth, each encoding block employs a relation-enhanced mechanism [55, 56] followed by a two-layer MLP with residual connections. The encoded observations are represented as (

), which integrate the information inherent in individual agents as well as the higher-level correlations through their interactions. An extra projection is added in the critic network to estimate the value function

and provide the environmental perceptions for actor network learning. The critic network will be trained with an update rule based on the squared Bellman error as follows:

()

where

represents the parameters of the target critic network, which can be periodically update to avoid oscillation during training [49].

3.5. Optimization Objective

GLSR offers an impressive action semantic encoder to help agents learn cooperation-aware action representation during the end-to-end training process. The overall objective function of the GLSR framework consists of the following three components:

()

where

is the minimization objective of the empirical Bellman error, which can encourage agents to learn their own policies by the value function based on the critic network,

is clipping PPO objective, and

is the action semantic embedding loss, with β a trade-off parameter. In cooperation-aware action representation learning for more diverse behaviors,

and

help embed action into a co-occurrence semantic space and explore the action semantic relations in joint action space for cooperative agents.

We describe the entire procedure in Algorithm 1. The cooperative-aware action representation learning is incorporated in the MARL, which further improves the global rewards by guiding agents to make more diversely cooperative behaviors rather than simple reward maximization of some homogeneous behavior. For each episode, there are M number of parallel threads for training in Table A2 threads with each thread collecting T timesteps of data. All hyperparameter settings can be found in Tables A1 and A2. Specifically, we provide the detailed calculation of the symmetric adjacency matrix. We first calculate the k-dimensional binary vector of co-occurring action types within all the agents on the current time step, where one denotes as the action occurring with zero standing for the nonexisting of the action at the same time step. Thus, we can obtain the k × M matrix by stacking M vectors that corresponds to the M parallel threads for training. We compute the self-correlation of the matrix and divide its κ-th column by the number of times that the κ-th type of action occurs within all the parallel threads. We set the diagonal elements of resulting matrix to be zeros to obtain conditional probability matrix and finally calculate the symmetric adjacency matrix according to (1).

3.6. Extension of GLSR to CTDE Framework

For better scalability, we also introduce a CTDE variant of GLSR called GLSR-var. GLSR-var preserves the centralized critic network for global value estimation while deploying fully decentralized semantic-guided actor networks for each agent. These actor networks only work with partial observations and the alternative adjacency matrices are constructed by one-hot vectors for eliminating dependency on previous agents’ actions. The loss function for actor networks is defined as:

()

where

denotes the local advantage estimation.

Algorithm 1: GLSR for MARL.

1.
Input: Batch size b, number of agents n, parallel threads M, episodes K, steps per episode T.
2.
Initialize: Semantic encoding network φ₀, actor network ϑ₀, critic network ϕ₀, replay buffer D.
3.
fork = 0, 1, 2, …, K − 1
4.
for step t = 0, 1, 2, …, T − 1
5.
/∗Semantic guided inference phase∗/
6.
form = 0, 1, 2, …, n − 1
7.
Count the occurrence number N_i (N_j) of each action type and the co-occurrence number N_ij of different actions i and j at each time step in all parallel threads M.
8.
Compute by conditional probability Pr(l_i|l_j) = N_ij/N_j.
9.
Infer in a sequential manner with and based on (3).
10.
Collect a set of trajectories and insert into D.
11.
end
12.
/∗Semantic guided training phase∗/
13.
Sample a random minibatch B from D.
14.
Calculate the joint advantage function with GAE.
15.
Input to generate E and cooperation representation z_i.
16.
Input , , and to generate at once with parallel training model.
17.
Compute L_SE(φ) with (4).
18.
Estimate L_Actor(ϑ) and L_Critic(ϕ) with (10) and (11).
19.
Update network by minimizing objectives in (12).
20.
end
21.
end

4. Experiments

GLSR provides a collaborative learning framework for cooperative MAS tasks. The fundamental principle of GLSR is the cooperative-aware action representation learning incorporated into the multiagent trust region policy optimization procedure, which inherits the merit of monotonic performance improvement during training. The structure information in action semantic space is graph modeled by encoding into the relations and dependencies among different action semantics, which is based on highly efficient implementation from a sequence modeling perspective. To validate the cooperation performance of our proposed GLSR, we conduct a series of experiments on the SMAC benchmark [51], which features comparatively complicated scene settings and is one of the most commonly used benchmarks in the cooperative MARL field. Figure 3 displays various task scenarios in SMAC.

We compared GLSR with three state-of-the-art methods, MAPPO, HAPPO, and MAT that are based on multiagent trust region optimization framework. During the experiment, the implementation of the baseline method was consistent with its official repository, and all hyperparameters stay unchanged in the original optimal performance state. Specific parameter settings for each of the methods are contained in Appendix A.

4.1. Performance on SMAC

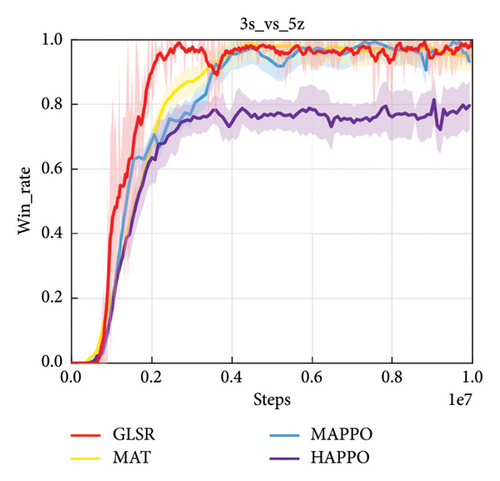
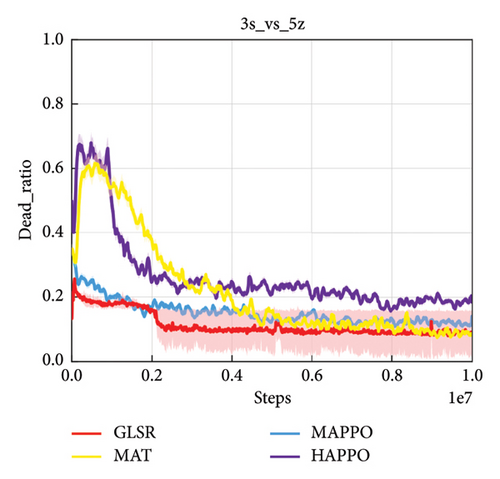
For the sake of generality, we first carried out algorithm performance verification experiments on hard and superhard maps, such as 3s_vs_5z, MMM2, 6h_vs_8z, 27m_vs_30m, and 3s5z_vs_3s6z. Figure 4 shows the performance comparison results on 3s_vs_5z map, which is one of the hard maps with asymmetric scenario. All the methods compared show similarly high win rate, but GLSR exhibits the fastest convergence and the lowest dead ratio which indicates that more cooperative behaviors can benefit not only high win rate but also the loss reduction of allied forces.

We further consider several superhard maps of MMM2, 6h_vs_8z, 27m_vs_30m and 3s5z_vs_3s6z, respectively, with more possibility of adopting diverse attempts for optimal policy. In these asymmetric maps, enemy outnumbers allied forces by one or more, especially in MMM2 and 3s5z_vs_3s6z, where each side contains more than one type of heterogeneous agent unit, so the cooperative behavior may be more important than simple independent behavior with high reward to help win the battle. Figures 5(a), 5(c), 5(e), and 5(g) show that the state-of-the-art algorithms, such as HAPPO, MAPPO, and MAT, tend to a suboptimal policy where agents preferentially take homogeneous behavior rather than potential heterogeneous behavior exploration. By contrast, GLSR significantly outperforms the other methods, which can provide a semantic relation guided cooperation-aware action representation learning for MARL to realize heterogeneous exploration and get rid of converge to the suboptimal joint policy. The cooperation-aware action rewards should be received where individual agents are able to adjust their policy in accordance with cooperative semantics and contribute to the success of the team. The proposed GLSR would explore more diverse action combinations instead of focusing on the individual action with current reward optimization, which would lead to the more fluctuations in win rate performance before convergence than conventional methods. After convergence, the fluctuations become trivial, which proves the ability of GLSR that can ensure consistent policy improvement from the global perspective.

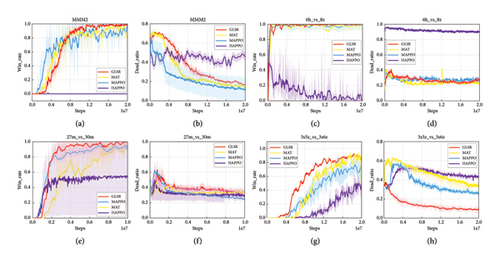
To demonstrate the effectiveness of the proposed method in complex tasks, a statistical analysis of the win rate and standard deviation comparison with MAT, MAPPO, HAPPO, and RODE are presented in Table 1. It is shown that GLSR outperforms the other methods. Although the algorithms like RODE are also based on action space modeling, they tend to require more samples to explore without exploiting the semantic information of action relation, which prevents them from performing better. By contrast, GLSR make an endeavor to incorporate the semantic relation encoding into action representation, which facilitates its competitive performance in the tasks that requires complex cooperation.

Table 1. Comparison results on SMAC maps for different methods.

Map	Difficulty	MAT	MAPPO	HAPPO	RODE	GLSR	Steps
3s5z	Hard	100 (1.9)	96.9 (0.7)	90.0 (3.5)	93.8 (2.0)	100 (0.3)	1e7
3s_vs_5z	Hard	95.1 (1.7)	100 (2.5)	91.9 (5.3)	78.9 (4.2)	100 (1.8)	1e7
5m_vs_6m	Hard	89.5 (5.7)	89.1 (2.5)	73.8 (4.4)	71.1 (9.2)	91.6 (4.4)	1e7
6h_vs_8z	Superhard	98.8 (1.3)	88.3 (3.7)	10.1 (1.4)	78.1 (37.0)	99.6 (0.9)	2e7
MMM2	Superhard	93.8 (2.6)	81.8 (10.1)	0.0 (0.0)	89.8 (6.7)	100 (0.0)	2e7
27m_vs_30m	Superhard	96.1 (5.7)	93.8 (2.4)	53.0 (37.0)	96.8 (1.5)	100 (0.7)	1e7

Note: The bold values indicate the best performance.

4.2. Ablation Experiments and Analysis

We analyze the primary factors of the GLSR performance. Ablation results have been provided on two superhard maps 3s5z_vs_3s6z and 27m_vs_30m.

4.2.1. Analysis of the Collaborative Learning

We compare a two-stage model denoted as GLSR-ts, which sequentially encodes the action semantics and learns the cooperation-aware action representations in two-stage manner instead of collaboratively learning. In other words, GLSR-ts firstly employs graph encoder to integrate semantic relations into action semantic embeddings with the objective in (4). Then, GLSR-ts obtains cooperation-aware action latent representations and performs action prediction with the clipping PPO objective , while the obtained action semantic embeddings are frozen. As is shown in Figure 6, the effectiveness of the collaborative learning can be validated, especially in modeling of more heterogeneous behaviors.

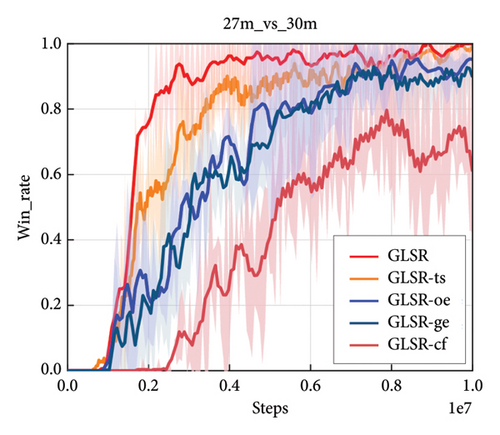
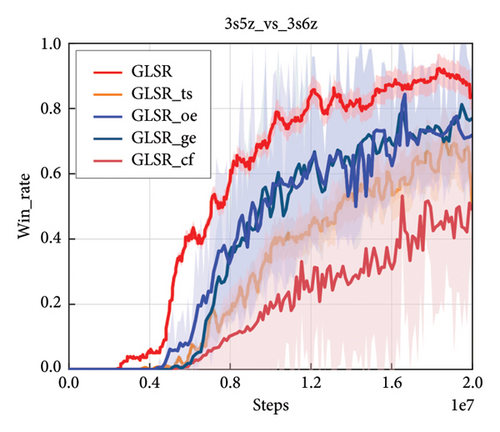
4.2.2. Analysis of the Semantic-Guided Interaction Based on Cross-Attention Mechanism

We also compare a simple interaction-based GLSR denoted as GLSR-cf, where embedded actions and cooperation embeddings are concatenated and fused through a two-layer MLP instead of the interaction through the cross-attention mechanism. As is shown in Figure 6, GLSR significantly outperforms GLSR-cf variation in terms of win rate.

4.2.3. Analysis of the Action Semantic Encoding

For validating the effectiveness of the GLSR, we compare two plain models denoted as GLSR-ge and GLSR-oe, which are implemented without action semantic encoding. They utilize the action embeddings generated by standard normal distribution function and one-hot vectors, respectively. Results in Figure 6 show the statistical effectiveness of the action semantic encoding. This is because the action embeddings of GLSR learn the structure of the action semantic space so that they can obtain more semantic relation information than Gaussian or one-hot-based embeddings.

4.3. Training Data Utilization

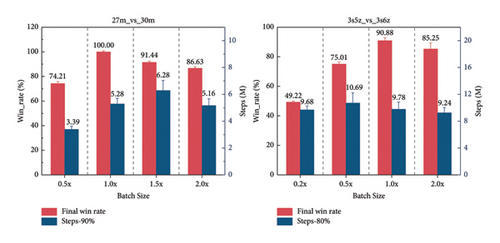
A key component of policy iteration is the use of importance sampling to sample reuse, and for the sake of data integrity, a large batch size is commonly used together with training for tens of epochs. In order to gain the deep insight of GLSR’s performance effected by the training data quantities, we consider different multiples of the batch size adopted in initial results, represented as 0.5x, 1x, 0.5x, and 2x, respectively, where x is the product of episode length and rollout threads as shown in Tables A1 and A2 of Appendix A. The final win rates are displayed by red bar clusters. The blue bar clusters show the total number of environment steps essential to achieve a high-level win rate (90% on 27m_vs_30m and 80% on 3s5z_vs_3s6z) as a measure of sample efficiency. From Figure 7, we observe that in superhard maps, larger data batches typically result in better convergence for GLSR, which benefits value function estimation and policy updating. However, an overabundance of data could place burdens on computational resources and result in the worsening sample efficiency. Therefore, we suggest using larger batches of data based on computing resources to attain optimal performance, and then fine-tuning the data batch to maximize data efficiency.

4.4. Parameter Sensitivity

Figure 8 gives an illustration on how the performance of GLSR changes with respect to win rate with the varying trade-off parameter β. The parameter β represents the impact of semantic relation learning on multiagent action prediction of multiagent, especially in complex tasks that require diversified behavior exploration and more skillful coordination. Figure 8 shows the comparison with parameter β between 0 and 2 on superhard SMAC tasks. When the β is large, GLSR exhibits a remarkably rapid growing trend with regard to win rate, which may benefit from the effective exploration of cooperative behavior via our action semantic encoding. In our experiment, we choose β = 1 for GLSR in various tasks.

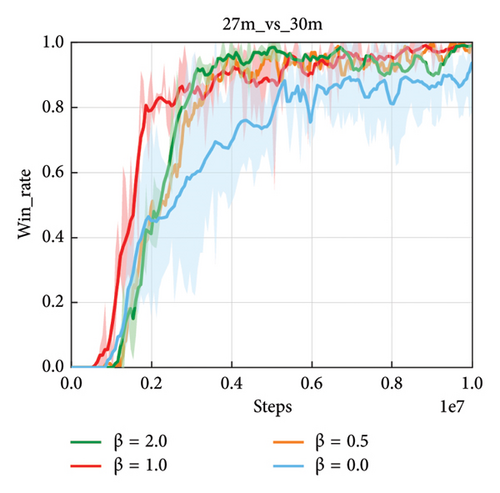
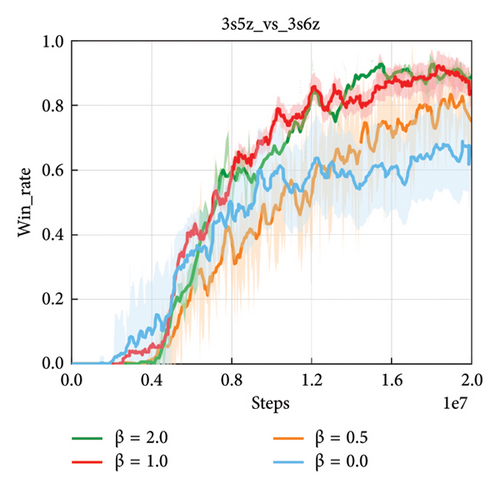
However, too small β may hinder the framework from achieving higher win rate, since the independence among the noncooperative action embeddings can hardly be guaranteed without the decoding with in (4). As is shown in Figure 8 that the case of β = 0 that corresponds to GLSR without suffers from the severe performance degradation. This indicates that is effective in decoding for the noncooperative action embeddings to pull apart from each other, which is necessary for complex cooperation modeling.

4.5. Comparison Results in Distributed Scenario

For fair comparison, we present statistical results of the win rate and standard deviation comparison of the GLSR-var with other CTDE-based methods such as MAPPO and MAT-Dec (CTDE variants of MAT), which use a completely decentralized actor network for each agent. The performance results are shown in Table 2. It is shown that our GLSR-var outperforms other CTDE-based methods, which is mainly attributed to the cooperation-aware representation.

Table 2. Comparison results on SMAC maps for CTDE-based methods.

Map	Difficulty	MAT-dec	MAPPO	GLSR-var	Steps
3s5z	Hard	100 (3.3)	96.9 (0.7)	100 (2.3)	1e7
3s_vs_5z	Hard	100 (1.7)	100 (2.5)	100 (0.6)	1e7
5m_vs_6m	Hard	83.1 (4.6)	89.1 (2.5)	86.1 (4.5)	1e7
6h_vs_8z	Superhard	93.8 (4.7)	88.3 (3.7)	95.1 (3.7)	2e7
MMM2	Superhard	91.2 (5.3)	81.8 (10.1)	92 (6.3)	2e7
3s5z_vs_3s6z	Superhard	85.3 (7.5)	74.3 (8.4)	89.3 (2.2)	2e7

Note: The bold values indicate the best performance.

5. Conclusion

We present the GLSR method within collaborative learning framework in this paper, where the learning of action semantics and action latent representation can mutually guide and reinforce each other. GLSR exploits the structure of the action semantic space for the learning of intricate cooperative relationship among actions, which facilitates the cooperation-aware representation and policy optimization of MARL. The action semantic relations captured by graph autoencoder are utilized to prompt actor network to learn the cooperation-aware joint action representation, which implicitly guides agent cooperation in joint policy space for more diverse behaviors of cooperative agents. We have demonstrated that GLSR achieves highly competitive performance against current well-established MARL methods. In the future, we will develop more sophisticated interaction between action semantics and latent representation since it may be significant to identify the most influential edge between two elements that contributes to the final performance.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the Key Research and Development Program of Shaanxi (Program No. 2022ZDLGY03-02), the National Natural Science Foundation of China (Grant Nos. 62106134, 62476159), and Qinchuangyuan Project of “Scientists + Engineers” Team Construction in Shanxi Province (Grant Nos. 2022KXJ-035, 2023KXJ-286).

Acknowledgments

Appendix A: Implementation Details of GLSR

In this paper, two GIN layers are employed in GLSR to encode action semantic relation for semantic embeddings. Table A1 shows the implementation details. Specifically, the dimensionality of the cooperation embeddings as shown in “embedding size” is used for a semantic specific learnable mapping. “GLSR_lr” refers to the learning rate of action semantic encoding network and “weight decay” simplifies the complexity of graph learning. The maximal training data length of action semantic encoding module should be set to override the collected action data in replay buffer.

In our experiments, the parameter settings of compared algorithms remain unchanged according to their best performance settings from their original repositories. The proposed method also adopts common practices including death masking, GAE with the PopArt value normalization and value clipping. The common hyperparameters adopted in the SMAC domain are listed in Table A2. The different hyperparameters used for respective algorithms and tasks are listed in Table A3. In these tables, “episode length” stands for the number of environment steps over a trajectory collected at once and “epoch number” represents the training number of sequence trajectory data in a “num mini-batch,” which is set to 1 especially in superhard maps. “Clip parameter” is the parameter for clipping term in the loss function. “Num_env_steps” stands for the total number of environment steps over the whole task. “Use huber loss” whether the huber loss function is applied to the optimized procedure and “huber delta” refers to δ in Huber loss function. “GLSR_coef” represents β in equation (12) which is set to 1. “Lr” represents the learning rate of critic and actor networks and “gamma” refers to the discount factor for rewards. “GAE_lambda” describes the GAE lambda parameter for balancing variance and bias of estimation value.

Table A1. Hyperparameters used in the semantic relation graph learning module.

Hyperparameters	Value
GLSR_lr	1e − 3
Weight decay	1e − 5
Embedding size	128
Activation	ReLU
Hidden layer	1
Max epoch length	800

Table A2. Hyperparameters adopted in SMAC.

Hyperparameters	Value
Actor	1
GLSR	1
lr	5e − 4
Gamma	0.99
gae_lambda	0.95
Use huber loss	True
Activation	ReLU
Optimizer	Adam
Use PopArt	True
Huber delta	10
Num mini-batch	1
Eval episodes	32
Training threads	1
Max grad norm	10
Rollout threads	32

Table A3. Different hyperparameters used for GLSR, MAT, MAPPO, and HAPPO in hard (H) and superhard (SP) maps.

Hyperparameters	GLSR		MAT		MAPPO		HAPPO
Hyperparameters	H	SP	H	SP	H	SP	H	SP
Episode length	200	400	100	100	100	100	100	100
Epoch number	5	5	5	15	5	15	5	15
Clip parameter	0.2	0.2	0.2	0.05	0.2	0.05	0.2	0.05
num_env_steps	1e7	2e7	1e7	2e7	1e7	2e7	1e7	2e7

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Troullinos D., Chalkiadakis G., Papamichail I., and Papageorgiou M., Collaborative Multiagent Decision Making for Lane-Free Autonomous Driving, Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, 2021, 1335–1343.
Google Scholar
2 Feriani A. and Hossain E., Single and Multi-Agent Deep Reinforcement Learning for Ai-Enabled Wireless Networks: A Tutorial, IEEE Communications Surveys and Tutorials. (2021) 23, no. 2, 1226–1252, https://doi.org/10.1109/comst.2021.3063822.
10.1109/COMST.2021.3063822
Web of Science® Google Scholar
3 Zhang C., Tian Y., Zhang Z. et al., Neighborhood Cooperative Multiagent Reinforcement Learning for Adaptive Traffic Signal Control in Epidemic Regions, IEEE Transactions on Intelligent Transportation Systems. (2022) 23, no. 12, 25157–25168, https://doi.org/10.1109/tits.2022.3173490.
10.1109/tits.2022.3173490
Google Scholar
4 Wang B., Gao X., and Xie T., An Evolutionary Multi-Agent Reinforcement Learning Algorithm for Multi-Uav Air Combat, Knowledge-Based Systems. (2024) 299, https://doi.org/10.1016/j.knosys.2024.112000.
10.1016/j.knosys.2024.112000
PubMed Google Scholar
5 Liu D., Zong Q., Zhang X., Zhang R., Dou L., and Tian B., Game of Drones: Intelligent Online Decision Making of Multi-Uav Confrontation, IEEE Transactions on Emerging Topics in Computational Intelligence. (2024) 8, no. 2, 2086–2100, https://doi.org/10.1109/tetci.2024.3360282.
10.1109/tetci.2024.3360282
Google Scholar
6 Piao H., Han Y., He S. et al., Spatiotemporal Relationship Cognitive Learning for Multirobot Air Combat, IEEE Transactions on Cognitive and Developmental Systems. (2023) 15, no. 4, 2254–2268, https://doi.org/10.1109/tcds.2023.3250819.
10.1109/tcds.2023.3250819
Google Scholar
7 Jiang T., Zhuang D., and Xie H., Anti-Drone Policy Learning Based on Self-Attention Multi-Agent Deterministic Policy Gradient, International Conference on Autonomous Unmanned Systems, 2021, Springer, 2277–2289.
Google Scholar
8 Cheng Z., Ye D., Zhu T., Zhou W., Yu P. S., and Zhu C., Multi-Agent Reinforcement Learning via Knowledge Transfer With Differentially Private Noise, International Journal of Intelligent Systems. (2022) 37, no. 1, 799–828, https://doi.org/10.1002/int.22648.
10.1002/int.22648
Web of Science® Google Scholar
9 Yang M., Zhao J., Hu X., Zhou W., Zhu J., and Li H., LDSA: Learning Dynamic Subtask Assignment in Cooperative Multi-Agent Reinforcement Learning, Advances in Neural Information Processing Systems. (2022) 35, 1698–1710.
Google Scholar
10 De Witt C. S., Gupta T., Makoviichuk D. et al., Is Independent Learning All You Need in the Starcraft Multi-Agent Challenge?, 2020, arXiv preprint arXiv:2011.09533.
Google Scholar
11 Yu C., Velu A., Vinitsky E. et al., The Surprising Effectiveness of Ppo in Cooperative Multi-Agent Games, Advances in Neural Information Processing Systems. (2022) 35, 24611–24624.
Google Scholar
12 Kuba J., Chen R., Wen M. et al., Trust Region Policy Optimisation in Multi-Agent Reinforcement Learning, ICLR 2022-10th International Conference on Learning Representations, the International Conference on Learning Representations, 2022, ICLR.
Google Scholar
13 Sunehag P., Lever G., Gruslys A. et al., Value-Decomposition Networks for Cooperative Multi-Agent Learning Based on Team Reward, Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, 2018, 2085–2087.
Google Scholar
14 Rashid T., Samvelyan M., Schroeder C., Farquhar G., Foerster J., and Whiteson S., QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning, International Conference on Machine Learning, 2018, PMLR, 4295–4304.
Google Scholar
15 Son K., Kim D., Kang W. J., Hostallero D. E., and Yi Y., QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning, International Conference on Machine Learning, 2019, PMLR, 5887–5896.
Google Scholar
16 Lowe R., Wu Y. I., Tamar A., Harb J., Pieter Abbeel O., and Mordatch I., Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments, Advances in Neural Information Processing Systems. (2017) 30.
Google Scholar
17 Foerster J., Farquhar G., Afouras T., Nardelli N., and Whiteson S., Counterfactual Multi-Agent Policy Gradients, Proceedings of the AAAI Conference on Artificial Intelligence, 2018.
Google Scholar
18 Liu S., Zhou Y., Song J. et al., Contrastive Identity-Aware Learning for Multi-Agent Value Decomposition, Proceedings of the AAAI Conference on Artificial Intelligence. (2023) 37, no. 10, 11595–11603, https://doi.org/10.1609/aaai.v37i10.26370.
10.1609/aaai.v37i10.26370
Google Scholar
19 Li C., Wang T., Wu C., Zhao Q., Yang J., and Zhang C., Celebrating Diversity in Shared Multi-Agent Reinforcement Learning, 2021, 3991–4002.
Google Scholar
20 Shao J., Lou Z., Zhang H., Jiang Y., He S., and Ji X., Self-Organized Group for Cooperative Multi-Agent Reinforcement Learning, 2022, 5711–5723.
Google Scholar
21 Wang T., Gupta T., Mahajan A., Peng B., Whiteson S., and Zhang C., Rode: Learning Roles to Decompose Multi-Agent Tasks, International Conference on Learning Representations, 2021.
Google Scholar
22 Munikoti S., Agarwal D., Das L., Halappanavar M., and Natarajan B., Challenges and Opportunities in Deep Reinforcement Learning With Graph Neural Networks: A Comprehensive Review of Algorithms and Applications, IEEE Transactions on Neural Networks and Learning Systems. (2024) 35, no. 11, 15051–15071, https://doi.org/10.1109/tnnls.2023.3283523.
10.1109/tnnls.2023.3283523
PubMed Google Scholar
23 Zhang B., Li L., Xu Z., Li D., and Fan G., Inducing Stackelberg Equilibrium Through Spatio-Temporal Sequential Decision-Making in Multi-Agent Reinforcement Learning, Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence. (2023) 40, 353–361, https://doi.org/10.24963/ijcai.2023/40.
10.24963/ijcai.2023/40
Google Scholar
24 Liu B., Liu Q., Stone P., Garg A., Zhu Y., and Anandkumar A., Coach-Player Multi-Agent Reinforcement Learning for Dynamic Team Composition, Proceedings of the 38th International Conference on Machine Learning. (2021) 139, 6860–6870.
Google Scholar
25 Vaswani A., Attention Is All You Need, 2017, arXiv preprint arXiv:1706.03762.
Google Scholar
26 Wen M., Kuba J., Lin R. et al., Multi-Agent Reinforcement Learning Is a Sequence Modeling Problem, Advances in Neural Information Processing Systems. (2022) 35, 16509–16521.
Google Scholar
27 Yang Y. and Wang J., An Overview of Multi-Agent Reinforcement Learning From Game Theoretical Perspective, 3. (2020) arXiv preprint arXiv:2011.0058.
Google Scholar
28 Claus C. and Boutilier C., The Dynamics of Reinforcement Learning in Cooperative Multiagent Systems, AAAI/IAAI 1998, 1998.
Google Scholar
29 Littman M. L., Markov Games as a Framework for Multi-Agent Reinforcement Learning, Machine Learning Proceedings 1994, 1994, Elsevier, 157–163.
10.1016/B978-1-55860-335-6.50027-1
Google Scholar
30 Foerster J., Chen R. Y., Al-Shedivat M., Whiteson S., Abbeel P., and Mordatch I., Learning With Opponent-Learning Awareness, Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, 2018, 122–130.
Google Scholar
31 Iqbal S. and Sha F., Actor-Attention-Critic for Multi-Agent Reinforcement Learning, International Conference on Machine Learning, 2019, PMLR, 2961–2970.
Google Scholar
32 Peng B., Rashid T., Schroeder de Witt C. et al., Facmac: Factored Multi-Agent Centralised Policy Gradients, Advances in Neural Information Processing Systems. (2021) 34, 12208–12221.
Google Scholar
33 Ding Z., Huang T., and Lu Z., Learning Individually Inferred Communication for Multi-Agent Cooperation, Advances in Neural Information Processing Systems. (2020) 33, 22069–22079.
Google Scholar
34 Li S., Gupta J. K., Morales P., Allen R., and Kochenderfer M. J., Deep Implicit Coordination Graphs for Multi-Agent Reinforcement Learning, Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, 2021, 764–772.
Google Scholar
35 Niu Y., Paleja R., and Gombolay M., Multi-Agent Graph-Attention Communication and Teaming, Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, 2021, 964–973.
Google Scholar
36 Dong S., Li C., Yang S., Li W., and Gao Y., Decentralized Counterfactual Value With Threat Detection for Multi-Agent Reinforcement Learning in Mixed Cooperative and Competitive Environments, Expert Systems With Applications. (2024) 257, https://doi.org/10.1016/j.eswa.2024.125116.
10.1016/j.eswa.2024.125116
Google Scholar
37 Gu S., Grudzien Kuba J., Chen Y. et al., Safe Multi-Agent Reinforcement Learning for Multi-Robot Control, Artificial Intelligence. (2023) 319, https://doi.org/10.1016/j.artint.2023.103905.
10.1016/j.artint.2023.103905
Google Scholar
38 Wang X., Tian Z., Wan Z., Wen Y., Wang J., and Zhang W., Order Matters: Agent-By-Agent Policy Optimization, The Eleventh International Conference on Learning Representations, 2023.
Google Scholar
39 Zhang Y., Zhang X., Wang J. et al., Generalized Relation Learning With Semantic Correlation Awareness for Link Prediction, Proceedings of the AAAI Conference on Artificial Intelligence. (2021) 35, no. 5, 4679–4687, https://doi.org/10.1609/aaai.v35i5.16598.
10.1609/aaai.v35i5.16598
Google Scholar
40 Na H., Seo Y., and Chul Moon I., Efficient Episodic Memory Utilization of Cooperative Multi-Agent Reinforcement Learning, The Twelfth International Conference on Learning Representations, 2024.
Google Scholar
41 van der Heiden T., Salge C., Gavves E., and van Hoof H., Robust Multi-Agent Reinforcement Learning With Social Empowerment for Coordination and Communication, 2020, arXiv preprint arXiv:2012.
Google Scholar
42 Xie A., Losey D., Tolsma R., Finn C., and Sadigh D., Learning Latent Representations to Influence Multi-Agent Interaction, Conference on Robot Learning, 2021, PMLR, 575–588.
Google Scholar
43 Wang W. Z., Shih A., Xie A., and Sadigh D., Influencing Towards Stable Multi-Agent Interactions, Conference on Robot Learning, 2022, PMLR, 1132–1143.
Google Scholar
44 Böhmer W., Kurin V., and Whiteson S., Deep Coordination Graphs, International Conference on Machine Learning, 2020, PMLR, 980–991.
Google Scholar
45 Majumdar S., Khadka S., Miret S., McAleer S., and Tumer K., Evolutionary Reinforcement Learning for Sample-Efficient Multiagent Coordination, International Conference on Machine Learning, 2020, PMLR, 6651–6660.
Google Scholar
46 Li P., Hao J., Tang H., Zheng Y., and Fu X., Race: Improve Multi-Agent Reinforcement Learning With Representation Asymmetry and Collaborative Evolution, International Conference on Machine Learning, 2023, PMLR, 19490–19503.
Google Scholar
47 Samarasinghe D., Barlow M., Lakshika E., and Kasmarik K., Exploiting Abstractions for Grammar-Based Learning of Complex Multi-Agent Behaviours, International Journal of Intelligent Systems. (2021) 36, no. 11, 6273–6311, https://doi.org/10.1002/int.22550.
10.1002/int.22550
Web of Science® Google Scholar
48 Hang J.-Y. and Zhang M.-L., Collaborative Learning of Label Semantics and Deep Label-Specific Features for Multi-Label Classification, IEEE Transactions on Pattern Analysis and Machine Intelligence. (2022) 44, no. 12, 9860–9871, https://doi.org/10.1109/tpami.2021.3136592.
10.1109/tpami.2021.3136592
Google Scholar
49 Kharbanda S., Gupta D., Schultheis E., Banerjee A., Hsieh C.-J., and Babbar R., Gandalf: Learning Label-Label Correlations in Extreme Multi-Label Classification via Label Features, Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2024, 1360–1371, https://doi.org/10.1145/3637528.3672063.
10.1145/3637528.3672063
Google Scholar
50 Chen Z.-M., Wei X.-S., Wang P., and Guo Y., Multi-label Image Recognition With Graph Convolutional Networks, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, 5177–5186.
Google Scholar
51 Littman M. L., Markov Games as a Framework for Multi-Agent Reinforcement Learning, Proceedings of the Eleventh International Conference on International Conference on Machine Learning, 1994, 157–163, https://doi.org/10.1016/b978-1-55860-335-6.50027-1.
10.1016/b978-1-55860-335-6.50027-1
Google Scholar
52 Espeholt L., Soyer H., Munos R. et al., Impala: Scalable Distributed Deep-Rl With Importance Weighted Actor-Learner Architectures, International Conference on Machine Learning, 2018, PMLR, 1407–1416.
Google Scholar
53 Xu K., Hu W., Leskovec J., and Jegelka S., How Powerful Are Graph Neural Networks?, 2018, arXiv preprint arXiv:1810.00826.
Google Scholar
54 Schulman J., Moritz P., Levine S., Jordan M., and Abbeel P., High-Dimensional Continuous Control Using Generalized Advantage Estimation, 2015, arXiv preprint arXiv:1506.02438.
Google Scholar
55 Hu S., Shen L., Zhang Y., and Tao D., Graph Decision Transformer, 2023, arXiv preprint arXiv:2303.03747.
Google Scholar
56 Cai D. and Lam W., Graph Transformer for Graph-To-Sequence Learning, Proceedings of the AAAI Conference on Artificial Intelligence. (2020) 34, no. 05, 7464–7471, https://doi.org/10.1609/aaai.v34i05.6243.
10.1609/aaai.v34i05.6243
Google Scholar
57 Mnih V., Kavukcuoglu K., Silver D. et al., Human-level Control Through Deep Reinforcement Learning, Nature. (2015) 518, no. 7540, 529–533, https://doi.org/10.1038/nature14236, 2-s2.0-84924051598.
10.1038/nature14236
CAS PubMed Web of Science® Google Scholar
58 Samvelyan M., Rashid T., Schroeder de Witt C. et al., The Starcraft Multi-Agent Challenge, Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, 2019, 2186–2188.
Google Scholar

All articles

Graph Learning of Semantic Relations (GLSR) for Cooperative Multiagent Reinforcement Learning

Abstract

1. Introduction

2. Related Work

2.1. MARL

2.2. Semantic Modeling for Cooperative MARL

2.3. Collaborative Learning

3. GLSR for MARL

3.1. Problem Formulation

3.2. Action Semantic Encoding

3.3. Semantic-Guided Actor Network

3.4. Critic Network

3.5. Optimization Objective

3.6. Extension of GLSR to CTDE Framework

4. Experiments

4.1. Performance on SMAC

4.2. Ablation Experiments and Analysis

4.2.1. Analysis of the Collaborative Learning

4.2.2. Analysis of the Semantic-Guided Interaction Based on Cross-Attention Mechanism

4.2.3. Analysis of the Action Semantic Encoding

4.3. Training Data Utilization

4.4. Parameter Sensitivity

4.5. Comparison Results in Distributed Scenario

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Appendix A: Implementation Details of GLSR

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley