The convergence of machine learning and searchable encryption enhances the ability to protect the privacy and security of data and enhances the processing power of confidential data. To enable users to efficiently perform machine learning tasks on encrypted data domains, we delve into oblivious keyword search with authorization (OKSA). The OKSA scheme effectively maintains the privacy of the user’s query keywords and prevents the cloud server from inferring ciphertext information through the searching process. However, limitations arise because the traditional OKSA approach does not support multi-keyword searches. If a data file is associated with multiple keywords, each keyword and corresponding data must be encrypted one by one, resulting in inefficiency. We introduce an innovative approach aimed at enhancing the efficiency of search processes while addressing the limitation of current encryption and search systems that handle only a single keyword. This method, known as the oblivious multiple keyword search with authorization (OMKSA), is designed for more effective keyword retrieval. One of our important innovations is that it uses the arithmetic techniques of bilinear pairs to generate new tokens and new search methods to optimize communication efficiency. Moreover, we present a detailed and rigorous demonstration of the security for our proposed protocol, aligned with the predefined security model. We conducted a comparative experiment to determine which of the two schemes, OKSA and OMKSA, is more efficient when querying multiple keywords. Based on our experimental results, our OMKSA is very efficient for data searchers. As the number of query keywords increases, the computational overhead of connected keyword searches remains stable. Finally, as we move into the 5G era, the potential applications of OMKSA are huge, with clear implications for areas such as machine learning and artificial intelligence. Our findings pave the way for further exploration and deployment of these frontier areas.

1. Introduction

In contemporary times, the convergence of machine learning (ML) [1, 2] and searchable encryption (SE) [3–5] is an important innovation. This combination will promote the enhancement of data privacy protection and the utility of big data. Known for their ability to self-learn and adapt, ML algorithms play a key role in retrieving huge datasets, recognizing patterns, and predicting outcomes. However, since these algorithms require access to large amounts of data for performance optimization, the task of maintaining data privacy and security is becoming increasingly important. To solve this problem, we can use SE technology [6], which can perform a secure search on encrypted data, ensuring data confidentiality while preserving the availability of encrypted information. The convergence of ML and SE enhances the ability to perform efficient secure data analysis on encrypted data to protect the privacy and security of the data.

However, there is an obvious problem in public key SE. The cloud server can infer the content and search keywords of outsourced data based on the frequency of retrieval, resulting in data privacy disclosure. However, most of the existing public-key SE schemes cannot solve the inside keyword guessing attack (IKGA) problem [7–10]. Specifically, an inside adversary is an honest but curious cloud server (and cloud server operator) that honestly executes search protocols but tries to infer user keywords and private information. Once the enemy obtains the keywords, it will threaten the security of the ciphertext data file, and it also means that the search preference, personal identity, and other information of the data receiver may be leaked. Therefore, solving the problem of internal keyword guessing attack is a very meaningful and important research topic. Several encryption schemes [11–15] have been designed to solve this problem. However, their search efficiency is relatively low. This highlights the need for a cryptographic search method that is resistant to internal keyword guessing attacks.

Ogata and Kurosawa proposed the oblivious keyword search (OKS) concept [16]. The OKS scheme protects the privacy of both the database and the client. On the one hand, it is to hide the user’s query database target, and on the other hand, it is to ensure that the client gets any other information except the corresponding value of the query target. At the same time, the privacy of keywords is protected, and the cloud server cannot carry out keyword guessing attacks by matching trap information and keyword information. However, in this scheme, each data file can only be associated with one keyword, and in the encryption process, each ciphertext supports only one keyword encryption search. If a file has multiple keywords, the file must be encrypted multiple times. Obviously, most files have more than one keyword.

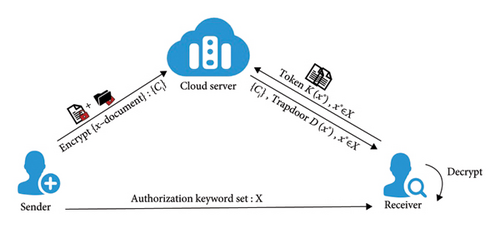
In addition, the existing OKS protocol has proven to be inefficient when applied to large databases. We need to consider a situation where a company intends to sell a portion of its encrypted data stored on cloud servers, and potential buyers face these restrictions because they want to keep the details of the specific data content of the intended purchase private. In this case, the sender may approve the set of keywords to be retrieved for the receiver and then restrict the receiver from querying the keywords in that set. Specifically, if X represents a set of authorization keywords, the recipient can only select the keyword w ∈ X. At the same time, while the sender allows the encrypted data associated with the keyword X to be retrieved from set X, they still do not know the specific keyword used, thus protecting the privacy of the receiver. In order to solve this problem, the oblivious keyword search with authorization (OKSA) [17] solution came into being. While OKSA protects the privacy of both recipients and senders, there is an obvious problem. This model binds a single keyword to a single data file, and if a file contains multiple keywords, then each keyword and file need to be encrypted individually, which is obviously inefficient. We introduced the oblivious multiple keyword search with authorization (OMKSA) scheme, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The framework of OMKSA.

1.1. Our Contributions

This paper’s primary advancements are detailed in the following ways:

1.
We came up with a new concept called OMKSA. It is based on the OKSA scheme. In the OKSA scheme, each encrypted data file is bound to a separate keyword. If the file contains a large number of keywords, we must encrypt each keyword and file one by one; otherwise, the retrieval will fail due to inaccurate keyword extraction. Furthermore, in the real world, where a single file often contains multiple keywords, OKSA cannot meet the need for efficiency. In the OMKSA scheme, we improved the encryption algorithm to allow the data provider to assign several keywords to each encrypted file. And the scheme can resist the internal keyword guessing attack problem.
2.
We designed OMKSA protocol. Compared with OKSA protocol, our algorithm has higher efficiency when searching multiple keywords. We have carefully designed our approach to disjunctive and conjunctive keyword search, which will meet the flexible needs of users and cloud storage providers. And it adds no additional communication or storage overhead compared to the OKSA scheme searching for the same number of keywords.
3.
We have compiled OMKSA scheme and analyzed the efficiency of OMKSA scheme compared with OKSA scheme through comprehensive simulation experiment. The results show that this scheme can effectively improve the efficiency of multi-keyword search. In addition, in-depth security assessments show that OMKSA meets the needs of artificial intelligence (AI) applications in the 5G era.

1.2. Related Works

Here are some pertinent studies.

1.2.1. Public Key Encryption With Keyword Search (PEKS)

As far as we know, PEKS [4] has undergone significant development and improvement since they were proposed by Boneh et al. The initial design was intended to address the limitations of symmetric searchable encryption (SSE) [18–21] by developing a unique mechanism. This mechanism allows the generation of searchable ciphertext using the user’s public key and specific keywords. This innovation makes it not only feasible to search on encrypted data, but it can be very efficient. This innovation began the history of SE, which later researchers introduced many improvements and tweaks aimed at enhancing security and enhancing functionality. The advent of secure channel-free PEKS (SCF-PEKS) scheme [22–25] is a big development in preventing keyword guessing attacks on cloud servers. The untrustworthiness of cloud servers can compromise search confidentiality. Functionality enhancements were not left behind. The advancement in multi-keyword search capabilities is significantly enhanced by the integration of public-key encryption with conjunctive keyword search (PECKS) [26–30]. The introduction of public-key cryptography with temporary keyword searches (PETKS) [31] by Abdalla et al. is another important research result, as it not only significantly improves the usability of database systems but also enables the flexibility of keyword searches. The transformation protocol connects identity-based encryption (IBE) [32] to encrypted data to enable search under ciphertext, further enriching the field of cryptography. The attribute-based encryption (ABE) scheme [33–35] provides subtle control over data search and enhanced privacy protection in the cloud environment [36, 37].

1.2.2. Oblivious Transfer

The origins of inadvertent diversion (OT) [38] can be traced back to Rabin’s seminal work. In the framework of the oblivious transfer protocol, the procedure is marked by an interaction between a sender, denoted as , and a receiver, indicated as . This interaction facilitates a transaction where the sender is unaware of which specific bit the receiver chooses, and the receiver is equally uninformed about the unselected bit. This approach to ensuring the privacy of both parties during transmission has led to the emergence of many OT variants [39–41], all of which contribute to enhanced security and functional diversity.

1.2.3. OKS

The design of OKS [16] is focused on ensuring rigorous privacy safeguards. It is meticulously designed to mask all informative traces, including access patterns, ensuring a user’s query and retrieval activities remain concealed. The pioneering OKS protocol, elucidated by Ogata and Kurosawa, is anchored in the oblivious polynomial evaluation and the oblivious transfer methodologies. The protocol facilitates a user’s engagement with a database in a manner that allows data acquisition without revealing any details about the search keywords or content to the data provider.

Ogata and Kurosawa developed two separate protocols. The first relies on the intricacies of the one-more RSA inversion problem, while the second depends on the difficulties inherent in polynomial reconstruction. Nonetheless, a constraint is manifested in these initial models, and the search is confined to a singular keyword per query. Rhee et al. advanced the narrative by unveiling an oblivious conjunctive keyword search (OCKS) protocol [42]. Rooted in the RSA known target inversion complexity, this enhancement expanded the search capacity. Simultaneously, Freedman and colleagues tackled the issue of privacy-preserving database access by proposing an efficient framework [43]. This structure links keyword search activities with the oblivious evaluation of pseudorandom functions, creating a cohesive framework. Zhu and Bao further enriched this dialog, leveraging enhanced OPEs [44] to craft an OKS protocol, and validated its security credentials. Notwithstanding these advancements, an inefficiency permeates previous OKS protocols; they are confined to a one-keyword-to-one-document architecture. This limitation amplifies both storage requisites and search durations, particularly pronounced when a document is tagged with multiple keywords, necessitating the replication of the document for each associated keyword. Jiang and Liu confronted this challenge, proposing an adept OKS protocol characterized by sublinear time search efficiency and compact ciphertexts [45]. However, it is circumscribed to disjunctive keyword search and is not configured for conjunctive keyword search applications. In this context, OKS continues to evolve, enhancing privacy while facing inherent operational constraints. Since Ogata and Kurosawa first introduced the OKS concept, new protocols have been developed to emphasize the need for coordination between strict privacy protection and operational efficiency. The exploration and resolution of these challenges are not only intrinsic to OKS’ progress but also a necessity in an era when data are ubiquitous and privacy is often under attack. Future research is expected to further address this complex problem, seeking innovative solutions for data privacy, search efficiency, and functional versatility in the OKS field. Zhang et al. introduced an advanced oblivious multiple keyword search (OMKS) service [46], designed to provide users and cloud storage providers with strong privacy protection while enabling efficient multi-keyword search. Jiang et al. introduced an innovative cryptographic primitive known as OKSA [17]. Specifically, OKSA streamlines the verification of search keywords, confirming their inclusion in the user’s authorized set prior to activating the OKS protocol. This feature enables user authorization and extends the level of privacy and security of traditional OKS.

1.2.4. The Integration of ML and SE

The combination of ML and SE is an emerging field that combines the efficient data processing of ML with the privacy protection principles of SE. In the era of big data, concerns about privacy are escalating, prompting people to seek solutions that can efficiently process data while protecting privacy. ML models can extract and process valuable information from massive datasets. However, when applied to sensitive data, a privacy-security conundrum emerges. SE has emerged as a viable solution that allows searching of encrypted data, thus ensuring data privacy [47]. One of the seminal works in this domain is CryptoNets [48], which explores the use of neural networks in encrypting data to make predictions about it while protecting data privacy. This method uses homomorphic encryption technology to convert data into encrypted form and realizes the calculation in ciphertext state. However, homomorphic encryption, while revolutionary, is computationally expensive. This leads to some solutions, such as personal data collection (PATE) [49]. It uses different private learning methods, aggregating the results of multiple models to protect privacy.

Kamil Khudhair et al. optimized image steganography [50–52] to support multiple scenes, high efficiency, and high security. This inspired us to improve the OKS scheme, combining it with deep learning to further achieve high efficiency and enable multi-scenario application. Raghunandan et al. used chaotic behavior [53] to encrypt data for greater security. How to easily access the encrypted data needs to be fully considered, and our scheme can achieve searchability in the encrypted state. Asmitha et al. perfected the problems of computer vision and deep learning in human authentication [54]. This further reinforces the need for ML and SE. ML needs to invoke a lot of private data, and our solution ensures the safe use of private data. Ramesh et al. introduced false modulus in the public key encryption process to improve the security of Rabin cryptosystem [55]. This is a very interesting study and encourages us to continue to investigate how to implement the security of SE on ML.

More recent advancements have broached efficient protocols like SecureML [56], which enhances scalability and efficiency, which improves the computational challenges inherent in privacy-protecting ML. Furthermore, innovations like oblivious neural network predictions (MiniONN) [57] have facilitated privacy-preserving by transforming existing neural network models into oblivious counterparts. With the convergence of ML and SE, the focus is shifting to ensuring data privacy without compromising the quality of ML predictions. The future trajectory may be to explore enhanced computing efficiency, robust security protocols, and common applications that span different data domains.

1.3. Organization

Section 2 presents essential foundational concepts, details the OMKSA algorithm, describes the security model, and discusses the underlying complexity assumptions. Section 3 introduces an efficient OMKSA protocol, while Section 4 offers a security proof. Section 5 focuses on conducting a thorough analysis and assessing the performance of the system. Additionally, Section 6 delves into applications in the field of ML. The paper concludes in Section 7.

2. Preliminaries

2.1. Notations

The symbols and terms utilized in this paper are efficiently compiled in Table 1.

Table 1. Notations.

Notation	Description
	A data sender
	The cloud server
	The receiver
X	Authorization keyword set
x^∗	Search keyword
α	The master secret key
K(x^∗)	Token of ^∗
D(x^∗)	Trapdoor cryptosystem of ^∗
L	A collection of search results
	The actual number of keywords retrieved
D	The maximum number of keywords that can be retrieved simultaneously

2.2. Bilinear Pairing

are two multiplicative cyclic groups of order p, any generator of

is g, and bilinear mapping

satisfies the following properties [58]:

1.
Bilinearity: For the generator g of , the other generator h of , and the positive integers a, b, we can get the equation: e(g^a, h^b) = e(g, h)^ab.
2.
Computability: For any element g, , we can efficiently compute e, which is a probabilistic polynomial algorithm.
3.
Non-degeneracy: There are two elements in , g and h, that satisfy the equation: e(g, h) ≠ 1. 1 is the identity element of . 1 is the identity element of .

e is a symmetric bilinear pair mapping, and the corresponding symmetric double planet pair system is denoted by .

2.3. Algorithm Definition

Our OMKSA solution interacts with three parties: the data sender, the cloud server, and the data receiver.

2.3.1. Setup

Commencing the procedure, the entity provides a security parameter denoted by 1^λ and an integer value n, subsequently generating the master key pair (MPK, MSK) for cryptographic system configuration. Furthermore, in collaboration with each user, establishes a distinct keyword set X, ensuring that the size of X does not exceed n².

2.3.2. Commit

processes a message m_i, a designated keyword x_i, and the MPK to produce the corresponding encrypted data C_i. Notably, each message m_i is coupled with a distinct keyword array . Subsequently, securely transmits the collection of ciphertexts {C_i} to the cloud storage .

2.3.3. Transfer

It is assumed that

establishes a distinct keyword set X in negotiations with each receiver

, where

: In this step, inputs the designated keyword set X, including specific keywords within X and MPK. This leads to the creation of the token of keywords, along with the user’s secret key sk and Γ which is proof of accountability. Then, the token and proof, represented as , are sent to . The token is derived from sk, , and MPK, with Γ aiding in verifying the token’s accountability, specifically ensuring it generates a trapdoor for a valid keyword in the set X.
: inputs the token and the MSK to affirm accountability, verifying that . It then generates a trapdoor D for delivery to .
: On the condition that the sequence aligns with , upon receiving inputs C_i, D, sk, will yield m_i; otherwise, it results in ⊥.

2.3.4. Correctness

For an OMKSA to be deemed effective, it is essential that the recipient accurately acquires the specified message, provided all involved parties comply with the outlined protocol. Furthermore, the authenticity is validated when accountability checks confirm that the trapdoor created from the acquired token corresponds exclusively to specific keywords. It is also crucial that these keywords fall within the scope of the authorized keyword collection.

2.4. Security Notions

Based on the previous article [4, 16], our framework establishes three key security criteria: confidentiality for the receiver, indistinguishability, and accountability. The first aspect, user confidentiality, ensures that during the i − th transaction phase, the sender, denoted as

, is unable to infer the search keywords from the user’s token. The principle of indistinguishability acts as a protective measure, preventing a potentially adversarial receiver, labeled

, from deciphering both the message and keyword embedded within the ciphertext. The accountability aspect primarily ensures that each trapdoor request by a user is distinctly linked to a specific keyword in the authorized keyword array.

Receiver privacy
For a receiver, discerning whether x is x₀ or x₁ becomes challenging when presented with (K(x), Γ) and the pair of keywords x₀, x₁.
Indistinguishability
When faced with a ciphertext C for (m, x) and two distinct message-keyword pairs (m₀, x₀) and (m₁, x₁), the receiver finds it difficult to determine if (m, x) matches (m₀, x₀) or (m₁, x₁).
Accountability
For scenarios where (K(X), X, sk) meets the condition |X| > 1, crafting (K(X), Γ) that successfully undergoes verification is a complex task.

In light of the specified requirements, our formulation of the security models is through a series of interactive games involving a challenger, denoted as , and an opponent, referred to as .

2.4.1. User Privacy

Setup.
executes the Setup procedure, thereby generating the system parameter MPK which is then transmitted to the adversary .
Challenge.
The adversary proposes two distinct keywords x₀, x₁ to the challenger . In response, selects a random θ ∈ 0, 1, sets x to x_θ, and produces (K(X), Γ).
Guess.
attempts to guess by announcing θ^′ and succeeds if θ^′ matches θ.

The advantage of is quantified as Adv = |Pr[θ^′ = θ] − 0.5|.

Definition 1. The OMKSA framework is deemed to adhere to user privacy standards when it is infeasible for any adversary operating in probabilistic polynomial-time to secure a substantial edge in the stipulated user privacy contest.

2.4.2. Indistinguishability

Setup.
The challenger executes the Setup protocol to produce the system parameter MPK and forwards it to adversary .
First Stage.
In this stage, requests a trapdoor for keyword X, and complies by providing trapdoor D.
Challenge.
presents two equally long message-keyword pairs (m₀, x₀) and (m₁, x₁) to , ensuring that x₀, x₁ were not previously queried for trapdoors in the First Stage. then issues a challenge ciphertext C^∗, selecting θ randomly from 0,1.
Second Stage.
continues to make trapdoor requests under the same constraints as the Challenge, with providing responses similarly to the First Stage.
Guess.
proposes a guess of θ^′ and is victorious if it matches θ.

The advantage of is defined as Adv = |Pr[θ^′ = θ] − 0.5|.

Definition 2. OMKSA achieves indistinguishability against chosen keyword attacks if no adversary, employing probabilistic polynomial time approaches, can significantly succeed in the described game.

2.4.3. Accountability

In OMKSA, the essence of accountability verification lies in confirming that each trapdoor produced is exclusively linked to a single permitted keyword. This process counteracts scenarios where an adversary, denoted as

, might construct a legitimate keyword token K(X^′), with X^′ being a fraction of the endorsed keyword set X, maintaining that 1 < |X^′| < |X| ≤ n, indicating

’s awareness of X^′, X, and the secret key sk used in the token’s formation.

Setup.
Executing the Setup phase, the challenger creates the system’s parameter MPK and subsequently dispatches this parameter to the adversary .
Challenge.
Here, presents (K(X^′), X, X^′, sk) alongside a numeral 1 for the challenge, deriving K(X^′) from X, X^′, sk, MPK with |X^′| exceeding 1.
Win.
The adversary submits (K(X^′), Γ) and is deemed victorious if this submission successfully clears the verification process.

The edge of in this scenario is determined as Adv in the formulation of (K(X^′), Γ).

Definition 3. Accountability within an OMKSA framework is established when no adversary, operating within polynomial time bounds, can achieve success in the previously outlined game with a notable margin.

2.5. Assumptions

The foundational security constructs of OKSA are built upon two complex challenges: the (f, n)-DHE Problem and the (f, q)-MSE-DDH Problem. While the former has been introduced in earlier works [59], here we provide only a brief overview, directing readers to these references for a thorough exploration of its complexities.

Definition 4. The challenge in the (f, n)-DHE Problem within a group of prime order p, involving elements and , is to compute (f(x), h^f(a)) from the given sequence . In this context, f(x) represents a polynomial within whose degree is greater than n.

The (f, q)-MSE-DDH Problem is a refined variant of the MSE-DDH Problem, preserving the original problem’s complexity. This problem stands as a particular case within the broader set of Diffie–Hellman exponent assumptions, as discussed in the previous article [60]. Detailed intractability analysis of this problem will be presented later. For more details, please refer to the paper [59].

3. OMKSA Protocol

In this segment, we introduce a protocol designed for OMKSA. This protocol seamlessly accommodates both disjunctive and conjunctive keyword searches, thanks to the integration of innovative token architectures and the implementation of sophisticated search algorithms as delineated in [59]. Moreover, our protocol endows the receiver with the capability to unobtrusively secure an authorized trapdoor by adaptively presenting a keyword token. A hallmark of this system is its efficiency, characterized by the constant size of communication overhead incurred between and . is enabled to construct a trapdoor nested within X without the capacity to ascertain the specific keyword in question. The OMKSA protocol engages three entities: a data sender , a cloud server , and a receiver , unfolding over three distinct phases: Setup, Commit, and Transfer.

3.1. Disjunctive Keyword Search

The scheme facilitates the execution of disjunctive keyword searches by innovatively creating tokens and applying sophisticated search techniques. Imagine a scenario where the data receiver, denoted as , aims to locate documents that include either keyword x₁ OR x₂. In such cases, the OMKSA scheme is implemented as follows.

3.1.1. Setup

Entity

begins by accepting a security parameter denoted as 1^λ, an integer value n, and the group system

. Following this,

selects generator elements g, h from

, and chooses random numbers α, x from

. It proceeds to calculate g^α and

for each i ranging from 1 to n + 1 for i = 1, 2, …, n + 1. A individual hash function H mapping from

to a binary string of length

is also selected. The ensuing steps involve the generation of the master key pair:

()

Entity makes the MPK available to everyone and maintains the confidentiality of K.

3.1.2. Commit

Within the framework, the complete keyword space is represented by

, encompassing a total of n² elements. Each message is paired with corresponding keywords. For a given message m_i within the binary set

and associated keywords

from

, the entity

selects a random value r_i from

, It then calculates β as the product of

and forms the encrypted message C_i in the following manner:

()

Subsequently, securely transmits the collection of ciphertexts {C_i} to the receiver .

3.1.3. Transfer

It is assumed that establishes a distinct keyword set X for each receiver, with and the size of X is denoted as |X| = k not exceeding n².

: With the predefined keyword set X, and specific keywords

alongside the MPK, the receiver

chooses a random number s from

and let sk = s. Then,

, formulate the tokens, where

and

correspond to the chosen keywords to be searched by

()

and the proof Γ is

()

Then sends and to .

: Given the tuple

, with the master public key MPK in hand,

proceeds to verify accountability using the subsequent equations,

()

and

()

When both equations are satisfied, it confirms that the tokens K₁, K₂ are associated with the authorized set of keywords, indicated as

()

In cases where this condition is not met, the algorithm terminates. Upon having the MSK and the keyword set

then proceeds to generate the trapdoors D₁, D₂ as

()

Then returns the trapdoor D₁, D₂ to .

: Upon receiving C_i, D₁, D₂, sk, the entity

initiates the process of searching by

()

Should the preceding equation be satisfied, the receiver

then proceeds with the decryption process by

()

adds to a list L⁽¹⁾ and adds to a list L⁽²⁾, and has L = L⁽¹⁾ ∪ L⁽²⁾ as final calculation.

3.1.4. Extension to D Keywords

The outlined OMKSA protocol, initially configured for disjunctive keyword search, is readily expandable to encompass D keywords. The data receiver computes for each where , subsequently recovering and compiling the list for every keyword. The final step entails aggregating the lists corresponding to all D keywords to yield the comprehensive disjunctive search outcome.

3.1.5. Correctness

With the (MPK, MSK) obtained from the Setup, and

at hand, the verification of accountability’s correctness hinges on the fulfillment of the following expression.

()

With the ciphertext C_i obtained through the execution of the Commit algorithm, coupled with the trapdoors D₁ and D₂ generated via Transfer, and the user’s sk, the process to validate the accuracy of the scheme’s function involves

()

3.2. Conjunctive Keyword Search

Imagine a scenario where the data receiver is inclined to retrieve documents that encompass both keywords x₁ AND x₂. An initial instinct might be to adapt the protocol aligned with the earlier elaborated disjunctive keyword search; essentially, would amass the list T⁽¹⁾ correlated with keyword x₁ and T⁽²⁾ associated with x₂, culminating in the intersection T = T⁽¹⁾∩T⁽²⁾ to finalize the conjunctive search outcome. However, this approach is riddled with the pitfall of information leakage, as inadvertently gains access to documents extraneous to the intersection T⁽¹⁾∩T⁽²⁾. In simple terms, if a file c₁ contains the keyword x₁, but does not contain the keyword x₂, then it belongs to set T₁, and if a file c₂ does not contain the keyword x₁, but contains the keyword x₂, it belongs to set T₂, and neither file should be searched by the data receiver . His searching scope includes these files which must contain two keywords x₁ and x₂. Therefore, the resulting set of files for the data recipient is required to be the intersection of T₁ and T₂. Otherwise, the search scope of the data receiver will be expanded, causing the pitfall of information leakage.

To navigate around this challenge, an enhancement of the protocol is requisite, one that curtails from accessing data that are not explicitly within the search range. The refinement of the protocol unfolds as delineated in the succeeding text.

3.2.1. Setup

Entity

, takes as input a security parameter 1^λ, an integer n and the group tuple

as Section 3.1.1. Then

selects generator elements g and h from

, along with random values α, x from the set

. It then calculates

for i = 1, 2, …, n + 1.

is also employed. The construction of the master key pair follows these steps.

()

Entity makes the MPK publicly available while ensuring the confidentiality of MSK.

3.2.2. Commit

In the defined keyword space

, which encompasses n elements, each message is linked to specific keywords. For any given message m_i within the binary space

and its associated set of keywords

from

, the system

selects a random r_i from

, and calculates

. C_i is

()

securely transfers the set of ciphertexts {C_i} to the recipient .

3.2.3. Transfer

It is assumed that establishes a distinct set of keywords, X, for each receiver. This set X, a subset of , is characterized by having a maximum size denoted as X, where |X| = k and does not exceed n².

: In the context of the authorized keyword collection X, encompassing specific keywords

within X, and with access to MPK, the participant

selects a random s from

to serve as sk = s and proceeds to calculate the corresponding token

()

and the proof Γ as

()

Then sends to .

: With the set

and the MPK at hand,

undertakes the verification of accountability through the application of specific equations,

()

When the conditions of both equations are satisfied,

confirms that the provided keyword token corresponds to a singular keyword trapdoor, indicated by

. In the event of a failure to meet these conditions, the operation is terminated. Upon possessing MSK and the keyword set X, entity

proceeds to generate the specific trapdoor D.

()

Subsequently, hands over the trapdoor D to .

: Upon this transfer, with C_i, the trapdoor D, and the secret key sk in possession,

commences the search operation

()

Upon verification,

proceeds with the next steps of the decryption process

()

3.2.4. Correctness

With the (MPK, MSK) obtained through the execution of the Setup algorithm, and equipped with the token or proof combination

, the validation of accountability’s accuracy is determined through a series of specific equations.

()

Upon receiving the ciphertext C_i generated through the Commit algorithm, along with the trapdoor D created via the Transfer, and the user’s sk, one can authenticate the effectiveness of the search and decryption processes

()

4. Security Analysis

Our analysis focuses on the security aspects of the OMKSA protocol, in accordance with the framework outlined in Section 2.3. This security reduction draws its foundation from the complex problems specified in Section 2.4. A thorough and systematic proofing process is outlined in the subsequent discussion.

4.1. Receiver Privacy

Theorem 1. In the framework, the assurance of absolute keyword privacy for the token, as it pertains to the receiver, is achieved within the context of the privacy game.

Proof 1. Consider X as the set of authorized keywords, and the pair (K(X), Γ) derived from the condition x = x₀. The resultant formulation of the keyword token and its corresponding proof is as follows:

()

In the case of a unique keyword x₁, and with s^′ chosen from , we adopt the implicit assignment s^′ = s · (α + x₁)/(α + x₀). This results in an equivalence of keyword tokens, namely, K(x₀) equals K(x₁), a fact that is substantiated through the following verification:

()

Let us consider Γ^′ to be composed of . In this scenario, the accountability proofs are found to be congruent, signifying Γ₁ is equal to and Γ₂ is equal to . This equivalency can be substantiated through the following validation:

()

The equivalence (K(x₀), Γ) = (K(x₁), Γ^′) holds true. Given that s is selected at random from , it follows that s^′ possesses uniform randomness within as well. Consequently, the distributions of (K(X), Γ) corresponding to both x₀ and x₁ are indistinguishable, offering no leverage to an adversary in predicting the keyword encapsulated in K(X). This argument forms the basis for the conclusion of Theorem 1.

4.2. Indistinguishability

Theorem 2. It is structured to ensure semantic security and indistinguishability, as per the criteria of the Indistinguishability game, under the assumption that solving the (f, q)-MSE-DDH Problem is an arduous task, as delineated in [60].

Proof 2. Imagine an adversary, referred to as , capable of undermining this indistinguishability. Under this hypothesis, we can devise an algorithm, named , specifically engineered to tackle the (f, q)-MSE-DDH Problem. Given a scenario with a (f, q)-MSE-DDH Problem instance and a variable Z in , the mission for is to ascertain if Z is equal to or if it is a randomly chosen element within . The strategic interplay between and is elaborated in the following explanation.

4.2.1. Setup

The foundational premise posits a universal keyword space, represented as

selects a specific keyword x_θ from

, with the associated message symbolized as m_θ. The algorithm tacitly establishes the polynomials.

()

Additionally, the algorithm lets

and it gets

. Following this,

forwards MPK to adversary

, where

()

4.2.2. H-Query

The entity

operates a hash list designated as L(a_i, X_i, hⁱ), starting in an empty state. When a query for H(a_i, X_i) is received and if the tuple (a_i, X_i) already exists within L, then

provides the associated hⁱ back to

. In cases where (a_i, X_i) is not present in L,

determines the hash value hⁱ using the following approach.

()

Selections for are made randomly from the binary set . Subsequently, incorporates (a_i, X_i, hⁱ) into the list and furnishes hⁱ back to .

4.2.3. Phase 1

In this phase, selects a set of keywords X, confined within the bounds of , and limited to a maximum size of |X| not more than n. For a trapdoor request corresponding to any keyword x_i from opts for a random as sk = s, and communicates (x_i, s) to .

Should x_i matches x_θ, the process is terminated.

In contrast, if x_i differs from delivers to , with q_i(α) defined as (q(α))/(α + x_i).

Subsequent steps involve verifying the trapdoor.

()

It becomes apparent that the expression can be computed from elements , as provided in the instance.

4.2.4. Challenge

When presents the pairs (m₀, x₀) and (m₁, x₁) as a challenge to , and assuming no prior trapdoor queries have been made for x₀ or x₁, the protocol proceeds as follows.

If x_θ is neither x₀ nor x₁, the process halts.

However, if x_θ matches either x₀ or x₁,

verifies the presence of (0, Z) and (1, Z) within the list L. If found,

retrieves and labels the corresponding hash values as

and

. In the absence of these entries,

randomly generates

and

from the binary set

and proceeds to set them accordingly.

()

Subsequently,

incorporates the pairs

and

into the compilation L. Following this,

furnishes

with the designated ciphertext for the challenge.

()

Verification of the condition

is feasible by assigning the value of r as r_if(α) in an implicit manner.

()

Hence, the ciphertext C^∗ constitutes an appropriate challenge.

In the scenario where Z represents a random variable within , from the perspective of , C^∗ emerges as a random ciphertext.

4.2.5. Phase 2

seeks further trapdoor queries for x_i, adhering to the constraint x_i ≠ x₀, x₁. In response, acts in accordance with the guidelines of Phase 1.

4.2.6. Guess

The adversary

generates a prediction, denoted as θ^′, aiming to ascertain the value of θ. With this step, our simulation narrative reaches its completion. Next, we transition to an analysis phase, probing the proficiency of

in unraveling the intricate hard problem. Let us assume q_T represents the total volume of trapdoor queries and n symbolizes the magnitude of the keyword space. In light of the preceding simulation dynamics, the probability of

persevering without an abortive outcome is delineated in the following sections.

()

Given that queries for x₀ and x₁ were not made in either Phase 1 or Phase 2, the quantity q_T is bounded by n − 2. Consequently, the probability Pr[abort] is no less than 2/n. Assuming

’s success in compromising the security game is at least ϵ, the reduction in advantage can be represented as

()

From this, the advantage of in resolving the (f, q) − MSE − DDH Problem is calculated to be at least , thus finalizing the proof of Theorem 2.

4.3. Accountability

Theorem 3. The framework’s competence in ensuring accountability is validated within the accountability game, contingent on the intractability of the (f, n) − DHE Problem [17].

Proof 3. Let us hypothesize the existence of an adversary who is capable of compromising the accountability security. In this case, an algorithm is formulated to address the (f, n) − DHE Problem. Confronted with a (f, n) − DHE challenge, engages with in the following manner.

4.3.1. Setup

Algorithm

assigns α = a, leading to the derivation of

, as per the (f, n) − DHE scenario. Subsequently,

selects H akin to the actual scheme. Then

circulates the MPK for

()

4.3.2. Challenge

selects two unique keyword sets, X and X^′, ensuring |X^′| > 1 and |X| ≤ n. A secret key sk is then established by randomly choosing a value s from

, with sk = s. Following this,

proposes (K(X^′), X, X^′, sk) along with a challenge indication set to 1. Here, the token K is characterized as

()

4.3.3. Win

The adversary

selects two keyword sets, X and X^′, conforming to the constraints |X^′| > 1 and |X| ≤ n. Upon choosing a random secret key s from

, denoted as sk = s,

then formulates and submits (K(X^′), X, X^′, sk) with a challenge indicator set to 1. The token within this setup is characterized as

()

Consequently, both the token and its associated proof are capable of successfully undergoing the matching process as follows:

()

Let ; then Γ = h^f(a). Given that the function f(x) is classified as a polynomial with a degree, deg f(x), surpassing n, it follows that furnishes the pair (f(x), Γ) as the resolution of the (f, n)-DHE Challenge. The conclusion of this proof of Theorem 3 leads to the deduction that the magnitude of X^′ is singular, |X^′| = 1, and correspondingly, the token K(X^′) also possesses a singular count, |K(X^′)| = 1.

5. Performance Evaluation

The experiment was conducted on the Ubuntu-22.04.3-desktop-amd64 operating system, with Linux hardware specifications: an 11th Gen Intel (R) Core i5-1135G7 CPU @2.40 GHz and 40.0 G of RAM. All program algorithms were implemented using the 8.3.1 20190311 (Red Hat 8.3.1-3) (GCC) compiler. The experimental data were derived from a dataset of n = 10, generated by random algorithms. We executed both the OKSA and OMKSA protocols on these data. OKSA is designed by Jang, which can only query keywords one by one. OMKSA is based on OMKSA made by us and can query multiple keywords at the same time. When we want to compare queries for the same keywords, our scheme is more efficient than the OKSA scheme.

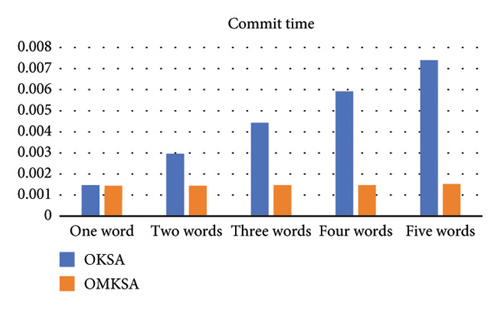
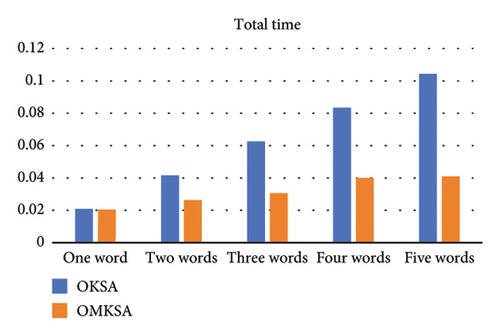
To illustrate the effectiveness of actual search terms, we varied the number of query keywords D from 1 to 5. The following figure compares the two scenarios and depicts an increase in search time with the augmentation of keyword quantity. The items from left to right are setup time2a, commit time2b, transfer to time2c, transfer to time2d, transfer time2e, and total time2f. We found that OMKSA is designed to query multiple keywords simultaneously, and the OMKSA protocol runtime does not increase with the number of queried words in the setup and commit algorithms. However, the OKSA scheme needs to query keywords one by one, and the query time will double as the number of query keywords increases.

As shown in Figure 2, at t = 1, the total time consumed by both protocols is almost the same; however, for t ≥ 2, the total time consumption of OMKSA is notably less than that of OKSA. Furthermore, the increase in duration for OMKSA is minimal, indicating its aptness for retrieval under multi-keyword scenarios.

Since cloud servers are not trusted, replay attacks are possible. We can further solve the problem of cloud server replay attacks in the future to further ensure the security of cloud storage. In addition, the proposed scheme works well in the laboratory environment, but the experimental data are limited, and it has not been applied in the real scene, which may cause unknown problems. It is necessary to further improve the scheme in the process of application.

6. Application in ML

The applications of OMKSA within the realm of ML are interesting. Users are able to execute ML tasks on encrypted data domains without revealing the contents of training data or the queries. Integrating this with ML poses both challenges and significant practical value. For instance, data in sectors like healthcare and finance, even when encrypted, may still require ML operations. In addition, users might not want to expose the specifics of their queries or the parameters and structure of their ML models.

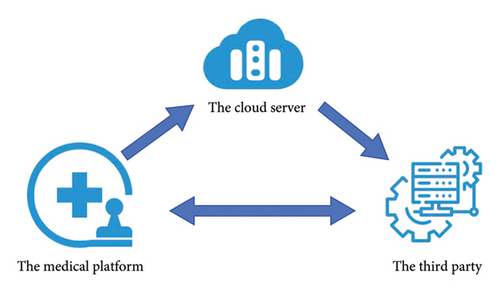
6.1. Applied on the Medical Platform

The convergence of AI and SE holds expansive prospects for application within the healthcare platform. This realm of possibility not only underscores the importance of leveraging technological advances but also signals a transformative shift in the way healthcare data are managed and accessed.

To expand on this, we must first understand the tremendous role that AI plays in healthcare. AI systems have the potential to revolutionize the medical field by offering personalized medicine, predictive analytics, and enhanced patient care. From analyzing medical images for early disease detection to predicting patient outcomes based on data trends, AI is pushing the boundaries of what is achievable in medicine. Also, AI is now poised to bridge the patient–doctor gap with automatic diagnostic tools that can operate round the clock. On the other hand, the significance of SE in protecting patient data cannot be overstated. The plethora of data generated in healthcare, from patient records to vital signs, necessitates a stringent data privacy policy. SE offers the solution by not only encrypting these data but also allowing them to be searched without being decrypted. It provides an avenue for secure querying of databases while safeguarding sensitive patient information.

Now, let us consider the combined force of AI and SE. When these technologies are integrated, we can pave the way for a reliable, encrypted database where AI can freely and securely extract insights. The use of SE can ensure the privacy of the data while AI can efficiently analyze the data to facilitate improved healthcare. This fusion of technologies can thus pave the way for a new era of medical treatment and patient management. For instance, consider a healthcare portal where users employ distinct keywords to classify their health issues. The company operating this medical platform employs Public Key SE to securely store user information and uploads encrypted data onto a cloud server. To broaden their business scope, the firm opts to delve deeper into research involving its user base, such as identifying common illnesses like “Hypertension,” “Periarthritis of Shoulder,” “Cervical Spondylosis,” “Osteoporosis,” and “Diabetes.” To achieve this objective, the organization delegates the task to an expert external agency, which is tasked with managing these activities while rigorously safeguarding the confidentiality of user health information. Figure 3 illustrates the framework, with the main steps outlined below.

1.
Data protection and encryption process: The company meticulously gathers user data, utilizing Public Key SE techniques to securely encrypt the information prior to its upload.
2.
Task transfer: The company establishes the parameters by collaborating with the third party, utilizing OMKSA for secure transformation of the encrypted data.
3.
Task computation: The external agency conducts analytical operations and then relays the findings back to the company.

6.2. Data Preprocessing and Feature Selection

In contemporary ML applications, data preprocessing is not just a prerequisite step, but it also profoundly influences the overall model performance and accuracy. To achieve optimal training results, it might be necessary to sift through vast encrypted data repositories to select critical data subsets for comprehensive analysis. This step often entails choosing and categorizing a myriad of features. With the introduction of the OMKSA technique, researchers can now employ multi-keyword searches to select specific data or features from encrypted datasets. Crucially, this process ensures that there is no disclosure regarding which particular keywords the researchers are keen on, thereby preserving search privacy.

6.3. Distributed ML

Distributed ML and federated learning have become essential strategies for multi-organizational collaborative ventures. In such settings, various entities or organizations aim to collaboratively develop a robust, shared ML model. However, due to concerns spanning data privacy, legal regulations, and intellectual property rights, the direct sharing of raw data becomes infeasible. The advent of OMKSA provides a novel solution to this conundrum. Using OMKSA, one organization can securely authorize another entity to search specific segments of its encrypted data. This means multiple entities can collaborate and train models without directly sharing any tangible data.

7. Conclusion

In this study, we introduced the advanced concept of OMKSA, which improves the traditional OKSA scheme to accommodate multi-keyword search. While traditional OKSA limits each encrypted data file to a single keyword association, OMKSA gives data providers the flexibility to extract multiple keywords for each encrypted dataset. Our analysis and experiments confirm that the OMKSA protocol is both practical and easy to implement for querying encrypted data in a cloud environment. A significant innovation of our approach lies in its integration of aggregation algorithms to generate the trapdoor. Consequently, the sender sent a fixed-size trapdoor to the receiver, enhancing the efficiency of communication.

Additionally, a comprehensive security analysis of the proposed protocol has been conducted, adhering to recognized security models. Notably, when benchmarked against existing OKSA protocols, our OMKSA stands out as exceptionally efficient for data seekers. Moreover, the computational overhead for conjunctive keyword searches remains stable, regardless of an increase in the volume of query keywords. Finally, for the replay attack problem, we may use the password accumulator tool in the future to further solve the problem of cloud server replay attack to ensure the security of cloud storage. Conclusively, as we transition into the 5G era, the potential applications for OMKSA are vast, with pronounced implications for domains like ML and AI. Our findings pave the way for further exploration and deployment in these cutting-edge fields.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 62402290, U24A20244, 62302280, and 62072276), Natural Science Foundation of Shandong Province (No. ZR2023QF133), and Youth Innovation Team of Shandong Higher Education Institutions (No. 2024KJN051).

Acknowledgments

Open Research

Data Availability Statement

The data used to support the findings of this study are available from the corresponding authors upon request.

References

1 Jia H., Aldeen M. S., Zhao C., Jing S., and Chen Z., Flexible Privacy-Preserving Machine Learning: When Searchable Encryption Meets Homomorphic Encryption, International Journal of Intelligent Systems. (2022) 37, no. 11, 9173–9191, https://doi.org/10.1002/int.22985.
10.1002/int.22985
Web of Science® Google Scholar
2 Shouval R., Fein J. A., Savani B. N., Mohty M., and Nagler A., Machine Learning and Artificial Intelligence in Haematology, British Journal of Haematology. (2020) 192, no. 2, 239–250, https://doi.org/10.1111/bjh.16915.
10.1111/bjh.16915
PubMed Web of Science® Google Scholar
3 Song D. X., Wagner D. A., and Perrig A., Practical Techniques for Searches on Encrypted Data, Proceeding 2000 IEEE Symposium on Security and Privacy. S&P 2000, 2000, 44–55.
Google Scholar
4 Boneh D., Di Crescenzo G., Ostrovsky R. M., and Persiano G., Public Key Encryption With Keyword Search, Lecture Notes in Computer Science. (2004) 506–522, https://doi.org/10.1007/978-3-540-24676-3_30.
10.1007/978-3-540-24676-3_30
Google Scholar
5 Liu J., Zhao B., Qin J., Zhang X., and Ma J., Multi-Keyword Ranked Searchable Encryption With the Wildcard Keyword for Data Sharing in Cloud Computing, The Computer Journal. (2021) 66, no. 1, 184–196, https://doi.org/10.1093/comjnl/bxab153.
10.1093/comjnl/bxab153
Google Scholar
6 Zhang X., Zhao B., Qin J., Hou W., Su Y., and Yang H., Practical Wildcard Searchable Encryption With Tree-Based Index, International Journal of Intelligent Systems. (2021) 36, no. 12, 7475–7499, https://doi.org/10.1002/int.22595.
10.1002/int.22595
Web of Science® Google Scholar
7 Byun J. W., Rhee H. S., Park H. A., and Lee D. H., Off-Line Keyword Guessing Attacks on Recent Keyword Search Schemes Over Encrypted Data, Lecture Notes in Computer Science. (2006) 75–83, https://doi.org/10.1007/11844662_6.
10.1007/11844662_6
Google Scholar
8 Jeong I. R., Kwon J. O., Hong D., and Lee D. H., Constructing PEKS Schemes Secure Against Keyword Guessing Attacks Is Possible?, Computer Communications. (2009) 32, no. 2, 394–396, https://doi.org/10.1016/j.comcom.2008.11.018, 2-s2.0-58249100325.
10.1016/j.comcom.2008.11.018
Web of Science® Google Scholar
9 Abdalla M., Bellare M., Catalano D. et al., Searchable Encryption Revisited: Consistency Properties, Relation to Anonymous IBE, and Extensions, Journal of Cryptology. (2008) 21, no. 3, 350–391, https://doi.org/10.1007/s00145-007-9006-6, 2-s2.0-43449138479.
10.1007/s00145-007-9006-6
Web of Science® Google Scholar
10 Yau W. C., Phan C. W., Heng S. H., and Goi B. M., Keyword Guessing Attacks on Secure Searchable Public Key Encryption Schemes With a Designated Tester, International Journal of Computer Mathematics. (2013) 90, no. 12, 2581–2587, https://doi.org/10.1080/00207160.2013.778985, 2-s2.0-84890119628.
10.1080/00207160.2013.778985
Web of Science® Google Scholar
11 Boneh D., Kushilevitz E., Ostrovsky R. M., and Skeith W. E., Public Key Encryption That Allows PIR Queries, Lecture Notes in Computer Science. (2007) 50–67, https://doi.org/10.1007/978-3-540-74143-5_4.
10.1007/978-3-540-74143-5_4
Google Scholar
12 Chen R., Mu Y., Yang G., Guo F., and Wang X., Dual-Server Public-Key Encryption With Keyword Search for Secure Cloud Storage, IEEE Transactions on Information Forensics and Security. (2016) 11, no. 4, 789–798, https://doi.org/10.1109/tifs.2015.2510822, 2-s2.0-84959234916.
10.1109/TIFS.2015.2510822
Web of Science® Google Scholar
13 Zhi-Yi S., On Security Against the Server in Designated Tester Public Key Encryption with Keyword Search, Information Processing Letters. (2015) .
PubMed Google Scholar
14 Tang Q. and Chen L., Public-Key Encryption With Registered Keyword Search, 2009.
Google Scholar
15 Huang Q. and Li H., An Efficient Public-Key Searchable Encryption Scheme Secure Against Inside Keyword Guessing Attacks, Information Sciences. (2017) 403–404, 1–14, https://doi.org/10.1016/j.ins.2017.03.038, 2-s2.0-85017123858.
10.1016/j.ins.2017.03.038
Web of Science® Google Scholar
16 Ogata W. and Kurosawa K., Oblivious Keyword Search, Journal of Complexity. (2004) 20, no. 2-3, 356–371, https://doi.org/10.1016/j.jco.2003.08.023, 2-s2.0-1942420748.
10.1016/j.jco.2003.08.023
Web of Science® Google Scholar
17 Jiang P., Wang X., Lai J., Guo F., and Chen R., Oblivious Keyword Search With Authorization, Lecture Notes in Computer Science. (2016) 173–190, https://doi.org/10.1007/978-3-319-47422-9_10, 2-s2.0-84996520658.
10.1007/978-3-319-47422-9_10
Google Scholar
18 Cash D., Jarecki S., Jutla C., Krawczyk H., Roşu M. C., and Steiner M., Highly-Scalable Searchable Symmetric Encryption With Support for Boolean Queries, Lecture Notes in Computer Science. (2013) 353–373, https://doi.org/10.1007/978-3-642-40041-4_20, 2-s2.0-84884472579.
10.1007/978-3-642-40041-4_20
Google Scholar
19 Curtmola R., Garay J., Kamara S., and Ostrovsky R., Searchable Symmetric Encryption: Improved Definitions and Efficient Constructions, Journal of Computer Security. (2011) 19, no. 5, 895–934, https://doi.org/10.3233/jcs-2011-0426, 2-s2.0-81255134906.
10.3233/JCS-2011-0426
Google Scholar
20 Jarecki S., Jutla C., Krawczyk H., Rosu M., and Steiner M., Outsourced Symmetric Private Information Retrieval, Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security-CCS’ 13. (2013) 875–888, https://doi.org/10.1145/2508859.2516730, 2-s2.0-84889073373.
10.1145/2508859.2516730
Google Scholar
21 Kamara S., Papamanthou C., and Roeder T., Dynamic Searchable Symmetric Encryption, 2012.
Google Scholar
22 Rhee H. S., Susilo W., and Kim H. J., Secure Searchable Public Key Encryption Scheme Against Keyword Guessing Attacks, IEICE Electronics Express. (2009) 6, no. 5, 237–243, https://doi.org/10.1587/elex.6.237, 2-s2.0-64949106593.
10.1587/elex.6.237
Web of Science® Google Scholar
23 Rhee H. S., Park J. H., Susilo W., and Lee D. H., Improved Searchable Public Key Encryption With Designated Tester, Proceedings of the 4th International Symposium on Information, Computer, and Communications Security. (2009) 376–379, https://doi.org/10.1145/1533057.1533108, 2-s2.0-71549160150.
10.1145/1533057.1533108
Google Scholar
24 Fang L., Susilo W., Ge C., and Wang J., Public Key Encryption With Keyword Search Secure Against Keyword Guessing Attacks Without Random Oracle, Information Sciences. (2013) 238, 221–241, https://doi.org/10.1016/j.ins.2013.03.008, 2-s2.0-84876842378.
10.1016/j.ins.2013.03.008
Web of Science® Google Scholar
25 Noroozi M. and Eslami Z., Public Key Authenticated Encryption With Keyword Search: Revisited, IET Information Security. (2019) 13, no. 4, 336–342, https://doi.org/10.1049/iet-ifs.2018.5315, 2-s2.0-85062873405.
10.1049/iet-ifs.2018.5315
Web of Science® Google Scholar
26 Ballard L., Kamara S., and Monrose F., Achieving Efficient Conjunctive Keyword Searches Over Encrypted Data, Lecture Notes in Computer Science. (2005) 414–426, https://doi.org/10.1007/11602897_35, 2-s2.0-33646736337.
10.1007/11602897_35
Google Scholar
27 Boneh D. and Waters B., Conjunctive, Subset, and Range Queries on Encrypted Data, IACR Cryptology ePrint Archive. (2007) 2006.
Google Scholar
28 Park D. J., Kim K., and Lee P. J., Public Key Encryption With Conjunctive Field Keyword Search, 2004.
Google Scholar
29 Ryu E. K. and Takagi T., Efficient Conjunctive Keyword-Searchable Encryption, 1, 21st International Conference on Advanced Information Networking and Applications Workshops (AINAW’07), 2007, 409–414, https://doi.org/10.1109/ainaw.2007.166, 2-s2.0-35248839565.
10.1109/ainaw.2007.166
Google Scholar
30 Sedghi S., van Liesdonk P., Nikova S., Hartel P. H., and Jonker W., Searching Keywords With Wildcards on Encrypted Data, Lecture Notes in Computer Science. (2010) 138–153, https://doi.org/10.1007/978-3-642-15317-4_10, 2-s2.0-77958060874.
10.1007/978-3-642-15317-4_10
Google Scholar
31 Abdalla M., Bellare M., Catalano D. et al., Searchable Encryption Revisited: Consistency Properties, Relation to Anonymous IBE, and Extensions, Journal of Cryptology. (2008) 21, no. 3, 350–391, https://doi.org/10.1007/s00145-007-9006-6, 2-s2.0-43449138479.
10.1007/s00145-007-9006-6
Web of Science® Google Scholar
32 Camenisch J., Kohlweiss M., Rial A., and Sheedy C., Blind and Anonymous Identity-Based Encryption and Authorised Private Searches on Public Key Encrypted Data, Lecture Notes in Computer Science. (2009) 196–214, https://doi.org/10.1007/978-3-642-00468-1_12, 2-s2.0-67049154037.
10.1007/978-3-642-00468-1_12
Google Scholar
33 Shi J., Lai J., Li Y., Deng R. H., and Weng J., Authorized Keyword Search on Encrypted Data, Lecture Notes in Computer Science. (2014) 419–435, https://doi.org/10.1007/978-3-319-11203-9_24, 2-s2.0-84906483101.
10.1007/978-3-319-11203-9_24
Google Scholar
34 Sun W., Yu S., Lou W., Hou Y. T., and Li H., Protecting Your Right: Attribute-Based Keyword Search With Fine-Grained Owner-Enforced Search Authorization in the Cloud, IEEE INFOCOM 2014-IEEE Conference on Computer Communications, 2014, 226–234, https://doi.org/10.1109/infocom.2014.6847943, 2-s2.0-84904444112.
10.1109/infocom.2014.6847943
Google Scholar
35 Zheng Q., Xu S., and Ateniese G., VABKS: Verifiable Attribute-Based Keyword Search Over Outsourced Encrypted Data, IEEE INFOCOM 2014-IEEE Conference on Computer Communications, 2014, 522–530.
Google Scholar
36 Li J., Li J., Chen X., Liu Z., and Jia C., Privacy-Preserving Data Utilization in Hybrid Clouds, Future Generation Computer Systems. (2014) 30, 98–106, https://doi.org/10.1016/j.future.2013.06.011, 2-s2.0-84888349708.
10.1016/j.future.2013.06.011
PubMed Web of Science® Google Scholar
37 Li J., Lin D., Squicciarini A. C., Li J., and Jia C., Towards Privacy-Preserving Storage and Retrieval in Multiple Clouds, IEEE Transactions on Cloud Computing. (2017) 5, no. 3, 499–509, https://doi.org/10.1109/tcc.2015.2485214, 2-s2.0-85029920502.
10.1109/TCC.2015.2485214
Google Scholar
38 Rabin M. O., How to Exchange Secrets with Oblivious Transfer, IACR Cryptology ePrint Archive. (2005) 2005.
Google Scholar
39 Chu C. K. and Tzeng W. G., Efficient K-Out-of-N Oblivious Transfer Schemes With Adaptive and Non-Adaptive Queries, Lecture Notes in Computer Science. (2005) 172–183, https://doi.org/10.1007/978-3-540-30580-4_12.
10.1007/978-3-540-30580-4_12
Google Scholar
40 Kurosawa K. and Nojima R., Simple Adaptive Oblivious Transfer Without Random Oracle, IACR Cryptology ePrint Archive. (2009) 2009.
Google Scholar
41 Camenisch J., Dubovitskaya M., and Neven G., Oblivious Transfer With Access Control, IACR Cryptology ePrint Archive. (2009) 2009.
Google Scholar
42 Rhee H. S., Byun J. W., Lee D. H., and Lim J., Oblivious Conjunctive Keyword Search, 2005.
Google Scholar
43 Freedman M. J., Ishai Y., Pinkas B., and Reingold O., Keyword Search and Oblivious Pseudorandom Functions, Lecture Notes in Computer Science. (2005) 303–324, https://doi.org/10.1007/978-3-540-30576-7_17.
10.1007/978-3-540-30576-7_17
Google Scholar
44 Zhu H. and Bao F., Oblivious Keyword Search Protocols in the Public Database Model, 2007 IEEE International Conference on Communications, 2007, 1336–1341.
Google Scholar
45 Jiang Z. and Liu L., Secure Cloud Storage Service With an Efficient DOKS Protocol, 2013 IEEE International Conference on Services Computing, 2013, 208–215, https://doi.org/10.1109/scc.2013.37, 2-s2.0-84891934139.
10.1109/scc.2013.37
Google Scholar
46 Zhang R., Xue R., Liu L., and Zheng L., Oblivious Multi-Keyword Search for Secure Cloud Storage Service, 2017 IEEE International Conference on Web Services (ICWS), 2017, Honolulu, HI, 269–276.
Google Scholar
47 Bost R., Popa R. A., Tu S., and Goldwasser S., Machine Learning Classification over Encrypted Data, IACR Cryptology ePrint Archive. (2015) 2014.
Google Scholar
48 Dowlin N., Gilad-Bachrach R., Laine K., Lauter K. E., Naehrig M., and Wernsing J. R., CryptoNets: Applying Neural Networks to Encrypted Data With High Throughput and Accuracy, 2016.
Google Scholar
49 Papernot N., Abadi M., Erlingsson Ú, Goodfellow I. J., and Talwar K., Semi-Supervised Knowledge Transfer for Deep Learning From Private Training Data, ArXiv. (2016) .
Google Scholar
50 Kamil Khudhair S., Sahu M., K R. R., and Sahu A. K., Secure Reversible Data Hiding Using Block-Wise Histogram Shifting, Electronics. (2023) 12, no. 5, https://doi.org/10.3390/electronics12051222.
10.3390/electronics12051222
Google Scholar
51 Sahu A. K. and Sahu M., Digital Image Steganography Techniques in Spatial Domain-A Study, International Journal of Pharmacy and Technology. (2017) 8, no. 4, 5205–5217.
Google Scholar
52 Swain G. and Sahu A. K., A Novel Multi Stego-Image Based Data Hiding Method for Gray Scale Image, Pertanika Journal of Science and Technology. (2019) 27, no. 2, 753–768.
Google Scholar
53 Raghunandan K. R., Dodmane R., Bhavya K., Rao N. S. K., and Sahu A. K., Chaotic-Map Based Encryption for 3D Point and 3D Mesh Fog Data in Edge Computing, IEEE Access. (2023) 11, 3545–3554, https://doi.org/10.1109/access.2022.3232461.
10.1109/ACCESS.2022.3232461
Google Scholar
54 Asmitha P., Rupa C., Nikitha S., Hemalatha J., and Sahu A. K., Improved Multiview Biometric Object Detection for Anti Spoofing Frauds, Multimedia Tools and Applications. (2024) 83, no. 33, 80161–80177, https://doi.org/10.1007/s11042-024-18458-8.
10.1007/s11042-024-18458-8
Google Scholar
55 Ramesh R. K., Dodmane R., Shetty S., Aithal G., Sahu M., and Sahu A. K., A Novel and Secure Fake-Modulus Based Rabin-3 Cryptosystem, Cryptography. (2023) 7, no. 3, https://doi.org/10.3390/cryptography7030044.
10.3390/cryptography7030044
Google Scholar
56 Mohassel P. and Zhang Y., SecureML: A System for Scalable Privacy-Preserving Machine Learning, 2017 IEEE Symposium on Security and Privacy (SP), 2017, 19–38, https://doi.org/10.1109/sp.2017.12, 2-s2.0-85024487501.
10.1109/sp.2017.12
Google Scholar
57 Liu J., Juuti M., Lu Y., and Asokan N., Oblivious Neural Network Predictions via MiniONN Transformations, Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, 2017.
Google Scholar
58 Galbraith S. D., Paterson K. G., and Smart N. P., Pairings for Cryptographers, Discrete Applied Mathematics. (2008) 156, no. 16, 3113–3121, https://doi.org/10.1016/j.dam.2007.12.010, 2-s2.0-53249117524.
10.1016/j.dam.2007.12.010
Web of Science® Google Scholar
59 Guo F., Mu Y., Susilo W., and Varadharajan V., Membership Encryption and Its Applications, Lecture Notes in Computer Science. (2013) 219–234, https://doi.org/10.1007/978-3-642-39059-3_15, 2-s2.0-84884497158.
10.1007/978-3-642-39059-3_15
Google Scholar
60 Boneh D., Boyen X., and Goh E. J., Hierarchical Identity Based Encryption with Constant Size Ciphertext, Lecture Notes in Computer Science. (2005) 440–456, https://doi.org/10.1007/11426639_26.
10.1007/11426639_26
Google Scholar

All articles

Machine Learning Meets Encrypted Search: The Impact and Efficiency of OMKSA in Data Security

Abstract

1. Introduction

1.1. Our Contributions

1.2. Related Works

1.2.1. Public Key Encryption With Keyword Search (PEKS)

1.2.2. Oblivious Transfer

1.2.3. OKS

1.2.4. The Integration of ML and SE

1.3. Organization

2. Preliminaries

2.1. Notations

2.2. Bilinear Pairing

2.3. Algorithm Definition

2.3.1. Setup

2.3.2. Commit

2.3.3. Transfer

2.3.4. Correctness

2.4. Security Notions

2.4.1. User Privacy

2.4.2. Indistinguishability

2.4.3. Accountability

2.5. Assumptions

3. OMKSA Protocol

3.1. Disjunctive Keyword Search

3.1.1. Setup

3.1.2. Commit

3.1.3. Transfer

3.1.4. Extension to D Keywords

3.1.5. Correctness

3.2. Conjunctive Keyword Search

3.2.1. Setup

3.2.2. Commit

3.2.3. Transfer

3.2.4. Correctness

4. Security Analysis

4.1. Receiver Privacy

4.2. Indistinguishability

4.2.1. Setup

4.2.2. H-Query

4.2.3. Phase 1

4.2.4. Challenge

4.2.5. Phase 2

4.2.6. Guess

4.3. Accountability

4.3.1. Setup

4.3.2. Challenge

4.3.3. Win

5. Performance Evaluation

6. Application in ML

6.1. Applied on the Medical Platform

6.2. Data Preprocessing and Feature Selection

6.3. Distributed ML

7. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information