International Journal of Intelligent Systems

Volume 2025, Issue 1 1458773

Research Article

Open Access

Knowledge-Driven and Low-Rank Tensor Regularized Multiview Fuzzy Clustering for Alzheimer’s Diagnosis

Yi Zhu

orcid.org/0009-0005-0333-9311

Jiangxi Engineering Technology Research Center of Nuclear Geoscience Data Science and System , East China University of Technology , Nanchang , 330013 , Jiangxi, China , ecit.edu.cn

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Chao Xi,

Chao Xi

orcid.org/0000-0002-5824-5540

Jiangxi Engineering Technology Research Center of Nuclear Geoscience Data Science and System , East China University of Technology , Nanchang , 330013 , Jiangxi, China , ecit.edu.cn

School of Mechanical and Electronic Engineering , East China University of Technology , Nanchang , 330013 , China , ecit.edu.cn

Search for more papers by this author

Sen Wang,

Corresponding Author

Sen Wang

[email protected]

orcid.org/0009-0003-5622-2972

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Lu Xu,

Lu Xu

orcid.org/0009-0001-2259-4167

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Xiang Chen,

Xiang Chen

orcid.org/0009-0005-2681-5413

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Zhicheng Wang,

Corresponding Author

Zhicheng Wang

[email protected]

orcid.org/0000-0002-0662-045X

School of Mechanical and Electronic Engineering , East China University of Technology , Nanchang , 330013 , China , ecit.edu.cn

Search for more papers by this author

Yi Zhu,

Yi Zhu

orcid.org/0009-0005-0333-9311

Jiangxi Engineering Technology Research Center of Nuclear Geoscience Data Science and System , East China University of Technology , Nanchang , 330013 , Jiangxi, China , ecit.edu.cn

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Chao Xi,

Chao Xi

orcid.org/0000-0002-5824-5540

Jiangxi Engineering Technology Research Center of Nuclear Geoscience Data Science and System , East China University of Technology , Nanchang , 330013 , Jiangxi, China , ecit.edu.cn

School of Mechanical and Electronic Engineering , East China University of Technology , Nanchang , 330013 , China , ecit.edu.cn

Search for more papers by this author

Sen Wang,

Corresponding Author

Sen Wang

[email protected]

orcid.org/0009-0003-5622-2972

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Lu Xu,

Lu Xu

orcid.org/0009-0001-2259-4167

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Xiang Chen,

Xiang Chen

orcid.org/0009-0005-2681-5413

School of Science , East China Jiaotong University , Nanchang , 330013 , China , ecjtu.jx.cn

Search for more papers by this author

Zhicheng Wang,

Corresponding Author

Zhicheng Wang

[email protected]

orcid.org/0000-0002-0662-045X

School of Mechanical and Electronic Engineering , East China University of Technology , Nanchang , 330013 , China , ecit.edu.cn

Search for more papers by this author

First published: 21 May 2025

https://doi.org/10.1155/int/1458773

Academic Editor: Eugenio Vocaturo

Share a link

Email
Wechat
Bluesky

Abstract

Alzheimer’s disease (AD), as a complex neurodegenerative disorder, is the most common cause of dementia. In recent years, the emergence of multiview data has brought new possibilities for the diagnosis of AD. However, due to uneven density and uncertainty in the multiview data, existing algorithms still face challenges in extracting consistent and complementary information across views. To address this issue, a multiview fuzzy clustering algorithm, which integrates high-density knowledge point extraction and low-rank tensor regularization (K-LRT-MFC), is proposed in this paper. First, high-density knowledge point extraction is employed to tackle the issue of uneven density in high-dimensional data, enhancing the stability and accuracy of single-view clustering. Second, low-rank tensor regularization is applied to effectively capture high-order complementary information among multiview data, significantly improving the precision and computational efficiency of multiview clustering. Experimental results on several publicly available AD diagnostic datasets demonstrate that the proposed method outperforms existing approaches in terms of accuracy, sensitivity, and specificity, providing an efficient and accurate solution for early AD diagnosis.

1. Introduction

Alzheimer’s disease (AD) is a highly complex neurodegenerative disorder, responsible for approximately 70% of dementia cases worldwide [1]. The disease is marked by progressive degeneration of the cerebral cortex, particularly affecting the frontal and temporal lobes, before gradually spreading to other neocortical regions. This process results in symptoms such as cognitive decline, memory impairment, and emotional instability [2]. It is estimated that approximately 6.7 million people aged 65 and older are currently affected by AD globally, making it one of the leading causes of death in the United States, where it ranks as the sixth most common cause [3]. Early symptoms of AD often manifest as mild cognitive impairment (MCI), and recent studies suggest that significant memory complaints (SMCs) or subjective cognitive decline (SCD) could also serve as early indicators of the disease [3]. Although the exact cause of AD remains unclear, early and accurate diagnosis is critical to slowing the progression, particularly in its initial stages before clinical symptoms become pronounced [4, 5].

In recent years, advancements in technologies such as medical imaging—including magnetic resonance imaging (MRI), positron emission tomography (PET), and blood plasma spectroscopy—have significantly enhanced the detection and quantification of AD [6–8]. The growing availability of multimodal data has led to an increased demand for utilizing these data sources in AD diagnosis. Machine learning techniques, particularly support vector machines (SVMs) [9], decision trees [10], and random forests [11], have been widely applied to the analysis of neuroimaging, genetic data, and cognitive test results, greatly improving the early diagnosis of AD [12–15]. However, despite advancements in the acquisition of medical imaging and genetic data, effectively processing these complex and heterogeneous multiview datasets remains a significant challenge. The inherent heterogeneity and complexity of multiview data call for the development of more efficient algorithms to extract complementary information from various modalities, ultimately enhancing diagnostic accuracy.

Various multiview or multimodal methods have been developed by researchers for the diagnostic prediction of AD. These methods are primarily categorized into two types: deep learning-based models and traditional machine learning methods. Deep learning-based approaches [16, 17] have leveraged the powerful representation capabilities of deep neural networks, achieving significant advancements. However, such methods often lack interpretability and rely heavily on large amounts of training data, which limits their practical application. On the other hand, traditional machine learning methods, such as latent space-based methods [18], multiple kernel learning [19], and multiview clustering [20], although slightly inferior in performance compared to deep learning, offer greater reliability in practical applications due to their mathematical rigor and lower data requirements. Particularly, multiview clustering, as an unsupervised feature learning method, has shown outstanding performance in capturing inter-modal correlations and dimensionality reduction [21].

Despite the promising results achieved by these methods, existing multiview approaches still face challenges in addressing the following issues:

1.
Data uncertainty and ambiguity: Medical data often contain uncertainties, such as the problem of fuzzy boundaries in imaging data, which can lead to inaccurate segmentation results. Additionally, the definition of diagnostic thresholds for AD poses challenges, as the transition between “diagnosed with AD” and “not diagnosed with AD” is often ambiguous [22].
2.
Sensitivity to initial points in clustering processes: Data related to AD diagnosis are typically high-dimensional and complex [23]. Traditional clustering algorithms, such as K-means and Fuzzy C-means (FCM), are sensitive to initial points and tend to perform unstably when dealing with uneven data distributions. Low-density regions may interfere with the identification of cluster centers, resulting in model instability and bias.
3.
Insufficient correlation in multiview data: Multiview data often consist of information from different modalities, which are complementary in nature. However, existing multiview clustering methods typically address only pairwise correlations between views, failing to fully capture higher-order complementary information, which results in insufficient diagnostic accuracy. Furthermore, the high dimensionality of multimodal data brings challenges in terms of computational complexity, reducing the model’s efficiency and consistency.

To address the aforementioned challenges, a knowledge-guided and low-rank tensor-constrained multiview fuzzy clustering (K-LRT-MFC) model is proposed. The framework of the proposed model is illustrated in Figure 1. This model employs fuzzy clustering to capture the uncertainty in the data. In addition, high-density knowledge point extraction technique is utilized to extract representative knowledge points from high-density regions, which serve as anchors to guide the clustering process. This approach resolves the issue in traditional clustering algorithms where cluster centers cannot be accurately identified in uneven density distributions, significantly improving the stability and accuracy of clustering in high-dimensional data. Furthermore, low-rank tensor regularization is applied, integrating multiview fuzzy partition matrices with low-rank constraints to capture higher-order complementary information across different views, thereby enhancing the clustering performance of multiview data and improving the accuracy and consistency of the AD diagnostic model.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The framework of K-LRT-MFC. The first module is feature extraction. We extract the feature data of p views and input them into the second module, namely, multiview fuzzy clustering. In the second module, the feature data of each view are optimized by knowledge-driven clustering to obtain the membership matrix U^(p) of each view. These membership matrices will be concatenated into a third-order tensor , which is then converted into a global member through tensor factorization (TF). This matrix represents the final probability distribution of each data point belonging to each cluster under all view angles. It reflects the global relationship between each data point and each cluster in the multiview data.

The main contributions of this paper are as follows:

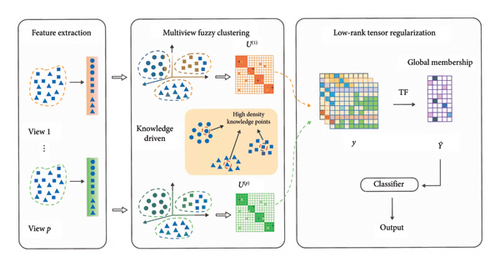
1.
This paper introduces a framework that combines high-density knowledge point extraction with low-rank tensor regularization, aiming to address feature extraction challenges in high-dimensional data and effectively capture higher-order correlations in multiview data.
2.
To tackle the challenges of high-dimensional data and uneven density distribution, a high-density knowledge point extraction method is proposed, which solves the difficulty faced by traditional clustering algorithms in identifying cluster centers under uneven density conditions. This method improves the stability and accuracy of the clustering process in high-dimensional data, making it particularly suitable for the complex data involved in AD diagnosis.
3.
The proposed low-rank tensor regularization model captures higher-order complementary information among multiview data and enhances the computational efficiency of the clustering process through effective tensor constraints. This method excels in multimodal data fusion and processing, providing higher accuracy and consistency for AD diagnosis tasks.

This paper is organized as follows. Section 1 makes an introduction of the problem to be solved and the adopted approach. Section 2 reviews recent multiview AD diagnosis algorithms as well as multiview fuzzy clustering algorithms. Section 3 focuses on explaining the proposed approach in detail. Section 4 discusses the optimization of the model. Section 5 presents the experimental results, and a further discussion is conducted in Section 6. Finally, Section 7 summarizes the paper and outlines future research directions.

2. Related Works

With the advancement of neural network technology, deep learning methods have greatly enhanced their capabilities in processing multimodal data. In particular, in AD diagnosis, deep learning models have significantly improved the handling of complex multimodal data by leveraging their powerful feature extraction and representation abilities. For example, Gao et al. integrated multimodal brain imaging data to improve the accuracy of AD image imputation and classification [24]. Additionally, Wang et al. proposed a 3D convolutional neural network (3D CNN) based on attention mechanisms, which enhanced AD classification accuracy by incorporating multiscale integration blocks [25]. These methods demonstrate the tremendous potential of deep learning in AD classification and diagnosis.

Although deep learning methods have demonstrated strong performance on several public AD datasets, they still exhibit certain limitations in practical applications. For instance, deep learning models typically require a large amount of labeled data for training, which is costly to obtain in the medical domain where high-quality, large-scale labeled datasets are scarce. Moreover, the interpretability of deep learning models is generally poor, which poses a significant issue in clinical applications, as medical diagnoses require the decision-making process of the model to be explainable.

Traditional machine learning methods have a long history of application in AD diagnosis. Although deep learning methods have shown superior performance in certain areas, traditional approaches retain their advantages in tasks requiring less data and greater interpretability. Latent space-based methods project multimodal data into a low-dimensional latent space, where classification or clustering is performed. Latent space methods effectively reduce data dimensionality and capture correlations between modalities. For example, Chen et al. significantly improved classification performance in multimodal AD diagnosis by employing feature weighting and graph learning [26]. MKL methods process data from different modalities using various kernel functions and dynamically adjust the weights of each kernel, allowing for better fusion of multimodal data. For instance, Wang et al. proposed a novel MKL algorithm that combines global and local information by optimizing the kernel coefficients through maximizing kernel alignment [27]. MKL has demonstrated excellent performance in several multimodal classification tasks, particularly in the early detection of AD, where it enhances diagnostic accuracy by jointly processing imaging and genetic data [28]. Multiview clustering utilizes shared features from different modalities to perform clustering analysis. This approach does not require labeled data and can be used to uncover unknown category structures. In the unsupervised diagnosis of AD, multiview clustering methods have been widely applied to integrate MRI, PET, and genetic data, improving the efficiency and accuracy of disease classification [29]. For example, Ning et al. proposed a relation-induced shared representation learning method that jointly analyzes multimodal data by combining structural and functional information [30].

In the processing of multimodal data, existing methods face several challenges, such as how to efficiently integrate heterogeneous data, how to handle the sparsity of high-dimensional data, and how to extract key features. These challenges become particularly difficult in the early diagnosis of AD, where the heterogeneity of multimodal data makes information fusion and the extraction of higher-order complementary information especially complex. To address these challenges, several methods have been improved in recent years in terms of data processing and feature extraction. For instance, some approaches have utilized graph embedding and latent space learning to capture correlations between different modalities, while others have reduced the dimensionality of data through feature selection techniques, thereby lowering computational complexity. However, further improvements in the accuracy and efficiency of data fusion remain an urgent problem that needs to be addressed.

3. Method

In this paper, we consider multiple view data matrices {X⁽¹⁾, …, X^(P)}, which contain N objects for clustering. The data matrix is composed of , where D_p represents the feature dimension of the data X^(p) in the p-th view. The goal of multiview clustering is to partition these N objects into C groups based on their similarities across different views. In the fuzzy clustering framework, the membership degree u_ic,p ∈ [0, 1] indicates the degree to which the i-th object in the p-th view belongs to the c-th cluster, and is the center of the c-th cluster in the p-th view.

3.1. Fuzzy C-Means

It is well known that FCM [31] is widely used in many fields due to its low computational time and effective results. FCM partitions N objects x_i(i = 1, 2, …, N) into C clusters by minimizing the following compactness measure of clustering:

()

where u_ic represents the membership degree of data point x_i to the cluster center v_c, satisfying

and u_ic ∈ [0, 1], and m > 1 is the fuzziness factor. Importantly, FCM is applicable to single-view data.

3.2. Knowledge-Driven Clustering

We introduce a method that combines high-density knowledge point extraction with the clustering process. This approach aims to leverage the advantage of using these knowledge points as initial cluster centers and further refine the clustering results through iterative optimization. Our proposed method consists of two key components: (1) extraction of high-density knowledge points and (2) clustering optimization based on these knowledge points. The first step of the method is to identify potential cluster centers by extracting high-density knowledge points from the dataset. High-density knowledge points are those data points that have both high local density and a significant distance from other high-density regions. These knowledge points can serve as initial cluster centers to guide the clustering process.

For any data point x_i, its local density ρ_i is defined as the inverse sum of the distances between it and its K-nearest neighbors:

()

where KNN(i) represents the set of the K-nearest neighbors of data point x_i, and

is the Euclidean distance between x_i and its neighboring point x_j. By calculating the local density of each data point, we can identify those points that are densely surrounded by other points.

The ultra-distance δ_i represents the minimum distance between data point x_i and the nearest data point with a higher density. The specific formula is as follows:

()

If the local density of x_i is the highest among all points, then its ultra-distance is defined as the average distance between it and all other points:

()

Algorithm 1: High-density knowledge point extraction.

Require: Data points X = {x₁, x₂, …, x_N}, number of nearest neighbors K
Ensure: Set of high-density knowledge points G
1.
for each data point x_i ∈ Xdo
2.
Calculate the local density ρ_i (equation (2)):
where KNN(i) is the set of K-nearest neighbors of x_i, and d_ij is the Euclidean distance between x_i and x_j.
3.
Calculate the ultra-distance δ_i (equation (3)):
If x_i has the highest local density, δ_i is the average distance to all other points (equation (4)):
4.
end for
5.
Sort data points based on ρ_i and δ_i to construct a decision graph.
6.
Select points with both high ρ_i and large δ_i as high-density knowledge points, forming the set G.
7.
ReturnG

Here, represents the set of high-density knowledge points obtained through K-LRT-MFC, which is used to guide the iterative process. The specific steps for extracting high-density knowledge points are shown in Algorithm 1.

By combining local density and ultra-distance, we can effectively identify high-density and isolated points in the data as knowledge points. Once these high-density knowledge points are extracted, they guide the clustering optimization process. In combination with FCM for clustering optimization, the objective is to further refine the clustering results by minimizing the following objective function:

()

where λ is a regularization parameter that controls the size of r_tc, preventing it from becoming too small or too large. q is an influence adjustment factor that determines the nonlinearity of the relationship between r_tc and the distance d_tc. The larger the value of q, the less sensitive r_tc becomes to distance, meaning that the influence of high-density knowledge points on the cluster center weakens at greater distances, where q > 1 and q ≠ 2. π is a coefficient that adjusts the influence of r_tc on the distance d_tc. r_tc represents the influence coefficient of high-density knowledge points on the cluster centers (r_tc ∈ [0, 1]), and the distance

is calculated using a multi-kernel distance

()

where

()

Here, in equation (7), φ₁, φ₂, …, φ_M are kernel functions, where each function φ_l re-encodes the q-dimensional data x into the vector φ_l(x). Assume that γ₁, γ₂, …, γ_M are the Mercer kernels corresponding to φ₁, φ₂, …, φ_M, respectively. Then, the following result can be derived:

()

φ is a multi-kernel function, which is the weighted sum of φ₁, φ₂, …, φ_M, subject to the constraint (i = 1, 2, …, N; c = 1, 2, …, C):

()

The first term of equation (5) corresponds to the standard mechanism between data points and cluster centers in the multi-kernel fuzzy clustering framework. The second term introduces the influence of high-density knowledge points, revealing the relationship between the knowledge points and the cluster centers. We map the high-density knowledge points into a high-dimensional space as information anchors. As a directional guide, this approach effectively brings the cluster centers closer to the knowledge points through iterations. The third term is a regularization term that prevents the influence coefficient r_tc from becoming too small or approaching zero. If the r_tc value is larger, the cluster centers should be closer to high-density points.

3.3. Low-Rank Tensor Regularized

To maintain consistency in clustering results across multiple views, the membership matrices U^(p) from each view are combined into a third-order tensor

, where

represents the membership degree of data point x_i in cluster k for view p. To capture shared information and higher-order correlations across views, we impose a low-rank constraint on the tensor

. The regularization term for the low-rank tensor is as follows:

()

where σ_r(Y) represents the r-th singular value of the tensor

, and R is the rank of the tensor. Low-rank regularization ensures that clustering results across different views remain consistent by minimizing the nuclear norm of the tensor while effectively suppressing noise. By introducing low-rank tensor regularization, our method can capture the high-order correlations in multiview data, ensuring consistency in clustering results across different views. This approach not only effectively handles the diversity of multiview data but also improves the quality of the initial cluster centers through high-density knowledge point extraction, thereby enhancing clustering accuracy and robustness.

3.4. Proposed Method: K-LRT-MFC

In multiview data, each view provides a different representation of the data. To leverage high-density knowledge points in multiview clustering, the knowledge points can be extracted separately from each view and combined to perform joint clustering using the information from all views. To capture high-order correlations in multiview data, inspired by tensor decomposition techniques [32–34], we introduce low-rank tensor regularization to ensure consistency across different views. For each view, we use a Gaussian kernel function to map the data into a high-dimensional space and perform fuzzy clustering separately. Our objective function is expressed as follows:

()

where

is the local density of data point x_i in the p-th view, calculated using the Gaussian kernel.

is the ultra-distance of data point x_i in the p-th view.

represents the membership degree of data point x_i belonging to cluster k in the p-th view.

is the distance between data point x_i and cluster center

in the p-th view.

4. Optimization

In this section, we introduce the augmented Lagrangian method (ALM) for optimizing the objective function of multiview fuzzy clustering guided by high-density knowledge points. Our optimization approach combines the guiding influence of high-density knowledge points with low-rank tensor regularization techniques, aiming to achieve consistency and accuracy in multiview clustering by progressively optimizing the membership matrices, cluster centers, tensor, and Lagrangian multipliers.

First, we introduce the augmented Lagrangian function by incorporating auxiliary variables H_t and Lagrange multipliers α_t to handle the low-rank constraint on the tensor

. This reformulates the objective function into a convex optimization problem:

()

where H_t is the unfolding matrix of the tensor

along mode t, α_t represents the Lagrange multipliers, μ is the penalty parameter in the ALM, and P^t is the unfolding operation that unfolds the tensor

into a matrix along mode t.

1.
Update the membership matrix U^(p):
Objective sub-problem:
()
To solve the above optimization problem, we independently optimize each . First, we take the derivative of the objective function with respect to and set it to zero:
()
where h_ic,t and α_ic,t are elements of the matrix H_t and the Lagrange multipliers α_t, respectively. The equation can be rearranged as follows:
()
Let , then:
()
This is a nonlinear equation for . To simplify the solution, we adopt an iterative update method, transforming it into an extended form of the standard FCM update rule. By solving the above equation, we obtain the update formula for :
()
However, considering the influence of the augmented Lagrangian term, we need to adjust the standard FCM update formula. Specifically, a correction term from H_t and α_t is introduced. Therefore, the update formula can be expressed as
()
2.
Update the cluster centers V^(p):
Fixing other variables, optimize the cluster centers V^(p):
()
For each cluster center , take the derivative and set it to zero to obtain:
()
3.
Update the influence coefficient of high-density knowledge points, R^(p):
Fixing other variables, the optimization problem for R^(p) is formulated as follows:
()
taking the derivative of r_tc and setting it to zero:
()
we can obtain
()
To avoid r_tc taking negative values, we adjust the above expression to obtain
()
4.
Update the tensor and the unfolded matrix H_t:
First, the third-order tensor is unfolded into a matrix along each mode t, denoted as P^tY. Assume that the dimensions of are I₁ × I₂ × I₃. The resulting matrix from unfolding along mode t, P^tY, will have the dimensions I_t × (I₁ × ⋯×I_t−1 × I_t+1 × ⋯×I₃). The unfolding operation can be represented as
()
Perform singular value decomposition (SVD) on the unfolded matrix P^tY:
()
where U_t is the left singular matrix with dimensions I_t × I_t, Σ_t is a diagonal matrix whose diagonal elements are the singular values of P^tY, with dimensions I_t × I_t, and is the right singular matrix with dimensions I_t × (I₁ × ⋯×I_t−1 × I_t+1 × ⋯×I₃).
To enforce the low-rank constraint on the tensor, the singular value matrix Σ_t is subjected to soft-thresholding. The soft-thresholding operation involves subtracting a threshold from each singular value (keeping only the non-negative part), where the threshold is related to the regularization parameter:
()
where η_t is the corresponding regularization parameter. After soft-thresholding, smaller singular values may be set to zero, thus achieving the effect of low-rank constraint. The unfolded matrix H_t is then reconstructed using the updated Σ_t:
()
Through this step, the unfolded matrix H_t is recombined, and the updated tensor is reconstructed. The reconstruction operation can be expressed as
()
The reconstructed tensor retains the low-rank structure, ensuring the consistency of clustering results across different views.
5.
Update the Lagrange multiplier α_t:
After the tensor is updated, the Lagrange multiplier α_t is updated using the new Y and H_t:
()

The optimization pseudo-code of K-LRT-MFC is shown in Algorithm 2.

Algorithm 2: The learning method of K-LRT-MFC.

Require: Multiview data matrices for p = 1, 2, …, P, the number of clusters C, the fuzziness factor m, regularization parameters λ, π, and ξ.
Ensure: Optimized membership matrices U^(p), cluster centers V^(p), and the low-rank tensor .
1.
Initialization: Initialize the membership matrices U^(p) for each view p with random values.
2.
for each view p = 1, 2, …, Pdo
3.
Compute high-density knowledge points using local density and ultra-distance (equation (2) and (3)).
4.
Initialize cluster centers V^(p) with the high-density knowledge points (equation (4)).
5.
end for
6.
repeat
7.
for each view p = 1, 2, …, Pdo
8.
Update membership matrix U^(p) according to equation (18).
9.
Update cluster centers V^(p) according to equation (20).
10.
Update influence coefficients according to equation (24).
11.
end for
12.
Construct third-order tensor from membership matrices U^(p).
13.
Apply low-rank tensor regularization on Y (equation (10)).
14.
Update the tensor and its unfolding matrices H_t according to equations (27) and (28).
15.
until convergence
16.
Output: Optimized membership matrices U^(p), cluster centers V^(p), and low-rank tensor .

5. Experiments

This section outlines the experiments carried out to evaluate the effectiveness of the K-LRT-MFC method. First, we introduce the datasets used in the experiments, followed by a description of the baseline methods and evaluation protocols. We then compare the performance of K-LRT-MFC with other related approaches. Finally, a comprehensive analysis is conducted to examine the impact of various K-LRT-MFC components on diagnostic accuracy.

5.1. Experimental Dataset

This study utilizes neuroimaging data from the ADNI database¹ [35]. Initiated in 2003, the ADNI project is a public–private partnership funded by various institutions including the National Institute on Aging and the National Institute of Biomedical Imaging and Bioengineering, as well as the FDA, private pharmaceutical companies, and non-profit organizations, with a budget of $60 million over 5 years. The main objective is to investigate if MRI, PET, other biological markers, and clinical as well as neuropsychological assessments can be integrated to monitor the progression of MCI and early AD. For our study, we use the ADNI-2 dataset, which includes preprocessed neuroimaging features available on the public ADNI website. This dataset comprises 757 patients: 144 with AD, 330 with MCI, and 283 normal controls (NCs). Patients with MCI are categorized into two subgroups: one consisting of individuals likely to develop AD within a certain timeframe (pMCI), and the other comprising those who are expected to either remain stable or return to normal cognitive function (sMCI). Extending the follow-up period facilitates earlier detection and intervention for AD. We choose a 3-year follow-up period because nearly all participants possess comprehensive follow-up data for this timeframe, and the majority of related research [36, 37] concentrates on forecasting the progression from MCI to AD during this period. Eleven MCI patients had only baseline diagnostic information and could not be categorized as either sMCI or pMCI. Consequently, the ADNI-2 dataset comprises 85 pMCI subjects and 234 sMCI subjects. Demographic details are provided in Table 1.

Table 1. Demographic information of subjects.

Category	NC	MCI	AD	sMCI	pMCI
Gender (male/female)	130/153	183/147	84/60	130/104	47/38
Age (mean±std)	72.2±9.5	70.9±10.0	73.0±13.3	70.4±10.8	70.2±14.9
MMSE (mean±std)	29.0±1.2	28.0±1.8	23.1±2.1	28.3±1.6	27.2±1.8
Education (mean±std)	16.6±2.5	16.4±2.6	15.7±2.7	16.4±2.7	16.2±2.5

To enhance reproducibility, we utilized features derived from MRI, PET-AV45, and PET-FDG scans, all of which are publicly accessible on the ADNI website. The MRI data were preprocessed, and features were extracted using the FreeSurfer image analysis suite, developed by a team at the University of California, San Francisco. This procedure included cortical reconstruction, volumetric segmentation, and corrections for gradient distortion, scaling, B1 field variation, and N3 bias field inhomogeneity. The extracted features include measurements of cortical volume, surface area, average thickness, and thickness variability from both cortical and subcortical regions. For PET data, the team from the University of California, Berkeley, used SPM8 for image alignment and calculated the standardized uptake value ratio (SUVR) for regions such as the frontal lobe and cingulate gyrus. Further details regarding the processing steps and data can be found on the ADNI website². After applying quality control procedures, the ADNI-2 dataset consisted of 115 PET features and 311 MRI features.

5.2. Comparative Experiment Algorithms

We conducted comparative experiments of the K-LRT-MFC method against several established methods:

•
A baseline is defined as a model that directly concatenates the original multimodal features and performs classification without employing any feature reduction techniques.
•
DGMM [38]: It identifies multimodal imaging phenotypes for Alzheimer’s research, enhancing imaging-genetic association accuracy.
•
MM-GNN [39]: It models brain networks using a graph neural network framework to improve Alzheimer’s diagnosis.
•
HGSCCA [40]: It uses hypergraph-based analysis for early-stage Alzheimer’s diagnosis by integrating genomic data.
•
MT-SGL [41]: It combines multitask learning and sparse regularization for predicting cognitive scores related to Alzheimer’s.
•
MvADL [42]: It enhances image classification by integrating information from different views through dictionary learning.
•
MvCCDA [43]: It learns a discriminative common subspace for cross-view classification, addressing view variance and nonlinearity.
•
OLFG [44]: It proposes an orthogonal latent space model for AD diagnosis, demonstrating superior results.
•
AWDR [45]: It improves classification by learning and fusing view-specific optimal weights into a discriminative subspace.

5.3. Experimental Settings

For the baseline method, along with other approaches that handled feature reduction and classifier training as separate steps, we utilized an SVM for classification using the LIBSVM toolbox [46]. The optimal margin parameter C was selected from the range {10⁻⁵, 10⁻⁴, …, 10⁵}. Following the strategies outlined in related works [47, 48], we assessed all comparison methods through a 10-fold cross-validation. The final results were obtained by averaging the outcomes across multiple experiments. The performance metrics included sensitivity (SEN), area under the curve (AUC), specificity (SPE), and accuracy (ACC). To ensure robustness, each experiment was repeated 15 times to calculate the average performance. The proposed K-LRT-MFC model features four custom hyperparameters: π, λ, and ξ, which were tuned through grid search within the range of {10⁻³, 10⁻², …, 10², 10³}. We performed three classification tasks: NC vs. AD, NC vs. MCI, and sMCI vs. pMCI.

5.4. Evaluation of Performance

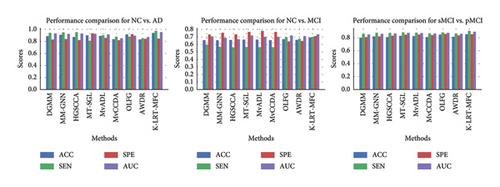
This section compares the performance of the K-LRT-MFC method against several state-of-the-art baseline approaches. Table 2 and Figure 2 present the average results for ACC, SEN, SPE, and AUC for each approach. The results demonstrate that K-LRT-MFC generally outperforms the other methods, confirming its effectiveness in multimodal AD diagnosis tasks. Notably, K-LRT-MFC surpasses the performance of other hidden space-based approaches, highlighting its ability to learn a more discriminative latent space. The strength of K-LRT-MFC lies in its capacity to focus on key features through adaptive feature weighting while applying orthogonality constraints to the projection matrix to retain discriminative information. Moreover, K-LRT-MFC outperforms other methods based on Laplacian regularization. This is due to two primary factors: first, traditional Laplacian regularization methods build the similarity graph directly within the original feature space, independently of subsequent processes. K-LRT-MFC integrates graph fusion with hidden feature learning into a single framework, enabling joint optimization and task-driven accurate graph construction. Second, traditional methods construct a separate similarity graph for each view, neglecting the need for a shared underlying graph structure across modalities, which is crucial for diagnosis. K-LRT-MFC creates a unified graph across multiple views, effectively capturing relationships among them. Additionally, for all models, the performance metrics for sMCI vs. pMCI and NC vs. MCI are typically lower compared to NC vs. AD. This is mainly due to the subtler brain differences between MCI patients and NCs, as well as between sMCI and pMCI patients. Conversely, the differences between NCs and AD patients are more pronounced, making them easier to distinguish. This methodology significantly enhances the diagnostic model’s ability to correctly differentiate between individuals with and without AD.

Table 2. Performance comparison of various methods on the ADNI-2 dataset for classifying NC vs. AD, NC vs. MCI, and sMCI vs. pMCI.

Method	NC vs. AD				NC vs. MCI				sMCI vs. pMCI
Method	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
DGMM	0.887	0.942	0.831	0.933	0.658	0.594	0.732	0.707	0.801	0.860	0.810	0.850
MM-GNN	0.909	0.951	0.840	0.925	0.656	0.570	0.756	0.688	0.820	0.876	0.820	0.860
HGSCCA	0.873	0.953	0.822	0.931	0.660	0.561	0.735	0.669	0.810	0.875	0.832	0.865
MT-SGL	0.900	0.813	0.934	0.927	0.664	0.566	0.767	0.719	0.830	0.884	0.847	0.875
MvADL	0.891	0.904	0.858	0.915	0.664	0.564	0.781	0.702	0.825	0.878	0.849	0.872
MvCCDA	0.837	0.878	0.821	0.852	0.658	0.564	0.767	0.702	0.810	0.868	0.840	0.865
OLFG	0.917	0.880	0.921	0.896	0.671	0.697	0.640	0.719	0.848	0.882	0.858	0.875
AWDR	0.833	0.851	0.843	0.872	0.661	0.673	0.647	0.712	0.815	0.865	0.835	0.860
K-LRT-MFC	0.940	0.975	0.847	0.955	0.693	0.700	0.711	0.736	0.854	0.906	0.854	0.893

Note: The bold values indicate best results.

5.5. Quantitative Component Assessment

We carry out an ablation study to assess the impact of the different components of the proposed model. We implement six different variants of the method:

•
K-LRT-MFC_M: A variant of K-LRT-MFC that is trained exclusively with MRI data.
•
K-LRT-MFC_PA: A variant of K-LRT-MFC that is trained exclusively with PET-AV45.
•
K-LRT-MFC_PF: A variant of K-LRT-MFC that is trained exclusively with PET-FDG.
•
K-LRT-MFC_T: A variant of K-LRT-MFC that disregards the tensor norm.
•
K-LRT-MFC_K: A variant of K-LRT-MFC that ignores knowledge-driven.

Each variant is designed to isolate the impact of specific data modalities or methodological components, thus highlighting the contribution of each element to the overall performance of the model.

Table 3 and Figure 3 present the results of K-LRT-MFC and its six variations. In most cases, K-LRT-MFC outperforms its variants, highlighting the effectiveness of each component in the diagnostic task. Specifically, by comparing K-LRT-MFC_M, K-LRT-MFC_PA, K-LRT-MFC_PF, and K-LRT-MFC, we find that K-LRT-MFC delivers superior diagnostic performance, illustrating the advantages of multimodal data fusion. Additionally, a comparison with K-LRT-MFC_T shows a drop in performance when the tensor norm is excluded. For example, in the NC vs. AD task, K-LRT-MFC achieves an ACC of 0.940 and an AUC of 0.955, whereas K-LRT-MFC_T reaches an ACC of 0.882 and an AUC of 0.921. This improvement can be attributed to K-LRT-MFC’s enhanced ability to perform low-rank approximation by minimizing the sparsity of the tensor norm, allowing it to capture more diagnostic information. Furthermore, comparing the results of K-LRT-MFC with K-LRT-MFC_K shows that K-LRT-MFC surpasses both. The ablation study results clearly show that incorporating knowledge-driven high-density point extraction and low-rank tensor regularization significantly improves performance. Particularly in the sMCI vs. pMCI classification, the complete K-LRT-MFC model outperforms the variants without these components. The addition of knowledge-driven extraction helps to stabilize clustering by reducing noise, while low-rank tensor regularization effectively captures high-order correlations in multiview data, enhancing both accuracy and consistency.

Table 3. Performance evaluation of K-LRT-MFC and its variants for classifying NC vs. AD, NC vs. MCI, and sMCI vs. pMCI.

Method	NC vs. AD				NC vs. MCI				sMCI vs. pMCI
Method	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
K-LRT-MFC_M	0.911	0.923	0.834	0.921	0.592	0.663	0.627	0.601	0.782	0.711	0.811	0.643
K-LRT-MFC_PA	0.902	0.917	0.851	0.931	0.583	0.598	0.603	0.673	0.773	0.842	0.812	0.863
K-LRT-MFC_PF	0.892	0.922	0.823	0.882	0.613	0.592	0.623	0.662	0.813	0.873	0.841	0.883
K-LRT-MFC_T	0.882	0.932	0.782	0.921	0.573	0.593	0.613	0.691	0.752	0.701	0.832	0.721
K-LRT-MFC_K	0.921	0.961	0.878	0.932	0.652	0.672	0.632	0.711	0.811	0.891	0.832	0.841
K-LRT-MFC	0.940	0.975	0.847	0.955	0.693	0.700	0.711	0.736	0.854	0.906	0.854	0.893

Note: The bold values indicate the best performance among all the methods for each metric under each classification task (NC vs. AD, NC vs. MCI, and sMCI vs. pMCI).

6. Discussion

6.1. Parameter Analysis

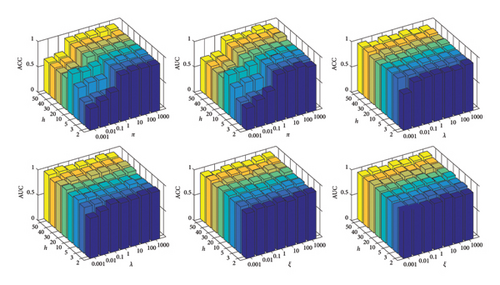
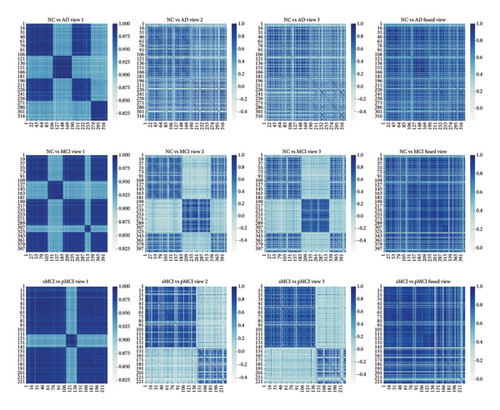
As illustrated in Figure 4 and Table 4, the performance of the K-LRT-MFC model is greatly influenced by key parameters such as π, λ, and ξ. When π is set too low, both ACC and AUC are reduced because the contribution of high-density knowledge points is diminished. By increasing π to around 1, the model achieves optimal performance. Similarly, tuning λ and ξ carefully is essential, with the best results observed when both parameters are set near 0.1, ensuring an effective balance between regularization strength and knowledge point contribution. Adjusting these parameters appropriately is crucial for maintaining high diagnostic accuracy, particularly in challenging cases such as distinguishing sMCI from pMCI. As shown in Figure 5. Columns 1–3 display input similarity maps based on individual modalities (e.g., MRI, PET), which often appear scattered due to noise and redundant features. In contrast, Column 4 shows the joint similarity map learned by the K-LRT-MFC method, revealing a clearer block diagonal structure. This demonstrates how K-LRT-MFC effectively captures the underlying correlations between samples through multimodal data fusion and joint graph learning, thereby enhancing the classification performance for AD-related diseases.

Table 4. Hyperparameter tuning and final values.

Hyperparameter	Tested range	Final value
π	{10⁻³, 10⁻², 0.1, 1, 10, 10², 10³}	10
λ	{10⁻³, 10⁻², 0.1, 1, 10, 10², 10³}	0.1
ξ	{10⁻³, 10⁻², 0.1, 1, 10, 10², 10³}	1
Fuzziness m	{1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5}	2
Number of clusters C	{2, 3, 4, 5, 6}	3
Gaussian kernel width	{0.1, 0.5, 1, 2, 5}	1

6.2. Comparison With Related Studies

This section presents a comparative analysis of the K-LRT-MFC model against various established methods for diagnosing AD, using multimodal datasets from the ADNI database. These methods, including both conventional machine learning and advanced deep learning techniques, are summarized in Table 5, with comparative outcomes shown in Table 2. Despite variations in dataset selection, preprocessing, and partitioning strategies across studies, the K-LRT-MFC model consistently outperforms most deep learning techniques, as highlighted in Table 2 and Figure 2. This advantage likely stems from K-LRT-MFC’s ability to integrate diverse features from medical images, whereas deep learning models often use whole-brain images, potentially overlooking critical regions. These findings emphasize K-LRT-MFC’s strengths in fusion learning and highlight opportunities to enhance deep learning methods in handling complex medical imaging data.

Table 5. Comparison of the multimodal classification performances reported in the literature.

Method	Subject	Dataset	NC vs. MCI				NC vs. AD				sMCI vs. pMCI
Method	Subject	Dataset	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
Suk et al. (2016)	51 AD, 52 NC, 43 pMCI, 56 sMCI	ADNI-1	0.7880	0.9080	0.5600	—	0.9510	0.9200	0.9800	—	0.7300	0.5300	0.8900	—
Hao et al. (2020)	211 NC, 160 AD	ADNI	—	—	—	—	0.8164	0.8560	0.8460	0.7860	—	—	—	—
Zhang et al. (2023)	215 AD, 246 NC, 331 MCI	ADNI	—	—	—	—	0.9107	0.9022	0.9187	0.9104	0.7550	0.4990	0.8870	0.6930
Shao et al. (2023)	168 NC, 125 MCI, 182 AD	ROSMAP	0.7630	0.8000	0.7430	0.7650	0.8200	0.8370	0.8030	0.8620	—	—	—	—
Chen et al. (2023)	144 AD, 330 MCI, 283 NC	ADNI-2	0.6710	0.6970	0.6400	0.7190	0.9470	0.8900	0.9820	0.9700	0.8020	0.4250	0.9530	0.8140
K-LRT-MFC	163 AD, 368 MCI, 183 NC	ADNI-2	0.6930	0.7000	0.7110	0.7360	0.9400	0.9750	0.8470	0.9550	0.8540	0.9060	0.8540	0.8930

7. Conclusion

In this study, we introduced a novel framework, K-LRT-MFC, to enhance AD diagnosis by integrating high-density knowledge extraction with low-rank tensor regularization. Our model addresses the challenges posed by high-dimensional, unevenly distributed multiview data, effectively capturing high-order complementary information between views. The experimental results on the ADNI-2 dataset demonstrate that K-LRT-MFC outperforms existing models in terms of ACC, SEN, and SPE. The superior performance of our method highlights its effectiveness in fusing multimodal data and improving clustering stability, offering a robust solution for AD diagnosis.

Although the K-LRT-MFC framework performs well in AD diagnosis, it still has some limitations. First, the imbalance of the dataset may lead to classification bias, which can be improved through data enhancement in the future. Second, the high computational complexity of low-rank tensor regularization may limit its application in real-time clinical environments. Finally, this method mainly targets specific types of multimodal data and can be expanded to more data sources in the future to improve the breadth of diagnosis.

Future research could extend the application of K-LRT-MFC to other neurodegenerative disorders and explore the integration of additional data modalities, such as genetic information and proteomic data, to further improve diagnostic accuracy. Additionally, refining the computational efficiency of the model can facilitate its implementation in clinical settings, enabling early detection and intervention for AD.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Yi Zhu and Chao Xi contributed equally to this work. Chao Xi is the co-first author.

Funding

This work was supported by an open fund from the Jiangxi Engineering Technology Research Center for Nuclear Geoscience Data Science and System (JETRCNGDSS202206), the Jiangxi Province Science and Technology Cooperation Special Project (20212BDH80008), the Jiangxi Province Major Science and Technology Special Project (20233AAE02008), and the Engineering Research Center of Ministry of Education for Nuclear Technology Application (HJSJYB2022-7).

Endnotes

¹https://surfer.nmr.mgh.harvard.edu.

²https://adni.loni.usc.edu/.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request.

References

1 Zhang L., Wang M., Liu M., and Zhang D., A Survey on Deep Learning for Neuroimaging-Based Brain Disorder Analysis, Frontiers in Neuroscience. (2020) 14, https://doi.org/10.3389/fnins.2020.00779.
10.3389/fnins.2020.00779
Web of Science® Google Scholar
2 Khojaste-Sarakhsi M., Haghighi S. S., Ghomi S. M. T. F., and Marchiori E., Deep Learning for Alzheimer’s Disease Diagnosis: A Survey, Artificial Intelligence in Medicine. (2022) 130, https://doi.org/10.1016/j.artmed.2022.102332.
10.1016/j.artmed.2022.102332
PubMed Google Scholar
3 Fisher D. W., Bennett D. A., and Dong H., Sexual Dimorphism in Predisposition to Alzheimer’s Disease, Neurobiology of Aging. (2018) 70, 308–324, https://doi.org/10.1016/j.neurobiolaging.2018.04.004, 2-s2.0-85046620961.
10.1016/j.neurobiolaging.2018.04.004
CAS PubMed Google Scholar
4 Braak H. and Braak E., Frequency of Stages of Alzheimer-Related Lesions in Different Age Categories, Neurobiology of Aging. (1997) 18, no. 4, 351–357, https://doi.org/10.1016/s0197-4580(97)00056-0, 2-s2.0-0030805991.
10.1016/S0197-4580(97)00056-0
CAS PubMed Web of Science® Google Scholar
5 Alzheimer’s Association, 2023 Alzheimer’s Disease Facts and Figures, 2023.
Google Scholar
6 Schelke M. W., Attia P., Palenchar D. J. et al., Mechanisms of Risk Reduction in the Clinical Practice of Alzheimer’s Disease Prevention, Frontiers in Aging Neuroscience. (2018) 10, https://doi.org/10.3389/fnagi.2018.00096, 2-s2.0-85045757433.
10.3389/fnagi.2018.00096
PubMed Google Scholar
7 Rathore S., Habes M., Iftikhar M. A., Shacklett A., and Davatzikos C., A Review on Neuroimaging-Based Classification Studies and Associated Feature Extraction Methods for Alzheimer’s Disease and Its Prodromal Stages, NeuroImage. (2017) 155, 530–548, https://doi.org/10.1016/j.neuroimage.2017.03.057, 2-s2.0-85018778702.
10.1016/j.neuroimage.2017.03.057
PubMed Web of Science® Google Scholar
8 Doecke J. D., Blood-Based Protein Biomarkers for Diagnosis of Alzheimer Disease, Archives of Neurology. (2012) 69, no. 10, 1318–1325, https://doi.org/10.1001/archneurol.2012.1282, 2-s2.0-84867339786.
10.1001/archneurol.2012.1282
PubMed Web of Science® Google Scholar
9 Paraskevaidi M., Morais C. L., Halliwell D. E. et al., Raman Spectroscopy to Diagnose Alzheimer’s Disease and Dementia With Lewy Bodies in Blood, ACS Chemical Neuroscience. (2018) 9, no. 11, 2786–2794, https://doi.org/10.1021/acschemneuro.8b00198, 2-s2.0-85048135533.
10.1021/acschemneuro.8b00198
CAS PubMed Google Scholar
10 Song Y.-Y. and Lu Y., Decision Tree Methods: Applications for Classification and Prediction, Shanghai Archives of Psychiatry. (2015) 27, no. 2, 130–135, https://doi.org/10.11919/j.issn.1002-0829.215044, 2-s2.0-84935075029.
10.11919/j.issn.1002-0829.215044
PubMed Google Scholar
11 Cortes C. and Vapnik V., Support-Vector Networks, Machine Learning. (1995) 20, no. 3, 273–297, https://doi.org/10.1007/bf00994018.
10.1007/BF00994018
Web of Science® Google Scholar
12 Rabin L. A., Smart C. M., and Amariglio R. E., Subjective Cognitive Decline in Preclinical Alzheimer’s Disease, Annual Review of Clinical Psychology. (2017) 13, no. 1, 369–396, https://doi.org/10.1146/annurev-clinpsy-032816-045136, 2-s2.0-85019134541.
10.1146/annurev-clinpsy-032816-045136
PubMed Google Scholar
13 Galvin J. E., Prevention of Alzheimer’s Disease: Lessons Learned and Applied, Journal of the American Geriatrics Society. (2017) 65, no. 10, 2128–2133, https://doi.org/10.1111/jgs.14997, 2-s2.0-85026741818.
10.1111/jgs.14997
PubMed Web of Science® Google Scholar
14 Breiman L., Random Forests, Machine Learning. (2001) 45, no. 1, 5–32, https://doi.org/10.1023/a:1010933404324, 2-s2.0-0035478854.
10.1023/A:1010933404324
Web of Science® Google Scholar
15 Cuingnet R., Gerardin E., Tessieras J. et al., Automatic Classification of Patients With Alzheimer’s Disease From Structural Mri: A Comparison of Ten Methods Using the Adni Database, NeuroImage. (2011) 56, no. 2, 766–781, https://doi.org/10.1016/j.neuroimage.2010.06.013, 2-s2.0-79955059574.
10.1016/j.neuroimage.2010.06.013
PubMed Web of Science® Google Scholar
16 Wu Y., Zhou Y., Zeng W., Qian Q., and Song M., An Attention-Based 3d Cnn With Multi-Scale Integration Block for Alzheimer’s Disease Classification, IEEE Journal of Biomedical and Health Informatics. (2022) 26, no. 11, 5665–5673, https://doi.org/10.1109/jbhi.2022.3197331.
10.1109/jbhi.2022.3197331
PubMed Google Scholar
17 Wu T.-R., Jiao C.-N., Cui X., Wang Y.-L., Zheng C.-H., and Liu J.-X., Deep Self-Reconstruction Fusion Similarity Hashing for the Diagnosis of Alzheimer’s Disease on Multi-Modal Data, IEEE Journal of Biomedical and Health Informatics. (2024) 28, no. 6, 3513–3522, https://doi.org/10.1109/jbhi.2024.3383885.
10.1109/jbhi.2024.3383885
PubMed Google Scholar
18 Chen Z., Liu Y., Zhang Y., and Li Q., Orthogonal Latent Space Learning With Feature Weighting and Graph Learning for Multimodal Alzheimer’s Disease Diagnosis, Medical Image Analysis. (2023) 84, https://doi.org/10.1016/j.media.2022.102698.
10.1016/j.media.2022.102698
Google Scholar
19 Liu F., Zhou L., Shen C., and Yin J., Multiple Kernel Learning in the Primal for Multimodal Alzheimer’s Disease Classification, IEEE Journal of Biomedical and Health Informatics. (2014) 18, no. 3, 984–990, https://doi.org/10.1109/jbhi.2013.2285378, 2-s2.0-84900841488.
10.1109/jbhi.2013.2285378
PubMed Google Scholar
20 Chen R., Tang Y., Zhang W., and Feng W., Adaptive-Weighted Deep Multi-View Clustering With Uniform Scale Representation, Neural Networks. (2024) 171, 114–126, https://doi.org/10.1016/j.neunet.2023.11.066.
10.1016/j.neunet.2023.11.066
PubMed Google Scholar
21 Fang U., Li M., Li J., Gao L., Jia T., and Zhang Y., A Comprehensive Survey on Multi-View Clustering, IEEE Transactions on Knowledge and Data Engineering. (2023) 35, no. 12, 12350–12368, https://doi.org/10.1109/tkde.2023.3270311.
10.1109/tkde.2023.3270311
Google Scholar
22 Tanveer M., Sajid M., Akhtar M. et al., Fuzzy Deep Learning for the Diagnosis of Alzheimer’s Disease: Approaches and Challenges, IEEE Transactions on Fuzzy Systems. (2024) 32, no. 10, 5477–5492, https://doi.org/10.1109/tfuzz.2024.3409412.
10.1109/tfuzz.2024.3409412
Google Scholar
23 Tang Y., Pan Z., Hu X., Pedrycz W., and Chen R., Knowledge-Induced Multiple Kernel Fuzzy Clustering, IEEE Transactions on Pattern Analysis and Machine Intelligence. (2023) 45, no. 12, 14838–14855, https://doi.org/10.1109/tpami.2023.3298629.
10.1109/tpami.2023.3298629
PubMed Google Scholar
24 Gao X., Shi F., Shen D., and Liu M., Task-Induced Pyramid and Attention Gan for Multimodal Brain Image Imputation and Classification in Alzheimer’s Disease, IEEE Journal of Biomedical and Health Informatics. (2022) 26, no. 1, 36–43, https://doi.org/10.1109/jbhi.2021.3097721.
10.1109/jbhi.2021.3097721
PubMed Google Scholar
25 Wang S., Wang H., Shen Y., and Shen D., An Attention-Based 3d Cnn With Multi-Scale Integration Block for Alzheimer’s Disease Classification, Neurocomputing. (2020) 403, 295–302.
Google Scholar
26 Chen Z., Liu Y., Zhang Y., and Li Q., Orthogonal Latent Space Learning With Feature Weighting and Graph Learning for Multimodal Alzheimer’s Disease Diagnosis, Medical Image Analysis. (2023) 84, https://doi.org/10.1016/j.media.2022.102698.
10.1016/j.media.2022.102698
Google Scholar
27 Wang Y., Liu X., Dou Y., Lv Q., and Lu Y., Multiple Kernel Learning With Hybrid Kernel Alignment Maximization, Pattern Recognition. (2017) 70, 104–111, https://doi.org/10.1016/j.patcog.2017.05.005, 2-s2.0-85020049098.
10.1016/j.patcog.2017.05.005
Google Scholar
28 Liu F., Zhou L., Shen C., and Yin J., Multiple Kernel Learning in the Primal for Multimodal Alzheimer’s Disease Classification, IEEE Journal of Biomedical and Health Informatics. (2014) 18, no. 3, 984–990, https://doi.org/10.1109/JBHI.2013.2285378, 2-s2.0-84900841488.
10.1109/JBHI.2013.2285378
PubMed Google Scholar
29 Liu M., Zhang D., and Shen D., View-Aligned Hypergraph Learning for Alzheimer’s Disease Diagnosis With Incomplete Multi-Modality Data, Medical Image Analysis. (2016) 36, 123–134.
10.1016/j.media.2016.11.002
PubMed Google Scholar
30 Ning Z., Xiao Q., Feng Q., Chen W., and Zhang Y., Relation-Induced Multi-Modal Shared Representation Learning for Alzheimer’s Disease Diagnosis, IEEE Transactions on Medical Imaging. (2021) 40, no. 6, 1632–1645, https://doi.org/10.1109/TMI.2021.3063150.
10.1109/TMI.2021.3063150
PubMed Google Scholar
31 Bezdek J. C., Ehrlich R., and Full W., FCM: The Fuzzy C-Means Clustering Algorithm, Computers and Geosciences. (1984) 10, no. 2-3, 191–203, https://doi.org/10.1016/0098-3004(84)90020-7, 2-s2.0-0021583718.
10.1016/0098-3004(84)90020-7
Web of Science® Google Scholar
32 Zhou P., Lu C., Lin Z., and Zhang C., Tensor Factorization for Low-Rank Tensor Completion, IEEE Transactions on Image Processing. (2018) 27, no. 3, 1152–1163, https://doi.org/10.1109/TIP.2017.2762595, 2-s2.0-85044256372.
10.1109/TIP.2017.2762595
PubMed Google Scholar
33 Madathil B. and George S., Twist Tensor Total Variation Regularized Reweighted Nuclear Norm Based Tensor Completion for Video Missing Area Recovery, Information Sciences. (2018) 423, 376–397, https://doi.org/10.1016/j.ins.2017.09.058, 2-s2.0-85030160279.
10.1016/j.ins.2017.09.058
Google Scholar
34 Han Z.-F., Feng R., Huang L.-T., Xiao Y., Leung C.-S., and So H. C., Tensor Completion Based on Structural Information, Neural Information Processing: 21st International Conference, ICONIP 2014, Kuching, Malaysia, November 3-6, 2014. Proceedings, Part II 21, 2014, Springer, 479–486.
Google Scholar
35 Weiner M. W., Aisen P. S., JackC. R.Jr. et al., The Alzheimer’s Disease Neuroimaging Initiative: Progress Report and Future Plans, Alzheimer′s & Dementia. (2010) 6, no. 3, 202–211, https://doi.org/10.1016/j.jalz.2010.03.007, 2-s2.0-77955474351.
10.1016/j.jalz.2010.03.007
PubMed Web of Science® Google Scholar
36 Moradi E., Pepe A., Gaser C., Huttunen H., Tohka J., and Initiative A. D. N., Machine Learning Framework for Early MRI-Based Alzheimer’s Conversion Prediction in MCI Subjects, NeuroImage. (2015) 104, 398–412, https://doi.org/10.1016/j.neuroimage.2014.10.002, 2-s2.0-84925058025.
10.1016/j.neuroimage.2014.10.002
PubMed Web of Science® Google Scholar
37 Wee C. Y., Yap P. T., Shen D., and Initiative A. D. N., Prediction of Alzheimer’s Disease and Mild Cognitive Impairment Using Cortical Morphological Patterns, Human Brain Mapping. (2013) 34, no. 12, 3411–3425, https://doi.org/10.1002/hbm.22156, 2-s2.0-84886240845.
10.1002/hbm.22156
CAS PubMed Web of Science® Google Scholar
38 Hao X., Yao X., Yan J. et al., Identifying Multimodal Intermediate Phenotypes between Genetic Risk Factors and Disease Status in Alzheimer’s Disease, Neuroinformatics. (2016) 14, no. 4, 439–452, https://doi.org/10.1007/s12021-016-9307-8, 2-s2.0-84973659671.
10.1007/s12021-016-9307-8
PubMed Google Scholar
39 Zhang Y., He X., Chan Y. H., Teng Q., and Rajapakse J. C., Multi-Modal Graph Neural Network for Early Diagnosis of Alzheimer’s Disease from sMRI and PET Scans, Computers in Biology and Medicine. (2023) 164, https://doi.org/10.1016/j.compbiomed.2023.107328.
10.1016/j.compbiomed.2023.107328
Google Scholar
40 Shao W., Xiang S., Zhang Z., Huang K., and Zhang J., Hyper-Graph Based Sparse Canonical Correlation Analysis for the Diagnosis of Alzheimer’s Disease From Multi-Dimensional Genomic Data, Methods. (2021) 189, 86–94, https://doi.org/10.1016/j.ymeth.2020.04.008.
10.1016/j.ymeth.2020.04.008
CAS PubMed Google Scholar
41 Liu X., Goncalves A. R., Cao P., Zhao D., Banerjee A., and Initiative A. D. N., Modeling Alzheimer’s Disease Cognitive Scores Using Multi-Task Sparse Group Lasso, Computerized Medical Imaging and Graphics. (2018) 66, 100–114, https://doi.org/10.1016/j.compmedimag.2017.11.001, 2-s2.0-85044527016.
10.1016/j.compmedimag.2017.11.001
PubMed Google Scholar
42 Wang Q., Guo Y., Wang J., Luo X., and Kong X., Multi-View Analysis Dictionary Learning for Image Classification, IEEE Access. (2018) 6, 20174–20183, https://doi.org/10.1109/access.2018.2791578, 2-s2.0-85041219674.
10.1109/access.2018.2791578
Google Scholar
43 You X., Xu J., Yuan W., Jing X. Y., Tao D., and Zhang T., Multi-View Common Component Discriminant Analysis for Cross-View Classification, Pattern Recognition. (2019) 92, 37–51, https://doi.org/10.1016/j.patcog.2019.03.008, 2-s2.0-85063239671.
10.1016/j.patcog.2019.03.008
Google Scholar
44 Chen Z., Liu Y., Zhang Y., Li Q., and Initiative A. D. N., Orthogonal Latent Space Learning With Feature Weighting and Graph Learning for Multimodal Alzheimer’s Disease Diagnosis, Medical Image Analysis. (2023) 84, https://doi.org/10.1016/j.media.2022.102698.
10.1016/j.media.2022.102698
Google Scholar
45 Yang M., Deng C., and Nie F., Adaptive-Weighting Discriminative Regression for Multi-View Classification, Pattern Recognition. (2019) 88, 236–245, https://doi.org/10.1016/j.patcog.2018.11.015, 2-s2.0-85057087289.
10.1016/j.patcog.2018.11.015
Google Scholar
46 Chang C.-C. and Lin C.-J., LIBSVM: A Library for Support Vector Machines, ACM Transactions on Intelligent Systems and Technology. (2011) 2, no. 3, 1–27, https://doi.org/10.1145/1961189.1961199, 2-s2.0-79955702502.
10.1145/1961189.1961199
Web of Science® Google Scholar
47 Zhu X., Suk H. I., Wang L., Lee S. W., Shen D., and Initiative A. D. N., A Novel Relational Regularization Feature Selection Method for Joint Regression and Classification in AD Diagnosis, Medical Image Analysis. (2017) 38, 205–214, https://doi.org/10.1016/j.media.2015.10.008, 2-s2.0-84949058046.
10.1016/j.media.2015.10.008
PubMed Web of Science® Google Scholar
48 Ning Z., Xiao Q., Feng Q., Chen W., and Zhang Y., Relation-Induced Multi-Modal Shared Representation Learning for Alzheimer’s Disease Diagnosis, IEEE Transactions on Medical Imaging. (2021) 40, no. 6, 1632–1645, https://doi.org/10.1109/tmi.2021.3063150.
10.1109/tmi.2021.3063150
PubMed Google Scholar

All articles

Knowledge-Driven and Low-Rank Tensor Regularized Multiview Fuzzy Clustering for Alzheimer’s Diagnosis

Abstract

1. Introduction

2. Related Works

3. Method

3.1. Fuzzy C-Means

3.2. Knowledge-Driven Clustering

3.3. Low-Rank Tensor Regularized

3.4. Proposed Method: K-LRT-MFC

4. Optimization

5. Experiments

5.1. Experimental Dataset

5.2. Comparative Experiment Algorithms

5.3. Experimental Settings

5.4. Evaluation of Performance

5.5. Quantitative Component Assessment

6. Discussion

6.1. Parameter Analysis

6.2. Comparison With Related Studies

7. Conclusion

Conflicts of Interest

Author Contributions

Funding

Endnotes

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley