Nanometer-Ranged Interfacial Interactions of the VRFB-Cell Electrolyte Species: An Implication of Molecular Dynamics Simulation
Abstract
In the large-scale energy storage technological sectors and many other state-of-the-art renewable energy subsidy policies, the vanadium redox flow battery (VRFB) stands as a low variable cost yet promising electrochemical assembly applicable to convert “all-vanadium” electrolyte stored chemical energy into electrical energy. Despite its ubiquitous attributes of grid-scale power storage and the remarkable charge–discharge cycles, there is still a dearth of MD simulation-based theoretical studies insighted into its Nafion-117 membrane-plunged electrolyte matrix comprising with the adjacent state polyvalent Vn+-hydrated complexes ([V (H2O)m]n+), monovalent HSO4− and H3O+ specimens, and the neutral H2O molecules. This specific simulation aiming at investigating very preliminary ideologies required for probing interfacial microstructures in the vicinity of SO3− conductive sites of the Nafion, most probable molecular/ionic obstructions or facilitations of their proton exchange rates, genius electrochemical impacts of the [V (H2O)m]n+ moieties in their mutual osmotic balance, disruption or maintenance of the hydrogen-bonded water channel across the electrolytic/polymeric matrices, etc., would be very crucial to the advancement of this battery technology. The RDF tools retrieved quantitative results presented herewith illuminate mainly the (a) predominant dynamics of the hydrated protons [H3O+] which when conducted H+ (proton) turn into Zundel [H5O2]+ and Eigen [H5O2+] states; (b) considerable water exchanging trends throughout the entire proton hopping occurring across the hydrogen-bonded water network; (c) outbound distributed water molecules and their reluctant propensities toward the central metal ion of the [V(H2O)m]n+; (d) absolute rejection of the predominant electrolyte ion HSO4− by all of those ionic specimens toward their chemical bonding affinities; (e) complete absence of the [V(H2O)m]n+ blockage in the proton exchange SO3− sites of the Nafion and the significant H2O/H3O+ number density retaining capacity of the latter into its hydrophilic tunnel. The author believes this article as a fundamental means of unveiling various interfacial complexities involved in driving the entire charge/mass transfer mechanisms of the VRFB cell.
1. Introduction
In the renewable energy sector, the vanadium redox flow battery (VRFB) technology stands as a standalone energy-producing candidate not only due to its promising electrochemical energy-storing capacities owing to the massive utilizations in electrical grid connections but also due to employing highly abundant vanadyl sulfate (VOSO4.5H2O) derived “all-vanadium” ((V (II)/V (III) and V (V)/V (IV)) redox couples (working electrolytes) via the state-of-art electrochemical cell assemblies [1–4]. The successful implementations of this battery technology worldwide and the overwhelming acceptance of it in the emerging industrial energy productions and consumption areas are further due to its exceptional working performance with recognizably longer yet stable lifespan cycles (> 10,000 cycles), low maintenance and operational costs, easily rechargeable and environment-friendly electroactive species of the single elemental form (vanadium with four adjacent oxidation states Vn+ (n = +2, +3, +4, and +5)), relatively more durable and no performance degradation attributes, very low chances of undergoing active Vn+ ion contaminations (V2+ solution is kept in an anolyte tank, and V5+ solution is in a catholyte tank) even within the considerable lapse of functioning time, negligible fire or smoke risk hazards, straightforwardly reusable and recyclable electrochemical cell ingredients, etc. [1–11]. In principle, this battery produces energy through the assembly of the electrochemical cells that are set in a compact form to convert chemical energy stored in the electroactive Vn+ ionic forms into electrical energy efficiently. The electrochemical cell is designed in the standard of the working principle of VRFB cell and is employed electrochemically so that the aqueous V (II) and V (V) species of the vanadium dispersed into their own matrices of aqueous 2M–5M H2SO4 (supporting electrolyte) undergo simultaneous oxidation and reduction reactions, respectively, in the anodic and cathodic half-cells separated by the low-resistance proton exchange membrane (in this case, Nafion-117). The separating membrane used in the electrochemical cell enables the battery to balance the “diffusion-gradient”-driven mass of the hydrated protons of different stable states (hydronium [H3O+], Zundel [H5O2+], and Eigen [H9O4+] [12]), electroactive charged–discharged hydrated complexes of Vn+, and the intermolecular hydrogen-bonded free water molecules (unbound state to the central Vn+ ion) in both half-cell compartments so that the net junction potential developed at the separator/electrode/electrolyte interfaces is substantially minimized or almost nullified at different state of charges (SOCs). According to density functional theory (DFT)–based quantum mechanical calculations and many other sophisticated experimental techniques probed investigations [5–9], all the adjacent state Vn+ ions show their existence in the bench aq.H2SO4 matrix as dissimilarly charged hydrated ions due to exhibiting exceptional hydration propensities and stabilizing tendencies. It means all the four Vn+ redox couples (V (II)/V (III) and V (V)/V (IV) of the anodic and cathodic half-cells) (“all vanadium”) employed in the VRFB cell immediately attain the most stable hydrated moieties (Figure 1) in the aqueous medium with distinguished colors and distinctive hydration number (n): V (II) complex [V (H2O)6]2+ (lilac, n = 6), V (III) complex [V (H2O)6]3+ (green, n = 6), V (IV) complex [VO (H2O)5]2+ (blue, n = 5), and V (V) complex [VO2 (H2O)4]+ (yellow, n = 4) [3, 4]. By the same experimental and theoretical means, none of the significant amounts of Vn+ ions and their hydrated moieties are detected in the form of HSO4−/SO42−-involved stable complexes/clusters despite their gracious presence in the VRFB-cell suit 2M–5M H2SO4-supported electrolyte matrices (the proportional concentration ratio is [HSO4−]:[SO42−] = 99:1 [10]). However, the positively charged and negatively charged complex ions of the V (II)/V (III) and V (V)/V (IV) redox couples are detected (electrophoresis experiment) by the present author, while the [H2SO4] was increased to the range of ≥ 8M (the specific results are yet to be reported), but it is insignificant to the typical operational VRFB-cell electrolytes. Similarly, by referring the charge–discharge reactions and the associated electrochemistry of the active Vn+ ions upon the completion of the series of charge–discharge cycles under different SOCs, the hydrated V (III) and V (IV) ions, viz., [V (H2O)6]3+ and [VO (H2O)5]2+ of the anodic and cathodic half-cells, respectively, gain and loss an electron e−, and changes into the hydrated forms of V (II) and V (V), viz., [V (H2O)6]2+ and [VO2 (H2O)4]+ (charging), and vice versa (discharging).
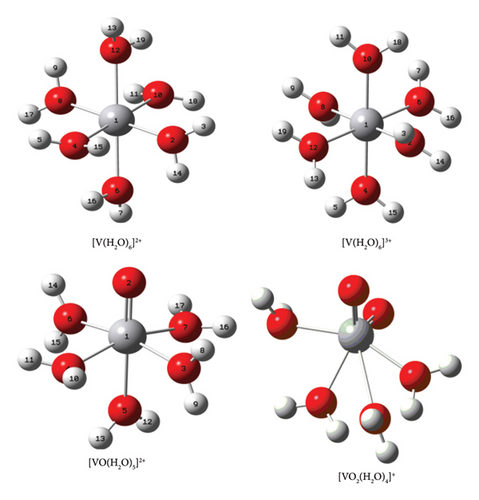
In order to cope with all those prospective VRFB-cell electrolyte scenarios comprising the aforementioned ionic/molecular specimens and their unique compositional distributions at different SOCs plus to understand their exclusive nanometer range dispersions and microstructures around themselves and in the vicinity of Nafion-117 and its proton-conducting functional group (SO3H, viz., SO3−) sites, the present author conducted molecular dynamics (MD) simulation-based theoretical study in the electrochemical cell designed for the VRFB technology. Even though a similar type yet quite preliminary study was already reported elsewhere [11] by the same author, the complete incorporation of the critical parts of such a complex electrolyte scenarios is still lacking. In that research work, the VRFB cell was designed with bare and nonhydrated “all-vanadium” redox couples in the presence of predefined number of free H2O molecules, H+-carried H2O, H3O+ ions, bare HSO4− ions, and Nafion-117 polymeric threads on the basis of which the benchmark quantitative discussions related to the (a) electrolyte–Nafion interfacial chemistry and its SO3− proton-conducting sites; (b) extreme hydration affinities of the adjacent state bare Vn+ ions; (c) closed ionic/molecular proximities of the H2O, H3O+, and Nafion-SO3− species; and (d) proton conduction phenomena and the direct/indirect involvement of the ionic/molecular specimens to initiate/accelerate the latter facilely were presented. However, the consequences raised by the extreme spontaneous hydration affinities of every adjacent state Vn+ ions owing to their settlement as low energy equilibrium-hydrated complexes, viz., [V (H2O)6]2+ and [V (H2O)6]3+ in anodic side and [VO2 (H2O)4]+ and [VO (H2O)5]2+ in cathodic side of the VRFB cell, and their interfacial microstructures nearby to the conductive SO3− sites of the Nafion-117 membrane, their affinities toward other potential cationic/anionic/molecular specimens of the electrolyte, and their direct/indirect impacts to the diffusion rates of the latter species across the polymeric membrane and H2SO4-supported electrolyte matrix were not studied. To the knowledge of the present author, not enough real-time-based MD simulation studies concentrated on each of these issues are reported despite being seriously taken as the most indispensable and imperative prerequisites for the comprehension of (a) “water-flooding” problems of the VRFB-cell technology and its resolving strategies at different SOCs; (b) interparticle interactions deterministic to the protonic and ionic mobility rates; and (c) Nafion’s proton conductivity. Since the MD simulation is a computer-aided mathematical formulation that allows the complete interactions between the designated number of atomic, molecular, and ionic specimens for a definite period of time t through the integrative package of Newton’s equations of motion and assesses their presumed microscopic properties directly before determine several measurable macroscopic observables statistically [11, 13], the present study serves as an imperative means of unveiling (a) microstructures of the electrochemically complex VRFB-cell electrolyte systems, (b) interfacial diffusion phenomena of the VRFB cell, (c) depletion and conglomeration attributes of the dissimilarly charged electrolyte particles throughout the electrolyte matrix, and (d) direct and indirect impacts of the spontaneously hydrated bigger sized Vn+ moieties. Additionally, the interfacial interactions of the real-world VRFB system insights into this article may expedite its new designations with efficient performances and workability and state-of-art internal architectures of the generic electrochemical assemblies. In the periphery of the same, this research article is drafted with “Theoretical approaches and Computational details” in Section 2, “Results and Discussions” in Section 3, and “Conclusions” in Section 4.
2. Computational and Theoretical Details
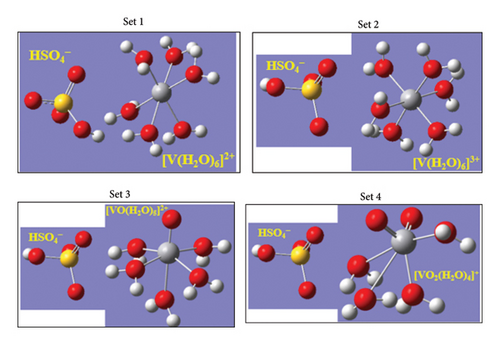
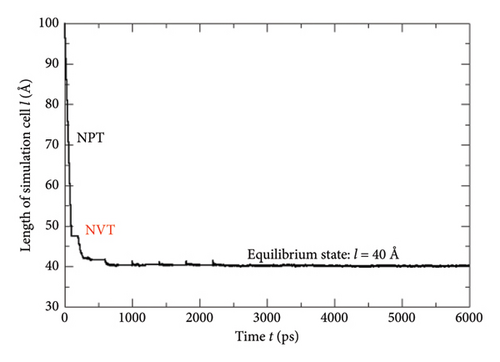
Based on the integrating assemblies of the VRFB cell and the complexities of the 2M–5M H2SO4 matrix-supported vanadium electrolytes, the four different MD simulation cells of the dimension 100 × 100 × 100 Å3 (Figure 2(a)) were designed explicitly, and the particular number density of all the ionic (HSO4−, H3O+, and Vn+-hydrated moieties), molecular (H2O), and polymeric membrane (Nafion-117) species were put together so that the net water content (λ) of the membrane attained a standard value 22 (an optimum scale that the membrane retains in an aqueous electrolyte system due to which the efficient protonic conduction is delivered [14]), and the entire simulation system became electrically neutral. Since the concentration ratio of the ions at VRFB-suit bench H2SO4-supporting electrolyte medium is approximately [HSO4−]:[SO42−] = 99:1 [10], the designated number density of the [HSO4−] species only was included in each simulation box. By referring spontaneous hydration affinities of each adjacent Vn+ (n = +2, +3, +4, +5) ions in their aqueous anolyte and catholyte matrices, the specific number density of the respective hydrated complexes of the form [V (H2O)6]2+ and [V (H2O)6]3+ (anodic side), and [VO2 (H2O)4]+ and [VO (H2O)5]2+ (cathodic side) was inserted (Figures 3, 2(b)). Again, based on the polymeric chain compositions of the Nafion-117 (perfluorosulfonic acid polymer) consisting of repeatedly arranged N7P units (polar SO3− (P) and nonpolar (N) groups) and its equivalent weight (EW) plus optimum water content λ features, the four chemically equivalent (N7P)10 threads (Figure 4) were incorporated into each simulation set (each (N7P)10 thread behaves as a better conductive membrane whenever its EW ≥ 1100 (EW = 100N + 446), and this value is only attained if 6 < N < 7 [14]). The detailed contents of the simulation cells and the precise determination of the λ are summarized in Table 1.

| Set | O.S. of V ions (conc.: 1M) | No. of hydrated Vn+ complexes | No. of Nafion chain (N7P)10 | No. of SO3− | No. of H3O+ | No. of HSO4− | No. of H2O | Water content (λ) |
|---|---|---|---|---|---|---|---|---|
| 1 | V (II); V2+ | [V (H2O)6]2+ = 16 | 4 | 40 | 24 | 16 | 760 | 22.0 |
| 2 | V (III); V3+ | [V (H2O)6]3+ = 16 | 4 | 40 | 8 | 16 | 776 | 22.0 |
| 3 | V (IV); VO2+ | [VO (H2O)5]2+ = 16 | 4 | 40 | 24 | 16 | 776 | 22.0 |
| 4 | V (V); VO2+ | [VO2 (H2O)4]+ = 16 | 4 | 40 | 40 | 16 | 776 | 22.0 |
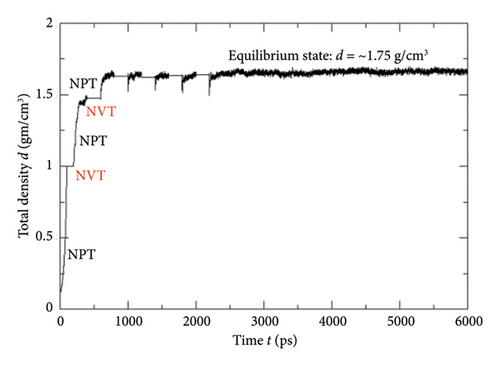
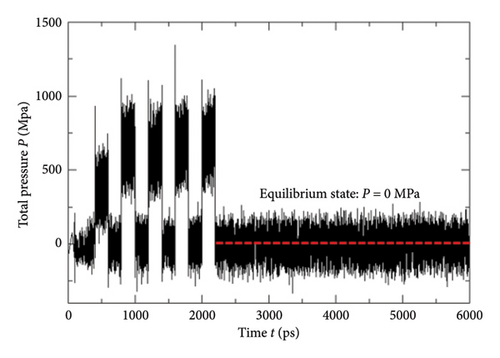
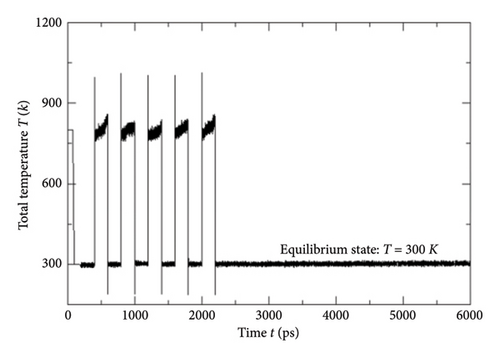
While implementing the entire MD simulation scripts designed for uniting all those specimens and their explicit interactions, several controlling parameters such as time step (Δt), length of the trajectory, intermittent geometry/energy, sampling intervals, and annealing conditions were set to the standard values lying into the practicable range of the available computational resources. The DREIDING force-field package [15] was employed for the hybridization-based force constants required for bonding potential and equilibrium geometrical parameters such as bond lengths, bond angles, and torsional parameters of each molecular/ionic/polymeric species and for the intermolecular Van der Waals and coulombic-type nonbonding interactions. Another database package “AMOEBA force field” and its extended features to metal ions (Mn+) were also called programmatically in order to address the nonbonding interactions of the Vn+-hydrated complexes with substantial short-range charge penetration, many-body charge transfer, and polarization effects [16, 17]. Similarly, the polarizable atomic multipole model, flexible three-centered water model [17], and the five-interacting-sites model with switching function [18] were also taken into account while dealing with the interactions between the H2O molecules themselves and with the H3O+ ions, respectively. At the time of simulating each cell, the specific annealing conditions were imposed on the system for about 6 ns before establishing an equilibrium state: The length of each simulation cell was reduced to 40 Å from the initial 100 Å, and the average internal kinetic temperature T was lowered to 300 K (from 850 K) so that the specific density (ρ) attained by the system reached to ∼1.75 gm/cm3, an experimentally determined value at 300 K (Figures 5, 6). While inspecting the equilibrium geometry of the molecular/ionic specimens of each simulation cell (Figure 2(b)), the computer-aided visual molecular dynamics (VMD)–based chemical graphics [19] were used. As soon as each simulation cell was found to attain all those equilibrium credentials, the NVE-type simulation was run where the constraints on change in number of moles (N), volume (V), and energy (E) were specifically applied computationally. Throughout the entire NVE iterations, the constancy of the total temperature T (Nose–Hoover thermostat), total pressure P (Andersen barostat), total density ρ, total volume of the simulation cell, and total conservation of the net sum of the potential and kinetic energy of each simulating particle was ensured.
3. Results and Discussion
3.1. Complexities of the VRFB-Cell Electrolytes
The electrochemical cell designed for the VRFB technology is comprised of the (a) anode, anolyte (anodic half-cell); (b) cathode, catholyte (cathodic half-cell); and (c) Nafion-117 proton exchange membrane (separator). In the normal operation process, the anolyte (an H2SO4 (aq.) matrix of V2+ [V (H2O)6]2+) and catholyte (an H2SO4 (aq.) matrix of VO2+ [VO2 (H2O)4]+) solutions are pumped into the electrochemical cell from the respective electrolyte storage tanks, and the former is oxidized while the latter is reduced electrochemically into the anodic and cathodic half-cells. Due to the exceptional hydration propensities of each adjacent state vanadium ions in the aqueous electrolyte systems, the anolyte tank stores V (II) fuel in [V (H2O)6]2+ form (lilac-colored), and the catholyte tank stores V (V) fuel in [VO2 (H2O)4]+ (yellow colored). Therefore, both the anodic and cathodic half-cells of the VRFB cell are supplied with the hydrated complexes of the active vanadium ions, viz., [V (H2O)6]2+ and [VO2 (H2O)4]+, respectively, along with the predominant quantity of free H2O molecules and the H+ carried H2O molecules. These dissimilarly charged vanadium fuels or electrochemically active hydrated vanadium ions undergo spontaneous charge/discharge reactions in the electrochemical cell as mentioned in Scheme 1 (for simplicity, the charge/discharge reactions in both negative and positive half-cells are separated, and the sum of these partial equations gives a net cell reaction of the VRFB cell). The Nafion-117 membrane (separator) is used to balance the diffusion-gradient governed H+ ion (or its hydrated forms), H2O molecule, HSO4−/SO42− ion, and hydrated vanadium ion concentrations in the two half-cells so that the net junction potential developed at the electrode–electrolyte and membrane–electrolyte interfaces is nullified to the most extent. At variable SOCs of the battery, the concentration gradients of these diffusing ionic/molecular specimens, mass/charge transfer toward/from the electrodes, the internal working mechanisms of the cell at different interfaces under variable concentrations, the charge–discharge processes under the depletions/depositions/agglomerations/asymmetric distributions of the molecular/ionic specimens throughout the anolyte/catholyte of the anodic/cathodic half-cell, the ionic/molecular blockage of the SO3− conductive sites of the Nafion-117, and their hindrance to the proton conductivity (Grotthuss and vehicular) procedures of the latter play very crucial roles deterministic to the exceptional performance of the cell and its integrities (battery). In addition to these, the consequences caused by the hydrated moieties of the adjacent state vanadium ions (released through the charge/discharge processes); their populations and abrupt increase/decrease in concentrations at the electrode/electrolyte and electrolyte/membrane interfaces at variable SOCs; their impacts to the smooth flow of the diffusion gradient-controlled ionic/molecular specimens across the electrolyte; their involvement in the unidirectional “water-flooding” and its prevention strategies; their physicochemical affinities toward the proton-conducting SO3− sites of the Nafion-117, free H2O molecules, HSO4−-type monovalent ions, and proton-carrying H3O+-type hydrated species; and the entire microdistributions/structural configurations of them in the nanometer range are imperative means of assessing internal complexities of the VRFB cell working electrolytes which in turn directs the optimum active material utilization strategies and the overall energy-storing capacities of the VRFB technology. Toward understanding these ideal prerequisites, the present study employed MD simulation as the most potential theoretical mean whose mathematically produced rigorous datasets and therein stored statistical microphysicochemical properties were accessed directly by the programmatically designed radial distribution function (RDF) tools (g (r)), and the required macroscopic statistical properties lying within the current MD simulation framework were retrieved. The detailed explanations of them are presented part by part in the following sections.
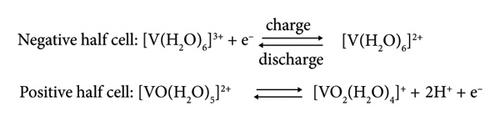
3.2. Microstructures Around Free Water Molecules
The radial distributions and the microstructures around any free water molecules (unbound state to the central Vn+ ion but bound each other by the intermolecular hydrogen bond) present in the entire simulation cell (designed to cope with the internal working conditions of VRFB cell) mostly depict the exact molecular network of water system, and its most probable breakage/cleavage of the hydrogen-bonded assembly while incorporating them with the Vn+-hydrated complexes, monovalent charged species (H3O+, HSO4−), and the proton exchange SO3− functional groups appended polymeric Nafion-117 membrane. The exact quantitative structural information related to the same explains the internal distributions of free water molecules in nanometer range which in principle stands as a standalone fact for outlining the proton conduction and ionic diffusion phenomena plus the most potential factors involved in retarding the ionic/molecular flow rates. As shown in Figure 7(a), the RDF g(r) tools derived radial distribution plot of the free water molecules computed over the last 900 ps of the MD run demonstrate the inhomogeneous number density (population) of them even within the radial distance framework of 5.0 Å. The abbreviations mentioned in the inset such as Ow and Hw indicate the central and centrally bound O and H atoms of the reference H2O molecule (Ref_H2O), respectively, and the functions and signify the typical radial O−O and O−H distances measured from that Ref_H2O, respectively. The sharp intense peaks appeared at 1.8 Å and peak at 2.8 Å justify the typical hydrogen bond length and the distance between the two O atoms of any two nearby H2O molecules, respectively. These RDF values ensure the existence of closed packing microstructures of water in VRFB-cell electrolyte; an identical network to that exists in pure bulk water systems. Moreover, no RDF peak shifting of these typical spectral bands is noticed while comparing with the MD simulation results associated with the simulation systems containing unhydrated Vn+ ions as reported by the present author elsewhere [11]. It means that the hydrated moieties of the vanadium ions (in the presence of monovalent charged species), viz., V (H2O)6]2+ and [V (H2O)6]3+ (anodic side) and [VO2 (H2O)4]+ and [VO (H2O)5]2+ (cathodic side) do not disrupt the water channel and its hydrogen bond bound assembly, further underscoring the excellent maintenance of proton conduction pathways (Grotthuss and vehicular) in VRFB-cell electrolyte system taking place facilely through the undisruptive hydrogen-bonded network of water assembly. Again, both of these and radial distributions with those two sharp and intense spectral bands are found to be as equal as the typical O−H and O−O distances of any two nearby H2O molecules present in the absolute aqueous environments with no Nafion-117 threads and monovalent H3O+ and HSO4− specimens (blank test) [11]. The and diffused type spectral patterns appeared at the radial distances of ∼3.6 Å and ∼4.5 Å, respectively, are simply due to the repetitive and periodic structural organizations of the H2O molecules in liquid state. The general conclusions we can extract from these quantitative explanations include no significant internal microstructural changes around any of the H2O molecules present in the aqueous H2SO4 matrix of the vanadium electrolytes, no disruption of the hydrogen-bonded network of water assembly (a schematic pathway for efficient proton conductions), and no internal inductions of the Vn+-adjacent state hydrated moieties, their electric charges, and their electrostatic interactions in making the VRFB-cell electrolyte systems electrochemically inactive.

3.3. Microstructures Around Hydronium Ions
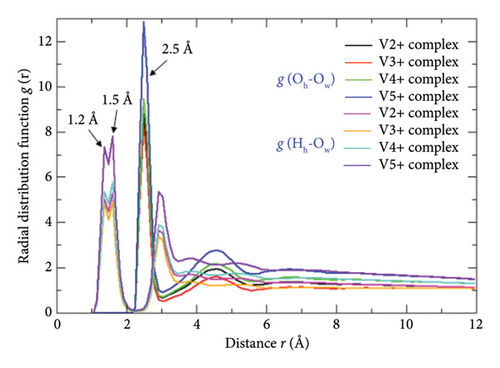
The quantitative radial distributions and the microstructural configurations of the water molecule around any H3O+ (a proton-carrying H2O molecule) specimen act as the descriptive parameters for identifying whether the proton hopping proceeded well through the Grotthuss and vehicular dynamics via the hydrogen-bonded water channel of the working electrolyte matrix or not. The movement of the H3O+ ions (proceeding of the proton conduction) across the water network can actually be inspected from the concerned RDF plot, which in fact demonstrates the same by specifying the formation and involvement of its other higher yet less stable hydrated states, viz., Eigen [H9O4]+ and Zundel [H5O2]+ states. The RDF-derived information confirms their existence in the electroactive electrolyte systems by quantizing the experimentally/theoretically determined specific interatomic distances and hydrogen bond length values. The concerned RDF plots computed over the last 900 ps of the MD run are shown in Figure 7(b) where the symbols and mentioned in the inset represent radial distribution functions of O atom of H3O+ (Oh) and O atom of water (Ow), and H atom of H3O+ (Hh) and O atom of water (Ow), respectively. The sharp spectral band appeared at 2.5 Å radial distance stands as a quantitative measures of the interoxygen distance of the two hydrated H2O molecules of the central H+; a characteristic length designated to the Zundel state of the proton (Figure 8(a)) (the Zundel state has hydration number (n) = 2, viz., [H2O------H+------OH2] or [(H3O) (H2O)]+; where the symbol ------ represents hydrogen bond), and the relatively less intense spectral peaks appeared at 1.2 Å and 1.5 Å radial distances serve as the distinctive yet distinguished hydrogen bond length values of the Zundel and Eigen states of the proton, respectively. Accordingly, the experimentally determined 2.55 Å distance exists between the central O atom of H3O+ and the central O atom of any one hydrated H2O molecule (out of three) of the Eigen ion, which is also confirmed by the sharp spectral peaks standing at the radial distance r = 2.5 Å (the Eigen ion has a hydration number (n) = 3 with a central H3O+ ion, viz., [(H3O) (H2O)3]+). All these RDF-predicted characteristic bands of the Zundel and Eigen ions at distinctive radial distances r are found to be as equal to those measured in their DFT-optimized equilibrium structures reported elsewhere [12, 20]. As per the blank tests conducted by the present author with and without including bare-state Vn+ ions, HSO4−, and polymeric (N7P)10-type Nafion-117 threads [11] in bulk water systems, none of those designated radial distances are found to be deviated significantly, suggesting the absence of predominant roles of the hydrated moieties of the adjacent state Vn+ ions deterministic to the proton conduction mechanisms and ionic/molecular flow rates existing in the VRFB-cell electrolyte systems. Furthermore, the characteristic bands of the and radial distribution functions appeared at radial distances r = ∼5.0 Å and ∼3.0 Å regions due to the periodicity of the water molecules hydrated around the central H+ and H3O+ ions of the Zundel and Eigen states, respectively; an unique distribution trends yet molecular arrangements of the hydrated proton in bulk water systems or water enriched electrolyte systems whose composition is alike to the present aq. H2SO4 matrix-supported VRFB-cell electrolytes. The relatively diffused RDF bands at r = ∼5.0 Å suggests that the considerable exchange of the water molecules used up in protonic hydration takes place between the first and second hydration shells, while the central protons start to diffuse or hop through the hydrogen-bonded water channel ubiquitously. As a whole, all these quantitative interpretations justified H3O+, [(H3O) (H2O)]+, and [(H3O) (H2O)3]+ ionic detections/conformations (Figure 8(a)) in all the four simulation cells designed for the VRFB-electrochemical cell verify the presence of predominant dynamisms of the hydrated protons (water carrying proton) in VRFB electrolyte systems, which in fact stand as the root cause of proving two mainstream Grotthuss and vehicular proton hopping dynamics; the mechanisms that govern the entire proton conduction processes of every aqueous electrolyte-fueled battery technologies and biochemical processes [21, 22].
3.4. Microstructures Around Adjacent State Vanadium Complexes
The nanometer-ranged radial distributions and microstructural configurations of the free water molecules around any hydrated complexes of adjacent Vn+ ions (V2+, V3+, VO2+, and VO2+) are quite essential to understand the hydration propensities of the latter and their free H2O molecules gaining/loosing and/or exchanging affinities in quantitative scales. The structural stabilities of these complexes with neutral monodentate H2O ligands during the entire annealing procedure of the MD simulation, after the successful ending of the same scheme, and within the parametrizations of the NVE iterations run over the significantly longer timescales can also be inspected and theorized from the MD trajectories linked RDF-based structural interpretations. The confirmation of their undisrupted hydrated moieties in equilibrium conditions even within the extreme parametrizations range of the annealing and NVE procedures ensures us to validate a few potential issues associated with the VRFB cell such as proton conductions, trends, retardations, or facilitations of the ionic/molecular flow rates, hindrance or simplistic of the conductive pathways, size dependencies of the active vanadium ions on their diffusion rates, and “water-flooding” problems of the VRFB cell. Similarly, the RDF-based distributional interpretations and population density analyses of the HSO4− ions nearby to the hydrated “all-vanadium” species specific to the anodic and cathodic half-cells are very much applicable to justify whether the highly dense HSO4− species ([HSO4−]:[SO42−] = 99:1) present in the bench H2SO4 matrix-supported vanadium electrolyte show remarkable or negligible affinities toward making anionic type complexes/clusters with the active vanadium ions or not, and to understand the effective roles of such type monovalent ions toward surpassing or restricting the conductivity rates and diffusion propensities of the protonic/ionic/molecular specimens residing into the same working electrolyte. Moreover, the closed chemical affinities of the SO3− functional groups of the Nafion threads toward the hydrated vanadium moieties and the most or the least probable blockage of them to the former sites (the bulkier sized hydrated motifs screen the former sites) can also be figured out from the concerned MD trajectories linked RDF distribution trends. Toward understanding all of these rigorous matters in question in quantitative scales, the MD-produced massive datasets of every simulation cell accessed over the last 900 ps of the MD run were assessed through the RDF means, and the required interpretations of thus retrieved RDF plots (Figures 8(b), 9, 10) were carried out. For easing the theoretical elucidations presented herewith explicitly, the representative symbols such as (n = +2, +3, +4, +5), , and are used in the insets that, respectively, stand for the radial distribution functions of the hydrated vanadium complexes (vn+_complex) in respect to the free water molecule (Ow = O atom of water), HSO4− ions (SHSO4 = S atom of HSO4−), and SO3− conductive sites of the Nafion−117 (SSO3− = S atom of SO3−).
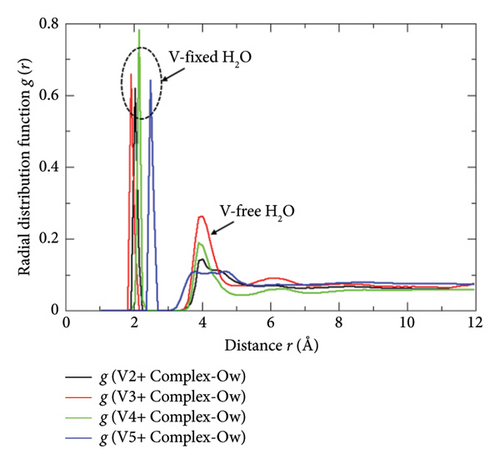
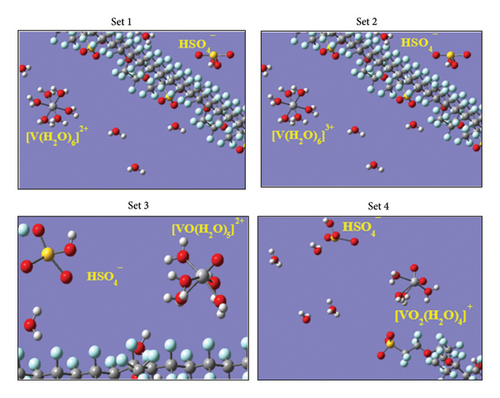
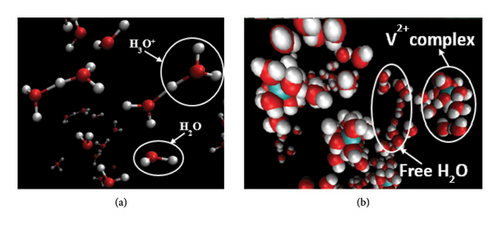
Since the simulation cells designed in this study contain both the free and fixed (solvated molecules of Vn+) water molecules separately, the undisrupted hydrated Vn+ complexes and the microdistributions of the free water molecules that tend to remain completely far away from the Vn+-centered hydrated moieties are clearly seen in the VMD-rendered graphical images (Figure 8(b)) produced over the 900 ps of the MD run (within this simulation timeframe, the annealing procedure was completed with the attainment of the absolute equilibrium descriptors underscored in Section 2, and the NVE simulation was run iteratively with extreme parametrizations). The dispersing propensities and the outbound distributions of the free water molecules from the central Vn+ ion of the given hydrated complexes are depicted quantitatively in Figure 9 where the symbols “V-free H2O” and “V-fixed H2O” mentioned in the inset abbreviated the interactions between the central Vn+ and outbound (mobile) water molecules, and the interactions between the central Vn+ and its inbound water molecules (hydrated), respectively. The intense and distinctive spectral bands appeared at the radial distance r in the range of ∼1.8 Å –∼2.5 Å illuminate the unequal inbound affinities of the adjacent states Vn+ ions with water molecules, which is however very typical to the intensities of the electric charges carried by them (V2+, V3+, VO2+, and VO2+) and their solvation propensities. These radial distance r ranges are justifiable to the DFT-derived Vn+-OH2 bond length of each hydrated complex in a respective low energy equilibrium state. The present author reported this bond length value elsewhere [5] for the adjacent state Vn+-hydrated complexes as 2.4 Å, 2.0 Å, 2.1 Å, and 2.1 Å, respectively, where the trial structures used for each of them were constructed in the graphical interface used with Gaussian and optimized explicitly into the global minima states via the DFT method. The considerable radial distance deviations to that of the DFT-predicted bond lengths are seen in the first two bivalent and trivalent complexes, viz., [V (H2O)6]2+ and [V (H2O)6]3+, which are however lying in the satisfactory range if we consider the extent of the polarizabilities induced by these two intensive electric charges and the moderate computing skills of the currently employed force-field databases [23]. In addition to this, the spectral bands standing at the radial distance r ∼ 4.0 Å present pictorially the exact location in which the optimum population density of the free water molecules is dispersed. This range of r explains quantitatively that none of the free water molecules dare to approach the vicinity/bonding regions of any of the hydrated Vn+ complexes (Figure 8(b)) unlike the cases of bare-state Vn+ ions that were found to show strong affinities toward the same while simulating them together in the presence of Nafion threads, H3O+ ions, and HSO4− ions as discussed elsewhere [11] by the present author. This reluctant tendency of the mobile water molecules toward going nearer to the hydrated complexes of adjacent state “all-vanadium” ions would be an esteemed fact to declare that every Vn+-hydrated complexes employed throughout this study attained their saturated levels of hydrations despite showing some degree of flexibility toward loosing closely inbound water molecule more especially by the [O = V = O]+ unit bearing [VO2 (H2O)4]+ species, but keeping it in the hydrogen bond bounding region [1]. Again, the radial distance r that lies in between 2.8 Å and 3.5 Å region of the same RDF plot bears no spectral peaks at all or represents a nodal plane into which no number density of free water molecules is residing, ensuring no exchange of any H2O molecules takes place in between the fixed-water (inbound state) and free water (outbound state) spheres. However, the nonzero region appeared immediately after the completion of the latter sphere (after the radial distance r = ∼5 Å) of the same plot indicates the spatial homogeneously distributed free water molecules, figuring out the internal pictures of the repeatedly aligned mobile H2O molecules dispersed throughout the electrolyte matrix designed for the VRFB cell.
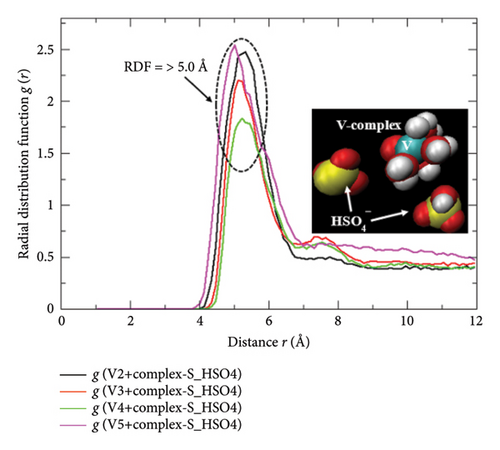
Alike to the aforementioned discussions, the closed interactive proximity of the HSO4− ions toward the hydrated complexes of adjacent state vanadium ions can be analyzed from the concerned RDF plot shown in Figure 10(a). The intense spectral bands standing at an abnormally higher radial distance r ≥ 5 Å region while varying the oxidation states of the hydrated vanadium complexes signify the least probability of forming new bonding moieties with the freely yet predominantly available monovalent type HSO4− ions. Despite their unwilling trends, the appearance of such intense peaks simply measures the approximate radial distance r region wherein the optimum number density of the HSO4− ions is accumulated. In fact, this specific region lies in the outbound distances in the perspectives of the covalent bonding principle between any two nearby atoms that are required to be departed by the distance shorter than the sum of their Van der Waals atomic radii rw for new bond formation. For example, if the rw of the central S atom (1.80 Å) of the HSO4− ion and the central V atom (1.79 Å) of each of the hydrated complexes are referred, their sum (rsum = 3.59 Å) does not exceed the radial distance value (r = ≥ 5 Å) speculated from the concerned RDF plot. This quantitative regime guaranties the null chances of developing bonding complexes between the HSO4− ion and the hydrated vanadium complexes within the present 2M−5M H2SO4 concentration frameworks used in preparing vanadium electrolytes. The same is diagrammatically depicted (in the inset of Figure 10(a)) by the VMD graphical image rendered from the MD simulation databases retrieved over the 900 ps. These quantitative justifications are very much useful to conclude the facts that none of the predominantly available monovalent HSO4− ions residing into the VRFB-cell electrolyte are used up to trap the electrochemically active hydrated vanadium complexes (the fuel materials that store chemical energy convertible into electrical energy). It means none of the “all-vanadium” fuel materials are wasted or electrochemically disabled to undergo complete oxidation/reduction reactions just only due to the excessive presence of HSO4−. However, a slight retardation of the diffusions or flow rates of the protons/ions/molecules throughout the conducting electrolyte medium may be caused by the [HSO4−] thickened viscous matrices. The similar type unopposed roles and negligible impacts of the HSO4− ions to the vanadium-based working electrolyte were also noticed while considering the bare-state Vn+ ions as the electrochemical-active species [11].
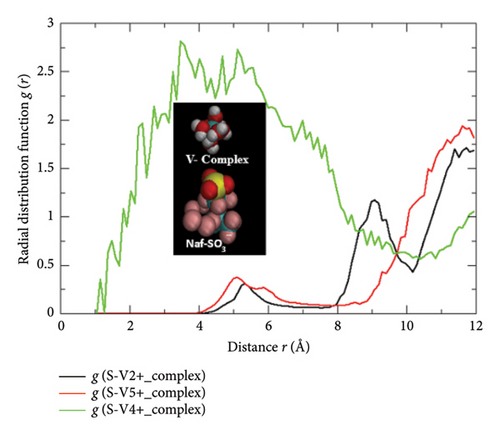
Accordingly, the ionic interactions and the microstructural distributions of the hydrated vanadium complexes with dissimilar charged states (electronic charges) in the vicinity of SO3− conductive sites of the Nafion-117 can be theorized from the concerned MD trajectories derived RDF plot shown in Figure 10(b). Except the case in V (IV)-hydrated state, viz., [VO (H2O)5]2+ ion, the relatively less intense RDF peaks are seen beyond the radial distance of ∼4 Å region, justifying the low number density of V (II)- and V (V)-hydrated complexes, viz., [V (H2O)6]2+ and [VO2 (H2O)4]+ accumulated in the relatively far away distance from the SO3− conductive sites of the Nafion-117. However, the case is pronouncedly different in V(IV) complex state: the relatively more intense, obtuse yet wide-range occupied RDF peak is observed at the radial distance ∼2 Å–∼8 Å region, signifying the asymmetric distributions of more number density of [VO (H2O)5]2+ ion in the both inbound and outbound regions of the SO3− conductive sites of the Nafion-117. The RDF g(r) spectral trends and the peak distributions for the V (III) complexes are excluded in the same diagram due to the negligible range expansions across the plotting scales. This might be due to the lack of proper databases in the designated force-field packages because of which the effects of the induced-charge polarizabilities created by the +3 unit electric charge of the [V (H2O)6]3+ ion were unable to be addressed properly. In terms of the covalent bond developing probabilities between the adjacent state hydrated vanadium complexes and the SO3− sites of Nafion, the aforementioned bonding principle is still applicable. Since the intense RDF peak position for the SO3− functional group (from the central S atom, rw = 1.80 Å) in respect to [VO (H2O)5]2+ and [V (H2O)6]2+, [VO2 (H2O)4]+ (from the central V atom, rw = 1.79 Å) is appeared at radial distance r = ∼4 Å and r > ∼4 Å regions, respectively, the sum of the Van der Waals radii rw of these atoms (rsum = 3.59 Å) never exceeds that value does not satisfy the critical conditions required for the bonding, illuminating that none of the Vn+-hydrated complexes can form covalent bond with any of the SO3− atoms of Nafion-117. It further means none of the SO3− groups of Nafion are obsessed by any of the Vn+ complexes, and therefore, they can exhibit exceptional conductivities and proton exchange rates even in the present complex electrolyte matrix functionalized battery system. Interestingly, this typical g (S−Vn+_complex) radial distance r = ∼4 Å specific to the V (IV)-hydrated complex is found to be as consistent as the closest separation distance maintained in between the two nearby groups, viz., a central V atom of [VO (H2O)5]2+ and a central S atom of SO3− Nafion (distance = 4.2 Å) as reported earlier by Intan et al. [24]. Therewith, the closest departing distance between the O atom of the former and the S atom of the latter is measured as 1.5 Å in their closely linked motifs developed in the electrolyte system while delivering ionic mobility/conductivity across the electrolyte–membrane interfaces. Nevertheless, this quantitative interpretation reveals the fact that none of the SO3− conductive sites of the Nafion experience either partial or complete blockage of the adjacent state hydrated vanadium complexes, ensuring that all the conductive sites and polymeric channel of the Nafion-117 remain completely unoccupied and activated by means of which protons/ions/molecules exhibit smooth diffusions and notable dynamism provided that the Nafion has priory attained the optimum water content (λ = 22) in its hydrophilic domains.
3.5. Microstructures Around SO3− Functional Groups of Nafion
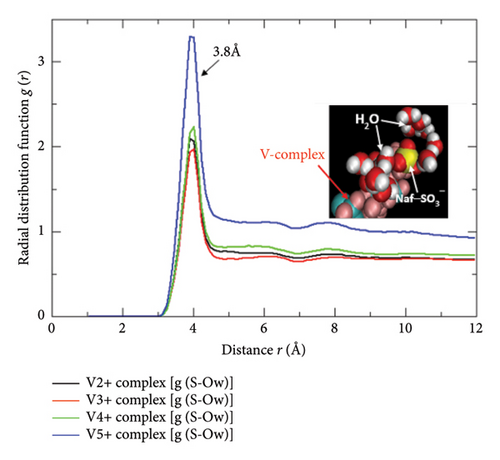
The complete protonic/ionic conduction abilities and the diffusive flow rates assessing propensities of the SO3− sites of the Nafion-117 are only be materialized if the microdistributions of the free water molecules and the hydrated protons H3O+ nearby to them are traced out thoroughly. Since the SO3− functional groups are regarded as the most electrochemically active conductive sites of the Nafion bearing a −1 unit electric charge, they chemically prefer to exhibit positively charged H+ exchanging abilities with the nearby H3O+ species leaving behind the free H2O molecules into the polymeric matrix, which in turn accept H+, and further participate in a similar type exchanging mechanisms with another nearby SO3− unit of the same polymeric thread, and so on. In addition to this, the protonic conduction takes place into the Nafion matrix (hydrophilic domain) through the Grotthuss mechanisms as well in which the H+ ions are hopped to the free H2O molecules dispersed into the same, and the continuous processes happen across the networking channels. Either of these schemes is pronouncedly affected by the water content λ of the Nafion, and its water retaining capacities (swelling property of Nafion: a distinguished characteristic feature when the (a) EWNafion ≥ 100 and (b) relative humidity RH = 0, λNafion ≅ 1; RH = 100, λNafion ≅ 14 and in a perfectly water enriched wet condition, λNafion ≅ 22) [14] plus the relative abundance of the H3O+ and H2O-type species nearer to its SO3− proton exchanging sites. Additionally, none of the SO3− functional groups of Nafion are found to be made electrochemically inactive by the excessive presence of the Vn+-hydrated complexes, and the HSO4− ions, and neither of the latter specimens plus their asymmetric distributions are found to involve in impeding the conductive potentialities of the former, and more importantly, none of them dare to form the bonding complexes with the SO3− groups as presented in Section 3.3. Therefore, the only way to inspect the facile conductivity rates of the Nafion membrane and the proton exchange abilities of its SO3− functional groups is to monitor the number density of H2O and H3O+ gathered nearby to them either due to their mutual electrostatic attractive forces or in the course of delivering protonic conductions. The theoretical mean that can correlate all these consequences quantitatively via the graphical representations is none other than radial distribution function plots. Herewith, the radial distribution functions for the H2O g(S − Ow) and H3O+g(S − Oh) species in reference to SO3− sites of Nafion are presented by varying the adjacent state Vn+-hydrated complexes as shown in Figures 11(a) and 11(b), respectively, and interpreted the results associated with them. In order to figure out their closed electrostatic interactions and the optimum nearest distance, the VMD graphical images rendered from the MD simulation datasets produced over the last 900 ps are also displayed in the respective insets. As can be seen in Figure 11(a), the four intense RDF spectral peaks of g(S − Ow) at radial distance r = 3.8 Å approximate the nearest region of H2O in reference to SO3− site of Nafion wherein the optimum number density of the former species are gathered. This S − Ow radial distance r is very much shorter relative to the r estimated for SO3−−SO3− (∼5.0 Å), SO3−−Vn+_complex (∼4.5 Å), and SO3−–bare_Vn+ (∼4.2 Å) (Figure 12), signifying that sufficient number density of the water molecules can be accommodated in between any two SO3− conductive sites of the Nafion by means of which the actual proton exchange and proton hopping processes are possible. In fact, the swelling properties of the Nafion and the length of its hydrophilic tunnel that separates any two of its SO3− groups made spherical micelles are dependable observables to the extent of which it can uptake and hold up freely moved polar solvents such as water into its conductive polymeric matrix. As per the literature analyses, these types of the micelles developed in the polymeric network of Nafion are of 4–6 nm diameter, and their water-filled connectors are of 1 nm width and 5 nm length, and more importantly, the water retention performance of it is a function of temperature [25]. It means the basic facts underlying the significant proton exchange and the ionic/protonic conduction deliveries of the Nafion membrane are none other than its net water retaining abilities for longer timescale which in turn is only furnished by its SO3− groups as discussed above. If the same diagram (Figure 11(a)) is furthermore referred, the most distinctive yet optimum number density of the H2O molecules holding g(S − Ow) spectral band is seen in the case for V (V) complex [VO2 (H2O)4]+ (this typical RDF peak has more height and width relative to others). This might be due to the least diffusion-gradient governed freely moved water obstructing abilities of the [VO2 (H2O)4]+ caused by its smallest ionic radii (mean bond distance dV=O = 1.6 Å, dV−O = 2.024 Å) with a distorted octahedral geometry [7, 24], and the least effects of the induced-charge polarizabilities (lie in the addressable range of currently employed force-field packages) caused by its lowermost electric charge unit. Again, the similar analyses of the diagram confer the symmetric, flat, and nonzero regions appeared beyond r ≅ 4.5 Å, further speculating the excessive presence of significant number density of water molecules aligned periodically in an absolute outbound region of the SO3− groups. This explanation justified one of the most indispensable requirements of the Nafion membrane to exhibit exceptional proton exchange and free water diffusions across its polymeric hydrophilic matrix in both extreme and nonextreme wet conditions.
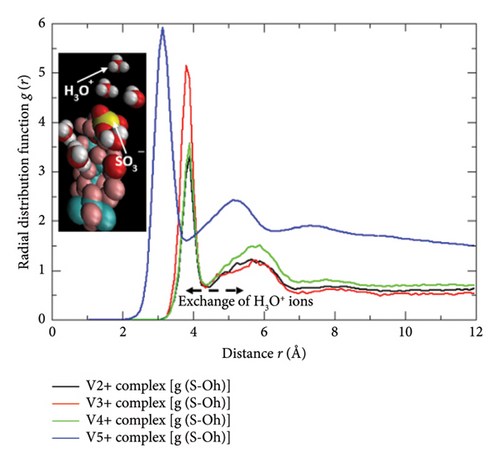
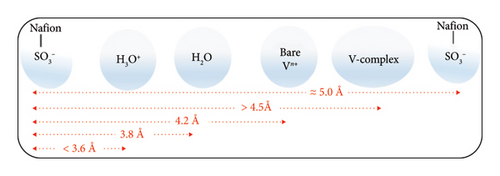
Alike to these interpretations, the microdistributions and the most possible involvements of the H3O+ ions in exchanging H+ with the SO3− sites of Nafion can be depicted on the basis of g(S − Oh) plot shown in Figure 11(b). The first and second sharp RDF peaks standing at the radial distances r ≅ 3.0 Å and ≅ 3.6 Å explain the stronger yet unequal strength electrostatic interactions, and the nonzero region lying in between ∼4.0 Å and ∼5.5 Å speculates the occurrence of reversible movements of H3O+ that takes place mainly in the time when the proton exchange between the SO3− and H3O+ groups is proceeded. In general, the approaching number density of the H3O+ species toward the SO3− sites of the Nafion is extremely affected by the size of the hydrated Vn+ complexes that remain there with them in an absolute working electrolyte condition of the VRFB cell. In this case, among the Vn+ complexes, the V (V) moiety [VO2 (H2O)4]+ is the smallest one in size and, hence, cannot screen fully the approaching number density of H3O+ toward the SO3− group of Nafion. Therefore, the relatively high abundance of the H3O+ species exposed directly to the SO3− groups is observed in the system containing [VO2 (H2O)4]+ complex. More importantly, the RDF plot predicted radial distance value r = 3.0 Å–3.6 Å between the SO3− and H3O+ groups is distinctly smaller than the separation gap of SO3−−SO3− and is noted as the lowest one (Figure 12); the optimum accommodation and the excellent involvement of the H3O+ species in proton exchange processes with the SO3− sites of Nafion are justifiable. Again, the nonzero H3O+ population density region of the same RDF plot even beyond the 7.0 Å radial distance indicates the presence of a symmetrically distributed hydrogen-bonded network of H3O+ across the polymeric matrix of Nafion, which is in principle a fundamental basis of conferring both the vehicular and/or the Grotthuss proton hopping dynamics. Actually, the first mechanism takes place with the obsolete movement of the H3O+ unit across the hydrogen-bonded water network retained inside the polymeric chain, and the second involves an exchange of H+ between the H3O+ and nearby H2O of the same matrix, either of them are absolutely facilitated by the symmetric population distributions of the both H3O+ and H2O specimens (Figures 11(a) and 11(b)) in the regions lying beyond the radial distance r = 6.0 Å in respect to SO3− group of Nafion.
4. Conclusion
This contribution was solely concentrated on the investigations of internal microstructures and nanometer range distributions of the sulfur-centered HSO4− ions, adjacent states Vn+-hydrated complexes ([V (H2O)6]2+, [V (H2O)6]3+, [VO (H2O)5]2+, and [VO2 (H2O)4]+), hydrated protons (H3O+), and free water molecules (H2O) in the vicinity of SO3− functional groups of Nafion-117-type polymeric cation exchange membrane dipped into the 2M–5M H2SO4 (aq.) matrix of “all-vanadium” electrolytes of the VRFB cell. These monovalent to polyvalent charged species made complex electrolyte composites are actually functionalized electrochemically through the VRFB cell, and the net chemical energy stored in them are converted into the electrical energy. Toward understanding the complexities of such type electrolyte system comprising with the drastically varied ionic/nonionic compositions and their explicit yet mutual chemical interactions, the MD simulation studies of the anodic and cathodic half-cells containing the [V (H2O)6]2+ and [V (H2O)6]3+, and VO (H2O)5]2+ and [VO2 (H2O)4]+, respectively, as principal working electrolyte species, and the H2O and H3O+ as predominant auxiliary molecular specimens were carried out separately in the presence of Nafion-117 threads holding essential SO3− proton exchange sites. Four different simulation cells compatible with such a complex internal electrolyte matrix of both anodic and cathodic half-cells were designed, and subjected to the extreme parametrizations of the annealing simulation (equilibrium state establishing strategies) for the specific time period followed by the NVE simulation under the constraints of constancy on number of particles N, volume V, and total energy E of the every microcanonical ensembles. The number of all those charged and uncharged particles incorporated into each of these simulation cells was determined in such a way that the net electric charge of the entire ensemble becomes fully neutral, and the net water content (λ) of the Nafion-117 thread reached 22. The statistical physicochemical properties that are associated with the operational principles of the VRFB-cell technology such as interfacial distributions of the Vn+-hydrated complexes, H2O, and H3O+ in the vicinity of SO3− and their intense chemical affinities toward themselves; internal dispersions of the former specimens into the polymeric matrix of the Nafion and their explicit contributions in enhancing proton-conducting abilities of the latter; electrochemical effects of the Vn+-hydrated complexes and their nearby shell structures in the osmotic balance of the electrolyte specimens; and inbound or outbound approaches of the HSO4− ions toward the freely dispersed H2O and H3O+ specimens plus the repeatedly aligned SO3− sites of the Nafion were retrieved from the MD-produced gigantic datasets accessed through the radial distribution function RDF g(r) tools.
The general results showed that in a VRFB-cell electrolyte system: (a) none of the hydrated vanadium moieties, viz., [V (H2O)6]2+, [V (H2O)6]3+, [VO2 (H2O)4]+, and [VO (H2O)5]2+, disrupt the internally bound water channel and its hydrogen bond bound networks, illuminated the excellent maintenance of the proton conduction pathways, and none of their internally induced electric charges, and their electrostatic interactions impact the electrochemical activity of the conducting ions/molecules, and the entire “all-vanadium” redox couples; (b) there is a presence of predominant dynamics of hydrated protons (H3O+) which when conducts H+ (proton) turn into Zundel [H5O2]+ and Eigen [H5O2+] states; and (c) considerable exchange of the H2O molecules used up in protonic hydrations takes place while the central protons proceed to hop through the channel of hydrogen-bonded water network. More importantly, the dispersing propensities and the outbound distributions of the freely aligned H2O molecules from the central Vn+ ion of the “all-vanadium” hydrated complexes were distinctly noted with the clear indications of their saturated hydration levels, and their unequal inbound hydration affinities. None of the freely moved water molecules were found to be exchanged between the fixed-water (inbound state, r ≅ 2–3 Å) and free water (outbound state, r ≅ 4 Å) spheres of the Vn+ complexes; instead, the spatial homogeneous distribution of the former was precisely observed immediately after the completion of the latter sphere, figuring out the internal microdispersion attributes of the water molecules occurred at various ion–molecule interfacial regions. In addition to these, the absolute rejection of the predominantly present monovalent HSO4− ions by the Vn+-hydrated complexes from their chemical bonding territories was confirmed based on their RDF-predicted nearest interatomic radial distance (r ≥ 5 Å) as this value does not satisfy the criteria required for the covalent bonding, reassuring the null retardations of the conductivity rates of “all-vanadium” redox couples simply due to the presence of HSO4− in an electrolyte matrix. A similar was the reluctant trends observed between all the adjacent state Vn+-hydrated complexes and the SO3− functional groups of the Nafion, the decisive descriptor verifying the complete absence of the vanadium blockage in the proton exchange sites of the latter. Accordingly, the significant H2O and H3O+ number density accommodating capacity of the Nafion-117 membrane in between any two of its SO3− functional groups was quantitatively justified: The radial distance (r ≥ 5 Å) between the two nearby SO3− functional groups was measured as the longest one, whereas the distances between the H2O and SO3− (r ≥ 3.8 Å), and H3O+ and SO3− (r ≤ 3.6 Å) were the shortest among the others; the most significant features that not only ease Nafion to exhibit exceptional proton exchange rates but also theorize its accessory pathways required for Grotthuss and vehicular proton hopping such as water-swelled clusters and hydrophilic tunnels. In view of all these concluding remarks, this research report is expected to serve as a doctrine means of probing VRFB-cell functionalities, operational mechanisms, charge–discharge stabilities, and energy-storing aptitudes.
Conflicts of Interest
The author declares no conflicts of interest.
Funding
No funding was received for this insightful work.
Acknowledgments
The author is indebted to the Institute of Fluid Science (IFS), Tohoku University, Sendai, Japan, for giving a direct access to the high-performance computing systems. This work was supported by Brother Industries, Ltd., Japan. The author has declared that no AI tools and the texts generated by them are used.
Open Research
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon reasonable request.




