Mathematical Analysis of a Resource-Based Dispersal Model With Gompertz Growth and Optimal Harvesting
Abstract
Gompertz dynamics offer significant applications for the growth of invasive species, cancer modeling, optimal harvesting policies, sustainable yield, and maintaining population levels due to its pattern formation in low-density cases. This paper examines a widely applicable nonhomogeneous diffusive Gompertz law with zero Neumann boundary conditions, where all coefficients are smooth periodic functions. The analytical approach explains the ubiquitous stability of a time-periodic solution and seeks the optimal strategy for harvesting under the Gompertz growth law, potentially generalizing the results for many small organisms, including plants and wild populations. The proposed model successfully investigates the dynamics with and without diffusion. Moreover, the spatio-temporal equation more precisely describes the population’s evolutionary processes using a generalized classical reaction-diffusion equation. Finally, we observe several potential applications, outlining the optimal strategies for real-world scenarios and related fields where optimal harvesting is utilized.
1. Introduction
A classical reaction-diffusion equation consisting of a reaction term and a diffusion term arises in numerous fields of science and technology such as in chemistry [1], in ecological invasions [2], in spread of epidemics [3], in tumor growth [4, 5], and in many other areas [6–9]. The area of population dynamics is recognized as the first application of mathematics to biology, exemplified by Malthus’ prediction of unbounded exponential growth and Verhulst’s proposal of the logistic equation. The first models were either differential or first-order difference equations. However, in many cases, we can not neglect either spatial distribution or dependence on the previous history of the population; thus, the passable models would be ordinary/partial differential [10], or fractional differential equations [11, 12].
In ecology, a classical reaction-diffusion equation plays a vital role in the study of different types of dynamics of species [9]. Due to the seasonal and climate issues in ecology, the resource distribution in multiple organisms is one of the main goal to survive the population. Besides foods, proper habitat and community structure are the another major challenge to survive the population maintaining density [13]. To maintain biodiversity in the ecosystems on conservation, the preface of spatio-temporal effects has become essential in recent decades [14–17]. The impulsive and harvesting population models were considered and was studied in [18] to display the scenario of time-dependent and independent facts. In [19], Henson and Cushing studied the consequence of seasonal natural territory amplifications for worm/moth population on a nonlinear model. Harvesting in a seasonal environment is studied in [20]. A general harvesting model with periodic capacity function is presented here, and a analytical ground is developed.
As for spatially distributed populations, if at each point the growth of the population size u was described by a specific law, such as logistic, Gompertz, or some other then, the simplest model follows that (du/dt) = g(u(t)). Here, the growth function can be modified to f(x, u) to involve the space variable, and the diffusion term is added to the right-hand side to describe population movements. Benjamin Gompertz investigated general growth equations, and those were successfully applied to ecological applications such as actual tumor data, which was published in 1825 that has become a foundational essay establishing the concept variously called “Gompertz’s Law” [21]. He fitted it to make a connection between increasing death rate and age. Gompertz discussed the two distinct behaviors of the human life table. 1n some cases, such as countries or range of ages, the function of age decays exponentially. Again as in real-life tables, when age is discrete, it decreases as a geometric series. By the mid −20th century, in models of population growth, Gompertz’s insight was applied that included mechanistic detail [22, 23]. It is frequently used to describe bird growth [24], fish growth [25], and growth of other animals and also used in plant growth [26]. To describe the number of bacteria in bacterial growth [27, 28] and the volume of cancer cells [29], it is also used.
- •
The existence of a lowest patch shape necessary to persist a population
- •
The extension of wave fronts corresponding to biological invasions, and
- •
The spatial pattern formations in the population distributions in homogeneous environments.
2. Model and Methods
Here, Δ is the Laplace operator in , the constant D > 0 is the diffusive coefficient. , are uniformly bounded from below and from above in where, Λ ≡ Ω × (0, +∞) and (similarly ∂Λ ≡ ∂Ω × (0, +∞)). Table 1 summarizes key symbols and their descriptions used throughout this study.
| Symbol | Description |
|---|---|
| u | Population density |
| r | Growth rate |
| H | Harvesting rate |
| K | Carrying capacity |
| t | Time |
| α | Higher-order smoothness |
| D | Diffusive coefficient |
While we are considering the model (1), then in the absence of growth function f(x, t, u, r, K), the organism has no change on their density level, which yields a uniform population distribution over the domain. Again if r = 0 or, D is very large, the solution of (1) tends to be uniformly distributed. The assumption is reasonable for uniform resources, which means the carrying capacity is not spatially dependent. In the case of nonuniform resource distribution, the model (1) suggests that the movement of the population to the areas with lower per capita available resources is contingent and biologically questionable. The idea of this type of diffusion in (1) was first considered in [8, 17] motivated by choice of optimal harvesting strategies. It is also noted that other diffusion types, specifically nonlinear, were considered in population dynamics which is based on the experimental data [30–34].
-
(h1) Function f is uniformly Hölder continuous in , where J is a sector between lower and upper solutions. Moreover, functions f and (∂f/∂u) are C1(0, t), Hölder continuous in in the x variable.
-
(h2) where is monotonically decreasing in and when and when .
-
(h3) .
J is a sector between lower and upper solution means the range within which the true solution of our equation exists. Specifically, a lower solution is a function that always stays below or equal to the true solution of the equation, while an upper solution is a function that always stays above or equal to the true solution. The sector J represents the interval or range where the true solution is found, lying between these lower and upper solutions. We can easily justify that the Gompertz function follows the (h1)–(h3) properties while r(x, t) is positive bounded, and we assume they hold always.
- 1.
For Gompertz law with time and space variable functions, the behavior of population is studied with or without diffusion. The existence and uniqueness of a periodic solution is presented
- 2.
For time-independent parameters, there is a positive stationary solution that attracts all positive solutions under certain conditions
- 3.
For periodic parameters, similar solution patterns have been found
- 4.
The analytical explanation of the global stability of optimal harvesting policy is presented
- 5.
The results are generalized using multiple growth functions with harvesting; and
- 6.
The theoretical results are verified in a series of numerical examples.
The paper is organized as follows. In Section 3, we describe the growth and harvesting of the model in absence of diffusion for constant coefficients (in sub-section 3.1) and then for periodic coefficients (sub-section 3.2). Then, we discuss in detail the Gompertz growth model with harvesting in Section 4. In Section 5, we present the existence, uniqueness of solutions of the diffusive Gompertz growth model. We establish the result of existence periodic solutions in a bounded domain. In Section 6, the optimal harvesting policy is discussed. In Section 7, we generalized the results using multiple growth functions with harvesting. A series of examples are presented in Section 8 for applications. Finally, Section 9 concludes the summary and discussion of the results.
3. Dynamics of Time Periodicity
3.1. Dynamics for Constant Coefficients
- i.
If is the globally asymptotically stable equilibrium.
- ii.
If H > r, then u decreases gradually and when t⟶∞, then u⟶0.
- iii.
If H = r then which is constant. These indicates that H = r is a critical value and under harvesting exploitation this H = r indicates the persistence or extinction of population.
- iv.
When the condition is H < r, the sustainable yield is h = Hu.
- v.
Here, the maximum yield is when and H∗ = r.
3.2. Dynamics for Time-Periodic Coefficients
Here, r(t), H(t) and are C1(0, ∞) functions. The above models are simple ODEs and do not include spatial and temporal environmental effects. Therefore, model (3) is extended to a periodic environment in [36–39]. A global asymptotically stable periodic solution is obtained and the harvesting policy is established. In real evolutionary processes, the density of population depends both on time and space. Considering this point, we get a unique model in the following sections.
3.2.1. Determination of Maximum Harvesting Yield
The maximum harvesting yield, , is derived by first identifying the optimal harvesting rate H∗(t) that maximizes the yield over the periodic cycle. The functional form of the yield with respect to the harvesting rate is crucial to determine the maximum sustainable yield.
4. Classical Diffusion With Harvesting
From the variational calculus method [40], here the maximum population label is , and the respective harvesting endeavor is and the maximum sustainable yield is [41]. This result is likewise to the specially homogeneous logistic equation considered in [35, 36].
5. Uniqueness and Existence of a Periodic Solution
-
J1: and r(x, t) are Hölder continuous in x, continuously differentiable functions and strictly positive for any .
-
J2: For a given function we denote ψm and ψl be the greatest and smallest of on .
Theorem 1. Assume that , Hmrm − Hlrl > 0. Then there exists while for , the solution of (6) u(x, t)⟶u∗(x, t) when t⟶∞.
Proof 1. Consider um and ul as the solutions of (12)
We get a unique positive solution um and ul if Hm/rl < 0, which are and .
It is obvious that um > ul and
That is, um and ul are the constant coupled upper and lower solutions of (1). Let, p and q are quasi-solutions and for they satisfy ul ≤ q(x, t) ≤ p(x, t) ≤ um. So
Now, subtracting the first two equations from (15), we can write
As p and q are periodic functions,
Now, from and yields Hm/Hl > rl/rm, for which it is obvious that p = q ≡ u∗ for a unique resolution u∗ over (ul, um) [42]. Therefore, for any the solution of (1) gratifies u(x, t)⟶u∗ as t⟶∞ and .
6. Sustainable Yield With Optimal Policy
According to Theorem 1 in Section 5, under the exploitative condition, the persistence of population is ensured by the condition and Hmrm − Hlrl > 0. Therefore, for t⟶+∞ and u0(x) > 0, x ∈ Ω, we find u∗(x, t; u0), a unique global asymptotically positive periodic solution. In this section, using the technique of variational calculus [43, 44] we are going to find out the optimal policy.
The functional of three variables generalizes (20) and (21). Now, the spatial case is to maximize the sustainable yield and the optimal H and p is .
As is periodic, we find the last equality valid. The previous discussion and the findings above lead to the following.
Theorem 2. Suppose and we denote . Then the optimal sustainable yield is
7. Classical Diffusion With Generalized Growth Function
-
(s1) Monotonically decreasing continuous function in .
-
(s2) There exists , and for it implies ; for and ϕ(x, t, 0) = 1.
-
(s3) ϕ(x, t, u) is a Hölder continuous and function and in some closed interval of R Lipschitz continuous in u. There exists l > 0 such that
For all (x, t) ∈ Λ and u, v ∈ [L, M]. We consider (s arabic)-(s arabic) are hold. We are going to use a similar method as in Theorem 1 to prove that (32) has a unique solution.
Theorem 3. Suppose −rm ln(lθ) < Hl < Hm < rl, l is Lipschitz constant that satisfies (33), in the interval (θ, ω) there exists a unique periodic solution u∗(x, t). Again for θ ≤ u0(x) ≤ ω, (32) satisfies u(x, t)⟶u∗ when t⟶∞ and .
Proof 2. We assume and and the constants θ and ω satisfy algebraic equations
It is easy to see
From assumption (s arabic) and (s arabic), and we know that θ and ω are unique. Moreover,
And this implies, θ and ω are the combined overhead and lower solutions of (32), respectively. Now, there exists quasi-solutions p and q [42] and they satisfy
From (38) and the periodicity of p and q, we have
We find ϕ(x, t, u) is a decreasing function on u from (s arabic) and (s arabic). Again 0 < ϕ(x, t, p) < 1, then ϕ(x, t, p) − ϕ(x, t, q) ≤ −(p − q)ln l. As p and q are periodic, we have
It follows from Hl + rm ln(lθ) > 0 that p = q ≡ u∗. Hence, according to the theorem, it is confirm that a unique solution u∗ exists over (θ, ω) the correspondent solution u(x, t) of (32) satisfies
Theorem 4. Suppose we find a unique positive periodic solution u∗(x, t) to the equation
The proof is similar to that of Theorem 2, so it is omitted here.
8. Numerical Simulation
This section aims to present the numerical simulations’ results that complement the previous sections’ theoretical results. We observe the behavior by diffusion coefficient D, intrinsic growth rate r, harvesting rate H, and carrying capacity of the model (1). First, let us consider the case of without harvesting, that is H = 0.
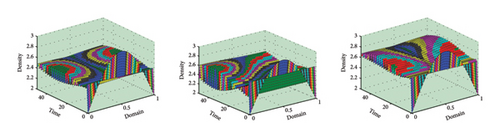
Example 1. We consider (1) on Ω ≡ x = (0, 1) with D = 1.0, harvesting H = 0.0, carrying capacity and different intrinsic growth rates r = 1.2, 1.2 + cos(πx), 1.2 + cos(πx)sin(πt). The numerical simulation in Figure 1 shows that in the absence of harvesting, we get a unique positive periodic solution whatever the initial density point is. Moreover, the result shows similar behavior in two dimensions (Figure 2). It is time to establish the unique solution for any initial density maps and for various growth rates. The existence and uniqueness of the solution of (1) are valid as designed in Figures 1 and 2. These figures justified the result of Theorem 1.

Example 2. Consider (1) on Ω = (0, 1) with D = 1.0 and H = 0.0, time variable carrying capacity and initial population u0(x) = 2.0 + sin(πx). For time-periodic carrying capacity and for various growth functions, the numerical simulation shows a positive unique solution. The equilibrium depends on the change of intrinsic growth rates r = 1.2, 1.2 + cos(πx), 1.2 + cos(πx)sin(πt) which is shown in left figure of Figure 3. Also in right figure of Figure 3, explains the uniqueness of the positive solution despite of different initial mass.
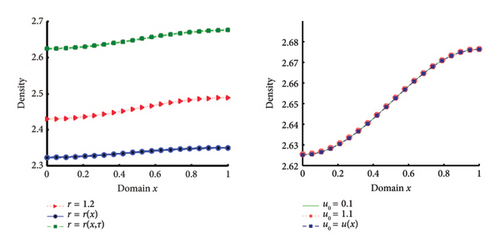
In both cases (Case 1 and Case 2), Theorem 1 is verified for random time-periodic carrying capacity functions . In the next example, we outline the impact of the dispersal coefficients D on the steady state level.
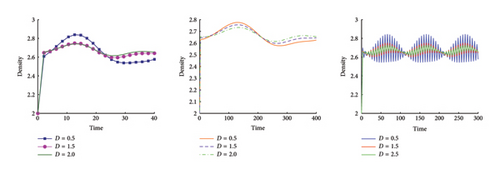
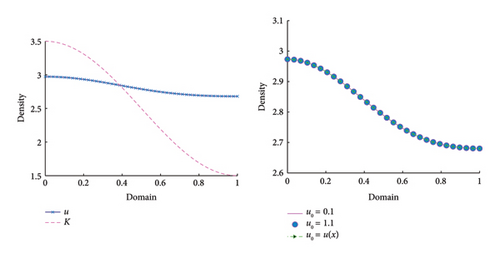
Example 3. Consider model (1) with time variable carrying capacity and intrinsic growth rate r(x, t) = 1.2 + cos(πx)sin(πt). Also consider H = 0, initial population density u0 = 1.1 for Ω = (0, 1). Numerically, it shows that the value of u(x, t) converges to the time periodic positive solution when t⟶∞. The more we increase the diffusion strategy, that is, increasing of D, the more we converge to the limit state for the same initial density and t > 0. See the illustration of Figure 4. There is a similar illustration in Figure 5 for a two-dimensional scenario. Finally, if we consider , carrying capacity only dependent on the environment, then we get a unique positive solution as shown in Figure 6.

Now, we consider the case with harvesting in (1). Here, first explore the behavior in the absence of diffusion.
Example 4. Let us consider model (1) in absence of diffusion, which is equivalent to (3) over the domain Ω = (0, 1). Since the diffusion is absent, so for D = 0 and the constant coefficients are constant. We verify the results of subsection 3.1. First we choose different values of harvesting rate H = {0.5, 1.2, 1.5} with growth rate r = 1.2 and carrying capacity . This shows that the results found in subsection 3.1 is justified. We also check for different initial values with a fixed harvesting rate, where the results are justified. See Figure 7.
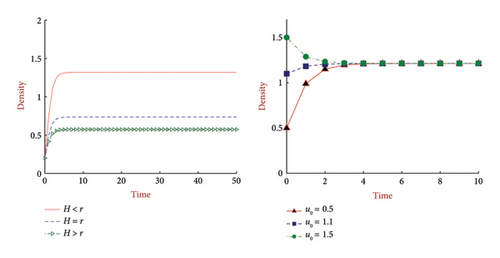
Example 5. Consider model (6) over Ω = (0, 1) and for D = 0.0. The coefficients are all time dependent, that is functions of time t. For growth rates r(t) = 1.3 + cos t, carrying capacity and different values of harvesting rates (H = {1.1 + cos t, 1.3 + cos t, 1.5 + cos t} in Figure 8 (left)) and initial densities (u0 = {0.3, 1.1, 1.7} with H = 1.2 + cos t in Figure 8 (right)), we observe the solution of (6). If we take smooth functions in the coefficients we get a unique positive T-periodic solution of equation (6).
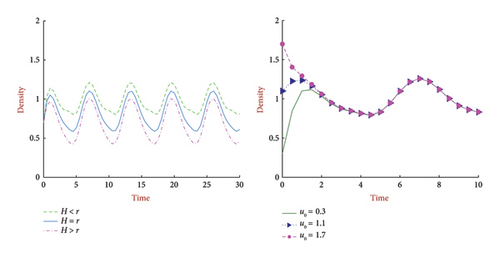
In the above two cases (Case 4 and Case 5; Figures 7 and 8), we verify the results in Section 3 for constant coefficients and time dependent coefficients, respectively.
In both cases, we have a delicate value H = r, which leads two different phases, either the population will persist or extinct under harvesting absorption. We also get a unique positive solution for H < r, whatever the starting point is.
Example 6. Consider equation (1) with all coefficients are only spatially distributed such that, which satisfies (∂u/∂η)|∂Ω = 0, which is discussed with the model (10).
The last inequality follows from the Green’s theorem [37]. Now, we explore the behavior of equation (10) in Figure 9 for D = 1.0, , u0(x) = 0.5 + sin2(πx), r(x) = 1.5 + cos(πx)sin(x), and H(x) = 0.75 + cos2(πx) on Ω = (0, 1) for t = (0, 100) and it verifies the result of Theorem 2.
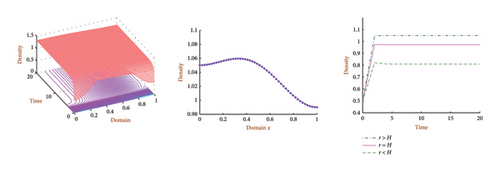
Example 7. Consider model (1) over the region Ω = (0, 1) with D = 1.0, carrying capacity and intrinsic growth rate r(x, t) = 1.2 + cos(πx)sin(πt).
We choose different harvesting rates H(x, t) = 0.75 + cos2(πx)sin(πt) < r(x, t), 1.2 + cos(πx)sin(πt) = r(x, t), 1.5 + cos(πx)sin(πt) > r(x, t).
The numerical simulation shows we get a unique positive periodic solution and explore the equilibrium on the change of intrinsic growth rates and harvesting rates.
In this example (Figure 10), Theorem 1 is verified for random time-periodic carrying capacity functions .
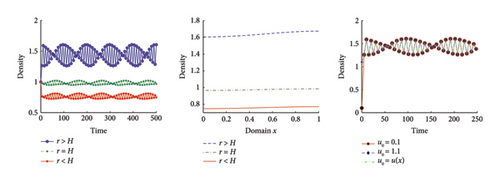
Now, we outline the significance of the dispersal coefficients D on the steady state level. With the increase of D, the convergence of the solution is faster than the limit state for the same initial density and t > 0.
Consider model (1) for various diffusion such as D = {0.5, 1.5, 2.5} with time varying carrying capacity , intrinsic growth rate r(x, t) = 1.2 + cos(πx)sin(πt), harvesting rate H(x, t) = 0.75 + cos2(πx)sin(πt) with initial population u0(x) = 1.0 + sin(πx). Figure 11 illustrates the speed of convergence clearly.

In all our numerical simulations, we used MATLAB, a high-level programming and numeric computing platform, to generate the figures presented in this paper. This software facilitated the precise rendering of data visualizations, ensuring accuracy, and clarity in demonstrating our results.
9. Conclusion
- 1.
Noncommunicable disease modeling, like tumor and cancer modeling since Gompertz law is specified as a highly increasing function in a certain density level
- 2.
Toxic problem in ecology and infections for multiple plants
- 3.
Delay type differential problems; and
- 4.
Introducing homogeneous and nonhomogeneous Dirichlet boundary conditions.
Additionally, future research could further explore the integration of economic controls, such as those described by Chatterjee and Pal, into ecological models to enhance sustainability and resource optimization [45].
Ethics Statement
No consent is required to publish this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Conceptualization, M.K. and S.I.A.; methodology, K.N.K., M.H.A.B., and K.M.A.K.; software, M.K. and S.I.A.; validation, M.H.A.B. and M.R.I.; formal analysis, M.K, S.I.A. and M.R.I.; investigation, K.N.K. and K.M.A.K.; resources, K.N.K. and M.R.I.; data curation, S.I.A.; original draft preparation, M.K. and S.I.A.; review and editing, M.H.A.B. and M.R.I. and K.M.A.K.; supervision, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research by Md. Kamrujjaman was both financially and non financially supported by the University Grant Commission (UGC), and the University of Dhaka, Bangladesh.
Open Research
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.




