Modified Semiseparation of Variables Methods for Solving the System of Nonlinear Fractional Partial Differential Equations
Abstract
The system of nonlinear fractional partial differential equations (SNFPDEs) are widely used in modeling various phenomena in applied sciences. Consequently, finding the solutions to SNFPDEs has become paramount. Recently, an analytic method known as the Semiseparation of Variables Method (S-SVM) has been applied to obtain the exact solution of the SNFPDEs by employing the Mittag–Leffler function method. The Salim function is a generalization of the Mittag–Leffler function with two additional parameters. These two additional parameters in the Salim function offer the flexibility and easier use of the Salim function as compared to the Mittag–Leffler function in one parameter. Similarly, the Salim and Faraj function extends the Salim function. In this paper, we introduce two modifications to the S-SVM, namely, the S-SVM via the Salim function (S-SVSFM) and the S-SVM via the Salim and Faraj function (S-SVSFFM). Interestingly, applying the S-SVSFM and the S-SVSFFM independently to solve the SNFPDEs yields an infinite series that converges easily to the exact solution of the SNFPDEs. In addition, the uniqueness of the exact solution of the SNFPDEs is established therein the paper. Choosing the value of α = 1, confirms the integer solution of the SNFPDEs which is depicted in tables. However, we observed that as the values of the α changes continuously from 0.1 to 1.0, the memory and hereditary properties are observed. The findings clearly show that the S-SVSFM and the S-SVSFFM are reliable and powerful analytic methods for finding the exact solution to the SNFPDEs.
1. Introduction
Fractional partial differential equations (FPDEs), as a generalization of integer partial differential equations have attracted significant attention due to their ability to model various physical and biological phenomena more accurately. They are frequently used in various disciplines such as physics, engineering, biology, and economics to describe anomalous diffusion, viscoelastic material behavior, control systems, signal processing, and many more [1–4]. The fractional-order models are more accurate than the integer-order models because fractional-order derivatives are endowed with memory and hereditary properties of different substances [5, 6]. Recently, the system of nonlinear FPDEs (SNFPDEs) has been of much interest because of their applicability in various domains [7, 8].
In recent years, finding the solution to the SNFPDEs has been at the heart of every scientist in the 21st century. Several numerical methods [9–11] have been introduced to solve the SNFPDEs. However, these methods require repeated iterations and are usually accompanied by errors. Conversely, analytic methods which provide a function that describes the underlying mechanism of the problem at hand have been observed by researchers to find the exact solution to the SNFPDEs. In addition, the solutions of the SNFPDEs yielded by analytic methods serve as a benchmark for validating the accuracy of numerical solutions obtained by these numerical methods. Various analytic methods for obtaining an exact solution to SNFPDEs have been introduced, such as the tanh-function method [12], exp-function method [13], Adomian decomposition method (ADM) [14], variational iteration method (VIM) [15], Laplace ADM [16], and Laplace residual power series method [17]. The ADM initially decomposes the nonlinear operators into an infinite sum of Adomian polynomials which is then followed by the inverse partial differential operator of the resulting equation to obtain the series. However, this series may not converge to the exact solution. The authors in [18–20] reported that even when the ADM converges, the solutions are limited to a small region. In addition, the authors in [21, 22] observed that in using the ADM, the obtained series does not converge to the exact solution of the given problem. Furthermore, using software based on the principles of the ADM to compute the exact solution of the SNFPDEs is challenging. For example, the author in [23] has observed this shortcoming of the ADM in searching for solutions to differential equations in functional spaces. In using VIM, the correction functional of the SNFPDEs must be constructed. The correction functional contains the Lagrangian multiplier that has to be determined first before the iteration to generate the series begins. However, determining the Lagrangian multiplier is challenging because several Lagrangian multiplier values are obtained after applying the stationarity condition and only one of them yields the convergent series solution to the SNFPDEs. How would one know the appropriate value of the Lagrangian multiplier to choose that will yield a convergent series solution of the SNFPDEs? This drawback has also been observed by the authors in [24, 25]. Furthermore, solving SNFPDEs using the VIM sometimes yields a divergent series. A similar observation has also been reported by the authors in [26, 27]. The homotopy analysis method (HAM) introduced by the author in [28] contains a convergence control parameter that has to be guessed arbitrarily in order to ensure a convergent solution to the SNFPDEs. One major disadvantage of using this method is that it heavily depends on the choice of the convergence control parameter. However, since there is no rule or procedure for choosing the value of the convergence control parameter, it thereby becomes a great challenge to rely on this method [29]. The homotopy perturbation method (HPM) as observed by the author in [30] is applicable when the convergence control parameter is chosen to be a negative one. Obviously, this HPM is only a special case of HAM [31–35]. The series obtained using HPM is divergent for solving some classes of differential equations [32, 36]. Recently, the S-SVM has been observed for solving FPDEs. This method assumes that a solution to a FPDE is a product of their component functions where one of the component functions is known and the other component is unknown [37]. Thus, the S-SVM due to [37] assumed that one of the component functions of the given FPDE is a Mittag–Leffler function in one parameter and the other component function is unknown. The S-SVM is applied to search for the unknown component function of the FPDE which in turn yields the solution of the FPDE in a functional space. The beauty of research in a class of S-SVM is not fully explored, as there are many functions that not only generalize the Mittag–Leffler function but also possess additional properties. One such function is the Salim function. The Salim function is a generalization of the Mittag–Leffler function in two parameters. Unlike the Mittag–Leffler function in two parameters, the Salim function has two additional parameters which makes its applications flexible. Similarly, the Salim and Faraj function also generalizes the Salim function with two additional parameters. These extra parameters influence the behavior of the function and allow for flexibility in using it to solve SNFPDEs.
In this paper, two modifications to the S-SVM are proposed. Thus, the S-SVM via the Salim function (S-SVSFM) and the S-SVM via the Salim and Faraj function (S-SVSFFM) for obtaining the exact solution of the SNFPDEs. The S-SVSFM and the S-SVSFFM yield the same series which converges rapidly to the exact solution.
The paper is organized as follows. In Section 2, relevant definitions of fractional derivatives and functional spaces are provided therein. The modifies methods of the S-SVM thus, the S-SVSFM and the S-SVSFFM are given in the Section 3 of this paper. In addition, the uniqueness of the exact solution of the SNFPDEs are presented in the same section. The numerical experiment of the exact solution of the SNFPDEs using the modified methods and the conclusion are seen in the Sections 4 and 5, respectively in the paper.
2. Preliminaries
In this section, we present the necessary definitions and preliminaries relevant to our studies.
Definition 1 (Caputo derivative [38]). The Caputo fractional derivative of f(t) is defined as
Lemma 1. If n − 1 < α ≤ n, n ∈ N and , then
- 1.
- 2.
Definition 2 (see [39].)One parameter of the Mittag–Leffler function is
Definition 3 (Pochhammer symbol [40]). The Pochhammer symbol is defined as
Definition 4 (Salim function [41]). The Salim function is defined as
Definition 5 (Salim and Faraj function [42]). The Salim and Faraj function is defined as
Definition 6 (Sobolev space [43]). Let Ω be in Rn. Then, the Sobolev space, denoted as Wk,p, is defined as
Definition 7 (Contraction mapping [44]). Let (X, | |) be a metric space and G a mapping of X into itself. The operator G is said to be a contraction or a contraction mapping if there exists a real number k, 0 < k < 1, such that
3. Methodology
The main concepts underlying the modifications of the S-SVM will be introduced in this section.
3.1. S-SVSFM
In this subsection, the S-SVM is modified by setting one of its component functions with the Salim function. The Salim function generalizes the Mittag–Leffler function and also possesses two additional parameters. The additional parameters allow for a greater flexibility in controlling the function and make it applicable to a wider range of problems.
3.1.1. Steps
- 1.
A solution to equation (8) is separated into its component functions as
() -
where λk is the unknown coefficient and (δ)k and (γ)k are the Pochhammer symbols. This method is termed as S-SVSFM.
- 2.
Substituting equation (10) into equation (8) yields
() - 3.
We find the partial derivatives in equation (11) with respect to their corresponding independent variables and simplify them to get
() - 4.
We now determine the values of lambda recursively from equation (12).
- 5.
The resulting lambda values obtained from Step 4 are then plugged into equation (10) to obtain the solution in a suitable functional space.
3.2. S-SVSFFM
In this subsection, another modification of the S-SVM is introduced by setting one of its component functions with the Salim and Faraj function. The Salim and Faraj function also generalizes the Salim function. Here, the Salim and Faraj function contains two extra parameters unlike the Salim function. These extra parameters influence the behavior of the function and allow for flexibility in modeling systems with complex memory effects.
3.2.1. Steps
- 1.
A solution to equation (8) is separated into its component function as
() -
where λk is the unknown coefficient and (γ)kq and (δ)kp are the Pochhammer symbols. This method is termed as a S-SVSFFM,
- 2.
Substituting equation (13) into equation (8) yields
() - 3.
We find the partial derivatives in equation (14) with respect to their corresponding independent variables and simplify them to get
() - 4.
We now determine the values of lambda recursively from equation (15).
- 5.
The resulting lambda values obtained from Step 4 are then plugged into equation (13) to obtain the solution in a suitable functional space.
3.3. Uniqueness of Solution of the SNFPDEs
In this section, the contraction mapping theorem is applied to determine the uniqueness of the solution. First, the contraction is stated before applying it to obtain the unique solution of the SNFPDEs.
Theorem 1 (see [45].)Let u(x, t) ∈ C1(Ω) and their partial derivatives exist, then u(x, t) is a solution of (8) if and only if
In order to obtain a unique solution to SNFPDEs, the contraction mapping theorem is given as follows.
Theorem 2. Let (X, |·|) be a Banach space, and G : X⟶X be a contraction mapping. Then, equations (8) with (9) has a unique solution u(x, t) whenever 0 < γ < 1.
Proof 1. The mapping G : C(Ω, |·|)⟶C(Ω, |·|) is defined as
Let u1, u2 ∈ C(Ω, |·|) be two different solutions of equations (8) with (9), then by using the above equations, we get the following:
3.4. Application of the S-SVSFM for Solving SNFPDEs
In this section, we now apply the S-SVSFM to obtain an exact solution to the SNFPDEs.
Example 1. Let us consider the following SNFPDEs:
We assume that a solution to equations (20) and (21) is given as follows:
Substituting the assumed solution and their respective partial derivatives of equations (24)–(26) into equations (20) and (21) yields
Expanding the Salim function by considering the first four terms of equations (27) and (28) yields
Expressing the inner product of equations (29) and (30) as
The above equation is written as
The following results are obtained after substituting equation (33) into equations (27) and (28)
By substituting the initial conditions of equations (22) and (23) into equation (34) and simplifying the results, we get
Following a similar procedure, equation (35) becomes
By using equations (37) and (38), we now determine the following coefficients. Starting from k = 0, we obtain the following lambda and theta values, where
Similarly, when k = 1, we obtain the following results:
Similarly, when k = 2, we obtain the following results:
Expanding equation (24) yields
Plugging the obtained λ0, λ1, λ2, …, λn values into equation (45) results in
Similarly,
When α = 1, we obtain the following:
We show in the following result that u(x, t) and v(x, t) are the unique solutions of equations (20) and (21).
3.5. Application of the S-SVSFFM for Solving SNFPDEs
In this section, we apply the S-SVSFFM to obtain an exact solution to the SNFPDEs.
We consider the SNFPDEs in equations (20) and (21) together with (22) and (23).
It can be observed that after substituting the λ and θ values obtained into equation (66) we obtain equation (67). Thus, the obtained λ and θ values are inversely proportional to the Pochhammer symbols introduced in the Salim function as well as in the Salim and Faraj function.
That is, λ1 = (δ)1/(γ)1 cancels the Pochhammer symbols (γ)1/(δ)1 in the Salim function. Similarly, λ2 = (δ)2/(γ)2 cancels the Pochhammer symbols (γ)2/(δ)2 in the Salim function. Similar observations can be seen in the Salim and Faraj function. Hence, the results obtained using the S-SVSFM and S-SVSFFM are the same for the SNFPDEs.
3.6. Solution in Sobolev Space
In this section, we show that the solution to the SNFPDEs exists in the Sobolev space.
Since ρϕ is finite, it shows that the solution u(x, t) exists in an L1 space. Similarly, v(x, t) exists in an L1 space.
Again, we show that (∂u(x, t)/∂x) ∈ L1(Ω).
Since ρϕ is finite, it shows that (∂u(x, t)/∂x) exists in an L1 space. Similarly, (∂v(x, t)/∂x) exists in an L1 space.
Finally, we show that (∂αu(x, t)/∂tα) ∈ L1(Ω).
Since ρϕ is finite, it shows that (∂αu(x, t)/∂tα) exists in an L1 space. Similarly, (∂αv(x, t)/∂tα) exists in an L1 space. Hence, the solution exists in the Sobolev space.
4. Numerical Experiment
In this section, the numerical results of the u(x, t) and v(x, t) for the given example are evaluated for various values of x and t and fractional order α using the S-SVSFM and the S-SVSFFM and are presented through tables and figures. Since the S-SVSFM and the S-SVSFFM give the same solution, their corresponding results are presented in the same tables and figures.
Tables 1 and 2 exhibit the behavior of the S-SVSFM and the S-SVSFFM solutions for different values of x and t and the fractional order α of equations (20) and (21). It can be observed that when α = 1, the S-SVSFM and the S-SVSFFM solutions of the given example are in excellent agreement with the integer solutions in equations (48) and (49). This confirms that both S-SVSFM and S-SVSFFM are more robust methods.
| x | t | α = 0.5 | α = 0.7 | α = 0.9 | α = 1.0 |
|---|---|---|---|---|---|
| −2 | 0.1 | 10.99813 | 9.27682 | 8.42973 | 8.16617 |
| 0.2 | 13.45977 | 10.78219 | 9.46156 | 9.02501 | |
| 0.3 | 16.21330 | 12.32888 | 10.56909 | 9.97418 | |
| −1 | 0.1 | 4.02936 | 3.41163 | 3.10107 | 3.00417 |
| 0.2 | 4.86301 | 3.96152 | 3.48035 | 3.32012 | |
| 0.3 | 5.69350 | 4.52198 | 3.88710 | 3.66930 | |
| −0.5 | 0.1 | 2.43689 | 2.06855 | 1.88086 | 1.82212 |
| 0.2 | 2.92847 | 2.39975 | 2.11071 | 2.01375 | |
| 0.3 | 3.41164 | 2.73564 | 2.35696 | 2.22554 | |
| 0 | 0.1 | 1.47153 | 1.25396 | 1.14076 | 1.10517 |
| 0.2 | 1.75807 | 1.45261 | 1.27999 | 1.22140 | |
| 0.3 | 2.03724 | 1.65245 | 1.42890 | 1.34986 | |
| 0.5 | 0.1 | 0.88715 | 0.75993 | 0.69187 | 0.67032 |
| 0.2 | 1.05403 | 0.87846 | 0.77614 | 0.74082 | |
| 0.3 | 1.22055 | 0.99652 | 0.86605 | 0.81873 | |
| 1 | 0.1 | 0.53504 | 0.46037 | 0.41961 | 0.40657 |
| 0.2 | 0.64162 | 0.53084 | 0.47056 | 0.44933 | |
| 0.3 | 0.77214 | 0.60099 | 0.52476 | 0.49659 | |
| 2 | 0.1 | 0.22637 | 0.16895 | 0.15432 | 0.14957 |
| 0.2 | 0.52999 | 0.19805 | 0.17291 | 0.16530 | |
| 0.3 | 1.35634 | 0.24726 | 0.19279 | 0.18268 | |
| x | t | α = 0.5 | α = 0.7 | α = 0.9 | α = 1.0 |
|---|---|---|---|---|---|
| −2 | 0.1 | 0.12031 | 0.10871 | 0.11877 | 0.12246 |
| 0.2 | 0.33045 | 0.09637 | 0.10603 | 0.11080 | |
| 0.3 | 0.98474 | 0.09772 | 0.09513 | 0.10026 | |
| −1 | 0.1 | 0.25955 | 0.29644 | 0.32296 | 0.33287 |
| 0.2 | 0.23452 | 0.25871 | 0.28864 | 0.30119 | |
| 0.3 | 0.24944 | 0.22995 | 0.25937 | 0.27253 | |
| −0.5 | 0.1 | 0.43022 | 0.48945 | 0.53251 | 0.54881 |
| 0.2 | 0.37709 | 0.42862 | 0.47613 | 0.49659 | |
| 0.3 | 0.35643 | 0.38228 | 0.42824 | 0.44933 | |
| 0 | 0.1 | 0.71431 | 0.80779 | 0.87802 | 0.90484 |
| 0.2 | 0.62821 | 0.70948 | 0.78529 | 0.81873 | |
| 0.3 | 0.58472 | 0.63553 | 0.70679 | 0.74082 | |
| 0.5 | 0.1 | 1.18442 | 1.33273 | 1.44766 | 1.49182 |
| 0.2 | 1.05119 | 1.17308 | 1.29504 | 1.34986 | |
| 0.3 | 0.98773 | 1.05475 | 1.16615 | 1.22140 | |
| 1 | 0.1 | 1.96120 | 2.19826 | 2.38684 | 2.45960 |
| 0.2 | 1.76073 | 1.93787 | 2.13548 | 2.22554 | |
| 0.3 | 1.69326 | 1.74770 | 1.92357 | 2.01375 | |
| 2 | 0.1 | 5.38414 | 5.97820 | 6.48824 | 6.68589 |
| 0.2 | 5.13871 | 5.28201 | 5.80572 | 6.04965 | |
| 0.3 | 5.77178 | 4.80093 | 5.23150 | 5.47395 | |
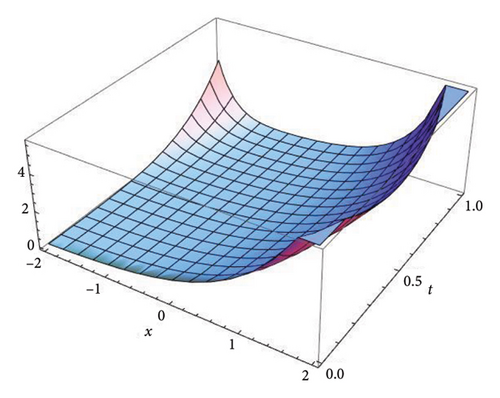
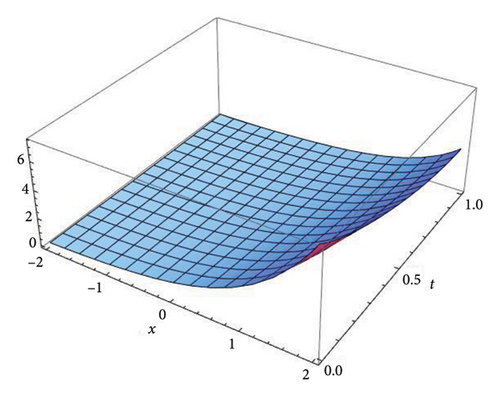
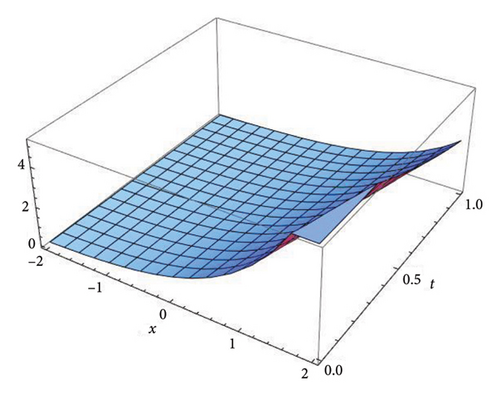
Figure 1 represents the three-dimensional plot for the solution u(x, t) at fractional order α = 0.5, 0.7, 0.9, and 1.0, respectively, using both the S-SVSFM and the S-SVSFFM. The subfigures in Figure 1 show the behavior of the solutions obtained by using the S-SVSFM and the S-SVSFFM. They also show the gradual changes in the behavior of the solution with different values of α, hence depicting the memory property of the SNFPDEs. The convergence of the fractional order solutions toward integer-order solutions has been observed by continuously varying the fractional order. Hence, the graphical representation has confirmed the strong agreement of the exact integer solution with the S-SVSFM and the S-SVSFFM solutions at fractional order α = 1.
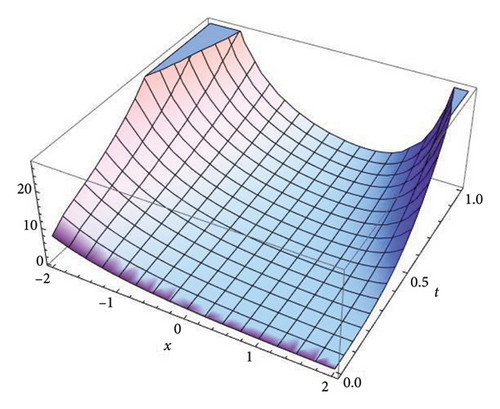
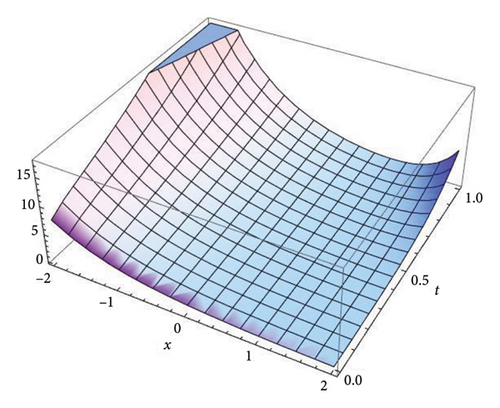
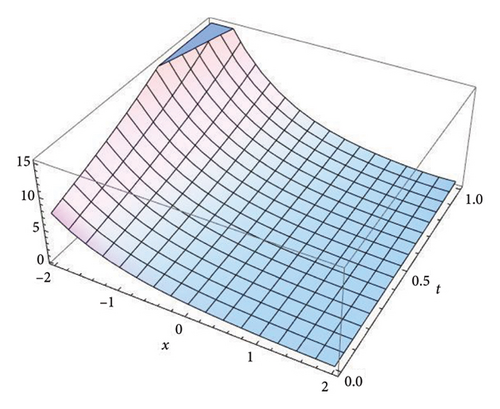
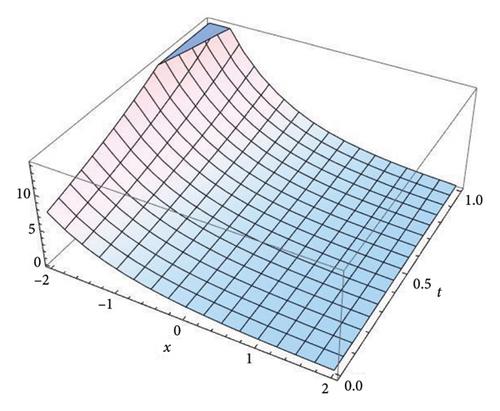
Figure 2 represents the three-dimensional plot for the solution v(x, t) at fractional order α = 0.5, 0.7, 0.9, and 1.0, respectively, using both the S-SVSFM and the S-SVSFFM. These subfigures show the behavior of the solutions obtained by using the S-SVSFM and the S-SVSFFM. They also show the gradual changes in the behavior of the solution with different values of α depicting the memory property of the SNFPDEs.

5. Conclusion
In this paper, we developed two analytic methods called the S-SVSFM and the S-SVSFFM and applied them independently to obtain the exact solution to SNFPDEs. The S-SVSFM and the S-SVSFFM yielded the same result when applied to the SNFPDEs because the lambda and theta values obtained using the S-SVSFM were inversely proportional to the Pochhammer symbols in the Salim function used in the S-SVSFM. Thus, we observed that the (δ)1/(γ)1 and (γ)1/(δ)1 canceled out when applying the S-SVSFM. A similar observation was seen in the S-SVSFFM. The numerical experiments were presented to observe the role of the fractional order α. Lastly, we determined that the solutions obtained exist in the Sobolev space. The analysis confirmed that the solutions obtained by the S-SVSFM and S-SVSFFM converged rapidly with a few terms. In the future, the proposed methods can be applied to find the analytic solutions of FPDEs and SNFPDEs.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
No funding was received for this research.
Open Research
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.




