Solving Systems of Linear Integral Equations via Fixed Point Theory in Extended Parametric Sb-Metric Spaces
Abstract
The purpose of this article is to present some fixed point theorems to guarantee the existence and uniqueness of common fixed points for two mappings (not necessary continuous), satisfying generalized contractions involving rational expressions in the setting of extended parametric Sb-metric spaces. To substantiate our findings, some examples with graphical representation are also given. Moreover, as an application of our findings, the existence and uniqueness of common solution to the system of integral equations followed by an example are presented.
1. Introduction and Relevant Literature
Fixed point theory is a fascinating field of study with vast applications, particularly in the sciences and engineering. Due to its numerous uses, it plays a crucial role in mathematical analysis, functioning as a highly efficient and extensively utilized method for problem-solving. Fréchet [1], in 1906, formulated the concept of metric space to establish a formal framework for analyzing the notion of distance in mathematical spaces. The concept of metrics, in the literature, has been broadened and modified by various approaches. Only a small number of the numerous generalizations are true (refer to [2–9]).
Motivated by the foundational works of Bakhtin [4] and Sedghi et al. [6], in 2016, Souayah and Mlaiki [7] introduced the concept of Sb-metric space. Rohen et al. [8], in 2017, further modified the definition of Souayah and Mlaiki [7] and introduced a more general form of Sb-metric space as follows.
Definition 1 (see [8].)A function Sb : Z3⟶[0, ∞) is said to be Sb-metric on a nonempty set Z, with b ≥ 1, if it satisfies the following properties: for each ϱ, ς, ϑ, τ ∈ Z
- i.
Sb(ϱ, ς, ϑ) = 0 if and only if ϱ = ς = ϑ;
- ii.
Sb(ϱ, ς, ϑ) ≤ b[Sb(ϱ, ϱ, τ) + Sb(ς, ς, τ) + Sb(ϑ, ϑ, τ)].
The pair (Z, Sb) is said to be Sb-metric spaces.
In 2023, Mani et al. [10] introduced the notion of extended parametric Sb-metric space (EPSb-metric space), which means that it is an extension of Sb-metric space and extended Sb-metric space. They also presented some of the topological properties of aforesaid space and have derived extensions of some well-known fixed point theorems within this framework.
Definition 2 (see [10].)Let Z be a nonempty set, and B : Z3⟶[1, ∞) be a positive real valued function. Then a function is said to be EPSb-metric on Z if for each ϱ, ς, ϑ, τ ∈ Z and λ > 0, it satisfies
-
if and only if ϱ = ς = ϑ;
-
.
The pair is called EPSb-metric space.
Here is an example of an EPSb-metric space.
Example 1. Let . Define function B : Z3⟶[1, ∞) by
Definition 3 (see [10].)Suppose is an EPSb-metric space. The pair is said to be symmetric EPSb-metric space, if for all ϱ, ς ∈ Z, λ > 0, it satisfies condition
Definition 4. [10] A sequence 〈ϱn〉 in an EPSb-metric space is said to be:
- i.
Convergent, and converges to ϱ if and only if for all n ≥ n0 and λ > 0.
- ii.
Cauchy sequence if for all n, m, λ > 0 with n > m.
Definition 5 (see [10].)The space “ is said to be complete if every Cauchy sequence is convergent in Z.”
Lemma 1 (see [10].)Let be a symmetric EPSb-metric space. Suppose there exist two sequences such that
If the sequence {ϱn} ∈ Z is such that limn⟶∞ ϱn = ϱ for some ϱ ∈ Z, then limn⟶∞ ςn = ϱ.
Lemma 2. Let be an EPSb-metric space and suppose there exist a sequence {ϱn} ∈ Z and a q ∈ (0, 1) such that the following inequality holds:
In the last few decades, various kinds of contractive conditions have been constructed to get common fixed points for pair of mappings in metric spaces and its variants. In early 80s, results were established by assuming conditions on maps such as commutativity, weakly commutativity, and compatibility [11–13]. In past so many years, a number of authors have proven the existence of common fixed point for pair maps that may exhibit a discontinuity in its domain. Among these, some of the authors derived the results without assuming the completeness property of the spaces. Considerable and valuable research has been undertaken in this area, and few of them are [14, 15]. Despite the aforementioned developments, only a limited number of results have been proven for two or more pairs of mappings on generalized metric spaces. In 2018, Sedghi et al. [16] derived some common fixed point theorems for four self-maps satisfying generalized contractive conditions in S-metric spaces. In 2021, Popa and Popa proved a common fixed point theorem for a pair of mappings satisfying implicit relation in S-metric spaces. For some further works on pair of mappings in metric spaces and its variants, we refer to [18–22].
In this article, motivated by the above mentioned discussions, we will further integrate and enhance the notion of common fixed point theory for pair of maps as we proceed. Hence, we will begin Section 2 by proving a lemma in order to guarantee the existence of fixed points in Theorem 2. Indeed, three theorems are established in which the maps are not necessarily continuous, by introducing a generalized contraction in complete EPSb-metric spaces. In Section 3, we also discuss some consequential outcomes of our primary findings including three examples with graphical representations that highlight the soundness of our findings. Moreover, we conclude our work by utilizing the results from Section 2 to explore the existence and uniqueness of solution of system of integral equations in Section 4.
2. Fixed Point Theorems for Two Maps
In this section, we now start to turn our attention to a lemma needed to prove our main results after first recalling the definition of auxiliary function ϕ.
Definition 6 (see [10].)Let Φ denote the class of all functions ϕ : [0, ∞)⟶[0, ∞) which is increasing, continuous, and such that , for all t > 0. Then ϕn(t)⟶0 as n⟶∞.
Lemma 3. Suppose that be an EPSb-metric spaces, and further suppose that there exists a sequence {ϱn} ∈ Z such that following inequality holds:
Proof 1. By iterating equation (7), we derive the following inequality:
From Definition 2, for all m > n we have
Since for all t > 0, ,
In what follows, {ϱn} is a Cauchy sequence.
Theorem 1. Suppose that two self-maps and defined on a complete symmetric EPSb-metric spaces are such that for each ϱ, ς, ϑ ∈ Z and λ > 0 with 0 < q < 1, it satisfies
Then and have unique common fixed point in Z.
Proof 2. Let us begin the proof by claiming that if ϱ is any arbitrary fixed point of the map , then it is also the fixed point of the map and vice versa.
First assume that , and claim that: .
Let us substitute ϱ = ς = ϱ and in equation (11), and we have
Thus, from equation (14), we have
This is only possible if , and hence we have our claim that . Similarly, if we assume that , one can get that . This proves that ϱ is a unique common fixed point of maps and .
In order to prove our theorem, it is sufficient to deduce that either or has a fixed point. Let ϱ0 ∈ Z be any arbitrary point. Since and are two self-maps defined on Z, there exists ϱ1, ϱ2 ∈ Z such that and .
Proceeding in this manner we can, in a general sense, choose two sequences ϱ2n, ϱ2n+1 ∈ Z such that
Assume that ϱ2n ≠ ϱ2n+1 for any n ∈ ℕ.
Substitute ϱ = ϱ2n, ς = ϱ2n, and ϑ = ϱ2n−1 in equation (11), and we obtain
Two alternatives emerge here.
-
Case 1 Either ,
-
Case 2 or .
Suppose Case 1 is true; then from equation (18) and using the fact that 0 < q < 1, we obtain that
This gives that ϱ2n = ϱ2n+1. This is a contradiction to our assumption that ϱ2n ≠ ϱ2n+1. Thus, Case 2 must be true.
Hence, from equation (18), we have
Again, on substituting ϱ = ς = ϱ2n and ϑ = ϱ2n+1, in equation (11), we obtain
By following the similar argument as above, we can get
On combining equations (21) and (24), we obtain
Thus, for all n ≥ 2, we can conclude that
On repeating the procedure n times, we obtain
On applying Lemma 2, we obtain our claim that the sequence {ϱn} is a Cauchy sequence. Since Z is a complete EPSb-metric space, there exist some ϱ ∈ Z such that
Next we will now prove that ϱ is the fixed point of , that is, we have to show that . On the contrary, assume that .
From equation (11), on substituting ϱ = ϱ2n, ς = ϱ2n and ϑ = ϱ, we obtain
By taking upper limit as n⟶∞ in above equality and utilizing equation (28), we get
By substituting equation (31) and utilizing the fact that 0 < q < 1 in equation (29), we obtain . Consequently, it follows that . Thus, the maps and have a fixed point in Z.
In order to guarantee the uniqueness of fixed point of maps, assume on contrary that there exists another common fixed point κ, different from ϱ, of maps and in Z such that .
Consider
Thus, from above equality, we have
This is possible only if and so κ = ϱ. Thus, ϱ is a unique common fixed point of and . This finally completes the theorem proof.
In the subsequent result, an auxiliary function ϕ, as outlined below, is employed to derive a unified fixed point theorem within the context of symmetric complete EPSb-metric spaces.
Theorem 2. Suppose is an EPSb-metric space, which is symmetric and complete. Let be two self-mappings such that for all ϱ, ς, ϑ ∈ Z and λ > 0, it satisfies
Then the maps and have a unique common fixed point.
Proof 3. Let us begin the proof by claiming that if ϱ is any arbitrary fixed point of the map , then it is also the fixed point of the map and vice versa.
First assume that , and claim that: .
Let us substitute ϱ = ς = ϱ and in equation (35), and we have
Thus, from equation (37), we have
In order to prove our theorem, it is sufficient to deduce that either or has a fixed point. Let ϱ0 ∈ Z be any arbitrary point. Since and are two self-maps defined on Z, there exists ϱ1, ϱ2 ∈ Z such that and .
Proceeding in this manner, we can, in a general sense, choose two sequences ϱ2n, ϱ2n+1 ∈ Z such that
Assume that ϱ2n ≠ ϱ2n+1 for any n ∈ ℕ.
Let us substitute ϱ = ϱ2n, ς = ϱ2n, and ϑ = ϱ2n−1 in equation (35), and we obtain
Two alternatives emerge here.
-
Case 1 Either ,
-
Case 2 or .
Suppose Case 1 is true; then from equation (41),
Hence, from equation (41), we have
Again, on substituting ϱ = ϱ2n, ς = ϱ2n, and ϑ = ϱ2n+1, in equation (35), we obtain
By following the similar argument as above, we can get
From equations (44) and (47), we obtain
Thus, for all n ≥ 2, we can conclude that
On repeating the procedure n times, we obtain
Thus, on using Lemma 3, {ϱn} is a Cauchy sequence in Z. Since Z is a complete EPSb-metric space; therefore, there exists ϱ ∈ X such that
Next we will now prove that ϱ is the fixed point of , that is, we have to show that . On the contrary, assume that .
From equation (35), on substituting ϱ = ϱ2n, ς = ϱ2n, and ϑ = ϱ, we obtain
By taking upper limit as n⟶∞ in above equality altogether and utilizing equation (51), we get
This is a contradiction. Hence, . Consequently, it follows that . Thus, the maps and have a fixed point in Z.
In order to guarantee the uniqueness of fixed point of maps, assume on contrary that there exists another common fixed point κ, different from ϱ, of maps and in Z such that .
Consider
Thus, from above equality, we have
Theorem 3. Suppose that and are self-maps defined on a complete symmetric EPSb-metric spaces , such that for each ϱ, ς, ϑ ∈ Z and λ > 0, it satisfies
Proof 4. Given that maps and are self-maps such that for each ϱ, ς, ϑ ∈ Z and λ > 0, it satisfies
Since each ai > 0,
This expression reduces to the form of Theorem 1, and as a result, the remainder of the proof can be directly inferred from the conclusions of Theorem 1. Thus, the maps and have a unique common fixed point in Z.
3. Consequential Outcomes With Numerical Illustrations
In this section, we will first discuss the consequential outcomes of our primary findings. On letting in Theorems 1, 2, and 3, we have the following results.
Corollary 1. Suppose that is a self-map defined on a complete symmetric EPSb-metric space , such that for each ϱ, ς, ϑ ∈ Z and λ > 0 with 0 < q < 1, it satisfies
Then has a unique fixed point in Z.
Corollary 2. Suppose that is a self-map defined on a complete symmetric EPSb-metric space , such that for each ϱ, ς, ϑ ∈ Z and λ > 0, there exists a function ϕ ∈ Φ such that
Then the map has a unique fixed point.
Corollary 3. Suppose that is a self-map defined on a complete symmetric EPSb-metric space , such that for each ϱ, ς, ϑ ∈ Z and λ > 0, it satisfies
- i.
If we take a1 = a4 = a5 = 0 and a2 = a3 = k in Theorem 3, we obtain the generalization of Kannan [23] contraction for two maps in sense of EPSb-metric spaces.
- ii.
On taking a2 = a3 = a4 = a5 = 0, Corollary 3 reduces to the classical Banach contraction principle, and as an extension of the results of Sedghi et al. [6].
- iii.
If we take a1 = a4 = a5 = 0 and a2 = a3 = k in Corollary 3, we obtain the extension of classical Kannan [23] contraction in sense of EPSb-metric spaces.
- iv.
If we take a2 = a3 = a4 = 0 in Corollary 3, we obtain the extension of Jaggi [24] contraction in sense of EPSb-metric spaces.
The following examples further substantiate our findings.
Example 2. Let Z = [1, ∞) ∪ {0}. For each λ > 0 and ϱ, ς, ϑ ∈ Z, define function B : Z3⟶[1, ∞) by
Then, is an EPSb metric space.
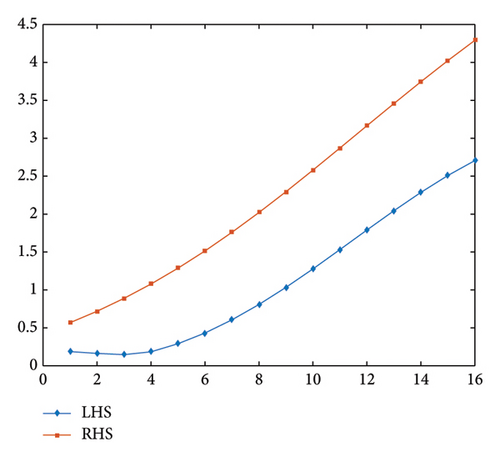
In Figure 1, the graphical interpretation of the inequality highlighting its behavioral characteristics is presented. Thus, all the necessary assumptions of Theorem 1 are satisfied. In addition, 0 is the unique common fixed point of the maps and .
Example 3. Let Z = (0, 1]. For each λ > 0 and ϱ, ς, ϑ ∈ Z, define function B : Z3⟶[1, ∞) by
Then, is an EPSb-metric space.
Then for all ϱ, ς, ϑ ∈ Z and λ > 0, inequality defined in (35) holds good.
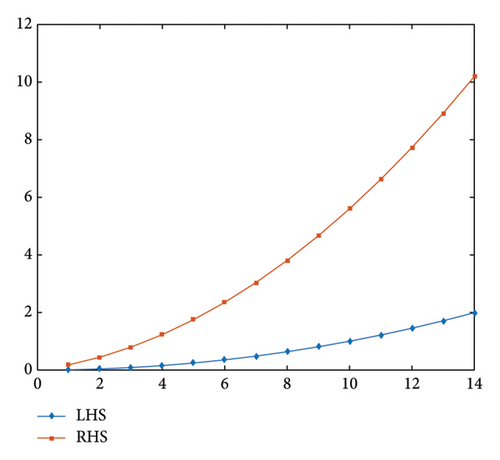
In Figure 2, the graphical interpretation of the inequality highlighting its behavioral characteristics is presented. Thus, all the assumptions of Theorem 2 are satisfied. In addition, 1 is the unique common fixed point of the maps and .
Example 4. Let Z = [0, 1). Define function B : Z3⟶[1, ∞) by
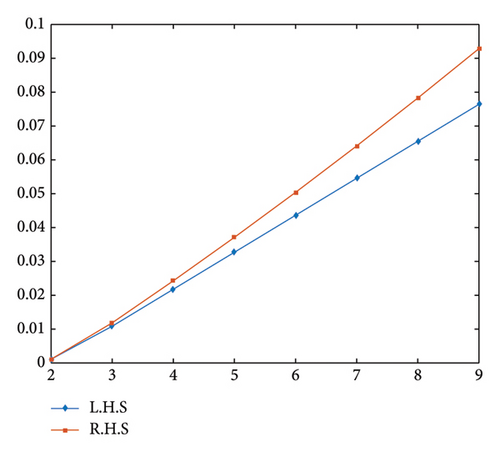
In Figure 3, the graphical interpretation of the inequality highlighting its behavioral characteristics is presented. Thus, all the assumptions of Theorem 2 have been verified. Moreover, 0 is the only fixed point that is common to the mappings and .
4. Applications: Existence of Solution of System of Integral Equations
In this section, we utilize the results from Section 3 to explore the existence of solution of system of integral equations.
It is clear that form complete EPSb-metric spaces.
Theorem 4. Suppose the set is closed and bounded on an interval [a, b]. Then, the system of linear integral equations
- i.
are continuous functions,
- ii.
for every ϱ, ς ∈ C[a, b],
() -
have a unique common solution ϱ(g2) ∈ C[a, b].
Proof 5. Define maps by:
It is evident to note that existence of the solution of system of integral equations is equivalent to find the common fixed point of the maps and .
For all ϱ, ς ∈ C[a, b], consider
On using Cauchy–Schwar inequality, we obtain
Assume that
Clearly, for every a > 0, b − a > 0, and so ((b − a)2/9) > 0. Thus, ϕ is positive, increasing, and continuous mapping, and so ϕ ∈ Φ.
As a result (from equation (87)), we have
Hence, all the conditions of Theorem 2 are satisfied. Therefore, there exists a unique common fixed point, say ϱ ∈ C[a, b] of the maps and . Consequently, ϱ(g2) is the unique common solution of the system of linear equations.
Consider the following example based on the aforementioned application.
Example 5. Consider the following system of integral equations:
Then it has solution in C[0, 1].
- i.
are continuous functions,
- ii.
Further, for all ϱ, ς ∈ C[0, 1] and g1, g2 ∈ [0, 1] with g1 > g2, we have
()
Thus, all the conditions of Theorem 4 are satisfied. Therefore, the system of integral equations considered in equation (90) has a unique common solution in C[0, 1].
5. Conclusion
In this article, we proved three theorems (Theorems 1, 2, and 3) for two self-maps (not necessarily continuous) satisfying a contraction that ensures the existence and uniqueness of common fixed points. Further, we have added three examples (Examples 2, 3, and 4) of our main findings with graphical representation. Our proved results extended and generalized some of the well-known previous existing results, particularly the results of Kannan [23], Jaggi [24], and Sedghi et al. [6]. Moreover, as an application, we have presented an existence theorem (Theorem 4) for a solution of the system of linear integral equations, further supported by an example (Example 5).
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Investigation, A.S., S.B., N.M., and R.S.; methodology, A.S., S.B., and N.M.; supervision, N.M. and R.S.; writing – original draft, A.S., N.M., and R.S.; and writing – review and editing, A.S., S.B., N.M., and R.S. All authors contributed to various stages of the study’s design and execution and have reviewed and approved the final manuscript for submission.
Funding
Open-access funding was enabled and organized by SANLiC Gold.
Open Research
Data Availability Statement
No data were used to support the findings of this study.




