International Journal of Antennas and Propagation

Volume 2025, Issue 1 9401985

Research Article

Open Access

A Novel TLBO-Based Antenna Array Imperfection Calibration for Effective DOA Estimation in mmWave mMIMO Systems

Aquino S.

orcid.org/0000-0002-7202-0049

Department of Electronics and Communication Engineering , Faculty of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , Tamil Nadu, 603203 , India , srmist.edu.in

Search for more papers by this author

G. Vairavel,

Corresponding Author

G. Vairavel

[email protected]

orcid.org/0000-0001-6460-3407

Department of Electronics and Communication Engineering , SRM Institute of Science and Technology , Tiruchirappalli , Tamil Nadu, 621 105 , India , srmist.edu.in

Search for more papers by this author

Aquino S.,

Aquino S.

orcid.org/0000-0002-7202-0049

Department of Electronics and Communication Engineering , Faculty of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , Tamil Nadu, 603203 , India , srmist.edu.in

Search for more papers by this author

G. Vairavel,

Corresponding Author

G. Vairavel

[email protected]

orcid.org/0000-0001-6460-3407

Department of Electronics and Communication Engineering , SRM Institute of Science and Technology , Tiruchirappalli , Tamil Nadu, 621 105 , India , srmist.edu.in

Search for more papers by this author

First published: 23 February 2025

https://doi.org/10.1155/ijap/9401985

Academic Editor: Raffaele Solimene

Share a link

Email
Wechat
Bluesky

Abstract

Antenna Array imperfection calibration is an important concern in direction-of-arrival (DOA) estimation in 5 G millimeter Wave (mmWave) massive Multiple Input Multiple Output (mMIMO) systems. As the number of elements in mMIMO systems increases, array imperfections tend to increase, degrading the DOA estimation performance. Existing calibration techniques use the local optimum solution as the gain/phase, and the location error is high. The present work proposes an inter-disciplinary learning teaching-learning-based optimization (IDL-TLBO) to estimate the DOA. This algorithm exploits the joint sparse properties of the DOA vector and array perturbation matrix. Benefitting from inter-disciplinary learning and sparse properties, the global search capability of the proposed method enhances the accuracy of DOA estimation. The efficacy of the proposed IDL-TLBO was validated using various simulation scenarios. Simulation results reveal that the proposed method achieves a better performance-complexity trade-off than conventional methods for DOA estimation.

1. Introduction

Enhanced Mobile Broadband (eMBB) is one of the 5G use cases that aims to provide higher bandwidth, higher throughput, and high data rates. The mmWave and mMIMO are key techniques to enable eMBB services. The massive MIMO systems employ beamforming techniques to focus the radio signal on a specified user and provide greater user capacity in high-traffic locations. To improve signal reception and reduce interference, the DOA of the incident signal was estimated to evaluate beamforming vectors to steer the beam to the intended user. DOA is a subset of effectual beamforming techniques [1], and these vectors subsequently track the appropriate signal sent from the User Equipment (UE). Accurate DOA estimation is essential to maximize the power of the received signal and reduce the interference signal from nearby sources, which subsequently increases the capacity of mMIMO systems [2].

In practical scenarios, the array manifold is prone to random errors and noise, and it increases as the mMIMO size increases, which successively degrades the DOA estimation performance. Owing to the imperfections in the calibrated array, array perturbations such as gain/phase uncertainties and position perturbations exist. Different techniques have been proposed using a minimal number of antenna elements in MIMO systems to annihilate gain/phase perturbations [3–6]. To obtain a certain array geometry, the inter-element spacing (d) is required to place the elements in the array. Owing to the imperfect placement of the array elements, it introduces a few unavoidable position errors, perturbing the ideal array manifold. Hence, unknown location errors were estimated to compensate for perturbations, and a DOA estimation was performed [7–9]. In [10] a PARAFAC decomposition model with imperfections in an antenna array was used to estimate the DOA. Subsequently, the 2D-DOA estimation with imperfections is proposed by utilizing calibration techniques [11], and a framework for the 2D-DOA estimation within a specified grid is presented with the assumption of gain/phase imperfections in a uniform rectangular array [12]. In recent studies [13, 14], many sparse reconstructions were performed to estimate imperfections based on a discrete dictionary. The -norm [15] was employed to enforce the sparse solution of the perturbation matrix. A sparse technique is employed to estimate the DOA with respect to gain and phase errors in the array [16]. The sparse techniques in [17, 18] have proposed 2D DOA estimation with V and L shaped arrays. The antenna array imperfections considered in the proposed study are gain/phase errors and antenna element location errors in mMIMO systems. Hence, these perturbations must be minimized to achieve a high-resolution DOA estimation.

The sparsity of DOAs is typically explored by creating a dictionary matrix comprising the possible steering vectors in the spatial domain. The -norm based methods in DOA estimation techniques offer superior performance compared to traditional subspace methods [19] despite having limited snapshots and a low signal-to-noise ratio (SNR). The major limitation of the existing array calibration technique using the MUSIC-based objective function is that it requires the approximate DOA to be known and then estimates the banded array perturbation matrix [20]. Hence, the joint estimation of the DOA and perturbation matrix becomes challenging with array imperfections using a subspace-based algorithm.

In the sparse-based DOA estimation [21], the norm-based objective function is solved sequentially using convex optimization, which requires a greater number of iterations until the adjunct DOA estimation is less than the threshold. The teaching-learning-based optimization (TLBO) is a meta-heuristic algorithm [22] and it has been applied to many practical applications in diverse fields. As the array imperfections tend to grow in mMIMO systems, the TLBO converges easily at local optimum solution. To alleviate the limitations of joint estimation of direction finding and perturbation matrix, a novel method combining inter-disciplinary learning with TLBO (IDL-TLBO) is proposed, which optimizes norm-based objective function to estimate the DOA and perturbation matrix. Henceforth, the proposed IDL-TLBO improves the global search ability with the help of interdisciplinary learning incorporated in TLBO, which outperforms conventional subspace-based methods with TLBO and PSO [23]. IDL-TLBO improves the accuracy of the DOA estimation by utilizing two different disciplines of interdisciplinary learners in the search space. In the presence of array imperfections, the proposed work jointly estimates the array perturbation matrix and DOA of the UE. The calibration of the array is performed with the help of the estimated array perturbation matrix, and further the channel state information, target parameter estimation can be characterized to estimate the doppler shift, DOA, multipath delay using an iterative estimation method [24] in mMIMO systems.

In the proposed work, a unified framework for DOA estimation using the IDL-TLBO algorithm is proposed in the presence of perturbations such as array element position errors and gain/phase uncertainty. The significant part of this study is to utilize the sparse property of the signal. The DOA vector remains sparse in accordance with the spatial dictionary, and array perturbations such as gain/phase uncertainty, array element position error can also be represented by a sparse matrix. The rest of this paper is arranged as follows. Section 2 presents the modelling of the DOA estimation problem. In Section 3, the framework for antenna array perturbations is presented. In Section 4 and 5, the basic TLBO and the proposed IDL-TLBO techniques are described. Section 6 illustrates the DOA estimation with array perturbations using the proposed IDL-TLBO technique. The simulation results are presented in Section 7, and Section 8 represents the conclusion of the study.

2. The Problem Modelling

2.1. System Model

A uniform rectangular array is considered with an inter-element spacing of d, which is equivalent to half of the signal wavelength along the X and Y axes. Here, we consider a mmWave mMIMO uplink system with a gNodeB (gNB) comprising a Uniform Rectangular Array (URA) of M × N antennas. For the URA shown in Figure 1, the uplink received signal model for DOA estimation [25] can be formulated as

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

URA geometry for massive MIMO system.

The narrowband far-field incoherent signals s_i transmitted from the user impinge on the antenna array with elevation and azimuth angles as

where θ_i represents the inclination of the position vector of the ith signal vector relative to z-axis, ϕ_i represents the inclination of the position vector relative to the XY plane and the X-axis. N_m,n represents the additive noise vector in the (m, n)^th array element and u_i, v_i are the spatial signatures of the signals along the X, Y axis and are given as

()

Thus, the signal received at gNB can be given as

()

Vectorizing the above equations, the signal model can be written as

()

The DOA estimation problem can also be designed with sparse signal properties. The signal sources impinging on the antenna array is randomly selected from the grid of azimuth angle ϕ ϵ [−180^°, 180^°] and elevation angle θ ϵ [−90^°, 90^°]. The dictionary matrix Ψ signifies the steering matrix which is articulated as a column vector and depends on the angular pairs J on the grid as follows:

()

Finally, the measured signal in (4) related to the dictionary matrix Ψ can be rewritten as

()

Therefore, the sparsity-based DOA estimation can be expressed as

()

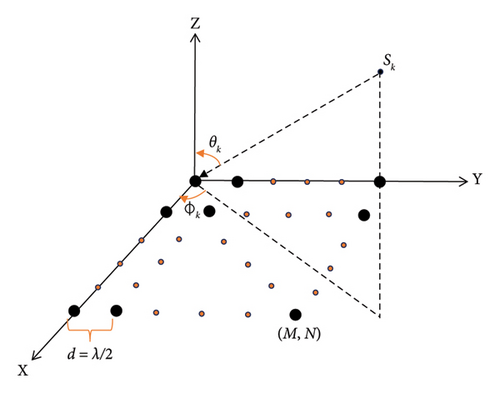
The DOA estimation technique estimates the sparse DOA s from the measured signal y.

2.2. Channel Model

Accurate channel modelling is essential for mmWave massive MIMO systems that use narrow beam antenna arrays to steer at the signal source. An open-source channel simulator NYUSIM was developed by scholars at New York University (NYU), which relies on real-world propagation at mmWave frequencies ranging from 28 to 73 GHz in several outdoor environments, such as rural microcell (RMa), urban macrocell (Uma) and urban microcell (UMi) environments [26].

Channel parameters contain basic input parameters for the channel, which comprises of carrier frequency, RF bandwidth, scenario, environment, upper bound of the T-R separation distance(m), lower bound of T-R separation distance(m), TX power(dBm), number of receive locations, temperature, barometric pressure, humidity, polarization, foliage loss, rain rate, distance within foliage, and attenuation of foliage. The panel incorporates input parameters appropriate to the transmit and receive arrays such as the number of antenna elements, array type, transmit and receive inter-element Spacing, Number of transmit and receive antenna elements per row, transmit and receive antenna azimuth HPBW, transmit and receive antenna elevation HPBW.

The proposed work considers a mMIMO system operating at 28 GHz with an RF bandwidth of 800 MHz in an UMi environment, is illustrated in Table 1. The gNB comprises 256 antenna elements that comprise a uniform rectangular array, and the uplink channel coefficients from the single user to gNB [27] are given by

()

where h_t,r represents the mmWave mMIMO channel coefficient between the t^th transmit antenna and the r^th receive antenna, α is the complex gain of coherent multipath components and l is the multipath component. The received signal at gNB is the combined version of coherent signals into a single incoherent signal with maximum gain. Subsequently, the channel matrix H of size N_r × N_t are obtained with the help of NYUSIM GUI in the UMi scenario with mMIMO of size 16 × 16 at the gNB, and the channel coefficients are mainly used for modelling the received signal to estimate DOA in mmWave mMIMO systems with array imperfections. These channel coefficients contain the angular information of the signal to be transmitted to the gNB, and this angular information is considered as ground truth angle for simulation purposes.

Table 1. The basic uplink parameters in NYUSIM simulator.

Channel parameters		Antenna parameters
Frequency	28 GHz	No of Tx antenna elements	8
RF bandwidth	800 MHz	No of Rx antenna elements	256
Scenario	Urban microcell (UMi)	No of Rx antenna per row	16
Environment	LOS	RX antenna spacing	0.5

3. Antenna-Array Perturbations

3.1. Gain/Phase Uncertainties

Each gain/phase of an array element is subject to unintentional errors due to aging rates and various manufacturing defects. The perturbation matrix is represented by B_gain/phase and the gain/phase uncertainty for the ith element is given by

()

where Δa_i and Δφ_i indicate the change in the gain and phase uncertainties, respectively, with standard deviations of σ_gain and σ_phase. The B_gain/phase matrix is a diagonal matrix, where the diagonal elements in matrix depicts unknown gain/phase perturbations of each element in antenna array [28]. Gain and phase errors were generated with a mean of zero according to the normal distribution and a standard deviation of 0.25. The responses of gain or amplitude perturbations and phase perturbations on a URA of 256 elements are shown in the below Figures 2 and 3, respectively. It interprets that the perturbed arrays have shallow nulls in the pattern response than the ideal array responses.

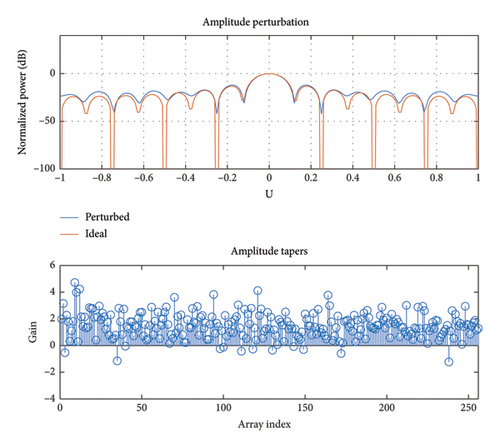
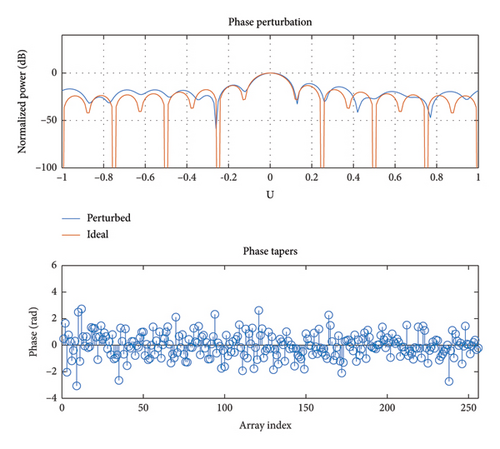
3.2. Position Perturbation

In the configuration of an antenna array, the location of each element must be precise according to the geometry of the array configuration [28]. It is impossible to satisfy this requirement in a practical scenario. The elements in the antenna array are prone to unintentional errors owing to deviation of the elements from their nominal positions. The perturbed array steering vector

of the ith received signal vector [12] can be written as

()

where

and

are the steering vectors with u_i, v_i comprising the DOA information along with the offset value due to position perturbation. To model this error, let Δ_l define the deviation of elements from their nominal position and the DOA information u_i, v_i along x and y axis are represented as

()

The steering vector

and

associated with these perturbations is written as

()

In appropriate to facilitate the expression in (10), the vectorization is performed by utilising Kronecker product (hereafter denoted by ⊗). This array steering vector is slightly different from Saleh-Valenzuela model due to array imperfections [29]. The array perturbation matrix (b) gets associated with the ideal steering vector due to the element deviation factor Δ_l and the steering vector with position perturbation is written as

()

Finally, the system model with position perturbation can be simplified as

()

where B_location = diag(b_M×N) is a diagonal matrix with elements of b being the diagonal elements [21]. The position error in our simulation is generated with a mean of zero and a standard deviation of 0.25. Figures 4(a) and 4(b) depict the position of ideal element and perturbed element across the plane. Figure 5 shows the pattern of both ideal and perturbed element in which the pattern of perturbed element is outside the main lobe of ideal pattern.

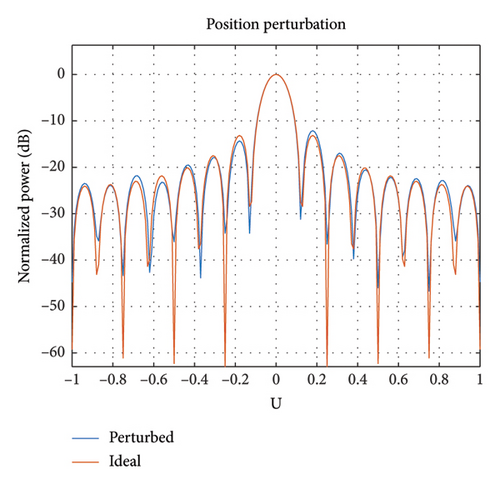
3.3. Combined Perturbations

The perturbations considered here are the gain/phase uncertainty and position perturbation. The steering vector of the received signal can be written as

()

where B_gain and B_location are the diagonal matrices. Equation (15) can be expressed as

()

The received signal with array perturbations is given as

()

Specifically [30], we have the following.

()

Substituting (18) into (17),

()

where B is the perturbation matrix that includes the gain/phase uncertainty and the position error of elements in the antenna array. To refine the precision of the DOA estimate, the overshadow of uncertainties must be removed. To compensate for perturbations in the received signal, the estimation of perturbation matrix B and DOA vector s utilizing sparse signal recovery techniques [21] is given as

()

where s indicates the sparse DOA vector, B indicates the antenna array perturbation matrix, Ψ signifies the dictionary matrix, τ is defined as the regularization constant and ϵ is a precision parameter. The main goal is to jointly estimate DOA and the antenna array perturbation matrix B using nonconvex optimization in (20). To proficiently solve the joint estimation problem, an IDL-TLBO is proposed.

4. TLBO

The main idea of TLBO emanates from the influence of a teacher on the output of learners in a class and the interaction among the learners [22]. This optimization technique comprises of teacher phase and learner phase.

4.1. Teacher Phase

This phase activates the process of teaching. Consider a cost function f(s), s represents the DOA vector in (20) and assume that the population consists of m learners. Initialize the population in accordance with the population size and search space of DOA vector that lies between 0 and 1. Among the number of learners in the classroom population, the best performing learner is chosen as s_teacher. Then, the teacher enhances the overall marks of the class. The mean result of learners is calculated as

. The learners update their position as follows:

()

where s_new and s_old represents the position of the learner after and before learning in each iteration. s_mean specifies the mean value of search agents in the population. The teaching factor (TF) regulates the variation of mean value and rand is a uniform random number between 0 and 1. The value of TF is randomly decided by the algorithm according to TF = round (1+rand (0,1) {2-1}).

4.2. Learner Phase

In this phase, the learners can enhance their knowledge from other learners. A learner acquires knowledge from other learners randomly with a better grade which refers to the fitness value of the cost function. The update equation can be expressed as

()

where s_i indicate the position of the ith learner and s_p indicates the position of random partner among the population. The rand is a uniformly distributed random numbers between 0 and 1. As the number of elements in mMIMO increases, the array imperfections tend to grow larger and this makes the local convergence of optimal solution easily. Thus, an improved TLBO is proposed to mitigate the premature convergence and the DOA vector is estimated from the

norm-based objective function.

5. The Proposed IDL-TLBO

IDL-TLBO is mainly based on IDL, it enables learners from multiple disciplines to solve complex problems from their discipline perspectives and through collaborative learning. IDL-TLBO also consists of teaching and learning phase similar to the basic TLBO.

5.1. Teacher Phase

In the interdisciplinary learning environment, learners from each discipline are divided into two groups comprising of superior and underachiever learners. The superior and underachiever learners are identified based on the mean mark of learners in each discipline. If the learner’s mark is higher than the mean mark of the class, the learner is regarded as a superior learner, else the learner is considered as an underachiever learner. As we need to minimize the cost function [31], the superior group consists of learners whose comprehensive mark is lower than the mean mark of the class, and the underachiever group consists of learners whose marks are higher than the mean mark of the class. The objective function of first discipline is f(s) to estimate the DOA vector s. The learners in superior group gains knowledge from the teacher as s_best and self-study, the update equation for superior group is shown in equation (23). The learners in underachiever group, update knowledge from the teacher to attain the mean mark of the group. The update equation [31] for underachiever learners is shown in equation (24):

()

where s_mean is the mean mark, ω₁ and ω₂ are the inertia weights which increases the convergence speed, iter represents the ongoing iteration and Maxiter is the maximum number of iterations. Initially the mark of underachiever is improved close to the mean mark by using the inertia weight ω₁ and later the teacher enhances the learner’s knowledge by utilising inertia weight ω₂.

5.2. Learner Phase

The fitness values of all learners are sorted in ascending order and the learners are divided into superior and underachiever group. In superior learner group, the learners acquire knowledge from the neighbour and furthermore learn independently. The update equation for superior learners is given as

()

The learner s_neighbour is randomly selected from the superior group and if it has lesser fitness value than s_old, the learner acquires knowledge from the neighbour, else the learner learns by himself. The upperlimit denotes the maximum capability of the learner to acquire knowledge and lowerlimit depicts the minimum capability of a learner to acquire knowledge. The update equation for underachiever learners is written as

()

The inertia weight ω₂ accelerates the difference between the teacher and learner to improve the learner’s mark and convergence speed. If there are two unknowns s and B, two discipline learners are initialised. The first discipline of learners works to estimate the optimized solution for s by using the initialised/estimated solution of B and the other discipline works to estimate the optimized solution for B by using the initialised/estimated solution of s. In each iteration, the optimized solution of each discipline is shared with the other discipline and this represents the collaboration in interdisciplinary learning.

6. DOA Estimation Using Proposed IDL-TLBO

In this section, we propose an IDL-TLBO technique to estimate DOA vector from the received signal as in (20). As there are two unknowns (design variables) namely DOA vector (s) and array perturbation matrix (B), the proposed optimization approach utilizes two disciplines to estimate the DOA and perturbation parameter. The incorporation of interdisciplinary learning in TLBO enhances the global searchability and accuracy of DOA estimation. The block diagram of DOA estimation using proposed IDL-TLBO is shown in Figure 6.

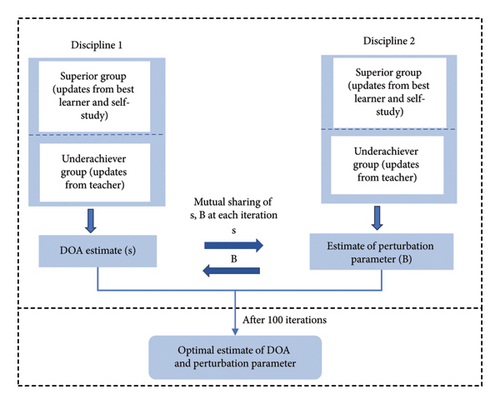
The two design variables namely array perturbation matrix (B) and DOA vector (s) must be estimated, in accordance with the objective function (20). Figure 6 infers that the IDL-TLBO is iterated with the initialized B within the search space to estimate the sparse DOA vector (s) by discipline 1 learners. Simultaneously, the perturbation matrix B is estimated with the initialized DOA vector within the search space by the discipline 2 learners. Then the optimized variables determined by each discipline are shared with another discipline to optimize the results of the array perturbation matrix (B) and the sparse DOA vector (s) in further iterations. The main hyperparameters of the algorithm are the number of learners (N) and the maximum number of iterations (T). The number of learners is initialized according to the number of elements in the antenna array and the maximum number of iterations is chosen as 100 for each discipline to balance the computational feasibility and solution accuracy. The search space of sparse DOA vector and array perturbation matrix lies between 0 and 1. More iterations are chosen to balance the exploration and exploitation to obtain an optimized solution and to avoid the risk of getting trapped in local optima. The two disciplines work in parallel to estimate the perturbation matrix, DOA vector as shown in Figure 6. The pseudocode of the IDL-TLBO algorithm is given in Table 2.

Table 2. Pseudocode of IDL-TLBO algorithm.

1	Objective function of first discipline f(s), (i = 1, 2 , …, N) with ‘B’ being initialized/estimated using (20)
2	Objective function of second discipline f(B), (i = 1, 2 , …, N) with ‘s’ being initialized/estimated using (20)
3	Initialize algorithm parameters
4	Generate initial population
5	Evaluate the fitness of population
6	/Teaching phase/
7	Update the mean value and divide the learners into two groups for each discipline
8	For each learner in population of each discipline do
9	If a learner is superior then,
10	Update new solution by using equation (23)
11	Else
12	Update new solution by using equation (24)
13	End If
14	Evaluate and update better solutions.
15	End For
16	/Learning phase/
17	Learners are partitioned into two groups for each discipline
18	For each learner in superior group do,
19	Select a neighbour learner randomly
20	Update new solution by using equation (27)
21	End For
22	For each learner in underachiever group do,
23	Update new solution by using equation (28)
24	End for
25	Evaluate and update the best solution of s, B from two disciplines.
26	The updated solution of each discipline is mutually shared with the other discipline
27	Iter = iter+1.
28	Output the best solution found

6.1. Computational Complexity Analysis

The IDL-TLBO algorithm comprises of initialization, cost function evaluation, and updating the position [32] of the variables from two disciplines. Initialization with the size of the population N is performed with [33]. Fitness evaluation is carried out in two disciplines with complexity of . The complexity of updating the position is indicated by , where T is the maximum iteration and D is the dimension size of the problem [34]. Henceforth, the computational complexity of the proposed IDL-TLBO is , as two disciplines are involved in IDL-TLBO.

7. Results and Discussion

7.1. Simulation Conditions

The performance of the proposed method is validated using the simulation results. We consider a gNB with a uniform rectangular array of size 16 × 16 with 256 elements and an inter-element distance of half the wavelength (λ/2) to collect the signals from the user. The channel coefficients were generated with NYUSIMv1.6 for accurate channel modelling and simulations for mmWave systems were used with an electrically steerable and narrow beam antenna array. The simulation results were executed using MATLAB R2022 to estimate the perturbation matrix of array and the DOA. The simulation parameters used to estimate the DOA are listed in Table 3.

Table 3. The simulation parameters.

Simulation parameters	Values
Number of transmit antenna—N_t	8
Number of elements in receive array—M × N	256
Antenna array	URA
Interelement spacing—d	λ⁄2
Number of user—K	1
Channel model	mmWave mMIMO statistical spatial channel model
Channel scenario	Umi
SD of position perturbation σ_maxper	0.5
SD of inconsistent gain σ_maxgain	0.5
SD of inconsistent phase σ_max phase	0.5

The 2D DOA estimation performance metrics were evaluated using the root mean square error (RMSE), and is written as

()

where RMSE_θ and RMSE_ϕ indicate the RMSE of elevation and azimuth angles defined as

()

where

and

are the estimates of elevation and azimuth angles, respectively, N_sim is the number of Monte Carlo simulations which is considered as 100 trials. The regularization parameter τ is set to be 0.1 and the dictionary of steering matrix ψ is generated on angular domain of θ ϵ [0, 90], ϕ ϵ [0, 180] with a uniform grid interval of 2^°. The single user transmits the signal to the base station with ground-truth DOA of the user as (ϕ, θ) = (70^°, 4^°) and the additive white Gaussian noise is considered. The signals received in gNB consist of the array perturbation matrix due to perturbations in the antenna array. The position error is generated by a Gaussian distribution with a mean of zero and, SD σ_per is selected by a uniform distribution σ_per ϵ [0, σ_maxper]. The position error in our simulation was generated with a mean of zero, standard deviation of 0.25.Similarly, inconsistent gains/phases are generated by a zero-mean Gaussian distribution with the SD σ_gain and σ_phase being σ_gainϵ[0, σ_maxgain] and σ_phaseϵ[0, σ_maxphase]. Gain and phase errors were generated with a mean of zero according to the normal distribution and a standard deviation of 0.25.

7.2. Simulation Results

First, the proposed method is compared with sparse DOA estimation [21] and TLBO [23] as benchmarks for estimation accuracy by varying the SNR from 0 to 30 dB with a single snapshot accompanied by gain/phase inconsistencies and position perturbation. The results in Figure 7 show that the proposed technique has the lowest estimation error compared to sparse estimation and TLBO estimation. It also implies that the proposed technique has lowest RMSE at the low-SNR regime owing to enhanced learning in IDL-TLBO.

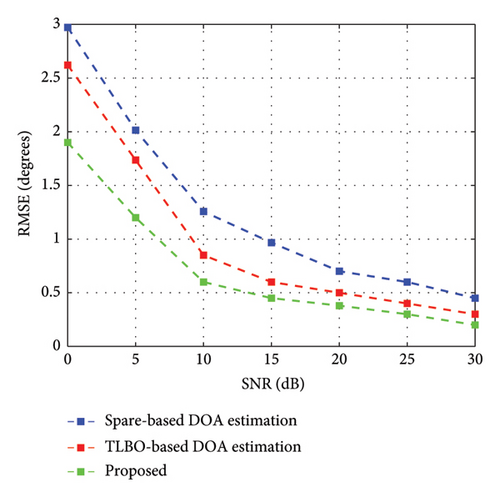
The traditional subspace-based method such as MUSIC performs well at high SNR region, as it requires a greater number of snapshots to estimate precise DOA and its performance depreciates, as the error grows larger in mMIMO systems. The sparse-based techniques and subspace-based MUSIC [35] estimation is implemented in mMIMO systems for comparison purposes. The performance of the existing work with the proposed work at SNR of 10 dB with single snapshot are tabulated in Table 4. It is observed that the estimated DOA using proposed work are closer to actual ones than the sparse-based and subspace-based techniques.

Table 4. Comparison of proposed work with existing studies.

DOA estimation techniques	Actual DOA (deg)		Estimated DOA (deg)		Estimation error (deg)
DOA estimation techniques	Azimuth	Elevation	Azimuth	Elevation	Azimuth	Elevation
TLBO-based DOA estimation [23]	70	4	69.16	3.35	0.84	0.65
Sparse-based DOA estimation [21]	70	4	68.85	5.34	1.15	1.34
Subspace-based MUSIC [35]	70	4	72.06	2.63	2.06	1.37
Proposed work	70	4	69.27	4.56	0.73	0.56

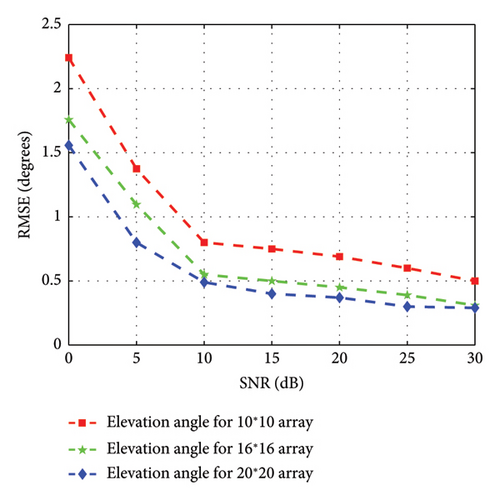
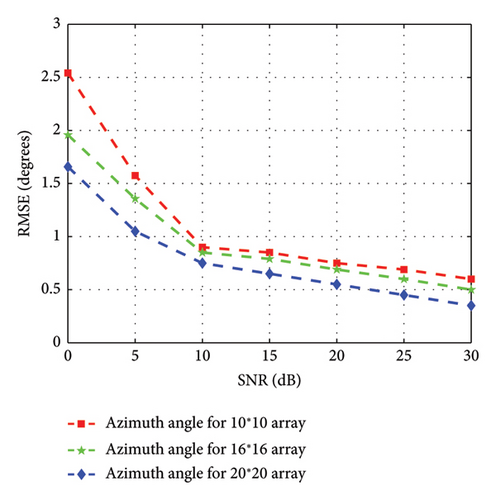
In the second scenario, the performance of the proposed technique is evaluated by varying the array sizes. The average RMSE for the elevation and azimuth angles versus the SNR are depicted in Figures 8 and 9, with the presence of gain/phase inconsistencies and position perturbation in this simulation. In accordance with Figures 8 and 9, it infers that the proposed technique provides better estimation accuracy for varying array sizes as the IDL-TLBO enhances the global search capability of learners. It is also observed that the proposed technique has lower RMSE with an increase in the size of the array.

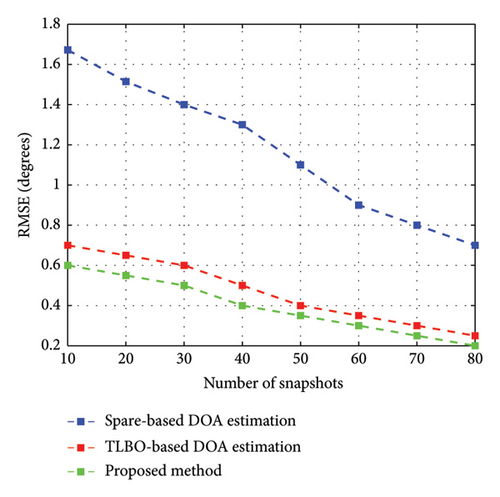
In simulation scenario 3, the performance of the DOA estimation was evaluated using different number of snapshots at a SNR of 10 dB. The number of snapshots varies from 10 to 80 at 10 intervals and this evaluation criteria infers that the DOA estimation performance improves as the number of snapshots increases in below Figure 10. In accordance with Figure 10, it infers that the proposed method has lowest estimation error than the benchmark algorithms because it is enhanced with global search capabilities.

The computational cost of the proposed work with existing studies is listed in Table 5. The complexity of the sparse-based DOA estimation [21] is given by , where K represents the number of column users in the dictionary steering matrix and n specifies the number of rows in the sparse DOA vector. The TLBO-based DOA estimation comprises of initialization process and position updation , where T represents the maximum iterations, N represents the population size and D represents the dimension size of problem. Thus, the total number of computations required for TLBO-based DOA estimation is given as [36]. The complexity of subspace-based DOA estimation [37] is , where M × N represents the number of array elements in URA. The computational complexity of the proposed IDL-TLBO is , as two disciplines are involved in IDL-TLBO. The number of computations involved in the proposed algorithm is more than the sparse-based TLBO in the estimation of DOA. The estimation of DOA accuracy increases in the low SNR region, as shown in the simulation results, and when compared with the traditional methods it brings about performance complexity trade-off for obtaining an accurate DOA estimate in the low SNR region.

Table 5. Comparison of computational cost of proposed work with existing studies.

DOA estimation techniques	Computational complexity
Sparse-based DOA estimation [21]
TLBO-based DOA estimation [23]
Subspace-based MUSIC [35]
Proposed work

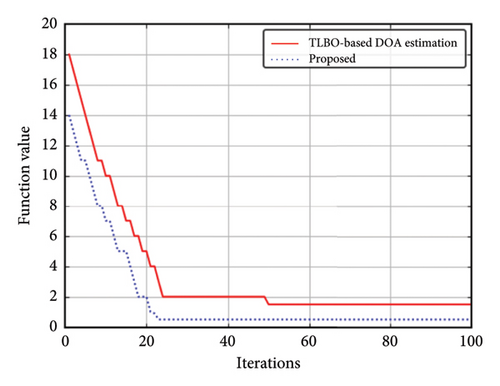
The convergence behaviour of the IDL-TLBO- and TLBO-based DOA estimation at SNR of 10 dB is depicted in Figure 11. It implies that the proposed optimization technique has enhanced convergence performance than the TLBO optimization technique. In our future work, we will further improve the DOA estimation performance with array imperfections for Hybrid Analog and Digital (HAD) architectures by using the IDL-TLBO. The sub-connected (SC) hybrid architectures could achieve the same performance as that of fully digital arrays. The proposed IDL-TLBO technique can be integrated with the switches-based (SE) hybrid architectures using switch optimization (SWO) [38] to estimate DOA and array perturbation matrix in mMIMO systems.

8. Conclusion

In this study, a novel optimization technique for estimation of 2D-DOA in 5G mmWave mMIMO systems in the presence of antenna position perturbation and inconsistent gain/phases have been proposed. The major motivation of the proposed method is inspired by the goal of applying sparse signal recovery methods. The joint estimation approach is formulated under the IDL-TLBO optimization framework by incorporating interdisciplinary learning strategies in TLBO. This mechanism improves the global search capability of DOA and increases the accuracy of the estimation in low SNR region. The simulation results reveal that the DOA estimation with the proposed IDL-TLBO outperforms the other existing DOA estimation schemes under different evaluation criteria.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funds were received.

Open Research

Data Availability Statement

The data supporting the findings of this research are available on request from the first author upon reasonable request.

References

1 Ali E., Ismail M., Nordin R., and Abdulah N. F., Beamforming Techniques for Massive MIMO Systems in 5G: Overview, Classification, and Trends for Future Research, Frontiers of Information Technology & Electronic Engineering. (2017) 18, no. 6, 753–772, https://doi.org/10.1631/fitee.1601817, 2-s2.0-85021730009.
10.1631/FITEE.1601817
Web of Science® Google Scholar
2 Liu Z., Liu Y., Long X., Zhang Y., and Qiu T., Improved Block Sparse Bayesian Learning Based DOA Estimation for Massive MIMO Systems, AEU-International Journal of Electronics and Communications. (2023) 166, https://doi.org/10.1016/j.aeue.2023.154666.
10.1016/j.aeue.2023.154666
Web of Science® Google Scholar
3 Liu A., Liao G., Zeng C., Yang Z., and Xu Q., An Eigenstructure Method for Estimating DOA and Gain-phase Errors, IEEE Transactions on Signal Processing. (Dec. 2011) 59, no. 12, 5944–5965.
10.1109/TSP.2011.2165064
Web of Science® Google Scholar
4 Li Y. and Er M. H., Theoretical Analyses of Gain and Phase Error Calibration with Optimal Implementation for Linear Equispaced Array, IEEE Transactions on Signal Processing. (Feb. 2006) 54, no. 2, 712–723, https://doi.org/10.1109/tsp.2005.861892, 2-s2.0-31344462722.
10.1109/TSP.2005.861892
Web of Science® Google Scholar
5 Weiss A. J. and Friedlander B., Eigenstructure Methods for Direction Finding with Sensor Gain and Phase Uncertainties, Circuits, Systems, and Signal Processing. (1990) 9, no. 3, 271–300, https://doi.org/10.1007/bf01201215, 2-s2.0-0024985730.
10.1007/BF01201215
Web of Science® Google Scholar
6 Soon V. C., Tong L., Huang Y. F., and Liu R., A Subspace Method for Estimating Sensor Gains and Phases, IEEE Transactions on Signal Processing. (1994) 42, no. 4, 973–976, https://doi.org/10.1109/78.285666, 2-s2.0-0028407259.
10.1109/78.285666
Web of Science® Google Scholar
7 Liu Z.-M. and Zhou Y.-Y., A Unified Framework and Sparse Bayesian Perspective for Direction-Of-Arrival Estimation in the Presence of Array Imperfections, IEEE Transactions on Signal Processing. (Aug. 2013) 61, no. 15, 3786–3798, https://doi.org/10.1109/tsp.2013.2262682, 2-s2.0-84880544581.
10.1109/TSP.2013.2262682
Web of Science® Google Scholar
8 Weiss A. J. and Friedlander B., Array Shape Calibration Using Sources in Unknown Locations—A Maximum Likelihood Approach, IEEE Transactions on Acoustics, Speech, & Signal Processing. (Dec. 1989) 37, no. 12, 1958–1966, https://doi.org/10.1109/29.45542, 2-s2.0-0024912185.
10.1109/29.45542
Web of Science® Google Scholar
9 Wong K. T., Wu Y. I., Hsu Y.-S., and Song Y., A Lower Bound of DOA-Estimates by an Array Randomly Subject to Sensor-Breakdown, IEEE Sensors Journal. (May 2012) 12, no. 5, 911–913, https://doi.org/10.1109/jsen.2011.2165704, 2-s2.0-84859790596.
10.1109/JSEN.2011.2165704
Web of Science® Google Scholar
10 Ruan N. J., Wen F. Q., Ai L., and Xie K., A PARAFAC Decomposition Algorithm for DOA Estimation in Colocated MIMO Radar with Imperfect Waveforms, IEEE Access. (2019) 7, 14680–14688, https://doi.org/10.1109/access.2019.2894747, 2-s2.0-85061719647.
10.1109/ACCESS.2019.2894747
Web of Science® Google Scholar
11 Liu S., Zhang Z., and Guo Y., 2-D DOA Estimation with Imperfect L-Shaped Array Using Active Calibration, IEEE Communications Letters. (2021) 25, no. 4, 1178–1182, https://doi.org/10.1109/lcomm.2020.3047222.
10.1109/LCOMM.2020.3047222
Web of Science® Google Scholar
12 Afkhaminia F. and Azghani M., Sparsity-based DOA Estimation of 2-D Rectangular Array in the Presence of Gain and Phase Uncertainty, Circuits, Systems, and Signal Processing. (Oct 2021) 40, no. 10, 5014–5032, https://doi.org/10.1007/s00034-021-01705-w.
10.1007/s00034-021-01705-w
Web of Science® Google Scholar
13 Zhu H., Leus G., and Giannakis G. B., Sparsity-cognizant Total Least-Squares for Perturbed Compressive Sampling, IEEE Transactions on Signal Processing. (May 2011) 59, no. 5, 2002–2016, https://doi.org/10.1109/tsp.2011.2109956, 2-s2.0-79954496453.
10.1109/TSP.2011.2109956
Web of Science® Google Scholar
14 Stoica P., Babu P., and Li J., SPICE: A Sparse Covariance-Based Estimation Method for Array Processing, IEEE Transactions on Signal Processing. (February 2011) 59, no. 2, 629–638, https://doi.org/10.1109/tsp.2010.2090525, 2-s2.0-78651376363.
10.1109/TSP.2010.2090525
Web of Science® Google Scholar
15 Xu X., Wei X., and Ye Z., DOA Estimation Based on Sparse Signal Recovery Utilizing Weighted $l_{1}$-Norm Penalty, IEEE Signal Processing Letters. (Mar. 2012) 19, no. 3, 155–158, https://doi.org/10.1109/lsp.2012.2183592, 2-s2.0-84863054157.
10.1109/LSP.2012.2183592
CAS Web of Science® Google Scholar
16 Zhang X., Liu L., Chen P., Cao Z., and Chen Z., Gridless Sparse Direction-Finding Method for Correlated Signals with Gain-phase Errors, Electronics. (2019) 8, no. 5, https://doi.org/10.3390/electronics8050557, 2-s2.0-85066813743.
10.3390/electronics8050557
Web of Science® Google Scholar
17 Wang D., You K., Zuo P., Wang Y., Guo W., and Peng T., Grid Adaptive Sparse Bayesian Learning for 2d-Doa Estimation with L-Shape Array, 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), 2019, IEEE, 1–6.
10.1109/PIMRC.2019.8904291
Google Scholar
18 Elbir A. M., V-shaped Sparse Arrays for 2-D DOA Estimation, Circuits, Systems, and Signal Processing. (2019) 38, no. 6, 2792–2809, https://doi.org/10.1007/s00034-018-0991-5, 2-s2.0-85065909905.
10.1007/s00034-018-0991-5
Web of Science® Google Scholar
19 Aquino S. and Vairavel G., A Review of Direction of Arrival Estimation Techniques in Massive MIMO 5G Wireless Communication Systems, Proceedings of Fourth International Conference on Communication, Computing and Electronics Systems: ICCCES 2022, 2023, Singapore, Springer Nature Singapore.
Google Scholar
20 Friedlander B., Antenna Array Calibration for a General Linear Transformation of the Array Manifold, International Journal of Antennas and Propagation. (2019) 2019, 1–11, https://doi.org/10.1155/2019/9257853, 2-s2.0-85065616941.
10.1155/2019/9257853
Web of Science® Google Scholar
21 Liu H., Zhao L., Li Y., Jing X., and Truong T. K., A Sparse-Based Approach for DOA Estimation and Array Calibration in Uniform Linear Array, IEEE Sensors Journal. (Jun 7 2016) 16, no. 15, 6018–6027, https://doi.org/10.1109/jsen.2016.2577712, 2-s2.0-84978253773.
10.1109/JSEN.2016.2577712
Web of Science® Google Scholar
22 Venkata Rao R. and Waghmare G., A Comparative Study of a Teaching–Learning-Based Optimization Algorithm on Multi-Objective Unconstrained and Constrained Functions, Journal of King Saud University-Computer and Information Sciences. (2014) 26, no. 3, 332–346, https://doi.org/10.1016/j.jksuci.2013.12.004, 2-s2.0-85006210786.
10.1016/j.jksuci.2013.12.004
Google Scholar
23 Jiang Z.o et al., A Novel Algorithm for DOA Estimation and Array Calibration in Monostatic MIMO Radar, 2021.
10.1049/icp.2021.0680
Google Scholar
24 Zhang R., Cheng L., Wang S. et al., Integrated Sensing and Communication with Massive MIMO: A Unified Tensor Approach for Channel and Target Parameter Estimation, IEEE Transactions on Wireless Communications. (2024) 23, no. 8, 8571–8587, https://doi.org/10.1109/twc.2024.3351856.
10.1109/TWC.2024.3351856
Web of Science® Google Scholar
25 Shen F. F., Liu Y.-M., Zhao G.-H., Chen X.-Y., and Li X.-P., Sparsity-Based Off-Grid DOA Estimation with Uniform Rectangular Arrays, IEEE Sensors Journal. (2018) 18, no. 8, 3384–3390, https://doi.org/10.1109/JSEN.2018.2800906, 2-s2.0-85041397064.
10.1109/JSEN.2018.2800906
Web of Science® Google Scholar
26 Ju S., Kanhere O., Xing Y., and Rappaport T. S., A Millimeter-Wave Channel Simulator NYUSIM with Spatial Consistency and Human Blockage, In2019 IEEE Global Communications Conference (GLOBECOM), December 2019, IEEE, 1–6.
Google Scholar
27 Fan D., Gao F., Wang G., Zhong Z., and Nallanathan A., Angle Domain Signal Processing-Aided Channel Estimation for Indoor 60-GHz TDD/FDD Massive MIMO Systems, IEEE Journal on Selected Areas in Communications. (Jun 2017) 35, no. 9, 1948–1961, https://doi.org/10.1109/jsac.2017.2720938, 2-s2.0-85023761253.
10.1109/JSAC.2017.2720938
Web of Science® Google Scholar
28 Moghaddam M. H., Rezaei Aghdam S., and Eriksson T., Statistical Analysis of Antenna Array Systems with Perturbations in Phase, Gain and Element Positions, 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP), 2019, Ottawa, ON, Canada, 1–5, https://doi.org/10.1109/GlobalSIP45357.2019.8969083.
10.1109/GlobalSIP45357.2019.8969083
Google Scholar
29 Yu X., Shen J. C., Zhang J., and Letaief K. B., Alternating Minimization Algorithms for Hybrid Precoding in Millimeter Wave MIMO Systems, IEEE Journal of Selected Topics in Signal Processing. (2016) 10, no. 3, 485–500, https://doi.org/10.1109/jstsp.2016.2523903, 2-s2.0-84966417086.
10.1109/JSTSP.2016.2523903
Web of Science® Google Scholar
30 Zhou J., Array Imperfection Calibration for Wireless Channel Multipath Characterisation, 2018, Diss. UCL (University College London).
Google Scholar
31 Ma Y., Zhang X., Song J., and Chen L., A Modified Teaching–Learning-Based Optimization Algorithm for Solving Optimization Problem, Knowledge-Based Systems. (2021) 212, https://doi.org/10.1016/j.knosys.2020.106599.
10.1016/j.knosys.2020.106599
PubMed Web of Science® Google Scholar
32 Wu X., Li S., Wu F., and Jiang X., Teaching–Learning Optimization Algorithm Based on the Cadre–Mass Relationship with Tutor Mechanism for Solving Complex Optimization Problems, Biomimetics. (2023) 8, no. 6, https://doi.org/10.3390/biomimetics8060462.
10.3390/biomimetics8060462
Web of Science® Google Scholar
33 Zhang H., He P., and Yang X., Fault Detection Based on Multi-Scale Local Binary Patterns Operator and Improved Teaching-Learning-Based Optimization Algorithm, Symmetry. (2015) 7, no. 4, 1734–1750, https://doi.org/10.3390/sym7041734, 2-s2.0-84952787282.
10.3390/sym7041734
Web of Science® Google Scholar
34 Singh R., Chaudhary H., and Singh A. K., A New Hybrid Teaching–Learning Particle Swarm Optimization Algorithm for Synthesis of Linkages to Generate Path, Sādhanā. (2017) 42, no. 11, 1851–1870, https://doi.org/10.1007/s12046-017-0737-2, 2-s2.0-85033409225.
10.1007/s12046-017-0737-2
Web of Science® Google Scholar
35 Zhen J. and Guo B., DOA Estimation for Far-Field Sources in Mixed Signals with Mutual Coupling and Gain-phase Error Array, EURASIP Journal on Wireless Communications and Networking. (2018) 2018, 295–310, https://doi.org/10.1186/s13638-018-1324-x, 2-s2.0-85059068261.
10.1186/s13638-018-1324-x
Google Scholar
36 Wu Di, Wang S., Liu Q., Abualigah L., and Jia H., An Improved Teaching-Learning-Based Optimization Algorithm with Reinforcement Learning Strategy for Solving Optimization Problems, Computational Intelligence and Neuroscience. (2022) 2022, 1–24, https://doi.org/10.1155/2022/1535957.
10.1155/2022/1535957
Web of Science® Google Scholar
37 Karim B. A. and Ali H. K., Computationally Efficient MUSIC Based DOA Estimation Algorithm for FMCW Radar, Journal of Electronic Science and Technology. (2023) 21, no. 1, https://doi.org/10.1016/j.jnlest.2023.100192.
10.1016/j.jnlest.2023.100192
Google Scholar
38 Zhang R., Shim B., and Wu W., Direction-of-arrival Estimation for Large Antenna Arrays with Hybrid Analog and Digital Architectures, IEEE Transactions on Signal Processing. (2022) 70, 72–88, https://doi.org/10.1109/tsp.2021.3119768.
10.1109/TSP.2021.3119768
Web of Science® Google Scholar

All articles

A Novel TLBO-Based Antenna Array Imperfection Calibration for Effective DOA Estimation in mmWave mMIMO Systems

Abstract

1. Introduction