International Journal of Antennas and Propagation

Volume 2025, Issue 1 5582517

Research Article

Open Access

Investigation of a Rectangular Dielectric Resonator Antenna Working in Higher Order Modes Using Perturbation Theory

Neetu

orcid.org/0000-0001-6003-2002

Department of Electronics and Communication Engineering , National Institute of Technology , New Delhi , 110036 , India , int.gov.br

Department of Electronics and Communication Engineering , Maharaja Surajmal Institute of Technology , New Delhi , 110058 , India , msit.in

Search for more papers by this author

Sachin Kumar,

Corresponding Author

Sachin Kumar

[email protected]

orcid.org/0000-0002-6260-6353

Department of Electronics and Communication Engineering , Galgotias College of Engineering and Technology , Greater Noida , 201310 , India , galgotiacollege.edu

Search for more papers by this author

Binod Kumar Kanaujia,

Binod Kumar Kanaujia

orcid.org/0000-0003-1272-1561

Department of Electronics and Communication Engineering , Dr. B. R. Ambedkar National Institute of Technology , Jalandhar , 144011 , India , nitj.ac.in

Search for more papers by this author

Sandeep Kumar Palaniswamy,

Corresponding Author

Sandeep Kumar Palaniswamy

[email protected]

orcid.org/0000-0001-5270-0242

Department of Electronics and Communication Engineering , Faculty of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , 603203 , India , srmist.edu.in

Search for more papers by this author

Gaurav Varshney,

Gaurav Varshney

orcid.org/0000-0002-7001-9095

Department of Electronics and Communication Engineering , National Institute of Technology , Patna , 800005 , India , int.gov.br

Search for more papers by this author

Neetu,

Neetu

orcid.org/0000-0001-6003-2002

Department of Electronics and Communication Engineering , National Institute of Technology , New Delhi , 110036 , India , int.gov.br

Department of Electronics and Communication Engineering , Maharaja Surajmal Institute of Technology , New Delhi , 110058 , India , msit.in

Search for more papers by this author

Sachin Kumar,

Corresponding Author

Sachin Kumar

[email protected]

orcid.org/0000-0002-6260-6353

Department of Electronics and Communication Engineering , Galgotias College of Engineering and Technology , Greater Noida , 201310 , India , galgotiacollege.edu

Search for more papers by this author

Binod Kumar Kanaujia,

Binod Kumar Kanaujia

orcid.org/0000-0003-1272-1561

Department of Electronics and Communication Engineering , Dr. B. R. Ambedkar National Institute of Technology , Jalandhar , 144011 , India , nitj.ac.in

Search for more papers by this author

Sandeep Kumar Palaniswamy,

Corresponding Author

Sandeep Kumar Palaniswamy

[email protected]

orcid.org/0000-0001-5270-0242

Department of Electronics and Communication Engineering , Faculty of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , 603203 , India , srmist.edu.in

Search for more papers by this author

Gaurav Varshney,

Gaurav Varshney

orcid.org/0000-0002-7001-9095

Department of Electronics and Communication Engineering , National Institute of Technology , Patna , 800005 , India , int.gov.br

Search for more papers by this author

First published: 15 April 2025

https://doi.org/10.1155/ijap/5582517

Academic Editor: Rajashik Paul

Share a link

Email
Wechat
Bluesky

Abstract

Dielectric resonator antennas (DRAs) operating in higher order modes provide wideband, enhanced gain, and circularly polarized performance. This paper presents a simple perturbation theory for predicting the resonant frequency of higher order modes in perturbed rectangular DRAs (RDRAs). The proposed theory has been validated for isolated RDRA, two-layer DRA, and RDRA with rectangular- and cylindrical-shaped perturbations. To determine the accuracy of the proposed theory, the frequency computed from it is compared to simulated and measured results of higher order mode perturbed antennas available in the literature. The proposed theory can be easily applied to the design of perturbed DRAs that operate at higher order modes. Also, the theory can be extended to compute other antenna parameters.

1. Introduction

The dielectric resonator antenna (DRA) is a potential candidate for future wireless communication systems, particularly at microwave and millimeter-wave frequencies, because of its inherent advantages of wide bandwidth and lower losses [1]. DRA can be implemented in a variety of shapes, including circular, rectangular, spherical, and conical [2, 3]. Among all of these shapes, the rectangular shape of the dielectric resonator drew the most attention due to its numerous features that make antenna implementation simple and efficient. The use of rectangular dielectric resonator allows for greater freedom in selecting the resonant frequency of the antenna [4]. Also, the rectangular DRA (RDRA) [5] offers less cross-polarization and can be easily used in arrays [6]. Furthermore, it is simple to excite accurately predictable resonant modes and design a RDRA with the correct dimensions based on the required operating mode. The term “required operating mode” is important in this context as it refers to obtaining the desired operating and radiation characteristics of the antenna. The radiation behavior of an antenna can be accurately defined if its operating modes are completely known. A number of research articles are available in the literature, which reported on the design of DRA operating with the fundamental and multiple higher order modes [2, 3, 7]. It is already known that a RDRA operating in higher order modes provides a higher gain than an antenna operating in fundamental mode [8]. In advanced wireless communication systems that require high data transfer rates over long distances, obtaining high gain and wide impedance bandwidth is required [9].

There are several methods in the literature that describe gain and bandwidth enhancement techniques [10, 11]. Moreover, the perturbation technique has been investigated for obtaining high gain and wideband response. The concept of DRAs with material wall perturbation in the form of vias and metal wall perturbation in the form of metal strips is also used to design band notch filtering [12], wide stop band filtering [13], and circularly polarized DRAs [14, 15]. The calculation of the resonant frequencies of the operating modes of the perturbed RDRA (PRDRA) has been a long-standing research topic, with a brief discussion of techniques provided in [16, 17]. However, unlike higher order modes, the perturbation approach is capable of easily calculating the resonant frequency of the fundamental mode. No research has been conducted on calculating the resonant frequency of the higher order mode. And, as previously discussed, the generation of higher order modes in the RDRA can offer enhanced characteristics that can make future communication systems fluent with high-end technology. In the literature, two-layer inhomogeneous structures are simulated and fabricated to generate higher order modes at lower frequencies while increasing gain and bandwidth. These are the principles of material perturbation. These reported DRAs are simulated and fabricated, but no specific theory is provided for the change in resonant frequency of the perturbed structure. In this paper, the authors proposed a very simple and accurate perturbation theory for predicting the resonant frequency of higher order modes in such inhomogeneous PRDRA structures.

This study presents a method for calculating the resonant frequency of a PRDRA operating in higher order modes. For the first time, perturbation theory is proposed in this paper for higher order RDRAs and PRDRAs. The perturbation shape of RDRA is rectangular or cylindrical. The higher order mode frequencies associated with each type of perturbation are computed using the proposed theory and compared to simulated and measured frequencies of PRDRAs coated with dielectric materials. It also explains how the permittivity and perturbation position are used to enhance the bandwidth and gain. The main advantage of the proposed theory is that it bridges the gap between simulated and measured results by providing the precise dimension and position of perturbation required to design an antenna with the desired performance. In the future, the theory can be applied to RDRA subjected to spherical-shaped perturbations.

2. Theory

Consider a RDRA with dimensions a × b × d and relative permittivity of ε_r, as shown in Figure 1. The RDRA is excited to work in the higher order mode. The field components for the

mode are given in [18]. The following transcendental equations describe the relationship between wave numbers (K_x, K_y, K_z, and K_mn) and resonant frequency (f_mn).

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Rectangular dielectric resonator antenna (RDRA).

The perturbation theory is used to accurately calculate the resonant frequency of higher order DRA modes. Equation (2) calculates the difference (Δf_mn) between the frequency obtained from perturbation theory (f_p) and frequency calculated from the DWM model (f_mn).

()

The perturbation approach for dielectric resonators is given in the following equation.

()

where E₀ represents the electric field in the unperturbed region, while E_p represents the electric field in the perturbed region, Δω_m − Δω_e represents the change in stored energies due to perturbation, and ω_m + ω_e represents the total stored energy in the original DRA. There is no evidence of the existence of TM modes in RDRA with ground plane [19], and TM modes have not been observed experimentally in RDRA [20], so only TE modes are discussed in this paper.

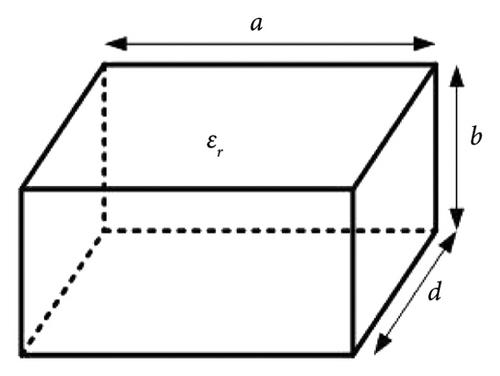
The perturbation concept is used in the design of inhomogeneous DRAs. Material perturbation and heterogeneous DRAs include two-layer DRAs, stacked DRAs, and RDRA with rectangular- and cylindrical-shaped inserts. The quasi-static approximation is used at a dielectric-dielectric discontinuity, and the continuity of electric field intensity in the perturbed region and the original DRA is maintained.

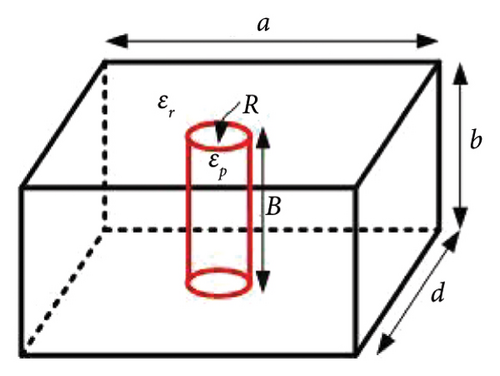
The perturbation theory for higher order RDRA modes with rectangular- and cylindrical-shaped perturbations is shown in Figures 2 and 3. Figure 2 depicts the RDRA with a rectangular-shaped perturbation, while Figure 3 depicts the RDRA with a cylindrical-shaped material perturbation. The perturbed cylinder is concentric with the RDRA. Table 1 shows the quasi-static approximation for the electric field relation at the dielectric-dielectric discontinuity, as well as the perturbation approach for all perturbation cases. Equation (4) is used to calculate the resonant frequency of the mode.

Table 1. Perturbation approach with rectangular- and cylindrical-shaped perturbations.

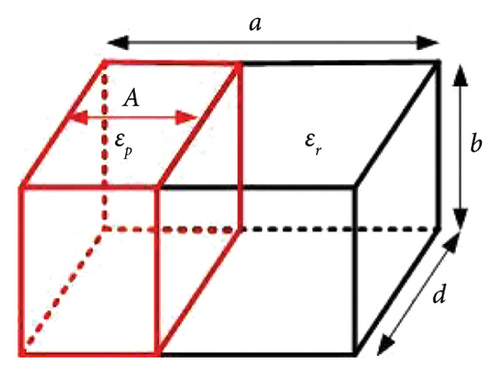
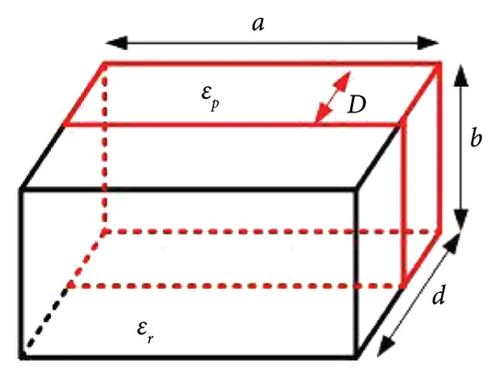
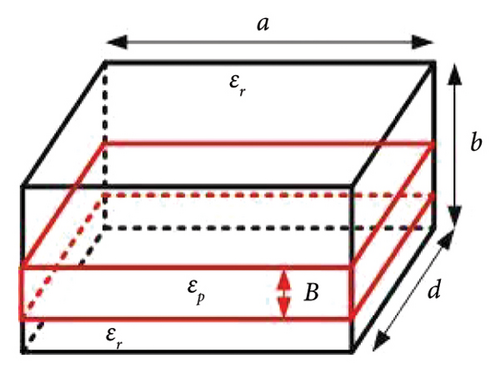
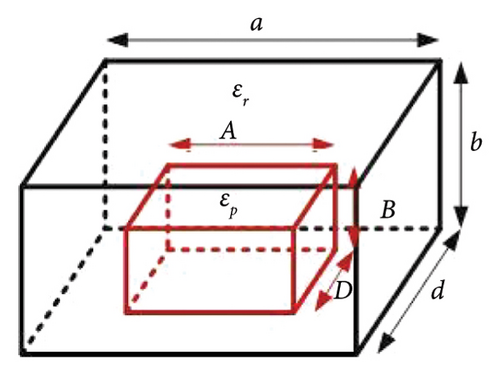
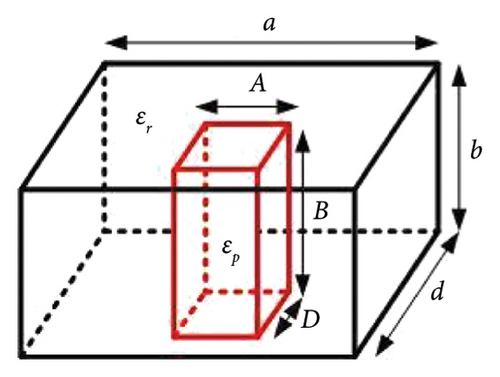
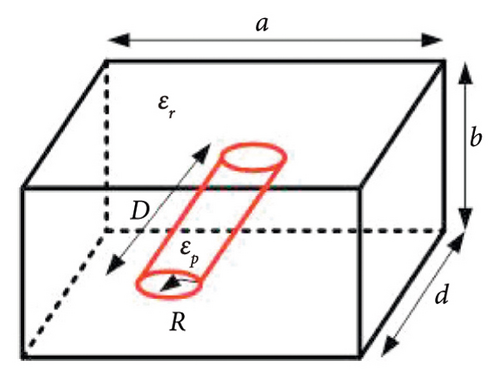
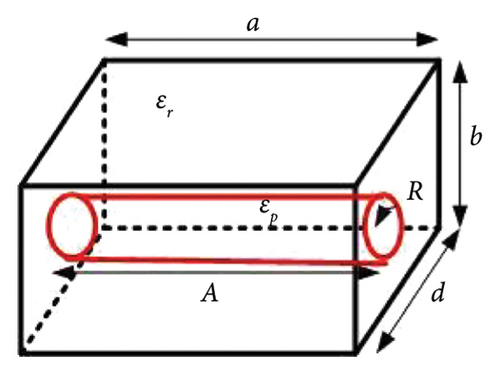
Shape of perturbation (dimensions)	Structure	Quasi-static approximation electric field intensity relationship between perturbed region (E_P) and original region (E₀)	Perturbation approach
Rectangular (A × b × d)	Figure 2(a)	E_P = E₀	(Δf_mn)/f_p = K(A/a)((Δε)/ɛ_r)((1+sin c(k_xA)cos(k_x(A − a)))/(1 + sin c(k_xa)))
Rectangular (a × b × D)	Figure 2(b)	E_P = E₀	(Δf_mn)/f_p = K(D/d)((Δε)/ɛ_r)
Rectangular (a × B × d)	Figure 2(c)		(Δf_mn)/f_p = (K/2)(B/b)((Δε)/ɛ_p)
Rectangular (A × B × D)	Figure 2(d)	E_P = E₀	(Δf_mn)/f_p = K((Δε)/ɛ_r)(BD(a − A)/abd)((1+sinc(k_x(a − A)))/(1 + sinc(k_xa)))
Rectangular (A × B × D)	Figure 2(e)	E_P = E₀	(Δf_mn)/f_p = K(ABD/abd)((Δε)/ɛ_r)
Cylindrical (radius = R, height = A = a)	Figure 3(a)	E_P = (2ɛ_r)/(ɛ_p + ɛ_r)E₀	(Δf_mn)/f_p = 2K(πR²/bd)((Δε)/(ɛ_r + ɛ_p))
Cylindrical (radius = R, height = D = d)	Figure 3(b)	E_P = (2ɛ_r)/(ɛ_p + ɛ_r)E₀	(Δf_mn)/f_p = 2K(πR²/ab)((Δε)/(ɛ_r + ɛ_p))
Cylindrical (radius = R, height = B = b)	Figure 3(c)	E_P = E₀	(Δf_mn)/f_p = K(πR²/ad)((Δε)/ɛ_r)

In Table 1, and Δε = ɛ_r − ɛ_p, and a, b, and d are the dimensions of RDRA along the x, y, and z directions, respectively. A, B, and D are the dimensions of the perturbed structure in the x, y, and z directions for RDRA. The dimensions of perturbed structures along the x, y, and z directions are A, B, and D, respectively, for RDRA with rectangular-shaped perturbation. R is the radius of the cylinder and sphere for the cylindrical- and spherical-shaped perturbed regions. Table 1 contains simple equations that can be used to predict the resonant frequency of higher order modes of PRDRA. The proposed theory is verified and validated with the simulated and fabricated PRDRA results.

3. Results

The accuracy of perturbation theory compared to dielectric waveguide model (DWM) [21], modified DWM method [22], weighted average model method (WAM) [23, 24], modified WAM method [25], mode matching technique [26], and transverse transmission line technique [27] is validated for the dominant mode of isolated RDRA [16, 28]. The proposed perturbation theory for higher order modes of RDRA and PRDRA for different perturbation shapes is validated by comparing the results of the proposed method to simulated and measured results reported in the literature. The theory is validated in three stages:

(i)
Validation of higher order modes for unperturbed RDRA
(ii)
Validation of higher order PRDRA modes with rectangular-shaped perturbations
(iii)
Validation of higher order PRDRA modes using cylindrical-shaped perturbations

In Table 2, the proposed theory is used to compute the resonant frequency of an unperturbed RDRA. In [21], the RDRA with different dimensions is excited in higher order modes. The calculated errors between frequencies are within the acceptable range.

Table 2. Validation of the proposed perturbation theory for higher order modes in unperturbed RDRA.

References	ɛ_r	Dimensions (a × b × d) (mm³)	f_sim (GHz)	f_meas (GHz)	f_prop (GHz)	% Δf_sim = (f_sim − f_prop)/f_sim	%Δf_meas = (f_meas − f_prop)/f_meas
[21]	12.7	12 × 20 × 8	8.44	8.30	8.6977	−3.05	−4.79
	12.7	12 × 20 × 8	12.18	12.01	12.5660	−3.17	−4.63
	12.7	8 × 24 × 10	7.54	7.24	7.7373	−2.62	−6.87
	12.7	8 × 24 × 10	10.52	10.25	10.391	1.23	−1.38
	12.7	8 × 20 × 12	10.03	9.7	10.2767	−2.46	−5.95
	12.7	8 × 20 × 12	10.84	10.40	10.775	0.60	−3.61
	12.7	12 × 16 × 10	11.54	11.25	11.8795	−2.94	−5.60
	12.7	12 × 16 × 10	10.70	10.40	10.91	−1.96	−4.90
	12.7	10 × 24 × 8	11.85	11.62	12.2491	−3.37	−5.41

[29]	10	18 × 58 × 20	3.52	3.54	3.4395	2.29	2.84
[29]	10	18 × 58 × 20	4.28	4.15	3.9058	−0.25	−3.39

[30]	10	3.96 × 3.96 × 12.2	24.06	23.86	23.9744	0.36	−0.48
[30]	10	4.27 × 4.27 × 21.36	24.05	23.87	24.0262	0.09	−0.65

[31]	12	28 × 32 × 24	3.51	—	3.4824	0.79	—
	12	28 × 32 × 24	3.76	—	3.7431	0.45	—
	12	27 × 33 × 24	3.44	—	3.4330	0.20	—
	12	27 × 33 × 24	3.82	—	3.8265	−0.17	—
	12	30 × 30 × 24	3.62	—	3.5992	0.58	—
	12	30 × 30 × 24	3.62	—	3.5992	0.58	—

[8]	10	6 × 6 × 30	11	10.65	10.899	0.92	−2.34
[8]	10	5 × 5 × 60	11	10.85	10.948	0.47	−0.90

In [29], RDRA is excited in , , and modes to achieve dual-band operation. The lower band is obtained by merging and modes, while the upper band corresponds to the mode. The lower band frequency calculated from the perturbation theory is 3.29 GHz, which is very close to the measured frequency of 3.25 GHz and gives an error of 1.47%. Table 2 shows the percentage error for the and modes.

In [30], the higher order mode RDRA is designed to operate at 24 GHz; the frequency computed using perturbation is very close to the design frequency, and the calculated error is less than 0.5%. In [31], RDRA with different dimensions are excited in and modes. The simulated results are compared to those calculated from the proposed theory and give an error of less than 1%.

In [8], the higher order and modes are excited to design an antenna with enhanced gain at 11 GHz. The frequencies corresponding to each mode for the specified dimensions are very close to the simulated and measured frequencies.

The above discussion shows that perturbation theory can be used to design an antenna excited in higher order modes.

In this case, RDRA with dimensions of 20 × 20 × 82 and permittivity (ɛ_r) = 3.5 is placed on the ground plane. The given RDRA is then subjected to material perturbation with a rectangular shape. An RDRA with dimensions of 4 × 4 × 80 is drilled to obtain an inhomogeneous PRDRA with a rectangular hole, which is then filled with a dielectric coat of the same dimensions. The dielectric coat has a dielectric constant (ε_p) of 10. This is the example of a perturbation shown in Figure 2(e). The perturbation formula for calculating the resonant frequency is simplified to

()

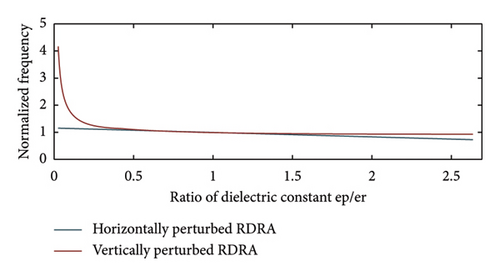
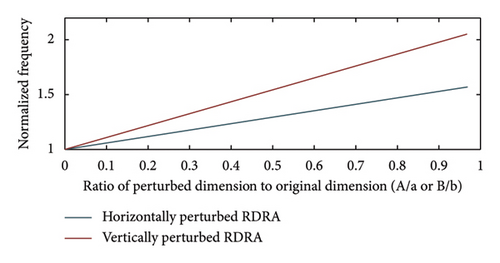
The resonant frequencies of PRDRA calculated using the proposed theory for and modes are in good agreement with simulated and measured frequencies. In [32], the concept of RDRA with rectangular-shaped perturbation is used to achieve a wider impedance bandwidth and higher gain by exciting higher order modes at lower resonant frequencies. This is achieved by maintaining a higher ε_p/ε_r ratio. Higher ε_p/ε_r ratios lead to lower changes in RDRA and PRDRA resonant frequencies. This is supported by the normalized frequency graph of PRDRA with rectangular-shaped perturbation in Figure 4. When a perturbation is made along the length or width of the RDRA, it is horizontally perturbed, and if it is made along the height, it is vertically perturbed. When a higher dielectric constant material is surrounded by a lower dielectric constant material, more fields will be confined in the higher dielectric constant region, resulting in a shorter distance between two adjacent magnetic dipoles. In [32], the same concept of perturbation is used to generate mode at a lower resonant frequency of 12 GHz. Furthermore, the accuracy of perturbation theory for PRDRA with rectangular-shaped perturbation, excited in the dominant mode, is already verified by authors in [16, 28].

An RDRA with dimensions of 3.84 × 3.84 × 38.44 and permittivity (ɛ_r) = 9.8 is placed on the ground plane and excited in the

mode. The given RDRA is then subjected to a cylindrical material perturbation. To create an inhomogeneous PRDRA with a cylindrical hole, a 0.4-mm diameter hole is drilled. The dielectric constant (ɛ_p) of the cylinder is equal to 1. This is the perturbation shown in Figure 3(c), with the cylinder placed along the z-axis. The perturbation formula for determining the resonant frequency is simplified to

()

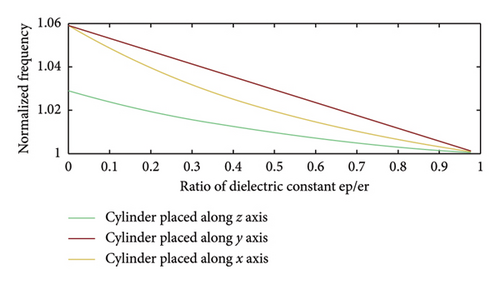
The results of the proposed theory closely match the simulated and fabricated results. PRDRA has a small change in the resonant frequency compared to RDRA due to the minimal ε_p/ε_r and radius/height ratios of the cylinder. This can be validated by the normalized frequency graphs shown in Figures 5(a) and 5(b) for RDRA with cylindrical shape perturbations. The reason that both RDRA and PRDRA in [33] resonate at 15 GHz is the same. The concept of perturbation results in reduced effective dielectric constant without much changing the operating frequency of RDRA, and thus, utilized for gain and bandwidth enhancement for 5G applications in [33] by exciting higher order modes in PRDRA.

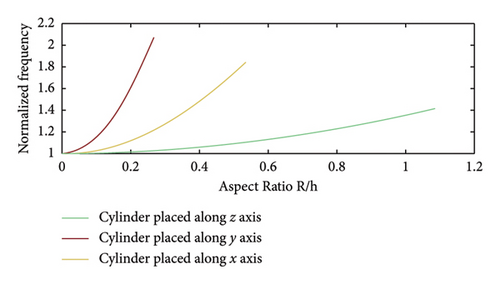
Tables 3 and 4 show that the position of the perturbation is the same in both cases; one is PRDRA with a rectangular-shaped perturbation with a higher dielectric constant material perturbation, and the other is PRDRA with a cylindrical-shaped perturbation with a lower dielectric constant. In Table 3, the concept of perturbation is used to generate higher order modes at lower resonant frequencies, with a wider bandwidth and higher gain. In Table 4, the concept of perturbation is used to increase antenna gain and bandwidth without significantly affecting the operating frequency of the antenna. As a result, RDRAs with various perturbation shapes can be used to design antennas with higher order modes, wider bandwidth, and higher gain. The proposed theory validated that the shape, dielectric constant, and position of perturbation will be deciding factors for the operational behavior of PRDRA.

Table 3. Validation of the proposed theory for higher order modes in PRDR with rectangular-shaped perturbations [32].

DRA	ɛ_r	ɛ_p	Dimensions (a × b × d)(mm³)	Dimensions of the rectangle (A × B × D) (mm³)	f_sim (GHz)	f_meas (GHz)	f_prop (GHz)	% Δf_sim = (f_sim − f_prop)/f_sim	%Δf_meas = (f_meas − f_prop)/f_meas
Unperturbed RDRA	3.5	—	20 × 20 × 82	—	—	—	11.03	—	—
Unperturbed RDRA	3.5	—	20 × 20 × 82	—	—	—	12.78	—	—

Perturbed RDRA	3.5	10	20 × 20 × 82	4 × 4 × 80	10.67	10.70	10.34	3.09	3.36
Perturbed RDRA	3.5	10	20 × 20 × 82	4 × 4 × 80	11.7	11.23	11.93	−1.96	−6.23

Table 4. Validation of the proposed perturbation theory for higher order modes in PRDRA with cylindrical-shaped perturbations [33].

DRA	Mode	ɛ_r	ɛ_p	Dimensions (a × b × d) (mm³)	Radius of the cylinder (r) (mm)	f_sim (GHz)	f_meas (GHz)	f_prop (GHz)	% Δf_sim = (f_sim − f_prop)/f_sim	%Δf_meas = (f_meas − f_prop)/f_meas
RDRA		9.8	—	3.84 × 3.84 × 38.44	—	15	14.98	14.8	1.33	1.20
PRDRA		9.8	1	3.84 × 3.84 × 38.44	0.4	14.9	14.9	14.893	0.04	0.04

4. Conclusion

Perturbed DRAs operating in higher order modes are used to design antennas with large impedance bandwidth and high gain. The perturbation theory is proposed for higher order modes of RDRAs with rectangular- and cylindrical-shaped perturbations. The proposed theory is verified and validated using simulated and measured results, and it is found to be in good agreement with the published data. A further theory can be used to explain the process of generating higher order modes and increasing bandwidth through perturbation. The combination of dielectric constant, shape, and perturbation position will help in the design of higher order perturbed DRAs. The new theory will bridge the gap between simulated and measured results by providing a precise measure of dimensions for the given design frequency. The theory can be extended for perturbed structures obtained through a combination of different shapes of perturbation.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was obtained for this study.

Acknowledgment

The authors have nothing to report.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Mukherjee B., Patel P., and Mukherjee J., A Review of the Recent Advances in Dielectric Resonator Antennas, Journal of Electromagnetic Waves and Applications. (2020) 34, no. 9, 1095–1158, https://doi.org/10.1080/09205071.2020.1744484.
10.1080/09205071.2020.1744484
Web of Science® Google Scholar
2 Leung K. W., Lim E. H., and Fang X. S., Dielectric Resonator Antennas: From the Basic to the Aesthetic, Proceedings of the IEEE. (2012) 100, no. 7, 2181–2193, https://doi.org/10.1109/jproc.2012.2187872, 2-s2.0-84862640618.
10.1109/JPROC.2012.2187872
Web of Science® Google Scholar
3 Wang Q., Li P., Rocca P. et al., Interval-based Tolerance Analysis Method for Petal Reflector Antenna with Random Surface and Deployment Errors, IEEE Transactions on Antennas and Propagation. (2023) 71, no. 11, 8556–8569, https://doi.org/10.1109/tap.2023.3314097.
10.1109/TAP.2023.3314097
Web of Science® Google Scholar
4 Luk Km L. K., Dielectric Resonator Antennas, 2003, Research studies press Ltd.
Google Scholar
5 Petosa A. and Ittipiboon A., Dielectric Resonator Antennas: A Historical Review and the Current State of the Art, IEEE Antennas and Propagation Magazine. (2010) 52, no. 5, 91–116, https://doi.org/10.1109/map.2010.5687510, 2-s2.0-78651487572.
10.1109/MAP.2010.5687510
Web of Science® Google Scholar
6 Huang X., Design of Miniaturized SIW Filter Loaded with Improved CSRR Structures, Electronics. (2023) 12, no. 18, https://doi.org/10.3390/electronics12183789.
10.3390/electronics12183789
Web of Science® Google Scholar
7 Gotra S., Varshney G., Pandey V. S., and Yaduvanshi R. S., Super-wideband Multi-Input–Multi-Output Dielectric Resonator Antenna, IET Microwaves, Antennas & Propagation. (2019) 14, no. 1, 21–27, https://doi.org/10.1049/iet-map.2018.6112.
10.1049/iet-map.2018.6112
Web of Science® Google Scholar
8 Petosa A. and Thirakoune S., Rectangular Dielectric Resonator Antennas with Enhanced Gain, IEEE Transactions on Antennas and Propagation. (2011) 59, no. 4, 1385–1389, https://doi.org/10.1109/tap.2011.2109690, 2-s2.0-79953769432.
10.1109/TAP.2011.2109690
Web of Science® Google Scholar
9 Fakhte S., Oraizi H., and Matekovits L., Gain Improvement of Rectangular Dielectric Resonator Antenna by Engraving Grooves on its Side Walls, IEEE Antennas and Wireless Propagation Letters. (2017) 16, 2167–2170, https://doi.org/10.1109/lawp.2017.2702584, 2-s2.0-85029456798.
10.1109/LAWP.2017.2702584
Web of Science® Google Scholar
10 Chang T. and Kiang J., Bandwidth Broadening of Dielectric Resonator Antenna by Merging Adjacent Bands, IEEE Transactions on Antennas and Propagation. (2009) 57, no. 10, 3316–3320, https://doi.org/10.1109/tap.2009.2029372, 2-s2.0-76149096824.
10.1109/TAP.2009.2029372
Web of Science® Google Scholar
11 Soren D., Ghatak R., Mishra R. K., and Poddar D. R., Dielectric Resonator Antennas: Designs and Advances, Progress in Electromagnetics Research B. (2014) 60, no. July, 195–213, https://doi.org/10.2528/pierb14031306, 2-s2.0-84905223969.
10.2528/PIERB14031306
Google Scholar
12 La D. S., Zhang C., Li H. C., Wang M. Y., Guo J. W., and Qu M. J., A Band-Notched Filtering Omnidirectional Dielectric Resonator Antenna with Metal Patches, Alexandria Engineering Journal. (2022) 61, no. 12, 11511–11522, https://doi.org/10.1016/j.aej.2022.05.020.
10.1016/j.aej.2022.05.020
Web of Science® Google Scholar
13 La D. S., Liu H., Wang R. L., Tian K., and Qu M. J., A Wide Stopband Filtering DDPA with Metal Vias and Metal Strips, IEEE Transactions on Antennas and Propagation. (March 2024) 72, no. 3, 2843–2848, https://doi.org/10.1109/tap.2024.3350187.
10.1109/TAP.2024.3350187
Web of Science® Google Scholar
14 Bari I., Iqbal J., Ali H. et al., Bandwidth Enhancement and Generation of CP of Yagi-Uda-Shape Feed on a Rectangular DRA for 5G Applications, Micromachines. (2022) 13, no. 11, https://doi.org/10.3390/mi13111913.
10.3390/mi13111913
PubMed Web of Science® Google Scholar
15 Illahi U., Iqbal J., Ramay S. M., and Sulaiman M. I., Design and Development of a New Circularly Polarized MIMO Wearable DRA for WBAN Applications, AEU: International Journal of Electronics and Communications. (2024) 177, https://doi.org/10.1016/j.aeue.2024.155208.
10.1016/j.aeue.2024.155208
Web of Science® Google Scholar
16 Sehrawat N., Kanaujia B. K., and Agarwal A., Calculation of the Resonant Frequency of a Rectangular Dielectric Resonator Antenna Using Perturbation Theory, Journal of Computational Electronics. (2018) 18, no. 1, 211–221, https://doi.org/10.1007/s10825-018-1284-8, 2-s2.0-85058149450.
10.1007/s10825-018-1284-8
Web of Science® Google Scholar
17 Fakhte S. and Oraizi H., Derivation of the Resonant Frequency of Rectangular Dielectric Resonator Antenna by the Perturbation Theory, Applied Computational Electromagnetics Society Journal. (2016) 31, no. 8, 894–900.
Web of Science® Google Scholar
18 Petosa A., Thirakoune S., and Ittipiboon A., Higher-order Modes in Rectangular DRAs for Gain Enhancement, Proceedings: 2009 13th International Symposium on Antenna Technology and Applied Electromagnetics and the Canadian Radio Sciences Meeting, 2009, ANTEM/URSI 2009, 13–16.
Google Scholar
19 Petosa A., Dielectric Resonator Antenna Handbook, 2007, Artech House, London, UK.
Google Scholar
20 Pan Y. M., Leung K. W., and Lu K., Study of Resonant Modes in Rectangular Dielectric Resonator Antenna Based on Radar Cross Section, IEEE Transactions on Antennas and Propagation. (2019) 67, no. 6, 4200–4205, https://doi.org/10.1109/tap.2019.2911198, 2-s2.0-85067041263.
10.1109/TAP.2019.2911198
Web of Science® Google Scholar
21 Mongia R. K., Theoretical and Experimental Resonant Frequencies of Rectangular Dielectric Resonators, IEE Proceedings H Microwaves, Antennas and Propagation. (1992) 139, no. 1, https://doi.org/10.1049/ip-h-2.1992.0016, 2-s2.0-0026819844.
10.1049/ip-h-2.1992.0016
Web of Science® Google Scholar
22 Petosa A., Simons N., Siushansian R., Ittipiboon A., and Cuhaci M., Design and Analysis of Multisegment Dielectric Resonator Antennas, IEEE Transactions on Antennas and Propagation. (2000) 48, no. 5, 738–742, https://doi.org/10.1109/8.855492, 2-s2.0-0034187707.
10.1109/8.855492
Web of Science® Google Scholar
23 Rashidian A., Forooraghi K., and Tayefeh M. R., Design Algorithm of Multisegment Dielectric Resonator Antennas (MSDRAs), 2004.
Google Scholar
24 Rashidian A., Forooraghi K., and Aligodarz M. T., Investigations on Two-Segment Dielectric Resonator Antennas, Microwave and Optical Technology Letters. (2005) 45, no. 6, 533–537, https://doi.org/10.1002/mop.20871, 2-s2.0-20444438780.
10.1002/mop.20871
Web of Science® Google Scholar
25 Gürel Ç. S., Coşar H., and Akalın Ö., Accurate Resonant Frequency Computation of Multisegment Rectangular Dielectric Resonator Antennas, Journal of Electromagnetic Waves and Applications. (2010) 24, no. 5–6, 839–847, https://doi.org/10.1163/156939310791036313, 2-s2.0-77950526454.
10.1163/156939310791036313
Web of Science® Google Scholar
26 Maity S. and Gupta B., Theory and Experiments on Horizontally Inhomogeneous Rectangular Dielectric Resonator Antenna, AEU: International Journal of Electronics and Communications. (2017) 76, 158–165, https://doi.org/10.1016/j.aeue.2017.04.001, 2-s2.0-85018288495.
10.1016/j.aeue.2017.04.001
Web of Science® Google Scholar
27 Lu K., Leung K. W., and Pan Y. M., Theory and Experiment of the Hollow Rectangular Dielectric Resonator Antenna, IEEE Antennas and Wireless Propagation Letters. (2011) 10, 631–634, https://doi.org/10.1109/lawp.2011.2158977, 2-s2.0-79960110557.
10.1109/LAWP.2011.2158977
Web of Science® Google Scholar
28 Sehrawat N., Kanaujia B. K., Agarwal A., and Varshney G., Analysis of an Inhomogeneous Circularly Polarized Hollow Dielectric Resonator Antenna Using Perturbation Theory, 2021.
10.3390/electronics10182273
Google Scholar
29 Zhang M., Li B., and Lv X., Cross-slot-coupled Wide Dual-Band Circularly Polarized Rectangular Dielectric Resonator Antenna, IEEE Antennas and Wireless Propagation Letters. (2014) 13, 532–535, https://doi.org/10.1109/lawp.2014.2310241, 2-s2.0-84898427578.
10.1109/LAWP.2014.2310241
Web of Science® Google Scholar
30 Pan Y. M., Leung K. W., and Luk K. M., Design of the Millimeter-Wave Rectangular Dielectric Resonator Antenna Using a Higher-Order Mode, IEEE Transactions on Antennas and Propagation. (2011) 59, no. 8, 2780–2788, https://doi.org/10.1109/tap.2011.2158962, 2-s2.0-80051478865.
10.1109/TAP.2011.2158962
Web of Science® Google Scholar
31 Zou M. and Pan J., Investigation of Resonant Modes in Wideband Hybrid Omnidirectional Rectangular Dielectric Resonator Antenna, IEEE Transactions on Antennas and Propagation. (2015) 63, no. 7, 3272–3275, https://doi.org/10.1109/tap.2015.2425421, 2-s2.0-84936857265.
10.1109/TAP.2015.2425421
Web of Science® Google Scholar
32 Abdulmajid A. A., Khalil Y., and Khamas S., Higher Order Mode Circularly Polarized Two-Layer Rectangular Dielectric Resonator Antenna, IEEE Antennas and Wireless Propagation Letters. (2018) 17, no. 6, 1114–1117, https://doi.org/10.1109/lawp.2018.2834981, 2-s2.0-85046792610.
10.1109/LAWP.2018.2834981
Web of Science® Google Scholar
33 Ali I., Jamaluddin M. H., Gaya A., and Rahim H. A., A Dielectric Resonator Antenna with Enhanced Gain and Bandwidth for 5G Applications, Sensors. (2020) 20, no. 3, https://doi.org/10.3390/s20030675.
10.3390/s20030675
Web of Science® Google Scholar

All articles

Investigation of a Rectangular Dielectric Resonator Antenna Working in Higher Order Modes Using Perturbation Theory

Abstract

1. Introduction

2. Theory

3. Results

4. Conclusion

Conflicts of Interest

Funding

Acknowledgment

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Investigation of a Rectangular Dielectric Resonator Antenna Working in Higher Order Modes Using Perturbation Theory

Abstract

1. Introduction

2. Theory

3. Results

4. Conclusion

Conflicts of Interest

Funding

Acknowledgment

Open Research

Data Availability Statement

References

Figures

References

Related

Information