The selection of a fourth-generation fighter aircraft for the Algerian Air Force is a complex multicriteria decision-making (MCDM) process, marked by ambiguity and subjectivity. In the face of such challenges, the hybrid framework has applied the fuzzy analytic hierarchy process (fuzzy AHP), Shannon entropy, and fuzzy technique for order of preference by similarity to ideal solution. This approach utilizes linguistic variables represented by triangular fuzzy numbers to enhance adaptability and transparency in the decision-making process. Fuzzy AHP and entropy methods calculate the weights of selection criteria, while fuzzy TOPSIS ranks alternatives. The study is applied on a set of aircrafts, including SU-34, MIG-29, Rafale, and F-16, using technical and operational criteria such as range, autonomy, and climb rate. Results indicate that SU-34 is the optimal choice when using fuzzy AHP, while the F-16 ranks highest with the entropy method, with minimal score differences underscoring the precision and reliability of the methodology. This study overcomes traditional limitations, such as subjective bias and inflexibility, by leveraging fuzzy logic, enabling systematic assessments aligned with real-world constraints. The findings refine procurement decisions and provide a framework for balanced military evaluations. Future work may extend to advanced aircraft or unmanned systems.

1. Introduction

This section is divided into three parts: Background and Motivation (Section 1.1), Related Work Analysis and Gaps in Research (Section 1.2), and Contributions (Section 1.3) of this study in the context of fighter aircraft selection. It provides a foundation for the subsequent sections, establishing the research context and highlighting key advancements in the field.

1.1. Background and Motivation

In military environments, weapon systems are critical in determining the outcome of any war. Among these systems, the choice of fighter aircraft is a pivotal decision for armies worldwide. A poor selection of military weapons can negatively impact the overall performance and effectiveness of a defense system. However, selecting a new weapon also represents a significant opportunity for armies to enhance their capabilities. This process is long and complex and demands advanced knowledge and experience [1]. The rapid advancement of military technologies has further complicated and escalated the cost of weapon systems. Also, geographical constraints such as a country’s location, surface area, and external disturbances aggravate any decision-making process. Particular air forces have a key role to play in defense strategy in every country, especially for countries like Algeria, whose vast territory and long borders would find it impossible to control under the responsibility of ground forces alone. Border disturbances and security threats make the role of air power indispensable.

Driven by this, this work introduces an in-depth study on fighter aircraft selection for the Algerian Air Force, advancing multicriteria decision-making (MCDM) methodologies to enhance selection accuracy. This study is aimed at providing a structured approach for evaluating fighter aircraft alternatives. The research considers key factors, including cost, internal fuel, unloaded weight, … act., ensuring a well-informed procurement strategy aligned with Algeria’s defense needs.

1.2. Related Work Analysis and Gaps in Research

The search for optimal methods to select military systems has drawn considerable academic interest. One of the earliest notable studies was conducted by authors in [2], who applied fuzzy analytic hierarchy process (FAHP) to evaluate tactical missile systems for military applications. Their criteria included tactics, technology, maintenance, economics, and advancement, with subcriteria such as effective range, reliability, system cost, and mobility. Similarly, they applied the same techniques to evaluate small antiaircraft artillery weapons, incorporating interval calculations, alpha cutoffs, symmetric trigonometric fuzzy numbers, and optimism indices to address ambiguity and imprecision.

Over the years, numerous studies have employed various MCDM methods. For instance, the authors in [3] used tools such as AHP and equal trade-offs method to evaluate aircraft selection for a small airline, considering factors like cost per seat mile, take-off mass, price, baggage, and seat capacity. Similarly, in [4], the authors developed a model using Type II Fuzzy TOPSIS and IT2FAHP to optimize military aircraft fleet management, factoring in technical, financial, and environmental considerations, particularly during crises like coronavirus disease. The authors in [5] applied MCDM tools to airline fleet management, using Interval Type 2 Fuzzy TOPSIS for ranking alternatives and IT2FAHP for weighting criteria. Their model considered eight subcriteria categorized into technical, economic, and environmental issues. Further advancements in fuzzy logic have been introduced by researchers such as [6], who used a single-valued neutrosophic score function (SVNSF) to evaluate stealth fighter aircraft, focusing on criteria like stealth and performance metrics under uncertainty. The authors also applied proximity fuzzy measurement (PMM) methods to select airborne firefighting aircraft, integrating inputs from multiple decision-makers to rank and identify optimal solutions.

Other researchers have applied fuzzy and MCDM methods in diverse contexts. For example, in [7], the authors utilized fuzzy intuitive evaluation to select the best attack helicopter for the Brazilian Navy, assessing models based on speed, tactical gun, ammunition, missiles, shells, and operational range. The authors in [8] applied the Grey Step-wise Weight Assessment Ratio Analysis (SWARA) method for military helicopter pilot selection, focusing on health, psychomotor skills, and education, thereby enhancing decision-making transparency in high-stakes environments. Recent studies have further explored MCDM applications in the aviation industry. The authors in [9] used the ranking of alternatives using fuzzy similarity index (RAFSI) method to select aircraft types for airlines, prioritizing revenue drivers, capacity, customer experience, operating costs, and competition. Similarly, in [10], the authors employed the best–worst Bayes method and intuitionistic fuzzy evaluation to assess alternative aircraft models for sustainable transportation, balancing accuracy and reliability. In [11], the authors applied the VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), translated as multicriteria optimization and compromise solution method, and Shannon’s entropy to select fifth-generation fighter aircraft for the Indian Air Force, addressing technical, economic, and performance aspects. Table 1 summarizes key findings and methodologies from recent studies relevant to this research while also focusing on the most important research gaps.

Table 1. Key findings from related works.

Ref.	Methods	Advantages	Research gaps
[2]	Fuzzy AHP	Evaluated tactical missile systems and small antiaircraft artillery using fuzzy logic, considering factors like range, reliability, cost, and mobility. Interval calculations and optimism indices enhanced decision accuracy	Complexity of fuzzy models increases computational demands. Limited validation for broader military applications
[3]	AHP, equal trade-offs	Applied to aircraft selection for small airlines, balancing cost per seat mile, take-off mass, price, baggage, and seat capacity. Demonstrated effectiveness in structured airline decision-making	Limited to small airlines, not scalable to large fleet or military applications. Subjectivity in trade-offs may introduce bias
[4]	Type II Fuzzy TOPSIS, IT2FAHP	Optimized military aircraft fleet management by integrating technical, financial, and environmental factors, particularly during crises like COVID-19	High sensitivity to expert inputs. May not fully adapt to rapidly changing crises or combat situations
[5]	Interval Type 2 Fuzzy TOPSIS, IT2FAHP	Enhanced airline fleet management by ranking alternatives and weighting criteria across technical, economic, and environmental dimensions	Model lacks real-world validation. Subjective judgment introduces potential bias in weight assignments
[6]	SVNSF, PMM	Evaluated stealth fighter aircraft based on stealth and performance metrics under uncertainty. Applied PMM methods for airborne firefighting aircraft selection	High computational complexity. Limited adaptability beyond aircraft evaluation
[7]	Fuzzy intuitive evaluation	Selected best attack helicopter for Brazilian Navy, considering speed, armament, missiles, and operational range	Lacks sensitivity analysis. Limited applicability to diverse military aviation needs
[8]	Grey SWARA	Applied to military helicopter pilot selection, enhancing transparency by focusing on health, psychomotor skills, and education	Not tested on larger datasets. May not account for evolving pilot training needs
[9]	Fuzzy triangles, RAFSI	Selected optimal aircraft types for airlines by prioritizing revenue, capacity, customer experience, operating costs, and competition	Limited applicability to military contexts. Lack of real-time adaptability
[10]	Best–Worst Bayes, intuitionistic fuzzy evaluation	Assessed alternative aircraft for sustainable transport, balancing accuracy and reliability	Requires further validation. High reliance on expert opinions
[11]	VIKOR, Shannon entropy	Selected fifth-generation fighter aircraft for Indian Air Force, addressing technical, economic, and performance aspects	Lacks adaptability to other defense procurement areas. High dependency on input data accuracy

1.3. Contributions

In attempt to cover up for previous research gaps, this paper introduces a novel fuzzy systematic evaluation approach for weapon systems, aimed at assisting the Algerian Air Force in selecting an ideal fourth or fourth-plus generation fighter aircraft from a set of available options. The objectives of this research are twofold: (1) to analyze the defense selection structure and determine the weighting coefficients of the criteria and (2) to select the most suitable aircraft, balancing subjectivity and objectivity in the evaluation process.

In this context, this study develops several significant contributions to the field of MCDM and military procurement, particularly in the context of selecting fighter aircraft for the Algerian Air Force.

•
Hybrid framework: A new hybrid framework is proposed based on integrating the FAHP, Shannon entropy, and fuzzy TOPSIS to deal with the complexity and subjectivity introduced with military procurement. The combined use of these techniques or methodologies seems to tug at each individual strength and allow for much stronger and more flexible decision-making processes.
•
The use of fuzzy logic and triangular fuzzy numbers to depict linguistic variables really enhances their flexibility and visibility, thus taking care of all the uncertainty and vagueness inherent in expert evaluations and real phenomena.
•
Criteria weighting: The study employs the FAHP and entropy, two methods employed for the calculation of the weights of selection criteria as a combination of subjective opinions from experts and objective data-driven analysis toward a balanced way of weighting.
•
Aircraft evaluation and ranking: The framework will evaluate and rank several fourth-generation jet fighters, including the SU-34, MIG-29, Rafale, and F-16, in terms of their technical and operational characteristics such as range, autonomy, climb rate, and cost.
•
Incorporating fuzzy logic into the study of MCDM tackles limitations, such as subjectivity and inflexibility, allowing for assessments far more systematic and realistic. The opinion of real-world constraints and experts comes into play.

The rest of the paper is divided into several sections: Section 1 forms the introduction, which includes motivations, state of the art, and contributions. Section 2 is the methodological discussion, wherein a description of the methodology used is presented, including FAHP, Shannon entropy, the unified (UNI) AHP–entropy model, and fuzzy TOPSIS. Section 3 presents the numerical application that includes an application of the abovementioned methodologies in the selection of fighter aircraft for the Algerian Air Force. Section 4 contains a discussion, while Section 5, the conclusions, features analysis of results, key findings, and avenues for future research. The References section contains all works that were referred to in the text. Such an explanation helps retain a coherence and logic in the exposition of the problem, methodology, application, and conclusions of the research in one format.

2. Methodology

This section introduces methods used in this work and their structured hybridization (see Figure 1). Accordingly, three methods for calculating criteria weights, namely, FAHP, entropy, and UNI AHP–entropy model, are used. To classify the alternatives, the fuzzy TOPSIS method is employed. Each of these methods is explained in detail in the subsections below.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Overview of the research framework and analytical steps.

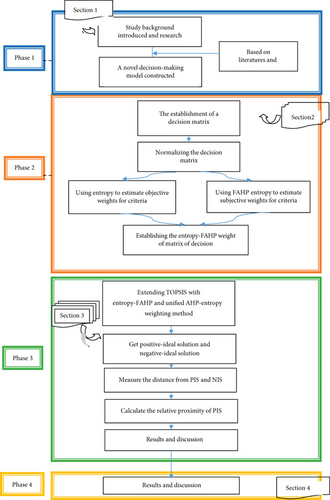
2.1. FAHP

FAHP is a widely used MCDM method based on fuzzy set theory, developed to solve hierarchical fuzzy problems. Various FAHP methods have been proposed by several authors, each with its advantages and disadvantages, as shown in Table 2. For instance, in [12], the authors extended Saaty’s AHP method using triangular fuzzy numbers, whereas Buckley [13] employed trapezoidal fuzzy numbers and the geometric mean method. The authors in [12] introduced synthetical degree values, while Cheng (1996) incorporated entropy concepts to calculate aggregate weights. Among these, Buckley’s [13] method, which determines fuzzy priorities using trapezoidal membership functions, is considered more reliable in our study. The measurement analysis method, on the other hand, has limitations, as it does not fully utilize all the information in fuzzy comparison matrices and may produce irrational zero weights [14].

Table 2. Comparison of different fuzzy AHP methods.

Sources	The main characteristics of the method	Advantages (A) and disadvantages (D)
AHP by van Laarhoven and Pedrycz [12]	Direct extension of Saaty’s AHP method with triangular fuzzy numbers Lootsma’s logarithmic least square method is used to derive fuzzy weights and fuzzy performance scores	(A) The opinions of multiple decision-makers can be modeled in the reciprocal matrix (D) There is not always a solution to the linear equations (D) The computational requirement is tremendous, even for a small problem (D) It allows only triangular fuzzy numbers to be used
AHP by Buckley [13]	Extension of Saaty’s AHP method with trapezoidal fuzzy numbers Uses the geometric mean method to derive fuzzy weights and performance scores	(A) It is easy to extend to the fuzzy case (A) It guarantees a unique solution to the reciprocal comparison matrix (D) The computational requirement is tremendous
AHP by Boender, de Grann, and Lootsma (1989)	Modifies van Laarhoven and Pedrycz’s method Presents a more robust approach to the normalization of the local priorities	(A) The opinions of multiple decision-makers can be modeled (D) The computational requirement is tremendous
AHP by Chang [14]	Synthetical degree values Layer simple sequencing Composite total sequencing	(A) The computational requirement is relatively low (A) It follows the steps of crisp AHP. It does not involve additional operations (D) It allows only triangular fuzzy numbers to be used
AHP by Cheng (1996)	Builds fuzzy standards Represents performance scores by membership functions Uses entropy concepts to calculate aggregate weights	(A) The computational requirement is not tremendous (D) Entropy is used when probability distribution is known The method is based on both probability and possibility measures

The procedure of Buckley’s [13] method consists of four steps. In Step 1, the pairwise comparison matrix is constructed by comparing criteria two by two using linguistic terms assigned according to Buyukozkan’s (2012) scale. The comparison matrix

is represented as shown in Equation (1), where

is presented in Equation (2). In Step 2, the fuzzy geometric mean matrix is computed using the geometric mean technique, as expressed in Equation (3). Step 3 involves calculating the fuzzy weights of each criterion using Equation (4). Finally, in Step 4, the best nonfuzzy performance (BNP) is determined using the center of gravity method, as shown in Equation (5). Here,

is the fuzzy weight of criterion i and

with Lw_i, Mw_i, and Uw_i representing, respectively, lower values and middle and upper fuzzy weights of criterion i.

()

2.2. Shannon Entropy

Entropy method is a measure of uncertainty of information formulated using probability theory. It states that a broad distribution represents uncertainty and then they have reached a peak [15]. To calculate the weights by the entropy method first, the information matrix is normalized using the following equations. The relative importance of criterion j in a decision situation is measured by the weight of the intrinsically set of alternatives with respect to that criterion. The entropy method was developed as an objective method of allocating weights depending on the decision matrix without affecting the decision-maker’s preference [16]. The criterion should be how much more variance there is in the assessments of the alternatives. Shannon’s well-established and widely recognized theory of entropy in an information channel serves as the conceptual foundation for this diversity [17]. The process begins by normalizing the decision matrix, which ensures that all criteria are comparable on a common scale. This is achieved using Equation (6). Next, the entropy E_j is calculated to measure the dispersion of values within each criterion, as shown in Equation (7). Finally, the normalized weight of each criterion w_j is determined based on the entropy values, as given in Equation (8):

()

2.3. UNI AHP–Entropy

The UNI AHP–entropy model is a hybrid decision-making approach that uses AHP and entropy method to calculate criteria weights. It balances subjective judgment with objective data analysis, addressing biases in either method. This approach is useful in complex decision-making scenarios where expert opinion and data variability are significant. The final set of criteria weights (W) is determined from both objective and subjective weights as in Equation (9):

()

2.4. Fuzzy TOPSIS

The TOPSIS method was proposed in [18] in order to solve the decision problems with uncertainty. In the extension of TOPSIS method (fuzzy TOPSIS), all assessments and weights are defined using linguistic variables. Different steps of the fuzzy TOPSIS method are presented as follows.

Step 1: Fuzzy decision matrix.

It is composed of m alternatives A_i(i = 1, 2, ⋯, m) and n criteria C_j(j = 1, 2, ⋯, n).

Table 3 presents the fuzzy decision matrix:

()

Table 3. Linguistic values according to the scale of Buyukozkan (2012).

Description	Numerical value
Both elements have equal importance	(1, 1, 1)
The element in line is little bigger than the one in column	(2, 3, 4)
The element in line is more important than the one in column	(4, 5, 6)
The element in line is much more important than the one in column	(6, 7, 8)
The element in line is absolutely more important than the one in column	(8, 9, 9)
The element in line is little less important than the one in column	(1/4, 1/3, 1/2)
The element in line is less important than the one in column	(1/6, 1/5, 1/4)
The element in line is much less important than the one in column	(1/8, 1/7, 1/6)
The element in line is absolutely less important than the one in column	(1/9, 1/9, 1/8)

Each criterion is associated with a weight w, either given by a set of experts or defined by one of the methods as FAHP, BNP, entropy analysis, eigenvector method, weighted least square method, and linear programming for multidimensions of analysis preference (LINMAP) with ; and of triangular fuzzy numbers with and .

represents the appreciation of the alternative A_i with respect to the criterion C_j, and represents the weight of the criterion C_j.

Step 2: Normalized fuzzy decision matrix.

The data are normalized, where the objective is to eliminate anomalies with different units of measurement used in a problem of MCDM. The normalized values of triangular fuzzy numbers are included in the interval [0, 1]. The normalized fuzzy decision matrix is given by

in Equation (11):

()

For triangular fuzzy numbers

, the normalized values are calculated by Equation (12):

()

Step 3: Construction of the decision matrix of fuzzy weights.

Given the different weights for each criterion, the normalized decision matrix of weights is calculated by multiplying the importance weights of the evaluation criteria by the normalized values.

The normalized values of decision matrix

are defined in Equations (13) and (14):

()

with

representing the weight of fuzzy number of criterion C_j.

Step 4: Calculation of the positive ideal solution and the negative ideal solution.

The positive ideal solution FPIRP (fuzzy positive ideal reference point) called A⁺ and the negative ideal solution FNIRP (fuzzy negative ideal reference point) called A⁻ are derived as in Equations (15) and (16):

()

Step 5: Calculation of distances between each alternative FPIRP and FNIRP.

The next step is to calculate the separation from the FPIRP and the FNIRP between the alternatives. The separation values can also be measured using the Euclidean distance as in Equations (17) and (18):

()

with

and

Step 6: Calculation of closeness coefficient called Cc_i and alternatives’ ranking.

For each alternative i, CC_i is given Equation (19):

()

The alternatives are classified with respect to their CC. The alternative with the biggest CC will be the best alternative.

3. Numerical Application

Following the need of the Algerian Air Force to renew and vary its fleet of fighting aircraft for fourth generation, a team of experts was formed from the crews of the Algerian Air Force and, specifically, the authors of this article.

The proposed model for the problem of the selection of fighting aircraft is based on the methods FAHP, entropy, UNI AHP–entropy model, and fuzzy TOPSIS. It includes three main phases: (1) identify the criteria to use in the model; (2) calculations of weight criteria using three methods FAHP, entropy, and UNI AHP–entropy; and (3) evaluating alternatives with fuzzy TOPSIS and determining the final ranking with a comparison between the three results. The first phase is to determine the criteria and alternatives to use and construct the hierarchical structure of suitable decision-making. The model AHP is structured so that the objective is in the first level, the criteria in the second level, and the alternatives in the third level. In the last step of the first phase, the hierarchy of decision is approved by the team of decision-making.

After the approval of the decision hierarchy in Figure 2, the criteria used in the selection of fighting aircraft are weighted using FAHP, entropy, and UNI AHP–entropy in the second phase.

In this phase, the pairwise comparison matrix is formed to determine the weights of the criteria. Experts of decision team make individual assessments using the scale provided in Table 3; the goal is to determine the values of elements of the pairwise comparison matrix. When calculating the geometric mean, the values are obtained from the individual assessments, the final matched comparison matrix on which there is a consensus found. The weights of the criteria are calculated on the basis of this final comparison matrix. In the last stage of this phase, the calculated weights of the criteria are approved by the decision-making team. The aircraft ranks are determined using fuzzy TOPSIS method in the third phase.

3.1. Determination of Criteria and Alternatives

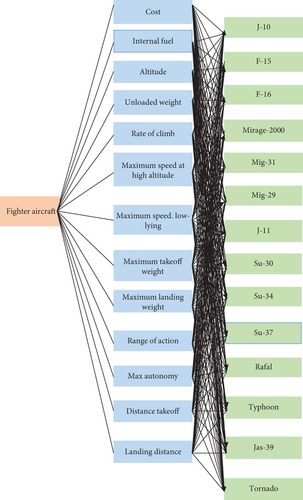
The criteria to be taken into account in the selection of fighting aircraft are determined by the team of experts. Past experience and prerequisites of the expert team are used in determining the criteria. The criteria and their definitions are shown in Table 4.

Table 4. Criteria and their definitions.

	Criteria	Description
C₁	Cost (m$)	Price of each aircraft
C₂	Internal fuel (tonne)	The amount of fuel stored in the aircraft structure without tank
C₃	Altitude max (km)	The maximum height that can reach the plane safely
C₄	Unloaded weight (tonnes)	Weight of the aircraft without fuel and tanks and without weapons
C₅	Rate of climb (m/s)	Is the rise time of the aircraft, it differs from one plane to another depending on the speed, weight, and the attack angle of the aircraft
C₆	Maximum speed at high altitude (Mach)	The maximum speed that the aircraft can reach to its maximum height safely, knowing that 1 Mach = 1234.8 km h
C₇	Maximum speed, low-lying (Mach)	The maximum speed that the aircraft can achieve in its lower altitude safely without crash, knowing that 1 Mach = 1234.8 km/h
C₈	Maximum takeoff weight (tonnes)	The maximum load with which the aircraft can take off safely, and if the aircraft exceeds this weight, it does not take off
C₉	Maximum landing weight (tonnes)	The maximum load with which the aircraft can land safely; if the aircraft exceeds this weight, it falls freely
C₁₀	Range of action (km)	The maximum range between takeoff and landing
C₁₁	Max autonomy (km)	The maximum distance at which the aircraft can stay aloft based on the fuel load
C₁₂	Distance takeoff (min)	The distance between the setting of the gas and when the aircraft reaches a height of 15 m
C₁₃	Landing distance (min)	The distance between the passage of 15 m and stopping the device

For the alternatives, we have taken practically most fighting aircrafts of fourth generation existing on the market except the so-called impossible choices either for political reasons or other reasons. Alternatives and their definitions are shown in Table 5.

Table 5. Different alternatives and their definitions.

Alternatives	Definitions
J-10	The J-10 is a fourth-generation multirole all-weather aircraft built by the firm Chengdu aircraft industry group based in Chengdu, China, for the Chinese air force. It is known in the west as the “vigorous dragon”
F-15	The McDonnell Douglas F-15 eagle is a fighter always says air superiority, designed by the American aircraft manufacturer McDonnell Douglas in the 1970s
F-16	The F-16 fighting falcon general dynamics is a multirole fighter aircraft developed by general dynamics for the United States in the 1970s
Mirage 2000	The Mirage 2000 is a fighter aircraft designed by the French company Dassault aviation in the late 1970s
Mig-31	The Mikoyan Mig-31 (NATO code “foxhound”) is an interceptor of Soviet origin (now Russian)
Mig-29	The Mikoyan Mig-29 is a Soviet air superiority fighter aircraft developed in the early 1970s and whose first flight took place on October 6, 1977
J-11	The Shenyang J-11 is a fourth-generation interceptor of the People’s Republic of China
Su-30	The Sukhoi Su-30 is a fighter multirole to Soviet and then Russian reaction
Su-34	The Sukhoi Su-34 is a Russian tactical bomber with antisurface warfare capabilities
Su-37	The Sukhoi Su-37 is a Russian fighter aircraft demonstrator. It is vectored thrust version of the Su-35
Jh-7	The Xian Jh-7 or FBC-1 flying leopard is an attack aircraft and two-seat jet built by Xi’an aircraft industrial corporation
Rafale	The Dassault aviation Rafale is a multirole combat aircraft developed for the French navy and French air force and delivered from May 18, 2001
Eurofighter Typhoon	The Eurofighter Typhoon is a twin-engine combat aircraft, gliders and canard, multiroles developed by the United Kingdom, Germany, Italy, and Spain gathered in the Eurofighter consortium
Jas 39 Gripen	The JAS 39 Gripen is a multirole combat aircraft fourth generation developed by Sweden in the 1980s
Tornado	The Tornado is a multirole combat aircraft developed jointly by Italy, the United Kingdom, and Germany during the 1970s

3.2. Determination of the Weight of the Criteria

There are different weighting methods, and each has its own advantages and disadvantages. In other words, no weighting system is superior to criticism [19]. In general, the weights of the criteria can be determined by equal weighting, principal component analysis (PCA) [20, 21, 22], the opinions of experts (for example, the FAHP [13, 14], allocation of budget (AB) [20], the entropy method [11], the eigenvector method, the weighted least squares method, and LINMAP. In this study, we combine three methods—FAHP, entropy, and the UNI FAHP–entropy approach—to provide a comprehensive weighting method. We adopt the FAHP method to evaluate the weights of the different criteria. After building the FAHP model, it is extremely important that the experts fill out the judgment matrix. The methodology for calculating the weights of dimensions is as follows.

A series of interviews with the evaluators were undertaken to calculate the weights of the criteria. Representatives were asked to express their degree of importance of perceptions for each evaluation criterion in linguistic variables according to the corresponding linguistic scales and triangular fuzzy numbers given in Table 3. The fuzzy geometric mean is then obtained. Each cell r_i is described by the geometric mean technique according to Equation (1). Following this, the fuzzy weights of each criterion are computed using Equation (2). To find the BNP, the center of gravity method is applied as described in Equation (3).

In fuzzy Shannon’s entropy, the first step is to compare the importance weights of the criteria and alternatives. Next, the criteria and options must be compared, and the weight must be determined. As a result, it is necessary to evaluate the criteria in accordance with the primary objective and to evaluate the alternatives for these criteria. The weights of the options can then be determined using all of these evaluation processes. These weights are then utilized in the second stage to calculate the fuzzy TOPSIS for the final assessment.

The UNI FAHP–entropy method is a hybrid approach that combines the FAHP and the entropy method. This method takes advantage of the strengths of both techniques to evaluate alternatives more comprehensively. The weights are calculated using Equation (9). Table 6 summarizes the weights obtained using the three methods. The values of criteria by different methods are visible in Figure 3. This integrated approach ensures a robust and balanced evaluation of criteria and alternatives, leveraging both subjective expert opinions and objective data-driven methods.

Table 6. Weights obtained using the three methods.

	FAHP	Entropy	Unified FAHP–entropy
C₁	0.0431	0.0935	0.0417
C₂	0.2315	0.1933	0.4625
C₃	0.1015	0.0064	0.0067
C₄	0.0472	0.0965	0.0471
C₅	0.1291	0.0255	0.0340
C₆	0.0425	0.0112	0.0049
C₇	0.0108	0.0148	0.0017
C₈	0.1104	0.0781	0.0891
C₉	0.0659	0.0781	0.0532
C₁₀	0.1045	0.0936	0.1011
C₁₁	0.1054	0.0214	0.0233
C₁₂	0.0398	0.0309	0.0127
C₁₃	0.0386	0.3057	0.1220

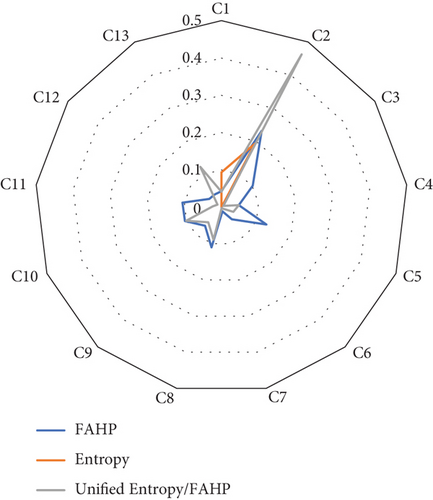
While the UNI FAHP–entropy method is a hybrid approach that combines the FAHP and the entropy method, this method takes advantage of the strengths of both techniques to evaluate alternatives more comprehensively. The weights are calculated using Equation (9). Table 6 summarizes the weights obtained using the three methods. Values of criteria by different methods are visible in Figure 3.

3.3. Evaluation of the Alternatives and Determination of the Final Ranking

In this step, to establish the decision matrix, the team members are asked to compare alternatives under each criterion separately. The fuzzy decision matrix is presented in Table 7. Table 7 shows the combined decision matrix used by Shannon entropy to calculate the weights using the approach previously explained in Paragraph 2.2.

Table 7. Fuzzy decision matrix.

	C₁−			C₂+			C₃+			C₄−			C₅+			C₆+			C₇+			C₈+			C₉+			C₁₀+			C₁₁+			C₁₂−			C₁₃−
A₁	5.625	6.750	7.941	2.280	2.400	3.600	5.400	6.480	7.200	4.592	5.422	6.000	4.500	5.625	6.300	4.275	4.950	6.075	3.240	3.960	5.760	2.782	3.158	3.436	4.846	5.727	7.000	2.829	3.343	3.394	2.916	3.330	3.366	4.186	4.500	5.625	4.813	5.000	6.923
A₂	4.219	4.821	5.192	3.480	3.660	4.920	6.120	6.552	7.308	2.866	3.125	3.462	4.613	5.715	6.458	4.950	5.625	6.525	3.960	5.040	6.840	4.582	5.040	5.400	2.333	2.520	2.864	4.688	5.058	5.091	4.950	5.580	5.634	6.000	6.569	8.571	4.128	4.217	4.737
A₃	6.136	7.105	8.438	1.500	1.560	3.360	4.680	5.472	6.264	4.945	5.696	6.429	4.613	5.715	6.458	4.050	4.500	5.625	2.880	3.600	5.040	2.373	2.782	3.093	4.065	4.667	6.000	4.757	5.143	5.194	6.300	7.002	7.056	7.826	9.000	9.000	6.767	7.031	08.250
A₄	5.192	5.870	6.750	1.800	1.860	4.200	4.680	5.472	6.264	4.945	5.921	6.522	5.625	6.413	6.750	4.275	4.950	6.075	3.600	4.320	5.760	2.373	2.782	3.093	6.300	7.159	8.630	3.394	3.986	4.037	5.400	6.003	6.048	0.984	1.000	1.241	6.767	7.031	08.250
A₅	2.077	2.250	2.700	5.400	6.600	7.800	6.480	7.416	8.208	1.965	2.064	2.368	4.388	4.680	5.288	5.625	6.368	6.750	3.600	4.320	5.760	7.036	7.560	7.855	2.266	2.423	3.000	3.137	3.729	3.780	5.004	5.400	5.454	1.475	1.500	1.800	5.422	5.625	7.500
A₆	4.091	4.821	5.625	1.920	2.100	3.300	5.760	6.480	7.200	3.462	4.091	4.737	6.750	7.425	7.875	4.500	5.063	6.188	3.780	4.500	5.940	2.782	3.273	3.600	3.938	4.345	5.478	2.957	3.343	3.420	3.420	3.780	3.834	1.104	1.125	1.333	4.369	4.500	6.000
A₇	3.857	4.500	5.000	5.400	5.580	6.600	5.760	6.840	7.920	2.542	2.744	3.000	6.300	6.750	7.425	4.725	5.288	6.413	3.960	4.680	6.300	4.582	5.400	5.727	3.706	4.200	5.250	4.371	4.886	4.963	5.760	6.354	6.408	2.338	2.400	3.600	4.369	4.500	6.000
A₈	3.214	3.418	3.857	5.400	5.640	6.720	5.400	6.228	7.128	2.273	2.446	2.727	6.300	6.750	7.425	3.825	4.500	5.175	3.060	3.960	4.932	5.645	6.349	6.676	2.451	2.625	3.150	2.829	3.343	3.420	4.860	5.400	5.454	1.463	1.500	1.800	4.865	5.000	6.923
A₉	3.068	3.375	3.649	7.080	7.260	9.000	4.680	5.400	6.120	1.867	2.000	2.250	6.750	7.425	7.875	3.375	4.050	5.400	3.420	4.320	5.292	6.873	7.380	7.789	2.172	2.423	3.000	2.443	2.906	2.957	6.750	7.200	7.254	2.338	2.400	3.600	4.390	4.500	6.000
A₁₀	2.250	4.500	4.821	5.580	5.700	6.900	6.120	6.480	7.236	2.250	2.432	2.727	4.950	5.513	6.413	4.500	5.288	5.963	4.680	5.472	6.804	5.073	5.727	6.055	2.172	2.333	2.739	3.986	4.713	4.778	5.400	5.940	5.994	1.935	2.000	2.400	3.376	3.462	4.500
A₁₁	5.400	6.429	7.105	1.980	2.100	3.300	5.040	5.760	6.552	2.813	3.103	3.462	4.410	4.658	5.265	2.925	3.938	4.455	2.520	3.060	4.680	3.764	4.664	4.909	3.000	3.316	4.200	3.729	4.523	4.575	4.320	4.860	4.914	1.748	1.800	2.118	3.664	3.750	4.737
A₁₂	2.077	2.250	2.455	2.700	2.820	4.080	5.040	5.472	6.264	2.647	3.000	3.462	6.413	6.818	7.425	3.150	4.050	4.500	3.420	3.960	5.040	3.273	3.895	4.222	3.150	3.500	4.500	4.191	4.765	4.816	5.580	6.300	6.354	2.169	2.250	3.273	6.541	6.818	10.000
A₁₃	1.929	2.109	2.288	2.280	2.400	4.440	5.220	6.048	6.804	3.462	4.091	4.737	4.950	5.715	6.458	3.825	4.500	5.175	3.060	3.600	4.680	3.600	4.418	4.745	3.000	3.316	4.200	4.243	4.762	4.814	5.760	6.822	6.876	1.714	1.765	2.000	4.945	5.056	7.500
A₁₄	2.328	2.700	3.000	1.620	1.800	3.600	5.040	5.472	6.264	5.056	6.618	9.000	3.938	4.500	4.950	3.825	4.500	5.175	2.664	3.240	5.400	1.800	2.291	2.749	5.727	7.000	9.000	4.320	5.099	5.143	5.310	5.760	5.814	2.500	2.571	3.600	4.399	4.500	6.000
A₁₅	4.655	5.625	6.750	1.320	1.500	2.580	5.040	5.486	6.271	2.778	3.103	3.462	2.700	3.375	3.825	4.725	5.265	6.143	3.060	3.960	5.400	3.764	4.451	4.893	3.333	3.706	4.345	2.700	3.574	3.651	3.150	3.600	3.654	1.532	1.565	1.895	4.639	4.737	6.923

The elements of the decision matrix of triangular fuzzy numbers are equivalent to linguistic variables.

Once the fuzzy matrix was determined, the second step is to obtain normalized decision matrix using the weights calculated by AHP (Tables 8 and 9).

Table 8. Normalized decision matrix.

	C₁−			C₂+			C₃+			C₄−			C₅+			C₆+			C₇+			C₈+			C₉−			C₁₀+			C₁₁+			C₁₂−			C₁₃−
A₁	0.287	0.338	0.405	0.253	0.267	0.400	0.658	0.789	0.877	0.380	0.421	0.497	0.571	0.714	0.800	0.633	0.733	0.900	0.474	0.579	0.842	0.357	0.405	0.438	0.326	0.398	0.470	0.545	0.644	0.653	0.402	0.459	0.464	0.405	0.507	0.545	0.329	0.456	0.474
A₂	0.449	0.484	0.553	0.387	0.407	0.547	0.746	0.798	0.890	0.674	0.747	0.814	0.586	0.726	0.820	0.733	0.833	0.967	0.579	0.737	1.000	0.588	0.642	0.688	0.815	0.926	1.000	0.902	0.974	0.980	0.682	0.769	0.777	0.272	0.355	0.389	0.493	0.553	0.565
A₃	0.178	0.211	0.244	0.167	0.173	0.373	0.570	0.667	0.763	0.233	0.263	0.303	0.586	0.726	0.820	0.600	0.667	0.833	0.421	0.526	0.737	0.305	0.354	0.394	0.250	0.321	0.369	0.916	0.990	1.000	0.868	0.965	0.973	0.138	0.167	0.192	0.182	0.213	0.222
A₄	0.146	0.168	0.189	0.200	0.207	0.244	0.570	0.667	0.763	0.151	0.166	0.199	0.714	0.814	0.857	0.633	0.733	0.900	0.526	0.632	0.842	0.305	0.354	0.394	0.114	0.137	0.156	0.653	0.767	0.777	0.744	0.828	0.834	0.792	0.984	1.000	0.087	0.140	0.145
A₅	0.546	0.656	0.710	0.600	0.733	0.867	0.789	0.904	1.000	0.623	0.715	0.751	0.557	0.594	0.671	0.833	0.943	1.000	0.526	0.632	0.842	0.903	0.963	1.000	0.492	0.609	0.375	0.604	0.718	0.728	0.690	0.744	0.752	0.820	0.984	1.000	0.197	0.262	0.272
A₆	0.196	0.229	0.270	0.213	0.233	0.367	0.702	0.789	0.877	0.233	0.270	0.319	0.857	0.943	1.000	0.667	0.750	0.917	0.553	0.658	0.868	0.357	0.417	0.458	0.202	0.254	0.280	0.569	0.644	0.658	0.471	0.521	0.529	0.828	0.982	1.000	0.184	0.245	0.253
A₇	0.468	0.519	0.606	0.600	0.620	0.733	0.702	0.833	0.965	0.779	0.852	0.919	0.800	0.857	0.943	0.700	0.783	0.950	0.579	0.684	0.921	0.588	0.688	0.729	0.445	0.557	0.631	0.842	0.941	0.955	0.794	0.876	0.883	0.649	0.974	1.000	0.390	0.519	0.535
A₈	0.379	0.428	0.455	0.600	0.627	0.747	0.658	0.759	0.868	0.537	0.598	0.644	0.800	0.857	0.943	0.567	0.667	0.767	0.447	0.579	0.721	0.725	0.808	0.850	0.465	0.557	0.597	0.545	0.644	0.658	0.670	0.744	0.752	0.813	0.976	1.000	0.211	0.293	0.301
A₉	0.512	0.553	0.609	0.787	0.807	1.000	0.570	0.658	0.746	0.830	0.934	1.000	0.857	0.943	1.000	0.500	0.600	0.800	0.500	0.632	0.774	0.882	0.940	0.992	0.622	0.771	0.860	0.470	0.559	0.569	0.931	0.993	1.000	0.257	0.259	0.277	0.311	0.415	0.427
A₁₀	0.401	0.430	0.860	0.620	0.633	0.620	0.746	0.789	0.882	0.710	0.796	0.860	0.629	0.700	0.814	0.667	0.783	0.883	0.684	0.800	0.995	0.651	0.729	0.771	0.707	0.829	0.891	0.767	0.907	0.920	0.744	0.819	0.826	0.806	0.968	1.000	0.430	0.559	0.573
A₁₁	0.246	0.272	0.324	0.220	0.233	0.367	0.614	0.702	0.798	0.505	0.563	0.621	0.560	0.591	0.669	0.433	0.583	0.660	0.368	0.447	0.684	0.483	0.594	0.625	0.471	0.597	0.660	0.718	0.871	0.881	0.596	0.670	0.677	0.825	0.971	1.000	0.418	0.528	0.540
A₁₂	0.846	0.923	1.000	0.300	0.313	0.453	0.614	0.667	0.763	0.600	0.692	0.785	0.814	0.866	0.943	0.467	0.600	0.667	0.500	0.579	0.737	0.420	0.496	0.538	0.482	0.620	0.688	0.807	0.917	0.927	0.769	0.868	0.876	0.635	0.923	0.958	0.217	0.318	0.332
A₁₃	0.749	0.813	0.889	0.253	0.267	0.493	0.636	0.737	0.829	0.362	0.419	0.495	0.629	0.726	0.820	0.567	0.667	0.767	0.447	0.526	0.684	0.462	0.563	0.604	0.408	0.517	0.571	0.817	0.917	0.927	0.794	0.940	0.948	0.857	0.971	1.000	0.229	0.339	0.347
A₁₄	0.540	0.600	0.696	0.180	0.200	0.400	0.614	0.667	0.763	0.180	0.245	0.320	0.500	0.571	0.629	0.567	0.667	0.767	0.389	0.474	0.789	0.231	0.292	0.350	0.180	0.231	0.283	0.832	0.982	0.990	0.732	0.794	0.801	0.450	0.630	0.648	0.270	0.360	0.368
A₁₅	0.196	0.235	0.284	0.147	0.167	0.287	0.614	0.668	0.764	0.381	0.425	0.475	0.343	0.429	0.486	0.700	0.780	0.910	0.447	0.579	0.789	0.483	0.567	0.623	0.304	0.356	0.396	0.520	0.688	0.703	0.434	0.496	0.504	0.697	0.843	0.862	0.191	0.279	0.285

Table 9. Normalized decision matrix of weights.

	C₁			C₂			C₃			C₄			C₅			C₆			C₇			C₈			C₉			C₁₀			C₁₁			C₁₂			C₁₃
A₁	0.007	0.013	0.026	0.033	0.058	0.138	0.038	0.074	0.134	0.011	0.018	0.034	0.045	0.087	0.150	0.017	0.029	0.054	0.003	0.006	0.013	0.024	0.042	0.070	0.012	0.024	0.047	0.034	0.063	0.100	0.024	0.045	0.073	0.010	0.019	0.031	0.008	0.017	0.026
A₂	0.011	0.019	0.036	0.051	0.089	0.188	0.043	0.075	0.136	0.020	0.033	0.056	0.046	0.088	0.153	0.020	0.033	0.058	0.004	0.007	0.015	0.039	0.066	0.111	0.031	0.055	0.100	0.057	0.096	0.150	0.041	0.075	0.123	0.007	0.013	0.022	0.011	0.020	0.031
A₃	0.004	0.008	0.016	0.022	0.038	0.128	0.033	0.063	0.117	0.007	0.011	0.021	0.046	0.088	0.153	0.017	0.026	0.050	0.003	0.005	0.011	0.020	0.037	0.063	0.010	0.019	0.037	0.058	0.097	0.153	0.053	0.094	0.154	0.003	0.006	0.011	0.004	0.008	0.012
A₄	0.004	0.007	0.012	0.026	0.045	0.084	0.033	0.063	0.117	0.004	0.007	0.014	0.056	0.099	0.160	0.017	0.029	0.054	0.004	0.006	0.013	0.020	0.037	0.063	0.004	0.008	0.016	0.041	0.075	0.119	0.045	0.081	0.132	0.020	0.037	0.057	0.003	0.005	0.008
A₅	0.014	0.026	0.046	0.079	0.160	0.298	0.045	0.085	0.153	0.018	0.031	0.052	0.044	0.072	0.126	0.023	0.037	0.060	0.004	0.006	0.013	0.060	0.100	0.161	0.019	0.036	0.037	0.038	0.070	0.111	0.042	0.073	0.119	0.021	0.037	0.057	0.005	0.010	0.015
A₆	0.005	0.009	0.018	0.028	0.051	0.126	0.040	0.074	0.134	0.007	0.012	0.022	0.067	0.115	0.187	0.018	0.030	0.055	0.004	0.007	0.013	0.024	0.043	0.074	0.008	0.015	0.028	0.036	0.063	0.100	0.029	0.051	0.084	0.021	0.037	0.057	0.004	0.009	0.014
A₇	0.012	0.020	0.040	0.079	0.136	0.252	0.040	0.078	0.148	0.023	0.037	0.063	0.063	0.104	0.176	0.019	0.031	0.057	0.004	0.007	0.014	0.039	0.071	0.117	0.017	0.033	0.063	0.053	0.092	0.146	0.048	0.085	0.140	0.016	0.036	0.057	0.009	0.019	0.030
A₈	0.009	0.017	0.030	0.079	0.137	0.257	0.038	0.071	0.133	0.016	0.026	0.044	0.063	0.104	0.176	0.016	0.026	0.046	0.003	0.006	0.011	0.048	0.084	0.137	0.018	0.033	0.059	0.034	0.063	0.100	0.041	0.073	0.119	0.021	0.036	0.057	0.005	0.011	0.017
A₉	0.013	0.022	0.040	0.104	0.176	0.344	0.033	0.062	0.114	0.024	0.041	0.069	0.067	0.115	0.187	0.014	0.024	0.048	0.004	0.006	0.012	0.059	0.097	0.160	0.024	0.046	0.086	0.030	0.055	0.087	0.056	0.097	0.158	0.007	0.010	0.016	0.007	0.015	0.024
A₁₀	0.010	0.017	0.056	0.082	0.138	0.213	0.043	0.074	0.135	0.021	0.035	0.059	0.049	0.085	0.152	0.018	0.031	0.053	0.005	0.008	0.015	0.044	0.075	0.124	0.027	0.050	0.089	0.048	0.089	0.140	0.045	0.080	0.131	0.020	0.036	0.057	0.010	0.021	0.032
A₁₁	0.007	0.012	0.024	0.029	0.051	0.126	0.035	0.066	0.122	0.015	0.025	0.043	0.044	0.072	0.125	0.012	0.023	0.040	0.003	0.005	0.010	0.032	0.061	0.101	0.018	0.036	0.066	0.045	0.085	0.134	0.036	0.065	0.107	0.024	0.041	0.064	0.009	0.017	0.027
A₁₂	0.022	0.038	0.068	0.040	0.069	0.156	0.035	0.063	0.117	0.017	0.030	0.054	0.064	0.105	0.176	0.013	0.024	0.040	0.004	0.006	0.011	0.028	0.051	0.087	0.018	0.037	0.069	0.051	0.090	0.141	0.047	0.085	0.138	0.017	0.036	0.057	0.006	0.011	0.018
A₁₃	0.019	0.032	0.058	0.033	0.058	0.170	0.037	0.069	0.127	0.011	0.018	0.034	0.049	0.088	0.153	0.016	0.026	0.046	0.003	0.005	0.010	0.031	0.058	0.097	0.016	0.031	0.057	0.051	0.090	0.141	0.048	0.092	0.150	0.022	0.036	0.057	0.005	0.012	0.019
A₁₄	0.013	0.024	0.045	0.024	0.044	0.138	0.035	0.063	0.117	0.005	0.011	0.022	0.039	0.070	0.118	0.016	0.026	0.046	0.003	0.005	0.012	0.015	0.030	0.056	0.007	0.014	0.028	0.052	0.096	0.151	0.044	0.078	0.127	0.011	0.023	0.037	0.006	0.013	0.020
A₁₅	0.005	0.009	0.019	0.019	0.036	0.099	0.035	0.063	0.117	0.011	0.019	0.033	0.027	0.052	0.091	0.019	0.031	0.055	0.003	0.006	0.012	0.032	0.059	0.100	0.012	0.021	0.039	0.033	0.068	0.107	0.026	0.048	0.080	0.018	0.031	0.049	0.004	0.010	0.016

Data are normalized to eliminate anomalies with different units of measure. The normalized fuzzy decision matrix is given by Equation (12).

The elements V_i j∀ i, j are normalized fuzzy triangular positive numbers and their values belong to the closed interval [1, 0]. Then, we can define the fuzzy positive ideal solution (FPIS, A⁺) and the fuzzy negative ideal solution (FNIS, A⁻) as and for the criteria of profit characters and and for the criteria of character.

In our problem, the criteria C₁, C₄, C₁₂, and C₁₃ are the criteria to be minimized and the others to be maximized. For the next step, the distance for each alternative D^∗ and D⁻ is computed by Equations (17) and (18).

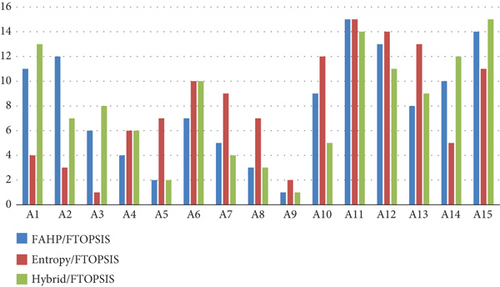
The calculation of closeness coefficient Cc_i, used to classify the alternatives for each alternative i, is found by Equation (19). Table 10 compares the evaluation of 15 alternatives (A₁A₁ to A₁₅A₁₅) using three methods: FAHP/FTOPSIS, entropy/FTOPSIS, and UNI FAHP–entropy/FTOPSIS. Each method evaluates alternatives based on three criteria: D⁻ (distance from the ideal solution), D⁺ (distance from the anti-ideal solution), and Cc_i (closeness coefficient), followed by a ranking, and with data illustration shown in Figure 4.

Table 10. Rankings yielded by three methods.

	D⁻	D⁺	Cc_i	Rank	D⁻	D⁺	Cc_i	Rank	D⁻	D⁺	Cc_i	Rank
	FAHP/FTOPSIS				Entropy/FTOPSIS				Hybrid/FTOPSIS
A₁	5.235	7.807	0.4014	11	4.887	8.117	0.3758	4	5.174	7.831	0.3978	13
A₂	5.232	7.819	0.4009	12	4.902	8.101	0.3770	3	5.241	7.763	0.4030	7
A₃	5.305	7.737	0.4068	6	5.035	7.971	0.3871	1	5.240	7.771	0.4027	8
A₄	5.323	7.719	0.4081	4	4.838	8.170	0.3719	6	5.258	7.757	0.4040	6
A₅	5.371	7.678	0.4116	2	4.829	8.177	0.3713	7	5.420	7.587	0.4167	2
A₆	5.294	7.744	0.4060	7	4.798	8.207	0.3689	10	5.208	7.798	0.4004	10
A₇	5.325	7.729	0.4079	5	4.806	8.202	0.3695	9	5.354	7.650	0.4117	4
A₈	5.345	7.703	0.4096	3	4.828	8.175	0.3713	7	5.376	7.627	0.4135	3
A₉	5.382	7.679	0.4121	1	5.025	7.978	0.3864	2	5.447	7.559	0.4188	1
A₁₀	5.250	7.800	0.4023	9	4.759	8.247	0.3659	12	5.315	7.688	0.4088	5
A₁₁	5.168	7.876	0.3962	15	4.685	8.320	0.3603	15	5.161	7.845	0.3968	14
A₁₂	5.206	7.843	0.3989	13	4.705	8.304	0.3616	14	5.206	7.800	0.4003	11
A₁₃	5.252	7.799	0.4024	8	4.735	8.271	0.3641	13	5.228	7.784	0.4018	9
A₁₄	5.246	7.796	0.4022	10	4,866	8.142	0.3741	5	5.199	7.813	0.3995	12
A₁₅	5.194	7.842	0.3984	14	4.794	8.210	0.3687	11	5.157	7.849	0.3965	15

4. Sensitivity Analysis

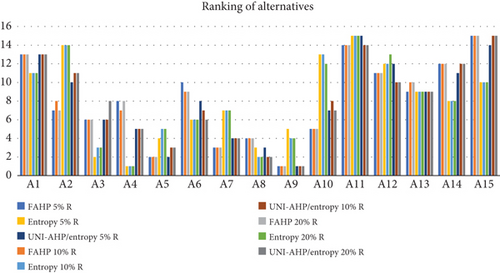
In this sensitivity study, criteria C₂ (internal fuel capacity), C₅ (rate of climb), and C₁₀ (range of action) were specifically chosen for modification because they represent critical operational performance factors in fighter aircraft selection and have a substantial influence on mission effectiveness. C₂ (internal fuel capacity) directly affects the aircraft’s endurance and autonomy without reliance on external fuel tanks, crucial for long-range operations and combat sustainability. C₅ (rate of climb) measures how quickly an aircraft can gain altitude, which is vital for air superiority missions, evasion maneuvers, and engagement flexibility; thus, it is a key tactical performance indicator. C₁₀ (range of action) defines the maximum operational distance between takeoff and landing, directly influencing the strategic deployment and reach of air operations. Moreover, these criteria showed relatively high weight values in the original FAHP, entropy, and UNI methods, indicating their strong impact on final rankings. By modifying these influential criteria, we can meaningfully assess the stability and robustness of the decision model under realistic operational uncertainties, where slight changes in key performance attributes could significantly affect procurement outcomes. Therefore, selecting C₂, C₅, and C₁₀ ensures that the sensitivity analysis remains both practically relevant and analytically insightful. The sensitivity analysis compares three methodologies—FAHP, entropy, and UNI—evaluating the robustness of rankings for 15 alternatives under parameter changes of 5%, 10%, and 20%. FAHP, relying on expert judgment, shows high stability across changes; entropy, an objective method based on data dispersion, displays greater volatility, especially for midtier alternatives, while UNI blends both approaches, offering moderate sensitivity. Alternatives A₉, A₅, and A₈ consistently rank among the top across all methods and scenarios, while A₁₁ and A₁₅ consistently perform poorly, demonstrating consensus at the extremes. Midtier alternatives like A₃ and A₁₀ show noticeable variability, especially under entropy, reflecting methodological influence. FAHP rankings remain largely stable, entropy rankings shift more with larger changes, and UNI rankings experience minor fluctuations. The findings highlight that decision-makers can confidently select robust options like A₉ and A₅ but should be cautious with midranked alternatives whose performance varies depending on the method. Entropy, while objective, may require validation through FAHP or UNI due to its greater sensitivity to data changes. The study also notes limitations, such as the limited range of change magnitudes tested and the assumption of equal criterion importance, suggesting that future work could explore hybrid methods and finer parameter variations. Overall, the results emphasize that method selection and sensitivity awareness are critical for reliable decision-making. The sensitivity analysis results are shows in Table 11, while Figure 5 shows ranking of alternatives in the sensitivity study.

Table 11. Sensitivity analysis results.

	5%		10%		20%		5%		10%		20%		5%		10%		20%
	FAHP						Entropy						UNI
	Cc_i	R	Cc_i	R	Cc_i	R	Cc_i	R	Cc_i	R	Cc_i	R	Cc_i	R	Cc_i	R	Cc_i	R
A₁	0.4110	13	0.4098	13	0.4106	13	0.3849	11	0.3861	11	0.3861	11	0.3920	13	0.3964	13	0.3972	13
A₂	0.4174	7	0.4154	8	0.4164	7	0.3821	14	0.3835	14	0.3836	14	0.3937	10	0.3983	11	0.3993	11
A₃	0.4186	6	0.4165	6	0.4173	6	0.3949	2	0.3962	3	0.3962	3	0.3970	6	0.4015	6	0.4024	8
A₄	0.4170	8	0.4155	7	0.4164	8	0.3973	1	0.3986	1	0.3986	1	0.3982	5	0.4032	5	0.4040	5
A₅	0.4236	2	0.4222	2	0.4234	2	0.3936	4	0.3949	5	0.3953	5	0.4027	2	0,4068	3	0.4079	3
A₆	0.4145	10	0.4135	9	0.4144	9	0.3932	6	0.3947	6	0.3946	6	0.3957	8	0.4015	7	0.4024	6
A₇	0.4232	3	0.4215	3	0.4228	3	0.3881	7	0.3897	7	0.3900	7	0.3992	4	0.4048	4	0.4061	4
A₈	0.4216	4	0.4206	4	0.4218	4	0.3946	3	0.3962	2	0.3964	2	0.4017	3	0.4072	2	0.4084	2
A₉	0.4267	1	0.4260	1	0.4273	1	0.3936	5	0.3953	4	0.3956	4	0.4036	1	0.4097	1	0.4111	1
A₁₀	0.4189	5	0.4173	5	0.4185	5	0.3837	13	0.3852	13	0.3855	12	0.3965	7	0.4012	8	0.4024	7
A₁₁	0.4094	14	0.4077	14	0.4085	14	0.3799	15	0.3811	15	0.3811	15	0.3908	15	0.3946	14	0.3954	14
A₁₂	0.4134	11	0,4117	11	0.4127	11	0.3839	12	0.3854	12	0.3853	13	0.3932	12	0.3987	10	0.3997	10
A₁₃	0.4153	9	0.4134	10	0.4143	10	0.3861	9	0.3874	9	0.3875	9	0.3946	9	0.3992	9	0.4001	9
A₁₄	0.4129	12	0.4108	12	0.4116	12	0.3865	8	0.3876	8	0.3876	8	0.3932	11	0.3968	12	0.3976	12
A₁₅	0.4077	15	0.4062	15	0.4068	15	0.3859	10	0.3867	10	0.3868	10	0.3919	14	0.3946	15	0.3951	15

5. Discussion and Conclusion

The table showcases the outcomes of three distinct MCDM methods: FAHP/FTOPSIS, entropy/FTOPSIS, and hybrid/FTOPSIS. Each method assesses 15 alternatives (A₁ to A₁₅) by calculating their distances to the ideal solution (D⁺ and D⁻) and their closeness coefficient (Cc_i), which determines their rankings. In the FAHP/FTOPSIS results, A₉, A₅, and A₈ emerge as the top three alternatives, with A₉ achieving the highest Cc_i value of 0.4121, while A₁₁, A₁₅, and A₁₂ rank at the bottom. The Cc_i values in this method range narrowly from 0.3962 to 0.4121, indicating relatively close performance among the alternatives. In the entropy/FTOPSIS results, A₃, A₉, and A₂ are the top performers, with A₃ having the highest Cc_i value of 0.3871. A₉, which was the top alternative in FAHP/FTOPSIS, ranks second here, and A₁₁, A₁₂, and A₁₅ remain the least preferred. The Cc_i values in this method range from 0.3603 to 0.3871, showing an even narrower spread. For hybrid/FTOPSIS, A₉, A₅, and A₈ again dominate the top ranks, with A₉ achieving the highest Cc_i value of 0.4188, while A₁₅, A₁₁, and A₁ are the least favorable. The Cc_i values here range from 0.3965 to 0.4188, indicating slightly more differentiation among the alternatives compared to the other methods.

A comparative analysis reveals that A₉ consistently ranks as the top performer across all three methods, demonstrating its robustness as the best alternative, while A₅ and A₈ also perform well, consistently appearing in the top three. On the other hand, A₁₁ and A₁₅ are consistently ranked as the least favorable alternatives, regardless of the method used. However, there is variability in the middle ranks, as seen with A₃, which ranks sixth in FAHP/FTOPSIS but jumps to first in entropy/FTOPSIS, highlighting that the choice of MCDM method can influence the ranking of midtier alternatives.

In conclusion, A₉ is the best performing alternative across all methods, making it the most reliable choice, while A₁₁ and A₁₅ are the least favorable. The sensitivity of midtier alternatives to the method used suggests that decision-makers should consider multiple approaches or conduct further analysis when evaluating closely ranked options. Overall, the results emphasize the importance of selecting an appropriate MCDM method and considering the consistency of rankings across different approaches to ensure informed and robust decision-making.

6. Conclusion

This study presents an extensive and systematic approach to selecting a fourth-generation fighter aircraft for the Algerian Air Force based on a hybrid MCDM procedure integrating FAHP, Shannon entropy, and fuzzy TOPSIS. The methodology overcomes the subjectivity, imprecision, and complexity in defense procurement by integrating subjective expert judgment and objective information to enable a balanced consideration of technical, operational, and strategic factors. By employing fuzzy logic and triangular fuzzy numbers, the model enhances flexibility, transparency, and adherence to real-world decision-making constraints. Coupling FAHP for calculating the weights and entropy for weighting assignments and subsequently fuzzy TOPSIS to rank the alternatives is a robust flexible approach that minimizes the biases of single techniques. Fifteen fighter jets were compared based on 13 features—cost, internal fuel, maximum height, climb rate, and action range—selecting the SU-34 as top-ranked alternative in FAHP and the F-16 in entropy, with low score differences demonstrating the model’s precision and alternatives’ competitiveness. Sensitivity analysis also complements the model’s robustness since top performers (e.g., A₉, A₅, and A₈) are stable across weighting variations in significant criteria (C₂, C₅, and C₁₀), whereas middle-ranked options are volatile, emphasizing the importance of balanced evaluation. The study points out the effect of method selection in MCDM: FAHP provides consistent rankings with the expert’s judgment, entropy introduces variability depending on data dispersal, and the FAHP–entropy approach combines into a balanced compromise. In the future, other studies could expand the scope of application of the framework by incorporating dimensions such as sustainability, maintenance cost, or innovation (such as stealth or electronic warfare) and extend its application to fifth-generation aircraft or unmanned platforms. Methodological advances could include hybridization with other MCDM methods (such as VIKOR, PROMETHEE, and ELECTRE) or machine learning integration for real-time data dynamic updation of rankings. Validation by broader panels of experts, simulations, or consultation with defense agencies is also recommended to increase operational relevance. The model demonstrates flexibility to larger defense procurement environments, naval platforms, missile platforms, or land platforms, and comparative cross-country analysis can further enhance strategic knowledge. Ultimately, this work has significant policy implications by enabling open, data-driven defense acquisition policy. It contributes to the body of academic work on MCDM and provides a scalable, practical, and robust decision support tool that strikes a balance between objectivity and subjectivity. The proposed hybrid model thus provides a standard for future application and research in military procurement and other complicated decision-making environments.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this manuscript.

Acknowledgments

We would like to thank Tarek Berghout for his valuable instructions during the revision stage including his help in conceptualization and methodology, reading, writing, and editing of both draft and revised paper.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Kiracı K. and Akan E., Aircraft Selection by Applying AHP and TOPSIS in Interval Type-2 Fuzzy Sets, Journal of Air Transport Management. (2020) 89, 101924, https://doi.org/10.1016/j.jairtraman.2020.101924, 32989347.
10.1016/j.jairtraman.2020.101924
PubMed Web of Science® Google Scholar
2 Mon D.-L., Cheng C.-H., and Lin J.-C., Evaluating Weapon System Using Fuzzy Analytic Hierarchy Process Based on Entropy Weight, Fuzzy Sets and Systems. (1994) 62, no. 2, 127–134, https://doi.org/10.1016/0165-0114(94)90052-3, 2-s2.0-38149147739.
10.1016/0165-0114(94)90052-3
Web of Science® Google Scholar
3 Dožić S. and Kalić M., Comparison of Two MCDM Methodologies in Aircraft Type Selection Problem, Transportation Research Procedia. (2015) 10, 910–919, https://doi.org/10.1016/j.trpro.2015.09.044, 2-s2.0-84959338954.
10.1016/j.trpro.2015.09.044
Google Scholar
4 Ali Y., Asghar A., Muhammad N., and Salman A., Selection of a Fighter Aircraft to Improve the Effectiveness of Air Combat in the War on Terror: Pakistan air Force–A Case in Point, International Journal of the Analytic Hierarchy Process. (2017) 9, no. 2, https://doi.org/10.13033/ijahp.v9i2.489.
10.13033/ijahp.v9i2.489
Google Scholar
5 Prabowo L. P. and Zagloel Y. M., Aircraft Selection for Cargo Purposes in Air Charter Company Using the Fuzzy AHP -- TOPSIS Method, Proceedings of the 5th International Conference in Industrial and Mechanical Engineering and Operations Management (IMEOM). (2022) https://doi.org/10.46254/BD05.20220140.
10.46254/BD05.20220140
Google Scholar
6 Ardil C., Fighter Aircraft Selection Using Neutrosophic Multiple Criteria Decision Making Analysis, International Journal of Computational Systems Engineering. (2022) 16, no. 1, 5–9.
Google Scholar
7 Maêda S. M., Costa I. P., Castro Junior M. A., Fávero L. P., Costa A. P., Corriça J. V., Gomes C. F., and Santos M. D., Multi-Criteria Analysis Applied to Aircraft Selection by Brazilian Navy, Production. (2021) 31, https://doi.org/10.1590/0103-6513.20210011.
10.1590/0103-6513.20210011
Google Scholar
8 Kurnaz S., Özdağoğlu A., and Keleş M. K., Method of Evaluation of Military Helicopter Pilot Selection Criteria: A Novel Grey SWARA Approach, Aviation. (2023) 27, no. 1, 27–35, https://doi.org/10.3846/aviation.2023.18596.
10.3846/aviation.2023.18596
Web of Science® Google Scholar
9 Deveci M., Çiftçi M. E., Isik M., Pamucar D., Wen X., Chin T., and Kadry S., Aircraft Type Selection Using Fuzzy Trigonometric Based OPA and RAFSI Model, Information Sciences. (2024) 673, 120688, https://doi.org/10.1016/j.ins.2024.120688.
10.1016/j.ins.2024.120688
Web of Science® Google Scholar
10 Arı E. and Dursun M., An Integrated Bayesian Best–Worst Method and Consensus-Based Intuitionistic Fuzzy Evaluation Based on Distance From Average Solution Approach for Evaluating Alternative Aircraft Models From a Sustainability Perspective, Symmetry. (2024) 16, no. 8, https://doi.org/10.3390/sym16081086.
10.3390/sym16081086
PubMed Web of Science® Google Scholar
11 Dwivedi P. P. and Sharma D. K., Selection of Combat Aircraft by Using Shannon Entropy and VIKOR Method, Defence Science Journal. (2023) 73, no. 4, 411–419, https://doi.org/10.14429/dsj.73.17996.
10.14429/dsj.73.17996
Web of Science® Google Scholar
12 van Laarhoven P. J. M. and Pedrycz W., A Fuzzy Extension of Saaty’s Priority Theory, Fuzzy Sets and Systems. (1983) 11, no. 1–3, 229–241, https://doi.org/10.1016/S0165-0114(83)80082-7, 2-s2.0-0020843523.
10.1016/S0165-0114(83)80082-7
Web of Science® Google Scholar
13 Buckley J. J., Fuzzy Hierarchical Analysis, Fuzzy Sets and Systems. (1985) 17, no. 3, 233–247, https://doi.org/10.1016/0165-0114(85)90090-9, 2-s2.0-46549093655.
10.1016/0165-0114(85)90090-9
Web of Science® Google Scholar
14 Chang D.-Y., Applications of the Extent Analysis Method on Fuzzy AHP, European Journal of Operational Research. (1996) 95, no. 3, 649–655, https://doi.org/10.1016/0377-2217(95)00300-2, 2-s2.0-0000672127.
10.1016/0377-2217(95)00300-2
Web of Science® Google Scholar
15 Deng H., Yeh C.-H., and Willis R. J., Inter-Company Comparison Using Modified TOPSIS With Objective Weights, Computers & Operations Research. (2000) 27, no. 10, 963–973, https://doi.org/10.1016/S0305-0548(99)00069-6, 2-s2.0-0034074074.
10.1016/S0305-0548(99)00069-6
Web of Science® Google Scholar
16 Zeleny M., High Technology Management, Human Systems Management. (1982) 3, no. 2, 57–59, https://doi.org/10.3233/HSM-1982-3201, 2-s2.0-0007848714.
10.3233/HSM-1982-3201
Web of Science® Google Scholar
17 Shannon C. E., A Mathematical Theory of Communication, Bell System Technical Journal. (1948) 27, no. 3, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, 2-s2.0-84940644968.
10.1002/j.1538-7305.1948.tb01338.x
Web of Science® Google Scholar
18 Hwang C.-L. and Yoon K., Multiple Attribute Decision Making, 1981, 186, Springer Berlin Heidelberg, https://doi.org/10.1007/978-3-642-48318-9.
10.1007/978-3-642-48318-9
Google Scholar
19 Frederick S., Loewenstein G., and O’donoghue T., Time Discounting and Time Preference: A Critical Review, Journal of Economic Literature. (2002) 40, no. 2, 351–401, https://doi.org/10.1257/002205102320161311.
10.1257/jel.40.2.351
Web of Science® Google Scholar
20 OECD, European Union, and EC-JRC, Handbook on Constructing Composite Indicators: Methodology and User Guide, 2008, OECD Publishing, https://doi.org/10.1787/9789264043466-en.
10.1787/9789264043466-en
Google Scholar
21 Gitelman V., Doveh E., and Hakkert S., Designing a Composite Indicator for Road Safety, Safety Science. (2010) 48, no. 9, 1212–1224, https://doi.org/10.1016/j.ssci.2010.01.011, 2-s2.0-77955086108.
10.1016/j.ssci.2010.01.011
Web of Science® Google Scholar
22 Wegman F. C. M., Commandeur J., Doveh E., Eksler V., Gitelman V., Hakkert S., Lynam D., and Oppe S., SUNflowerNext: Towards A Composite Road Safety Performance Index, 2008. [Online]. Available: https://api.semanticscholar.org/CorpusID:108043116.
Google Scholar

All articles

A Hybrid Fuzzy Multicriteria Decision-Making Approach for Fighter Aircraft Selection: Application to the Algerian Air Force

Abstract

1. Introduction

1.1. Background and Motivation

1.2. Related Work Analysis and Gaps in Research

1.3. Contributions

2. Methodology

2.1. FAHP

2.2. Shannon Entropy

2.3. UNI AHP–Entropy

2.4. Fuzzy TOPSIS

3. Numerical Application

3.1. Determination of Criteria and Alternatives

3.2. Determination of the Weight of the Criteria

3.3. Evaluation of the Alternatives and Determination of the Final Ranking

4. Sensitivity Analysis

5. Discussion and Conclusion

6. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley