1. Introduction

Multipath planning for guided vehicles is a global optimization issue that aims to program an optimal path for each vehicle from a common initial waypoint to a common terminal waypoint, under the condition that specific indicators meet specific constraints. Whether online, offline, optimal, or cooperative, path planning is basically divided into four types of basic methods: intelligent optimization algorithms, including simulated annealing algorithms, genetic algorithms [1–3], particle swarm optimization (PSO) algorithms [4–6], grey wolf algorithm [4], evolutionary algorithm [7], gravitational search algorithm [8], and ant colony algorithm; artificial potential field (APF) method [9]; mathematical-based planning methods, including nonlinear planning algorithms and dynamic planning algorithms; and graphical-based methods, including the Voronoi diagram method [10], rapidly exploring random tree (RRT) and variants, visibility binary tree algorithm, and A ^∗ algorithm [11].

In the literature, there are several proposals for addressing optimal path planning and multipath planning problems. Multipath planning for guided vehicles represents a global optimization challenge, aiming to devise an optimal path for each vehicle as it traverses from a common starting waypoint to a common terminal waypoint, all while ensuring that specific performance indicators satisfy predefined constraints. Path planning, regardless of whether it is conducted online, offline, with an emphasis on optimality, or in a cooperative context, can be comprehensively categorized into four principal types of methodologies.

Intelligent optimization algorithms include simulated annealing algorithms, genetic algorithms [1–3], PSO algorithms [4–6], grey wolf algorithm [4], evolutionary algorithm [7], gravitational search algorithm [8], and ant colony algorithm. Based on Bellman’s optimality principle, a dynamic programming-genetic algorithm (DPGA) [1] is developed. By dividing the entire planning space into multiple sequential stages and applying genetic algorithms for optimization at each stage, the DPGA not only has a higher computational efficiency than the dynamic programming algorithm but also has a higher convergence probability and efficiency than the genetic algorithm. For the delivery problem in chain restaurants, [2] introduces an adaptive genetic algorithm. This algorithm refines traditional crossover and mutation operations by making adaptive adjustments according to the fitness of individuals and the population, thus effectively avoiding local optima. In the UAV/UGV cooperative system, a hybrid path planning algorithm [3] is proposed, which is a mixture of a genetic algorithm for global path planning and a local rolling optimization that constantly optimizes the results of the genetic algorithm. The improved PSO algorithm [4] integrates the grey wolf optimization algorithm [4], chaos theory, and adaptive inertial weights. During the evolutionary process, the grey wolf optimizer sorts particles to identify those with optimal fitness values, which then guide the search of other particles, enhancing the PSO algorithm’s global search ability. The parallel implementation of genetic and PSO algorithms, as studied in [5, 6], improves the real-time performance of UAV route planning. By separately evaluating and evolving waypoints, an evolutionary algorithm for single UAV path planning in complex 3D environments [7] is proposed. This method addresses the challenges of 3D space expansion, path smoothness and safety requirements for fixed-wing UAVs, and the rapid increase in calculation scale due to more obstacles and waypoints. A hybrid strategy based on the gravitational search algorithm for UAV path planning was presented in [8]. This strategy includes an adaptive adjustment mechanism for the gravity constant attenuation factor and the Cauchy mutation strategy. By constructing an objective function considering flight length cost, threat area cost, and turning angle constraints, this method reduces flight risks and generates smoother paths, demonstrating advantages in solution quality, robustness, and constraint-handling capabilities. Although not elaborated in detail in the reviewed literature, ant colony algorithms are an important part of intelligent optimization algorithms for path planning.

In [9], future movement prediction was integrated into the APF method. This innovation enables autonomous ground vehicles (AGVs) to reduce travel route length, improve path smoothness, and avoid local minima, enhancing the overall path-planning performance.

Mathematical-based planning methods consist of nonlinear planning algorithms and dynamic planning algorithms. Although not extensively detailed in the previously reviewed literature, these methods form the fundamental theoretical frameworks for path planning. They often serve as the basis for more complex path-planning strategies, frequently combined with other techniques to achieve optimal or suboptimal path solutions.

Graphical-based methods include the Voronoi diagram method [10], RRT and variants, visibility binary tree algorithm, and A ^∗ algorithm [11] or its special case, Dijkstra algorithm [12]. The A ^∗ algorithm [11] is a well-known heuristic optimal search method. It selects the node with the smallest heuristic function value in the search space for expansion during each iteration. Scholars, both domestic and international, have made numerous improvements to the A ^∗ algorithm, including modifications to the dynamic or optimal weight heuristic function [13, 14], the implementation of an adaptive modifying step [15], integration with the dynamic window method [15], combination with the APF method [16], the use of the potential energy field to more accurately represent the environment [17], the adoption of a bidirectional search strategy [18], the incorporation of reinforcement learning strategies [19], and the utilization of meta-heuristics [20].

In addition to the abovementioned path-planning methods, there are other notable research efforts. For example, a suboptimal path-planning solution based on the game theory framework was proposed in [21].

In the area of multipath planning, which has become a focal point of research among scholars globally, the main goal is to preplan multiple routes and then select an appropriate route according to specific requirements during mission execution. To solve the rendezvous problem of multiple UAVs traveling from different initial waypoints to a common terminal waypoint, [22] proposed a solution based on reaching a consensus among the UAVs regarding the estimated time of arrival at the rendezvous point. This approach, involving velocity control, wandering maneuvers, inter-UAV communication, and the application of lateral accelerations to increase the line-of-sight rate between UAVs on a potential collision course, enables rendezvous while ensuring collision avoidance. Existing multipath planning methods include the evolutionary algorithm based on topological diversity [23], the genetic algorithm using path construction of a binary tree [24], the homotopic path- planning approach for a UAV swarm [25], the multipopulation chaotic grey wolf optimization algorithm [26], the personalized multigroup sparrow search algorithm [27], and the improved PSO [28]. As generalized shortest path algorithms, the k-shortest path algorithms, such as the multilabel algorithm [29] and the k-shortest paths based on A ^∗ (KSPA) algorithm [30], also fall within the category of multipath planning. However, it is important to note that these methods are mainly applicable to vector maps or multigraphs and are not suitable for digital raster or grid maps.

Because the optimal path planning generated by the intelligent optimization algorithm has a random solution, the existing multipath planning algorithms do not share the initial waypoint and terminal waypoint, and avoidance between multipaths is rarely considered in 3D. To overcome these limitations, a guided vehicle multipath planning method based on an improved A ^∗ search algorithm is proposed to realize a saturation attack from preset angles in a manner that obeys a uniform symmetric distribution, which is useful for antisurface target operations and simulations.

We propose the following six assumptions: (a) Guided vehicles can avoid threats by making sharp turns rather than coordinated turns [12]. (b) Considering that the movement of the no-fly zone is relatively static with respect to the flight speed of a guided vehicle, it can be simplified as a known fixed threat. (c) Even if the vehicle’s launching point and target are in the normal maneuvering state, the route planned in this study is effective within a certain time range. If it exceeds the time range, it will be periodically replanned by the vehicle planning system until the launch moment. The planned route is uploaded to the vehicle at the launch moment and is effective during the entire flight phase. (d) Only one vehicle is assigned to a planned path. (e) In order to ensure that the vehicle follows the planned route, the wind speed is required to be no more than 15 m/s, and the sea condition is lower than Level 5.

The remainder of this paper is organized as follows. Section 2 describes the procedure and formulation of the proposed improved algorithm. Section 3 provides the application scenarios and presents the results of simulations that demonstrate the performance of the proposal. Finally, the conclusions of this study is drawn in Section 4.

2. Improved Algorithm

Considering only the motion of the vehicle’s center of mass and ignoring the rotation around the center of mass, a right-handed and inertial simulation coordinate system oxyz is created, whose origin o selects the position of the acquisition radar, x-axis points east, y-axis points north, and z-axis points vertically upwards.

To obtain the space vector and displacement of each waypoint, the waypoint coordinate system OXYZ is set up by translating the simulation coordinate system, whose origin O represents the position of the current waypoint, x-axis points east, y-axis points north, and z-axis points vertically upwards. The grid data of the raster digital map are stored in three m × n matrices $$, $$, and $$, where matrix $$ stores the geographically horizontal coordinates of the j_th column of the grid, matrix $$ stores the geographically vertical coordinates of the i^th row of the grid, and matrix $$ stores the height of the i^th row and j^th column of the grid. The actual geographic coordinates are (a_ij, b_ij, z_ij) = (x_i, y_j, z(x_i, y_j)), corresponding to the grid (i, j, z(i, j)) on the raster digital map. The continuous coordinates of the planned waypoints can be derived from discretized grid points but are not limited to grid points.

2.2. Horizontal Margin Vector

The l^th waypoint vector is $$, whose base unit vector is$$ and the horizontal turning limit angle [7, 12] is θ_horizontal. If the horizontal margin vector shown in Figure 1 is $$, then the upper margin vector $$ and the lower margin vector $$ are derived by solving Equation (2).

$$ ()

where base unit vector rotates θ_horizontal around Z-axis with the same height.

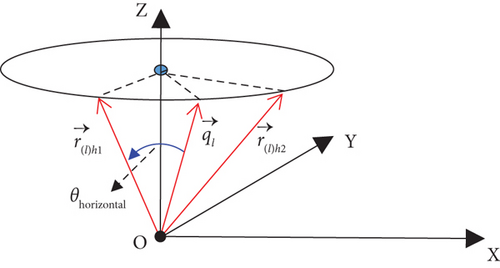
2.3. Vertical Margin Vector

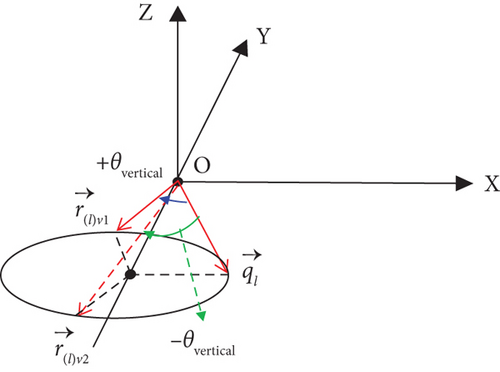
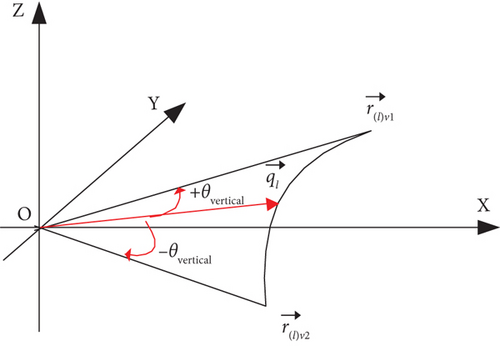
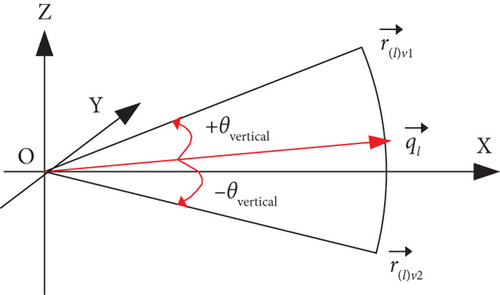
The l^th waypoint vector is $$, whose base unit vector is $$ and the vertical turning limit angle [7, 12] is θ_vertical; if the vertical margin vector is $$, the upper margin vector $$ and the lower margin vector $$ are obtained through three different degrees of freedom modes.

2.3.1. Mode 1

Around the y-axis with a certain horizontal margin vector, the vector direction of the vertical margin vector $$ is rotated θ_vertical and calculated using Equation (3). The model for Mode 1 is illustrated in Figure 2.

$$ ()

where the base unit vector rotates θ_vertical around the Y-axis at the same distance from the XOZ plane. The planned path is relatively jumpy and encounters situations in which obstacles cannot be avoided.

2.3.2. Mode 2

Around O in the XOZ projecting plane with a certain horizontal margin vector, the vector direction of the vertical margin vector $$ is rotated θ_vertical and solved using Equation (4). The model for Mode 2 is illustrated in Figure 3.

$$ ()

where the projection plane of XOZ is unique unless the base unit vector is perpendicular to the XOZ plane. The planned path is relatively smooth with both horizontal and vertical turns.

2.3.3. Mode 3

Around O in the projecting plane of XOY with a certain horizontal margin vector, the vector direction of the vertical margin vector $$ is rotated θ_vertical and solved using Equation (5). The model for Mode 3 is illustrated in Figure 4.

$$ ()

where the projection plane of XOY is unique, unless the base unit vector is perpendicular to the XOY plane. Although it has a strong obstacle-avoiding capability, this path-planning mode produces a relatively jumpy path similar to the model for mode 1, whose movements along the X- and Y-axes are coupled with each other.

2.4. Candidate Subnode Vectors

A spatial region can be constructed by setting the l^th waypoint as the origin from step size h and the horizontal and vertical turning restriction angles, θ_horizontal, and θ_vertical. According to Equations (6)–(9), the spatial region can be divided into 16 equal parts to attain 25 candidate subnode vectors depicted in Figure 5, from which the next waypoint will be selected as the optimal solution without constraining the path to grid edges to find “any-angle” path [31] within the turning angle range.

Based on Equations (2)–(5), the components of the subnode vectors are defined as follows:

$$ ()

Subnode vectors:

$$ ()

Unit subnode vectors:

$$ ()

With step size h, the $$ candidate subnode vector is calculated using Equation (9).

$$ ()

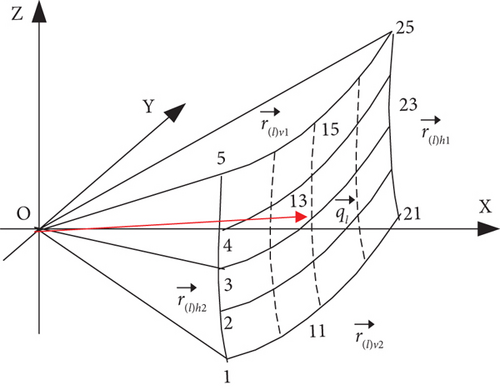
2.5. Subnode Vectors Filtered by Multiple Avoidance Tactics

2.5.1. Terrain Avoidance

Candidate subnode vectors under the Earth’s surface are filtered. Let the candidate subnode vector $$and adjacent digital map data shown in Figure 6 be (x_i−1, y_j−1, z(x_i−1, y_j−1)), (x_i, y_j−1, z(x_i, y_j−1)), (x_i−1, y_j, z(x_i−1, y_j)) and(x_i, y_j, z(x_i, y_j)), $$, and $$; then,

$$ ()

$$ ()

The Earth surface height responding to the candidate subnode $$ is calculated using Equation (12), relying on the bilinear interpolation of the digital map data.

$$ ()

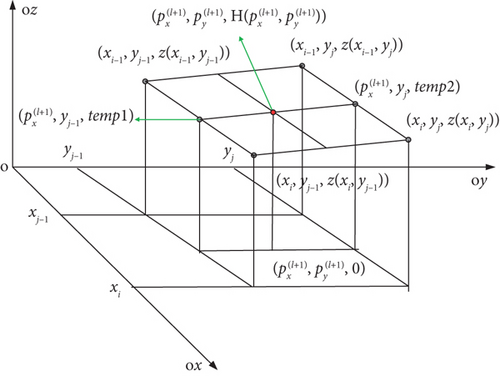
All $$ are deleted [7] from the candidate subnode vector table $$.

In fact, it is necessary to determine that the entire course between the previous waypoint and the candidate subnode to be filtered is above Earth’s surface, but such a computational amount is unacceptable. It is possible to add 1/2, 1/3, and even 1/n equivalent points between the two nodes to judge the feasibility of the entire course. Taking n = 2 as an example, we obtain

$$ ()

According to Equations (10)–(12), $$ can be obtained. All $$ and $$ are deleted from the candidate subnode vector table $$.

2.5.2. No-Fly Zone Avoidance

For the safe concealment of vehicle flights, the no-fly zone is considered as an area centered at (W_i,W_j) with threat radius r according to assumption b.

The complete coordinates corresponding to the grid (i, j, z(i, j)) in the digital map are (xi, yj, z(xi, yj)), and the coordinates corresponding to the center (W_i, W_j) of the no-fly zone are (x_Wi, y_Wj). If ml is the length from point (i, j) to point (W_i, W_j), the altitude of the no-fly zone can be acquired as follows:

$$ ()

Equation (14) is decomposed into Equations (15)–(17). Suppose

$$ ()

Build a discriminant matrix $$ and $$.

$$ ()

$$ ()

The altitude of the no-fly zone is

$$ ()

2.5.3. Horizontal Multipath Collision Avoidance

When planning a multipath, a route with a smaller terminal attack angle is generally planned before that with a larger angle. To avoid the horizontal intersection of two adjacent routes with different terminal attack angles, a route channel with a certain width can be established for a route with a smaller absolute value of the attack angle, and a route with a larger absolute value of the attack angle can be planned outside the route channel to achieve horizontal route avoidance.

• 1.

  Route channel polygon.

Let k waypoint vectors of the planned route i with a smaller absolute value of attack angle successively be $$, $$,…, $$, excluding the initial waypoint vector $$ and the terminal waypoint vector $$, whose coordinates of the xoy plane are (P_i1x, P_i1y),(P_i2x, P_i2y),…,(P_ikx, P_iky). If the width of the route channel is 2d, then (P_i1x, P_i1y + d), (P_i2x, P_i2y + d),…,(P_ikx, P_iky + d), (P_ikx, P_iky − d), (P_{i(k − 1)x}, P_{i(k − 1)y} − d),…,(P_i1x, P_i1y − d), and (P_i1x, P_i1y + d) form the route channel polygon $$.

Given $$, $$, $$, $$

where

$$ ()

$$ ()

$$ ()

$$ ()

• 2.

  Quadrant number vector.

Thus, the quadrant number [32] vector $$ is defined as follows:

$$ ()

where the symbol & represents a logical “and” and q_i1∈{0, 1, 2, 3}.

• 3.

  Cross product vector.

Find the cross product vector $$ of the vectors $$ and $$.

$$ ()

The symbol vector $$ corresponding to the cross product $$ is expressed as

$$ ()

Define the dot product vector $$ of the vectors $$ and $$.

$$ ()

• 4.

  Quarter angle vector.

Define the quarter angle [32] vectors $$, where $$, $$−q_i1 and i = 1, 2, ⋯, 2k.

Therefore, introduce adjusted quarter angle vectors $$ as follows:

$$ ()

• 5.

  Logical criterion.

For any detection point vector $$ on the XOY plane, detect whether it is in the closed-route channel polygon $$ route or on the boundary using Equations (28)–(29).

where the criterion of logical “in” is expressed by

$$ ()

where the criterion of logical “on” is expressed by

$$ ()

After completing the detection, we set the height of the grid points in and on the boundary of the planned route channel as the maximum height of the terrain and no-fly zone.

2.7. Iteration and Convergence

Path plan from initial waypoint:

$$ ()

Path plan from terminal waypoint:

$$ ()

If the condition is not satisfied by Equation (34) or (35), it is necessary to iterate and determine the next waypoint by using the aforementioned five steps. If the condition is satisfied by Equation (34) or (35), the path planning of this route converges and is completed. All routes with different terminal attack angles are path planned in the above manner.

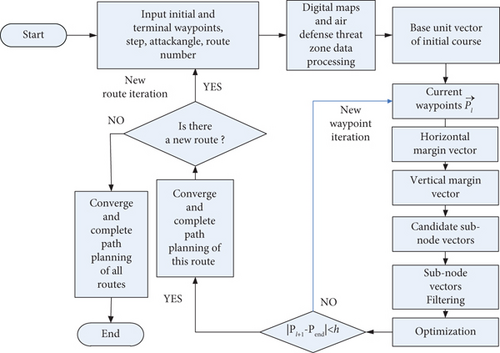
A flowchart of the 3D multipath planning method for guided vehicles using the improved A ^∗ algorithm based on multiple avoidance tactics and terminal attack angles is shown including above 7 steps in Figure 7. And the advantages of the proposed algorithm will be analyzed and verified through the following simulation experiments.

3. Simulation Analysis

Referring to the application scenarios in [33–35], the effectiveness of the proposed method is verified and explored based on two types of typical attack situations and 10 real-world scenarios as shown in Table 1. Among them, Scenarios 1, 3, and 4 are used for the hidden initial waypoint situation without no-fly zone or with five no-fly zones near initial waypoint (islands and reefs) or terminal waypoint on the sea; Scenarios 2, 5, 6, and 7 are used for the hidden terminal waypoint situation without no-fly zone or with five no-fly zones near terminal waypoint (islands and reefs) or in the midway or near initial waypoint on the sea; Scenario 8 is used for algorithm comparison; Scenario 9 as the combination of Scenarios 1 and 4, near initial waypoint (islands and reefs) and near terminal waypoint on the sea; Scenario 10, as the combination of Scenarios 2, 6, and 7, is used for the hidden terminal waypoint situation near initial waypoint and in the midway on the sea and near terminal waypoint (islands and reefs).

3.1. In Hidden Initial Waypoint Situation

The terminal waypoint is located at the grid position (1109, 1069, z(1109, 1069)) at sea, and the initial waypoint is located at the grid position (489, 449, z(489, 449)) near the islands and reefs. Plans 2–8 path for guided vehicles one-to-one in coordinated and stealthy attacks and carry out terrain, no-fly zones, and collision avoidance between multipaths.

Actual digital map parameters for a certain zone: The island sea zone is at the grid position (460–918, 420–838, 1–16), the entire zone is at the grid position (1–1836, 1–1676, 1–16), the accuracy of the grid is 0.09266 km, and the highest elevation is 1.4488 km.

Given that θ_horizontal = θ_vertical = pi/6 rad, waypoint number k ≤ 15, and the basic step size h = 8 km.

3.1.1. Mode 1

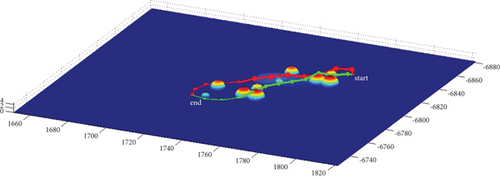
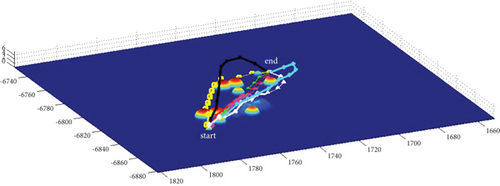
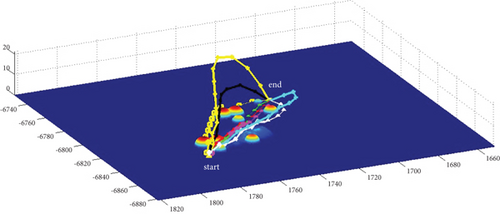
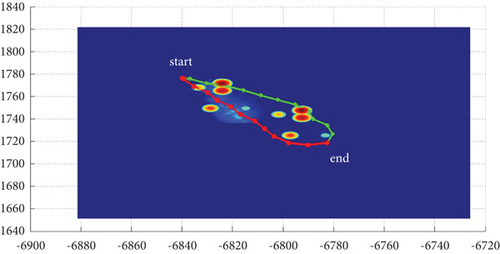
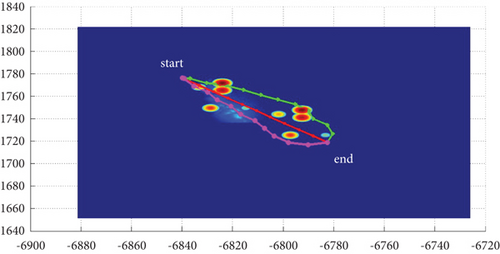
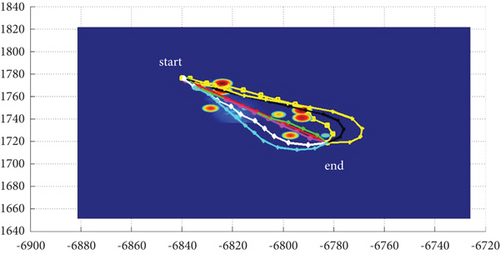
In Scenario 1/9, the azimuth of the reference attacking direction is 3 pi/4 rad, and the multipath planning is shown in Table 2 and Figures 8 and 9. “Start” in all the following figures represents the initial waypoint, and “end” represents the terminal waypoint.

Table 2. Simulation data in Mode 1, Scenario 1/9.

Path count	Attack angle (rad)	Path length (step size) (km)
2-path	-pi/2, pi/2	92.15/91.11, 90.97/90.97
3-path	0, -pi/2, pi/2	83.14/83.14, 92.15/91.11, 90.97/90.97
4-path	-pi/4, pi/4, -pi/2, pi/2	83.30/83.45, 83.14/83.14, 92.15/91.11, 90.97/90.97
5-path	0, -pi/4, pi/4, -pi/2, pi/2	83.14/83.14, 83.30/83.45, 83.14/83.14, 92.15/91.11, 90.97/90.97
6-path	-pi/4, pi/4, -pi/2, pi/2, -2pi/3, 2pi/3	83.30/83.45, 83.14/83.14, 92.15/91.11, 90.97/90.97, 110.81/110.81 (12), 118.48/118.48 (15)
7-path	0, -pi/4, pi/4, -pi/2, pi/2, -2pi/3, 2pi/3	83.14/83.14, 83.30/83.45, 83.14/83.14, 92.15/91.11, 90.97/90.97, 110.81/110.81 (12), 118.48/118.48 (15)
8-path	0, -pi/4, pi/4, -pi/2, pi/2, -2pi/3, 2pi/3, 9pi/10	83.14/83.14, 83.30/83.45, 83.14/83.14, 92.15/91.11, 90.97/90.97, 110.81/110.81 (12), 118.48/118.48 (15), 144.38/144.38 (15)

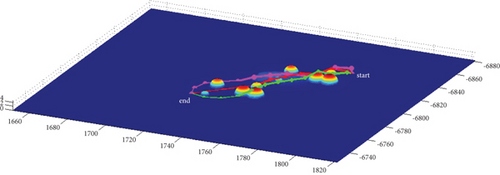
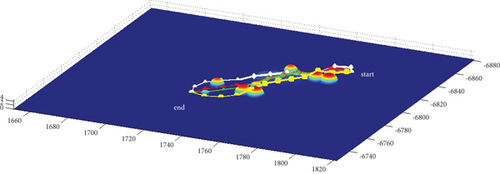
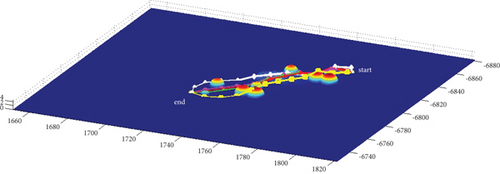
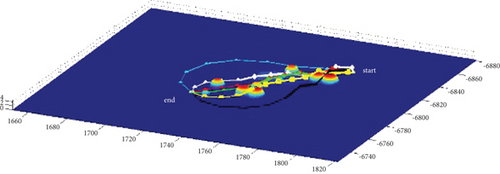
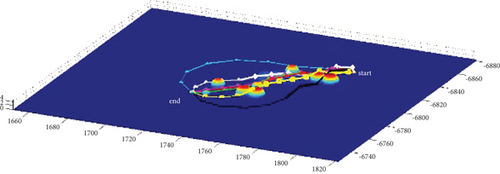
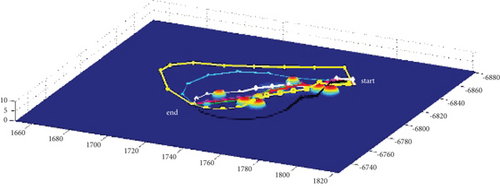
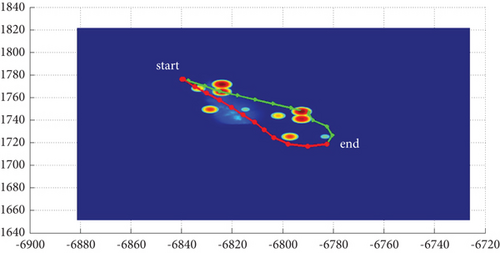
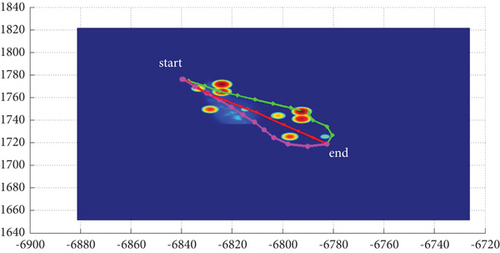
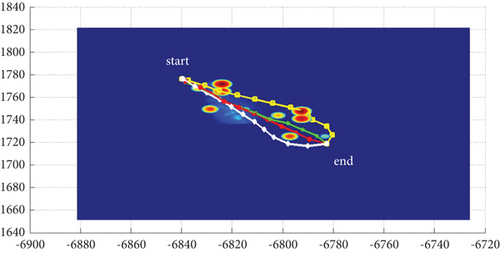
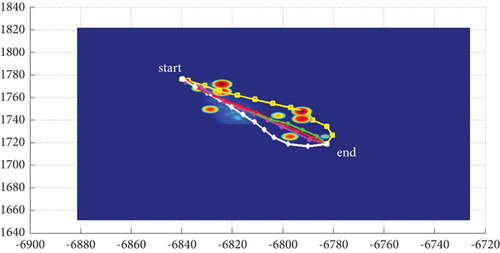
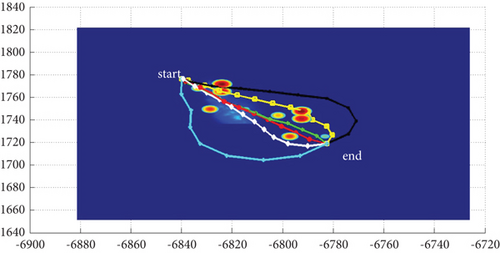
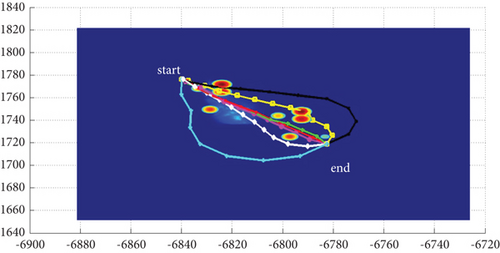
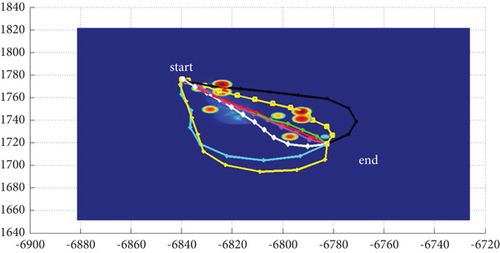
3.1.2. Mode 2

In Scenario 1, the azimuth of the reference attacking direction is 3pi/4 rad, and the multipath planning is shown in Table 3 and Figures 10 and 11.

Table 3. Simulation data in Mode 2—Scenario 1.

Path count	Attack angle (rad)	Path length (h/d ) (km)
2-path	-pi/2, pi/2	101.34, 94.73
3-path	-pi/2, pi/2, -2pi/3	101.34 (d = 10), 94.73, 124.84 (h = 13)
4-path	-pi/2, pi/2, -2pi/3, 2pi/3	101.34 (d = 10), 94.73 (d = 10), 124.84 (h = 13), 107.65 (h = 10)
5-path	-pi/2, pi/2, -2pi/3, 2pi/3, -4pi/5	101.34 (d = 10), 94.73 (d = 10), 124.84 (d = 10, h = 13), 107.65 (h = 10), 156.11 (h = 14)
6-path	-pi/2, pi/2, -2pi/3, 2pi/3, -4pi/5, 4pi/5	101.34 (d = 10), 94.73 (d = 10), 124.84 (d = 10, h = 13), 107.65 (d = 5, h = 10), 156.11 (h = 14), 120.00 (h = 15)
7-path	-pi/2, pi/2, -2pi/3, 2pi/3, -4pi/5, 4pi/5, -9pi/10	101.34 (d = 10), 94.73 (d = 10), 124.84 (d = 10, h = 13), 107.65 (d = 5, h = 10), 156.11 (d = 5, h = 14), 120.00 (h = 15), 172.62 (h = 12)
8-path	-pi/2, pi/2, -2pi/3, 2pi/3, -4pi/5, 4pi/5, -9pi/10, 9pi/10	101.34 (d = 10), 94.73 (d = 10), 124.84 (d = 10, h = 13), 107.65 (d = 5, h = 10), 156.11 (d = 5, h = 14), 120.00 (d = 5, h = 15), 172.62 (h = 12), 136.53 (h = 15)

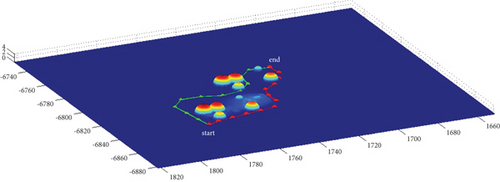
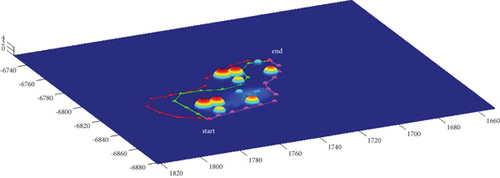
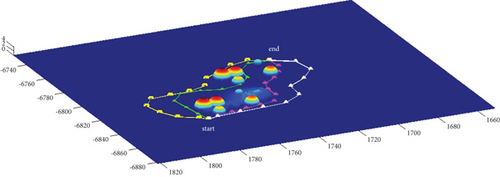
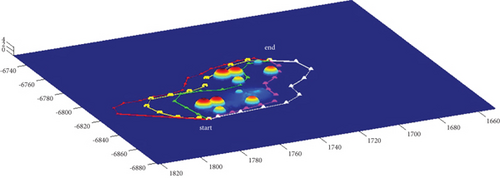
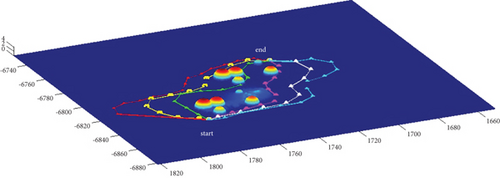
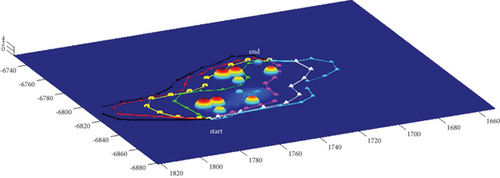
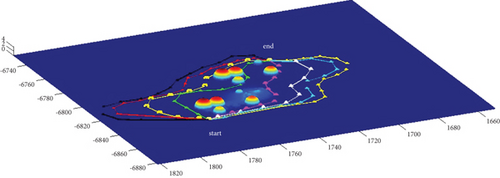
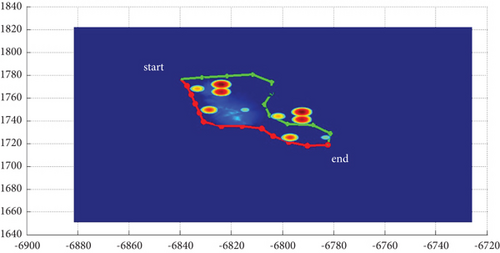
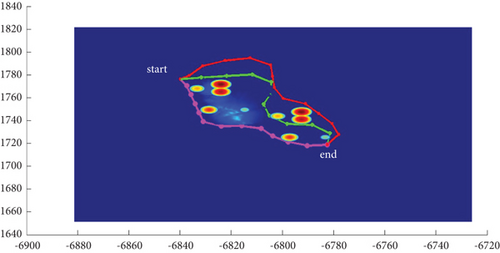
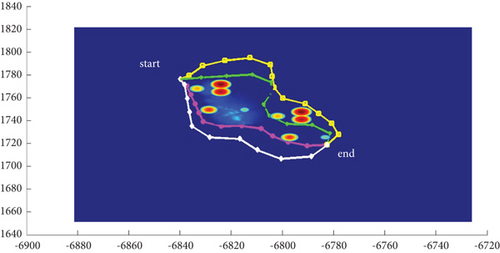
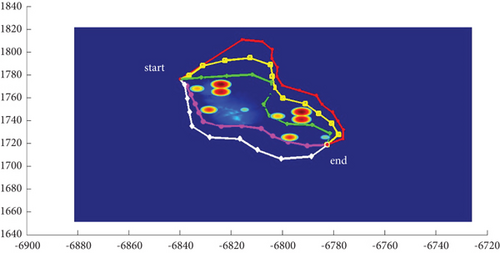
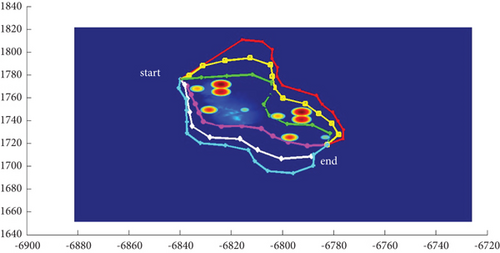
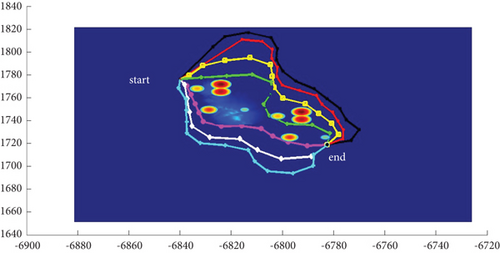
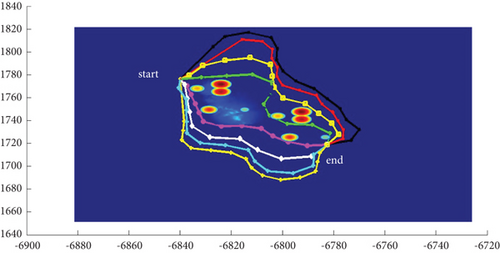
In Scenario 9, the multipath planning is shown in Table 4 and Figures 10 and 11.

Table 4. Simulation data in Mode 2—Scenario 9.

Path count	Attack angle (rad)	Path length (h/d ) (km)
2-path	-5pi/9, 5pi/9	108.37 (h = 10), 94.41
3-path	-5pi/9, 5pi/9, -2pi/3	108.37 (d = 10, h = 10), 94.41, 124.62 (h = 10)
4-path	-5pi/9, 5pi/9, -2pi/3, 2pi/3	108.37 (d = 10, h = 10), 94.41 (d = 10), 124.62 (h = 10), 113.48 (h = 12)
5-path	-5pi/9, 5pi/9, -2pi/3, 2pi/3, -4pi/5	108.37 (d = 10, h = 10), 94.41 (d = 10), 124.62 (d = 10, h = 10), 113.48 (h = 12), 154.19
6-path	-5pi/9, 5pi/9, -2pi/3, 2pi/3, -4pi/5, 4pi/5	108.37 (d = 10, h = 10), 94.41 (d = 10), 124.62 (d = 10, h = 10), 113.48 (d = 5, h = 12), 154.19, 137.91 (h = 10)
7-path	-5pi/9, 5pi/9, -2pi/3, 2pi/3, -4pi/5, 4pi/5, -9pi/10	108.37 (d = 10, h = 10), 94.41 (d = 10), 124.62 (d = 10, h = 10), 113.48 (d = 5, h = 12), 154.19 (d = 5), 137.91 (h = 10), 170.80 (h = 10)
8-path	-5pi/9, 5pi/9, -2pi/3, 2pi/3, -4pi/5, 4pi/5, -9pi/10, 9pi/10	108.37 (d = 10, h = 10), 94.41 (d = 10), 124.62 (d = 10, h = 10), 113.48 (d = 5, h = 12), 154.19 (d = 5), 137.91 (d = 5, h = 10), 170.80 (h = 10), 149.40

3.1.3. Mode 3

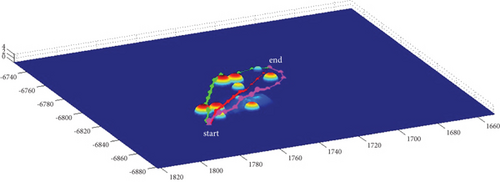
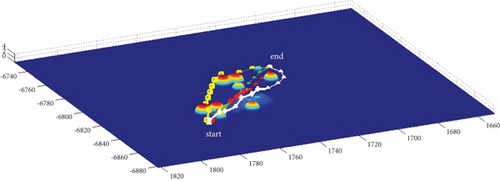
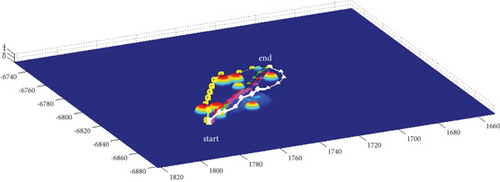
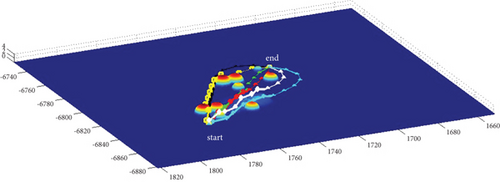
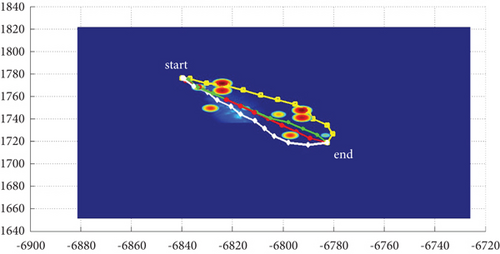
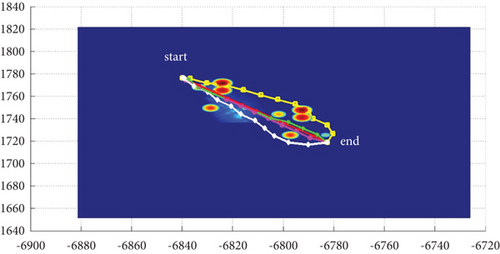
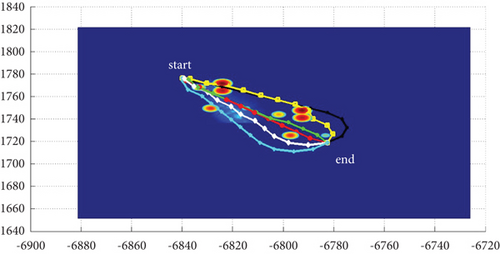
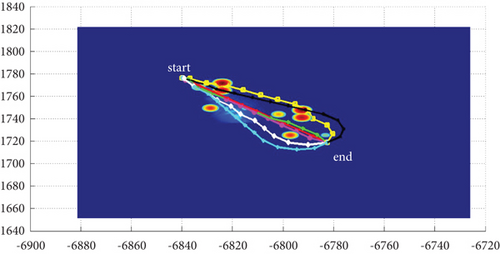
In Scenario 1/9, the azimuth of the reference attacking direction is 3 pi/4 rad, and the multipath planning is shown in Table 5 and Figures 12 and 13.

Table 5. Simulation data in Mode 3, Scenario 1/9.

Path count	Attack angle (rad)	Path length (step size) (km)
2-path	-pi/2, pi/2	90.72/91.47, 90.41/90.41
3-path	0, -pi/2, pi/2	82.44/82.44, 90.72/91.47, 90.41/90.41
4-path	-pi/4, pi/4, -pi/2, pi/2	82.82/83.15, 83.06/83.06, 90.72/91.47, 90.41/90.41
5-path	0, -pi/4, pi/4, -pi/2, pi/2	82.44/82.44, 82.82/83.15, 83.06/83.06, 90.72/91.47, 90.41/90.41
6-path	-pi/4, pi/4, -pi/2, pi/2, -2pi/3, 2pi/3	82.82/83.15, 83.06/83.06, 90.72/91.47, 90.41/90.41, 98.66/98.57, 98.86/98.86
7-path	0, -pi/4, pi/4, -pi/2, pi/2, -2pi/3, 2pi/3	82.44/82.44, 82.82/83.15, 83.06/83.06, 90.72/91.47, 90.41/90.41, 98.66/98.57, 98.86/98.86
8-path	0, -pi/4, pi/4, -pi/2, pi/2, -2pi/3, 2pi/3, -9pi/10	82.44/82.44, 82.82/83.15, 83.06/83.06, 90.72/91.47, 90.41/90.41, 98.66/98.57, 98.86/98.86, 120.48/120.48 (10)

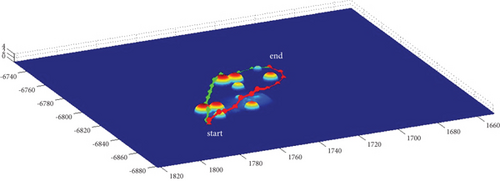
3.2. In Hidden Terminal Waypoint Situation

The terminal waypoint is located at the grid position (489, 449, z(489, 449)) near islands and reefs, and the initial waypoint is located at the grid position (1509, 1469, z(1509, 1469)) on the sea. Plans 2–8 route for guided vehicles one-to-one in coordinated way, perform terrain and no-fly zones, and avoid multiple routes between routes. The parameter settings for actual digital map and no-fly zone, the horizontal turning limit angle θ_horizontal, the vertical turning limit angle θ_vertical, waypoint number, and the basic step size in Scenario 2, Attack Situation 2, are the same as those for Scenario 1, Attack Situation 1.

3.2.1. Mode 1

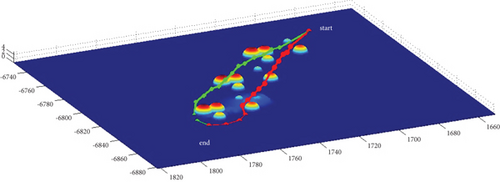
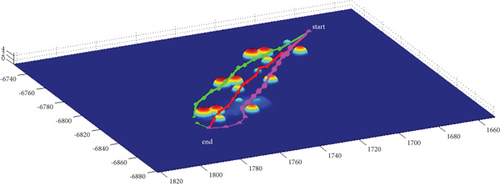
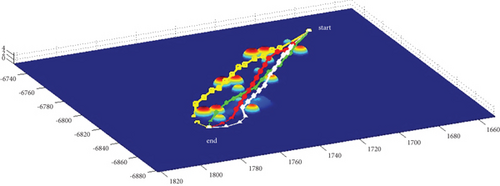
In Scenario 2/10, the azimuth of the reference attacking direction is -pi/4 rad. Each planned path can effectively avoid the no-fly zone and terrain under various constraints, as shown in Table 6 and Figures 14 and 15, respectively.

Table 6. Simulation data in Mode 1, Scenario 2/10.

Path count	Attack angle (rad)	Path length (step size) (km)
2-path	pi/2, -pi/2	141.58/141.58, 140.47/140.93
3-path	0, pi/2, -pi/2	135.19/135.19, 141.58/141.58, 140.47/140.93
4-path	pi/4, -pi/4, pi/2, -pi/2	135.92/135.88, 136.10/136.10, 141.58/141.58, 140.47/140.93
5-path	0, pi/4, -pi/4, -pi/2, pi/2	135.19/135.19, 135.92/135.88, 136.10/136.10, 141.58/141.58, 140.47/140.93
6-path	pi/4, -pi/4, pi/2, -pi/2, 2pi/3, -2pi/3	135.92/135.88, 136.10/136.10, 141.58/141.58, 140.47/140.93, 158.05/158.70 (12), 163.19/163.19 (15)
7-path	0, pi/4, -pi/4, pi/2, -pi/2, 2pi/3, -2pi/3	135.19/135.19, 135.92/135.88, 136.10/136.10, 141.58/141.58, 140.47/140.93, 158.05/158.70 (12), 163.19/163.19 (15)
8-path	0, pi/4, -pi/4, pi/2, -pi/2, 2pi/3, -2pi/3, 9pi/10	135.19/135.19, 135.92/135.88, 136.10/136.10, 141.58/141.58, 140.47/140.93, 158.05/158.70 (12), 163.19/163.19 (15), 175.48/175.98 (12)

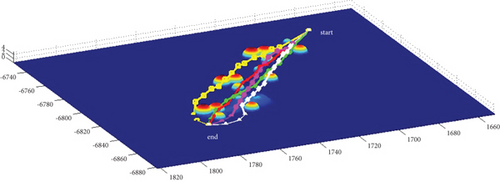
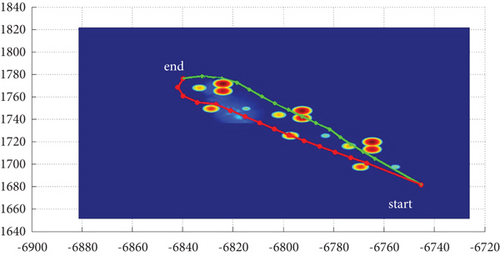
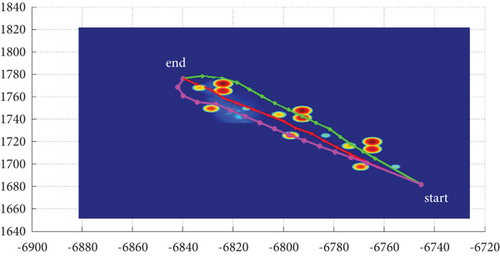
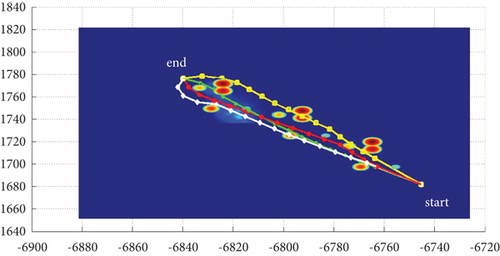
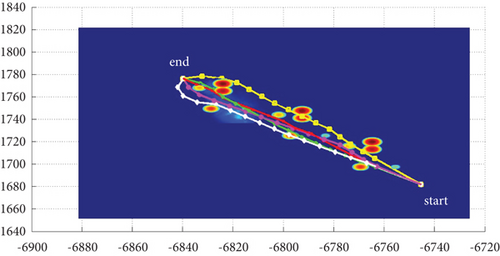
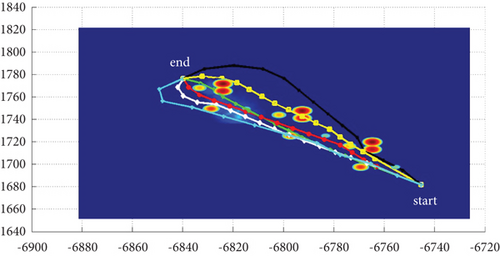
3.2.2. Mode 2

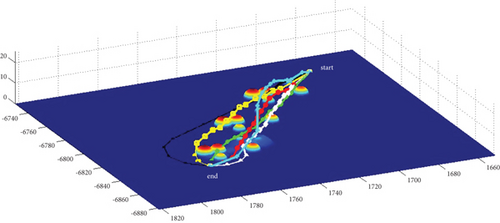
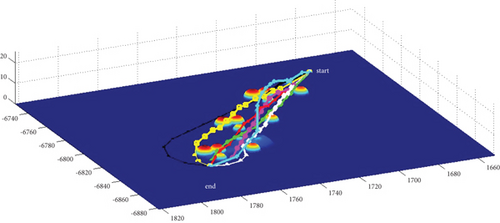
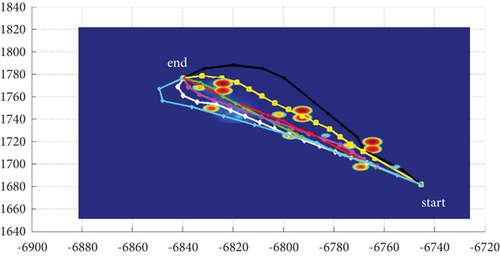
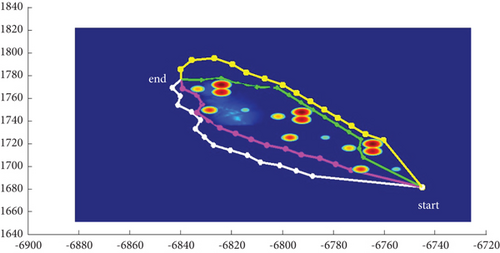
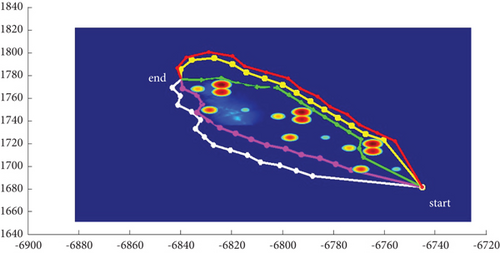
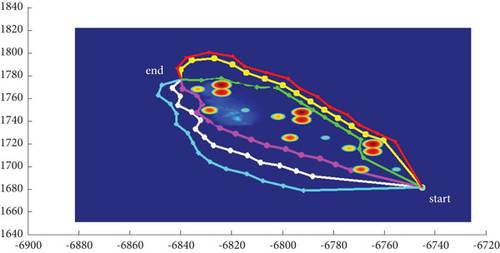
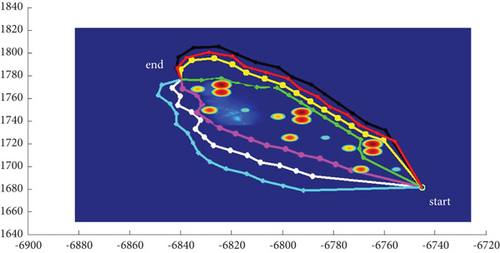
In Scenario 2/10, the azimuth of the reference attacking direction is -pi/4 rad. All the planned paths can effectively avoid the no-fly zone and terrain under larger attack angles with absolute values above pi/2 rad. Most paths are in level flight over the sea with collision-free between horizontal paths, as shown in Table 7 and Figures 16 and 17.

Table 7. Simulation data in Mode 2, Scenario 2/10.

Path count	Attack angle (rad)	Path length (h/d ) (km)
2-path	pi/2, -pi/2	144.43/146.86, 143.53/143.58
3-path	pi/2, -pi/2, 4pi/5	144.43/146.86 (d = 4), 143.53/143.58, 156.32/157.59
4-path	pi/2, -pi/2,2pi/3, -2pi/3	144.43/146.86 (d = 4), 143.53/143.58 (d = 15), 168.78/169.78 (h = 9), 156.00/156.00
5-path	pi/2, -pi/2, 2pi/3,-2pi/3, 4pi/5	144.43/146.86 (d = 4), 143.53/143.58 (d = 15), 168.78/169.78 (d = 4, h = 9), 156.00/156.00, 180.73/181.71 (h = 10)
6-path	pi/2, -pi/2, 2pi/3,-2pi/3, 4pi/5, -4pi/5	144.43/146.86 (d = 4), 143.53/143.58 (d = 15), 168.78/169.78 (d = 4, h = 9), 156.00/156.00 (d = 15), 180.73/181.71 (h = 10), 172.63/172.63 (h = 9)
7-path	pi/2, -pi/2, 2pi/3,-2pi/3, 4pi/5, -4pi/5, 9pi/10	144.43/146.86 (d = 4), 143.53/143.58 (d = 15), 168.78/169.78 (d = 4, h = 9), 156.00/156.00 (d = 15), 180.73/181.71 (d = 4, h = 10), 172.63/172.63 (h = 9), 191.88/191.88 (h = 10)
8-path	pi/2, -pi/2, 2pi/3,-2pi/3, 4pi/5, -4pi/5, 9pi/10, -9pi/10	144.43/146.86 (d = 4), 143.53/143.58 (d = 15), 168.78/169.78 (d = 4, h = 9), 156.00/156.00 (d = 15), 180.73/181.71 (d = 4, h = 10), 172.63/172.63 (d = 15, h = 9), 191.88/191.88 (h = 10), 190.86/190.86 (h = 9)

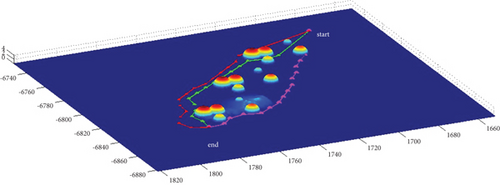
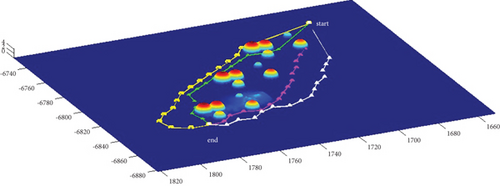
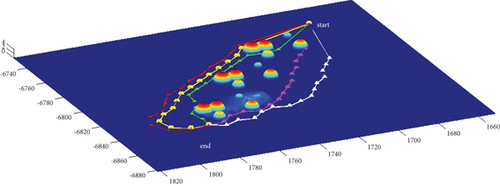
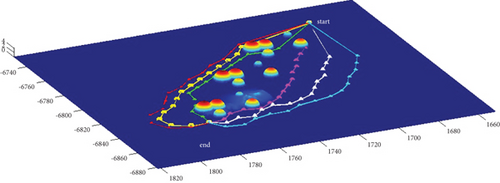
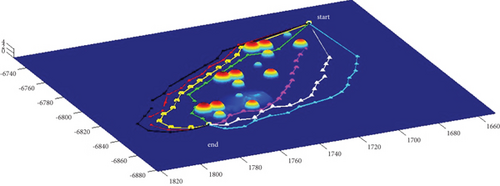
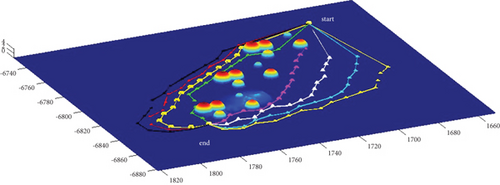
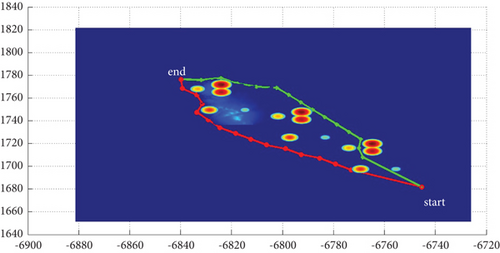
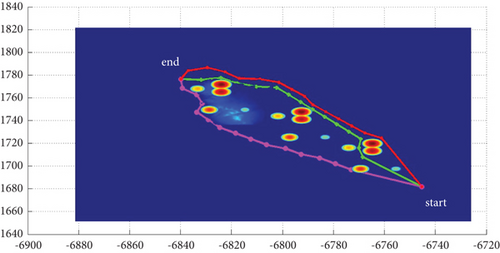
3.2.3. Mode 3

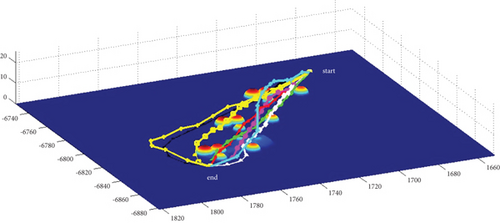
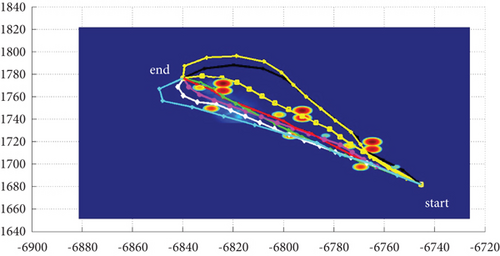
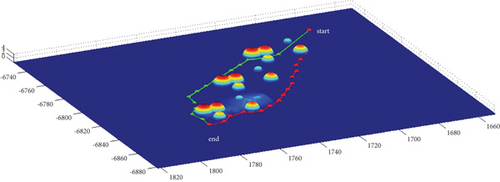
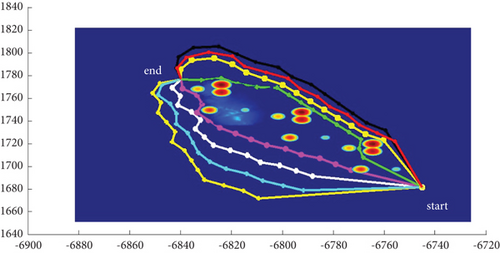
In Scenario 2/10, the azimuth of the reference attacking direction is -pi/4 rad. All the planned paths can effectively avoid the no-fly zone and terrain under various constraints, as shown in Table 8 and Figures 18 and 19, respectively. Although the route in the penetration stage is relatively gentle after crossing the obstacles, that in the launch stage is relatively steep. Therefore, it is suitable for the vertical launch method, and the route during the cruise stage fluctuates significantly.

Table 8. Simulation data in Mode 3, Scenario 2/10.

Path count	Attack angle (rad)	Path length (step size) (km)
2-path	pi/2, -pi/2	142.10/142.10, 140.68/141.35
3-path	0, pi/2, -pi/2	136.73/136.73, 142.10/142.10, 140.68/141.35
4-path	pi/3, -pi/3, pi/2, -pi/2	137.45/137.45, 135.97/135.97, 142.10/142.10, 140.68/141.35
5-path	0, pi/3, -pi/3, pi/2, -pi/2	136.73/136.73, 137.45/137.45, 135.97/135.97, 142.10/142.10, 140.68/141.35
6-path	pi/3, -pi/3, pi/2, -pi/2, 2pi/3, -2pi/3	137.45/137.45, 135.97/135.97, 142.10/142.10, 140.68/141.35, 149.35/149.35, 149.35/149.35
7-path	0, pi/3, -pi/3, pi/2, -pi/2, 2pi/3, -2pi/3	136.73/136.73, 137.45/137.45, 135.97/135.97, 142.10/142.10, 140.68/141.35, 149.35/149.35, 149.35/149.35
8-path	0, pi/3, -pi/3, pi/2, -pi/2, 2pi/3, -2pi/3, 9pi/10	136.73/136.73, 137.45/137.45, 135.97/135.97, 142.10/142.10, 140.68/141.35, 149.35/149.35, 149.35/149.35, 162.19/162.19

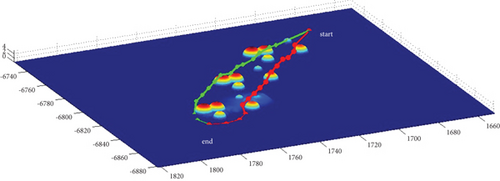
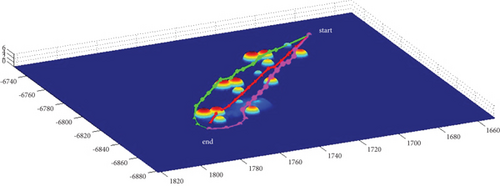
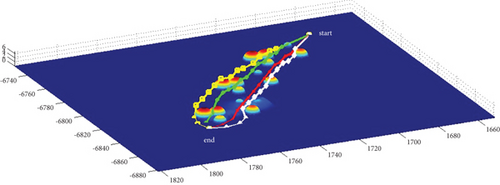
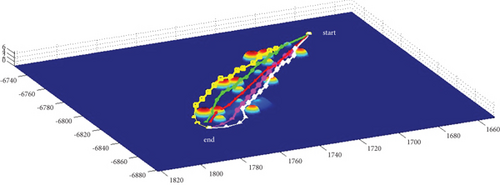
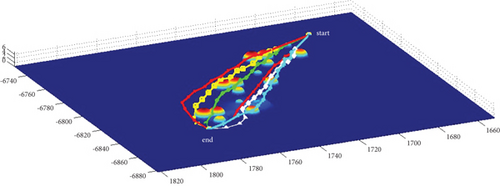
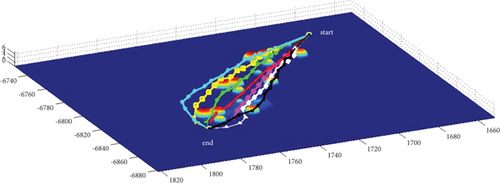
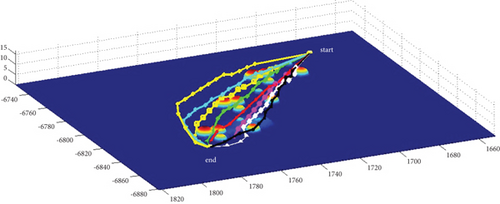
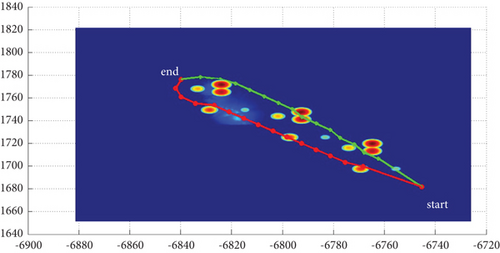
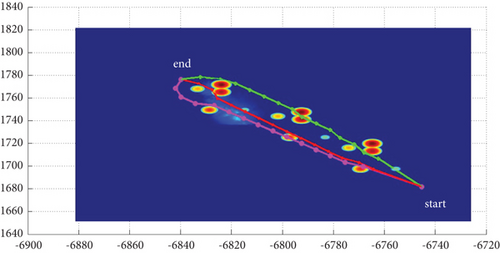
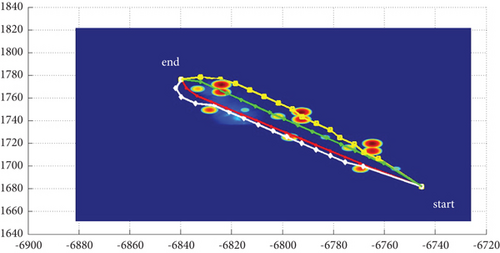
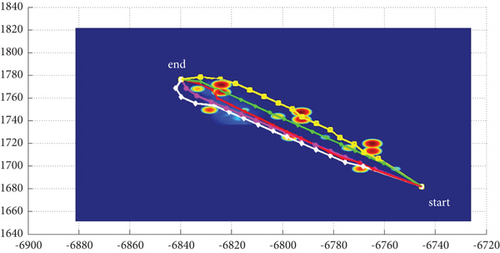
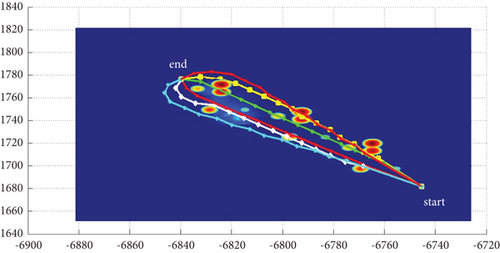
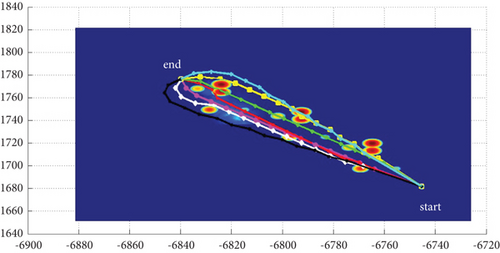
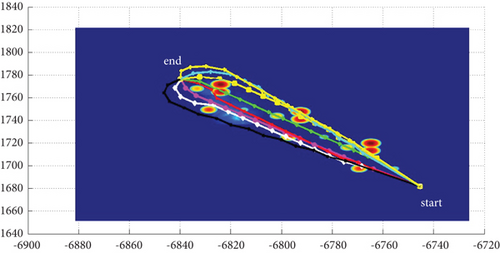
3.3. Algorithms Comparison

3.3.1. Path Smoothness

Path planning performance indicators commonly include the network life cycle, average delay, energy consumption, throughput, packet loss rate [33], path length, average success rate, average execution time [34], path smoothness [35], speed up [36, 37], and number of turns [38]. For a better comparison of different route planning algorithms, path smoothness [35, 39] in 3D space is further decomposed into direction smoothness D_s and pitch smoothness P_s. Pitch smoothness P_s is defined by Equation (36).

$$ ()

where m is the number of waypoints, the i^th waypoint vector is $$, and e_i is calculated using Equation (37).

$$ ()

If ε is a preset micro positive real number, q_i is calculated using Equation (38).

$$ ()

Direction smoothness D_s is defined by Equation (39).

$$ ()

where b_i is calculated using (40) and n_i is calculated using Equation (41).

$$ ()

$$ ()

3.3.2. Comparison With Different Modes and Situations

Multipath planning for guided vehicles in different modes and Scenarios 3–7 is simulated and compared, as shown in Figure 20. Mode 1 has strong applicability to both operational situations, with strong horizontal and vertical planning capabilities and a more jumpy course, mainly preventing obstacle penetration. Mode 2 is inclined to plan in the horizontal plane, with less altitude change throughout, a smooth pitch trajectory, and better concealment. However, multipath collision must be avoided, and a larger attack angle is required, which often requires a planning step size larger than the basic step size. This will lead to no convergence if it cannot be satisfied. Mode 3 is more oriented to plan in the vertical plane, with a strong obstacle avoidance capability and route fluctuation degree in the obstacle crossing stage similar to mode 1; however, it requires high maneuverability for the vehicle. Mode 1 and Mode 3 can use a combination of a 0 rad attack angle route with positive and negative attack angle routes when planning odd-numbered routes, whereas Mode 2 generally uses a combination of positive and negative attack angle routes plus the attack angle route with an absolute value greater than pi/2 rad when planning odd-numbered routes.

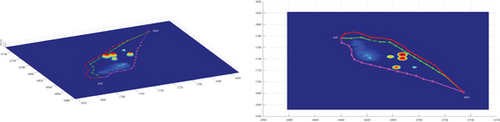
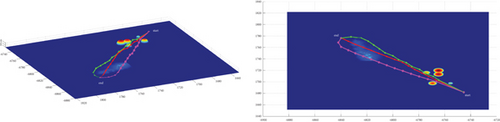
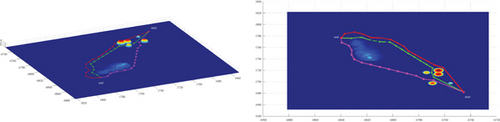
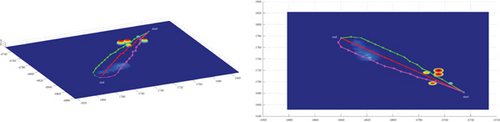
Multipath planning for guided vehicles is simulated and compared in hidden initial waypoint situations, hidden terminal waypoint situations, and Scenarios 3–7, as shown in Figure 20. For the same mode, the planned path length in Attack Situation 2 is much longer than that in Attack Situation 1. Under Modes 1 and 3, only the route jumps during the obstacle crossing stage in Attack Situation 1. The route during the cruise stage is relatively flat, and the multipath collision in the horizontal plane is not obvious. However, in Attack Situation 2, most of the routes fluctuate; only the small section after obstacle crossing becomes smooth, and multipath collision in the horizontal plane is obvious. In Mode 2, a large heading change occurs during the initial obstacle avoidance phase in Attack Situation 1, and the heading of the main cruise stage is close to the reference attacking direction. However, the heading of the entire route deviates significantly from the reference attacking direction in Attack Situation 2.

A data-driven analysis of the impact of no-fly zones on path planning performance is conducted. The comparative analysis of Scenario 1 (with no-fly zones) and Scenario 3 (without no-fly zones) across three operational modes reveals significant trends in computational efficiency, path optimality, waypoint inflation, fixed step sizes, mode-specific trade-offs, and no-fly zone complexity as shown in Table 9. The runtime difference is minimal (≤ 0.01 s), suggesting that no-fly zones do not significantly increase computational overhead in Modes 1 and 3. A 2.8% runtime reduction in Scenario 3 indicates that no-fly zones impose higher computational demands in Mode 2. No-fly zones force a 12.0% longer path in Scenario 1, highlighting inefficiencies in Mode 2’s obstacle circumvention logic. This suggests that the algorithm prioritizes safety over optimality, generating conservative detours. The minor path length differences (≤ 0.7%) indicate that Modes 1 and 3 exhibit resilience to no-fly zones. Scenario 1 requires 10 waypoints versus nine in Scenario 3, indicating that no-fly zones force additional intermediate nodes to navigate complex geometries and Mode 2’s waypoint inflation. Despite no-fly zones, step sizes remain unchanged, suggesting rigid resolution parameters. Mode 2’s larger step size (12 km) may exacerbate detour lengths when avoiding obstacles. Modes 1 and 3 prioritize path optimality with minimal runtime penalties, and Mode 2 sacrifices path length for robustness, reflecting reactive planning strategies. Increased path length and waypoints correlate with obstacle density and spatial distribution (e.g., Mode 2’s 11.96 km detour implies clustered or large no-fly zones). No-fly zones impose measurable penalties on path planning performance, particularly in Mode 2 prioritizing safety over optimality. Modes 1 and 3 demonstrate resilience through efficient threat handling, suggesting their suitability for environments with static obstacles.

Table 9. Performance comparison of mode and scenario.

Mode and scenario	Mode 1 scenario 1	Mode 1 scenario 3	Mode 2 scenario 1	Mode 2 scenario 3	Mode 3 scenario 1	Mode 3 scenario 3
Runtime/s	2.52	2.51	2.82	2.74	2.58	2.57
Number of waypoints	9	9	10	9	9	9
Path length/km	83.21	82.90	111.48	99.52	82.79	82.25
Step size/km	10	10	12	12	10	10

3.3.3. Comparison With Traditional Algorithms

This study proposes a path planning method with three modes to form and filter a set of subnode vectors.

In Scenario 8, the grid part (460–918, 420–838, 1–16) of the digital map in 4.1 and 4.2 is taken as the island sea zone and translated to (1–459, 1–419, 1–16); the map size is 459 × 419 × 16. The grid position (1, 1, z(1, 1)) is taken as the initial waypoint, the grid position (450, 410, z(450, 410)) is taken as the terminal waypoint, and the no-fly zone is neglected.

Because the planned route is an ideal route or a planned, not the actual flight route, no matter how many experiments are carried out, all performance parameters remain unchanged except runtime and are unique solutions. As shown in Table 10 and Figure 21, the BFS algorithm with cost function f = 0^∗g + h, the adding-weight A ^∗ algorithm with increased heuristic function weights in the cost function f = g + 2^∗h [14], and the A ^∗ algorithm optimizing the OPEN table [15] to save only the subsequent nodes of the current expansion node and the three modes in this study, adopting terminal attack angles of 0 rad, -pi/2 rad, and 0 rad, are compared in search time/runtime, path length, and number of search nodes and waypoints, respectively. The method in this study shortens the search time by 91.4%, reduces the number of path nodes by 96.9% to meet the requirements of k ≤ 15, and has better real-time performance. Mode 1 has the fastest search speed; Mode 3 has the shortest and smoothest planned path on the horizontal plane, which is 100% better than the traditional method; Mode 2 has the smoothest path on the vertical plane, which is 99.6% better than the traditional method, although the planned path is slightly longer than the other two modes. The method in this study does not rely on the arc of the curvature circle between the tangent points of the two adjacent path segments [12] or the Bezier curve [15] to improve smoothness, but on limited rotation of the trajectory in multiple degrees of freedom.

Table 10. Performance comparison of each algorithm.

Algorithm type	BFS	f = g + 2∗h	Optimizing OPEN A ∗	Mode 1	Mode 2	Mode 3
Runtime/s	28.17	46.81	5.26	3.62	4.03	3.72
Number of search nodes	449	449	449	14	14	14
Number of waypoints	450	450	450	15	15	15
Path length (km)	58.66	59.93	57.71	56.73	62.35	56.64
Terrain avoidance capability	No	No	No	Yes	Yes	Yes
Terminal attack angle is settable or no	No	No	No	Yes	Yes	Yes
Direction smoothness (°)	45	45	45	2.21	16.26	0.00
Pitch smoothness (°)	37.29	35.26	35.26	8.85	0.13	8.33

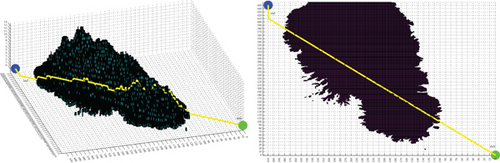
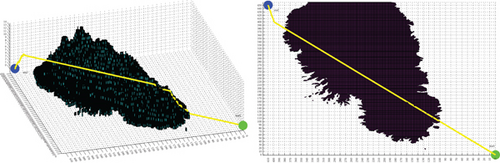
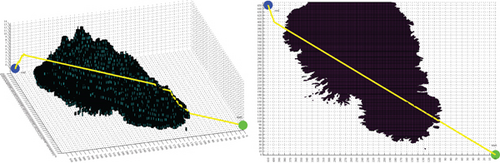
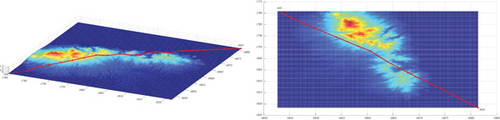
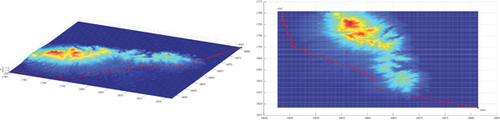
The standard A ^∗ algorithm with cost function f = g + h and Dijkstra algorithm [12, 40] with cost function f = g + 0^∗h take much longer to search than the data in Table 2. Assuming that the number of search nodes is n, the time complexity [27] or the computational complexity [41–43] of the various algorithms in Table 2 is O (n). Although these algorithms have the same form of computational complexity, algorithms with fewer search nodes have smaller computational complexity and shorter runtime, which also can explain why the traditional methods have significantly longer runtime than the three modes in this study in Table 2. In traditional methods, the optimizing OPEN A ^∗ method has the shortest runtime because its OPEN table only contains subsequent nodes of the current extension node, while the BFS algorithm and the A ^∗ algorithm with cost function f = g + 2^∗h have a longer runtime because their OPEN table contains all subsequent nodes of previous generations of extension nodes and removes the extended nodes. All planning methods were implemented using script and function m file programming in MATLAB 8.3 and executed on a 2.9 GHz Intel Core i5 with 32 GB of RAM.

4. Conclusion

In this work, the proposed 3D multipath planning method using an improved A ^∗ algorithm based on multiple avoidance tactics and terminal attack angles successfully solves the multipath planning problems of guided vehicles. This method can overcome the drawbacks of classical A ^∗ approaches, such as time consumption, insufficient smoothness, unsettable terminal attack directions, and collisions between multiple paths. All the simulation results demonstrate that the proposed multipath planning method can improve the planning speed, smoothness and coordination of multiple paths.

For two types of typical attack situations, a uniform and symmetrical attack from a single starting point to a unique target and a new practical engineering approach of implicitly extending the parent-child node are established. New tactics for terrain and threat zone avoidance are developed by filtering subnodes below the Earth’s surface, and a detection tactic based on point-in-polygon is used to realize horizontal route avoidance with a better effect. Compared with the traditional A ^∗ algorithms, the method in this study shortened the search time by 91.4%, reduced the number of path nodes by 96.9%, improved direction smoothness by 100%, and pitch smoothness by 99.6%.

We presented different real-world scenarios to evaluate the multipath planning method. The results obtained in two typical attack situations with different no-fly zones show that the proposed multipath planning method efficiently solves four major problems: symmetrically distributed terminal attack angles, limited rotation of trajectory in multiple degrees of freedom, terrain avoidance, and collision-free between routes. This makes the proposed multipath planning appropriate to find competitive results for guided vehicles in complex and real scenarios.

Moreover, the 3D multipath planning method using an improved A ^∗ algorithm based on multiple avoidance tactics and terminal attack angles could be useful for many mission planning applications, including land-attack vehicles, UAVs, unmanned underwater vehicles, and war game systems.

There are three possible directions to extend this work in the future. Firstly, in the iterative process of multipath planning, the fixed step size needs to be adaptive or variable in numerous complex environments. Secondly, for guided vehicles with coordinated turn, an explicit node extension approach should be developed by adjusting the heading at the parent node for a smooth turn to the child node with a larger radius. Thirdly, considering the current technical limitations of guided vehicles in sensing, memory, and computing power for online path planning, the realization of online planning with the solution of these technical bottlenecks will be a future trend.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research is supported by the National Science Foundation of China (62073334).