For the obstacle avoidance and formation maintenance issues of spacecraft formation, a control method with prescribed performance is proposed. Firstly, an error description system based on SE (3) is established. Secondly, to simplify the control system, collision avoidance, formation control of leading spacecraft, and containment control of following spacecraft are combined. Finally, the control errors are kept within the prescribed performance function range using prescribed performance control. Simulation results of spacecraft formation completing complex tasks under external disturbances validate the effectiveness of the proposed control scheme.

1. Introduction

With the development of modern science and space technology, people’s demand for space exploration has also increased. Spacecraft formation is an essential tool for space missions and plays an essential role in spacecraft rendezvous and docking, asteroid companion flight, in-orbit satellite maintenance, and space debris management [1–3]. However, as space missions become increasingly complex and diverse, the technical requirements for spacecraft formations are becoming more demanding. The attitude and orbit control of spacecraft and collision avoidance within spacecraft formations have received significant attention as the core technology for the formation to complete the mission in orbit.

Modeling spacecraft is the basis of controller design. Spacecraft attitude trajectory integration modeling methods, which consider the coupling of spacecraft attitude motion and positional motion, effectively improve the accuracy and response speed of spacecraft control and have received widespread attention. Most current modeling methods that consider spacecraft attitude trajectory integration are based on dual quaternions [4, 5]. The six-degree-of-freedom (6DOF) motion of the next spacecraft is simulated in [4] using dyadic quaternions, accounting the coupling between spacecraft position and attitude. An artificial potential function based on dyadic quaternions is proposed in [5] to address the problem of integrated position and attitude control during autonomous spacecraft rendezvous and docking.

However, these methods have the disadvantages of ambiguity and rewinding, which, in practice, reduce the response time of the spacecraft and lead to higher energy consumption. SE (3), as a new modeling method that avoids the issues of ambiguity, singularity, and receding winding that arise in the description of rigid body attitudes, is also widely used in the field of attitude orbit integration control and modeling of spacecraft [6–8]. A robust adaptive controller based on SE (3) with integrated extended state observer (ESO) is proposed in [6], which addresses the tracking maneuvers of coupled spacecraft under model uncertainty and external disturbances. In [7], an adaptive terminal sliding mode controller with SE (3) modeling is proposed to improve the spacecraft docking accuracy. In [8], the relative error dynamics equations for attitude and orbit between two spacecraft under SE (3) modeling are developed for the parameter uncertainty of the spacecraft model. In addition to the above error description systems, which are mostly based on the exponential coordinates of SE (3), there is also an error description system based on the bit-shaped error function obtained on SE (3). In [9], a new construction error function based on SE (3) is designed, and a controller based on this function developed to ensure that the rigid body remains stable with a bounded construction error for a fixed period. Based on SE (3), a more diverse error description system can be obtained, which allows greater flexibility in the design of spacecraft formation controllers.

When spacecraft formations are on space missions, one of the most important tasks is to avoid collisions between spacecraft. However, none of the previously mentioned literature addresses collision avoidance. However, there are some studies that focus on this issue [10–12]. In [10], a decentralized collision avoidance vehicle formation flight tracking control scheme using virtual leading state trajectories is proposed based on SE (3). Lee et al. [11] investigated the finite-time stabilization problem of dispersed collision avoidance in spacecraft formation flight, combining dispersed collision avoidance with finite-time control to achieve convergence of spacecraft motion to the desired state trajectory in finite time while achieving collision avoidance. In the process of solving collision avoidance, the above method does not consider the simultaneous constraints of formation, collision avoidance, and containment and thus cannot address other difficulties encountered during the formation process, which poses challenges in practical applications.

There has been some research on the optimization of control schemes. In [13], a unified control scheme is designed to achieve both formation control and suppression control, and an adaptive robust constraint is proposed to address collision avoidance constraints, formation constraints, and suppression constraints for the satellite. Compared with designing two independent control schemes, this unified approach is more concise and more feasible to solve practical problems. In order to simplify the control scheme and increase its feasibility for solving practical problems, this paper establishes a unified control scheme that transforms the three desired objectives—formation containment, leader, and follower—into a set of servo constraints.

In addition, to achieve collision avoidance and formation maintenance, this paper uses prescribed performance controls to constrain the following errors to a consistent and ultimately bounded level. The spacecraft studied in this paper is highly nonlinear and has a model that has uncertainties and dynamic coupling. In any dynamic system, the presence of uncertainty impacts the performance of the system. Therefore, a control method which is significantly robust to modeling uncertainties and external disturbances is required. Much research has been conducted on control methods modeled using SE (3). In [14], in order to solve the problem of spacecraft orbit maneuvering coupling under uncertain parameters and external interference, an adaptive fixed-time sliding mode control law is proposed. In [15], for the virtual structure control problem of multiagent systems, a formation adaptive super-twisting sliding mode controller is proposed. In [16], an integrated guidance and feedback control scheme was designed. However, the tracking of predetermined steady-state and transient indices is lacking in the literature cited above. These specifications, which are crucial for spacecraft, ensure safety and time constraints.

In [17], an improved prescribed performance control scheme is proposed to achieve prescribed performance trajectory tracking for three-degree-of-freedom UAVs. To this end, this paper applies an improved prescribed performance control protocol to assist in the completion of multiple tasks in spacecraft formation. The control design does not rely on the accuracy of the system model. One of the key features makes it possible to track time-varying trajectories with a degree of accuracy that can be prespecified for both the transient and steady-state responses of the system.

The contributions of this paper are as follows.

1.
The formation configuration error modeling of formation configuration error is performed on the Riemannian manifold SE (3) that is applied, which avoids the singularity and the unwinding phenomenon.
2.
Collision avoidance, formation control of leading spacecraft, and containment control of following spacecraft are combined into a new simplified control method. Furthermore, the consistency constraint of formation–containment error is addressed using a prescribed performance function.
3.
A prescribed performance controller for spacecraft is proposed to handle model uncertainties and ensure that the performance of the spacecraft formation is within the prescribed limits when completing multiple missions.

2. Problem Statement

2.1. Spacecraft Dynamic Model

In this section, a configuration error description system based on SE (3) is applied. For the integrated attitude–orbit motion of the spacecraft, its configuration space SE (3) is a six-dimensional nonlinear manifold embedded in a 16-dimensional Euclidean space. The generalized velocity and driving force of the integrated attitude–orbit motion lie in the tangent and cotangent spaces of SE (3). The configuration of the 6-DOF spacecraft, including attitude and position, can be uniquely described by SE (3) uniquely. According to Reference [9], the kinematic and dynamic equations can be described as follows:

()

where

is the generalized velocity. Ω ∈ ℝ³ is the angular velocity. V ∈ ℝ³ is the linear velocity of the spacecraft. The operation on

()

In Formula (1), the projection

is the dual projection of ad_ξ, which can be described as

()

where

is described as

m ∈ ℝ₊ is the mass of the spacecraft and J ∈ ℝ^3×3 is the rotational inertia. Therefore, the inertial parameter Π ∈ ℝ^6×6 is

()

Furthermore, f_V ∈ ℝ³ is the resultant external torque in the body-fixed frame, and f_Ω ∈ ℝ³ is the resultant external force.

is the generalized force in the spacecraft system, which can be described as

()

where

is a generalized controller input, which is composed by the input torque τ ∈ ℝ³ and the input force F ∈ ℝ³. d_Ω ∈ ℝ³ is the disturbance torque. d_V ∈ ℝ³ is the disturbance force. The generalized external disturbance can be described as

is the generalized potential force. M_g ∈ ℝ³ and F_g ∈ ℝ³ are the known moment and force caused by the potential forces, respectively.

According to Formulae (1), (2), (3), and (5), the spacecraft kinematic and dynamic equations can be described as

()

Remark 1. SO(3) is the modeling space for spacecraft attitude, and the elements are represented as R ∈ SO(3). ℝ³ is the modeling space of spacecraft position, and the elements are represented as p ∈ ℝ³. The set of elements on SO(3) can be characterized as SO(3) = {R ∈ ℝ^3×3|R^TR = I, det[R] = 1.

Remark 2. The map [∙]^∧ : ℝ³⟶so(3) represents the skew–symmetric matrix operation. The corresponding Lie algebras of Lie group SE (3) are se(3) = so(3) × ℝ³. The map [∙]⁻ : ℝ⁶⟶se(3) is a bijection map, where se(3) is a Lie algebra of a special Euclidean group and so(3) is a Lie algebra of the three-dimensional special orthogonal group.

2.2. Error Design on SE (3)

SE (3) is a nonlinear space with 16 elements and 10 constraints, but the input in this paper contains only 6 elements. This makes the controller based on SE (3) redundant. Therefore, according to [9, 18], the configuration error function is applied to address this problem.

The error function is φ_g = SE(3) × SE(3)⟶ℝ, where g_d and ξ_d are desired configurations and g and ξ are generalized velocities. The attitude error function is

; the position error function on

is defined as the actual attitude and desired attitude of the spacecraft; (p, p_d) is defined as the actual position and desired position. It can be rewritten as

()

Hence, the configuration error vector e_g = SE(3) × SE(3)⟶ℝ⁶ and the generalized velocity error vector e_ξ : SE(3) × ℝ⁶ × SE(3) × ℝ⁶ can be expressed as

()

where e_R is the attitude error vector and e_p is the position error vector. Angular velocity error and translational velocity error are represented by e_Ω and e_V.

Taking the derivative of Formula (8) yields

()

where

2.3. Formation–Containment Design

In this paper, the spacecraft formation system consists of N spacecraft, which include K leader spacecraft and N − K follower spacecraft. N = {1, 2, ⋯, N} is the total sequence number set of spacecrafts; L≔{1, 2, ⋯, K} and H≔{K + 1, K + 2, ⋯, N} are the leader and follower spacecrafts, respectively.

In this paper, collision avoidance constraints, formation constraints, and containment constraints are used to obtain that the leader spacecrafts form the desired formation. Meanwhile, the follower spacecraft must enter the formation space defined by the leader spacecraft.

Based on Reference [13], the first leader spacecraft performs trajectory tracking, and the remaining spacecraft form a formation relative to the position of the first leader spacecraft. Consequently, there are variations in the formation constraints and collision avoidance constraints. Formation constraints are redefined, and the permutations and combinations of collision avoidance constraints are adjusted. Some results can be obtained as follows.

A collision avoidance error function e_ih is set i(i = ∈{1, 2, ⋯, N}) between spacecraft h(h = ∈{1, 2, ⋯, N}) h ≠ i and spacecraft. A formation error function e_jk is set for the formation between the leader spacecraft j(j = ∈{1, 2, ⋯, N}) and the leader spacecraft k(k = ∈{1, 2, ⋯, L}), k ≠ j. The containment error functions e_s are set for follower spacecraft s(s = ∈{1, 2, ⋯, H}); the specific expressions for these functions are shown below:

()

where the space measure between two spacecraft i and h is given by

; Q is the maximum distance of the spacecraft from the center of mass.

is the desired relative position.

is a containment restriction when s ∈ H, j ∈ L, and μ_j ≥ 0 satisfy

The three constraints are set as

()

where l_jk and l_s are positive constant scalars.

Definition 1. It can be obtained from Reference [13], for any initial states p_j(t₀) and p_s(t₀), there exists a time T_j < ∞ such that

()

Moreover, ς_jk > 0 and ς_jk > 0 are the arbitrarily small positive constants and there exist t⩾T_j, k ∈ L, j ≠ k, s ∈ H.

If S_ih(t₀) > 0, the spacecraft can avoid collisions with each other. If S_ih(t) > 0, h ∈ N, i ≠ h, the spacecraft will avoid collisions.

Make

()

Then, the formation constraint is described as

()

where j ∈ {2, 3, ⋯, N}; the above formation constraint shows a general form.

Collision–avoidance constraint is described as

where

The containment constraint is described as where .

In order to simplify the control design, a unified statement of the constraints on each spacecraft is required i, i ≠ 1. Make

()

Then, the constraint on each spacecraft i, i ≠ 1 can be described as

()

The constraint-following error is defined as

()

2.4. Prescribed Performance Control

In this section, the main design process of prescribed performance control (PPC) is introduced. Based on [17], in order to make the error e(t) converge to a prescribed set of arbitrarily small residuals, the convergence rate is greater than the given value. This set of residuals is denoted by e(t) in a prescribed region whose boundary depends on a function of time. This region is defined as

()

where the bounded and smooth time function ρ(t) satisfies

. The exponentially decaying performance function is described as follows:

()

where ρ₀, ρ_∞, and λ are parameters greater than 0.

It is necessary to choose the constant ρ₀, which requires the condition ρ₀ > |e(0)| to be satisfied and dictates the rate of decrease of ρ(t). In addition, λ is designed to ensure that the convergence rate of e(t) has a lower bound. Furthermore, the parameter represents the steady-state maximum allowable error value. Therefore, choosing a suitable performance function ρ(t) can make the tracking error e(t) have certain steady-state or transient performance characteristics.

The PPC can adjust e(t) to encapsulate the performance function ρ(t) according to the corresponding performance characteristics. The bijective, odd, and strictly increasing mapping T : (−1, 1)⟶(−∞, ∞) is used, which is defined as follows:

()

where the modulated error

Moreover, the derivative of T(ξ) is strictly positive and is expressed as

()

Due to the properties of the transformation described above, it can be shown that ensuring the boundedness of ε(t) is sufficient to achieve prescribed performance.

3. Control Design

In this section, the design process of the controller is introduced, as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flowchart of the control scheme.

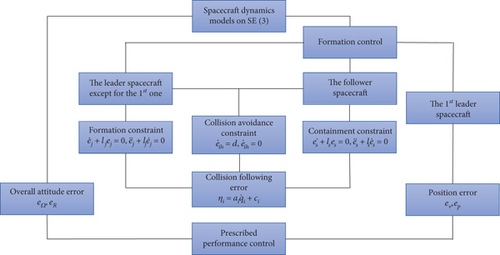
3.1. Overall Attitude Controller Design

According to the error design in (8), the sliding surface is defined as

()

where m is a constant.

The prescribed performance function is selected as

()

where ρ_q0, ρ_q1, andλ₁ are parameters greater than 0.

The normalized sliding-mode error is defined as

()

The integral of Formula (26) is

()

where

is selected constant. The corresponding transformed error is defined as

()

where T : (−1, 1)⟶(−∞, ∞) is selected according to Formula (22).

To guarantee Formula (24) is bounded, the overall attitude control law is designed as follows:

()

where

; ζ_q is defined as ζ_q = ε_q + (k₂/k₁)ξ_q, k₁ and k₂ are constants, and k₁ ≠ 0.

Theorem 1. Aiming at the SE (3) model mentioned in Section 2, if the overall attitude control law is used, the sliding surface in Formula (24) exists and it ensures that the angle and angular velocity of the system always remain within a small neighborhood of the sliding surface; specifically, for any t⩾0, there always exists |s_q| ⩽ |ρ_q|. Meanwhile, the system error e_r and e_ω can converge in finite time with the prescribed performance.

Proof 1. Design the Lyapunov candidate function as

()

Taking the derivative of both sides of (30) yields

()

According to Formulae (22) and (28), Formula (31) can be rewritten as

()

Substituting (29) into (32) yields

()

where

Furthermore, by using the mean value theorem for the term tanh(ε_q), there exist , where . Then, , which means

()

Based on Formulae (33) and (34), we can get

()

Moreover, by using can be transformed into

()

where κ_q is a positive constant such that

. By denoting

can be finally transformed into

()

Then, based on Reference [17], the existence of positive and finite constants and can be proved, and for all implies from (32) that

()

Therefore, there always exists |s_q| ⩽ |ρ_q| for any t⩾0.

3.2. Position Controller Design of the First Leader Spacecraft

According to the error design in (8), the sliding surface of the first leader spacecraft is defined as

()

where n is a constant.

Select the prescribed performance function as

()

where ρ_l0, ρ_l∞, and λ are parameters greater than 0.

The normalized sliding-mode error is defined as follows:

()

The integral of Formula (41) is

()

where

is selected constant. The corresponding transformed error is defined as

()

where T : (−1, 1)⟶(−∞, ∞) is selected by referencing Formula (22).

To guarantee Formula (39) is bounded, the position control law of the first leader spacecraft is designed as follows:

()

where

, ζ_l is defined as ξ_l = ε_l + (k₄/k₃)ξ_l, and k₃ and k₄ are constant.

Theorem 2. Aiming at the SE (3) model mentioned in Section 2, if the overall attitude control law is used, the sliding surface in Formula (39) exists and it can ensure the input and the position of the system always slides near a small region of the sliding surface; namely, for any t⩾0, there always exists |s_l| ⩽ |ρ_l|. Meanwhile, the signal of the closed-loop system can be ensured to be bounded. The system error e_p and e_V can converge in finite time with the prescribed performance.

Proof 2. Design the Lyapunov candidate function as

()

Taking the e derivative of both sides of (45) yields

()

According to Formulae (22) and (39), Formula (46) can be rewritten as

()

Substituting (44) into (47) yields

()

where

Furthermore, according to the mean value theorem for the term sinh(ε_q), there exist , which implies

()

According to Formulae (48) and (49), we can get

()

Furthermore, by using can become

()

where κ_l is positive constant such that

. By denoting

can finally become

()

Then, by invoking [17], the existence of positive and finite constants can be obtained, , such that and for all t ∈ [0, τ_max). Hence, (47) can be rewritten as

()

Therefore, there always exists |s_l| ⩽ |ρ_l| for any t⩾0.

3.3. Formation Controller Design

The normalized sliding-mode error of the spacecrafts i (except the first leader spacecraft) is defined as

()

where

is the prescribed performance function. ρ_i0, ρ_i1, and λ_i are parameters greater than 0.

The integral of Formula (54) is

()

where

is selected constant. The corresponding transformed error is defined as

()

where T : (−1, 1)⟶(−∞, ∞) is selected by Formula (22).

To guarantee Formula (54) is bounded, the formation–containment control law is designed as follows:

()

Theorem 3. Aiming at the SE (3) model mentioned in Section 2, if the formation–containment control law is applied, the constraint-following error in Formula (54) exists and it can ensure the system state always slides near a small area of the sliding surface; namely, for any t⩾0, there will always |η_i| ⩽ |ρ_i|. Meanwhile, the signal of the closed-loop system can be ensured to be bounded. The formation of the spacecraft will satisfy the conditions for collision avoidance, formation maintenance, and containment constraints.

Proof 3. Design the Lyapunov candidate function as

()

It can be calculated from (58) that

()

According to Formulae (22) and (54), Formula (59) can be rewritten as

()

Substituting (57) into (60) yields

()

where

Furthermore, by using the mean value theorem for the term sinh(ε_q), there exist , where , such that which implies

()

According to Formulae (61) and (62), we can get

()

Furthermore, by using can become

()

where k_l is positive constant and

; by denoting

can finally become

()

Then, based on Reference [17], the existence of positive and finite constants can be obtained, , such that and for all t ∈ [0, τ_max). Hence, it can be rewritten as

()

Therefore, there always exists |η_i| ⩽ |ρ_i| for any t⩾0.

4. Simulation

4.1. Formation Design

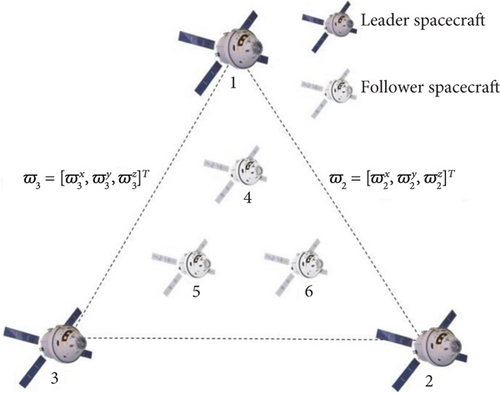
This section considers a spacecraft formation flying system with three Leader Spacecrafts 1, 2, 3 and three Follower Spacecrafts 4, 5, 6. The equation of motion of spacecraft i in the SE (3) is described as (6).

The mass d_Ω and d_V are chosen as

The first leader spacecraft tracks the desired trajectory; other leader spacecrafts are expected to form a formation structure of an equilateral triangle based on the position of the first spacecraft, while the follower spacecrafts are expected to fly inside the equilateral triangle. Moreover, Figure 2 shows the formation structure. In this diagram, ϖ₂ and ϖ₃ represent the expected relative positions between Spacecrafts 1 and 2 and 1 and 3, respectively.

According to the constraint-following error

, constraint-following error can be represented as

()

In the formula,

()

4.2. Parameter Setting

In this section, the parameters of the spacecraft are shown.

The parameters of the spacecrafts are set as Table 1.

Table 1. Control parameters.

Parameter	Value
m	0.9
n	0.3
k₁	6
k₂	4
ω₂₁	[100 0 − 10]^T
k₃	8
k₄	1
k₅(2, 3, 4, 5, 6)	8
k₆(2, 3, 4, 5, 6)	1
ω₃₁	[0 100 − 10]^T

The selected exponentially decaying functions are set as ρ_q(t) = (5 − 0.1)e^−t + 0.1, ρ_l(t) = (50 − 1)e^−t + 1, ρ_2,3(t) = (25 − 1)e^−t + 1, ρ_4,5(t) = (120 − 1)e^−t + 1, and ρ₆(t) = (100 − 1)e^−t + 1.

The initial attitude and the angular velocity of the spacecraft are set as [0.18π − 0.24π 0.4π]^T and [2.5 − 1.5 − 2]^T, respectively. The expected attitude and angular velocity are set as [0 0 0]^T. The expected position and velocity of the first leader spacecraft are set as p_d = [8t 8t 5t + 25sin(t/5)]^T and v_d = [8 8 5 + 5cos(t/5)]^T. The initial value of the spacecrafts is set in Table 2 as [0 0 0]^T.

Table 2. Initial value of spacecrafts.

Conditions	Position (m)	Velocity (m/s)
Leader 1	[0 0 5]^T	[0 0 0]^T
Leader 2	[110 − 10 5]^T	[0 0 0]^T
Leader 3	[0 110 5]^T	[0 0 0]^T
Follower 4	[80 80 0]^T	[0 0 0]^T
Follower 5	[50 − 40 − 5]^T	[0 0 0]^T
Follower 6	[−40 50 − 5]^T	[0 0 0]^T

4.3. Simulation Results

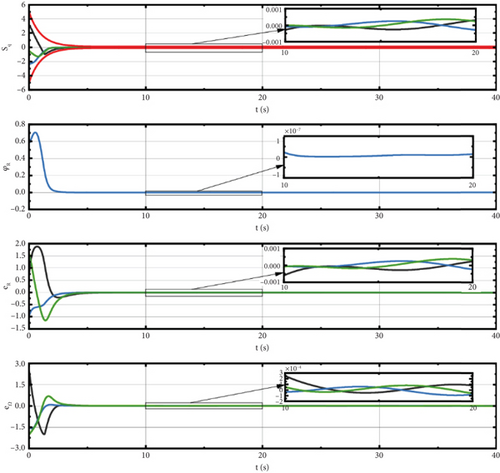
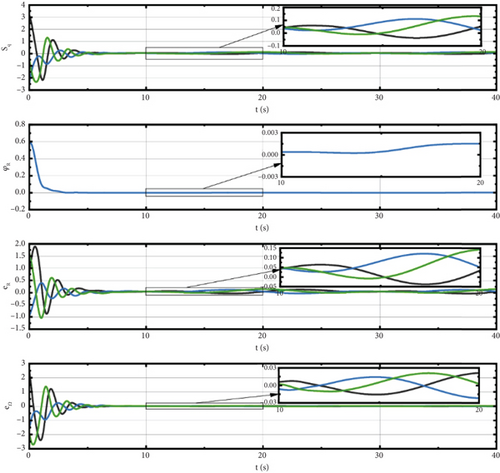
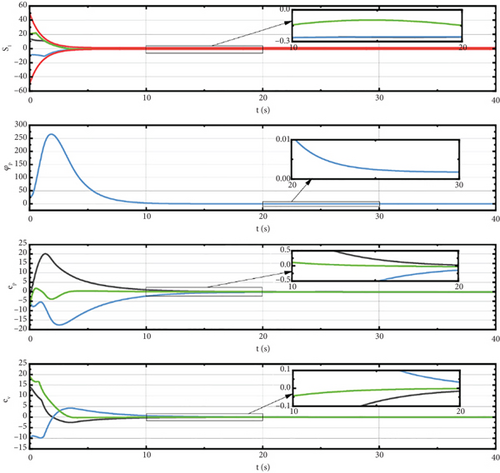
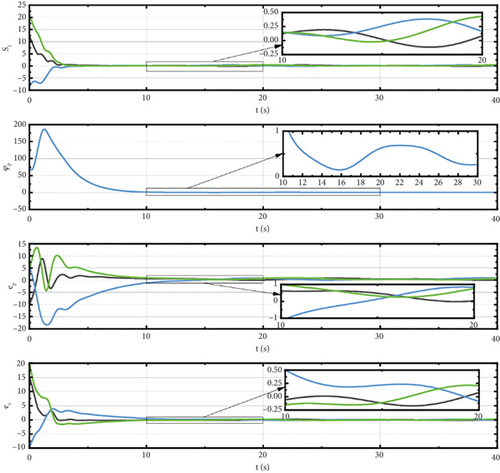
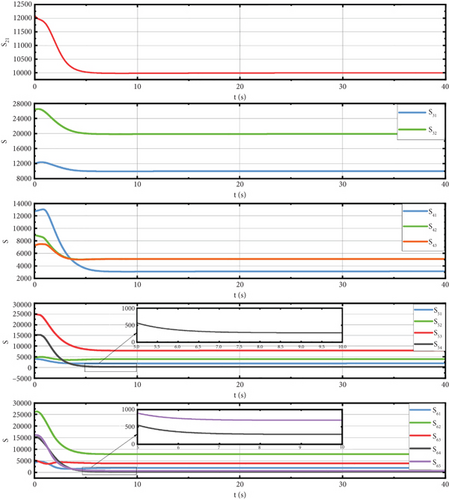
In this section, the simulation results are analyzed in detail. Figure 3 shows the trajectories of the spacecrafts. Figures 4 and 5 illustrate the sliding surface, attitude error, and angular velocity error of the spacecrafts using our method (a) and sliding mode control (SMC) method (b). Figure 6 displays the spatial measurements between any two spacecrafts. Figure 7 presents the errors of the leader spacecrafts. Figure 8 shows the containment error of the follower spacecrafts. Figure 9 shows the constraint-following error under the PPC of spacecraft i.

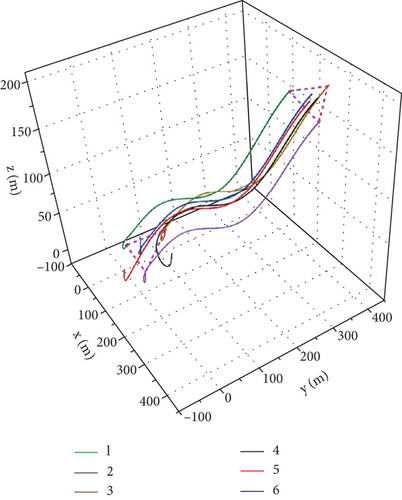
In Figure 3, for a limited time, Leader Spacecrafts 1–3 form the desired triangular formation, and Follower Spacecrafts 4–6 enter the triangular region constructed by the three leader spacecrafts, verifying the leader formation and follower containment performance. Additionally, this figure illustrates that none of the spacecraft trajectories intersect at any time, indicating high effectiveness in collision avoidance.

It can be seen in Figures 4 and 5 the clear trend that the errors in overall attitude, angular velocity, position, and velocity of the first leader spacecraft are converged to around 0 as the variation of the exponentially decaying functions. Compared to the SMC method, our controller can make the error reduction faster and larger, demonstrating higher control accuracy and greater stability.

As shown in Figure 6, the spatial measurements S_ih and ΔS_ih(i, h ∈ {1, 2, 3, 4, 5, 6}, i ≠ 1) are always positive. As demonstrated, the method achieves the expected collision avoidance performance.

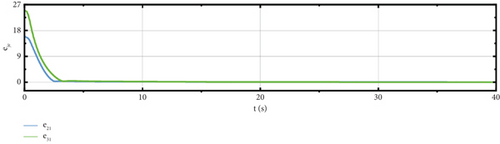
Figure 7 shows that the formation errors e₂₁ and e₃₁ converge to around 0 before t = 5 s and remain stable with ς₂₁ ≈ 0.2, ς₃₁ ≈ 0.37. Therefore, the result in this diagram demonstrates that our method can achieve the desired performance of formation.

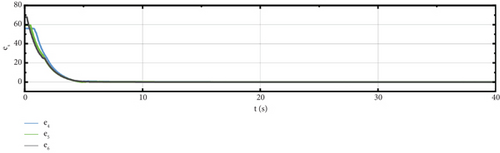
From Figure 8, we can see that the containment errors e₄, e₅, and e₆ converge to around 0 before t = 5 s and keep stable with ς₄ ≈ 0.81, ς₅ ≈ 0.49, ς₆ ≈ 0.59. Therefore, the paper demonstrates the expected performance of containment. In the simulation, with uncertainties in d_Ω and d_V, both the dynamics model of spacecraft and the constraints are nonlinear. Therefore, the results shown in Figure 8 indicate that our controller can solve the formation–containment, collision avoidance, uncertainty, and nonlinearity problems.

Looking at Figure 9, it is apparent that all constraint-following errors remain within the range of the prescribed performance function. These errors converge to around zero before t = 4 s. From this result, indicates that our control scheme can achieve containment, formation, and collision avoidance effectively, and its performance function can be applied to the transient and steady-state responses of the system to achieve high-precision control.

5. Conclusions

The present study was designed to determine the effect of spacecraft formation multimission execution problem modeled on the nonlinear manifold SE (3) with prescribed performance. First, for spacecraft attitude trajectory integration, the error vector of each spacecraft is set using the configuration error function on SE (3). Formation containment control is then employed to design formation errors for multiple spacecraft, enabling them to perform formation, collision avoidance, and containment tasks simultaneously. Finally, the prescribed performance control is applied to ensure that the formation error is continuously limited and the convergence rate is higher than expected. The simulation results illustrate the effectiveness of the proposed control scheme for multitask completion and high-precision control. The results indicate that the control scheme not only avoids singularity and the unwinding phenomenon but also ensures that the performance of the spacecraft formation is within the prescribed limits while completing multiple missions.

Ethics Statement

The authors have nothing to report.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research received no external funding.

Open Research

Data Availability Statement

Data will be made available on request.

References

1 Zhang Z., Deng L., Feng J., Chang L., Li D., and Qin Y., A survey of precision formation relative state measurement technology for distributed spacecraft, Aerospace. (2022) 9, no. 7, https://doi.org/10.3390/aerospace9070362.
10.3390/aerospace9070362
Google Scholar
2 D′Souza C., Hannak C., Spehar P., Clark F., and Jackson M., Orion rendezvous, proximity operations and docking design and analysis, AIAA guidance, navigation and control conference and exhibit, 2007, Hilton Head, South Carolina, https://doi.org/10.2514/6.2007-6683.
10.2514/6.2007-6683
Google Scholar
3 Singla P., Subbarao K., and Junkins J. L., Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty, Journal of Guidance, Control, and Dynamics. (2006) 29, no. 4, 892–902, https://doi.org/10.2514/1.17498, 2-s2.0-33747081935.
10.2514/1.17498
Web of Science® Google Scholar
4 Wang J. and Sun Z., 6-DOF robust adaptive terminal sliding mode control for spacecraft formation flying, Acta Astronautica. (2012) 73, no. 2, 76–87, https://doi.org/10.1016/j.actaastro.2011.12.005, 2-s2.0-84856442176.
10.1016/j.actaastro.2011.12.005
Web of Science® Google Scholar
5 Dong H., Hu Q., and Akella M. R., Dual-quaternion-based spacecraft autonomous rendezvous and docking under six-degree-of-freedom motion constraints, Journal of Guidance, Control, and Dynamics. (2018) 41, no. 5, 1150–1162, https://doi.org/10.2514/1.G003094, 2-s2.0-85045519580.
10.2514/1.G003094
Web of Science® Google Scholar
6 Zhang J., Ye D., Sun Z., and Liu C., Extended state observer based robust adaptive control on SE (3) for coupled spacecraft tracking maneuver with actuator saturation and misalignment, Acta Astronautica. (2018) 143, 221–233, https://doi.org/10.1016/j.actaastro.2017.11.034, 2-s2.0-85036655609.
10.1016/j.actaastro.2017.11.034
Web of Science® Google Scholar
7 Lee D. and Vukovich G., Robust adaptive terminal sliding mode control on SE (3) for autonomous spacecraft rendezvous and docking, Nonlinear Dynamics. (2016) 83, no. 4, 2263–2279, https://doi.org/10.1007/s11071-015-2479-1, 2-s2.0-84958114787.
10.1007/s11071-015-2479-1
Web of Science® Google Scholar
8 Ren J., Tang S., and Chen T., Adaptive sliding mode control of spacecraft attitude-orbit dynamics on SE (3), Advances in Space Research. (2023) 71, no. 1, 525–538, https://doi.org/10.1016/j.asr.2022.09.007.
10.1016/j.asr.2022.09.007
Google Scholar
9 Wang Y., Hong H., Guo J., Wang X., and Shang W., Configuration error function design and application to fixed-time geometric terminal sliding-mode control on SE(3), Acta Astronautica. (2020) 174, 61–71, https://doi.org/10.1016/j.actaastro.2020.03.018.
10.1016/j.actaastro.2020.03.018
Web of Science® Google Scholar
10 Lee D., Sanyal A. K., and Butcher E. A., Asymptotic tracking control for spacecraft formation flying with decentralized collision avoidance, Journal of Guidance, Control, and Dynamics. (2015) 38, no. 4, 587–600, https://doi.org/10.2514/1.G000101, 2-s2.0-84936741722.
10.2514/1.G000101
Web of Science® Google Scholar
11 Xue X., Yue X., and Yuan J. P., Distributed connectivity maintenance and collision avoidance control of spacecraft formation flying, 2019 Chinese Control Conference (CCC), 2019, Guangzhou, China, 8265–8270, https://doi.org/10.23919/ChiCC.2019.8866017.
10.23919/ChiCC.2019.8866017
Google Scholar
12 Lee D. and Vukovich G., Almost global finite-time stabilization of spacecraft formation flying with decentralized collision avoidance, International Journal of Control, Automation and Systems. (2017) 15, no. 3, 1167–1180, https://doi.org/10.1007/s12555-016-0239-8, 2-s2.0-85019914986.
10.1007/s12555-016-0239-8
Web of Science® Google Scholar
13 Sun Q., Wang X., and Chen Y. H., Satellite formation-containment control emphasis on collision avoidance and uncertainty suppression, IEEE Transactions on Cybernetics. (2023) 53, no. 8, https://doi.org/10.1109/TCYB.2022.3173683.
10.1109/TCYB.2022.3173683
Google Scholar
14 Gong K., Liao Y., and Wang Y., Adaptive fixed-time terminal sliding mode control on SE (3) for coupled spacecraft tracking maneuver, International Journal of Aerospace Engineering. (2020) 2020, no. 1, https://doi.org/10.1155/2020/3085495, 3085495.
10.1155/2020/3085495
Google Scholar
15 Ghasemi K., Ghaisari J., and Abdollahi F., Robust formation control of multiagent systems on the Lie group SE(3), International Journal of Robust and Nonlinear Control. (2020) 30, no. 3, 966–998, https://doi.org/10.1002/rnc.4806.
10.1002/rnc.4806
Web of Science® Google Scholar
16 Viswanathan S. P., Sanyal A. K., and Samiei E., Integrated guidance and feedback control of underactuated robotics system in SE (3), Journal of Intelligent Robotic Systems. (2018) 89, no. 1-2, 251–263, https://doi.org/10.1007/s10846-017-0547-0, 2-s2.0-85017116331.
10.1007/s10846-017-0547-0
Google Scholar
17 Verginis C. K., Bechlioulis C. P., Soldatos A. G., and Tsipianitis D., Robust trajectory tracking control for uncertain 3-DOF helicopters with prescribed performance, IEEE/ASME Transactions on Mechatronics. (2022) 27, no. 5, 3559–3569, https://doi.org/10.1109/TMECH.2021.3136046.
10.1109/TMECH.2021.3136046
Google Scholar
18 Bullo F. and Murray R. M., Tracking for fully actuated mechanical systems: a geometric framework, Automatica. (1999) 35, no. 1, 17–34, https://doi.org/10.1016/S0005-1098(98)00119-8, 2-s2.0-0032714958.
10.1016/S0005-1098(98)00119-8
Web of Science® Google Scholar

All articles

Predetermined Performance Control of Spacecraft Formation Based on SE(3) Error Description

Abstract

1. Introduction

2. Problem Statement

2.1. Spacecraft Dynamic Model

2.2. Error Design on SE (3)

2.3. Formation–Containment Design

2.4. Prescribed Performance Control

3. Control Design

3.1. Overall Attitude Controller Design

3.2. Position Controller Design of the First Leader Spacecraft

3.3. Formation Controller Design

4. Simulation

4.1. Formation Design

4.2. Parameter Setting

4.3. Simulation Results

5. Conclusions

Ethics Statement

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Predetermined Performance Control of Spacecraft Formation Based on SE(3) Error Description

Abstract

1. Introduction

2. Problem Statement

2.1. Spacecraft Dynamic Model

2.2. Error Design on SE (3)

2.3. Formation–Containment Design

2.4. Prescribed Performance Control

3. Control Design

3.1. Overall Attitude Controller Design

3.2. Position Controller Design of the First Leader Spacecraft

3.3. Formation Controller Design

4. Simulation

4.1. Formation Design

4.2. Parameter Setting

4.3. Simulation Results

5. Conclusions

Ethics Statement

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information