International Journal of Aerospace Engineering

Volume 2024, Issue 1 7720612

Research Article

Open Access

Response Analysis of Projectile System Under Gaussian Noise Excitation Using Path Integral Method

Liang Wang

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Xinyi Li,

Corresponding Author

Xinyi Li

[email protected]

orcid.org/0009-0008-2521-0350

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Jiahui Peng,

Jiahui Peng

orcid.org/0009-0008-1532-125X

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Zhonghua Zhang,

Zhonghua Zhang

orcid.org/0009-0000-1641-3334

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Shuangqi Dong,

Shuangqi Dong

orcid.org/0009-0009-0641-1752

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Liang Wang,

Liang Wang

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Xinyi Li,

Corresponding Author

Xinyi Li

[email protected]

orcid.org/0009-0008-2521-0350

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Jiahui Peng,

Jiahui Peng

orcid.org/0009-0008-1532-125X

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Zhonghua Zhang,

Zhonghua Zhang

orcid.org/0009-0000-1641-3334

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Shuangqi Dong,

Shuangqi Dong

orcid.org/0009-0009-0641-1752

Department of Applied Probability and Statistics , School of Mathematics and Statistics , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

First published: 02 December 2024

https://doi.org/10.1155/ijae/7720612

Academic Editor: Tuo Han

Share a link

Email
Wechat
Bluesky

Abstract

During flight, projectiles are subject to uncertainties such as aerodynamic forces, wind gusts, and measurement errors; all of which significantly affect their stability and accuracy. As a result, studying the response of projectile systems under stochastic excitation is essential. This paper focuses on the solution and analysis of projectile system responses under stochastic excitation. We employed the path integral method to compute the transient and stationary probability density functions for projectile systems subjected to Gaussian stochastic external and parametric excitations. Based on the probabilistic responses, we analyzed the evolution of the system’s probability density function over time under Gaussian white noise excitation, as well as the changes in the stationary probability density function with air density and flight speed as bifurcation parameters. The analysis results indicate that within a specific range of parameter variations, air density can induce stochastic P-bifurcation phenomena. Furthermore, increasing air density and flight speed can enhance the stability of the projectile.

1. Introduction

In the field of engineering, a critical aspect of studying exterior ballistics is the analysis of projectile stability [1]. Ensuring ballistic reliability in shooting applications is heavily dependent on this stability analysis.

In the 1950s, Murphy and other researchers studied the angular motion of projectiles, focusing on system modeling and dynamic analysis [1–3]. Since then, researchers have focused on two main aspects of the system: first, improving the intricacy of system modeling, and second, investigating its complex dynamic behavior. Ren and Ma investigated the coning motion of spinning missiles in flight, concentrating on the mechanisms of longitudinal static stability, lateral moments affecting coning, and the impact of aerodynamic damping [4]. Liaño, Castillo, and García-Ybarra examined the impact on the steady states of the coupled roll–yaw motion when using a high-order roll-dependent yaw moment, in an effort to provide tools to explore the dynamic free-flight behavior in the high angle-of-attack regime [5]. Xu et al. investigated the angular motion of rolling projectiles with configurational asymmetries, delving into the system’s nonlinear characteristics [6]. Zhong et al. studied the periodic stability analysis and Hopf bifurcation of the nonlinear angular motion equations of projectiles [7, 8]. Additionally, methods such as Lyapunov stability theory, bifurcation analysis, the homotopy analysis method [9], and the cell mapping (CM) method [10] have been applied in the study of projectile systems.

However, research on projectile systems under stochastic excitation is limited, primarily due to the challenge of solving the probability density function (PDF) for high-dimensional systems. Huang and Yang provided an approximate analytical representation of the stationary PDF using the stochastic center manifold method and analyzed the stochastic dynamic behavior of the system [11]. This study focuses on the approximate solution of the stationary PDF for projectile systems, introducing stochastic dynamics into the stability analysis of projectile flight. The stochastic center manifold method does not address the solution of the transient PDF, which is also important for analyzing stochastic responses. Additionally, other methods are employed to solve stochastic systems. These include numerical methods such as the Monte Carlo (MC) method [12, 13], as well as semianalytical methods like the stochastic averaging method [14] and equivalent linearization method. Nevertheless, many flight dynamics systems, including projectile systems, face the curse of dimensionality when extending research to stochastic dynamics, leading to significant challenges and time-consuming computations, particularly with the MC method.

In summary, investigating precise and efficient methods to solve the Fokker–Planck (FPK) equation for these systems is crucial yet highly demanding. The path integral (PI) method is an approach for exploring stochastic dynamic systems. Since Wiener applied the PI method to solve stochastic differential equations [15, 16], many experts have been devoted to improving the computational efficiency and accuracy of the PI method and applying it to practical problems [10, 17, 18]. In recent years, a PI based on probability mapping was proposed [19, 20]. This paper uses the PI method based on decoupling probability mapping to analyze the stochastic response of projectile systems and further analyzes the behavior of projectile systems under stochastic excitations. By employing the PI method, we addressed both transient and stationary stochastic responses. With the flight speed of the projectile and air density as varying parameters, our analysis of the stationary PDF revealed the occurrence of stochastic P-bifurcation phenomenon. The findings indicate that, within a specific range of parameter variations, increasing air density and flight speed can significantly enhance the stability of the projectile.

This paper is organized as follows: In Section 2, the basic principles of the PI method based on decoupled probability mapping used in this paper are introduced. Additionally, models for missile angular motion under Gaussian white noise external excitation and parameter excitation are developed. Section 3 presents the stochastic response solution results for the two stochastic systems and analyzes the stochastic bifurcation phenomena of the systems. The conclusion is provided in Section 4.

2. Introduction of Algorithm and Model

2.1. System of Projectile Angular Motion

During the flight of a spinning projectile, an angle of attack develops between the projectile’s axis and its velocity direction, as shown in Figure 1. If the projectile maintains a small angle of attack during flight (below a certain threshold), its nose will remain nearly aligned with the flight direction, resulting in stable forward flight. Conversely, a significant increase in the angle of attack can lead to instability in the projectile’s flight. To explore the laws of angular motion in projectiles, a deterministic model is established based on coordinate transformations, Newton’s second law, and the conservation of angular momentum, as shown in Equation (1):

(1)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Angular motion of spinning projectiles.

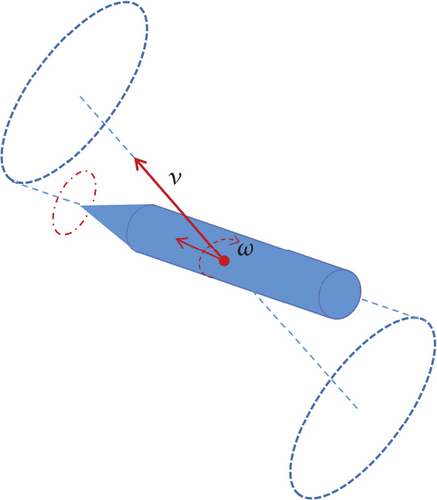
As illustrated in Figure 2, the angle of attack δ₁ and δ₂ represents rotation angles of the projectile’s axis coordinate system relative to the trajectory coordinate system, playing a key role in determining the projectile’s trajectory and flight stability. ω_η and ω_ζ represent the angular rate in the projectile coordinate system. m and v stand for the mass and velocity of the projectile, respectively. M_ξ, M_η, and M_ζ represent the components of the moment about the three axes of the projectile coordinate system. F_x, F_y, and F_z, respectively, denote the components of the moment about the three axes of the velocity coordinate system. A and C stand for the equatorial moment of inertia and polar moment of inertia of the projectile.

Furthermore, considering the simplest nonlinear forms of aerodynamic forces and moments and substituting the force and moment terms, we can obtain the deterministic nonlinear angular motion Equation (2). This equation includes trigonometric terms and does not linearize trigonometric functions and their product terms, preserving geometric nonlinearity as much as possible [7, 8]:

(2)

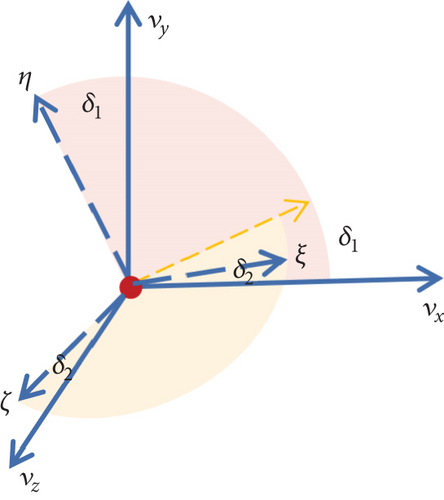
The flight speed of the projectile is symbolized by v. ρ denotes the density of the air. S, l, and d, respectively, represent the reference area, length, and diameter of the projectile. , , , and are the aerodynamic parameters of the projectile.

Using

to represent the four state variables

and ξ(t) = (ξ₁(t) ξ₂(t) ⋯ ξ_K(t)) to represent mutually independent Gaussian white noise excitations, the stochastic system of the projectile under Gaussian white noise excitation can be expressed in the following standard form:

(3)

where

is the first-order derivative of X(t). F(X(t)) is a four-dimensional column vector of functions. G(X(t)) is a matrix of functions with a size of 4 × K, and its structure depends on the method of noise addition. Equation (3) is the standard form of the stochastic model, and the relationship between the matrices is standard matrix multiplication. Next, we will specifically discuss the model under Gaussian white noise external excitation and parameter excitation.

2.1.1. Projectile System Under Gaussian White Noise External Excitation

During flight, a projectile is subjected to various environmental factors such as atmospheric pressure, temperature, air density, and turbulence, as well as loads and uncertainties in aircraft parameters. These stochastic factors introduce deviations between theoretical predictions and actual responses. Stochastic dynamical systems refer to whose states or behaviors are influenced by stochastic factors, including noise, stochastic disturbances, and uncertainties. These systems are typically modeled using stochastic differential equations or stochastic difference equations. Both the excitation and response of stochastic systems are stochastic processes, requiring characterization by statistical methods such as PDF and mean square responses. Stochastic bifurcation refers to the phenomenon in which the stationary probability density characteristics of a stochastic dynamical system experience abrupt changes due to minor variations in system parameters. This phenomenon is a vital tool for analyzing system stability and can be categorized into two primary types: stochastic P-bifurcation and stochastic D-bifurcation. Stochastic P-bifurcation specifically addresses changes in the shape of the stationary PDF, such as transitions of the marginal PDF from unimodal to bimodal forms. In summary, developing a stochastic system model and deriving the PDF are essential for analyzing projectile systems subjected to stochastic disturbances [21].

Multiple complex stochastic factors act simultaneously on the projectile, causing stochastic fluctuations in the forces and torques experienced by it. Under ideal conditions, it is assumed that the disturbances in force and torque experienced by the projectile follow a Gaussian white noise ξ(t) = (ξ₁(t), ξ₂(t)) with intensity δ². The model for projectile angular motion under Gaussian white noise external excitation is described by Equation (4):

(4)

(5)

where K₁ = ρSv/2m and K₂ = ρSlv²/2A.

2.1.2. Projectile System Under Gaussian White Noise Parametric Excitation

If the projectile is influenced by wind during flight, the analysis of aerodynamic forces and moments differs from the ideal scenario. The magnitude and direction of the aerodynamic forces and moments experienced by the projectile in a wind field are determined by the velocity of the projectile relative to the air, known as the airspeed v_r. We use v to represent the velocity of the projectile relative to the ground (ground speed) and w to represent the wind speed. Lead wind is usually not considered, and wind speed can be decomposed into crosswind w_x and headwind w_z. The relationship between wind speed, ground speed, and airspeed can be represented by Formula (6):

(6)

Decomposing the velocity into the coordinate system of the velocity vector, we can obtain .

The actual stochastic wind disturbances are highly complex. However, in order to study the angular motion model of projectiles under suitable stochastic wind disturbances, it is necessary to appropriately idealize the stochastic wind disturbances. There are many assumptions about atmospheric turbulence, such as the assumptions of stationarity and homogeneity and the assumption of isotropy [22, 23]. The assumption of Gaussian distribution considers atmospheric turbulence to be of Gaussian type, meaning that the velocity magnitude follows a normal distribution. Among these, the calculation of probabilities related to the Gaussian distribution assumption is very useful. For example, under the Gaussian assumption background, the angular motion of projectiles can be modeled as a stochastic differential equation excited by Gaussian white noise parameters.

Therefore, in this paper, we assume that the stochastic crosswind w_x and headwind w_z are two mutually independent Gaussian white noises ξ₁(t) and ξ₂(t), respectively. Combining the aerodynamic forces and moments of the projectile under windy conditions, we can derive the stochastic differential Equation (7), which is an equation under Gaussian white noise parameter excitation:

(7)

Both F(X) and G(X) are function matrices:

(8)

(9)

where K₁ = ρSv²/2sinδ, K₂ = ρS/2sinδ, K₃ = ρSl/2sinδ, and K₄ = ρS/2sinδ.

2.2. PI Method Based on a Decoupling Probability Mapping

The PI method is a numerical approach for solving stochastic dynamical systems. The method is based on the Chapman–Kolmogorov (CK) equation, which involves discretizing the equation in both spatial and temporal domains and then replacing integrals with path sums. By linking short-time TPDF, the joint PDF of states at any given moment can be obtained. An essential step in employing the PI method involves constructing the short-time TPDF matrix. Once the short-time TPDF matrix is established, this matrix enables the computation of the PDF at any given moment through successive matrix operations.

For the system (3) satisfying the Markov property, the region of interest D for four-dimensional state variables is discretized into M subintervals D₁, D₂, ⋯D_M, with the center points X₁, X₂, ⋯X_M of each subinterval chosen as their integration points. The initial time is set to t₀, and the time interval is Δt. Using the classical PI method, the PDF of the state X_i at time t₀ + rΔt can be expressed as

(10)

q(X_i, Δt|X_j, 0) represents the short-time TPDF from X_j to X_i within the time interval Δt. Construct a matrix of short-time TPDF from all q = {q(X_i, Δt|X_j, 0), i, j = 1, 2, ⋯M}. It is easy to see that the size of the short-time TPDF matrix is M × M. Discretizing the space for high-dimensional systems will result in a large value for M, which makes continuous operations on the short-time TPDF matrix time-consuming. Next, we will introduce the construction method for the short-time TPDF matrix and the PI method based on decoupling probability mapping.

For the stochastic differential Equation (3), the iteration of the state variables over a small time interval τ can be expressed as follows:

(11)

The iteration process can be replaced by using the stochastic Runge–Kutta (RK) method.

Initially, discretize the integration step Δt size of the short-time TPDF matrix into n smaller iterative steps, that is, Δt = iτ, i = 1, 2, ⋯n. Correspondingly, the continuous stochastic process ξ(t) within this interval Δt is also discretized into ξ(iτ), i = 1, 2, ⋯n. For each

, where ξ_j(iτ) is a Gaussian white noise with noise intensity

and Δξ_j(iτ) is a stochastic variable that follows a Gaussian distribution

. We denote the discretized set as ξ(t = (0, Δt]), where Δξ(t = (0, Δt]) = {Δξ(iτ), i = 1, ⋯, n}. The values of Δξ(iτ) and Δξ(t = (0, Δt]) are represented as Δξ_i and Δξ, respectively. The sample space of Δξ is represented by Ω_Δξ, with a probability measure of 1, that is,

(12)

Then, we define the probability space of Θ = (Ω_Δξ, Δξ(t = (0, Δt]), P). Through the use of the GF-difference method [24], we can discretize the probability space and select S representative points from the sample subspace. Assuming the representative points selected after discretization are denoted as {Δξ_k(iτ), k = 1, ⋯, S} and the subspace corresponding to each representative point is denoted as

, then, based on the discretization of the probability space, Equation (13) can be obtained:

(13)

To enhance computational efficiency, we define a short-time TPDF that depends on the initial state label and representative point label. For example, selecting X_j as the initial point and choosing the representative point Δξ_k for the noise input would yield a solution X. Assuming this solution X is contained within a subinterval D_c of the region of interest, then

(14)

Represent q(X_c|(X_j, Δξ_k)) by q_kj = c.

Finally, the PDF of the stochastic system at any given time can be obtained using the following iterative expression:

(15)

Compared to the classical TPDF matrix, the size of the new TPDF matrix is reduced to S × M, significantly reducing the time cost of PI in practical calculations.

The MC method is a numerical computation technique based on stochastic sampling, widely used for solving various problems in SDEs. This method fundamentally estimates the characteristics and behaviors of complex systems through random sampling. The K-dimensional state space is divided into D₁, D₂, ⋯D_M, with the center points defined as X₁, X₂, ⋯X_M. For the system (3), N stochastic samples are generated using numerical solution methods for SDEs, such as the RK-4 method. The locations of the samples at a given time t are recorded, yielding their distribution in the state space. Let M_i be the number of samples in the state space D_i. Based on the principle of the law of large numbers, when the sample size N is sufficiently large, the probability of space D_i can be approximated by P_i = M_i/N, which can further lead to the PDF in the state space.

The MC method requires a substantial number of samples to achieve high precision. In high-dimensional spaces, the dramatic increase in the required sample size can significantly affect computational efficiency. Furthermore, compared to the PI method, the MC method does not provide distinct advantages in capturing the temporal evolution of probability densities. In summary, the PI method based on decoupled probability mapping offers an effective approach for exploring high-dimensional systems such as projectile angular motion models.

3. Numerical Examples

In Section 2, the projectile model under stochastic disturbances and the PI method have been introduced. Next, we will focus on a specific type of rocket projectile during its passive flight phase and apply the PI method for stochastic analysis. The structural and aerodynamic parameters selected are detailed in Tables 1 and 2 [11].

Table 1. Structural parameters.

m(kg)	C(kg × m²)	A(kg × m²)	S(m²)	l(m)
44.2	0.12466	30.627	0.01269	2.7

Table 2. Aerodynamic parameters.

**w_ζ(rad/s)**				m_y0	m_y2
79.0064	6.5	−1.3546	0.46	−5.7	29

3.1. Projectile System Under Gaussian White Noise External Excitation

Initially, we investigate the transient PDF of Equation (4). Select ρ = 0.5 kg/m³, ρ = 0.53 kg/m³, δ² = 0.01, and v = 600 m/s, and then, utilize the PI method mentioned in Section 2 to compute the response of Equation (4). The results obtained by the PI method are compared with those of the MC method depicted in Figures 3 and 4, where dots represent results from the MC method and lines represent results obtained using the PI method. Different colors denote different moments in time. It is evident that the numerical solutions obtained from the PI method at transient moments are in good agreement with those of the MC method within the overall probability levels. Furthermore, we can see that within short durations of motion, the PDF of system (4) remains unimodal, with the peak position close to 0. This phenomenon indicates that the projectile’s motion state is stable over short durations. Specifically, it suggests that the projectile is likely to maintain a small angle of attack under these conditions, thereby sustaining a stable flight attitude.

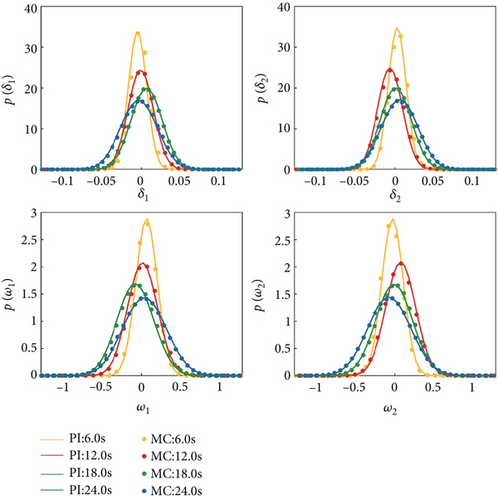
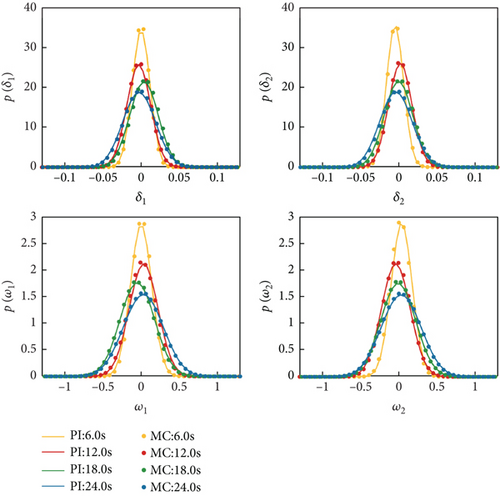
Through the investigation of deterministic projectile systems, we have discovered that under the aforementioned parameter combination, the system (2) exhibits bifurcation phenomena with ρ as the bifurcation parameter. Next, we will continue to use ρ as the bifurcation parameter to verify whether the PI method can capture the bifurcation behavior of the system (4).

Select ρ = 0.5 kg/m³, 0.51 kg/m³, 0.52 kg/m³, 0.53 kg/m³, and δ² = 0.01, and then, utilize the PI method to compute the stationary marginal PDF of the system (4). The stationary marginal PDF obtained by the PI method is compared with that of the MC method depicted in Figure 5, where dots and lines represent the results obtained by the MC method and the PI method, respectively. Different colors indicate different values of parameter ρ. As shown in Figure 5, the results obtained by the PI method closely match those from the MC method. The marginal PDF transitions from bimodal shape to a unimodal shape. When ρ = 0.50 kg/m³, the system undergoes stochastic oscillations around the displacements corresponding to the two peaks, and with the decrease of ρ, the instability of the motion intensifies. To better observe the phenomenon of system variation with respect to ρ, we plotted the system’s two-dimensional contour plots representing the joint PDF of system variables, as shown in Figure 6. Taking Figure 6(a) as an example, where the axes represent the elevation angle δ₁, azimuth angle δ₂, and the angular velocity of the coordinate system’s rotation w₁, w₂, the top two plots depict the results obtained using the MC method, while the bottom two plots represent the results obtained using the PI method. When v = 600 m/s, air density leads to a stochastic P-bifurcation phenomenon. For ρ = 0.50 kg/m³ and ρ = 0.51 kg/m³, the system’s joint PDF takes the shape of a symmetric volcano shape, indicating that the system undergoes random oscillations within the corresponding range. When ρ = 0.53 kg/m³, the PDF becomes single peak, with the peak value corresponding to the state (0, 0, 0, 0). This indicates that as air density increases, the flight state of the projectile becomes more stable.

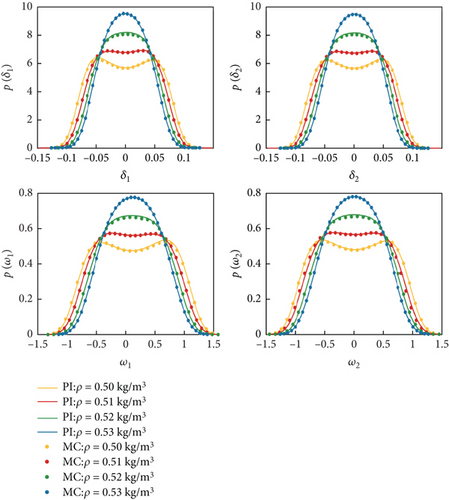
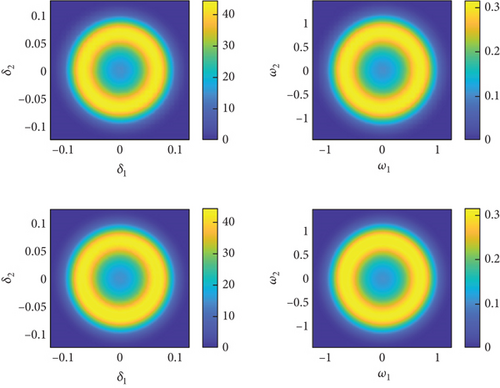
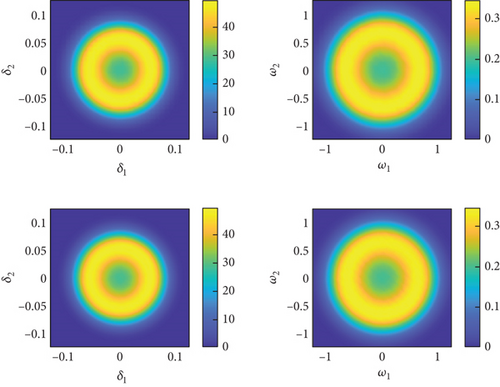
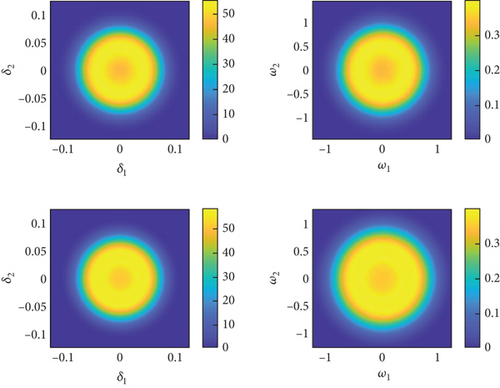
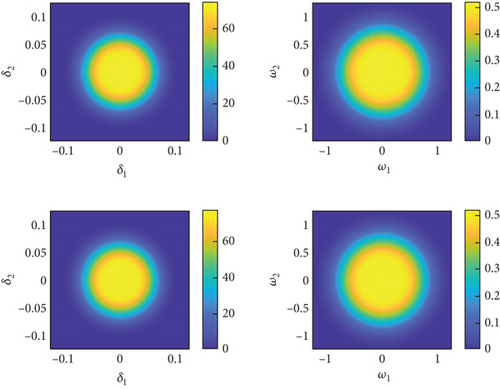
Table 3 lists the time consumed by the PI method and MC method calculations of the transient and stationary PDF, achieving the same level of accuracy. The state space is divided into 40 × 40 × 40 × 40 subintervals (M = 40 × 40 × 40 × 40), with the number of representative points for the PI method set to 50 (S = 50). Transient PDF in Table 3 represents the results at t = 6.0 s, while the system reaches stationary at 500 s. It is worth noting that the PI method mainly consists of two steps: solving the TPDF matrix and iterating the TPDF matrix to obtain the PDF. This algorithmic process dictates that regardless of which moment’s PDF is being computed, the transition probability density matrix only needs to be calculated once. In contrast, the MC method requires resolving and recording sample data for computing the PDF at any given moment, leading to longer computation time for both continuous and stationary PDF. Therefore, in Table 3, T₁ represents the time taken for solving the TPDF matrix using the PI method, while T₂ represents the duration for iterating the transient PDF.

Table 3. The real execution time utilizing the PI method and the MC method for solving the transient and stationary PDF.

	Transient PDF (6.0 s)	Stationary PDF
The execution time of the PI method
The execution time of the MC method	561.56 s	45,860.02 s

Through analysis of Figures 5 and 6 and Table 3, we can draw three conclusions: (1) The PI method can yield accurate marginal PDF and joint PDF. (2) Due to the high dimensionality of the system, the MC method requires a sufficient number of samples to obtain smooth results. Therefore, when computing the transient and stationary PDF of the system, the PI method has advantages in computational efficiency compared to the MC method. In particular, the PI method can rapidly obtain the evolution of the PDF with time, which is time-consuming for the MC method. (3) The system undergoes P-bifurcation phenomena between ρ = 0.52 kg/m³ and ρ = 0.53 kg/m³, indicating that as the air density increases, the flight of the projectile gradually becomes more stable. In conditions of low air density, the reduced number of air molecules leads to a deterioration in the conditions for generating lift, making it difficult for the projectile to maintain stable lift during flight. Additionally, low air density also affects the magnitude of drag, thereby collectively impacting the flight stability of the projectile.

3.2. Projectile System Under Gaussian White Noise Parametric Excitation

Equation (7) is a complex nonlinear system excited by Gaussian white noise parameters. To verify the applicability and efficiency of the PI method in solving such models, we still compare with the MC method. Figures 7 and 8 present the transient solution results for two parameter combinations. In the figures, dots and lines represent the results of the MC and PI methods, respectively, with different colors indicating different moments in time. Analysis of Figures 7 and 8 indicates that, under stochastic wind disturbances, the marginal PDF of the system exhibits irregular variations in the short term.

Next, the PI method is used to solve the stationary PDF at ρ = 0.8 kg/m³. The results are shown in Figures 9 and 10, where Figure 9 displays the marginal PDF and Figures 10(a), 10(b), 10(c), and 10(d) show the joint PDF of two states. In Figure 9, dots and lines represent the results of the MC and PI methods, respectively, with different colors indicating different parameter combinations. In contrast to the volcano shape shown in Figure 8, the joint PDF under the aforementioned parameter combination exhibits a bimodal distribution. This suggests that the projectile, when disturbed, may oscillate between two different flight states. Although the amplitude of the oscillations is relatively small, it can still be observed that the amplitude decreases slightly as the flight speed increases.

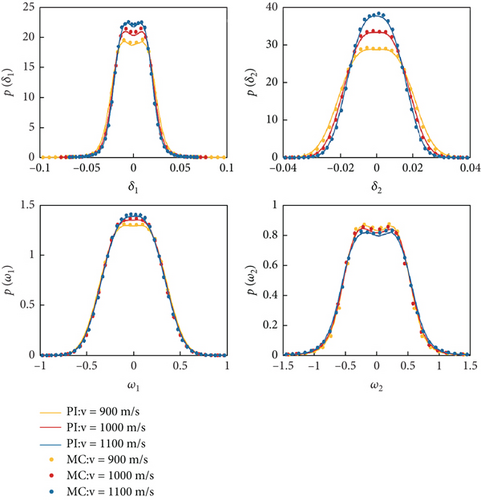
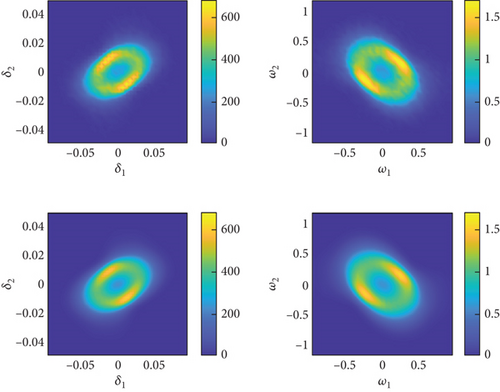
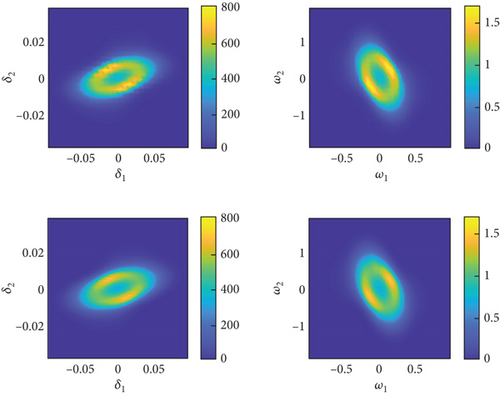
Table 4 illustrates the time consumption for solving the PDF using both methods at the same level of accuracy. The number of subspaces and representative points is 40 × 40 × 40 × 40 and 50. Transient PDF in Table 4 represents the results at t = 0.6 s, while the system reaches stationary at 30 s. The table validates the efficiency of the PI method. It not only allows for the computation of the stationary PDF at a lower time cost but also enables the continuous computation of transient PDF, a limitation of the MC method.

Table 4. The real execution time utilizing the PI method and the MC method for solving transient and stationary PDF.

	Transient PDF (0.6 s)	Stationary PDF
The execution time of the PI method
The execution time of the MC method	10,753.75 s	16,307.2 s

4. Conclusions

Considering the importance of studying projectile systems under stochastic excitation, the challenge lies in analyzing their stochastic response due to the high system dimensionality. The key issue is solving PDF of the systems. In this paper, the PI method based on decoupling probability mapping is applied to solve the transient and stationary PDF. In principle, the PI method reconstructs the short-time TPDF matrices in the classical PI method, significantly improving computational efficiency. The numerical results also demonstrate the accuracy of the PI method in analyzing the response of high-dimensional systems. Additionally, the PI method offers a viable technical approach for future related studies. For higher-dimensional projectile systems, such as six-degree-of-freedom equations, the PI method still requires improvements in computational efficiency.

Analysis of the numerical results indicates that air density ρ and projectile flight speed v are the key parameters influencing flight stability. Under Gaussian white noise external excitation, the system undergoes stochastic P-bifurcation when air density is treated as a bifurcation parameter. Specifically, as air density decreases, the stationary joint PDF of the system transitions from the volcano shape to a unimodal form, while the marginal PDF shifts from a bimodal to a unimodal distribution. As air density increases, the range of stochastic oscillations within the system diminishes, leading to a higher probability that the projectile will fly in a state close to the peak value. This indicates that higher air density can reduce the instability of projectile motion, likely due to its direct impact on factors such as lift and drag. This phenomenon aligns with the potential occurrence of flight instability observed in projectile tests conducted at high altitudes. When flight speed is considered as the parameter, the system under Gaussian white noise parametric excitation consistently exhibits a bimodal stationary joint PDF, indicating the presence of stochastic oscillations. Moreover, with increasing flight speed, the amplitude of these oscillations decreases, leading the projectile to favor a more stable low-angle-of-attack flight state.

The analytical results of this study can provide insights for the design of projectile stability. In establishing the stochastic model, we assumed that random wind disturbances follow a Gaussian white noise model; however, there is still room for further research on other forms of random wind disturbances, such as colored noise and non-Gaussian noise.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 12472034 and 12372034).

Open Research

Data Availability Statement

The data is available upon request by contacting the provided email address.

References

1 Murphy C. H., Free Flight Motion of Symmetric Missiles, 1963, US: Ballisties Research Laboratory, Aberdeen Proving Ground.
10.21236/AD0442757
Google Scholar
2 Murphy C. H., Response of an asymmetric missile to spin varying through resonance, AIAA Journal. (1971) 9, no. 11, 2197–2201, https://doi.org/10.2514/3.50025, 2-s2.0-84962148006.
10.2514/3.50025
Google Scholar
3 Nicolaides J. D., On the free flight motion of missiles having slight configurational asymmetries, Institute of the Aeronautical Sciences. (1953) 395.
Google Scholar
4 Ren T. R. and Ma J. M., Coning motion analysis of spinning missile based on gyrodynamics, Journal of Astronautics. (2010) 31, no. 9, 2082–2087.
Google Scholar
5 Liaño G., Castillo J. L., and García-Ybarra P. L., Steady states of the rolling and yawing motion of unguided missiles, Aerospace Science and Technology. (2016) 59, 103–111, https://doi.org/10.1016/j.ast.2016.10.016, 2-s2.0-84993965514.
10.1016/j.ast.2016.10.016
Google Scholar
6 Xu Y., Yue B., Yang Z., Zhao L., and Yang S., Study on the chaotic dynamics in yaw–pitch–roll coupling of asymmetric rolling projectiles with nonlinear aerodynamics, Nonlinear Dynamics. (2019) 97, no. 4, 2739–2756, https://doi.org/10.1007/s11071-019-05159-3, 2-s2.0-85070201797.
10.1007/s11071-019-05159-3
Google Scholar
7 Zhong Y. W., Wang L. M., Chang S. J., and Fu J., Stability analysis of periodic solutions for nonlinear angle motion of projectiles and rockets, Journal of Ballistics. (2015) 27, no. 3.
Google Scholar
8 Zhong Y. W., Wang L. M., Fu J., and Chang S. J., Hopf bifurcation analysis of nonlinear angular motion stability of projectile, Acta Armamentarii. (2015) 36, no. 7, 1195–1202.
Google Scholar
9 Chang S. and Li D., Homotopy-analysis-method-based solutions of quintic nonlinear angular motion for projectiles, Journal of Spacecraft and Rockets. (2018) 55, no. 3, 669–680, https://doi.org/10.2514/1.A33864, 2-s2.0-85048075383.
10.2514/1.A33864
Google Scholar
10 Yu J. S., Cai G. Q., and Lin Y. K., A new path integration procedure based on Gauss-Legendre scheme, International Journal of Non-Linear Mechanics. (1997) 32, no. 4, 759–768, https://doi.org/10.1016/S0020-7462(96)00096-0.
10.1016/S0020-7462(96)00096-0
Web of Science® Google Scholar
11 Huang Y. and Yang C., Stability analysis of the projectile based on random center manifold reduction, Theoretical & Applied Mechanics Letters. (2023) 13, no. 1, article 100385, https://doi.org/10.1016/j.taml.2022.100385.
10.1016/j.taml.2022.100385
Google Scholar
12 Eason R. P. and Dick A. J., A parallelized multi-degrees-of-freedom cell mapping method, Nonlinear Dynamics. (2014) 77, no. 3, 467–479, https://doi.org/10.1007/s11071-014-1310-8, 2-s2.0-84905081725.
10.1007/s11071-014-1310-8
Google Scholar
13 Li Z., Jiang J., and Hong L., Noise-induced transition in a piecewise smooth system by generalized cell mapping method with evolving probabilistic vector, Nonlinear Dynamics. (2017) 88, no. 2, 1473–1485, https://doi.org/10.1007/s11071-016-3323-y, 2-s2.0-85008466134.
10.1007/s11071-016-3323-y
Web of Science® Google Scholar
14 Xu Y., Guo R., Jia W., and Li J., Stochastic averaging for a class of single degree of freedom systems with combined Gaussian noises, Acta Mechanica. (2014) 225, no. 9, 2611–2620, https://doi.org/10.1007/s00707-013-1040-x, 2-s2.0-84906321018.
10.1007/s00707-013-1040-x
Web of Science® Google Scholar
15 Wehner M. F. and Wolfer W. G., Numerical evaluation of path-integral solutions to Fokker-Planck equations. II. Restricted stochastic processes, Physical Review A. (1983) 28, no. 5, 3003–3011, https://doi.org/10.1103/PhysRevA.28.3003, 2-s2.0-5544294159.
10.1103/PhysRevA.28.3003
Web of Science® Google Scholar
16 Wehner M. F. and Wolfer W. G., Numerical evaluation of path-integral solutions to Fokker-Planck equations. III. Time and functionally dependent coefficients, Physics. (1987) 35, no. 4, 1795–1801, https://doi.org/10.1103/PhysRevA.35.1795, 2-s2.0-5544243785.
10.1103/PhysRevA.35.1795
CAS Google Scholar
17 Naess A. and Moe V., Efficient path integration methods for nonlinear dynamic systems, Probabilistic Engineering Mechanics. (2000) 15, no. 2, 221–231, https://doi.org/10.1016/S0266-8920(99)00031-4, 2-s2.0-0033874591.
10.1016/S0266-8920(99)00031-4
Web of Science® Google Scholar
18 Wang Y., Generalized Fokker–Planck equation with generalized interval probability, Mechanical Systems and Signal Processing. (2013) 37, no. 1-2, 92–104, https://doi.org/10.1016/j.ymssp.2012.02.013, 2-s2.0-84876894364.
10.1016/j.ymssp.2012.02.013
CAS Google Scholar
19 Peng J., Wang L., Wang B., Yuan M., and Xu W., A new path integration method for the stochastic system under Poisson white noise excitation based on a probability mapping, Journal of Sound and Vibration. (2024) 571, article 118037, https://doi.org/10.1016/j.jsv.2023.118037.
10.1016/j.jsv.2023.118037
Google Scholar
20 Peng J. H., Wang L., Wang B. C., Dong S. Q., and Xu W., Path integration method based on a decoupling probability mapping for fast solving the stochastic response of dynamical systems, International Journal of Non-Linear Mechanics. (2023) 156, article 104504, https://doi.org/10.1016/j.ijnonlinmec.2023.104504.
10.1016/j.ijnonlinmec.2023.104504
Google Scholar
21 Namachchivaya N. S., Stochastic bifurcation, Applied Mathematics and Computation. (1990) 39, no. 3, 37s–95s, https://doi.org/10.1016/0096-3003(90)90003-L, 2-s2.0-44949290285.
10.1016/0096-3003(90)90003-L
Google Scholar
22 Reeves P. M., Campbell G. S., Ganzer V. M., and Joppa R. G., Development and application of a non-Gaussian atmospheric turbulence model for use in flight simulators, NASA Contractor Report NASA CR-2451, 1974, University of Wash-ington.
Google Scholar
23 Robinson P. A. and Reid L. D., Modeling of turbulence and downbursts for flight simulators, Journal of Aircraft. (1990) 27, no. 8, 700–707, https://doi.org/10.2514/3.25343, 2-s2.0-0025475464.
10.2514/3.25343
Google Scholar
24 Chen J., Yang J., and Li J., A GF-discrepancy for point selection in stochastic seismic response analysis of structures with uncertain parameters, Structural Safety. (2016) 59, 20–31, https://doi.org/10.1016/j.strusafe.2015.11.001, 2-s2.0-84949492533.
10.1016/j.strusafe.2015.11.001
Google Scholar

All articles

Response Analysis of Projectile System Under Gaussian Noise Excitation Using Path Integral Method

Abstract

1. Introduction

2. Introduction of Algorithm and Model

2.1. System of Projectile Angular Motion

2.1.1. Projectile System Under Gaussian White Noise External Excitation

2.1.2. Projectile System Under Gaussian White Noise Parametric Excitation

2.2. PI Method Based on a Decoupling Probability Mapping

3. Numerical Examples

3.1. Projectile System Under Gaussian White Noise External Excitation

3.2. Projectile System Under Gaussian White Noise Parametric Excitation

4. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Response Analysis of Projectile System Under Gaussian Noise Excitation Using Path Integral Method

Abstract

1. Introduction

2. Introduction of Algorithm and Model

2.1. System of Projectile Angular Motion

2.1.1. Projectile System Under Gaussian White Noise External Excitation

2.1.2. Projectile System Under Gaussian White Noise Parametric Excitation

2.2. PI Method Based on a Decoupling Probability Mapping

3. Numerical Examples

3.1. Projectile System Under Gaussian White Noise External Excitation

3.2. Projectile System Under Gaussian White Noise Parametric Excitation

4. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information