International Journal of Aerospace Engineering

Volume 2025, Issue 1 5522713

Research Article

Open Access

Adaptive Feedforward Vibration Control of Helicopter Cabin Floor Driven by Piezoelectric Stack Actuators: Modeling, Simulation and Experiments

Laishou Song,

Corresponding Author

Laishou Song

[email protected]

orcid.org/0000-0002-5417-7245

National Key Laboratory of Helicopter Aeromechanics , College of Aerospace Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , China , nuaa.edu.cn

Search for more papers by this author

Yingquan Wang,

Yingquan Wang

National Key Laboratory of Helicopter Aeromechanics , College of Aerospace Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , China , nuaa.edu.cn

Search for more papers by this author

Xiaoyu Shen,

Xiaoyu Shen

National Key Laboratory of Helicopter Aeromechanics , College of Aerospace Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , China , nuaa.edu.cn

Search for more papers by this author

Laishou Song,

Corresponding Author

Laishou Song

[email protected]

orcid.org/0000-0002-5417-7245

National Key Laboratory of Helicopter Aeromechanics , College of Aerospace Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , China , nuaa.edu.cn

Search for more papers by this author

Yingquan Wang,

Yingquan Wang

National Key Laboratory of Helicopter Aeromechanics , College of Aerospace Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , China , nuaa.edu.cn

Search for more papers by this author

Xiaoyu Shen,

Xiaoyu Shen

National Key Laboratory of Helicopter Aeromechanics , College of Aerospace Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , China , nuaa.edu.cn

Search for more papers by this author

First published: 24 March 2025

https://doi.org/10.1155/ijae/5522713

Academic Editor: Ke Feng

Share a link

Email
Wechat
Bluesky

Abstract

Active control of structural response is the most practical and effective approach to mitigate helicopter vibration and enhance ride quality. In this paper, adaptive feedforward vibration control is constructed for the helicopter cabin floor driven by piezoelectric stack actuators (PSAs). A scale helicopter airframe model, preserving the local geometric similarity of the cabin floor structure, is developed and optimized to capture the low-order global dynamic characteristics of a reference airframe. The model of PSA is integrated into the attached beam element based on the conditions of force equilibrium and displacement compatibility, and adaptive feedforward control is implemented by the filtered-x least mean square (Fx-LMS) algorithm. Simulations and experimental studies under diverse excitations have been carried out. Results indicate that the adaptive PSA-driven ride quality improvement system can effectively reduce the cabin floor vibration, and the responses under multidirection excitations can also be reduced by more than 90%. It is also observed that the responses at different control points exhibit inconsistent convergence due to the interference of modes under multidirection excitations.

1. Introduction

Vibration is a key factor for comfort evaluation of an aircraft [1, 2]. Reducing helicopter vibration continues to be an area of intense interest in helicopter dynamics [3]. Owing to its better control effectiveness than passive devices, active vibration control has become the most practical and effective technology to reduce helicopter vibration [4]. Active control of structural response (ACSR), with actuators positioned in the airframe structure, presents a lot of advantages such as better control effectiveness, greater reliability, and lower power consumption [5, 6]. The power consumption of airframe-based ACSR has been estimated at an order of magnitude lower than the rotor-based higher harmonic control (HHC) system [7, 8]. Several studies about the actuator, control law, modeling technology, and model experiment have been carried out to improve the control performance. ACSR, using inertial actuators, has been extensively investigated and extended to the compound helicopter [9, 10].

Piezoelectric stack actuator, thanks to its lightweight, high efficiency, and wide operating frequency range, has become an attractive actuator in active vibration control of aerospace structure [11] and has been comprehensively reviewed in a recent reference [12]. To improve the drive efficiency, a novel concept of piezoelectric actuator, named offset piezoelectric stack actuator (OPSA) is proposed and tested [13, 14]. The optimal offset distance can be determined by the criterions of the stiffness matching [13] or modal damping ratio [15]. This actuation concept has been investigated for vibration control of the aircraft [16] and space structures [15, 17]. The piezoelectric actuator can overcome the weight penalty problem of inertia actuators. It is also suitable for multiharmonic vibration control and the rotational speed change of the rotor. Hanagud and Badu [18] investigated the feasibility of using piezoelectric actuators in active vibration control of a helicopter airframe. A single-input–single-output (SISO) control for a beam model is constructed, and simulation results show that the vibration response at the control point was reduced by 60%. Friedmann and Millott [6, 19, 20] numerically investigated the placement influence and control ability of the PSAs in active helicopter vibration control using a reduced-order elastic linear finite element airframe model. They also conducted experimental studies on a cantilever tail beam model by installing the piezoelectric stack actuators at its clamped end. Results indicate that the PSA could be effectively used for reducing helicopter vibration, and the distributed actuation strategy has a stronger ability of vibration suppression and requires less control power than a centralized actuation configuration around the gearbox. Song and Xia [21] proposed a harmonic synchronous identification-updating method for active control of helicopter structural response, and experiments were conducted on a free–free beam driven by PSAs. Meng et al. [22] modeled the cabin floor structure as a cantilever frame structure. Simulations of the multi-input–multioutput–multiharmonic (MIMOMH) feedforward vibration control were carried out on this model. Singhvi and Vennkatesan [23] conducted a conceptual research in which the PSA was installed between the gearbox and airframe based on a highly simplified two degrees of freedom model, and the control performance was examined by simulation. Further, based on the rigid model assumption of the rotor/gearbox and airframe, Lang and Xia [24] constructed a vibration control model consisting of the rotor/gearbox, airframe, and four active struts driven by PSAs, and the control performance was examined by simulations.

Owing to the available frequency information of the helicopter vibration, the frequency-domain control algorithm and frequency-shaping control have been used for helicopter vibration control. The HHC algorithm, a frequency-domain control method, using discrete Fourier transform (DFT) has been effectively used in active helicopter vibration control [25]. In order to overcome the shortcomings of the DFT-based frequency-domain control method, Song and Xia [21] proposed the harmonic synchronous identification-updating method by harmonic coefficient identification, and then, this method was extended to the adaptive hybrid control of helicopter vibration [24]. Time-domain feedback control methods such as the H_∞ control [18], feedback control based on the internal model principle [26], and linear quadratic feedback control [27] have been redesigned by the frequency-shaping methodology for helicopter vibration control studies. The partial pole placement based on the receptance method has been tentatively used for helicopter vibration control [28]. The filtered-x least mean square (LMS), an adaptive time-domain filtering algorithm, is effectively used in active noise and vibration control when the reference signals are easy to obtain [29, 30]. For the helicopter vibration control, the revolution speed transducer of the rotor facilitates the acquirement of the reference signal, so the adaptive feedforward control based on filtered-x LMS is employed to construct the helicopter vibration control system.

In this paper, adaptive feedforward vibration control of helicopter cabin floor driven by piezoelectric stack actuators has been constructed. A scale airframe model is developed based on a reference helicopter. The scale model, preserving the local geometric similarity of the cabin floor structure, is optimized to capture the low-order global dynamic characteristics of the reference airframe, and then, the modal test is conducted to verify its dynamic characteristics. The concept of OPSA is employed, and the PSA is parallelly integrated into the structural beam though through rigid brackets. Adaptive feedforward control is implemented by the filtered-x LMS algorithm, and the simulation and experiment system have been constructed. Simulations and experimental studies under different excitations are carried out to investigate the effectiveness and performance of the constructed active vibration control system.

2. Scaled Airframe Structure

A scale airframe model characterized by dynamic similarity is an effective equipment to assess the vibration control performance. A laboratory dynamic similarity model used to design and evaluate the active control system should not be overly complex nor expensive to produce. However, it should be sophisticated enough to preserve the low-order global dynamic characteristics of the reference structure. It also has a local geometric similarity to the cabin floor, which means the locations of the sensors and actuators on the scale model can match the layout of the active vibration control system for the reference helicopter.

2.1. Scaled Modeling of an Airframe Structure

A 1/3 scale airframe model that can represent the global dynamic characteristics and local cabin floor features of a reference helicopter is shown in Figure 1. The overall dimensions of the model are L = 5.0 m in length, W = 0.6 m in width, and H = 0.95 m in height, respectively. This model is composed of the forward cabin floor, middle and intermediate airframe, tail boom, and main gearbox system. The cabin floor, middle and intermediate airframe, and the tail boom are made up of Euler–Bernoulli’s beams with a rectangular cross-section. The main gearbox and supporting system are modeled as a rigid body and rods, respectively. The modal parameters of the scale model are optimized by adjusting the width and height of the beam. In order to improve the optimization efficiency and extend the parameter feasible domain, several lumped mass elements on the cabin floor are also selected as optimization parameters. The cabin floor structure is the most important part, and it consists of 11 different types of beams. The middle and intermediate airframe with high stiffness is composed of two different types of beams, and the tail boom is also composed of two different types of beams. Each beam has two variable cross-section parameters (height and width), and there are five pairs of variable concentrated masses denoted by black spots on the floor. The numbers of the different beams are shown in Figure 1, and the more detailed information is listed in Table 1. There are a total of 35 parameters of the scale model that can be optimized. The finite element model is established in MATLAB, and the optimization problem is defined as follows:

()

where ω_i is the i^th modal frequency of the scale model;

is the reference frequency; w_i is the weighting factor for i^th modal frequency; b_j is j^th section parameter (width or height) of the beam, and

and

are the lower and upper bounds of the parameter b_j, respectively; m_k is the k^th concentrated mass, and

and

are the lower and upper bounds of the parameter m_k, respectively; MAC is the modal assurance criterion, and the MAC_i is defined as follows:

()

where φ_i is the i^th mode shape of the scale model and

is the reference mode shape. The value of MAC_i will be from zero, representing no correlation, to one, representing complete consistency. The threshold Z_i is set to 0.9, which means a very good correlation in practice [31].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

1/3 scale airframe model.

Table 1. Position and direction of the beam and mass and their optimal values.

Number	Position	Direction	Optimal values (mm, kg)
1	Lower cabin floor	y	6 × 10
2	Lower cabin floor	z	14 × 2
3	Lower cabin floor (outside)	x	10 × 16
4	Lower cabin floor (inside)	x	10 × 2
5	Upper cabin floor	y	12 × 2
6	Upper cabin floor	z	18 × 8
7	Upper cabin floor (outside)	x	12 × 6
8	Upper cabin floor (inside)	x	18 × 20
9	Lower cabin floor	y	4 × 6
10	Lower cabin floor	z	18 × 16
11	Connection between upper and lower cabin floor	z	12 × 10
12	Middle airframe	/	20 × 40
13	Intermediate airframe	/	35 × 45
14	Tail beam	x	40 × 40
15	Oblique tail beam	/	35 × 30
16~20	Concentrated masses from the nose of airframe to the back	/	0, 1.3, 0.5, 0, 1.2

Low-order mode is an important factor of the dynamic analysis. Relative to the high-order modes, the low-order modes are required to achieve higher dependability in the design of helicopter airframe structure. On the other hand, a laboratory scale model is difficult to simultaneously capture the low-order and high-order reference modes due to the structural simplification and manufacturing costs. Referring to the literature [32], the first four modes are selected to be optimized for the dynamical similarity. The reference frequencies are extracted from the ground vibration tests of a helicopter, and the mode shapes used for calculating MAC_i are the modal displacements (excluding the rotational degrees of freedom) at the measure points along the airframe. The optimal parameter values are shown in Table 1. The modal parameters of the optimized model and reference modes are shown in Table 2. The material is steel with elastic modulus E = 2.09 × 10¹¹ Pa, density ρ = 7890 kg/m³, and Poisson’s ratio μ = 0.27. It can be seen that the maximum error of the natural frequency between the optimized scale model and reference airframe is 3.13%, and all the MAC_i are greater than 0.92.

Table 2. Modal parameters of the optimized model versus reference modes.

Modes	Calculated (Hz)	Reference (Hz)	Error	MAC
First (vertical bending)	10.06	9.75	3.13%	0.97
Second (lateral bending)	10.15	10.18	0.28%	0.98
Third (vertical bending)	16.76	16.86	0.62%	0.97
Fourth (lateral bending)	18.46	18.96	2.61%	0.92

2.2. Dynamic Test of the Scale Model

The physical model is fabricated and is shown in Figure 2a. During the test, the model is suspended to simulate a free–free boundary condition. The suspension frequency is 2.93 Hz, and the ratio of the suspension frequency to the first elastic frequency is less than 1/3, which is a practicable criterion in the sense of engineering [33, 34]. The schematic diagram of the test system is shown in Figure 2b, and the distributed dots indicate the layout of the measuring points. The modal test and analysis are performed by the LMS test. The lab system is operating in the mode of the impact hammer test method. The modal parameters of the physical model versus reference are shown in Table 3, and the mode shapes are shown in Figure 3. It can be seen that the dynamic characteristics of the fabricated model are in good agreement with the reference modes except for the third natural frequency. Fortunately, the control frequency of 25.5 Hz is a considerable distance away from the third mode frequency of 19.07 Hz. The steady-state harmonic response at 25.5 Hz is less affected by the low-damping structure. The transient response due to the closer natural frequency has an adverse effect on steady-state harmonic control, especially on the convergence characteristics. Compared with the calculated results, experimental modes have a little greater error. Considering the dynamic similarity characteristic and severe vibration environment of the manufactured scale model, it can be used to evaluate the control performance of the proposed control system in the sense of laboratory tests.

Table 3. Modal parameters of the scale physical model versus reference modes.

Modes	Experimental (Hz)	Reference (Hz)	Error	MAC
First (vertical bending)	9.90	9.75	1.54%	0.90
Second (lateral bending)	9.98	10.18	1.97%	0.91
Third (vertical bending)	19.07	16.86	13.11%	0.96
Fourth (lateral bending)	18.05	18.96	4.8%	0.95

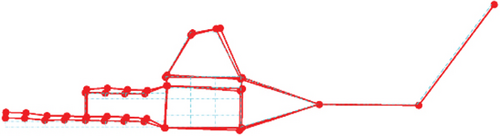
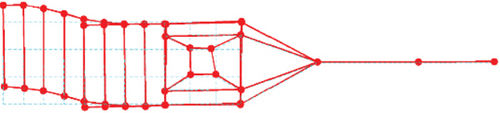
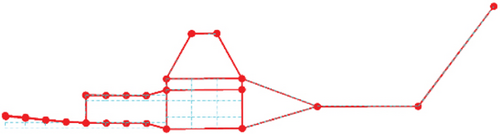
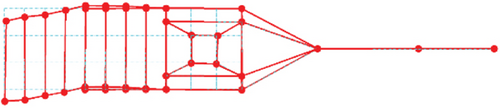
3. Adaptive Feedforward Cabin Floor Vibration Control Driven by Piezoelectric Stack Actuators

Piezoelectric stack actuator is made of multilayer piezoceramic disks mechanically in series and electrically in parallel. It can produce large force and displacement outputs under low voltage input (0~150 V) and has become an effective and practical actuator in active control of aerospace structure.

3.1. PSA–Structure Coupling Model

In this research, the concept of OPSA is employed in that the PSA is installed parallel to the beam through rigid brackets and is connected to a flexible hinge to avoid a large moment exerting on itself. The advantages of OPSA are summarized in Ref. [15]. The schematic diagram and its prototype are shown in Figure 4. δ is the offset distance of the piezoelectric stack actuator to the neutral axis of the attached beam and is optimized by the criterions of the stiffness matching to maximize the control ability [13]. The coupled model of the PSA and beam is constructed based on the conditions of force equilibrium and displacement compatibility at the connected points.

The constitutive equation of piezoelectric material in actuation direction 3–3 is expressed as

()

where σ₃ is the stress, ε₃ is the strain, E₃ is the applied electric field,

is the modulus of elasticity at zero or constant electric field, and e₃₃ is the piezoceramic stress constant.

The electric field E₃ related to the applied voltage v is given as E₃ = v/t, where t is the thickness of each piezoceramic disk. Then, the model of the piezoelectric stack actuator can be derived as

()

where

and

denote the nodal forces and displacements at the ends of PSA, respectively. A and L are the cross-section and length, respectively.

The element stiffness and mass matrix of the beam with PSA are denoted as

and

. The degree of freedom of the beam is

, and the corresponding nodal control forces generated by the PSA are given by

()

where

The relationships of the nodal control forces

and displacements

of the beam and the actuation force

and displacement

of the PSA are expressed as

()

Substituting Equation (7) into Equation (4) and then substituting Equation (4) into Equation (5), the nodal control forces

can be given by

()

Matrix

and Ae₃₃/t[1 − 1 δ − δ]^T are denoted by K_pzt and B_pzt, respectively. Incorporating the stiffness contribution of the PSA into the structural finite element, the stiffness matrix

and the control force vector

of the electromechanical coupling element become as follows:

()

The inertial contribution of the PSA is incorporated into the structural finite element. The mass matrix of the electromechanical coupling element becomes as follows:

()

Replacing the conventional beam element with the electromechanical coupling element, the dynamic equation of the PSA-driven airframe structure can be obtained as

()

where M_c, C_c, K_c are the mass, damping, and stiffness matrix of the coupling structure with the mechanical contribution of the PSAs; F and V are the exciting forces from a rotor and control voltage, respectively; B₁ and B₂ are the input matrices for the exciting forces F and control voltages V, respectively.

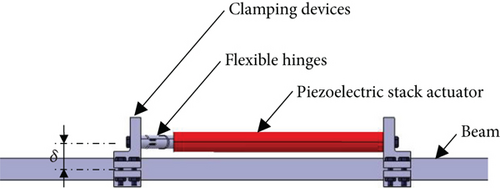
It can be seen from Equation (8) that the resultant control force exerted by PSA depends on not only the control voltage but also the displacement response at the driving point. The power output of PSA is discussed in detail in Reference [35]. The optimal power output of PSA is determined by the stiffness matching principle K_pzt = K_str(ω). K_str(ω) is the dynamic stiffness of the actuation point at control frequency ω. This stiffness-matched principle can be achieved by distributed multi-PSAs around the structure.

In engineering application, a practical actuation concept for an actual helicopter structure could be the formulation of an active PSA-driven frame member to replace an existing passive frame member of the airframe. The active frame member would generate a force and displacement distribution around its perimeter. The control forces can be also applied at the intersection of stringers and adjacent frame members by multi-PSAs. Active struts driven by distributed multi-PSAs have been employed to reduce the dynamic loads of the main gearbox for interior noise control, and control performance is demonstrated by the flight tests [36].

3.2. Adaptive Feedforward Control Based on Filtered-x LMS

The helicopter vibration mainly comes from the main rotor excitations, and it is characterized by the steady-state harmonic response at the blade passing frequency and its higher harmonic frequencies. The clear frequency information facilitates the acquirement of the reference signal, so the adaptive feedforward control is an effective way to control the helicopter vibration. The schematic of adaptive feedforward control of helicopter vibration based on the filtered-x LMS algorithm is shown in Figure 5. H is a dynamic description of the N_c-inputs/N_m-outputs secondary path, including the dynamic characteristic of the PSAs, control path of the model, and the measurement system. N_c and N_m are the numbers of the actuators and sensors, respectively.

and

are the vectors of the control inputs and control error responses.

and

are the vectors of the rotor excitation responses and actuation responses, respectively. The secondary path H is defined as

()

where

is the secondary path from the i^th control input to the j^th control outputs in the form of the finite impulse response (FIR) filter. x(n) is the reference signal which must be well-correlated with the rotor excitation. r(n) is the matrix of filtered reference signals, and its element r_ij(n) = h_ij ⊗ x(n) (symbol ⊗ denotes the discrete convolution) is the filtered reference signal x by the secondary path h_ij.

is a N_c-dimension adaptive controller.

is a

FIR filter, and its weight coefficients are updated by the LMS algorithm to minimize the error signals (accelerations) in the least squares sense. The cost function J is defined as

()

where e_i is the control error signal from the i^th accelerometer, which can be written as

()

where d_i is the rotor excitation response and

is the additional response caused by all actuators at the i^th control point.

()

The control signal that is fed to the j^th actuator v_j(n) is given by

()

where w_jk is the k^th weights of the j^th FIR control filter and x is the reference signal and has the same frequency information with the rotor excitation. During the control procedure, the reference signal x = sin(NΩ) is generated in the digital signal processor, and the frequency information Ω can be provided by the revolution speed transducer of the rotor (N is the number of rotor blades). The weights w_j are updated as

()

Based on the assumption that the adaptive filter w_j varies slowly, the adaptive updating process is given by [29].

()

where r_i,j is the reference signal x filtered by the secondary path from the j^th actuator to the i^th accelerometer and the factor μ is the step-size. The weights of the controller are updated by the filtered reference signal r_i,j and real-time response e_i(n), which can track the changes in the vibration environment.

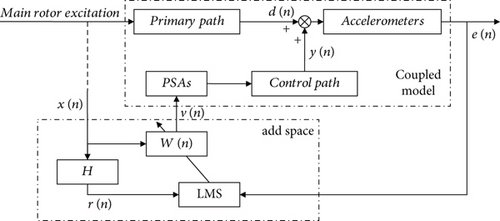
The adaptive control process can be summarized as follows: The weight coefficients of the adaptive controller are initialized firstly (usually W(0) = 0). The gradient of the cost function J is calculated by the filtered-x signal r_ij(n) and sampled control error signals e(n) at time n, and the next-step weight coefficients w_j(n + 1) are updated by recursive Formula (17). And then, the control voltage v_j(n + 1) for the j^th actuator is calculated by Formula (15). The stability of the filtered-x LMS and the effects of secondary path modeling errors on this algorithm have been investigated extensively [37]. Errors in the magnitude of the secondary path will alter the maximum stable value of step-size μ through an inverse proportional relationship. In other words, there is a step-sizeμthat made this algorithm stable, provided the error in the estimation of the phase of the secondary path does not exceed 90°. Comprehensive summaries can be found in Ref. [38].

4. Simulations of Adaptive Feedforward Cabin Floor Vibration Control

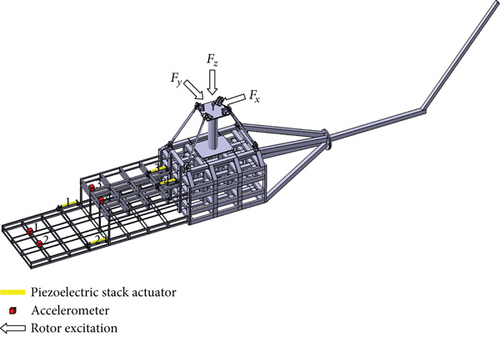
Reducing the vibration level of the cabin floor is the most important to improve ride quality. Four positions on the cabin floor are selected as control points, and the locations of PSAs are determined through optimization. The layout of accelerometers and PSAs is shown in Figure 6. The PSA used in simulation is PSt150/10/160VS15, a mechanical packaged piezoelectric stack actuator. The parameters of the PSt150/10/160VS15 and its offset distance δ are listed in Table 4. Normally, the vibration caused by the main rotor at blade passing frequency NΩ (N =5 is the number of blades, and Ω = 306 rpm is the rotational speed) is the control objective. The forces F_x, F_y, and F_z are applied to the hub to simulate the rotor vibratory loads. The excitation frequency is the blade passing frequency NΩ = 25.5 Hz of the reference helicopter. Simulations with different excitations are carried out. In simulations, the control system turns on 5 s after the excitation is applied. The sampling frequency is 1000 Hz.

Table 4. Parameters of the piezoelectric stack actuator (PSt150/10/160VS15).

Parameters (units)	Values
Free displacement (μm)	152
Block force (N)	2300
Stiffness (N/m)	13 × 10⁶
First natural frequency (Hz)	6000
Working voltage range (V)	−30~150
Length (mm)	154
Mass (g)	130
Offset distance (δ/mm)	20

4.1. Simulation Under Single Vertical Excitation

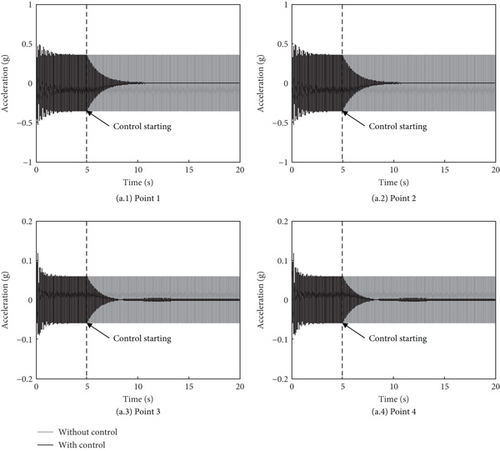
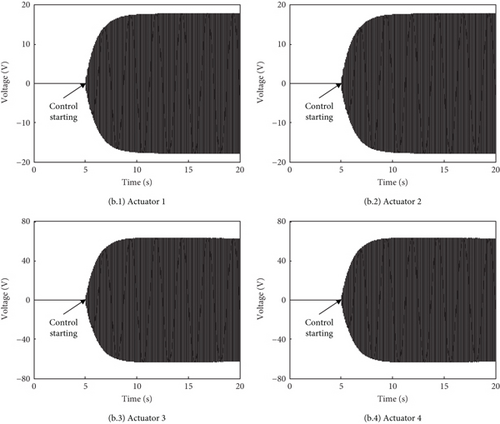
Simulation under a single vertical force F_z = 300 sin (2π·25.5 t N is carried out firstly to investigate the effectiveness of the constructed active control system. The amplitude of F_z is determined by the vibratory environment similarity on the cabin floor between the scale model and reference helicopter. In simulation, the vertical accelerations of the four control points are selected to be controlled. The maximum amplitude at the control points achieves 0.35 g under the excitation F_z. The adaptive feedforward control turns on at 5 s after the excitation is applied. The acceleration responses with and without control are shown in Figure 7a, and the associated control voltages of the PSAs are given in Figure 7b. It can be seen that when the control reaches a steady state, the amplitudes at Points 1, 2, 3, and 4 decrease by 99%, 99%, 96%, and 96%, respectively. All the responses decay more than 80% in 1.5 s. The control voltage amplitudes of the four PSAs are about 18, 18, 63, and 63, respectively.

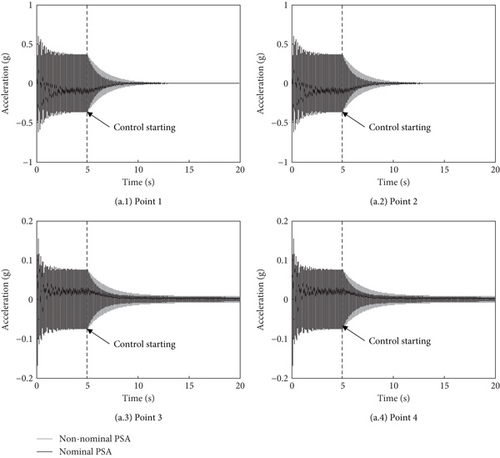
In order to assess the influence of the nonnominal behavior in the actuator, a simulation with half-drive ability is conducted. Figure 8 shows the comparative analysis with nominal and nonnominal PSAs. It can be seen that both simulations are stable and the convergence rate with nominal PSAs faster than nonnominal PSAs. It is worth noting that although the nonnominal behavior used in simulation is only a theoretical possibility and there are more possibilities in engineering applications, robustness is an important characteristic of the filtered-x LMS algorithm [33].

4.2. Simulation Under Three-Directional Excitations

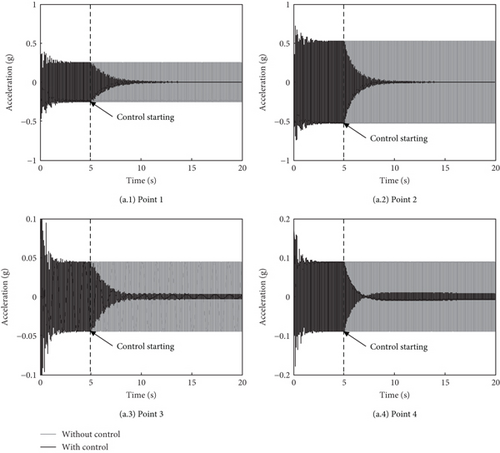
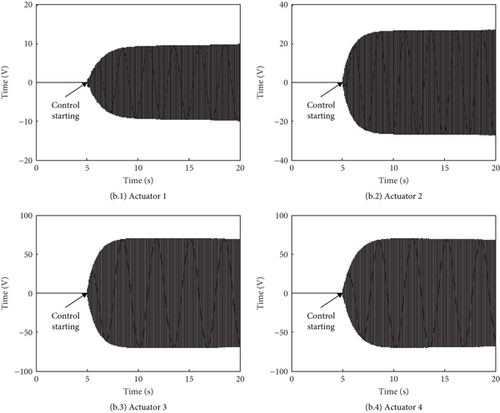
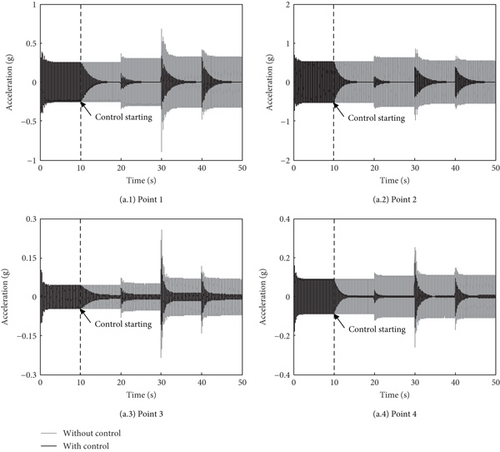
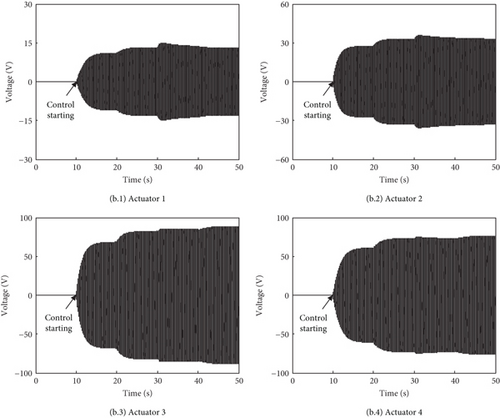
The three-directional forces F_x, F_y, and F_z are F_x = 100 sin (2π·25.5 t N, F_y = 100 sin (2π · 25.5 t + π/2 N), F_z = 300 sin (2π · 25.5 t + π/2 N). These excitations are set based on the ratio of 1/10 of the vertical dynamic load to the thrust (the mass of the model is about 300 kg) as the reference helicopter and then checked by the vibration level of about 0.5 g at the cabin floor. The relative amplitude and phase of the forces F_x and F_y to F_z are determined according to the characteristics of rotor excitations. The amplitudes of the steady-state responses without control at Points 1, 2, 3, and 4 are 0.25, 0.53, 0.045, and 0.09 g, respectively. The adaptive feedforward system turns on at 5 s after the excitations are applied. The acceleration responses with and without control are shown in Figure 9a, and the control voltages of the four PSAs are shown in Figure 9b. It can be seen that after the control reaches a steady state, the amplitudes at Points 1, 2, 3, and 4 decrease by 99%, 99%, 92%, and 94%, respectively, and all the responses decay more than 80% in 2 s. The control voltage amplitudes of the four PSAs are about 10, 27, 70, and 68 V, respectively. Simulation results indicate the excellent performance and convergence speed of the constructed active control system. Compared with the single vertical excitation, it is observed that the convergence rate becomes slightly complex and slower when the responses include more modes. Responses at some points converge faster than others, and responses at some points have an increasing phenomenon in the process of convergence. This inconsistent convergence is caused by the coupling effect of the MIMO control system associated with the condition number of the secondary Path H at the control frequency. And this inconsistent phenomenon becomes more serious as the condition number increases [37]. Due to the symmetrical characteristic, the control system under the vertical excitation essentially runs in a 2-inputs/2-outputs state and the condition number is 14.5. The torsion modes can be excited by the transversal excitation, so the control system under the three-directional excitations runs in a 4-inputs/4-outputs state, and the condition number is 105.6. So the inconsistent convergence is easier to observe with the three-directional excitations.

4.3. Simulation Under Excitation–Changes

In order to verify the adaptive tracking performance of the constructed active vibration control system, simulations under excitation–change situations are carried out. These changes are implemented by altering the excitation amplitude, frequency, and phase. The initial excitations are the same as those used in Section 4.2; then, the amplitude of excitation increases by 20% at 20 s, the frequency of excitation changes by 5% at 30 s, and the phase of excitation increases by π/6 at 40 s. Figure 10a shows the acceleration responses at measuring Points 1, 2, 3, and 4 under excitation–change situations, and Figure 10b shows the control voltages of the four piezoelectric stack actuators. It can be seen that under the excitations with changes in the amplitude, phase, and frequency, the active control system has an adaptive capability of tracking the changes in excitation. The vibration suppression can achieve more than 80% in 2 s after the excitations change.

5. Experimental Investigations of Adaptive Forward Cabin Floor Vibration Control

Based on the scale airframe model and adaptive feedforward control strategy, an experimental system of active cabin floor vibration control driven by PSAs has been developed. The modal test is carried out to examine the influence on dynamic characteristics of the overall system with PSA installation, and the results are listed in Table 5. The results show that overall modes are scarcely influenced, and the third modal frequency slightly increases due to stiffness contribution. Experiments under different excitations are carried out to investigate the effectiveness and performance of the constructed active vibration control system.

Table 5. Modal parameters with and without PSAs.

Modes	With PSAs (Hz)	Without PSAs (Hz)	Error
First (vertical bending)	9.90	9.88	−0.2%
Second (lateral bending)	9.98	10.01	0.3%
Third (vertical bending)	19.07	19.50	2.3%
Fourth (lateral bending)	18.05	18.13	0.4%

5.1. Experimental System

The experimental setup is shown in Figure 11. The control objective is focused on the lower cabin floor where the vibration level is high. The layout of the accelerometers and PSAs is shown in Figure 11. The vibratory loads are applied by electromagnetic exciters. The experimental studies also include two excitation cases: (1) a single vertical force and (2) the combination of the vertical and horizontal forces. The PSA PSt150/10/160VS15 used in the experiment is the same as in the simulation. In the experiments, the control system turns on a few seconds after the excitation is applied, and the sampling frequency is 1000 Hz.

5.2. Experiment Results and Analyses

5.2.1. Experiment Under Single Vertical Excitation

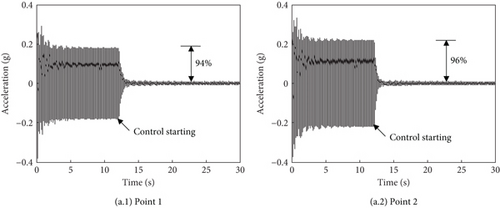
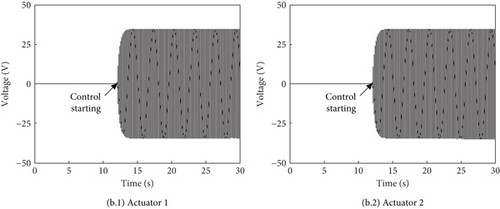
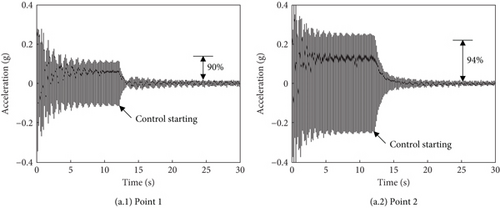
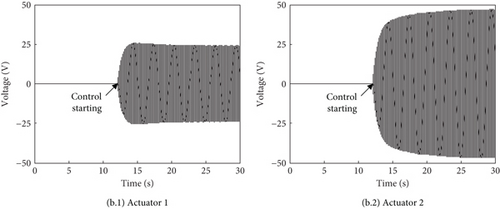
In the experiment, a single vertical force is applied at the hub center, and the excitation frequency is the blade passing frequency NΩ = 25.5 Hz. After the exciting force turns on, the active control system starts at 10 s. Points 1 and 2 on the lower cabin floor are selected to be controlled, and a 2-input–2-output control system is constructed. Figure 12a shows the acceleration responses at the two control points. The responses decrease from about 0.2–0.01 g in less than 1 s and keep stable. The vibration amplitudes at these two points decrease by 94% and 96%, respectively. It can be seen that the constructed active vibration control system driven by PSAs can effectively reduce the cabin floor vibration. When the control objective is focused on the high-vibration region, the responses have a faster convergence rate. The maximum amplitudes of the control voltages are both about 28 V as shown in Figure 12b.

5.2.2. Experiment Under Combined Vertical and Horizontal Excitations

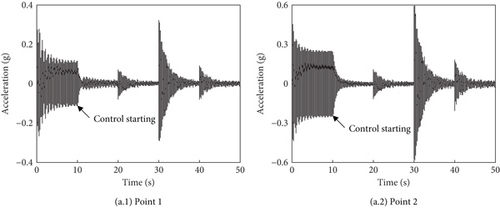
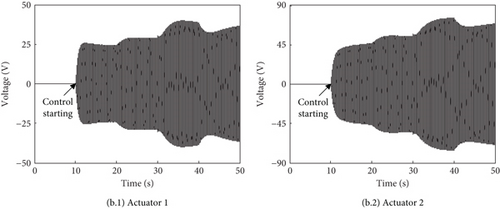
In this experiment, the excitations contain the vertical force and horizontal force. Both forces are applied at the hub center. The horizontal force can excite the torsional and coupled modes of vibration. Figure 13a shows the acceleration responses at the two points, and the vibration of asymmetrical modes is obviously observed. The response at Point 1 decreases by 80% from 0.12 to 0.024 g after 4 s, and the response at Point 2 decreases by 80% from 0.25 to 0.05 g in less than 1 s. Vibrations at these two points decrease by 90% and 94% after converging to a quasisteady state, respectively. It can be seen that the constructed active vibration control system can effectively reduce the cabin floor vibration under the combined vertical and horizontal excitations. Compared with the single vertical excitation, the vibration under the combined excitations has a slightly lower and inconsistent convergence rate. The responses at some points converge faster than others, and responses at some points have an increasing phenomenon in the process of convergence. This phenomenon is also observed in the simulation analysis. The maximum amplitudes of the control voltages are 25 and 47 V, respectively, as shown in Figure 13b.

5.2.3. Experiment Under Excitation–Changes

In order to verify the adaptive tracking performance of the constructed active vibration control system experimentally, tests under excitation–change situations are carried out. These changes are implemented similarly by altering the excitation amplitude, frequency, and phase. The initial excitations are the same as those used in the previous Section 5.2, and then, the amplitude of excitation increases by 20% at 20 s, the frequency of excitation changes by 5% at 30s, and the phase of excitation increases by π/6 at 40 s. Figure 14a shows the acceleration responses, and Figure 14b shows the control voltages. It also can be seen that under the excitations with changes in the amplitude, phase, and frequency, the active control system has an adaptive capability of tracking the changes of excitation. The vibration suppression can achieve more than 80% in 3 s after the excitations change, in which the larger transient responses lead to slower convergence than simulation.

6. Conclusions

In this paper, a scale model characterized by the local geometric and low-order global dynamic similarity characteristics is developed; then, the model is fabricated, and modal tests are conducted to verify its similar dynamic characteristics.

Active vibration control of cabin floor structure driven by piezoelectric stack actuators has been constructed for the constructed scale model, and the filtered-x LMS algorithm is employed to construct the simulation and experiment system. Simulations and experimental studies under different excitations have been carried out. The results indicate that the adaptive feedforward vibration control system can effectively reduce the cabin floor vibration and has an adaptive ability of tracking control. Moreover, the responses under multidirectional excitations can also be reduced by more than 90%.

In comparing the single vertical excitation, the responses under multidirectional excitation exciting more modes have a slightly lower and inconsistent convergence rate in both the experiment and simulation results. Responses at some points converge faster than others, and responses at some points have an increasing phenomenon in the process of convergence.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (51505214).

Open Research

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Tamer A., Muscarello V., Masarati P., and Quaranta G., Evaluation of Vibration Reduction Devices for Helicopter Ride Quality Improvement, Aerospace Science and Technology. (2019) 95, 105456, https://doi.org/10.1016/j.ast.2019.105456, 2-s2.0-85072947565.
10.1016/j.ast.2019.105456
Web of Science® Google Scholar
2 Esposito A., Orlando C., and Alaimo A., Cabin Aircraft Comfort Evaluation Over High Fidelity Simulated Flight, Aeronautical Journal. (2023) 14, no. 2, 491–508, https://doi.org/10.1007/s13272-023-00640-7, 36743353.
10.1007/s13272-023-00640-7
PubMed Google Scholar
3 Konstanzer P., Enenkl B., and Aubourg P., Recent Advances in Eurocopter’s Passive and Active Vibration Control, Annual Forum Proceedings-American Helicopter Society. (2008) 64, no. 1.
Google Scholar
4 Kim D. H., Kwak D.-I. I., and Song Q., Demonstration of Active Vibration Control System on a Korean Utility Helicopter, International Journal of Aeronautical and Space Sciences. (2019) 20, no. 1, 249–259, https://doi.org/10.1007/s42405-018-0106-3, 2-s2.0-85063775770.
10.1007/s42405-018-0106-3
Web of Science® Google Scholar
5 Heverly D., Wang K. W., and Smith E. C., An Optimal Actuator Placement Methodology for Active Control of Helicopter Airframe Vibrations, Journal of the American Helicopter Society. (2001) 46, no. 4, 251–261, https://doi.org/10.4050/JAHS.46.251.
10.4050/JAHS.46.251
Web of Science® Google Scholar
6 Friedmann P. P. and Millott T. A., Vibration Reduction in Rotorcraft Using Active Control: A Comparison of Various Approaches, Journal of Guidance, Control, and Dynamics. (1995) 18, no. 4, 664–673, https://doi.org/10.2514/3.21445, 2-s2.0-0029346745.
10.2514/3.21445
Web of Science® Google Scholar
7 Welsh W. A., Von Hardenberg P. C., and Von Hardenberg P. W., Test and Evaluation of Airframe Vibration Utilizing Active Control of Structural Response (ACSR) Optimized to ADS-27, 46th American Helicopter Society Annual Forum, 1990, Washington, DC, https://vtol.org/store/product/test-and-evaluation-of-fuselage-vibration-utilizing-active-control-of-structural-response-acsr-optimized-to-ads27-1034.cfm.
Google Scholar
8 Kessler C., Active Rotor Control for Helicopters: Motivation and Survey on Higher Harmonic Control, CEAS Aeronautical Journal. (2011) 1, no. 1-4, 3–22, https://doi.org/10.1007/s13272-011-0005-9, 2-s2.0-84880829102.
10.1007/s13272-011-0005-9
Google Scholar
9 Blackwell R. and Millott T., Dynamics Design Characteristics of the Sikorsky X2 TechnologyTM Demonstrator Aircraft, 64th American Helicopter Society Annual Forum, 2008, https://vtol.org/store/product/dynamics-design-characteristics-of-the-sikorsky-x2-technologytm-demonstrator-aircraft-3270.cfm.
Google Scholar
10 Lee Y. L., Kim D. H., Park J. S., and Hong S. B., Vibration Reduction Simulations of a Lift-Offset Compound Helicopter Using Two Active Control Techniques, Aerospace Science and Technology. (2020) 106, 106181, https://doi.org/10.1016/j.ast.2020.106181.
10.1016/j.ast.2020.106181
Web of Science® Google Scholar
11 Giurgiutiu V., Review of Smart-Materials Actuation Solutions for Aeroelastic and Vibration Control, Journal of Intelligent Material Systems and Structures. (2000) 11, no. 7, 525–544, https://doi.org/10.1106/HYTV-NC7R-BCMM-W3CH, 2-s2.0-0034216656.
10.1106/HYTV-NC7R-BCMM-W3CH
Web of Science® Google Scholar
12 Shivashankar P. and Gopalakrishnan S., Review on the Use of Piezoelectric Materials for Active Vibration, Noise, and Flow Control, Smart Materials and Structures. (2020) 29, no. 5, 053001, https://doi.org/10.1088/1361-665X/ab7541.
10.1088/1361-665X/ab7541
CAS Web of Science® Google Scholar
13 Noyer M. B. D. and Hanagud S., Modal Analysis and Optimization of the Offset Piezoceramic Stack Actuator, 41st structures, structural dynamics, and materials conference and exhibit, 2000, Atlanta, GA, U.S.A., https://doi.org/10.2514/6.2000-1792.
10.2514/6.2000-1792
Google Scholar
14 Wei W. and Zhichun Y., A Compact Piezoelectric Stack Actuator and Its Simulation in Vibration Control, Tsinghua Science and Technology. (2009) 14, no. S2, 43–48, https://doi.org/10.1016/S1007-0214(10)70029-8.
10.1016/S1007-0214(10)70029-8
Google Scholar
15 Callipari F., Sabatini M., Angeletti F., Iannelli P., and Gasbarri P., Active Vibration Control of Large Space Structures: Modelling and Experimental Testing of Offset Piezoelectric Stack Actuators, Acta Astronautica. (2022) 198, 733–745, https://doi.org/10.1016/j.actaastro.2022.05.058.
10.1016/j.actaastro.2022.05.058
Web of Science® Google Scholar
16 Hanagud S., Noyer M. B. D., Luo H., Henderson D., and Nagaraja K. S., Tail Buffet Alleviation of High-Performance Twin-Tail Aircraft Using Piezostack Actuators, AIAA Journal. (2002) 40, no. 4, 619–627, https://doi.org/10.2514/2.1718, 2-s2.0-0036530853.
10.2514/2.1718
Web of Science® Google Scholar
17 Angeletti F., Gasbarri P., Sabatini M., and Iannelli P., Design and Performance Assessment of a Distributed Vibration Suppression System of a Large Flexible Antenna During Attitude Manoeuvres, Acta Astronautica. (2020) 176, 542–557, https://doi.org/10.1016/j.actaastro.2020.04.015.
10.1016/j.actaastro.2020.04.015
Web of Science® Google Scholar
18 Hanagud S. and Babu G., Smart Structures in the Control of Airframe Vibrations, Journal of the American Helicopter Society. (1994) 39, no. 2, 69–72, https://doi.org/10.4050/JAHS.39.69.
10.4050/JAHS.39.69
Web of Science® Google Scholar
19 Heverly D., Optimal Actuator Placement and Active Structure Design for Control of Helicopter Airframe Vibrations, 2002, The Pennsylvania State University.
Google Scholar
20 Walchko J. C., Wang K. W., and Smith E. D., Hybrid Feedforward-Feedback Control for Active Helicopter Vibration Suppression, 63rd American Helicopter Society International Annual Forum 2007, 2007, Virginia Beach VA.
Google Scholar
21 Song L. S. and Xia P. Q., A harmonic Synchronous Identification-Updating Method for Active Control of Helicopter Structural Response Driven by Piezoelectric Stack Actuators, Journal of the American Helicopter Society. (2015) 60, no. 3, 1–14, 032013, https://doi.org/10.4050/JAHS.60.032013, 2-s2.0-84936984843.
10.4050/JAHS.60.032013
Web of Science® Google Scholar
22 Meng D., Xia P. Q., and Song L. S., MIMOMH Feed-Forward Adaptive Vibration Control of Helicopter Fuselage by Using Piezoelectric Stack Actuators, Journal of Vibration and Control. (2018) 24, no. 23, 5534–5545, https://doi.org/10.1177/1077546318757840, 2-s2.0-85045296371.
10.1177/1077546318757840
Web of Science® Google Scholar
23 Singhvi R. and Vennkatesan C., Vibration Control of an Idealized Helicopter Model Using Piezo Stack Sensor-Actuator, 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 2005, Austin, Texas, https://doi.org/10.2514/6.2005-2275.
10.2514/6.2005-2275
Google Scholar
24 Lang K. and Xia P. Q., Hybrid Active Vibration Control of Helicopter Fuselage Driven by Piezoelectric Stack Actuators, Journal of Aircraft. (2019) 56, no. 2, 719–729, https://doi.org/10.2514/1.C034965, 2-s2.0-85063971920.
10.2514/1.C034965
Web of Science® Google Scholar
25 Patt D., Liu L., Chandrasekar J., Bernstein D. S., and Friedmann P. P., Higher-Harmonic-Control Algorithm for Helicopter Vibration Reduction Revisited, Journal of Guidance, Control, and Dynamics. (2005) 28, no. 5, 918–930, https://doi.org/10.2514/1.9345, 2-s2.0-26244448901.
10.2514/1.9345
Web of Science® Google Scholar
26 Mathews A., Sule V. R., and Venkatesan C., Order Reduction and Closed-Loop Vibration Control in Helicopter Fuselages, Journal of Guidance, Control, and Dynamics. (2002) 25, no. 2, 316–323, https://doi.org/10.2514/2.4884, 2-s2.0-0036493898.
10.2514/2.4884
Web of Science® Google Scholar
27 Gupta N., DuVal R., and Fuller J., A New Approach for Active Control of Rotorcraft Vibration, Journal of Guidance, Control, and Dynamics. (1982) 5, no. 2, 143–150, https://doi.org/10.2514/3.56151, 2-s2.0-0020099674.
10.2514/3.56151
Web of Science® Google Scholar
28 Mottershead J. E., Tehrani M. G., James S., and Court P., Active Vibration Control Experiments on an AgustaWestland W30 Helicopter Airframe, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2012) 226, no. 6, 1504–1516, https://doi.org/10.1177/0954406211423609, 2-s2.0-84864489958.
10.1177/0954406211423609
Web of Science® Google Scholar
29 Elliott S. J., Stothers I. M., and Nelson P. A., A Multiple Error LMS Algorithm and Its Application to the Active Control of Sound and Vibration, Signal Processing. (1987) 35, no. 10, 1423–1434, https://doi.org/10.1109/TASSP.1987.1165044, 2-s2.0-6444228583.
10.1109/TASSP.1987.1165044
Google Scholar
30 Rodriguez J., Cranga P., Chesne S., and Gaudiller L., Hybrid Active Suspension System of a Helicopter Main Gearbox, Journal of Vibration and Control. (2018) 24, no. 5, 956–974, https://doi.org/10.1177/1077546316655707, 2-s2.0-85043605300.
10.1177/1077546316655707
Web of Science® Google Scholar
31 Allemang R. J. and Brown D. L., A Correlation Coefficient for Modal Vector Analysis, Proceedings of the 1st International Modal Analysis Conference & Exhibit, 1982, Orlando FL.
Google Scholar
32 Bang S. W., Hong S. B., Lee Y. B., Shin H. C., Park B. H., and Park J. S., Active Airframe Vibration Control Study Using a Small-Scale Model for Lift-Offset Compound Helicopter, International Journal of Aeronautical and Space Sciences. (2023) 24, no. 1, 77–91, https://doi.org/10.1007/s42405-022-00501-3.
10.1007/s42405-022-00501-3
Web of Science® Google Scholar
33 Wolf J. A., The Influence of Mounting Stiffness on Frequencies Measured in a Vibration Test, 1984, No. 840480. SAE Technical Paper.
Google Scholar
34 Qin J., Gong L., and Wang P. Y., Modal Analysis and Test of the Main Structure of an Aircraft, Noise and Vibration Control. (2020) 40, no. 1, 234–238, https://doi.org/10.3969/j.issn.1006-1355.2020.01.044.
10.3969/j.issn.1006-1355.2020.01.044
Google Scholar
35 Giurgiutiu V. and Rogers C. A., Power and Energy Characteristics of Solid-State Induced-Strain Actuators for Static and Dynamic Applications, Journal of Intelligent Material Systems and Structures. (1997) 8, no. 9, 738–750, https://doi.org/10.1177/1045389X9700800903, 2-s2.0-0031222907.
10.1177/1045389X9700800903
CAS Web of Science® Google Scholar
36 Hoffmann F., Maier R., Jänker P., Hermle F., and Berthe A., Helicopter Interior Noise Reduction by Using Active Gearbox Struts, 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), 2006, Cambridge, Massachusetts, https://doi.org/10.2514/6.2006-2604.
10.2514/6.2006-2604
Google Scholar
37 Snyder S. D. and Hansen C. H., The Effect of Transfer Function Estimation Errors on the Filtered-x LMS Algorithm, IEEE Transactions on Signal Processing. (1994) 42, no. 4, 950–953, https://doi.org/10.1109/78.285659, 2-s2.0-0028408306.
10.1109/78.285659
Web of Science® Google Scholar
38 Simon H., Adaptive Filter Theory, 2002, Prentice-Hall.
Google Scholar

All articles

Adaptive Feedforward Vibration Control of Helicopter Cabin Floor Driven by Piezoelectric Stack Actuators: Modeling, Simulation and Experiments

Abstract

1. Introduction

2. Scaled Airframe Structure