A Data Decomposition and End-to-End Optimization-Based Monthly Carbon Emission Intensity of Electricity Forecasting Method
Abstract
Accurate high-resolution carbon emission intensity of electricity forecasting (CIF) can assist multi-staker in timely adjusting their electricity consumption strategies to gain benefits. Few studies attempt to perform high-resolution (monthly and above) CIF due to the limited carbon emission data. High-resolution electricity data is easily available, and there is a coupling relationship between electricity and carbon emission data, making it possible to perform high-resolution CIF. Therefore, the paper proposes an end-to-end monthly CIF approach using annual carbon emission and monthly electricity consumption data, which can be divided into two stages. In Stage I, a monthly carbon emission data generator based on the Denton decomposition method is proposed. In Stage II, support vector machine (SVM), known for their effectiveness in small-sample prediction, are employed for monthly CIF. To ensure that the decomposed data effectively improves the predictor’s performance, we propose an end-to-end optimization strategy. This strategy feeds back the predictor’s performance on actual monthly data as optimization target to the generator and uses differential evolution algorithms (DEA) to optimize and adjust the decomposed data. Case studies conducted using actual data from Guangdong Province, China, demonstrate that the proposed method can effectively enhance monthly data, thereby improving prediction accuracy.
1. Introduction
Since the electrical revolution, humanity has continually produced electricity by consuming fossil fuels, which has generated and releases significant amounts of carbon dioxide and had a profound impact on the environment. According to the International Energy Agency (IEA), the power sector is the largest contributor to global carbon emissions, accounting for 40% of total emissions in 2022, with this percentage trending upward [1]. Consequently, many countries and organizations have implemented measures to promote low-carbon reforms in the power industry. For example, Chinese government announced its “30–60” dual-carbon plan at the 75th General Debate of the United Nations General Assembly in September 2020 [2]. The UK government has introduced its 10 Plans for a Green Industrial Revolution in November 2020, utilizing over £12 billion of government funding to foster sustainable, future-proof green industries in the UK and worldwide [3].
With the increasing emphasis on the electricity carbon emissions, a rapid and high-resolution system for accounting and forecasting carbon emissions is crucial. In order to account the carbon emission in the electricity power industry, many researchers have conducted extensive studies. Currently, the carbon accounting methods can be divided into three main categories: emission factors method, mass balance method and monitoring method. The emission factors method is the most commonly used approach for accounting carbon emissions [4], which relies on constructing emission factors and activity data for each emission source [5]. The mass balance approach is another carbon emission accounting method which has been used in accounting carbon emission [6, 7]. This method allows for a quantitative analysis of energy consumption and carbon emissions throughout the entire energy input and output process [8]. The carbon factors method and mass balance method all rely on the statistical data of energy consumption and therefore they are not suitable for high-resolution (monthly and above) carbon emission accounting [9, 10]. To enhance the high-resolution carbon emission accounting, the monitoring method based on the continuous emission monitoring systems (CEMS) is proposed [11, 12]. However, the monitoring method is limited by the CEMS equipment costs and cannot be widely applied to large-scale carbon emission accounting.
In response, scholars have proposed a power carbon accounting method based on the carbon emission intensity of electricity to achieve high-resolution and low-cost accounting of electricity carbon emission [13]. The carbon emission intensity of electricity is defined as the amount of carbon dioxide emitted per unit of electricity consumed. It is used to obtain electricity carbon emissions by multiplying it with the electricity consumption [14, 15]. The feasibility of this method lies in the high real-time capability, accuracy, resolution, and wide collection scope of electricity data [16–18]. Currently, the carbon emission intensity of electricity is usually updated yearly [19]. However, with the rapid development of renewable energy, the carbon emission intensity of electricity may fluctuate significantly due to the uncertainty characteristic of renewable energy. The study result of [20] shows that there is a up to 30% error with using the conventional low-resolution carbon emission intensity of electricity for daily accounting of electricity carbon emission.
In order to achieve accurate high-resolution electricity carbon emission accounting, there is an increasing focus on the high-resolution forecasting of the carbon emission intensity of electricity [15]. According to the definition of carbon emission intensity of electricity, achieving high-resolution forecasting of carbon emission intensity requires a substantial amount of high-resolution electricity carbon emission data [21]. However, in many developing countries whose carbon accounting research started relatively late, it is challenging to be obtain enough historical high-resolution carbon emission data. Insufficient data prevents predictive models from fully learning, making accurate predictions difficult [22, 23]. Therefore, achieving high-resolution forecasting of carbon emission intensity of electricity in these countries faces significant data challenges.
- 1.
Due to the lack of actual high-resolution data for feedback, the authenticity of the decomposed high-resolution data is difficult to ensure.
- 2.
Data decomposition and high-resolution forecasting are treated as two independent tasks, lacking coordination between them. This disconnect can lead to error propagation, thereby limiting the accuracy of high-resolution forecasting.
In order to address these issues, an end-to-end monthly CIF method based is proposed in this paper, which consists of two main stages. In the first stage, we develop a high-resolution carbon emission data generator based on the correlation between electricity data and carbon emissions, thereby obtaining high-resolution historical carbon emission intensity of electricity data for training. In the second stage, a predictor is trained on the decomposed monthly dataset to achieve monthly CIF. In order to ensure that the decomposed data can improve the prediction accuracy CIF effectiveness, we integrate above two stages into a single end-to-end model, creating a feedback loop that simultaneously improves data decomposition and prediction during training.
- 1.
An end-to-end optimization framework is proposed in this paper, which integrates data decomposition and forecasting into a single model and creates a feedback linkage between them. In this framework, the performance evaluation of predictor will serve as the optimization objective for the data decomposition based high-resolution data generator, ensuring that the decomposed data contributes to high-resolution prediction.
- 2.
In this paper, an annual electricity carbon emission data decomposition method is proposed to generate monthly carbon emission intensity of electricity. The method is based on the correlation between ‘carbon-electricity’ data and utilizes the monthly electricity consumption data as additional information input.
The rest of this paper is organized as follows. Section 2 presents the implementation details of the proposed approach. Comprehensive simulation results based on actual data are reported in Section 3. Section 4 draws the conclusions and future works.
2. Methodologies
In this section, we first give the detail definition of carbon emission intensity of electricity and analyze the problems of the existing CIF methods. Then, the overall framework of the proposed CIF approach is introduced. Finally, all modules in proposed method are illustrated in detail, respectively.
2.1. Problem Statement
The conventional monthly CIF methods generally build the forecasting problem as a one-step forecasting model, which forecasts the next FM of a historical monthly carbon emission intensity of electricity series. It is obviously a small sample learning problem since there are insufficient training samples can be constructed from limited historical monthly carbon emission intensity of electricity. For data-driven based AI forecasting methods, the limitation on the number of training samples tends to give rise to the overfitting of the forecasting algorithms [27]. Therefore, the conventional monthly CIF methods cannot provide a satisfactory forecasting accuracy.
2.2. Framework of the Proposed Approach
- •
Stage I: Data decomposition. The first stage aims to generate more historical monthly electricity carbon emission data, then divide it by corresponding electricity consumption to obtain the monthly carbon emission intensity of electricity. In this stage, Denton method is adopted and improved as generator. This generator takes annual carbon emission data and monthly electricity consumption data as inputs and outputs monthly carbon emission data. The details of Stage I are described in Section 2.3.
- •
Stage II: Data-driven forecasting. The second stage aims to achieve the monthly forecasting of carbon emission intensity of electricity. In this stage, the support vector machine (SVM) is used as forecasting model, and trained and optimized on decomposed monthly dataset. The details of Stage II are described in Section 2.4.
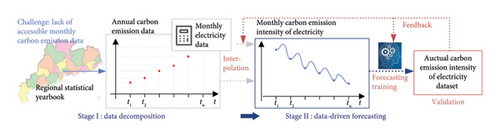
The separation of the two stages can lead to propagation errors, thereby affecting the accuracy of the prediction. To address this problem, we aim to integrate both tasks into one end-to-end learning model and optimized this model with the performance of predictor to achieve high accuracy of CIF. The details of end-to-end optimizing process are described in Section 2.5.
2.3. Denton Method-Based High-Resolution Data Generator
The Denton method is a nonsmooth data decomposition technique for time series data, commonly used to distribute low-resolution data into high-resolution data [24]. The key idea of the Denton method is to estimate data through high-resolution reference data relative with data to be decomposed. The decomposition process can be regarded as solving a constrained optimization problem which consists of three key parts: inputs, constraints, and objective function.
Therefore, the task of generator is to solve several simple constrained optimization problems. These problems can be solved quickly by using the least squares method.
2.4. Forecasting Model
In this paper, SVM is selected as the forecasting model of proposed CIF method. SVM is based on the structural risk minimization principle, and ensures a good generalization performance even on limited training set. Additionally, the training time required for SVM is relatively short, which contributes to enhancing the overall efficiency of the method. Therefore, SVM is suitable for our method. The input of SVM is the historical monthly carbon emission intensity of electricity series , where n1 denotes the length of input and it is set as 12 in our paper, and the output is the next one . The training process of SVM only uses the decomposed monthly carbon emission intensity of electricity, and the validation of model is set on actual monthly carbon emission intensity of electricity dataset.
2.5. Integrated Optimization
In our task, data decomposition and prediction are sequential steps, with the predictor’s performance being constrained by the authenticity of the decomposed data, but it cannot be ensured due to the lack of actual data. To address this issue, we propose an end-to-end model optimization approach, which feeds the performance evaluation of the downstream predictor back into the upstream data decomposition process and uses it as a target to guide the optimization of the decomposed data, thereby ensuring that the decomposed data can effectively enhance the accuracy of the predictions.
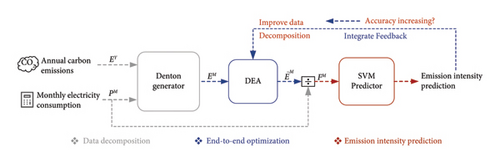
- 1.
DEA effectively explores the entire solution space through operations like mutation and crossover, helping to avoid getting trapped in local optima. This makes it particularly suitable for our global optimization tasks.
- 2.
DEA has simple operational steps and requires only small amounts of computational resources, allowing to save significant time.
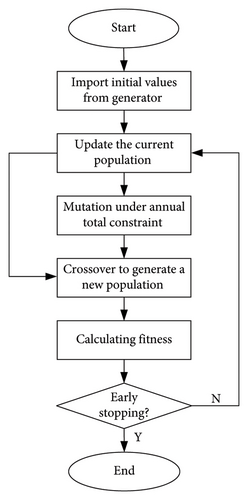
It is notable that DEA employs an early stopping mechanism to control whether the optimization process should be terminated. Specifically, the optimization stops if the DEA’s fitness does not decrease after 10 iterations.
3. Case Study
The case study is performed using Python 3.8 on a computer equipped with Intel Core i5-12400 CPU, 32 GB useable RAM and Nvidia RTX 3080. In this section, we first introduce the data set and accuracy assessments. Then, two cases are conducted based on the collected data.
3.1. Data Description
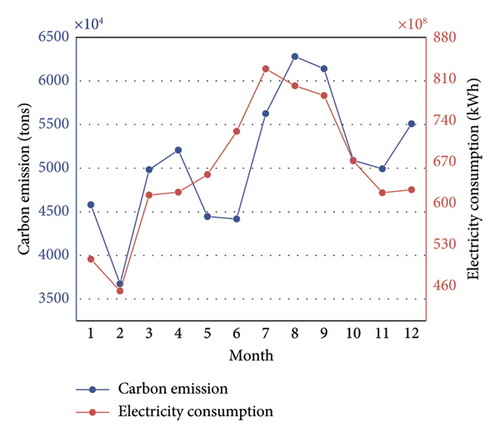
The electricity consumption data and electricity carbon emission data used in this study are sourced from the Guangdong Power Grid Corporation. Specifically, the annual electricity carbon emission data spans from 2011 to 2022 and the monthly electricity carbon emission data covers the period from January 2022 to June 2024. The monthly electricity consumption data encompasses the period from January 2011 to June 2024.
In this paper, the dataset is divided into three subsets: the training set (from Jan. 2011 to Dec. 2021), the validation set (from Jan. 2022 to Dec. 2023) and the testing set (from Jan. 2024 to Jun. 2024).
3.2. Accuracy Assessment
To verify the practicability of the proposed approach, two forecasting algorithms commonly used for small sample learning were employed, including backpropagation (BP) neural network model and auto regressive integrated moving average (ARIMA) model. The hyperparameters of these models are optimized automatically in the validation by Bayesian algorithm.
3.3. Experiment Setting
- 1.
Extrapolation CIF method (EM): It is a commonly investigated method as mentioned in [29–31], with few training samples and short steps to be forecasted. To highlight the idea of the proposed approach, only actual historical monthly carbon emission intensity of electricity is employed to train models. Therefore, the actual monthly dataset is divided into three subsets in this method: the training set (from Jan. 2022 to Aug. 2023), the validation set (from Sep. 2023 to Dec. 2023) and the testing set (from Jan. 2024 to Jun. 2024). The input and output of the model are monthly carbon emission intensity of electricity of the previous 6 months and the next month.
- 2.
Liner interpolation and end-to-end optimization based-CIF method (LEM): It decomposes annual carbon emission data using linear interpolation and adjusts the decomposed data using end-to-end optimization method proposed in this paper. The predictor is trained on the decomposed dataset and validated and tested on the actual monthly data. The dataset partitioning is consistent with the proposed approach. The input and output of the model are monthly carbon emission intensity of electricity of the previous 12 months and the next month.
- 3.
Denton method-based CIF method (DM): It generates monthly carbon emission data using Denton decomposition method but does not adjust them. The predictor is trained on the decomposed dataset and validated and tested on the actual monthly data. The dataset partitioning is consistent with the proposed approach. The input and output of the model are monthly carbon emission intensity of electricity of the previous 12 months and the next month.
- 4.
Denton interpolation method and end-to-end optimization based-CIF method (DEM): It is the method proposed in our paper, which generates monthly carbon emission data using Denton decomposition and adjusts the decomposed data using end-to-end optimization method proposed in this paper. The predictor is trained on the decomposed dataset and validated and tested on the actual monthly data. The input and output of the model are monthly carbon emission intensity of electricity of the previous 12 months and the next month.
4. Results
Figures 5(a), 5(b), and 5(c) show the forecast results using EM, LEM, DM, and proposed CIF method in three forecasting models, respectively. The evaluation metrics are enumerated in Table 1. It can be seen from Figure 5 that, compared with the EM method, all other methods provide more satisfactory forecast results, indicating that insufficient monthly data do not allow these models to be fully trained. Simulation results show that due to the increased scale of training samples from data decomposition, all three forecasting algorithms exhibit higher accuracy when using DM, LEM, and DEM compared to EM (see Table 1).
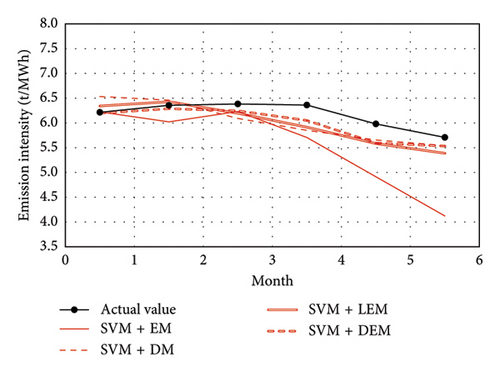
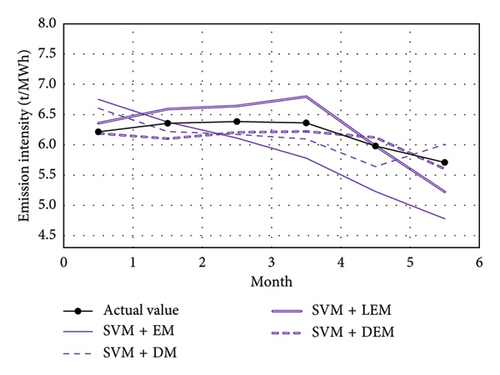
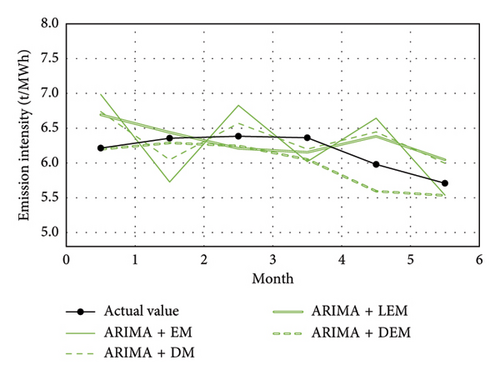
| Algorithm | Forecasting method | MAPE (%) | RMSE |
|---|---|---|---|
| BP | EM | 8.54 | 0.110 |
| LEM | 4.24 | 0.038 | |
| DM | 4.48 | 0.041 | |
| DEM | 2.27 | 0.029 | |
| SVM | EM | 10.62 | 0.078 |
| LEM | 4.23 | 0.040 | |
| DM | 4.61 | 0.037 | |
| DEM | 2.98 | 0.020 | |
| ARIMA | EM | 8.13 | 0.071 |
| LEM | 4.61 | 0.041 | |
| DM | 5.27 | 0.046 | |
| DEM | 3.96 | 0.035 | |
Based on the provided data, the predictive performance of different forecasting models and methods shows significant variation in terms of MAPE (%) and RMSE. Across all methods, the DEM consistently outperforms other approaches, achieving the lowest MAPE and RMSE values for all models, indicating its superior accuracy and reliability.
For the BP model, the DEM method achieves a remarkably low MAPE of 2.27% and an RMSE of 0.029, substantially better than the other methods, such as EM with a MAPE of 8.54% and RMSE of 0.110. Similarly, for the SVM model, DEM also performs best with a MAPE of 2.98% and RMSE of 0.020, compared to the EM method, which records the highest error metrics (MAPE 10.62%, RMSE 0.078).
The ARIMA model shows a consistent trend, where DEM achieves the lowest error values (MAPE 3.96%, RMSE 0.035), while EM yields higher errors (MAPE 8.13%, RMSE 0.071). Interestingly, the LEM and DM methods show competitive results across all models, with their errors generally lower than EM but higher than DEM.
These results highlight the superior performance of the DEM method in improving prediction accuracy across all tested models. This can be attributed to its ability to effectively capture dynamic and complex data patterns, making it the most reliable method among the options analyzed.
In comparing the models, SVM demonstrates overall superior predictive performance compared to BP and ARIMA models. Specifically, SVM achieves lower MAPE (2.98%) and RMSE (0.020) with the DEM method, while the best results for BP and ARIMA are 2.27%, 0.029 (BP) and 3.96%, 0.035 (ARIMA), respectively. Although BP slightly outperforms SVM in certain cases, its predictive performance is highly influenced by the choice of method.
The underperformance of BP compared to SVM is primarily attributed to overfitting. As a neural network-based model, BP is highly sensitive to the complex patterns in training data. When the sample size is insufficient or the data contains significant noise, the model tends to overfit the training data, leading to reduced generalization ability and suboptimal performance on test data. The experimental results indicate that although the Denton method was used to generate monthly carbon emission data for the past 10 years, the overall sample size is still insufficient to support the training of complex models such as neural networks.
Table 2 records the actual values and forecasting values of monthly carbon emission intensity of electricity using EM, LEM, DM, and DEM methods, while the best results under the same forecasting algorithm are in grey. It is obvious that the forecasting accuracy based on the proposed DEM method tends to be higher than others method in most months.
| Month | True values | Forecasting values | |||||
|---|---|---|---|---|---|---|---|
| BP + EM | BP + DM | SVM + EM | SVM + DM | ARIMA + EM | ARIMA + DM | ||
| Jan. | 6.214 | 6.224 | 6.534 | 6.751 | 6.603 | 6.985 | 6.738 |
| Feb. | 6.356 | 6.023 | 6.460 | 6.377 | 6.219 | 5.727 | 6.047 |
| Mar. | 6.384 | 6.231 | 6.092 | 6.111 | 6.172 | 6.829 | 6.570 |
| Apr. | 6.362 | 5.707 | 5.852 | 5.780 | 6.097 | 6.019 | 6.200 |
| May | 5.980 | 4.913 | 5.656 | 5.228 | 5.640 | 6.644 | 6.447 |
| Jun. | 5.708 | 4.122 | 5.544 | 4.778 | 6.008 | 5.538 | 5.996 |
| BP + LEM | BP + DEM | SVM + LEM | SVM + DEM | ARIMA + LEM | ARIMA + DEM | ||
| Jan. | 6.214 | 6.343 | 6.197 | 6.358 | 6.189 | 6.694 | 6.383 |
| Feb. | 6.356 | 6.429 | 6.289 | 6.591 | 6.103 | 6.440 | 6.490 |
| Mar. | 6.384 | 6.197 | 6.246 | 6.642 | 6.206 | 6.210 | 6.148 |
| Apr. | 6.362 | 5.916 | 6.051 | 6.797 | 6.222 | 6.155 | 5.893 |
| May | 5.980 | 5.585 | 5.595 | 5.981 | 6.121 | 6.383 | 5.704 |
| Jun. | 5.708 | 5.389 | 5.534 | 5.223 | 5.602 | 6.047 | 5.522 |
- Note: The bold values represent the best prediction results.
Figure 6 shows the comparison of the time consumption of different forecasting methods. It can be seen that all DEM and LEM method spend more time than all EM and DM method, which illustrates the integrated optimization consumed the majority of the processing time. In terms of forecasting algorithms, the BP model requires the most time (about 17 min). That is because the BP network has numerous hyperparameters and requires multiple training sessions with averaging to avoid unstable predictions. The ARIMA model requires the least time due to its simple structure and fewer hyperparameters (about 7 min). The SVM model, with its more complex hyperparameter settings, requires a certain amount of time (about 11 min) for optimization.
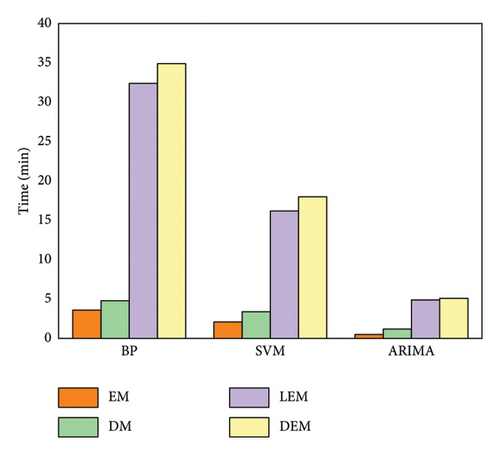
The experiments discussed above illustrate that the proposed DIE method can effectively improve the accuracy of monthly CIF.
5. Conclusion
In order to achieve accurate high-resolution CIF under limited high-resolution data, a data decomposition and end-to-end optimization-based monthly CIF method is proposed in our paper. Specifically, we design a high-resolution data generator based on ‘electric-carbon’ coupling characteristics and Denton method and integrate it with predictor into an end-to-end CIF framework. In this way, the performance evaluation of the forecasting task will guide the optimization of data decomposition. Therefore, the decomposed data are able to improve the accuracy of CIF effectively. We use actual monthly carbon emission intensity of electricity dataset to validate the proposed CIF method. The result shows that the proposed method can reach achieve satisfactory forecasting performance and provide a feasible approach for high-resolution forecasting of carbon emission intensity of electricity.
- 1.
The case study only explored the performance of the proposed method in monthly forecasting. In the future, we will further test the effectiveness of proposed method in higher-frequency forecasting tasks.
- 2.
The generator only considered electricity data for decomposition. In the future, we will investigate more relevant factors to further improve the accuracy of the decomposition.
- 3.
The lack of historical monthly carbon emission intensity of electricity data has prevented the accuracy of the augmented data from being validated. In the future, we will collect more high-resolution data to comprehensively validate the effectiveness of the decomposition method.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work was funded by the Science and Technology Project of BDC of State Grid Corporation of China, Project Name: Research on Key Technologies of Electricity-Carbon Market Collaboration Based on Green Electricity Contract, Grant No. SGSJ0000NYJS2400037.
Open Research
Data Availability Statement
Research data are not shared.




