An Improved Communication-Free Dual Characteristic Over Current-Based Protection Scheme for AC Microgrids
Abstract
The entry of distributed generation causes the network to become complicated, and as a result, the protection coordination between the network equipment is lost. In previous studies, three decision variables were considered for each directional overcurrent relay: time dial setting in the main mode, time dial setting in the backup mode, and pickup current (Ip). However, the minimum coordination time interval between the main and backup relay was lost. In this paper, communication-free dual characteristics directional overcurrent relays are used, considering six decision variables: Ip, time dial setting of the relays in the main and backup mode, breakpoint current, and the type of curves in main and backup operations. The proposed scheme maintains the minimum time interval between the main and backup relays, which reduces the operation time of the relays compared to previous studies. The proposed scheme is implemented on the modified IEEE 30-bus network distribution section. DIGSILENT software is used for simulation, and load currents and fault currents of protection relays in grid-connected and islanded conditions are extracted based on load flow and short circuit studies. Then, the optimization problem is solved using the genetic algorithm in MATLAB software, and optimal settings are obtained to minimize the operation time of the relays. The simulation results of the proposed method shows that the operation time of the relays can be improved by 17% compared with the previous existing method.
1. Introduction
Microgrids will have many benefits for both consumers and electricity production companies; from the perspective of consumers, microgrids can simultaneously provide electricity and heat, increase reliability, reduce greenhouse gas emissions, and improve quality, and from the perspective of companies, the use of microgrid electricity has the potential to reduce consumption demand as well as reduce the facilities for the development of transmission lines and eliminate peak load, which also reduces network losses [1, 2]. Despite all the advantages of microgrids in the presence of distributed generation (DG), there are possible adverse effects on the distribution network, which include complicating the network and, as a result, the development of the network protection system and the operation and coordination of the network protection relays are associated with problems. Connecting DGs to the network causes harmonics and reduces short-circuit impedance. Also, when DGs enter distribution networks, these networks lose their radial structure. Therefore, due to the circularization of the distribution network, to detect the direction of the fault current, relays that operate based on the direction of the fault current are needed [3, 4]. Directional over current relays (DOCRs) can detect current direction by measuring current, voltage, and angle between current and voltage. This equipment recognizes the direction of the power passing through the line and only issues permission to pass the power in a specific direction.
A protection plan aims to isolate the faulty parts from the healthy parts and minimize the consequences of the faults by reducing the operating time of the protective equipment. However, coordinating protective relays is challenging [5, 6].
- 1.
Methods based on the communication system
- 2.
Methods without the need of the communication system
The communication system-based methods usually use adaptive protection, which uses communication links to change the settings. In [8], the protection coordination scheme for microgrids using DOC relays with dual settings and with the help of a communication platform has been presented. In this scheme, both relays in one line are connected with each other. The possibility of cyber-attacks and loss of the communication link, which leads to failure of the relay’s functionality, are the main disadvantages of this method. In [9, 10], an adaptive protection scheme has been proposed to identify the fault areas and achieve coordination between relays. This method requires a lot of measurements, such as the voltage and current of all DGs. In [11], the authors have utilized intelligent electronic devices and a communication channel to obtain real-time system information to update relay settings. This method was implemented in distribution networks with dynamically changing operating conditions, which include loss of loads, generations, and lines. A review of communication failure impacts on adaptive microgrid protection schemes has been carried out by authors in [12].
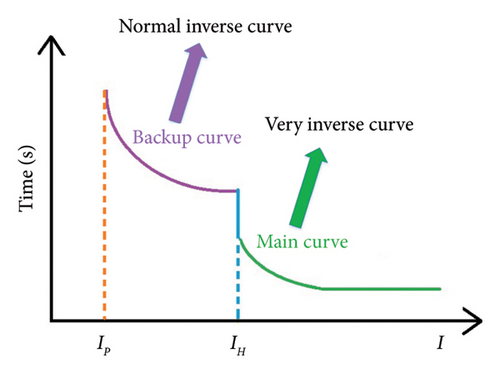
The second category includes methods that do not require a communication system, which establishes coordination between relays through local measurement. In [13], a communication-free protection coordination scheme of DOC relays with dual settings and voltage-dependent protection characteristics has been presented. This design adds a voltage characteristic to the relay operation time relationship. Among its disadvantages is the ineffectiveness of the presented plan for faults with high currents. In [14], a scheme for protection coordination for microgrids using DOC relays with dual settings and without the need for a communication platform has been presented. One of the advantages of using the double characteristic curve is the reduction of the operation time of the relays, but the disadvantage of the mentioned method is the loss of the minimum coordination time interval (CTI) between the main and backup relays. Some studies have presented protection schemes that do not use IEEE and IEC standard curves for synchronizing relays. For example, in [15–17], designs using nonstandard characteristics for DOC relays have been presented. The advantages of using nonstandard curves are higher flexibility and accuracy, while the disadvantages are increased cost, complexity, and networking to coordinate relays, which is not practical in reality. Another approach that does not require the communication system is using fault current limiters (FCLs) to coordinate relays [18–20]. However, using FCLs has some disadvantages, such as the complexity of finding the optimal locations to install FCLs, and the increase in costs. In [21–23], metaheuristic optimization methods have been used for communication-free protection coordination of DOC relays. The objective functions of these studies have only considered the reduction of the total operation time of the main relays. Therefore, as a disadvantage, the operation time between the main and backup relays was not optimal. One of the most recent works in the field of coordination relays without a communication platform is [24]. Three decision variables have been considered for each DOCR, which include time dial setting in main mode (TDSPm) and time dial setting in backup mode (TDSbk) and pickup current (Ip). As shown in Figure 1(a), the proposed dual characteristic scheme consists of two protection curves: the Very Inverse (VI) curve for the main function and the Normal Inverse (NI) curve for the backup function. There is also a breakpoint (IH) where the two curves, VI and NI, are connected. The use of a combination of NI and VI curves in all relays has led to the loss of the CTI between the main and backup relays, which is the main drawback of this study.
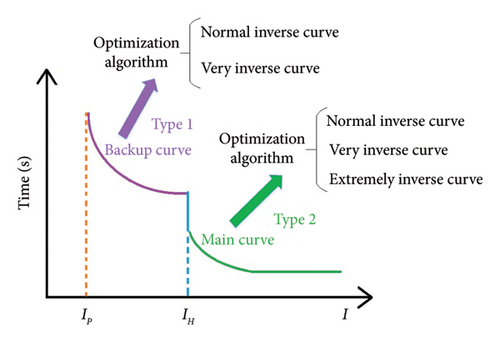
In this paper, an attempt is made to eliminate problems such as the loss of CTI that existed in [24]. In Figure 1(b), the proposed communication-free dual characteristic coordination scheme is shown. The curve is divided into two parts, which include the characteristic curves of types 1 and 2. The type-1 characteristic curves are used for relay operation in the backup mode, and their slope will be less than or equal to that of type-2 curves. The optimization algorithm selects the type of curve from NI and VI curves. The type-2 characteristic curve is used for relay operation in the main mode, which has a higher slope and shorter operation time, and the type of curve is selected by the optimization algorithm from NI, VI, and Extremely Inverse (EI) curves. Therefore, in the proposed method, six decision variables are considered for the ith DOCR, which include (, , Ip, IH, and main and backup curves).
-
Q1. Do the relays have dual characteristics?
-
Q2. Have adaptive protection measures been used for coordination?
-
Q3. Have FCLs been used?
-
Q4. Has the characteristic curve selection been optimized?
-
Q5. Have both modes of operation (grid connected and islanded) been considered in the coordination scheme?
-
Q6. Has the breakpoint of the characteristic curve been optimized?
-
Q7. Do the relay settings include all symmetrical and unsymmetrical faults?
| Reference | Category | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 |
|---|---|---|---|---|---|---|---|---|
| Reference [8] | With communication | Yes | No | No | No | Yes | No | No |
| Reference [9] | No | Yes | No | No | Yes | No | No | |
| Reference [10] | Yes | Yes | No | No | Yes | No | No | |
| Reference [11] | No | Yes | No | No | No | No | No | |
| Reference [13] | Communication free | Yes | No | No | No | Yes | No | No |
| Reference [14] | Yes | No | No | No | Yes | No | No | |
| Reference [17] | No | No | No | Yes | Yes | No | No | |
| Reference [18] | No | No | Yes | No | Yes | No | No | |
| Reference [24] | Yes | No | No | Yes | Yes | No | No | |
| Proposed method | Yes | No | No | Yes | Yes | Yes | Yes |
- Note: The last row of Table 1 indicate the contributions of this paper compared to the previous studies (other rows).
- •
Improving the performance of the protection system by optimizing the IH.
- •
The use of different curves for the performance of each relay in the main and backup modes, which is obtained by the optimization algorithm.
- •
The obtained settings for the relays are valid for both modes of operation (grid connected and islanded), and there is no need to change the settings when the operating mode is changed.
- •
Providing optimized relay settings for both symmetrical and unsymmetrical faults and for both modes of operation (grid connected and islanded).
2. Proposed Protection Coordination Scheme
Despite of many previous studies in which the optimal settings of the relays have just given for the grid-connected mode or islanded mode, in the proposed coordination scheme, the optimal settings are provided for both grid-connected and islanded operation modes. In this section, the decision variables are defined in the first subsection. In the second subsection, the objective function is described and then the constraints of the problem and their limits are defined. Thereafter, the optimization algorithm, the number of decision variables, and the problem-solving flowchart are explained next.
2.1. Decision Variables
- 1.
(TDSPm)
- 2.
(TDSbk)
- 3.
Ip
- 4.
Break point current (IH)
- 5.
Main protection curve
- 6.
Backup protection curve
2.2. Objective Function
In most of the previous studies, objective functions were considered to reduce the operation time of the relays in the optimization algorithm. In [15, 21–23], the aim of the objective function is only the reduction of the total operation time of the main relays. In previous studies, the objective function for reducing the operation time of relays in both symmetrical and unsymmetrical faults has not been presented for both modes of operation (grid connected and islanded). Therefore, considering the difference in the nature of faults (symmetrical and unsymmetrical faults), two objective functions are proposed, which are presented in Sections 2.2.1 and 2.2.2.
2.2.1. Objective Function for Symmetrical Faults
In equation (1), the symbols nc, nf, npm, and nbk indicate the number of different operating modes (grid-connected and islanded), number of fault locations, number of main relays, and number of backup relays, respectively. is the time of operation of the ith main relay for cth operating mode at jth fault location. is the time of operation of the kth backup relay for cth operating mode at jth fault location. When the time difference between the backup relay and the main relay for the jth fault location is more than CTI, the penalty function in equation (1) returns zero, as shown in equation (2). Also, when the time difference between the backup relay and the main relay for the jth fault location is less than CTI, the penalty function in equation (1) returns δ. δ is a big value, and in the proposed method, it is considered equal to 100. CTI usually takes a value between 0.2 and 0.5 s, which in this paper is set to be 0.2 s.
2.2.2. Objective Function for Symmetrical and Unsymmetrical Faults
2.3. Constraints
The following constraints are considered in the optimization procedure to ensure having a reliable operation.
2.3.1. Ip
2.3.2. TDS
2.3.3. IH
2.3.4. Curves
| Curve type | A | B |
|---|---|---|
| Normal Inverse | 0.14 | 0.02 |
| Very Inverse | 13.5 | 1 |
| Extremely Inverse | 80 | 2 |
Superscripts pm and bk indicate main and backup modes, respectively.
2.4. Optimization Algorithm
To minimize the objective function, various optimization algorithms such as GA particle swarm optimization (PSO) algorithm, shuffled frog leaping algorithm (SFLA), teaching learning optimization algorithm (TLBO), and other metaheuristic algorithms can be used. However, according to the results of previous studies, the GA has favorable behavior and convergence in objective functions with many decision variables [15]. Therefore, GA is used to find the optimal values of the decision variables in the proposed protection coordination scheme. In the genetic algorithm, the values of the decision variables are initially created randomly within the range of their variation. Then, by calculating the fitness function and minimizing the operation time of each relay, the optimal values of the decision variables are selected. Table 3 presents the settings considered for the genetic algorithm parameters in the proposed design.
| Parameter | Value |
|---|---|
| Population size | 200 |
| Iterations | 4000 |
| Crossover rate | 0.6 |
| Mutation rate | 0.4 |
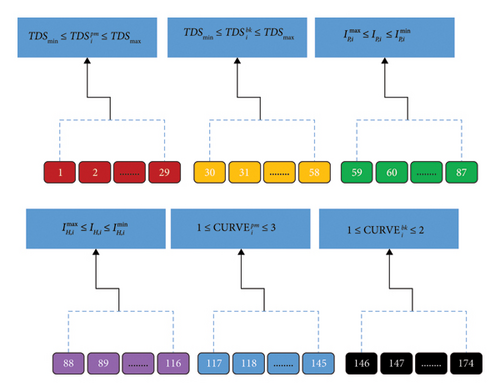
In Figure 2, the chromosomes of the decision variables of the DOC relays are shown. In the studied network, 29 DOC relays are used. Therefore, in the GA, the first 29 genes of each chromosome (1–29) include the relays’ TDSs in the main mode. The following 29 genes (30–58) include the relays’ TDSs in the backup mode. The next 29 genes (59–87) include the relays Ip and the next 29 genes (88–116) include the point H current. The following 29 genes (117–145) include the main relay curve type, and the final 29 genes (146–174) include the backup relay curve type. The NI, VI, and EI curves are considered as numbers 1, 2, and 3, respectively. Therefore, the number of decision variables in the proposed algorithm for the specific study case is equal to 174.
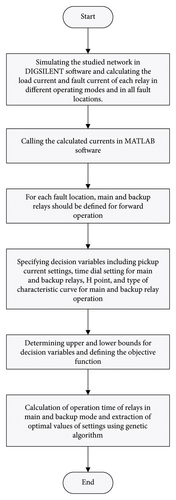
2.5. Flowchart
In Figure 3, the flowchart of the proposed protection coordination scheme is presented. First, the test system is simulated in DIGSILENT software, and based on load flow studies, the load currents that pass through the relays are obtained. These studies are carried out in both grid-connected and islanded modes. Then, the obtained currents are fed into the MATLAB software, and the GA optimization is run to obtain the optimal values of the decision variables.
3. Description of the Test System
The proposed protection coordination scheme is tested on the modified IEEE 30-bus distribution system [26]. As shown in Figure 4, this network comprises 14 buses and 16 feeders, whose parameters are given in [26]. In addition, the network utilizes 29 directional overcurrent relays. The network nominal voltage is 33 kV, the frequency is 60 Hz, and the test system consists of three subtransmission substations with 132/33 kV and 50 MVA transformers. The studied network also includes 11 synchronous-based DGs in buses (2–10, 12, and 14). In the case of the islanded mode of operation, synchronous-based DGs can supply all the local loads. Synchronous-based DGs are connected to the network by 11 transformers of 6.6/33 kV [26].
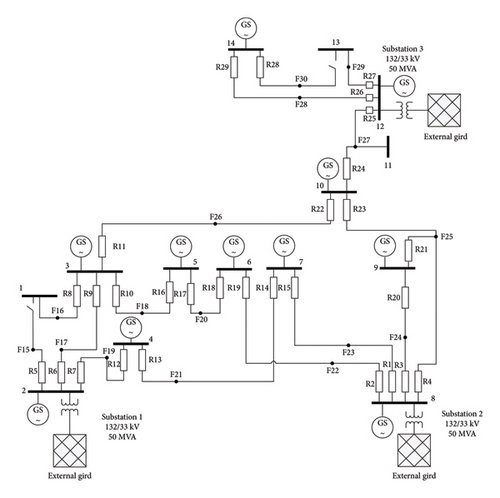
4. Simulation Results and Analysis
In this section, the first subsection presents the operation time of the relays in both grid-connected and islanded modes, as well as the optimal settings of the protection relays, obtained using the method described in reference [24]. Then, in the second subsection, the operation time of the relays in both grid-connected and islanded modes, along with the optimal settings of the relays, are obtained using the proposed method. In both subsections, by applying a symmetrical fault in the middle of each line, the fault current of each relay is recorded. The CTI used in reference [24] and the proposed method are identical and equal to 0.2 s. In addition, at the end of the second subsection, it is demonstrated that the relay operation time achieved by the proposed method is reduced compared with the reference method. Then, in the third subsection, the operation times of the relays in grid-connected and islanded modes, as well as the optimal settings of the relays for all symmetrical and unsymmetrical faults, are obtained using the proposed method.
4.1. The Method of Optimizing Dual Characteristic in Reference [24] With Symmetrical Faults
In reference [24], using the dual characteristic, which consists of two protection curves (VI curve for the main relay and NI curve for the backup relay), has been proposed. In that reference, three decision variables have been considered for each DOCR, which include (, , and Ip). The optimum relay setting for this method is given in Table 4. Table 5 presents the operation time of the relays in the islanded mode, and Table 6 displays the operation time of the relays in the grid-connected mode.
| Relay | Ip (pu) | TDS (main) | TDS (backup) | H setting |
|---|---|---|---|---|
| 1 | 0.0714 | 0.05 | 0.1474 | 24.88 |
| 2 | 0.2341 | 0.05 | 0.0561 | 5.535 |
| 3 | 0.0459 | 0.05 | 0.1125 | 31.85 |
| 4 | 0.0295 | 0.05 | 0.0965 | 16.76 |
| 5 | 0.0435 | 0.05 | 0.0807 | 17.48 |
| 6 | 0.1557 | 0.05 | 0.0689 | 7.697 |
| 7 | 0.2607 | 0.05 | 0.0502 | 4.826 |
| 8 | 0.0314 | 0.05 | 0.0578 | 27.34 |
| 9 | 0.0976 | 0.05 | 0.1069 | 14.72 |
| 10 | 0.0628 | 0.05 | 0.1067 | 19.99 |
| 11 | 0.0263 | 0.05 | 0.0941 | 30.28 |
| 12 | 0.0799 | 0.05 | 0.0932 | 15.19 |
| 13 | 0.2095 | 0.05 | 0.0747 | 5.911 |
| 14 | 0.3422 | 0.05 | 0.0516 | 3.712 |
| 15 | 0.0742 | 0.05 | 0.0941 | 16.46 |
| 16 | 0.0891 | 0.05 | 0.0668 | 12.11 |
| 17 | 0.0964 | 0.05 | 0.1035 | 10.75 |
| 18 | 0.0281 | 0.05 | 0.1721 | 37.39 |
| 19 | 0.0774 | 0.05 | 0.0685 | 13.61 |
| 20 | 0.0595 | 0.05 | 0.0513 | 24.73 |
| 21 | 0.1061 | 0.05 | 0.0523 | 9.744 |
| 22 | 0.1002 | 0.05 | 0.0511 | 6.793 |
| 23 | 0.0227 | 0.05 | 0.1399 | 34.36 |
| 24 | 0.0293 | 0.05 | 0.1015 | 23.29 |
| 25 | 0.1062 | 0.05 | 0.0526 | 4.758 |
| 26 | 0.0531 | 0.05 | 0.0779 | 10.74 |
| 27 | 0.0161 | 0.05 | 0.1428 | 26.76 |
| 28 | 0.0263 | 0.05 | 0.1958 | 11.55 |
| 29 | 0.0101 | 0.05 | 0.1654 | 38.89 |
| Fault location | Main relay operation time | Backup relay operation time | Backup relay operation time | Backup relay operation time |
|---|---|---|---|---|
| F15 | R5 | R9 | R12 | — |
| 0.0356 | 0.3591 | 0.3402 | ||
| F16 | R8 | R6 | R16 | R22 |
| 0.0357 | 0.4017 | 0.2814 | 0.2934 | |
| F17 | R6 | R12 | — | — |
| 0.2527 | 0.4529 | |||
| R9 | R16 | R22 | — | |
| 0.0474 | 0.2478 | 0.2479 | ||
| F18 | R10 | R6 | R22 | — |
| 0.0356 | 0.3792 | 0.2824 | ||
| R16 | R18 | — | — | |
| 0.1895 | 0.3903 | |||
| F19 | R7 | R9 | — | — |
| 0.2314 | 0.4353 | |||
| R12 | R14 | — | — | |
| 0.2444 | 0.4446 | |||
| F20 | R17 | R10 | — | — |
| 0.0632 | 0.2871 | |||
| R18 | R2 | — | — | |
| 0.0356 | 0.3327 | |||
| F21 | R13 | R7 | — | — |
| 0.1282 | 0.3719 | |||
| R14 | R1 | — | — | |
| 0.2247 | 0.4267 | |||
| F22 | R2 | R15 | R20 | R23 |
| 0.1396 | 0.3397 | 0.1918 | 0.3404 | |
| R19 | R17 | — | — | |
| 0.1856 | 0.3879 | |||
| F23 | R1 | R19 | R20 | R23 |
| 0.0356 | 0.2426 | 0.2364 | 0.3172 | |
| R15 | R13 | — | — | |
| 0.2442 | 0.4446 | |||
| F24 | R3 | R15 | R19 | R23 |
| 0.0355 | 0.2728 | 0.2355 | 0.3172 | |
| R20 | R23 | R4 | — | |
| 0.1172 | 0.3172 | 0.3174 | ||
| F25 | R4 | R15 | R19 | — |
| 0.0355 | 0.2861 | 0.2504 | ||
| R21 | R3 | — | — | |
| 0.0579 | 0.2584 | |||
| R23 | R11 | R25 | — | |
| 0.0356 | 0.2916 | 0.3761 | ||
| F26 | R11 | R6 | R16 | — |
| 0.0359 | 0.5569 | 0.3555 | ||
| R22 | R4 | R21 | R25 | |
| 0.0803 | 0.4541 | 0.3262 | 0.4668 | |
| F27 | R24 | R4 | R11 | R21 |
| 0.0355 | 0.4153 | 0.2873 | 0.3618 | |
| R25 | R29 | — | — | |
| 0.1748 | 0.3751 | |||
| F28 | R26 | R24 | — | — |
| 0.0623 | 0.2627 | |||
| R29 | — | — | — | |
| 0.0357 | ||||
| F29 | R27 | R24 | R29 | — |
| 0.0356 | 0.2577 | 0.3751 | ||
| F30 | R28 | R26 | — | — |
| 0.0356 | 0.2896 | |||
- Note: The first row of Table 5 is bold to emphasize the titles.
| Fault location | Main relay operation time | Backup relay operation time | Backup relay operation time | Backup relay operation time |
|---|---|---|---|---|
| F15 | R5 | R9 | R12 | — |
| 0.0365 | 0.4665 | 0.4181 | ||
| F16 | R8 | R6 | R16 | R22 |
| 0.0357 | 0.2372 | 0.2888 | 0.2848 | |
| F17 | R6 | R12 | — | — |
| 0.0978 | 0.6347 | |||
| R9 | R16 | R22 | — | |
| 0.0396 | 0.4682 | 0.4056 | ||
| F18 | R10 | R6 | R22 | — |
| 0.0356 | 0.2363 | 0.2579 | ||
| R16 | R18 | — | — | |
| 0.0534 | 0.3903 | |||
| F19 | R7 | R9 | — | — |
| 0.1192 | 0.4251 | |||
| R12 | R14 | — | — | |
| 0.0401 | 0.2927 | |||
| F20 | R17 | R10 | — | — |
| 0.0475 | 0.2485 | |||
| R18 | R2 | — | — | |
| 0.0355 | 0.2359 | |||
| F21 | R13 | R7 | — | — |
| 0.1008 | 0.3011 | |||
| R14 | R1 | — | — | |
| 0.1196 | 0.3343 | |||
| F22 | R2 | R15 | R20 | R23 |
| 0.0688 | 0.4151 | 0.2821 | 0.4061 | |
| R19 | R17 | — | — | |
| 0.0491 | 0.3307 | |||
| F23 | R1 | R19 | R20 | R23 |
| 0.0356 | 0.2583 | 0.3378 | 0.3172 | |
| R15 | R13 | — | — | |
| 0.0374 | 0.3129 | |||
| F24 | R3 | R15 | R19 | R23 |
| 0.0355 | 0.2668 | 0.2461 | 0.4073 | |
| R20 | R23 | R4 | — | |
| 0.0363 | 0.4074 | 0.2704 | ||
| F25 | R4 | R15 | R19 | — |
| 0.0355 | 0.2993 | 0.2923 | ||
| R21 | R3 | — | — | |
| 0.0355 | 0.2552 | |||
| R23 | R11 | R25 | — | |
| 0.0356 | 0.2361 | 0.2362 | ||
| F26 | R11 | R6 | R16 | — |
| 0.0359 | 1.2431 | 0.3763 | ||
| R22 | R4 | R21 | R25 | |
| 0.0599 | 0.3042 | 0.2604 | 0.2892 | |
| F27 | R24 | R4 | R11 | R21 |
| 0.0355 | 0.3278 | 0.2714 | 0.3084 | |
| R25 | R29 | — | — | |
| 0.0431 | 0.5072 | |||
| F28 | R26 | R24 | — | — |
| 0.0359 | 0.4224 | |||
| R29 | — | — | — | |
| 0.3751 | ||||
| F29 | R27 | R24 | R29 | — |
| 0.0356 | 0.3653 | 0.5261 | ||
| F30 | R28 | R26 | — | — |
| 0.0356 | 0.2365 | |||
The operation time of all relays in the main mode and in all operating modes is mostly 0.035 s, and this operation time with curve VI cannot be less than this value; this result means that at these points, the short-circuit current is more than 20 times the load current of the relays. In fault location (F22) and in the island operation mode that is marked with bold in Table 5, the operation time of the main relay R2 is equal to 0.1396 s, and the operation time of the backup relay R20 is equal to 0.1918 s, which indicates that CTI is less than 0.2 s. Operation of these relays has caused the loss of CTI. The optimum relay setting for this method is given in Table 5.
4.2. Proposed Dual Characteristic Optimization Method With Symmetrical Faults
In this subsection, the results obtained from the proposed protection coordination method, using the objective function in equation (1), are presented. In addition, a comparison is made between the operation times of the relays in all operating modes for the proposed method and the reference method [24]. In the proposed protection method for each DOCR, six decision variables are considered, which include (, , Ip, IH, and main protection curves and backup protection curves).
Table 7 shows the optimal settings obtained for the decision variables in the proposed protection method. Table 8 presents the operation time of the relays in the islanded mode, and Table 9 displays the operation time of the relays in the grid-connected mode.
| Relay | Ip (pu) | TDS (main) | TDS (backup) | H setting | Type 2 | Type 1 |
|---|---|---|---|---|---|---|
| 1 | 0.0213 | 0.05 | 0.1031 | 84.83 | EI | NI |
| 2 | 0.0356 | 0.05 | 0.1024 | 39.01 | EI | NI |
| 3 | 0.0785 | 0.05 | 0.2319 | 21.51 | EI | VI |
| 4 | 0.0238 | 0.05 | 0.2275 | 27.38 | EI | VI |
| 5 | 0.0207 | 0.05 | 0.3125 | 73.51 | EI | NI |
| 6 | 0.1487 | 0.05 | 0.0635 | 9.06 | EI | NI |
| 7 | 0.2186 | 0.05 | 0.0536 | 5.74 | EI | VI |
| 8 | 0.0312 | 0.05 | 0.2745 | 53.87 | EI | VI |
| 9 | 0.0593 | 0.05 | 0.2158 | 25.21 | EI | VI |
| 10 | 0.0923 | 0.05 | 0.1826 | 14.59 | EI | VI |
| 11 | 0.0549 | 0.05 | 0.0609 | 18.67 | EI | NI |
| 12 | 0.0482 | 0.05 | 0.1887 | 22.81 | EI | VI |
| 13 | 0.2431 | 0.05 | 0.0609 | 5.42 | EI | NI |
| 14 | 0.1236 | 0.05 | 0.1309 | 11.16 | EI | VI |
| 15 | 0.0165 | 0.05 | 0.0937 | 81.47 | EI | NI |
| 16 | 0.0428 | 0.05 | 0.0801 | 26.31 | EI | NI |
| 17 | 0.0771 | 0.05 | 0.2107 | 14.61 | EI | VI |
| 18 | 0.0905 | 0.05 | 0.1871 | 12.81 | EI | VI |
| 19 | 0.0177 | 0.05 | 0.0953 | 57.26 | EI | NI |
| 20 | 0.0511 | 0.05 | 0.0623 | 24.59 | EI | NI |
| 21 | 0.0409 | 0.05 | 0.1465 | 32.75 | EI | VI |
| 22 | 0.0225 | 0.05 | 0.0906 | 42.11 | EI | NI |
| 23 | 0.0201 | 0.05 | 0.1507 | 42.37 | EI | NI |
| 24 | 0.0277 | 0.05 | 0.0863 | 32.07 | EI | NI |
| 25 | 0.0276 | 0.05 | 0.0901 | 18.75 | EI | NI |
| 26 | 0.0298 | 0.05 | 0.2518 | 21.25 | EI | VI |
| 27 | 0.0141 | 0.05 | 0.1371 | 59.62 | EI | VI |
| 28 | 0.0102 | 0.05 | 0.0678 | 76.32 | EI | VI |
| 29 | 0.0193 | 0.05 | 0.0743 | 16.06 | EI | VI |
| Fault location | Main relay operation time | Backup relay operation time | Backup relay operation time | Backup relay operation time |
|---|---|---|---|---|
| F15 | R5 | R9 | R12 | — |
| 0.0107 | 0.2491 | 0.2575 | ||
| F16 | R8 | R6 | R16 | R22 |
| 0.0101 | 0.3559 | 0.2308 | 0.2289 | |
| F17 | R6 | R12 | — | — |
| 0.2271 | 0.4346 | |||
| R9 | R16 | R22 | — | |
| 0.0105 | 0.2111 | 0.2113 | ||
| F18 | R10 | R6 | R22 | — |
| 0.0198 | 0.3366 | 0.2249 | ||
| R16 | R18 | — | — | |
| 0.1814 | 0.3839 | |||
| F19 | R7 | R9 | — | — |
| 0.1672 | 0.3672 | |||
| R12 | R14 | — | — | |
| 0.1341 | 0.3397 | |||
| F20 | R17 | R10 | — | — |
| 0.0191 | 0.3241 | |||
| R18 | R2 | — | — | |
| 0.0264 | 0.2321 | |||
| F21 | R13 | R7 | — | — |
| 0.1435 | 0.3543 | |||
| R14 | R1 | — | — | |
| 0.0326 | 0.2337 | |||
| F22 | R2 | R15 | R20 | R23 |
| 0.0101 | 0.2124 | 0.2147 | 0.3505 | |
| R19 | R17 | — | — | |
| 0.0162 | 0.4169 | |||
| F23 | R1 | R19 | R20 | R23 |
| 0.0101 | 0.2162 | 0.2602 | 0.3418 | |
| R15 | R13 | — | — | |
| 0.2124 | 0.4161 | |||
| F24 | R3 | R15 | R19 | R23 |
| 0.0102 | 0.2124 | 0.2162 | 0.3417 | |
| R20 | R23 | R4 | — | |
| 0.1413 | 0.3417 | 0.3414 | ||
| F25 | R4 | R15 | R19 | — |
| 0.0108 | 0.2124 | 0.2162 | ||
| R21 | R3 | — | — | |
| 0.0108 | 0.3042 | |||
| R23 | R11 | R25 | — | |
| 0.0101 | 0.2852 | 0.2657 | ||
| F26 | R11 | R6 | R16 | — |
| 0.0112 | 0.4865 | 0.2701 | ||
| R22 | R4 | R21 | R25 | |
| 0.0101 | 0.7003 | 0.2885 | 0.2896 | |
| F27 | R24 | R4 | R11 | R21 |
| 0.0103 | 0.5948 | 0.2789 | 0.3269 | |
| R25 | R29 | — | — | |
| 0.0114 | 0.2123 | |||
| F28 | R26 | R24 | — | — |
| 0.0104 | 0.2186 | |||
| R29 | — | — | — | |
| 0.0154 | ||||
| F29 | R27 | R24 | R29 | — |
| 0.0105 | 0.2145 | 0.2311 | ||
| F30 | R28 | R26 | — | — |
| 0.0101 | 0.3301 | |||
| Fault location | Main relay operation time | Backup relay operation time | Backup relay operation time | Backup relay operation time |
|---|---|---|---|---|
| F15 | R5 | R9 | R12 | — |
| 0.0107 | 0.4166 | 0.3797 | ||
| F16 | R8 | R6 | R16 | R22 |
| 0.0101 | 0.2134 | 0.2351 | 0.2258 | |
| F17 | R6 | R12 | — | — |
| 0.0452 | 0.7105 | |||
| R9 | R16 | R22 | — | |
| 0.0105 | 0.3196 | 0.2616 | ||
| F18 | R10 | R6 | R22 | — |
| 0.0105 | 0.2114 | 0.2155 | ||
| R16 | R18 | — | — | |
| 0.0101 | 0.2671 | |||
| F19 | R7 | R9 | — | — |
| 0.0582 | 0.3512 | |||
| R12 | R14 | — | — | |
| 0.0103 | 0.2108 | |||
| F20 | R17 | R10 | — | — |
| 0.0112 | 0.2121 | |||
| R18 | R2 | — | — | |
| 0.0142 | 0.2321 | |||
| F21 | R13 | R7 | — | — |
| 0.0941 | 0.2957 | |||
| R14 | R1 | — | — | |
| 0.0117 | 0.2337 | |||
| F22 | R2 | R15 | R20 | R23 |
| 0.0101 | 0.2124 | 0.3049 | 0.4149 | |
| R19 | R17 | — | — | |
| 0.0102 | 0.2944 | |||
| F23 | R1 | R19 | R20 | R23 |
| 0.0101 | 0.2162 | 0.3577 | 0.3417 | |
| R15 | R13 | — | — | |
| 0.0102 | 0.2808 | |||
| F24 | R3 | R15 | R19 | R23 |
| 0.0102 | 0.2124 | 0.2162 | 0.4161 | |
| R20 | R23 | R4 | — | |
| 0.0102 | 0.4161 | 0.2319 | ||
| F25 | R4 | R15 | R19 | — |
| 0.0108 | 0.2124 | 0.2162 | ||
| R21 | R3 | — | — | |
| 0.0108 | 0.2116 | |||
| R23 | R11 | R25 | — | |
| 0.0101 | 0.2112 | 0.2124 | ||
| F26 | R11 | R6 | R16 | — |
| 0.0103 | 1.0224 | 0.2801 | ||
| R22 | R4 | R21 | R25 | |
| 0.0101 | 0.3094 | 0.2114 | 0.2357 | |
| F27 | R24 | R4 | R11 | R21 |
| 0.0103 | 0.3669 | 0.2566 | 0.2684 | |
| R25 | R29 | — | — | |
| 0.0101 | 0.3799 | |||
| F28 | R26 | R24 | — | — |
| 0.0104 | 0.3472 | |||
| R29 | — | — | — | |
| 0.1825 | ||||
| F29 | R27 | R24 | R29 | — |
| 0.0105 | 0.3016 | 0.4035 | ||
| F30 | R28 | R26 | — | — |
| 0.0101 | 0.2131 | |||
As can be seen, the CTI is maintained at all fault locations. In addition, due to the use of the curve EI, the operation time of most relays in the main mode has been reduced to 0.01 s in both islanded and grid-connected operating modes, compared with 0.035 s in Tables 5, 6.
The operation time of the relays in the backup mode has also been reduced. Some comparisons between the results of reference [24] and the proposed method are as follows.
As shown in Figure 5 for the fault at the F15 location in the grid-connected mode, relay R5 operates as the main relay, while relays R9 and R12 serve as backup relays. If relay R5 fails to operate, the backup relays operate after 0.4166 s and 0.3797 s, respectively, to isolate the fault. According to the method described in reference [24], the backup relays operate with response times of 0.4665 s and 0.4181 s, respectively, which show that the proposed method has improved the relays’ operating times.
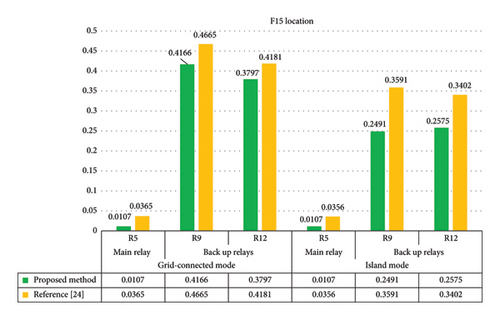
For faults at the F15 location and in the islanded mode, relay R5 operates as the main relay, while relays R9 and R12 function as backup relays. If relay R5 fails to operate, the backup relays operate after 0.2491 s and 0.2575 s, respectively, to isolate the fault. According to the method described in reference [24], the backup relays operate with the times of 0.3591 s and 0.3402 s, respectively. The proposed method demonstrates improvement over the previous study.
As shown in Figure 6 for the fault in the F22 location in the grid-connected mode, relays R2 and R19 operate as the main relays, while relays R15, R20, R23, and R17 operate as backup relays. If relay R2 fails to operate, the backup relays operate after 0.2124 s, 0.3049 s, and 0.4149 s, respectively, to isolate the fault. If relay R19 fails to operate, the backup relay operates after 0.2944 s. While using the method presented in reference [24], the backup relays operate with the times of 0.4151 s, 0.2821 s, 0.4061 s, and 0.3307 s, respectively.
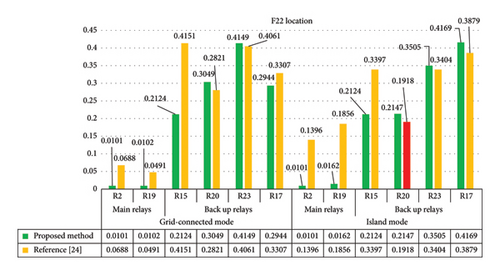
For the fault in the F22 location and in the islanded mode, relays R2 and R19 operate as the main relays, while relays R15, R20, R23, and R17 operate as backup relays. If relay R2 fails to operate, the backup relays operate after 0.2124 s, 0.2147 s, and 0.3505 s, respectively, to isolate the fault. If relay R19 fails to operate, the backup relay operates after 0.4169 s. While using the method presented in reference [24], the backup relays operate with times of 0.3397 s, 0.1918 s, 0.3404 s, and 0.3879 s, respectively.
In reference [24], the CTI between the main and backup relays was considered to be 0.2 s. As you can see, here, the time interval between relay R2 and R20 has disappeared, which is why the R20 relay diagram is shown in red. But the proposed method maintains the CTI between the main and backup relays.
Another notable point in Figure 6 is the slight increase in the operation time of some backup relays in the proposed design compared with the reference. This increase in time is negligible compared with the decrease in time in other main and backup relays and also helps to maintain CTI.
In Table 10, the operation time of the relays in the proposed coordination method is compared with that in reference [24]. As can be seen, the proposed method reduces the operation time of the relays by 17% in all operating modes.
| Operating mode | Benchmark method with symmetrical faults [24] (s) | Proposed method with symmetrical faults (s) | Percentage of improvement (%) |
|---|---|---|---|
| Grid-connected operation mode | 18.7 | 15.2 | 19 |
| Islanded operation mode | 19.1 | 16.3 | 15 |
| Summation (both modes) | 37.8 | 31.5 | 17 |
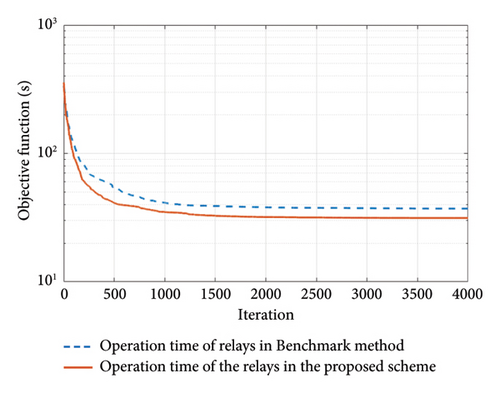
Simulations have been carried out using a Core i7-7500U/8GB RAM laptop, and it takes approximately 20 min. In Figure 7, the convergence of the genetic algorithm and its comparison with reference [24] are presented.
4.3. Proposed Dual Characteristic Optimization Method With Symmetrical and Unsymmetrical Faults
The settings of directional overcurrent relays should cover all possible fault scenarios, including the worst-case scenario and the highest current, such as a three-phase fault or faults with lower current, such as single-phase to ground, two-phase, and two-phase to ground faults. Therefore, in this subsection, using the objective function of equation (3), settings are presented that include all the mentioned modes, which were not considered in previous studies. Table 11 presents the optimal settings obtained for the decision variables in the proposed protection method for both symmetrical and unsymmetrical faults. Table 12 presents the operation time of the relays in the islanded mode, and Table 13 displays the operation time of the relays in the grid-connected mode.
| Relay | Ip (pu) | TDS (main) | TDS (backup) | H setting | Type 2 | Type 1 |
|---|---|---|---|---|---|---|
| 1 | 0.3596 | 0.05 | 0.0613 | 5.02 | EI | NI |
| 2 | 0.1665 | 0.05 | 0.0921 | 8.33 | EI | VI |
| 3 | 0.3201 | 0.11 | 0.0511 | 5.27 | VI | NI |
| 4 | 0.0418 | 0.05 | 0.1109 | 15.56 | EI | VI |
| 5 | 0.0207 | 0.05 | 0.2771 | 73.51 | EI | VI |
| 6 | 0.0522 | 0.05 | 0.0935 | 24.98 | EI | NI |
| 7 | 0.0938 | 0.19 | 0.0992 | 12.99 | VI | VI |
| 8 | 0.0312 | 0.05 | 0.1576 | 53.88 | EI | NI |
| 9 | 0.1223 | 0.05 | 0.1741 | 12.21 | EI | VI |
| 10 | 0.0634 | 0.05 | 0.0893 | 21.23 | EI | NI |
| 11 | 0.0818 | 0.05 | 0.0986 | 12.54 | EI | NI |
| 12 | 0.1042 | 0.05 | 0.0591 | 10.38 | EI | NI |
| 13 | 0.0192 | 0.05 | 0.0932 | 68.31 | EI | NI |
| 14 | 0.1249 | 0.05 | 0.1216 | 11.04 | EI | VI |
| 15 | 0.0165 | 0.05 | 0.1912 | 72.04 | EI | NI |
| 16 | 0.0275 | 0.05 | 0.0966 | 38.39 | EI | NI |
| 17 | 0.0674 | 0.05 | 0.1752 | 16.72 | EI | VI |
| 18 | 0.0598 | 0.05 | 0.2314 | 19.36 | EI | VI |
| 19 | 0.0699 | 0.05 | 0.1364 | 15.09 | EI | NI |
| 20 | 0.0635 | 0.05 | 0.1251 | 19.51 | EI | NI |
| 21 | 0.0799 | 0.05 | 0.1024 | 16.79 | EI | VI |
| 22 | 0.0338 | 0.05 | 0.0862 | 28.01 | EI | NI |
| 23 | 0.1281 | 0.08 | 0.1128 | 6.62 | NI | NI |
| 24 | 0.0304 | 0.05 | 0.0941 | 29.23 | EI | NI |
| 25 | 0.0877 | 0.05 | 0.1071 | 5.89 | EI | NI |
| 26 | 0.0856 | 0.05 | 0.0662 | 7.39 | EI | VI |
| 27 | 0.0141 | 0.05 | 0.3815 | 59.63 | EI | NI |
| 28 | 0.0179 | 0.05 | 0.3286 | 76.32 | EI | VI |
| 29 | 0.0181 | 0.05 | 0.0938 | 38.76 | EI | NI |
| Fault location | Main relay operation time | Backup relay operation time | Backup relay operation time | Backup relay operation time |
|---|---|---|---|---|
| F15 | R5 | R9 | R12 | — |
| 0.0101 | 0.4558 | 0.2486 | ||
| F16 | R8 | R6 | R16 | R22 |
| 0.0101 | 0.2707 | 0.2317 | 0.2629 | |
| F17 | R6 | R12 | — | — |
| 0.0101 | 0.2102 | |||
| R9 | R16 | R22 | — | |
| 0.0179 | 0.2191 | 0.2331 | ||
| F18 | R10 | R6 | R22 | — |
| 0.0101 | 0.2612 | 0.2533 | ||
| R16 | R18 | — | — | |
| 0.0101 | 0.2799 | |||
| F19 | R7 | R9 | — | — |
| 0.1755 | 0.3768 | |||
| R12 | R14 | — | — | |
| 0.0226 | 0.3118 | |||
| F20 | R17 | R10 | — | — |
| 0.0101 | 0.2389 | |||
| R18 | R2 | — | — | |
| 0.0102 | 0.3466 | |||
| F21 | R13 | R7 | — | — |
| 0.0101 | 0.2108 | |||
| R14 | R1 | — | — | |
| 0.1639 | 0.3659 | |||
| F22 | R2 | R15 | R20 | R23 |
| 0.0411 | 0.4335 | 0.4405 | 0.5749 | |
| R19 | R17 | — | — | |
| 0.0126 | 0.2779 | |||
| F23 | R1 | R19 | R20 | R23 |
| 0.1533 | 0.4463 | 0.3551 | 0.5226 | |
| R15 | R13 | — | — | |
| 0.0107 | 0.2114 | |||
| F24 | R3 | R15 | R19 | R23 |
| 0.2331 | 0.4335 | 0.4333 | 0.4338 | |
| R20 | R23 | R4 | — | |
| 0.0102 | 0.4338 | 0.3201 | ||
| F25 | R4 | R15 | R19 | — |
| 0.0104 | 0.4335 | 0.4668 | ||
| R21 | R3 | — | — | |
| 0.0101 | 0.2978 | |||
| R23 | R11 | R25 | — | |
| 0.2915 | 0.6352 | 0.6498 | ||
| F26 | R11 | R6 | R16 | — |
| 0.0189 | 0.3194 | 0.2655 | ||
| R22 | R4 | R21 | R25 | |
| 0.2638 | 0.7619 | 0.4681 | 0.8608 | |
| F27 | R24 | R4 | R11 | R21 |
| 0.0101 | 0.6704 | 0.6671 | 0.5691 | |
| R25 | R29 | — | — | |
| 0.0548 | 0.3594 | |||
| F28 | R26 | R24 | — | — |
| 0.0551 | 0.2562 | |||
| R29 | — | — | — | |
| 0.0101 | ||||
| F29 | R27 | R24 | R29 | — |
| 0.0102 | 0.2521 | 0.2128 | ||
| F30 | R28 | R26 | — | — |
| 0.0101 | 0.3343 | |||
| Fault location | Main relay operation time | Backup relay operation time | Backup relay operation time | Backup relay operation time |
|---|---|---|---|---|
| F15 | R5 | R9 | R12 | — |
| 0.0101 | 0.6482 | 0.2847 | ||
| F16 | R8 | R6 | R16 | R22 |
| 0.0101 | 0.2135 | 0.2341 | 0.2614 | |
| F17 | R6 | R12 | — | — |
| 0.0101 | 0.2177 | |||
| R9 | R16 | R22 | — | |
| 0.0111 | 0.2191 | 0.2111 | ||
| F18 | R10 | R6 | R22 | — |
| 0.0101 | 0.2121 | 0.2437 | ||
| R16 | R18 | — | — | |
| 0.0101 | 0.2106 | |||
| F19 | R7 | R9 | — | — |
| 0.1355 | 0.5171 | |||
| R12 | R14 | — | — | |
| 0.0123 | 0.2125 | |||
| F20 | R17 | R10 | — | — |
| 0.0101 | 0.2107 | |||
| R18 | R2 | — | — | |
| 0.0102 | 0.2111 | |||
| F21 | R13 | R7 | — | — |
| 0.0101 | 0.2104 | |||
| R14 | R1 | — | — | |
| 0.0102 | 0.2125 | |||
| F22 | R2 | R15 | R20 | R23 |
| 0.0157 | 0.4335 | 0.5434 | 0.6129 | |
| R19 | R17 | — | — | |
| 0.0101 | 0.2108 | |||
| F23 | R1 | R19 | R20 | R23 |
| 0.0304 | 0.4523 | 0.3499 | 0.5179 | |
| R15 | R13 | — | — | |
| 0.0106 | 0.2114 | |||
| F24 | R3 | R15 | R19 | R23 |
| 0.0933 | 0.4335 | 0.4328 | 0.2947 | |
| R20 | R23 | R4 | — | |
| 0.0101 | 0.2947 | 0.2111 | ||
| F25 | R4 | R15 | R19 | — |
| 0.0101 | 0.4335 | 0.5108 | ||
| R21 | R3 | — | — | |
| 0.0101 | 0.2103 | |||
| R23 | R11 | R25 | — | |
| 0.2538 | 0.4541 | 0.4572 | ||
| F26 | R11 | R6 | R16 | — |
| 0.0117 | 0.2358 | 0.2718 | ||
| R22 | R4 | R21 | R25 | |
| 0.0103 | 0.4465 | 0.6352 | 0.4973 | |
| F27 | R24 | R4 | R11 | R21 |
| 0.0101 | 0.4465 | 0.6352 | 0.4973 | |
| R25 | R29 | — | — | |
| 0.0101 | 0.2408 | |||
| F28 | R26 | R24 | — | — |
| 0.0163 | 0.3918 | |||
| R29 | — | — | — | |
| 0.0101 | ||||
| F29 | R27 | R24 | R29 | — |
| 0.0102 | 0.3394 | 0.2466 | ||
| F30 | R28 | R26 | — | — |
| 0.0101 | 0.2103 | |||
To test the obtained optimal settings using the objective function of equation (3) in the presence of high resistance faults, a new case study is considered. In this case study, the fault currents for single-phase to ground and two-phase short circuit faults are considered to be half and one-quarter of the three-phase fault current, respectively. Table 14 presents a comparison of the total operating time between the proposed method and the benchmark method [24] for symmetrical and unsymmetrical faults, both without and with resistance. It is clear from Table 14 that the proposed method outperforms the other methods at all faults.
| Faults type | Operating mode | Benchmark method [24] | Proposed method | Percentage of improvement (%) |
|---|---|---|---|---|
| Symmetrical faults | Grid-connected operation mode | 18.7 | 15.2 | 19 |
| Islanded operation mode | 19.1 | 16.3 | 15 | |
| Summation (both modes) | 37.8 | 31.5 | 17 | |
| Symmetrical and unsymmetrical faults without resistance | Grid-connected operation mode | 20.9 | 17.2 | 18 |
| Islanded operation mode | 24.1 | 20.2 | 16 | |
| Summation (both modes) | 45 | 37.4 | 17 | |
| Symmetrical and unsymmetrical faults with resistance | Grid-connected operation mode | 39.5 | 32.5 | 18 |
| Islanded operation mode | 49.7 | 40.4 | 19 | |
| Summation (both modes) | 89.2 | 72.9 | 18 | |
5. Conclusion
- •
Presenting a new objective function to consider both symmetrical and unsymmetrical faults in the optimization procedure.
- •
Reducing the operation time of the relays and thus the protection system by using dual characteristics in symmetrical and unsymmetrical faults by 17%.
- •
Maintaining the minimum CTI between the main and backup relays in all operating modes.
- •
Increasing reliability against cyber-attacks and possible failure of communication systems by using the communication-free scheme.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
No funding was received for this manuscript.
Open Research
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.




