This paper presents a new 3D analytical model based on the Fourier–Bessel series for electromagnetic modeling of the performance of slotless axial flux permanent magnet (AFPM) machines under no-load conditions. The machine geometry is divided into different domains including the permanent magnet (PM) domain, the air-gap domain, and so on. The Laplace equation in terms of scalar magnetic potential is solved in each domain, and their solutions are expressed based on the Fourier–Bessel series to accurately consider the radial variation of the air-gap magnetic field. A 2D geometry function based on the Fourier–Bessel series is introduced to accurately consider the different PM shaping in the magnet domain. The boundary condition is then used to determine the unknown constants in the general solutions. This 3D analytical model is prepared to calculate the no-load flux linkage of stator phases while considering different PM shapes and skewing effects. Two indexes including the amplitude of the fundamental component and the total harmonic distortion (THD) of no-load phase flux linkage are considered to investigate the effect of skewed PMs and other PM shapes. The capability of the proposed 3D analytical model is also presented to calculate the air-gap magnetic field due to the stator phases for determining the inductance matrix. Finally, the accuracy of the proposed 3D analytical model is verified by comparing it with the corresponding results obtained through the finite element method (FEM) and the experiment setup.

1. Introduction

Slotless axial flux permanent magnet (AFPM) machines have found various applications in industries due to the lack of cogging torque and low vibration [1, 2]. For this reason, the accurate 3D modeling of slotless AFPM machines is necessary to calculate the air-gap magnetic field. The finite element method (FEM) is the most famous technique for the performance analysis of the AFPM machines [3, 4]. The field reconstruction method which acts based on the FEM was used in [5] for the analysis of one AFPM machine. The FEM can accurately consider all nonideal effects such as the magnetic saturation and the slotting effect. However, the FEM is a time-consuming technique for 3D modeling of the AFPM machines. For this reason, it should be better only used in the final stage for verifying the analytical results [6]. The analytical techniques which have been so far used for modeling and analysis of the AFPM machines are, respectively, the quasi-3D models, the magnetic equivalent circuit (MEC) model, and the subdomain (S-D) model.

The most commonly used analytical model for the analysis of the AFPM machines is the quasi-3D analytical model. In this model, the geometry of the AFPM machine is divided into several annular slices in the radial direction to consider the curvature effect due to the radial variation of geometry. The 2D analytical models and the law of superposition are then used to analyze the 3D model. The quasi-3D model based on the FEM was used in [7]. The quasi-3D model based on the harmonic magnetic modeling in the Cartesian coordinate was proposed in [8]. The quasi-3D model based on one S-D model was presented in the mean radius of axial flux eddy current brakes [9, 10] and in different radii of the AFPM machines [11]. The quasi-3D model based on the MEC model was used in [12, 13] for the electromagnetic analysis of the AFPM machines. The quasi-3D model based on the combination of the solution of Maxwell’s equations in the air-gap region and the MEC model in the iron parts was presented in [14]. Generally, it can be said that the accuracy of quasi-3D models increases as the number of 2D models in different radii increases. Also, the edge effect which is caused by the unequal radial length of the rotor and the stator cannot be considered by using the quasi-3D models. For this reason, the correction factor obtained through the FEM was used to consider the edge effect in the air-gap magnetic field results of the quasi-3D model [15, 16]. The 3D MEC model can be used to model and analyze the AFPM machines [17]. However, the MEC model is not user-friendly and it is not accurate for calculating the air-gap magnetic field components. The 3D S-D model has been also used for electromagnetic analysis of the AFPM machines without considering the edge effect [18].

This paper presents a 3D analytical model for the electromagnetic analysis of the slotless AFPM machines which can consider the curvature effect of the PM geometry and the edge effect due to the different radial lengths of the stator and rotor cores. This paper is organized as follows.

The main parameters of analyzed AFPM machines are introduced in Section 2. The principle of the proposed 3D analytical model is presented in Section 3. The flux linkage calculation by using the proposed analytical model is presented in Section 4. The conclusions of the work are given in Section 5.

2. Parameters of the Studied AFPM Machine

The main parameters of the analyzed single-sided 3-phase slotless AFPM machine with the axial magnetized trapezoid and rectangle PMs are introduced in Table 1. The views of the rotor and stator disks of the studied AFPM machine with sector-shaped PM and radial coils have been illustrated in Figure 1.

Table 1. Parameters of the analyzed AFPM machine.

Parameter	Value (unit)
Outer radius of stator back-iron (r_so)	150 (mm)
Inner radius of stator back-iron (r_si)	100 (mm)
Height of stator back-iron	10 (mm)
Number of coils	24
Height of coil	4 (mm)
Width of coil	7 (mm)
Number of turns per coil	51
Air-gap length	2 (mm)
Outer radius of PM (r_mo)	155 (mm)
Inner radius of PM (r_mi)	95 (mm)
Number of PMs	16
Height of PM	2.5 (mm)
Ratio of pole arc to pole pitch (trapezoidal PM)	0.8
Width of rectangle PM	30 (mm)
Length of rectangle PM	60 (mm)
Outer radius of PM back-iron (r_ro)	160 (mm)
Inner radius of PM back-iron (r_ri)	90 (mm)
Height of PM back-iron	10 (mm)
Remanence of PM (B_R)	1.2 (T)
Relative permeability of PM	1.1

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Analyzed AFPM machine. (a) Rotor disk. (b) Stator disk.

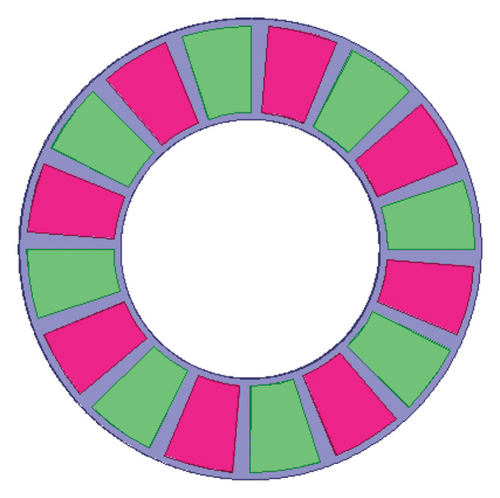
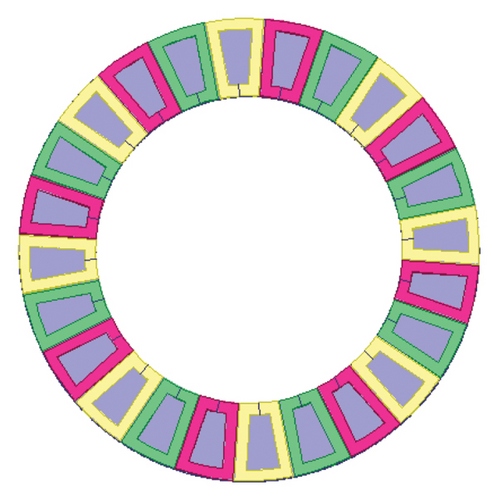
As shown, the stator phases and rotor PMs are illustrated with different colors for more clarity.

3. Proposed 3D Analytical Model

In the proposed 3D model, the machine geometry is divided into several domains. The 2D cross sections of the slotless AFPM geometry in the r − z plane and the φ − z plane are shown in Figure 2. The proposed 3D model can also consider the edge leakage fluxes and the leakage flux between adjacent PMs, which are shown in Figure 2.

The Laplace equation in terms of the scalar magnetic potential is written as

()

where Ψ_i is the scalar magnetic potential in the ith domain.

By using the continuity principle of the normal component of

and the tangential component of

across the boundaries in Figure 2, the necessary boundary condition for solving equation (1) in the air-gap domain can be defined as follows:

()

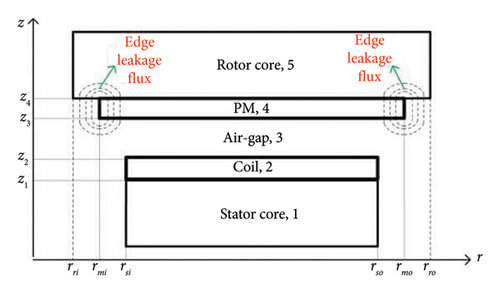
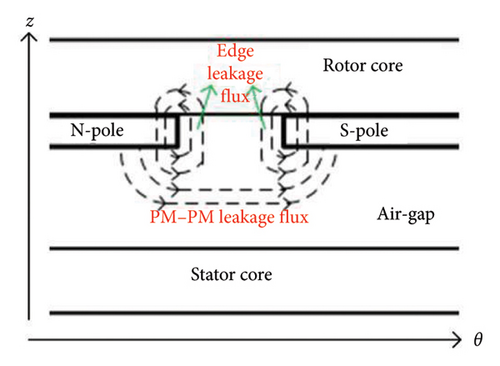
Laplace equation (1) is solved by using the variable separation method while assuming that the stator and rotor cores in the slotless AFPM machine have the infinite magnetic permeability. In Figure 2, the edge and overhang effects are due to the different radial lengths of domains. To accurately consider the geometrical variations in radial and tangential directions, the Fourier–Bessel series is used to represent the general solution of equation (1) in the ith domain, as shown in equation (7). j_{(k, l)} in equation (7) is the kth root of the first-kind Bessel function J_l(r).

The magnetic field strength in the ith domain can be calculated by using the following formula:

()

The components of

are obtained as shown in equations (8)–(10).

()

F((j_{(k, l)}/r_a)r) in equation (8) is defined as follows:

()

As shown in Figure 2(a), the PM magnetization (

) should be considered in the fourth domain to calculate the magnetic flux density as follows:

()

In equation (13), μ₀ is the magnetic permeability of air. The Fourier–Bessel series is used to express the distribution of axial magnetization of PMs, as shown in equation (11).

()

For the analyzed slotless AFPM machine with the trapezoid PM shape, the real distribution of M_z and the approximated distribution based on the Fourier–Bessel series are shown in Figure 3. To calculate the distribution of air-gap magnetic field due to only PMs, the unknown constants in equations (8)–(10) should be determined through applying the boundary condition at z = z₁, z = z₃, and z = z₄ while removing the coil region in Figure 2. The unknown constants for the domains of air-gap and PMs are determined by solving equation (14). For a typical no-load operating point and in different radii, the components of air-gap flux density for the analyzed slotless AFPM machine with the trapezoidal PMs are shown in Figure 4. It should be noted that the component of B_r is negligible at the mean radius (r = 125 mm). For this reason, Figure 4(c) shows the component of B_r at r = 101 mm.

()

The proposed 3D analytical method can be also used to calculate the air-gap magnetic field due to the stator currents while replacing the stator coils with the equivalent virtual PMs with axial magnetization. In this equalization process, the shape and magnetomotive force (MMF) of stator coils are completely maintained. The remanent flux density (B_r) of equivalent virtual PMs is calculated as follows:

()

where N_c is the number of turns of one coil, I_c is the magnitude of the coil current, and h_m is the height of PM poles.

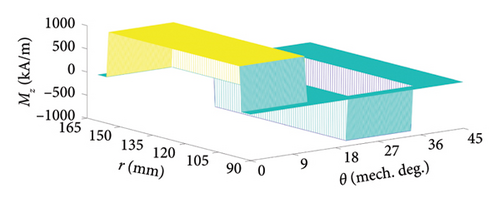
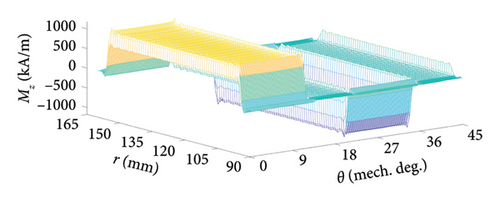
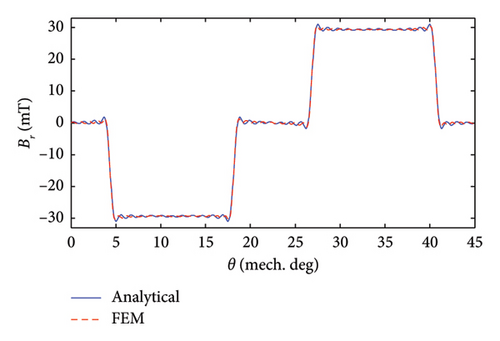
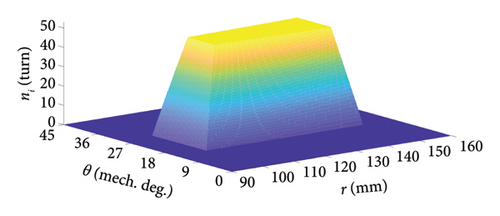
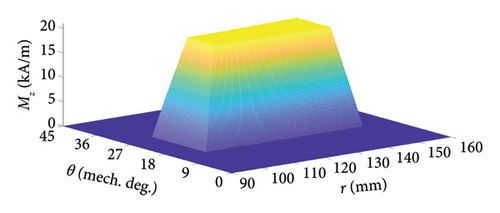
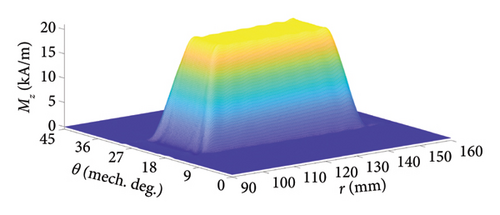
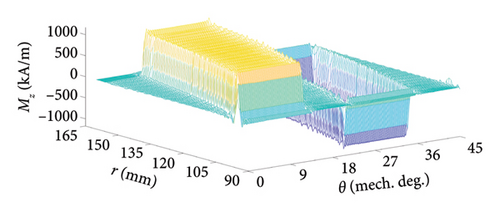
For the analyzed AFPM machine, the 2D turn function of one stator coil and the real and approximated distribution of M_z of corresponding virtual PM are shown in Figure 5 when assuming I_c = 1(A).

Similar to the no-load condition, the system of equation (15) is formed by applying the boundary condition at z = z₁, z = z₂, and z = z₄ while removing the PM region in Figure 2.

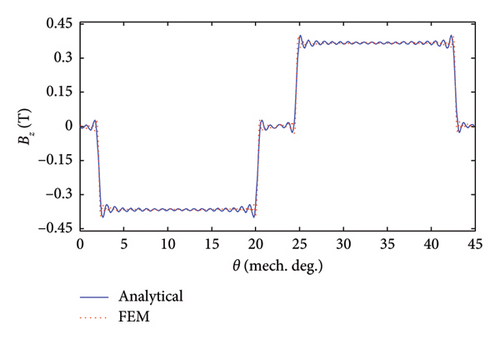
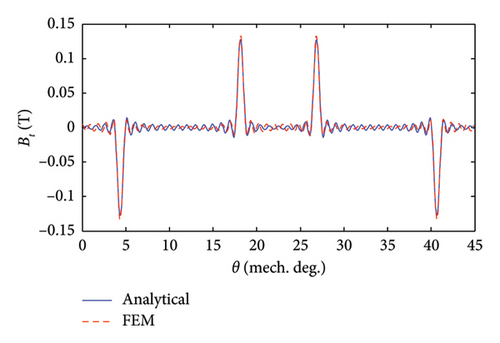
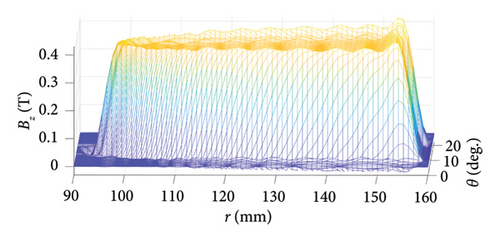
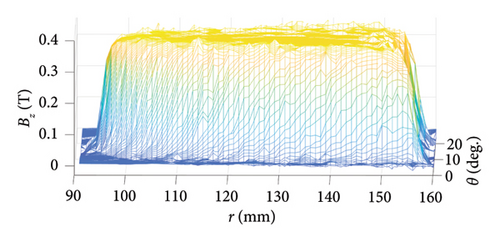
Under the excitation of Phase A with one ampere (I_A = 1[A], I_B = 0[A], I_C = 0[A]), the components of air-gap flux density are shown and verified in Figure 6. The rationale behind choosing these specific current conditions is to calculate the self and mutual inductances of stator phases in the next section.

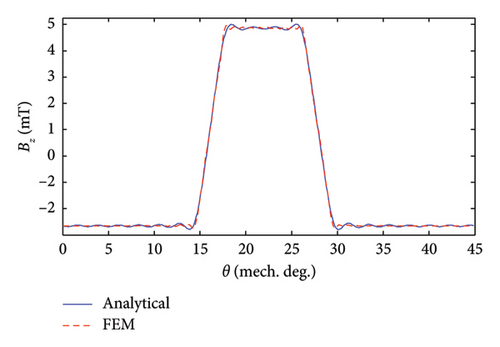
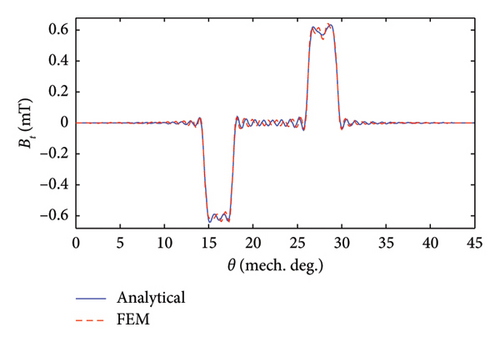
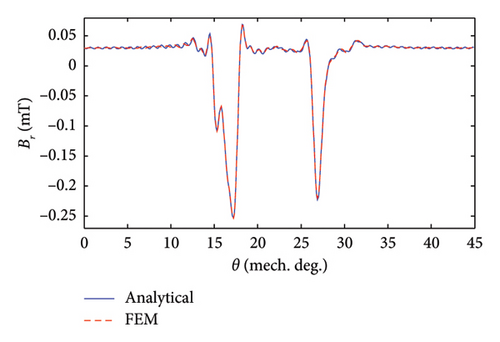
4. Flux Linkage Calculation

The flux linkage with one stator coil can be calculated as follows:

()

where θ_r is the rotor position, n_i(r, θ) is the turn function of the ith coil, B_z(r, θ) is the main component of the air-gap flux density, and ds(r, θ, θ_r) is the area of the relevant differential element.

The 2D distribution of the turn function of the ith coil has been illustrated in Figure 5(a) while considering the distribution of conductors in the coil sides. The flux linkage with other stator coils can be easily calculated through shifting the result obtained from equation (17).

Finally, the flux linkage with one stator phase is calculated through applying the law of superposition on the relevant results of stator coils as follows:

()

The calculation of phase flux linkage can be used to determine the elements of the inductance matrix while removing the PM poles. As shown in equation (19), n_A(r, θ) is the 2D distribution of the turn function of Phase A and B_z(r, θ) is the 2D distribution of the main component of air-gap flux density due to the excitation of the relevant phase.

As seen from equation (19), the self and mutual inductances are constant values due to the slotless geometry of the analyzed AFPM machine.

()

In the following, the phase flux linkage of the studied slotless AFPM machine is calculated and analyzed while considering different magnet shapes and without varying the area and the height of PM poles. Figure 7 shows the approximated distribution of PM magnetization obtained through equation (11) for different PM shapes including the skewed trapezoid PM, the skewed rectangle PM, the circular PM, and the sinusoidal PM. Figure 8 shows an illustration of one skewed trapezoid PM. As shown, the area of PM has not been varied due to the skewing effect. By keeping the area (1800 mm²) and the height (2.5 mm) of PM poles constant, some results of phase flux linkage of the analyzed slotless AFPM machine with different magnet shapes are illustrated in Figure 9. As shown in Figure 9(c), the phase flux linkage result obtained through the proposed 3D analytical model of this AFPM machine has been also verified by comparing it with the corresponding result obtained from the 3D FEM. Under this condition, an accurate comparison of the phase flux linkage results based on the Fourier analysis and the total harmonic distortion (THD) is presented in Table 2. The maximum allowed values of the skew angle are 30° and 25° for trapezoidal and rectangle shapes of PM poles, respectively. The following results have been obtained from Table 2:

1.
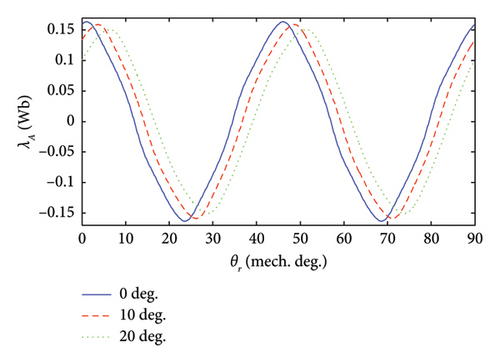
The fundamental component and THD of phase flux linkage are reduced using the skewed PMs.
2.
The highest fundamental component and the highest THD of phase flux linkage have been obtained from the slotless AFPM machine with the circular PMs.
3.
The lowest THD of phase flux linkage has been obtained from the slotless AFPM machine including the trapezoidal PMs with the skew angle of 30°.
4.
The AFPM machine with the skewed trapezoidal PMs has more optimal phase flux linkage than it with the skewed rectangle PMs.
5.
In general, the slotless AFPM machine with the sinusoid PMs has more optimal phase flux linkage than others.

Table 2. Result of flux linkage analysis.

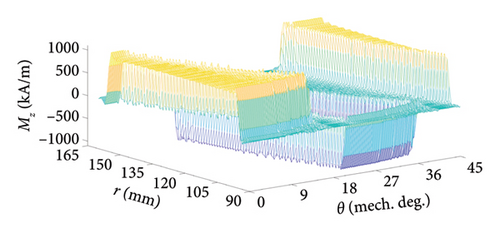
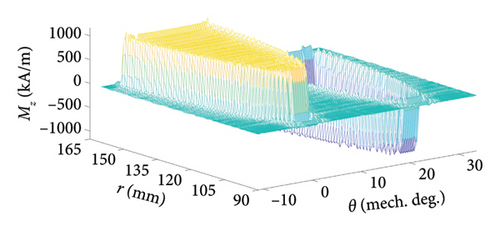
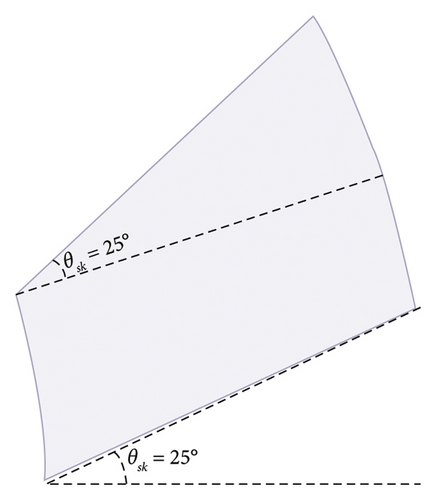
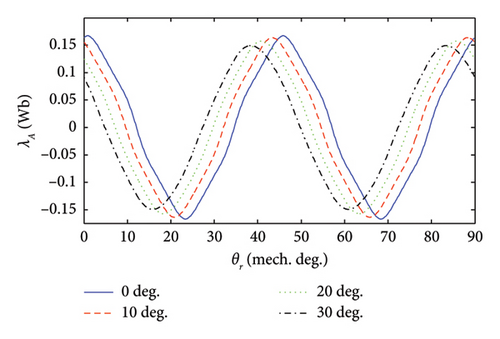
PM shape	Skew angle	Fundamental component (Wb)	THD (%)
Trapezoid	0°	0.1555	5.24
	5°	0.1548	5.11
	10°	0.1541	4.59
	15°	0.1528	3.89
	20°	0.1512	3.13
	25°	0.1488	2.48
	30°	0.1462	2.05

Rectangle	0°	0.1545	4.25
	5°	0.1536	3.88
	10°	0.1521	3.54
	15°	0.1497	3.37
	20°	0.1461	3.42
	25°	0.1416	3.51

Circular	—	0.1691	5.5

Sinusoid	—	0.1548	3.9

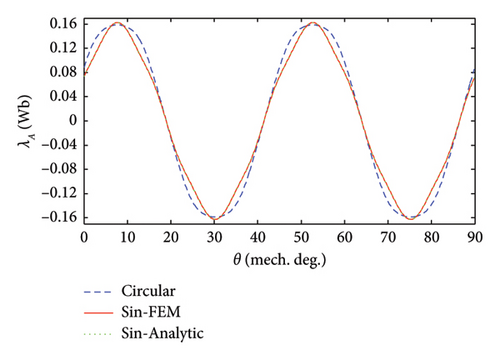
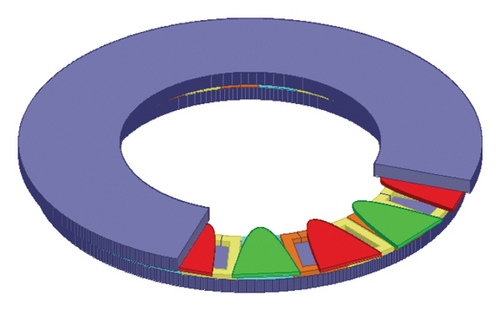
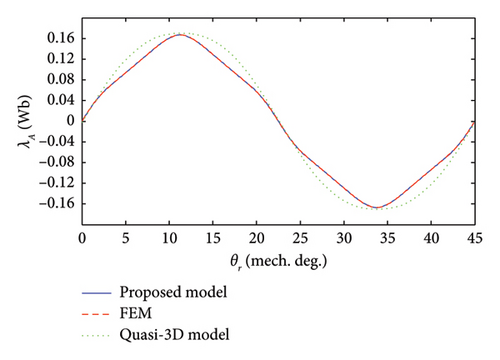
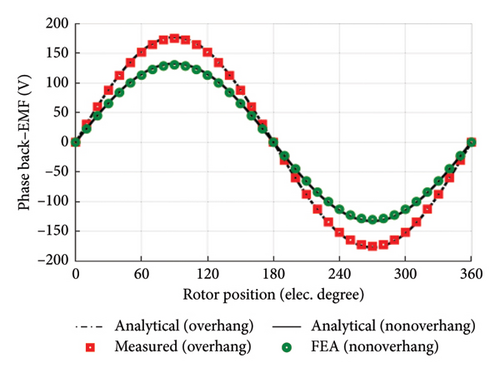
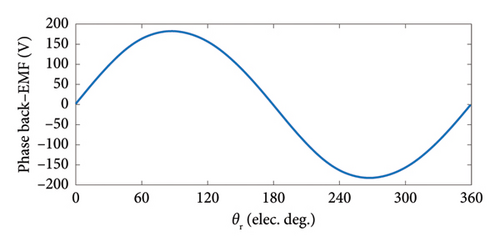
The 3D FEM model of the analyzed slotless AFPM machine with sinusoidal PM poles is shown in Figure 10. For this model of the analyzed AFPM machine, the capability and accuracy of the proposed 3D model for considering the edge effect have been shown and verified in Figure 11. In [19], the quasi-3D model based on the Hague solution has been used to calculate the z-component of air-gap flux density of the stator coreless AFPM machines. Figure 12 shows the high accuracy of the proposed 3D analytical model compared to the quasi-3D model. To verify with the experimental result, the phase back–EMF result of the manufactured slotless AFPM machine in [20] due to only PMs (dλ_A/dt) has been compared with the corresponding result obtained through the proposed 3D analytical model. As shown in Figure 13, there is a good agreement between both the results.

5. Conclusion

This paper proposed a new and fast 3D analytical model based on the scalar magnetic potential for electromagnetic analysis of the slotless AFPM machines. The geometry of the AFPM machine was divided into several domains, and the Laplace equation was solved in the air-gap region to determine the air-gap flux density components. To consider different PM shaping and skewing effects, the 2D distribution of PM magnetization was expressed in the Fourier–Bessel series. For this reason, the general solution of the Laplace equation was also expressed in the Fourier–Bessel series. The proposed approach was used to calculate the phase flux linkage while considering the PM shapes with or without the skewing effect. It was shown that the AFPM machine with skewed PMs has more sinusoidal phase flux linkage with a reduced fundamental component. Generally, it can be concluded that the AFPM machine with the sinusoidal PMs has more optimal phase flux linkage, which has low THD and high fundamental components, simultaneously. The proposed 3D analytical model can be extended to consider the slotting effect in future works.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

References

1 Liu Y., Zhang Z., Wang C., Geng W., and Yang T., Design and Analysis of Oil-Immersed Cooling Stator With Nonoverlapping Concentrated Winding for High-Power Ironless Stator Axial-Flux Permanent Magnet Machines, IEEE Transactions on Industrial Electronics. (Apr. 2021) 68, no. 4, 2876–2886, https://doi.org/10.1109/tie.2020.2978694.
10.1109/TIE.2020.2978694
Web of Science® Google Scholar
2 Taran N., Rallabandi V., Heins G., and Ionel D. M., Coreless and Conventional Axial Flux Permanent Magnet Motors for Solar Cars, IEEE Transactions on Industry Applications. (Nov. 2018) 54, no. 6, 5907–5917, https://doi.org/10.1109/tia.2018.2855123, 2-s2.0-85049789757.
10.1109/TIA.2018.2855123
CAS Web of Science® Google Scholar
3 Chan T. F., Wang W., and Lai L. L., Performance of an Axial-Flux Permanent Magnet Synchronous Generator From 3-D Finite-Element Analysis, IEEE Transactions on Energy Conversion. (Sep. 2010) 25, no. 3, 669–676, https://doi.org/10.1109/tec.2010.2042057, 2-s2.0-77956060142.
10.1109/TEC.2010.2042057
Web of Science® Google Scholar
4 Talebi D., Gardner M. C., Sankarraman S. V., Daniar A., and Toliyat H. A., Electromagnetic Design Characterization of a Dual Rotor Axial Flux Motor for Electric Aircraft, IEEE Transactions on Industry Applications. (Nov. 2022) 58, no. 6, 7088–7098, https://doi.org/10.1109/tia.2022.3191300.
10.1109/TIA.2022.3191300
CAS Web of Science® Google Scholar
5 Ajily E., Abbaszadeh K., and Ardebili M., Three-Dimensional Field Reconstruction Method for Modeling Axial Flux Permanent Magnet Machines, IEEE Transactions on Energy Conversion. (Mar. 2015) 30, no. 1, 199–207, https://doi.org/10.1109/tec.2014.2353299, 2-s2.0-85027920644.
10.1109/TEC.2014.2353299
Web of Science® Google Scholar
6 Cheng W., Cao G., Deng Z., Xiao L., and Li M., Torque Comparison Between Slotless and Slotted Ultra-High Speed AFPM Motors Using Analytical Method, IEEE Transactions on Magnetics. (Feb. 2022) 58, no. 2, 1–5, https://doi.org/10.1109/tmag.2021.3081175.
10.1109/tmag.2021.3081175
Web of Science® Google Scholar
7 Parviainen A., Niemelä M., and Pyrhönen J., Modeling of Axial Flux Permanent-Magnet Machines, IEEE Transactions on Industry Applications. (Sep. 2004) 40, no. 5, 1333–1340, https://doi.org/10.1109/tia.2004.834086, 2-s2.0-5444237052.
10.1109/TIA.2004.834086
Web of Science® Google Scholar
8 Zhao H., Chau K. T., Yang T., Song Z., and Liu C., A Novel Quasi-3D Analytical Model for Axial Flux Motors Considering Magnetic Saturation, IEEE Transactions on Energy Conversion. (2022) 37, no. 2, 1358–1368, https://doi.org/10.1109/tec.2021.3132618.
10.1109/TEC.2021.3132618
Web of Science® Google Scholar
9 Lubin T. and Rezzoug A., 3-D Analytical Model for Axial-Flux Eddy-Current Couplings and Brakes under Steady-State Conditions, IEEE Transactions on Magnetics. (Oct. 2015) 51, no. 10, 1–12, https://doi.org/10.1109/tmag.2015.2455955, 2-s2.0-84942326101.
10.1109/TMAG.2015.2455955
Web of Science® Google Scholar
10 Taghipour Boroujeni S., Abedini Mohammadi A., Oraee A., and Oraee H., Approach for Analytical Modelling of Axial-Flux PM Machines, IET Electric Power Applications. (2016) 10, no. 6, 441–450, https://doi.org/10.1049/iet-epa.2015.0645, 2-s2.0-84977110711.
10.1049/iet-epa.2015.0645
Web of Science® Google Scholar
11 Li W., Wang D., Kong D., Wang S., and Hua Z., A Novel Method for Modeling the Air Gap Flux Density of the Axial-Flux Permanent Magnet Eddy Current Coupler Considering the End-Effect, Energy Reports. (2021) 7, 508–514, https://doi.org/10.1016/j.egyr.2021.08.012.
10.1016/j.egyr.2021.08.012
Web of Science® Google Scholar
12 Kano Y., Kosaka T., and Matsui N., A Simple Nonlinear Magnetic Analysis for Axial-Flux Permanent-Magnet Machines, IEEE Transactions on Industrial Electronics. (Jun. 2010) 57, no. 6, 2124–2133, https://doi.org/10.1109/tie.2009.2034685, 2-s2.0-77952267308.
10.1109/TIE.2009.2034685
Web of Science® Google Scholar
13 Hemeida A., Lehikoinen A., Rasilo P. et al., A Simple and Efficient Quasi-3D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines, IEEE Transactions on Industrial Electronics. (Nov. 2019) 66, no. 11, 8318–8333, https://doi.org/10.1109/tie.2018.2884212, 2-s2.0-85058164819.
10.1109/TIE.2018.2884212
Web of Science® Google Scholar
14 Taqavi O. and Taghavi N., Development of a Mixed Solution of Maxwell’s Equations and Magnetic Equivalent Circuit for Double-Sided Axial-Flux Permanent Magnet Machines, IEEE Transactions on Magnetics. (Apr. 2021) 57, no. 4, 1–11, https://doi.org/10.1109/tmag.2021.3060538.
10.1109/TMAG.2021.3060538
Web of Science® Google Scholar
15 Sung S. Y., Jeong J. H., Park Y. S., Choi J. Y., and Jang S. M., Improved Analytical Modeling of Axial Flux Machine With a Double-Sided Permanent Magnet Rotor and Slotless Stator Based on an Analytical Method, IEEE Transactions on Magnetics. (Nov. 2012) 48, no. 11, 2945–2948, https://doi.org/10.1109/tmag.2012.2203112, 2-s2.0-84867776220.
10.1109/TMAG.2012.2203112
Web of Science® Google Scholar
16 Deng W. and Zuo S., Analytical Modeling of the Electromagnetic Vibration and Noise for an External Rotor Axial Flux In-Wheel Motor, IEEE Transactions on Industrial Electronics. (Mar. 2018) 65, no. 3, 1991–2000, https://doi.org/10.1109/tie.2017.2736487, 2-s2.0-85028806074.
10.1109/TIE.2017.2736487
Web of Science® Google Scholar
17 Alipour-Sarabi R., Nasiri-Gheidari Z., and Oraee H., Development of a Three-Dimensional Magnetic Equivalent Circuit Model for Axial Flux Machines, IEEE Transactions on Industrial Electronics. (2020) 67, no. 7, 5758–5767, https://doi.org/10.1109/tie.2019.2934065.
10.1109/TIE.2019.2934065
Web of Science® Google Scholar
18 Okita T. and Harada H., 3-D Analytical Model of Axial-Flux Permanent Magnet Machine With Segmented Multipole-Halbach Array, IEEE Access. (Jan. 2023) 11, 2078–2091, https://doi.org/10.1109/access.2022.3233922.
10.1109/ACCESS.2022.3233922
Web of Science® Google Scholar
19 Frank Z. and Laksar J., Analytical Design of Coreless Axial-Flux Permanent Magnet Machine With Planar Coils, IEEE Transactions on Energy Conversion. (Sep. 2021) 36, no. 3, 2348–2357, https://doi.org/10.1109/tec.2021.3050502.
10.1109/TEC.2021.3050502
Web of Science® Google Scholar
20 Min S. G., Analytical Design and Optimization of Axial Flux Permanent Magnet Machines With Slotless Structure, IEEE Transactions on Transportation Electrification. (Jun. 2022) 8, no. 2, 1994–2004, https://doi.org/10.1109/tte.2021.3124258.
10.1109/TTE.2021.3124258
Web of Science® Google Scholar

All articles

Magnet Shape Modeling in Slotless Axial Flux Permanent Magnet Machines Under No-Load Conditions

Abstract

1. Introduction

2. Parameters of the Studied AFPM Machine

3. Proposed 3D Analytical Model

4. Flux Linkage Calculation

5. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Magnet Shape Modeling in Slotless Axial Flux Permanent Magnet Machines Under No-Load Conditions

Abstract

1. Introduction

2. Parameters of the Studied AFPM Machine

3. Proposed 3D Analytical Model

4. Flux Linkage Calculation

5. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information