International Transactions on Electrical Energy Systems

Volume 2025, Issue 1 4373929

Research Article

Open Access

Optimal Control Strategy of Five-Phase PMSMs in a Wide Speed Range Using Third Harmonics

Danyal Ghasemi

orcid.org/0000-0001-8470-9604

Department of Electrical Engineering , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Energy Research Center , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Search for more papers by this author

Jafar Siahbalaee,

Corresponding Author

Jafar Siahbalaee

[email protected]

orcid.org/0000-0001-7234-6076

Department of Electrical Engineering , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Energy Research Center , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Search for more papers by this author

Mohammad Divandari,

Mohammad Divandari

orcid.org/0000-0002-9111-1552

Department of Electrical Engineering , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Energy Research Center , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Search for more papers by this author

Danyal Ghasemi,

Danyal Ghasemi

orcid.org/0000-0001-8470-9604

Department of Electrical Engineering , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Energy Research Center , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Search for more papers by this author

Jafar Siahbalaee,

Corresponding Author

Jafar Siahbalaee

[email protected]

orcid.org/0000-0001-7234-6076

Department of Electrical Engineering , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Energy Research Center , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Search for more papers by this author

Mohammad Divandari,

Mohammad Divandari

orcid.org/0000-0002-9111-1552

Department of Electrical Engineering , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Energy Research Center , Islamic Azad University , Aliabad Katoul Branch, Aliabad Katoul , Iran , azad.ac.ir

Search for more papers by this author

First published: 03 March 2025

https://doi.org/10.1155/etep/4373929

Academic Editor: Akshay Kumar Saha

Share a link

Email
Wechat
Bluesky

Abstract

The utilization of the third current harmonic in five-phase motors offers the potential to enhance their performance. This paper presents a comprehensive theory for optimally controlling five-phase permanent magnet synchronous motors (PMSMs) across all speeds, considering both motor and inverter limitations. A three-region speed profile is defined based on motor and inverter constraints, with precise relationships derived for determining region boundaries. Distinct control strategies are proposed for each region: maximum torque per ampere (MTPA) for copper loss minimization and maximum voltage–maximum current (Max V–Max I) and maximum power per voltage (MPPV) for core loss minimization. Optimal components of the first and third current harmonics are calculated for each strategy, serving as reference values for control methods such as FOC, DTC, or MPC in motor drives. Analysis results indicate that the proposed strategies significantly increase electromagnetic torque and output power and decrease power loss of five-phase PMSM motors.

1. Introduction

The five-phase permanent magnet synchronous motors (PMSMs) have superiorities such as reducing the stator current per phase leads to smaller sizes of switches for each phase, reduced torque ripple therefore less vibration and noise of the machine, simultaneous effects of both first and third current harmonics in torque generation, slighter current harmonics in DC bus, and enhanced fault tolerance, and as a result, higher reliability [1–5]. These advantages have made the motors come to attention for many applications [6, 7].

The research studies about third harmonic injection can be divided into four categories as follows:

•
Control methods of five-phase PMSMs
•
Design of five-phase PMSMs
•
Control strategies of five-phase PMSMs
•
Five-phase inverters to produce the first and third harmonics independently

The five-phase synchronous motors, similar to three-phase motors, can be controlled by three main methods: field-oriented control (FOC) [8, 9], direct-torque control (DTC) [10–12], and model predictive control (MPC) [13–15].

Unlike the three-phase motors with the Y connection, injection of the third harmonics is impossible, and in five-phase motors, the third harmonic can be injected independently of the first harmonic. For this reason, the optimal design of these motors and their control strategies are closely intertwined. Therefore, a lot of research studies have been performed in order to design the optimal shape of the permanent magnet with the aim of optimizing the contribution of the third harmonic in the electromagnetic torque and reduction of the peak flux density [16–19]. Implementation of control strategies on the five-phase PMSMs has a direct relationship with the capability of the five-phase inverters to produce the first and third voltage harmonics independently. Levi et al., in their research studies, found a region where five-phase inverters can independently generate the first and third voltage harmonics [20].

In the any control mentioned method, the control strategies determine the optimal reference values of the control variables according to the operating point. In five-phase PMSM, because of the first and third orthogonal current harmonics, there are four control variables (id₁, iq₁, id₃, iq₃). Researchers proposed different control strategies for different speed regions. A simple strategy in five-phase motors is to eliminate the third harmonic and apply only the first harmonic. Elimination of the third harmonic withdraws some of the capabilities of five-phase motors and causes increasing copper loss and decreasing maximum torque [18–20]. Hassan, Paul, and Mohan [21] have proposed a control strategy in two regions, below and above the rated speed or the flux-weakening area. They used numerical methods for optimization and considered only one flux-weakening region. In this paper, we have shown that the flux-weakening region should be divided into two regions. In addition, a new nominal speed must be defined, because the control strategy itself changes the nominal speed. In addition, nonanalytical methods are time-consuming and may face problems in practical applications. In [22–24], the optimal first and third current harmonic have been obtained. However, the inverter limitations are not considered and the flux-weakening region is not considered separately. In [25], the CBPWM technique and the extended mode observer (ESO) control scheme for a five-phase current source inverter (CSI) were studied. However, the machine model in this research does not consider the third harmonic component of the permanent magnet flux (λ_m3). Consequently, optimal control of the motor and the full exploitation of the inherent advantages of five-phase motors are not feasible with this method. In general, most research studies have focused on control strategies below the nominal speed or within the maximum torque per ampere (MTPA) region, aiming to minimize copper loss (i.e., i_ds1 = 0 and i_ds3 = 0). While at speeds higher than the nominal speed, core loss is also important. On the other hand, while optimal control of the five-phase PMSM faces two main limitations, motor and inverter, these limitations have not been considered simultaneously in all existing research studies. This paper addresses this gap by introducing constrained optimization, which incorporates both motor and inverter limitations. This novel approach leads to entirely new concepts and methodologies explored in detail within this work. In this paper, a comprehensive control strategy at all speeds and considering these limitations completely analytically is proposed. Here, the limitation of the motor is the maximum permissible current of the stator windings, and the limitation of the inverter is the ability to independently produce the first and third voltage harmonics according to the DC source amplitude. These limitations cause three-speed regions to be defined. In the first region, the MTPA control strategy has been studied, using completely analytical and simple mathematical relationships, with the aim of minimizing both the motor loss. For the second region, the maximum voltage–maximum current (Max V–Max I)control strategy has been used. In the third region, the maximum power per voltage (MPPV) control strategy has been applied in order to minimize iron losses of the motor.

The organization of the paper is as follows. In Section 2, modeling of the nonsalient five-phase PMSM of the five-phase motor is expressed in the orthogonal frame. Section 3 presents the proposed control strategies through the three subsections. In the first subsection, optimal values of the motor’s currents are derived, and in the second and third subsections, they are studied based on the control region boundary and geometrical interpretation. Finally, simulation and analysis remarks of the proposed method are drawn in Section 4. Section 5 presents the conclusion of the study.

2. Modeling of the Nonsalient Five-Phase PMSM

The equivalent electric circuit of the five-phase PMSM in the rotating reference frame of the rotor (dq) is illustrated in Figure 1 [26]. The five-phase synchronous motors have two separate and independent equivalent circuits, correspondingly, for the first and third harmonics. From this viewpoint, these motors are similar to two synchronous motors, one for each harmonic, whose shafts are coupled together. In this paper, the following assumptions have been made for a five-phase motor:

•
The windings distribution is completely sinusoidal.
•
There is no magnetic saturation within the core; in other words, the magnetic circuit is assumed to be linear.
•
The iron losses are negligible; using this assumption, the parallel resistance taken to model the iron losses will be ignored in the equivalent circuit.
•
There is no damping winding (starting cage) inside the rotor.
•
The rotor is of nonsalient type, but the distribution of the permanent magnet’s flux is nonsinusoidal; in other words, the motor is of surface permanent magnet type.
•
Variations of the motor’s parameters are omitted. This assumption does not invalidate the generality of the study since appropriate estimation methods for the machine’s parameters can be independently added.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The equivalent electric circuit of a five-phase PMSM in the rotor’s rotating reference frame (dq) [7].

The differential equations of the five-phase PMSM for the first harmonic, within the rotor’s rotating reference frame (d − q), are as follows [26]:

()

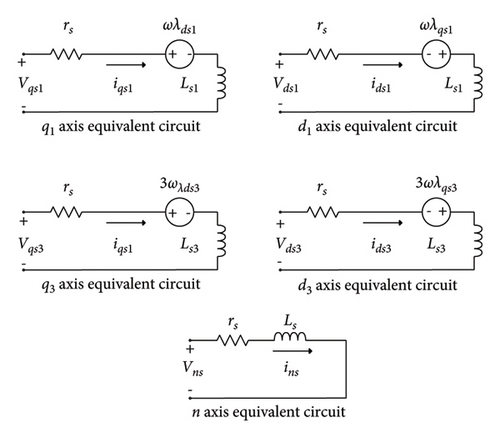
In (1)–(4), v_ds1, v_qs1, i_ds1, i_qs1, λ_ds1, and λ_qs1 are voltages, currents, and flux linkages of the d and q axes for the first harmonic within the rotor’s rotating reference frame, respectively. Also, λ_m1 is the flux linkage of the first harmonic of the permanent magnet.

For the third harmonic, the motor’s differential equations in the rotating reference frame will be as follows [7]:

()

In (5)–(8), v_ds3, v_qs3, i_ds3, i_qs3, λ_ds3, and λ_qs3 are, voltages, currents, and flux linkages of the d and q axes for the third harmonic within the rotor’s rotating reference frame, respectively. Also, λ_m3 is the flux linkage of the third harmonic of the permanent magnet.

The motor’s electromagnetic torque can be written as

()

where P shows the number of poles of the motor. For the steady state and by ignoring voltage drop over the stator resistance, from relationships (1)–(8), the first and third harmonic voltages can be simplified as

()

In (14)–(17), V_s1, V_s3, I_s1, and I_s3 are voltages and currents of the first and third harmonics of the motor, respectively.

3. Control Strategies

There are two limitations to motor control. The first is a limitation on the inverter capability in producing the desired voltage amplitude for a given DC voltage, and the second is the limitation on the current of the motor. Since control strategies of five-phase PMSMs are simultaneously applied to both first and third harmonics, the mentioned limitations must be decomposed for both harmonics. For the limitation on voltage, five-phase inverters are not able to independently produce any desirable voltage amplitudes in both first and third harmonics [20]. For the limitation on current, the sum value of the first and third effective current harmonics must not exceed the motor’s limit current. To determine the boundaries of control regions, first, by assuming to be inside a specific control region, optimal values of the first and third current harmonics are calculated using optimization methods. Then, the validity region boundary of the related equations is determined by applying limitations on the motor and inverter. Generally, three different control regions can be defined as follows:

a
First control region (V < V_Max and I < I_Max): In this region (Figure 2, R₁ region), torque is constant, and power can be controlled in the range of zero up to MTPA power, and speed can be controlled from zero up to MTPA speed (the upper limit of motor’s speed in the first region).
b
Second control region (V = V_Max and I = I_Max): In this region (Figure 2, R₂ region), torque decreases, and power increases from MTPA up to the maximum power, and speed can be controlled within the range of MTPA speed and critical speed (lowest speed for the maximum power performance).
c
Third control region (V = V_Max and I < I_Max): In this region (Figure 2, R₃ region), torque decreases gradually up to zero, and power is constant at the maximum value, and speed can be theoretically controlled, within the range of the critical speed and infinity.

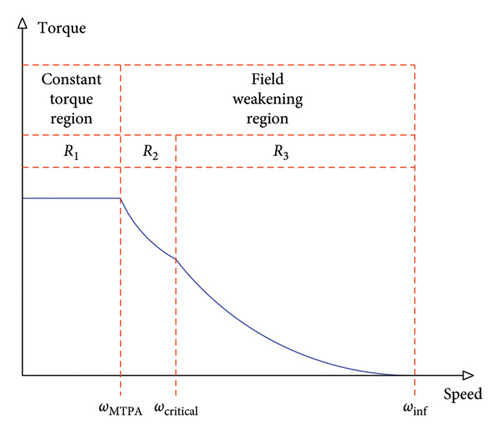
In the first control region, to minimize the machine’s copper losses and inverter losses, the MTPA method is chosen as the control strategy. In the second control region, the Max V–Max I control strategy is used in order to produce the maximum power. In the third control region, the MPPV control strategy is used for the minimization of the iron losses of the motor.

3.1. First Control Region

3.1.1. MTPA Control Strategy

In this study, to generate maximum torque with minimum copper loss, simultaneous minimizing of both first and third current harmonics is chosen as the cost function as follows:

()

The objective function must always satisfy the desired electromagnetic torque in (9). Using Lagrange’s duality theory and the problem’s constraint, we have

()

In (19), the derivative with respect to current components must be zero. After mathematical simplifications, the optimal current components can be obtained as follows:

()

3.1.2. Determination of Limit Conditions

The limitation of motor current is to be decomposed into its first and third harmonic limit components. If I_sm is the maximum of the limit current, then

()

By substituting (20)–(23) into (16), (17), and (25), the maximum current amplitude of the first and third harmonics, I_s1m, I_s1m, and I_s3m, are obtained as

()

By substituting (26) and (27) into (9), the maximum torque under the MTPA strategy with the guarantee of limit current would be

()

In the MTPA strategy, since optimal currents of the first and third harmonics are applied to the motor, the motor’s torque can be increased. One of the main assessment approaches of the MTPA control strategy can be comparing it with what is in the third harmonic elimination method. If only the first current harmonic is applied, then the maximum torque of the motor when the current is equal to the limit current, using (9), would be

()

Hence, a suitable criterion for performance comparison of MTPA strategy could be defined as

()

where the parameter K_T is greater than one. In other words, a higher electromagnetic torque can be produced by the MTPA control strategy.

Also, the limitation on voltage is obtained as follows:

()

By substituting (10)–(13) into (14) and (15), the maximum values of V_S1 and V_S3 under the MTPA strategy in boundary conditions are found according to

()

where ω_rMTPA is the MTPA’s speed boundary, and V_s1m and V_s3m are the maximum voltage amplitudes of the first and third harmonics, respectively. From (32) and (33), the coefficient K_MTPA can be defined based on the optimal ratio of the third to the first voltage harmonics as follows:

()

To provide voltages in (32) and (33), the capability of the two-level five-phase inverters must be considered. The upper limit of speed is obtained when the first and third voltage harmonics are at their maximum possible values. In other words, the operation point is on the voltage limit boundary. Based on the results from references [20, 21], and assuming that the first harmonic has a larger amplitude and main contribution in torque generation, the margin of the five-phase inverters in providing the first and third voltage harmonics will be determined by

()

The concept of (35) is illustrated in Figure 3, where values of A and B are 1.7013 and 1.0515, respectively. By substituting (34) into (35), the speed boundary of MTPA is obtained as

()

3.1.3. Geometrical Interpretation

According to (16) and (17), the locations of the first and third current harmonics on the planes d₁ − q₁ and d₃ − q₃ are circles with radii I_S1 and I_s1I_S3, with center at the coordinate origin (Figure 4). By increasing the load torque, the radii of the circles increase. The control strategy determines to which ratio the currents should be increased. On the MTPA lines in Figure 4 (green lines), the ratio of the currents is obtained from (20) and the radius of the largest circle as the boundary of the first region is defined by (26) and (27). By substituting (10)–(13) into (14) and (15), first and third harmonic voltage circles with respect to current harmonics are

()

where circles are with radii V_s1/(ω_rL_s1) and V_s3/(3ω_rL_s3) and centers (−λ_m1/L_s1, 0) and (−λ_m3/L_s3, 0). Hence, by increasing the speed, the radii of the voltage circles become smaller. The boundary of speed in the first region is where voltage circles of (37) and (38) intersect the circle of the limit current. The intersection point is equal to the MTPA speed boundary which is obtained from (36).

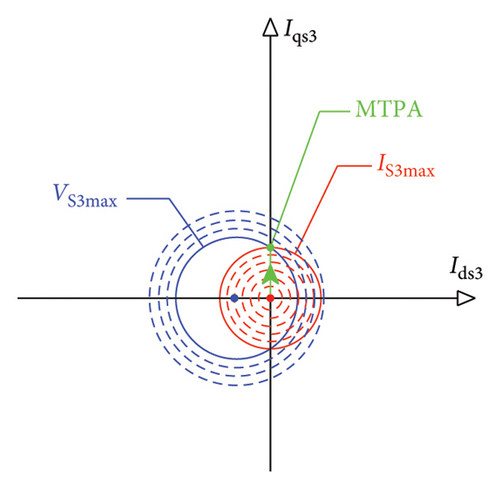
3.2. Third Control Region

To analyze the second control region, the speed’s range needs to be determined. As mentioned before, the second control region is located between the first and third regions. Therefore, a maximum speed of the first region can be considered as the beginning of the second region, and likewise, a minimum speed of the third region is the ending of the second region. Thus, to determine the final speed of the second region, the third region should be described first.

3.2.1. MPPV Control Strategy

The aim of this strategy is to achieve maximum power with minimum iron losses. Since iron loss is a function of voltage amplitude, thus, the objective function will be defined as follows:

()

Using (9), (10), and (12), the motor’s output power in terms of the voltage is obtained as

()

The objective function must always satisfy the desired maximum power in (40). Using Lagrange’s duality theory and the problem’s constraint, we have

()

In (41), the derivative with respect to voltage components must be zero. After mathematical simplifications, the optimal voltage ratio components can be obtained as follows:

()

By substituting (42) in (35), the boundaries of voltage components are obtained as follows:

()

By increasing the speed in the third region, the maximum power remains constant as follows:

()

3.2.2. Determination of Limit Conditions

According to Figure 2 for the maximum power performance, the minimum speed at the beginning of the third region is called critical speed. For speeds higher than the critical, the motor’s speed can be theoretically increased to infinity. As the motor’s speed increases in constant power, the torque and current of the motor decrease. Therefore, the critical speed is where the current of the motor is maximized.

From (43) and (10)–(15) and simplification, the motor’s critical speed can be simplified as

()

3.2.3. Geometrical Interpretation

By substituting (10)–(13) into (14) and (15), first and third harmonic voltage circles with respect to current harmonics are

()

where circles are with radii V_s1/(ω_rL_s1) and V_s3/(3ω_rL_s3) and centers (−λ_m1/L_s1, 0) and (−λ_m3/L_s3, 0) and the V_s1 and V_s3 are constant. By increasing the motor’s speed, the radii of the circles become smaller. So, the greatest circle will be at ω = ω_rc. The trajectory of the current is from the points (−λ_m1/L_s1, V_s1/(ω_rcL_s1)) and (−λ_m3/L_s3, V_s3/(3ω_rcL_s3)) to the points (−λ_m1/L_s1, 0) and (−λ_m3/L_s3, 0), respectively (Figure 5). The results of the geometrical interpretation of the MPPV control strategy are shown in Figure 5.

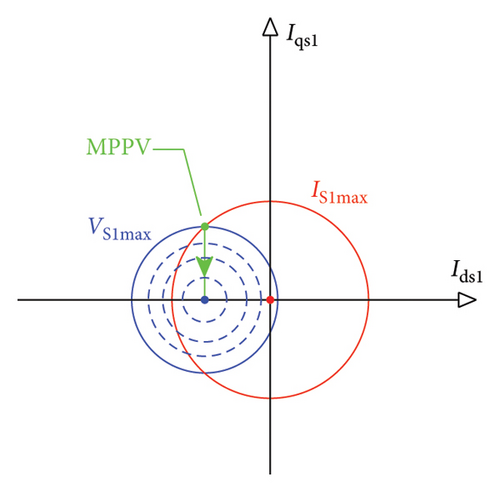
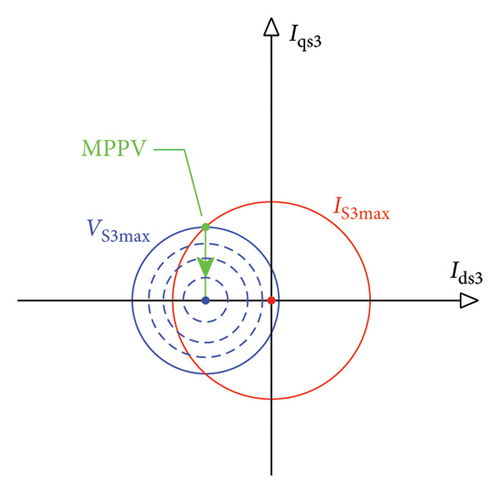
3.3. Second Control Region

3.3.1. Max V–Max I Control Strategy

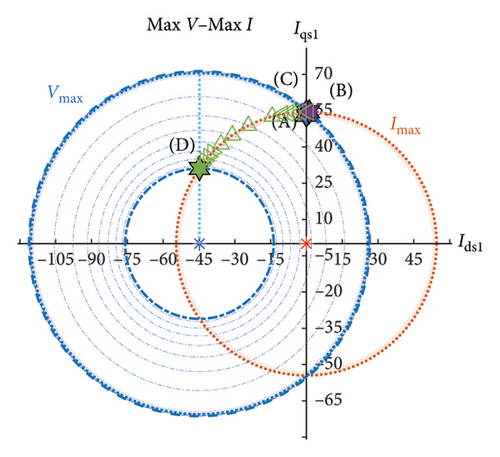
According to Figures 4 and 5, the second control region should be a path from the end of the first control region to the beginning of the third control region. A simple and solvable method is to divide the second area into three parts. In part one, the aim is to produce the maximum power while maintaining minimum copper losses. The control strategy in this section is similar to the first control region except that here, the voltage is changed on the boundary region of the inverter capability (Section 1 of Figure 6). The effective value of the first and third harmonic current must also be equal to the limit current of the motor (I_sm). Similar to the MTPA strategy, in order to reduce copper losses, the current component along d axis is considered to be zero. As the speed increases, the first harmonic current will continually increase from the current at the border of the first MTPA region to the current at the border of the third MPPV region, and the amplitude of the third harmonic current will decrease.

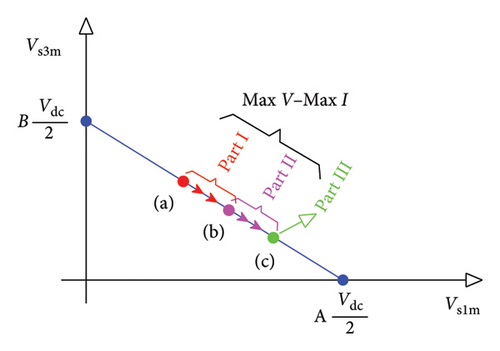
In the second part, the goal is only to produce the final power. To this end, as depicted in Section 2 of Figure 6, first, the voltage is increased over the inverter voltage limit up to the optimal value (MPPV voltage). It must be noted that by increasing the voltage, the optimal current limit will change which leads to the lost continuity in the third control region. To prevent from discontinuity, in the next step, contrary to Part 1 where the current component along axis d was considered to be zero, here, by changing the current along axis d, the current limit is maintained constant. In this way, both the maximum inverter voltage and maximum limit current of the motor are utilized to achieve the final power.

In Part 3, the control strategy is similar to the third control region with the difference that the location of the current changes on the constant current circle obtained at the border of the MPPV region. According to Figure 6, MPPV voltage is used in this part and the aim is to reach the maximum power. In this part, both the maximum voltage of the inverter and the maximum limit current of the motor are utilized. The analysis results of the Max V–Max I control strategy for the operational range of the inverter’s voltage are briefly illustrated in Figure 6.

3.3.2. Determination of Limit Conditions

In Part 1 of the second control region, it assumed that

()

To get the current values for any arbitrary speed (ω_r1) in this region, the first and third current harmonic components are obtained as follows:

()

where

and

are limit voltages of the first and third harmonics for every given speed in Part 1, respectively. For any arbitrary speed in this region, the first voltage harmonic will be obtained by solving the algebraic equation as follows:

()

where the coefficients a, b, and c are

()

Similar to (51), the third voltage harmonic can be calculated. As mentioned before, Part 1 of the second control region starts from MTPA speed and rises up until the value of the current becomes equal to the MPPV current. Hence, the final speed of Part 1 will be determined at the end of the first part. For this purpose, the final speed limit is obtained from the intersection of the first and third harmonic boundary voltages with the boundary conditions of the inverter voltage. Thus, the final speed limit at the end of the first part will be obtained by solving the algebraic equation as follows:

()

where the coefficients a, b, and c are

()

In the second part of the second control region, values of the first and third current harmonics derived from part one are maintained constant (intact, unchanged). By increasing the speed, based on (51), voltage amplitude will be increased up to the point of MPPV voltage. In this section, the current will be variable along the d axis. In order to calculate the current values along axis d, from (10)–(17), the first and third current harmonics are obtained as follows:

()

where ω_r2 denotes speed at every point of part two of the second control region. In Part 2, the speed must be increased until the current along axis d reaches those in I_ds1 = −λ_m1/L_s1 and I_ds3 = −λ_m3/L_s3. The final speed in Part 2 is derived as follows:

()

In Part 3 of the second control region, the speed increases up to the MPPV’s speed value. In this section, the voltage is equal to the MPPV’s voltage. In order to maintain the boundary values of the first and third harmonic currents and prevent the current from breaking, in this section, the current will be variable along the d axis. To calculate the current values along axis d, the first and third current harmonics are the same as Part 2 of the second control region, which is equal to (55) and (56).

3.3.3. Geometrical Interpretation

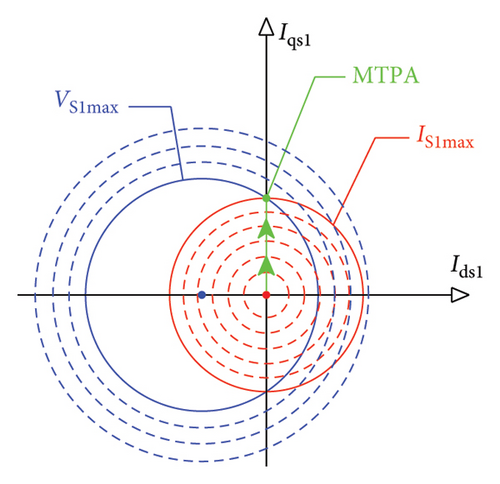
In Part 1 of the second control region, using (53), the location of the first and third voltage harmonics in the planes d₁ − q₁ and d₃ − q₃ are circles with radii and and centers (−λ_m1/L_s1, 0) and (−λ_m3/L_s3, 0). It must be noted that, as speed increases, the radii of the circles of the first and third voltage harmonics will increase and decrease, respectively.

Also, according to (49) and (50), the limitation of the first and third current harmonics can be drawn as circles with radii I_s1m and I_s3m and centers (0, 0). The results of the geometrical interpretation of Part 1 of the second control region are illustrated in Figure 7.

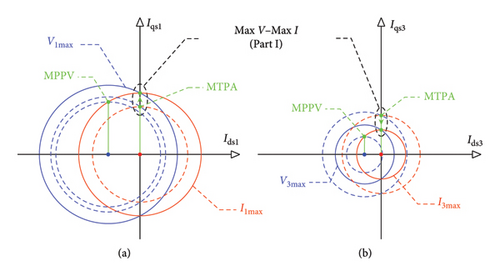
In Part 2 of the second control region, similar to Part 1, from equation (51), the location of the first and third voltage harmonics in the planes d₁ − q₁ and d₃ − q₃ are circles with radii and , and centers (−λ_m1/L_s1, 0) and (−λ_m3/L_s3, 0), respectively. Here again, the radii of the circles of the first and third voltage harmonics will, respectively, increase and decrease as speed increases. Due to constant currents’ limitation, from (49) and (50), limitation’s limit of the first and third current harmonics can be represented as circles with, respectively, radii I_s1m and I_s3m and center (0, 0). The geometrical interpretation obtained from Part 2 of the second control region is displayed in Figure 8.

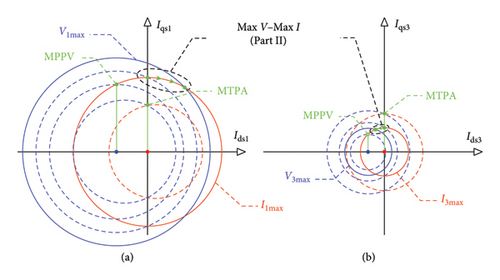
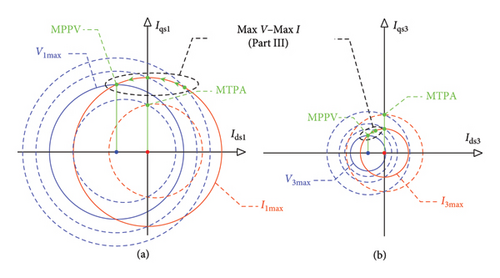
As stated before, in Part 3 of the second control region, the obtained values of current and voltage from Part 2 will be maintained unchanged. However, as speed increases from ω_r2 up to the final speed limit (MPPV speed), the radii of voltage circles become smaller. Therefore, the final point of the geometrical location of Part 3 of the second control region coincides with the geometrical location of the third control region. The geometrical interpretation of Part 3 of the second control region is illustrated in Figure 9.

4. Results’ Assessment and Discussion

In this section, for the purpose of assessment and comparison of the proposed strategies, several studies and discussion have been carried out on a typical motor. The parameters of the motor under study are shown in Table 1. The calculations have been performed by MATLAB software.

Table 1. Parameters of the five-phase PMSM.

Parameter	Symbol	Value
Rated power	PN	6 kw
DC-link voltage	U_dc	110 v
Rated speed	ω_r	360 rpm
Number of pole pairs	P	8
Fundamental PM flux linkage	λ₁	0.142 Wb
Third PM flux linkage	λ₃	0.016 Wb
d1 axis inductance	L_d1	3.17 mH
q1 axis inductance	L_q1	3.17 mH
Stator resistance	R_s	0.11 Ω
d3 axis inductance	L_d3	1.4 mH
q3 axis inductance	L_q3	1.4 mH

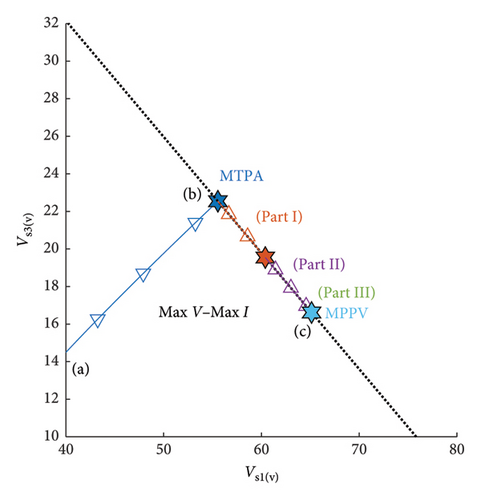
4.1. Optimal Voltage Path

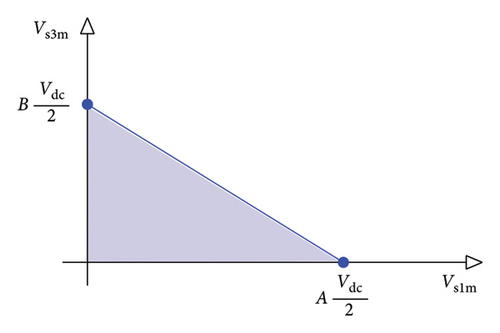
The optimal path curve of the first voltage harmonic amplitude to that of the third has been shown in Figure 10. As shown in Figure 10, by increasing the speed, the voltage’s optimal path within the first control region varies from the inside of the voltage operational region of the inverter up to the inverter voltage limit. This is represented by the segment between Points a and b. This optimal path, with more speed increase in the second and third control regions, has been located on the voltage limit line such that the second control region varies from Point b to Point c and the third control region corresponds exactly to Point c. According to Figure 10, up to the ending of the first control region, both optimal voltages of the first and third harmonics increase. However, in the second and third control regions, as speed increases the optimal share of the first voltage harmonic becomes higher than that of the third harmonic. According to simulation results, values of the optimal voltages in Part 2 of the second control region and also in the third control region remained unchanged at Point c.

4.2. Power–Speed and Torque–Speed Curves

Figures 11 and 12 show curves of power and torque versus speed in different control regions. When the third harmonic is not considered, the maximum resultant power and torque at nominal speed are 6 kW and 159.5 Nm, respectively. These values of power and torque are equal to the nominal ones listed in Table 1. By injecting the third harmonic, the maximum resultant power at the same nominal speed becomes 6.5 kW, which shows 8.8 percent increment in power. Also, the maximum resultant torque at the nominal speed with 4.3 percent growth is equal to 166.5 Nm.

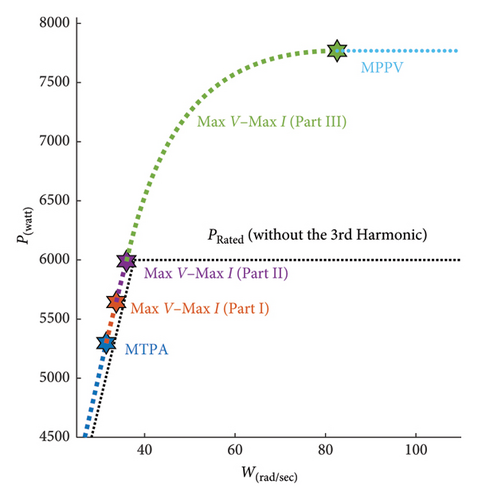
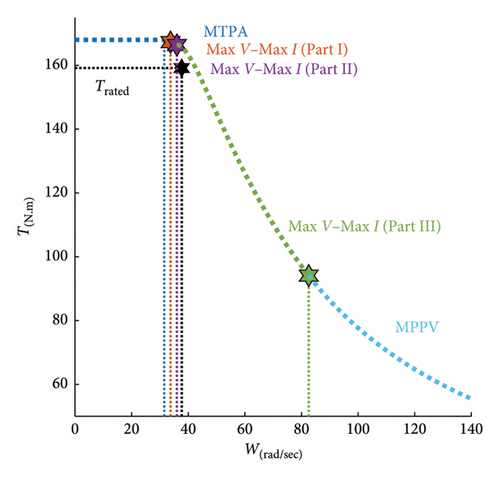
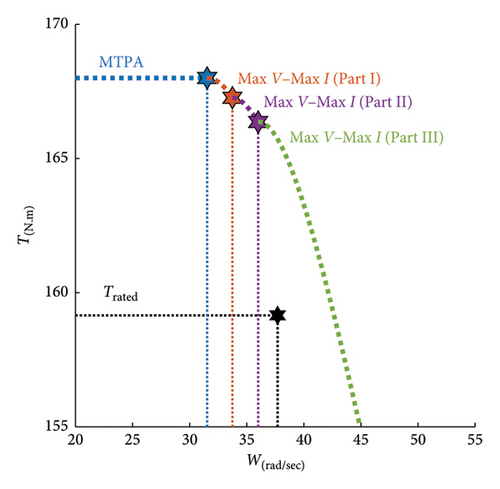
The power and torque curves are, respectively, shown in Figures 11 and 12. In the first control region corresponding to the blue curves, using the MTPA strategy at 252.24 rpm (ω_rMTPA), the motor’s power and torque have reached values of 5.29 kW and 168.00 Nm, respectively. In Part 1 of the second control region, corresponding to the red curves, using the Max V–Max I strategy at 269.95 rpm (ω_r1), the motor’s power and torque have reached 5.64 kW and 167.26 Nm, respectively. In Part 2 of the second control region, shown by green curves, using the Max V–Max I strategy at 660.53 rpm (ω_r2), the motor’s power and torque have reached, accordingly, 7.76 kW and 94.08 Nm. In the third control region, illustrated by cyan curves, using the MPPV strategy, the motor’s power is maintained constant at the maximum power of 77.68 kW. Theoretically, by increasing the speed towards infinity, torque tends to zero.

As shown in Figures 11 and 12, compared to the case with the lack of the third harmonic, by injecting the third harmonic in an optimal manner to a five-phase motor, higher powers and torques can be achieved. It must be noted that this feature has been achieved despite the limitations on the motor limit current and inverter limit voltage.

4.3. Control Regions

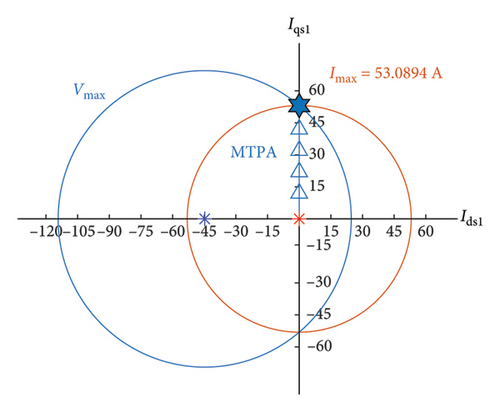
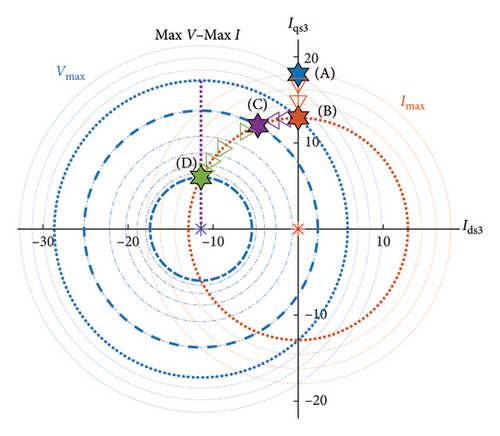
Table 2 shows the numerical results of the simulation for boundaries of different control regions. The performance of the different control regions is reported using the data obtained from Table 2. Figure 13 shows the limits of the simulated first control region in the planes d₁ − q₁ and d₃ − q₃, wherein the current limits of the first and third harmonics are 53.08 A and 17.94 A, respectively; these are revealed as red circles. Also, the voltage limits of the first and third harmonics, depicted as blue circles, are 55.54 V and 22.54 V, respectively. By increasing the load torque, the current optimal path of the MTPA strategy rises from the origin up to the intersection boundary of the current and voltage circles, along the q axis; this is illustrated in Figure 13 by blue arrows. It should be noted that over the intersection boundary of the current and voltage circles, the maximum MTPA torque has occurred at 252.24 rpm, which is equal to ω_rMTPA.

Table 2. Numerical results of simulation for different control strategies.

Parameter	R1	R2			R3
Parameter	R1	1	2	3	R3
T_r (Nm)	168.00	167.26	166.36	94.08	0
ω_b (rpm)	252.24	269.95	287.99	660.53	∞
P (watt)	5297.20	5644.20	5989.00	7768.30	7768.3
i_d1 (A)	0	0	1.20	−44.79	−44.79
i_q1 (A)	53.08	54.53	54.52	31.10	0
i_d3 (A)	0	0	−4.74	−11.42	−11.42
i_q3 (A)	17.94	12.90	11.99	5.98	0
I_s1 (A)	53.08	54.53	54.53	54.53	44.79
I_s3 (A)	17.94	12.90	12.90	12.90	11.42
I_s (A)	56.04	56.04	56.04	56.04	46.23
V_d1 (V)	−42.45	−46.66	−49.77	−65.12	−65.12
V_q1 (V)	35.81	38.33	42.00	0	0
V_d3 (V)	−19.01	−14.63	−16.51	−16.61	−16.61
V_q3 (V)	12.10	12.95	8.08	0	0
V_s1 (V)	55.54	60.39	65.12	65.12	65.12
V_s3 (V)	22.54	19.54	16.61	16.61	16.61
V_s (V)	59.94	63.47	67.21	67.21	67.21

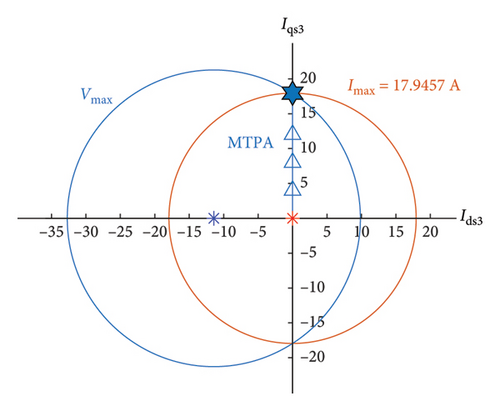
Simulation results of the third control region are shown in Figure 14. In the third control region, the limits of the first and third current harmonics are increased and decreased to 54.53 A and 12.90 A, respectively. This indicates a higher share of the first current harmonic compared to the third harmonic at high speeds; this feature has already been shown in Figure 10. As the motor’s speed increases, for preserving the maximal power, the current’s optimal path of the third control region is a perpendicular line. Starting from the intersection of the limit current and limit voltage, the path continues up to the center of the voltage circle along axis d; this is shown in Figure 14.

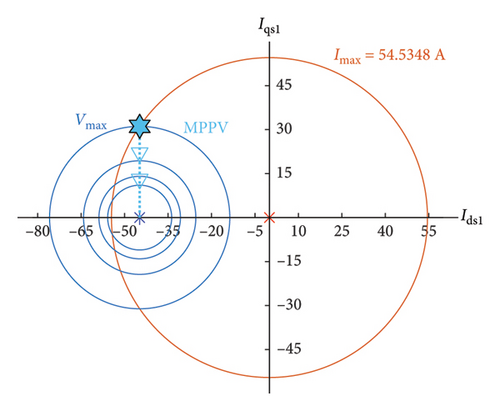
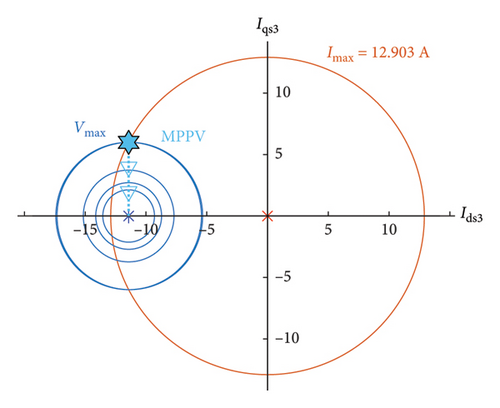
Figures 15 and 16 show the simulation results of the second control region for the first and third harmonics, which include two parts. In Part 1, the first and third current harmonics along axis d are zero. The first current harmonic along axis q increases from 53.08 A to 54.53 A and the third current harmonic decreases along axis q from 17.94 A to 12.90 A, such that the sum of current remains constant at 56.04 A. In this part, the motor’s speed has been increased from 252.24 rpm to 269.95 rpm. The optimal path of Part 1 has been specified from Point a to Point b. In Parts 2 and 3, due to keeping of the continuity of current, the third current harmonic along the axis d should be injected.

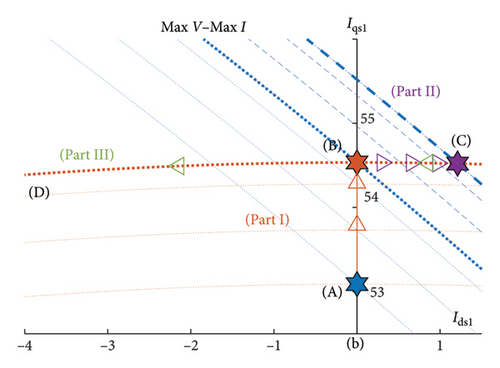
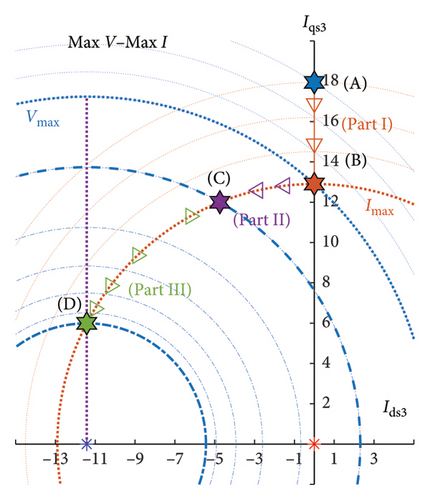
In Part 2, the d axis current of the first and third harmonics has been increased, in turn, in the positive and negative directions by 1.20 A and 4.74 A.

Also, considering movement on the boundary of the current circle, the q axis’ currents have been decreased for the first and third harmonics by, in turn, 54.52 A and 11.99 A. In this part, the motor’s speed has been increased from 269.95 rpm to 287.99 rpm. The optimal path of Part 2 has been shown from Point b to Point c. In Part 3, for the first and third harmonics, the d axis’ currents are decreased, in turn, up to −44.79 A and −11.42 A and q axis’ currents up to 31.10 A and 5.98 A. In this part, speed has been increased from 287.99 rpm to 660.53 rpm. The optimal path of Part 2 is depicted from Point c up to Point d.

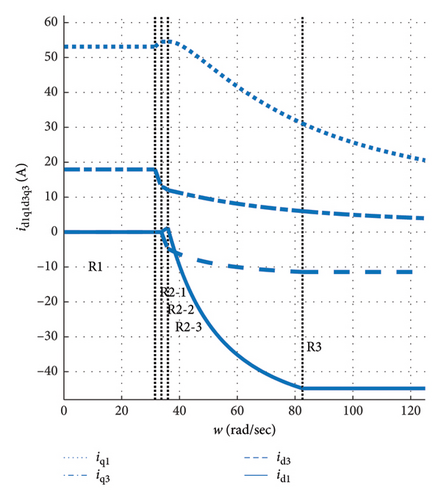
To better illustrate Figures 13, 14, 15, and 16, the optimal first and third harmonic components of the motor current and voltage at the maximum current limit and the inverter capability across all speed ranges are represented in Figures 17 and 18. As observed in Figure 17, in the first region and assuming maximum torque, the d axis’ current components are zero, and the q axis’ components are optimal. With increasing speed in regions two and three, the q axis’ current components decrease, and the d axis current. As the speed and motor power consumption increase, the q axis’ voltage components increase in the first region, and the d axis’ voltage components also increase with a negative sign until they reach the inverter capability limit. In regions two and three, the q axis’ voltage components decrease, while the d axis’ voltage components remain. One of the key points is that the proposed optimization should satisfy the continuity at the boundary of the regions. By observing the current and voltage components, it can be seen that this condition is fully met.

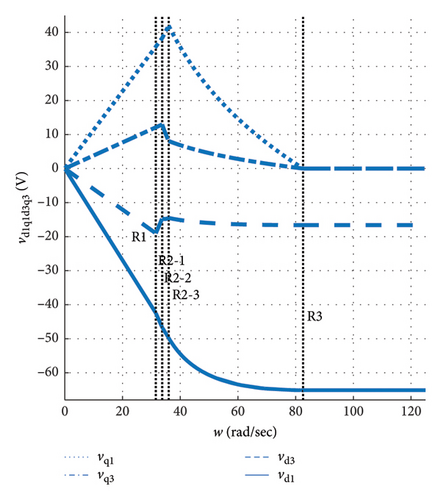
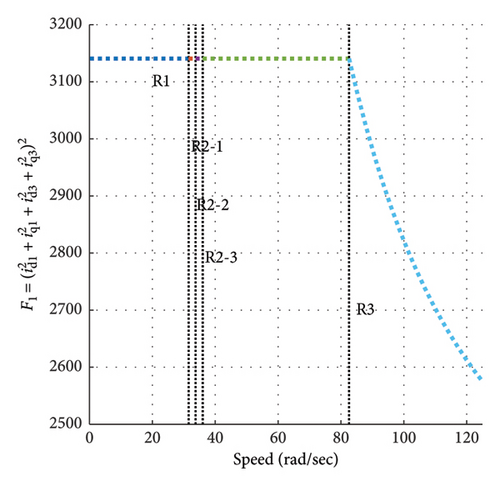
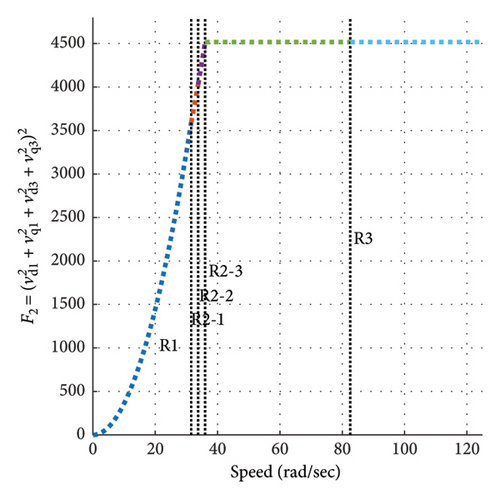
4.4. Power Losses

We know that copper losses can be calculated using the following equation:

()

Regarding the modeling of iron losses in five-phase PMSM motors, comprehensive research has not yet been reported. Typically, core losses are modeled with a parallel resistance (R_core). We do not know if the core resistance is the same for the first and third harmonics or if it is different (especially since the magnitude of the magnetic field is different at these two frequencies). Assuming that the core resistance is the same for the first and third harmonics, a relatively accurate model for core losses can be presented according to the following equation:

()

Therefore, the objective functions presented in the paper are proportional to copper losses and core losses, respectively. The results obtained from optimizing the objective functions from equations (18) and (39) for the sample motor are shown in the following Figure 19. In the first region, as torque increases, the optimal q axis current components also increase. Consequently, both copper and iron losses rise. Notably, Figure 19 depicts the function F₁, which corresponds to the machine’s copper losses, under the assumption of maximum torque (T_MTPAmax) or, in other words, at the current limit I_s = I_smax, effectively representing maximum copper losses. As speed increases, the magnitude of the voltage components also grows, leading to an increase in function F₂ and core losses. The second region is characterized by the highest current and voltage and can be termed as the constant loss region. In the third region, the current remains constant at the motor’s maximum value, thus copper losses stay constant. As speed increases and voltage components decrease, core losses are minimized.

One of the results of this research is that it seems that the nominal values of five-phase motors should be redefined. Common parameters such as speed, current, and torque do not fully represent all the characteristics of these motors. It was shown that optimal engine control has an effect on some nominal engine parameters such as power, speed, and torque. In a broader view, it seems that the motor and driver design should be integrated and the nominal values of the machine should be defined under optimal control.

5. Conclusion

A comprehensive analytical control strategy was proposed for nonsalient five-phase PMSMs, taking into account the limitations of the motor and inverter across all operating speeds. The study defined three distinct speed zones and established precise boundaries for each. Optimal control variables were then calculated for each region, accompanied by detailed geometric interpretations of all possible motor states. To validate the effectiveness of the proposed strategy, simulations were performed on a sample five-phase PMSM. The results demonstrated that by adhering to the permissible motor current limits, both the electromagnetic torque and motor power experienced significant. Specifically, the electromagnetic torque exhibited a 5.32% increase, while the power output of the motor rose by approximately 8%. Also, the results in the first region showed that the d axis currents (i_d1 and i_d3) were found to be zero, and as the speed approached, infinity and the torque decreased, and the q axis’ currents (i_q1 and i_q3) tended toward zero. Future research can build on these findings to develop generalized control strategies for internal magnet or salient pole motors. Due to the mutual effect of motor design and control strategies, it is suggested that the research related to engine design and proposed control strategies should be performed simultaneously.

Conflicts of Interest

The authors declare no conflicts of interest. We, the authors of the manuscript titled “Optimal Control Strategy of Five-Phase PMSMs in a Wide Speed Range Using Third Harmonics,” submitted to International Transactions on Electrical Energy Systems, hereby declare that there are no conflicts of interest related to this work.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Levi E., Bojoi R., Profumo F., Toliyat H. A., and Williamson S., Multiphase Induction Motor Drives—A Technology-Status Review, IET Electric Power Applications. (2007) 1, no. 4, 489–516, https://doi.org/10.1049/iet-epa:20060342, 2-s2.0-35148895423.
10.1049/iet-epa:20060342
Web of Science® Google Scholar
2 Levi E., Barrero F., and Duran M. J., Multiphase Machines and Drives—Revisited, IEEE Transactions on Industrial Electronics. (2016) 63, no. 1, 429–432, https://doi.org/10.1109/tie.2015.2493510, 2-s2.0-84960955219.
10.1109/TIE.2015.2493510
Web of Science® Google Scholar
3 Barrero F. and Duran M. J., Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part I, IEEE Transactions on Industrial Electronics. (Jan. 2016) 63, no. 1, 449–458, https://doi.org/10.1109/tie.2015.2447733, 2-s2.0-84960212108.
10.1109/TIE.2015.2447733
Web of Science® Google Scholar
4 Duran M. J. and Barrero F., Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part II, IEEE Transactions on Industrial Electronics. (2016) 63, no. 1, 459–468, https://doi.org/10.1109/tie.2015.2448211, 2-s2.0-84960308500.
10.1109/TIE.2015.2448211
Web of Science® Google Scholar
5 Mahmoud E. A., Abdel-Khalik A. S., and Soliman H. F., An Improved Fault Tolerant for a Five-Phase Induction Machine Under Open Gate Transistor Faults, Alexandria Engineering Journal. (2016) 55, no. 3, 2609–2620, https://doi.org/10.1016/j.aej.2016.04.040, 2-s2.0-84991833363.
10.1016/j.aej.2016.04.040
Web of Science® Google Scholar
6 Tatte Y. N. and Aware M. V., Torque Ripple and Harmonic Current Reduction in a Three-Level Inverter-Fed Direct-Torque-Controlled Five-Phase Induction Motor, IEEE Transactions on Industrial Electronics. (2017) 64, no. 7, 5265–5275, https://doi.org/10.1109/tie.2017.2677346, 2-s2.0-85028917272.
10.1109/TIE.2017.2677346
Web of Science® Google Scholar
7 Priestley M., Fletcher J. E., and Tan C., Space-Vector PWM Technique for Five-Phase Open-End Winding PMSM Drive Operating in the Over Modulation Region, IEEE Transactions on Industrial Electronics. (2018) 65, no. 9, 6816–6827, https://doi.org/10.1109/tie.2018.2795527, 2-s2.0-85040925008.
10.1109/TIE.2018.2795527
Google Scholar
8 Parsa L. and Toliyat H. A., Five-Phase Permanent-Magnet Motor Drives, IEEE Transactions on Industry Applications. (2005) 41, no. 1, 30–37, https://doi.org/10.1109/tia.2004.841021, 2-s2.0-13844256675.
10.1109/TIA.2004.841021
Web of Science® Google Scholar
9 Chen C., Zhou H., Wang G., and Liu G., Unified Decoupling Vector Control of Five-Phase Permanent-Magnet Motor With Double-Phase Faults, IEEE Access. (2020) 8, 152646–152658, https://doi.org/10.1109/access.2020.3017541.
10.1109/ACCESS.2020.3017541
Web of Science® Google Scholar
10 Cao B., Grainger B. M., Wang X., Zou Yu, Reed G. F., and Mao Z. H., Direct Torque Model Predictive Control of a Five-Phase Permanent Magnet Synchronous Motor, IEEE Transactions on Power Electronics. (2021) 36, no. 2, 2346–2360, https://doi.org/10.1109/tpel.2020.3011312.
10.1109/TPEL.2020.3011312
Web of Science® Google Scholar
11 Sharma T. and Bhattacharya A., Performance Analysis of Encoderless DTC of IPMSM for Wide Operating Range, Arabian Journal for Science and Engineering. (2020) 45, no. 8, 6501–6515, https://doi.org/10.1007/s13369-020-04550-2.
10.1007/s13369-020-04550-2
Web of Science® Google Scholar
12 Parsa L. and Toliyat H. A., Sensorless Direct Torque Control of Five-Phase Interior Permanent-Magnet Motor Drives, IEEE Transactions on Industry Applications. (2007) 43, no. 4, 952–959, https://doi.org/10.1109/tia.2007.900444, 2-s2.0-34547883180.
10.1109/TIA.2007.900444
Web of Science® Google Scholar
13 Bin Yu, Song W., Guo Y., and Saeed M. S. R., A Finite Control Set Model Predictive Control for Five-Phase PMSMs With Improved DC-Link Utilization, IEEE Transactions on Power Electronics. (2021) 37, no. 3, 3297–3307.
Google Scholar
14 Xiong C., Xu H., Guan T., and Zhou P., A Constant Switching Frequency Multiple Vector Based Model Predictive Current Control of Five-Phase PMSM With Non-Sinusoidal Back-EMF, IEEE Transactions on Industrial Electronics. (2020) 67, no. 3, 1695–1707, https://doi.org/10.1109/tie.2019.2907502.
10.1109/TIE.2019.2907502
Web of Science® Google Scholar
15 Xiong S. and Li J., Cascade Model Predictive Current Control for Five-Phase Permanent Magnet Synchronous Motor, IEEE Access. (2022) 10, 88812–88820, https://doi.org/10.1109/access.2022.3183138.
10.1109/ACCESS.2022.3183138
Web of Science® Google Scholar
16 Li Y., Zou J., and Lu Y., Optimum Design of Magnet Shape in Permanent-Magnet Synchronous Motors, IEEE Transactions on Magnetics. (2003) 39, no. 6, 3523–3526, https://doi.org/10.1109/tmag.2003.819462, 2-s2.0-0346276814.
10.1109/TMAG.2003.819462
Web of Science® Google Scholar
17 Zhu Z. Q., Wang K., and Ombach G., Optimal Magnet Shaping with Third Order Harmonic for Maximum Torque in Brushless AC Machines, 2012, 1–4.
Google Scholar
18 Wang K., Zhu Z. Q., and Ombach G., Torque Enhancement of Surface Mounted Permanent Magnet Machine Using Third-Order Harmonic, IEEE Transactions on Magnetics. (2014) 50, no. 3, 104–113, https://doi.org/10.1109/tmag.2013.2286780, 2-s2.0-84897083300.
10.1109/TMAG.2013.2286780
Web of Science® Google Scholar
19 Ullah W., Khan F., Ullah N., and Majid A., Investigation of Third Harmonic Utilization for Torque Performance Improvement in Novel H-Type Modular Stator Consequent Pole Machine, Electrical Engineering. (2022) 104, no. 4, 2703–2715, https://doi.org/10.1007/s00202-022-01508-5.
10.1007/s00202-022-01508-5
Web of Science® Google Scholar
20 Levi E., Dujic D., Jones M., and Grandi G., Analytical Determination of Dc-Bus Utilization Limits in Multiphase Vsi Supplied Ac Drives, IEEE Transactions on Energy Conversion. (2008) 23, no. 2, 433–443, https://doi.org/10.1109/tec.2008.921557, 2-s2.0-44349175607.
10.1109/TEC.2008.921557
Web of Science® Google Scholar
21 Hassan W., Paul L., and Mohan K., Optimum Flux-Weakening Characteristics for Five-Phase Surface Mount Permanent Magnet, 2018 International Symposium on Electrical Machines. (2018) Andrychow, Poland.
10.1109/ISEM.2018.8442571
Google Scholar
22 Zhao P. and Yang G., Torque Density Improvement of Five-Phase PMSM Drive for Electric Vehicles Applications, Journal of Power Electronics. (2011) 11, no. 4, 401–407, https://doi.org/10.6113/jpe.2011.11.4.401, 2-s2.0-79960805108.
10.6113/JPE.2011.11.4.401
Web of Science® Google Scholar
23 Sui Yi, Zheng P., and Fan Y., Research on the Vector Control Strategy of Five Phase Permanent-Magnet Synchronous Machine, 2017 IEEE International Electric Machines and Drives Conference. (2017) .
Google Scholar
24 Li J., Du B., Zhao T., Cheng Y., and Cui S., Third-Harmonic Current Injection Control of Five-Phase Permanent-Magnet Synchronous Motor Based on Third-Harmonic Current Reference Online Identification, IEEE Access. (2023) 11, 41840–41847, https://doi.org/10.1109/access.2023.3269282.
10.1109/ACCESS.2023.3269282
Web of Science® Google Scholar
25 Yang S., Zheng P., Sui Yi, Tong C., and Wang M., Carrier-Based PWM Technique and Extended State Observer-Based Current Control Scheme for Current-Source Inverter-Fed Five-Phase PMSM Drives, IEEE Transactions on Industrial Electronics. (2024) 71, no. 7, 6635–6646, https://doi.org/10.1109/tie.2023.3301518.
10.1109/TIE.2023.3301518
Web of Science® Google Scholar
26 Toliyat H. A., Waikar S. P., and Lipo T. A., Analysis and Simulation of Five-Phase Synchronous Reluctance Machines Including Third Harmonic of Air Gap MMF, IEEE Transactions on Industry Applications. (1998) 34, no. 2, 332–339, https://doi.org/10.1109/28.663476, 2-s2.0-0032028857.
10.1109/28.663476
Web of Science® Google Scholar

All articles

Optimal Control Strategy of Five-Phase PMSMs in a Wide Speed Range Using Third Harmonics

Abstract

1. Introduction

2. Modeling of the Nonsalient Five-Phase PMSM