Electric vehicle (EV) batteries may now be conveniently charged with wireless chargers. These systems are prized for their dependability and security in a range of weather scenarios. Generally speaking, there are two kinds of EV wireless charging systems: static (for parked cars) and dynamic (for moving cars). Traditionally, EV chargers have parts like a high-frequency direct current (DC)–alternating current (AC) converter that usually requires intricate cabling and an AC–DC converter that aids in power quality management. In these systems, a process called as “transformation” occurs when energy moves from a main component—the power source—to a secondary component—the vehicle’s receiver. Eliminating physical connections, such wires and charging outlets on the car, improves convenience and lessens wear and tear on the charger. This is another advantage of wireless chargers over plug-in varieties. In this study, we investigate a novel design that substitutes a single integrated AC–AC converter on the input side for the conventional AC–DC and DC–AC converters. This creative solution lowers the demand on power switches while raising voltage levels, which not only makes the system simpler but also more efficient. To further reduce the voltage stress on these switches, we additionally employ a multilevel diode clamp inverter, which not only helps to reduce the size of the switches but also greatly increases the efficiency of the system. To validate the performance of this new converter, we provide data from the laboratory as well as simulation results.

1. Introduction

More than ever, people are concerned about the depletion of fossil resources and the rising levels of air pollution. Consequently, more attention is being paid to the expanding use of fossil fuels in internal combustion engines [1]. Electric vehicle (EVs) are a suitable substitute for internal combustion engines to tackle these problems. These cars use the electricity in their batteries to provide kinetic energy instead of burning fuel or liquefied gas [2]. In addition, the adoption of EV has become more and more spurred by the rising expense of fuel [3].

Several factors make EV desirable, such as the depletion and growing price of fossil resources worldwide, the need to lessen environmental pollution, the fact that they produce less noise than vehicles powered by fossil fuels, and the fact that they are less expensive to operate than conventional vehicles [4]. In electric cars, the internal combustion engine is replaced by an electric motor, and a battery replaces the fuel tank. Batteries can be charged by off-grid electric sources like fuel cells, the vehicle’s regenerative braking system, and even grid connections. Fast start-up times, the ability to store kinetic energy when parked, almost zero pollutants, increased efficiency over gasoline-powered vehicles, no fuel usage, and low maintenance costs are just a few advantages of utilizing EV [5]. The drawbacks include reliance on batteries, a restricted operating range because of battery capacity, poor acceleration, a substantial weight penalty, and expensive starting expenses [6].

Assessing the effectiveness and suitability of various charging methods becomes essential as the shift to EV increases. These challenges are prompting scientists to look into alternative EV power sources. Scientists are investigating different ways to power EV due to these difficulties. One approach to providing energy is to use wireless power transmission (WPT). The users can send power ranging from several watts to tens of kilowatts via WPT, sometimes called contactless and magnetic coupling power transfer. This technology is highly dependable, safe, and practical. Water, chemicals, snow, and pollution do not affect WPT [7].

But even with these benefits, wireless charging methods have some significant drawbacks. Significant limitations include lower efficiency and greater starting expenses when compared to traditional plug-in chargers. Furthermore, even though WPT systems are usually safe, adverse weather or other environmental circumstances may have an impact on how well they function and how safe they are [8]. It is critical to support safety claims with particular research or technological modifications that deal with these issues. For example, to reduce such impacts and improve the operational safety and efficiency of WPT systems in different environmental circumstances, sophisticated shielding and adaptive control systems have been developed [9].

Table 1 offers a thorough comparison of aspects like convenience, charging speed, safety, energy efficiency, and environmental effect to highlight the advantages and disadvantages of wireless charging over conventional plug-in techniques.

Table 1. Comparative analysis of wireless and plug-in chargers for EVs.

Feature	Wireless chargers	Ref	Plug-in chargers
Convenience	- No need for physical connection; simply park over the charger - Ideal for public and home environments where accessibility is crucial	[9]	- Requires manual connection, which can be inconvenient in adverse weather or tight spaces

Charging speed	- Generally slower charging speeds due to energy transmission inefficiencies - Recent studies suggest advancements in high-frequency inductive charging can improve speeds significantly (up to 22 kW)	[10]	- Faster charging capabilities, especially with DC fast chargers (up to 350 kW) available

Safety	- Safer operation in various weather conditions (water, snow) - Reduced risk of electric shock due to lack of physical connections	[8]	- Safety risks associated with exposed connectors in wet conditions

Energy efficiency	- New designs, such as integrated AC–AC converters, can achieve efficiencies exceeding 90% - Still faces challenges with energy loss during transmission	[11]	- High efficiency, often above 95%, especially in DC fast charging systems

Installation cost	- Higher initial infrastructure costs due to the need for specialized equipment and installation	[12]	- Generally lower installation costs; widespread availability of plug-in stations

User experience	- Eliminates hassle of plugging and unplugging, enhancing user experience - Suitable for fleet operations and shared charging stations	[13]	- Familiar and straightforward for users but can be cumbersome for frequent charging

Maintenance	- Fewer mechanical components may lead to lower maintenance needs - However, the technology is still evolving, and long-term reliability is yet to be fully established	[6]	- Established technology with known maintenance requirements; issues typically arise from wear and tear on connectors

Environmental impact	- Potentially lower emissions if integrated with renewable energy sources. - Reduced reliance on fossil fuels for electricity generation can enhance sustainability	[14]	- Emissions depend on the energy source; renewable integration is crucial for minimizing environmental impact

Abbreviations: AC, alternating current; DC, direct current; EVs, electric vehicles.

Hidayah, Suryoatmojo, and Pamuji [15] investigated using a single-phase matrix converter in WPT to charge EV in parking lots. In line with global trends toward greener technology, this work introduces a novel resonant inductive coupling method that significantly improves the safety and practicality of EV charging. Vinod et al. [10] emphasized using primary side control techniques in EV applications when focusing on battery charge management in WPT systems. The paper compares and contrasts several control approaches to maximize charging process stability and effectiveness. Their research advances our knowledge of how precise control may boost WPT system efficiency, which directly increases the dependability of EV charging. In their critical analysis of modern power electronics interface topologies for renewable energy integration, Tasnim et al. [16] highlighted how they might improve and stabilize power quality. Although not limited to EVs, the topic of interface topologies is relevant to any WPT application where effective energy transfer is essential, including EVs. Because of its increased power density compared to other WPT methods, inductive power transmission (IPT) is utilized explicitly in EV [17]. IPT has low magnetic inductance; hence, both the primary (transmitter) and secondary (receiver) sides require adjustment. These techniques allow energy to be transferred without requiring a physical electrical connection, which frees the EV from needing to travel a predetermined path. There are no related mechanical connection issues because there is not a mechanical connection between the grid and the vehicle [18]. This method keeps batteries as energy storage devices rather than removing them entirely from the electric car system. They are smaller, less volumetric, and receive sporadic charging using contactless techniques [19].

A fault-tolerant multilevel inverter, invented by Zhang et al. [20], is needed for applications such as IPT systems where continuous operation is required. It is designed to retain output integrity under fault conditions. Their application of cutting-edge modulation techniques to lower power losses and boost efficiency is similar to the optimization methods we employ in our IPT research on electric cars. The objectives of our study to guarantee dependable and continuous EV charging are directly supported by this work, which provides significant insights into attaining robustness in IPT systems. Zhou et al. [21] devised a spread-spectrum modulation technique to minimize electromagnetic interference (EMI) in multiphase indirect matrix converters. This technique is very significant in reducing EMI in EV IPT systems. Their emphasis on improving power conversion efficiency and the harmonic spectrum aligns with our research’s goal of maximizing system safety and energy transfer efficiency in IPT-based EV charging. Their practical demonstration of less EMI and better waveform quality provides applicable standards for us to advance IPT technology in our study.

Series–series (S/S), series–parallel (S/P), parallel–series (P/S), parallel–parallel (P/P), and mixtures of series and parallel tanks, such as LCL and LCLC, are examples of several types of compensation networks [22]. In compensatory networks, S/S and S/P arrangements are frequently employed, although P/S and P/P tanks are less often used because of load-dependent escalation [11, 23]. In IPT applications, it is typically required to set the switching frequency at the resonant frequency of the resonant tank to guarantee that the power converter circuit receives the minimal amount of volt-ampere (VA), which lowers power loss and reduces converter size [12]. The majority of compensator networks employed on the primary side are series and have an LCL structure [24]. An LCLC tank is created when an extra capacitor is occasionally added to the LCL tank in series with the coil to improve system performance [13].

Ali et al. [25] examined the enhanced passive damping design for single-phase grid-connected LCL-filtered inverters. Since the concepts they cover can be utilized to lower harmonic distortion and improve the power quality in systems used to charge electric cars, their work is vital to any application utilizing WPT. The article [14] discusses optimizing a resonant inductive power transmission (RIPT) system for charging the battery banks of EV. This study assesses a RIPT system for light car charging and provides diagrams to clarify the system’s operational characteristics. The results indicate that the resonant frequency should be between 25 and 51 kHz, and the inductance coefficient of the coil should be between 111 and 151 µH for the best possible resonant WPT system design.

Despite these developments, there are still fundamental inefficiencies in the wireless charging solutions available today, which our study seeks to resolve. A few of these are the hefty infrastructure expenses related to charging, the sluggish energy transfer speeds, and the significant energy losses that occur throughout the process [26, 27]. By utilizing state-of-the-art technology, our research presents a revolutionary IPT system that addresses these particular problems and enhances the efficiency, accessibility, and affordability of EV charging infrastructure.

The design and assessment of a high-efficiency WPT system will be covered in this talk, emphasizing the novel alternating current (AC)–AC converter design. By directly converting AC from one waveform to another, this technology increases power density and streamlines the system design as a whole. Conventionally, systems use two stages—AC–direct current (DC) and DC–AC conversion—to convert AC to DC and back to AC. By eliminating these intermediary stages, our design lowers operating costs and energy losses. We also present a new component, a multilevel diode clamp inverter. This sophisticated inverter, in contrast to traditional inverters, improves system efficiency by precisely controlling electrical flow, which also makes smaller power switches possible. These developments show their efficacy in practical situations and indicate their potential for wider application. They are backed by solid modeling and empirical evidence.

In this article, an attempt is made to design an IPT system for wireless charging of EV, focusing on the power electronics part of this system. The main goals of this research are to design an induction power transmission system with high efficiency and its simulation by MATLAB/Simulink software and to implement a laboratory sample to provide a solution to improve the prosperity of this industry.

The main contributions of the paper are as follows:

•
Innovation in design: A revolutionary development in wireless charging technology, this integrated AC–AC converter efficiently raises voltage levels while decreasing current stress on power switches.
•
Enhanced system efficiency: The implementation of a multilevel diode clamp inverter markedly improved efficiency and reduced the size of power switches, signifying a major enhancement compared to conventional systems.
•
Validation through testing and simulation: Strong simulation and empirical data from lab samples were provided, supporting the suggested system’s practical viability and performance promises.
•
Strategic directions and improvements for next-generation wireless charging systems were outlined, to stimulate additional research and development in this vital field of electric car technology.

The remainder of the paper is as follows: The background information on wireless chargers and electric cars is covered in the second section, which also sets the scene for the advances that are presented. The architectures of isolated, nonisolated, and wireless charging systems are presented in the third section to improve comprehension of various integration strategies. The framework of our innovative wireless charging system, complete with comprehensive design schematics, is introduced in the fourth section, marking a significant advancement in the integration of charging technologies. In the fifth section, we show the efficacy and operational efficiency of the suggested system by validating it with simulation results and lab testing. The last section provides a thorough synopsis, broad conclusions, and recommendations for the future based on our research.

2. The Structure of the Proposed Wireless EV Charger

This article proposes a wireless EV charger system based on the dual LCC series structure to increase the DC link voltage and remove the diode bridge. In the proposed structure, the power switches’ current is reduced by using a voltage-increasing circuit. Also, to reduce the voltage stress of the power switches, the diode clamp inverter was used, which reduced the size of the switches and increased the efficiency of the proposed converter.

The proposed system consists of a high-frequency AC–AC converter, an LCC compensator, and a rectifier for battery charging. Figure 1 shows the proposed system’s circuit structure. Figure 1a shows that a single-stage AC–AC converter generates high-frequency AC voltage from the AC input source. The inductor at the input, together with the power switches, acts as a conventional boost converter and increases the input voltage with a gain of (D is the duty cycle of the power switches). Also, the capacitors are DC link capacitors, and their values are much larger than the resonant capacitors, so they will not have an effect on the resonant circuit performance.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The proposed wireless charger general structure of the (a) high-frequency AC–AC converter, (b) compensation LCC, and (c) output rectifier.

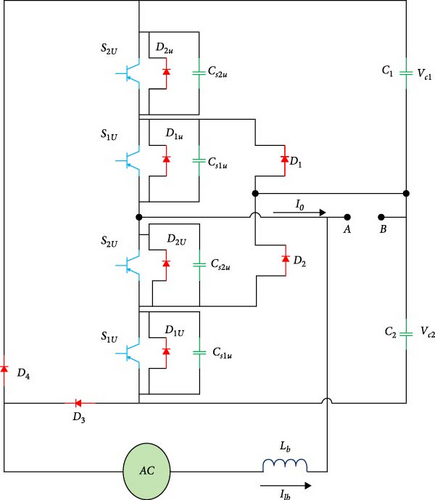
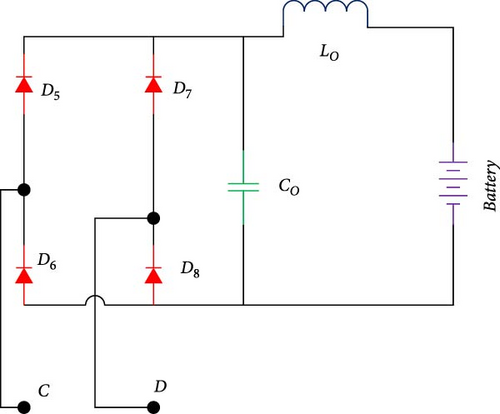
The output of the inverter in Figure 1a is a high-frequency AC voltage. The resonance circuit and the air-gap transistor transfer the input source energy to the secondary side of the transformer, which is connected to the rectifier coupled to the battery. Finally, the energy transferred to the secondary through fast rectifier diodes is rectified and charges the battery. The following presents the analysis and operation of each part of the wireless EV charger system.

2.1. The Suggested Inverter’s Structure

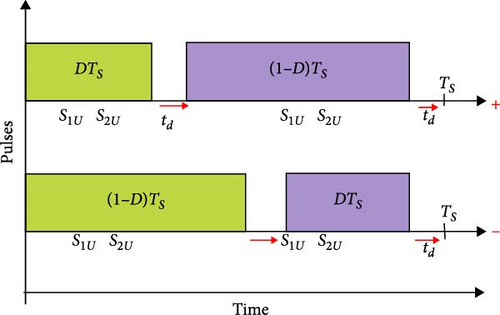
Figure 1a depicts the inverter’s construction as presented in this article. The average value of the input AC voltage following the diode bridge is equal to V_in, which is used to construct the inverter and establish the nominal values of its semiconductor elements. This article uses a resonant type of inverter. Resonant converters are used because they transmit higher powers, have a high conversion efficiency, produce soft switching, and eliminate switching losses. Figure 2 illustrates the suggested inverter’s switching mechanism and how the switches are pulsed during the input voltage’s positive and negative half cycles. This converter’s output voltage can be adjusted by pulse width modulation or switching frequency control. It should be remembered when pulsing the keys that 50% is the maximum duty cycle (D) that can be used to regulate this converter, independent of dead times.

2.2. Working Fashions

Considering that the DC link capacitors do not interfere on the resonance circuit and their values are much larger than the resonance capacitors (at least 10 times larger), these capacitors are used as a DC link with an increased voltage of () which are equal to the average value of the input voltage (V_in) after rectification. Also, considering the resonant compensation system and the rectified resistive load as an RLC resonant tank that work at a frequency higher than the resonant frequency, the modes of the operation of the proposed circuit along with the voltage and current waveforms of some key elements of the circuit are shown in Figure 3.

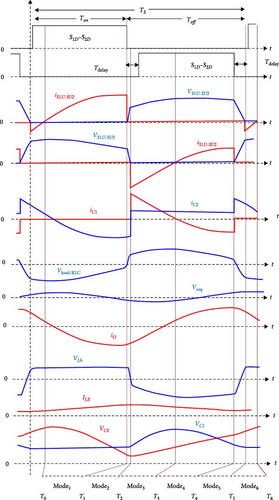
2.3. Working Modes of the Proposed Converter in the Positive Half Cycle of the Input

Considering the positive half cycle of the input voltage, different current paths and working modes are created during a switching period. These work modes are discussed as follows.

2.3.1. The First Work Mode

As seen in Figure 4a, in this mode, the lower leg keys of the inverter receive pulses and are turned on. The capacitor C₂ is discharged, and the input inductor is charged. Also, the resonant capacitor C_eq is also discharging. It should be noted that the capacitor C_eq is charged in the sixth mode that occurs before this mode.

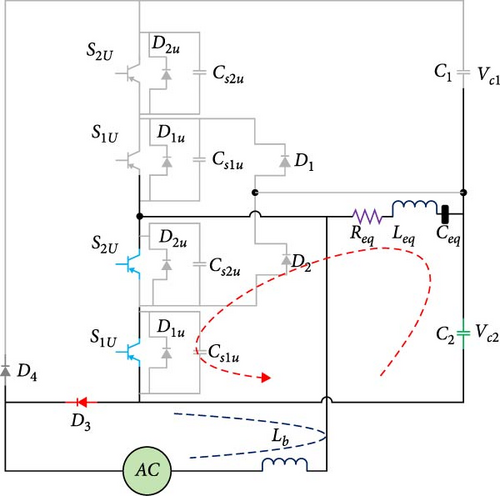
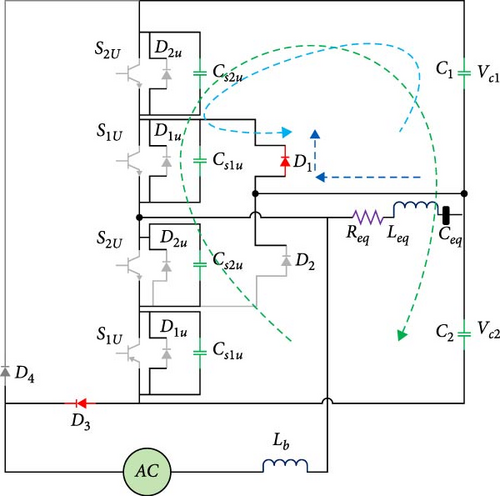
2.3.2. The Second Method

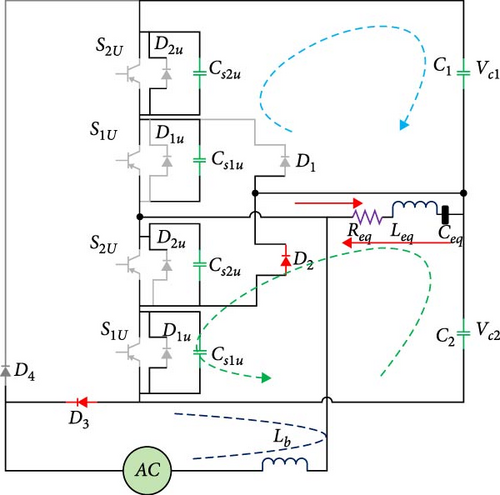
Considering that at the moment when the lower keys are turned off, the external snubber capacitors of the keys have zero voltage, so the keys are turned off in the form of zero voltage switching (ZVS). Also, in this mode, the external snubber capacitors of the upper leg power switches are discharged, and before turning on the keys, the voltage on them reaches zero. In other words, it prepares the upper keys to be turned on as ZVS. The positive half cycle of the second working mode is shown in Figure 4b.

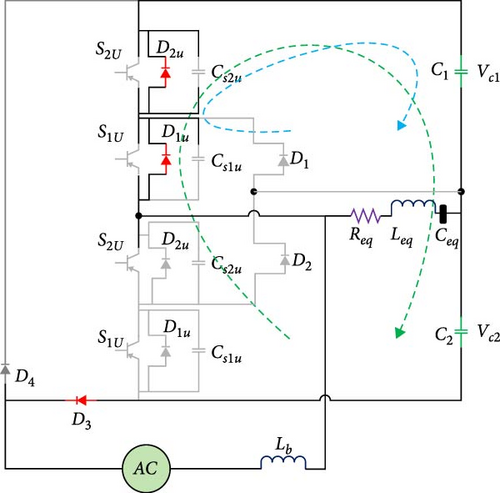
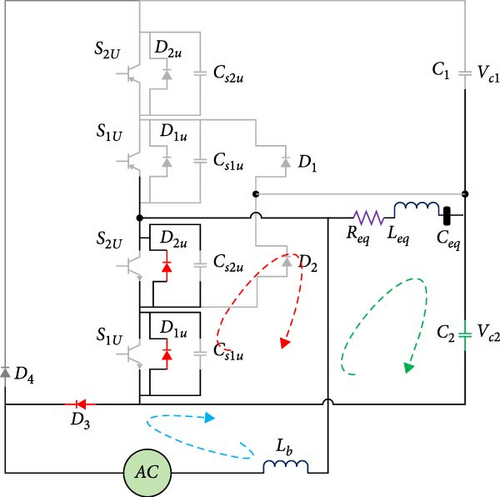
2.3.3. Third Operating Mode

As can be seen in Figure 4c, in this mode, the inverse parallel diodes related to the upper leg switches are conducted, and in addition to the zero voltage of the switches, the current passing through them also reaches zero. Therefore, after this working mode, the power switches will be turned on as ZVS and zero current switching (ZCS). Also, the DC link capacitors are charged through the inductor L_b and the input source; as a result, the inductor L_b is discharged.

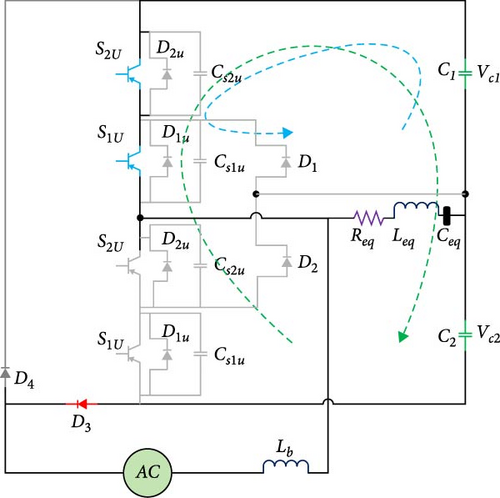
2.3.4. Fourth Operating Mode

As seen in Figure 4d, in the fourth working mode, capacitor C₂ is still charging, and capacitor C₂ starts discharging on the load through the upper leg switches. In addition, the input inductor is discharged on the load and capacitor C₂ and increases the output voltage.

2.3.5. Fifth Operating Mode

In the fifth method, as seen in Figure 4e, the capacitor C₁ is discharging on the external snubber capacitors of the upper leg switches, and by increasing their slow voltage, it causes the power switches to turn off in ZVS mode. Also, by discharging the external snubber capacitors of the lower leg keys, the conditions for turning on the ZVS of the said keys are provided.

2.3.6. Sixth Grade

In this working mode, the booster inductor is still discharging and leads to the charging of capacitor C₂. To continue the amplification process, diodes in reverse parallel with the lower leg switches are forced on and lead to zero current in the power switches before they are turned on. As happened in the previous mode, the voltage of the power switches has already gone to zero. Therefore, the lower leg power switches are turned on in the ZVS–ZCS state. Also, in this interval, the voltage of capacitor C₁ remains constant, and the power switches of the upper leg are still off. The positive half cycle of the sixth working mode is shown in Figure 4f.

2.4. Working Modes of the Proposed Converter in the Positive Half Cycle of the Input

2.4.1. The Initial Operational Mode

Figure 5a illustrates how the input current route is closed through the diode D₄ during the input voltage’s negative half cycle. In contrast, diode D₃, which was always on during the positive half cycle, is always off during this half cycle. Firstly, the input inductor is charged through the two upper leg keys, which are switched on. Additionally, the load causes the capacitor C₁ to discharge. The reverse parallel diodes of the keys are off, and the voltage of the capacitor C₂ stays constant when the key is in this operational mode.

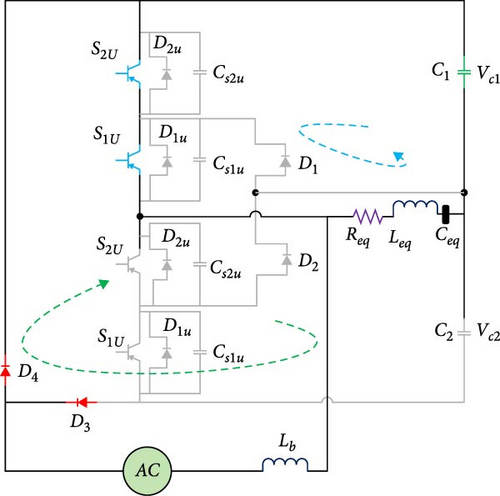
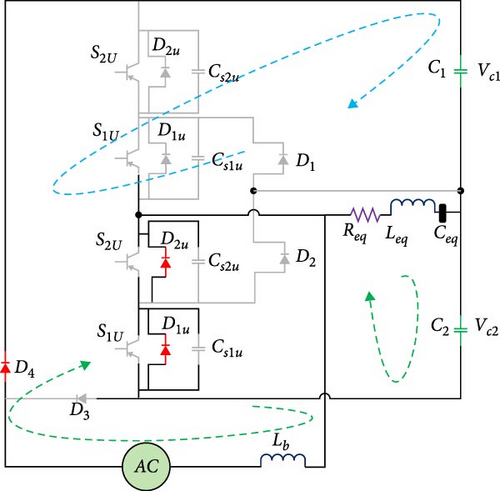
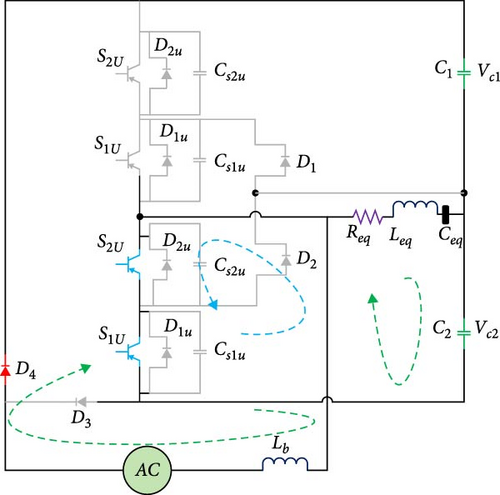
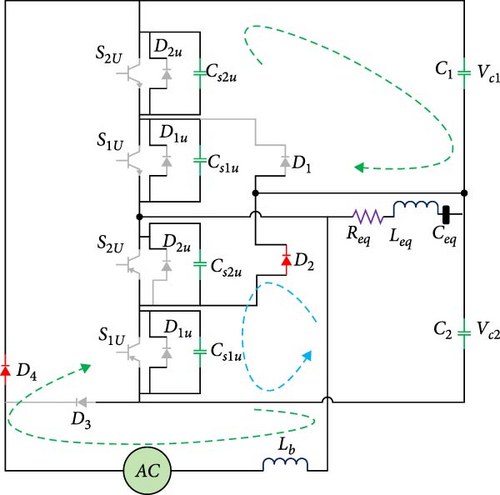
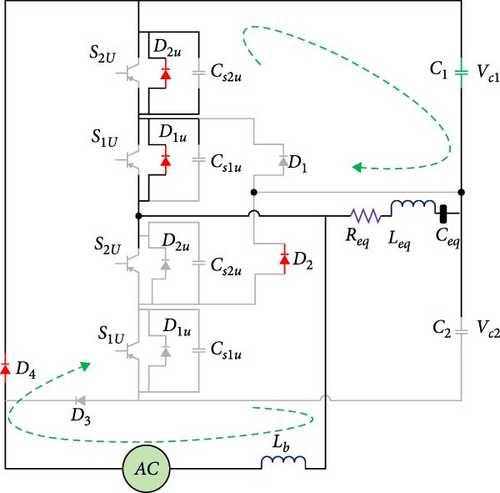
2.4.2. Second Working Mode

According to Figure 5b, in this method, the power switches of the upper leg are turned off, and the external snubber capacitors parallel to them are slowly charged and ensure the switch off under zero voltage (ZVS). Also, in this working mode, all the power switches are turned off, and the external snubber capacitors of the lower leg, by discharging themselves, prepare the conditions for turning on the power switches at zero voltage for the next working modes.

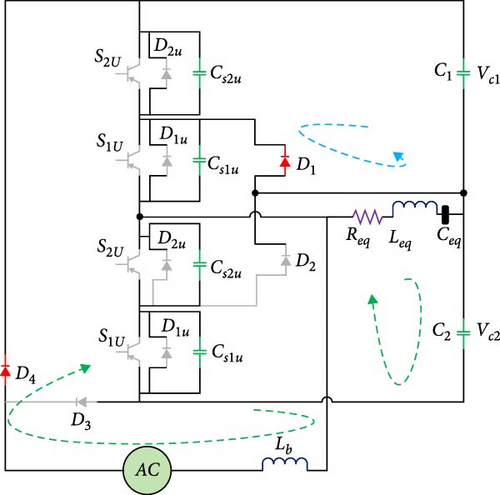
2.4.3. Third Working Mode

According to Figure 5c, in the third working mode, the resonant load is still completing its resonant process in the positive direction, and the amplifier inductor (L_b) is discharged on the DC link capacitors (C₂ and C₂). Also, because in the next mode, the power transistors of the lower leg will be turned on; the diodes D_1d and D_2d will start to conduct so that the current of the keys is equal to zero when they are turned on. In other words, the ZVS–ZCS conditions are fully established for the keys to be turned on in the next working mode.

2.4.4. Fourth Grade

As seen in Figure 5d, in this mode, the lower leg switches of the inverter are turned on under soft switching and in ZVS–ZCS conditions. Also, the capacitor C₁ is being charged and is preparing to complete the intensification process in the next working modes. Also, the resonant load is fed through the capacitor C₁ and the inductive current. In this working mode, the direction of feeding the load is also changed, and it remains like this for the next several working modes so that by creating an alternating voltage in the two ends of the resonant load, it can induce a voltage in its secondary side. This induced voltage will be used to charge the battery after rectification.

2.4.5. Fifth Working Mode

This method is similar to the second method. Of course, with the difference that this time, the zero voltage conditions are provided for the lower power switches to turn off as ZVS. Also, at the same time, the zero voltage conditions are provided for the upper leg switches before turning on. The negative half cycle of the fifth working mode is shown in Figure 5e.

2.4.6. Sixth Working Mode

The inverse parallel diodes of the higher leg switches are activated in this mode, as shown in Figure 5f, and they set the circumstances for the upper leg switches to switch on under zero current before being turned on. The S_1U and S_2U switches are turned on under the soft switching method and with ZVS–ZCS circumstances in the next operating mode, which is the same as the first mode.

The compensating circuit’s resonant frequency in Figure 1b is the same as the resonant frequency for the resonant load. In order for the circuit to function in the self-locking zone, the output voltage and current frequency must also be equal to the switching frequency and consistently higher than the circuit’s resonance frequency.

3. Necessary Conditions for Establishing ZVS With the External Snubber Capacitor of the Keys

To establish ZVS in the circuit by the external snubber capacitors of the keys, in the second mode, we have the following:

(1)

(2)

Also, in the fourth mode, the following relationship should be established:

(3)

3.1. LCC Compensation System

To transfer energy through the air gap (the distance between the vehicle charging system and the resonant circuit of the charger side), the compensating system of Figure 6 is used [28].

For the aforementioned compensation system, the resonance frequency is equal to the following:

(4)

Also, according to Jiang, Long, and Gaona [19] for currents I_Lf1, I_Lf2, I₁, and I₂, we have the following:

(5)

(6)

(7)

(8)

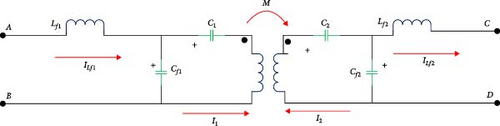
The parameters used in LCC are given in Table 2.

Table 2. Specifications of parameters used in LCC converter relations.

Characteristic	Parameter	Characteristic	Parameter
The first-order RMS value of the input voltage	u_AB	First-order phasor of the input voltage	U_AB
The first-order RMS value of the output voltage after rectification	u_CD	First-order phasor of output voltage before rectification	U_CD
		Inductance of coupled inductor	M

According to Equations (3)–(8), the output current to the rectifier and battery can be calculated using the RMS value of the input voltage. In other words, by controlling the input RMS voltage of the compensator, the output current of the secondary side is controlled. Also, for output power, we have the following:

As it is clear from the above relationships, the resonant frequency depends only on the values of the inductor and capacitor of the resonant circuit and has nothing to do with the load conditions and the coupling method. Also, by using this LCC structure, by increasing the mutual inductance, the transmitted power to the output increases, and by decreasing it, the amount of output power decreases. This means that the amount of power transmitted will increase as the vehicle approaches the charger coil. Of course, it is certain that there will be a minimum distance between the primary winding and the existing winding on the vehicle. Also, using Equations (3)–(6) for output power, it can be seen that factors such as resonance frequency and inductances L_f1 and L_f2 as well as input and output voltages are effective in transmission power.

Using relations Equations (3)–(5) and Equations (3)–(6), it can be seen that the input voltage and current of the compensator are in phase. Therefore, the unit power factor is obtained by the compensator system.

3.2. Rectifier System and Output Filter

As seen in Figure 1c, the alternating voltage output of the LCC compensator enters the rectifier circuit and is connected to the battery through an LC filter. The diodes used in this circuit must be of the fast type and the inductor and capacitor. Filters are used to remove current and voltage ripple.

3.3. Design of Inductor

The relation of the inductor current i_Lb is calculated according to Equation (9):

(9)

In order for the converter to operate in the continuous conduction mode (CCM) area, the inductor current must always be positive (i_Lb(T_s) > 0), so to calculate the inductor we have the following:

(10)

On the other hand, to calculate the DC link voltage, which is the sum of the two voltages of capacitors C₁ and C₂, we have the following:

(11)

Considering the current ripple ΔI_Lb for the inductor current I_Lb, the peak current I_Lb.Peak will be equal to the following:

(12)

And assuming the power factor of the circuit is equal to one and considering Z_in as the input impedance of the circuit, we will have the minimum value of the inductance for the converter to operate in the continuous region:

(13)

In order to clarify the calculations and calculate the impedance of the circuit in relation to the design of the inductor, a coefficient called ripple-factor (γ) is defined which is equal to the following:

3.4. Designing Circuit Parameters of Compensator

Calculation of inductor and capacitor values related to Figure 6 is explained as follows. First, assuming that the inductance of the primary side of the power transmission coil is equal to 360 μH, we solve the problem. To calculate the values of L_f1 and L_f2 and assuming the average input voltage is equal to a maximum of 265 V (the average voltage of the rectified city electricity is 197 V, and the maximum input value is considered as a coefficient of it), the output voltage (battery voltage) is equal to 280 V, and the maximum output power is one kilowatt, and assuming the maximum coupling coefficient k = 0.32, we have the following [2]:

(14)

(15)

(16)

Therefore, for the values of inductors L_f1 and L_f2, we have the following:

(17)

Having the values of L_f1 and L_f2, the values of capacitors C_f1 and C_f2 can also be calculated according to the following relations:

(18)

which according to relations Equations (3)–(21) for the values of capacitors C_f1 and C_f2, we have the following:

(19)

By placing the values of the parameters, we will have the following:

(20)

3.5. Proposed Converter Control System

To control the proposed converter, a closed loop control system with a PI controller has been used.

The proposed control system for the circuit is shown in Figures 7 and 8.

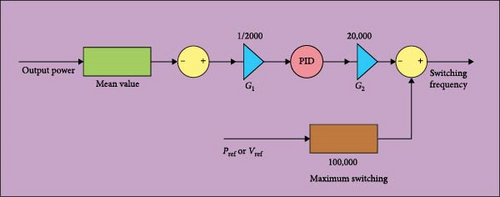
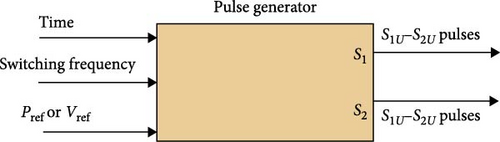
The basis of the work is that the controller should be able to control the switching frequency between 80 and 100 kHz. In the control system presented in Figure 7, the desired power is given to the system as a reference, then through a PI controller and fixed gain blocks, a signal is produced that is proportional to the switching frequency. The control signal created by control diagram block is given to the pulse generator block according to Figure 8 to create the gate signals of the keys.

Also, to control the output voltage, Equations (3)–(8) can be used, and the output current can be fixed at the desired value by controlling the input voltage. Since the output voltage is equal to the product of the output current multiplied by the constant value of the output resistance, therefore, by controlling the output current, the output voltage is also controlled.

3.6. Output Equivalent Circuit From Inverter Point of View

For the inverter circuit of the structure mentioned in Figure 1 in terminals A and B, the values of L_eq, R_eq, and C_eq are as follows:

(21)

(22)

(23)

3.7. Winding Design

To design the primary and secondary windings, we use the values of inductance L₁ and L₂ [27]. The relationship between the number of turns in terms of inductance in the inductor with air core is obtained from the following relationship:

(24)

where N is the number of turns and D is the distance D between the centers of the primary and secondary windings in an air-core inductor.

4. Simulation

In this section, in order to show the capabilities and confirm the performance of the proposed converter, the simulation results and the results of the experimental sample of the proposed converter in Figure 1a–c are presented and reviewed.

The simulation results have been obtained using MATLAB software and Simulink environment. The values and parameters used in the simulation for the proposed converter elements are presented in Tables 3–5:

Table 3. Values of the elements of the inverter section of the proposed converter (Figure 1a).

Characteristic or element	Value
V_ac	220 Vrms–50 Hz
L_b	500 μH
C_s1u − C_s2u − C_s1d − C_s2d	33 nF
C₁ − C₂	1 μF
f_s	85 kHz
R_O output load	100 Ω

Table 4. Values of elements of the compensating part of the proposed converter Figure 1b.

Characteristic or element	Value
L_f1 − L_f2	116 μH
C_f1 − C_f2	33 nF
C₁ − C₂	15 nF
L₁ − L₂	360 μH
M mutual inductance	100 μH

Table 5. Values of the elements of the output section (equivalent circuit of the load in Figure 1c).

Characteristic or element	Values
L_o	100 μH
C_o	1000 μH
R_o	100 Ω

In the simulation, a 100 Ω resistor is used instead of a battery. Also, the output voltage of the DC side is equal to 240 V.

4.1. Simulation Results of the Proposed Wireless Charging System

The simulation results of the proposed converter for a load of 650 W at the output are presented in this section. During the simulation, the duty cycle is constant at 40%, and the switching frequency is equal to 85 kHz. Also, the dead time between the pulses of the upper and lower leg switches of the inverter is considered equal to 1 µs. The waveform of the pulses applied to the gate related to the power switches S_1U − S_2U − S_1D − S_2D is shown in Figure 9.

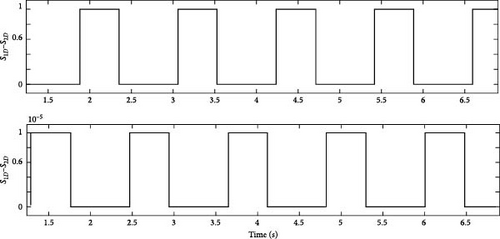
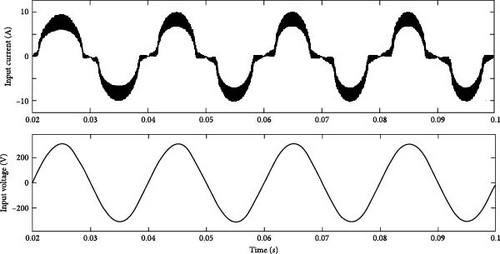
As can be seen in Figure 9a, the gate pulses of the upper and lower leg switches of the inverter have a phase difference of 180°, and a dead time interval (T_delay) is applied between these pulses so that the upper and lower leg switches under no circumstances do not turn on at the same time. Also, to complete the soft switching function by using the snubber capacitors on the power switches, the presence of this delay time is necessary. Considering that the input voltage of the proposed charger system is directly connected to the city electricity with a voltage of 220 V and a frequency of 50 Hz, the presence of current with a suitable quality and in phase with the input voltage can be effective in determining the quality of the current drawn from the network. For the proposed converter under simulated conditions, the waveform of voltage and input current can be seen in Figure 9b.

The current and voltage waveforms of diodes D₁ to D₄ of the inverter section of the proposed converters are shown in Figure 10a–d. The current of diodes D₃ and D₄ is equal to the input current from the city electricity side. Diode D₃ conducts in positive half cycle, and diode D₄ conducts in negative half cycle. As can be seen, diodes D₁ to D₂ conduct when the lower leg snubber is activated. Also, diodes D₃ and D₄ operate in positive and negative half cycles, respectively, and create the current conduction path in positive and negative voltage half cycles.

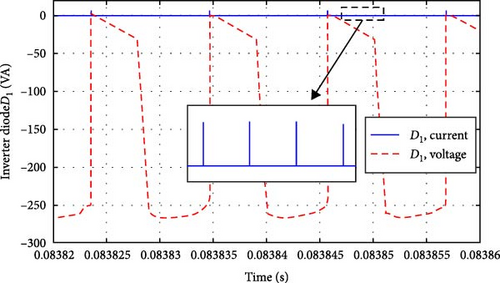
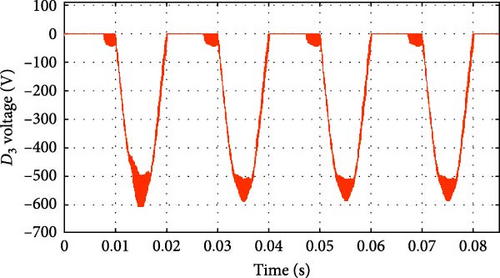
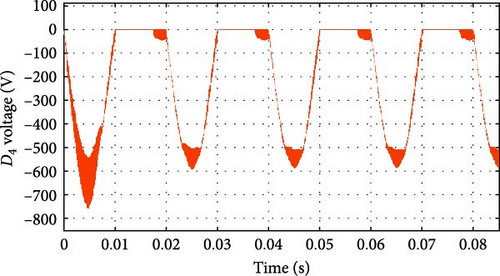
To show the soft switching performance of the proposed converter power switches according to the working modes mentioned in the previous section, the voltage and current waveforms of the S_1U − S_2U − S_1D − S_2D switches are shown in Figure 11a–d.

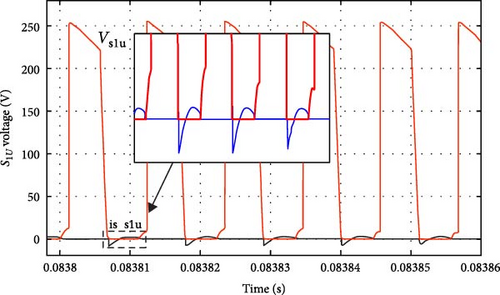
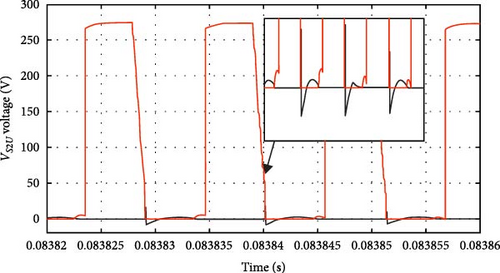
As seen in Figure 11a, the power switch is turned on as ZVS–ZCS and turned off as ZVS. Also, the voltage range of the power switch is equal to the product of half the input voltage and the gain of the boost converter. The occurrence of soft switching in power switches causes a significant reduction in switching losses, and the majority of losses in the proposed converter are caused by the conduction losses of diodes and switches.

The voltage of capacitors C₁ and C₂ is shown in Figure 12a,b, respectively. Figure 12b shows voltage waveform of capacitor C₂ in a cycle of input voltage. Also, the voltage waveform of DC link, which is equal to the sum of voltages of capacitors C₁ and C₂, is presented in Figure 12c. The waveform of the output voltage of the inverter is a high-frequency alternating voltage whose amplitude increases or decreases according to the switching frequency and duty cycle. The output voltage’s detailed waveform, depicted in Figure 12d, illustrates how operational alterations have an instantaneous impact. On the other hand, Figure 12e shows the range of these output voltages under various operating circumstances, emphasizing the inverter’s response over a wider range of parameters. For the current passing through the inductors L_f1 and L_f2 in the compensating system of Figure 1b, Figure 13a–c is presented. Additionally, these figures indicate stable and controlled voltage and current behaviors, characteristic of reduced stress on the system components due to the integrated design.

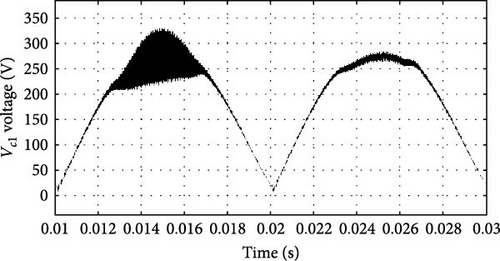
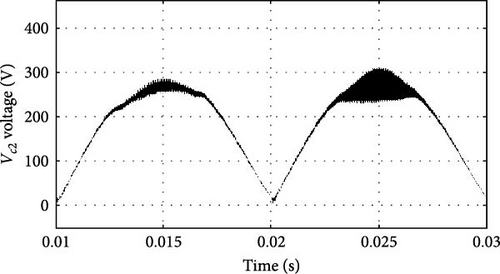
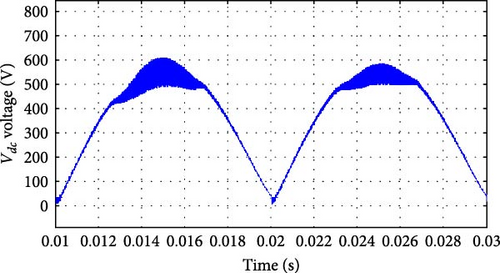
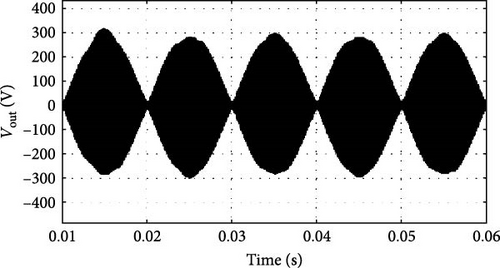
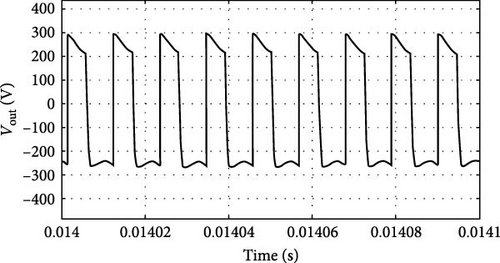
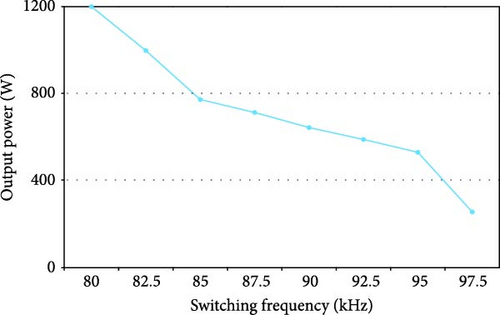
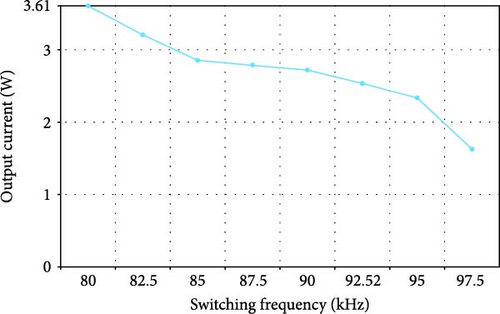
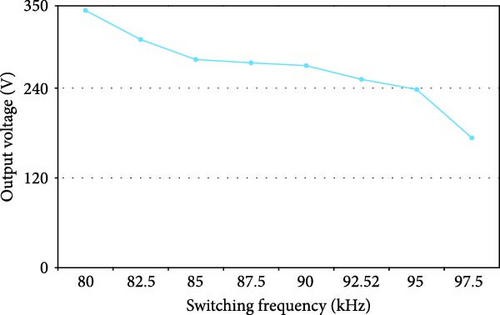
Due to the ability to control the output power by changing the switching frequency in the range of 80–100 kHz, it is possible to control the output power by changing the switching frequency. In series RLC circuits, as the frequency increases from the resonance frequency, the load impedance increases, and the output power and current decrease. The following figures show the changes in output power, current, and voltage according to changes in the switching frequency.

4.2. Checking the Performance of the Proposed Converter Control System

In order to check the dynamic behavior and correct operation of the control system presented in Figure 14a for the proposed converter, the output power reference value is changed step by step at the moment t = 0.4 s from 600 to 1000 W. Figure 14a shows the changes in the output power under the above conditions. As can be seen in this figure, it has been able to bring the output power value to its reference value in a period of about 100 milliseconds.

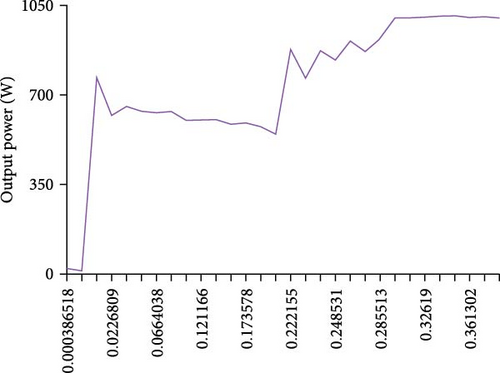
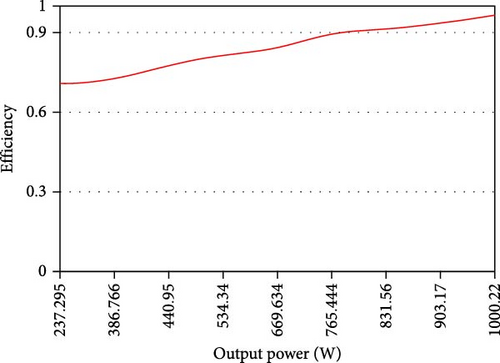
The efficiency of the proposed converter per load change from 400 to 1900 W is shown in Figure 14b. As it is known, the maximum efficiency has been obtained in the power of 1900 W and equal to 96.5%. As the output power decreases due to the dominance of switching losses over conduction, the efficiency of the converter decreases further. To achieve higher powers, a mutual inductance of 200 μH is included. From Figure 14, particularly Figure 14b which illustrates the efficiency curve across different output powers, it is evident that the integrated AC–AC converter achieves high efficiency. The maximum efficiency noted at higher powers indicates effective management of energy, likely translating into lower stress on system components over time.

The results of the simulation for different circuit elements as well as their functional modes are consistent with the items mentioned in the previous section, and according to the items mentioned in the previous section, changes in the current and voltage of the elements have occurred.

5. Laboratory Sample Results

This section uses comprehensive laboratory tests to validate the accuracy and show the capabilities of the proposed converter. The elements are redesigned to operate optimally at a resonance frequency of 21 kHz, reflecting the modifications required by the frequency limitations of the TLP250 (IGBT) drivers. A thorough examination of the modified converter components is included below, along with the practical results of these testing.

5.1. Design and Parameters of the Converter

5.1.1. Inverter Section (Figure 1a and Table 6)

To improve durability and performance under higher operating demands, the inverter’s operational specifications include a 100 Vrms input at 50 Hz, power switches (FGH 60N60), and diodes arranged in triples (4007 μF).

Table 6. Values of the elements of the inverter section of the proposed converter (Figure 1a).

Characteristic or element	Values
V_ac	100 Vrms–50 Hz
L_b	740 μH
C_s1u − C_s2u − C_s1d − C_s2d	33 nF
C₁ − C₂	2.2 μF
f_s	21 kHz
Power transistors	FGH 60N60
Diodes	4007 μF⁻³ to parallel (instead of each diode)

5.1.2. Compensator Section (Figure 1b and Table 7)

The compensator, which uses precisely tuned inductors (L_f1 and L_f2) and capacitors (C_f1, C_f2, C₁, and C₂) to manage the power flow and quality across the system accurately, is essential to preserving system stability and efficiency.

Table 7. Values of elements of the compensator section of the proposed converter (Figure 1b).

Characteristic or element	Values
L_f1 − L_f2	230 μH
C_f1 − C_f2	560 nF
C₁ − C₂	500 nF
L₁ − L₂	360 μH

5.1.3. Output Section (Table 8 and Figure 1c)

A 100 Vdc output voltage across a 250 Ω load is one of the output characteristics that are crucial for assessing the converter’s practical application since it shows the converter’s capacity to maintain a steady output even when under load.

Table 8. Values of the elements of the output section (load equivalent circuit (Figure 1c).

Characteristic or element	Values
L_o	100 μH
C_o	470 μF
R_o	250 Ω
V_o	100 Vdc

Figure 15 shows the overview of the implemented wireless inductive power transmission system.

5.2. Crucial Performance Findings

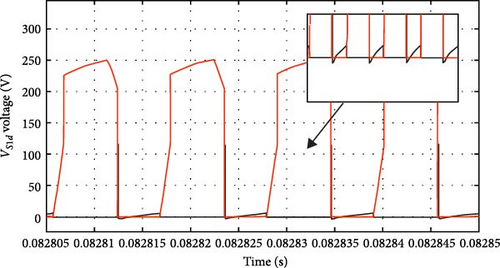
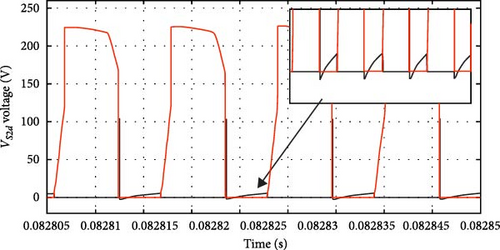
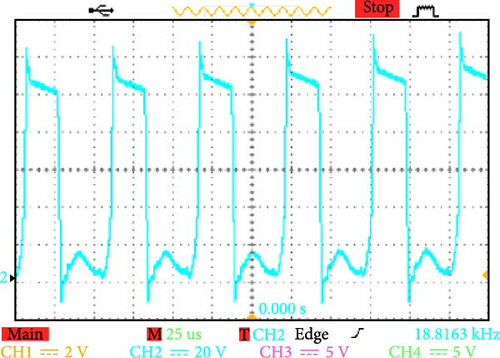
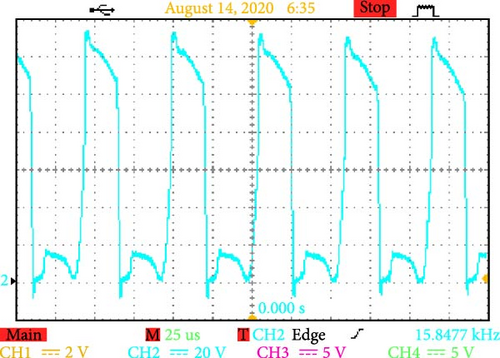
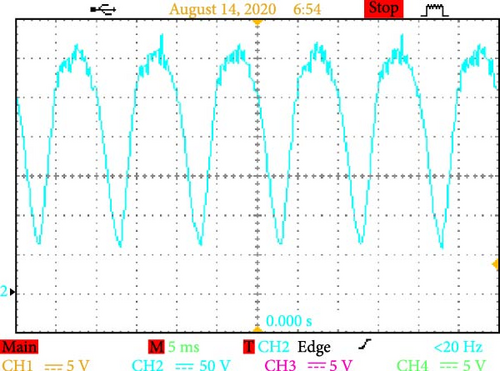
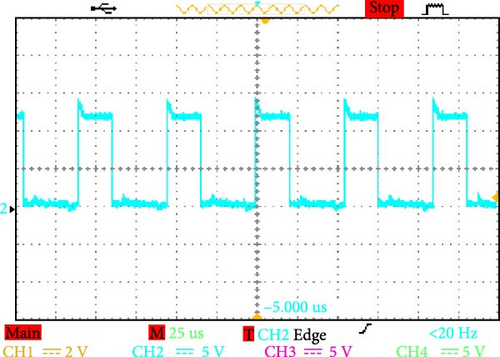
5.2.1. Dynamics of Voltage Waveforms (Figures 16a–d and 17a–d)

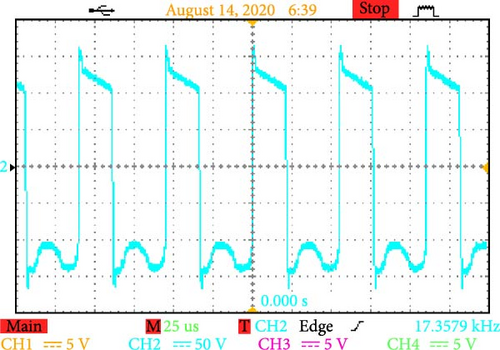
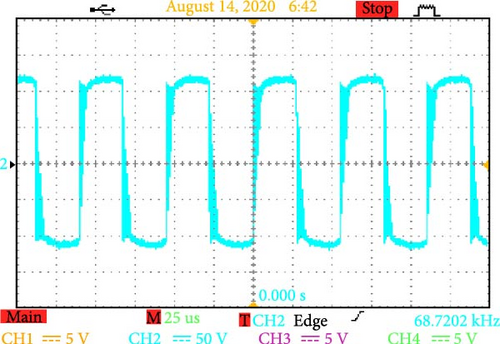
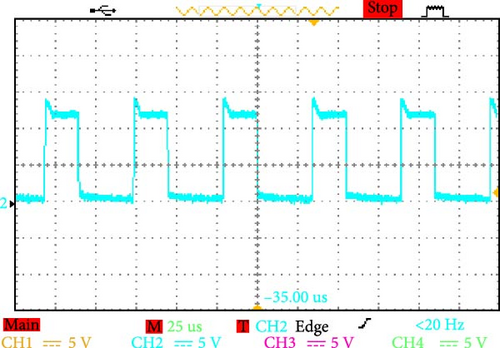
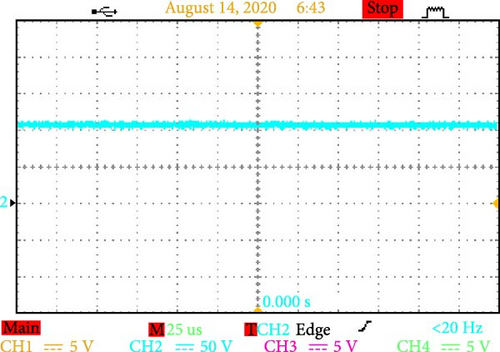
The converter can efficiently manage alternating voltage ranges, as evidenced by a detailed examination of the voltage across terminals AB and CD. It can also increase the working voltage in the DC connection to as high as 300 V (Figure 17a). These dynamics demonstrate how well the converter handles high-power applications and how resilient it is to operational stressors.

5.2.2. Charge Dynamics and System Efficiency (Figure 18a–d)

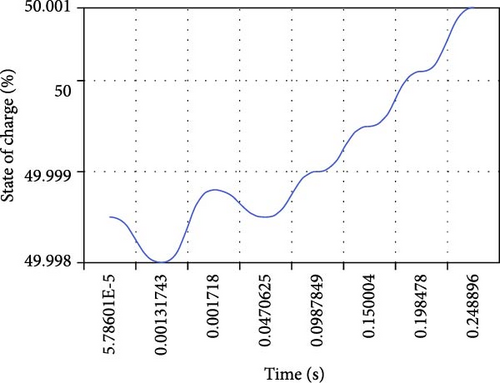
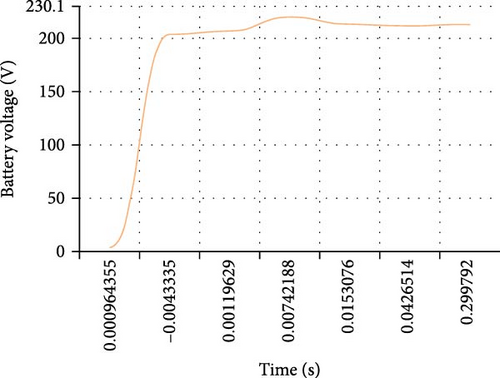
An evaluation is conducted on the converter’s performance under constant voltage and constant current charging conditions. The converter effectively controls the charging process, ensuring constant current and voltage levels for a battery with a capacity of 50 A.h and a full charge voltage of 215 V, as shown by Figure 18a–d. This demonstrates how well the system works in practical energy storage applications.

The laboratory assessments greatly improve our knowledge of the practical applications of the proposed converter by confirming its high efficiency and dependability. These outcomes validate the design improvements made to the converter and show its potential in commercial and industrial environments where reliability and effectiveness are critical. The laboratory data have been succinctly and clearly summarized in this part, which has been extended in response to prior requests for a more thorough and persuasive presentation of our results.

6. Conclusion

The working modes of the proposed converter were investigated considering a resonant load under different operating conditions. In order to reduce the losses and increase the efficiency of the system, the structure of the proposed converter is designed in such a way that the switches are disconnected and connected under soft switching conditions. As a result, the main losses of the converter are related to the conductive losses of the elements, and the converter provides an acceptable behavior in terms of efficiency in different power ranges. The calculations related to the compensation system and the output and input current values were presented. A closed loop control system was introduced to control output power or output voltage. Finally, the simulation and laboratory results of the manufactured sample were presented. Based on the analysis and simulation and laboratory results presented, the proposed wireless charger has the following advantages:

1.
Reducing the voltage stress of the input inverter switches
2.
Reducing the current of the power switches for constant output power compared to the half-bridge inverter without boost mode, due to the voltage increasing function
3.
No need for an input diode bridge
4.
High efficiency

While this work was on the power converter front of inductive EV charging, it does not fully realize real-world scenarios of variable magnetic coupling or coil geometrical issues. Optimization of inductor designs and their configurations is a suggested future work for realistic misalignment/coupling situations. Further work on increasing the scope to more integrated system analysis, looking into alternative inverter structures, and switching strategies will further improve the efficiency and scalability of the system.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Acharige S. S. G., Haque M. E., Arif M. T., Hosseinzadeh N., Hasan K. N., and Oo A. M. T., Review of Electric Vehicle Charging Technologies, Standards, Architectures, and Converter Configurations, IEEE Access. (2023) 11, 41218–41255, https://doi.org/10.1109/ACCESS.2023.3267164.
10.1109/ACCESS.2023.3267164
Web of Science® Google Scholar
2 Ullah I., Zheng J., and Jamal A., et al.EV Charging Infrastructure Planning: A Review, International Journal of Green Energy. (2023) 21, no. 7, 1710–1728.
10.1080/15435075.2023.2259975
Google Scholar
3 Patil H. and Kalkhambkar V. N., Grid Integration of EV for Economic Benefits: A Review, Journal of Modern Power Systems and Clean Energy. (2021) 9, no. 1, 13–26, https://doi.org/10.35833/MPCE.2019.000326.
10.35833/MPCE.2019.000326
CAS Google Scholar
4 Zand M., Alizadeh M., Nasab M. A., Nasab M. A., and Padmanaban S., Electric Vehicle Charger Energy Management by Considering Several Sources and Equalizing Battery Charging, Renewable Energy Focus. (2024) 50, https://doi.org/10.1016/j.ref.2024.100592, 100592.
10.1016/j.ref.2024.100592
Google Scholar
5 Alizadeh M., Tightiz L., and Azimi Nasab M., Providing an Intelligent Frequency Control Method in a Microgrid Network in the Presence of Electric Vehicles, World Electric Vehicle Journal. (2024) 15, no. 7, https://doi.org/10.3390/wevj15070276, 276.
10.3390/wevj15070276
Google Scholar
6 Mazumdar D., Biswas P. K., Sain C., Ahmad F., and Al-Fagih L., An Enhanced MPPT Approach Based on CUSA for Grid-Integrated Hybrid Electric Vehicle Charging Station, International Journal of Energy Research. (2024) 2024, no. 1, 14, https://doi.org/10.1155/2024/7095461, 7095461.
10.1155/2024/7095461
Google Scholar
7 Venkatesan R., Savio A. D., and Balaji C., et al.A Comprehensive Review on Efficiency Enhancement of Wireless Charging System for an EV Application, IEEE Access. (2024) 12, 46967–46994.
10.1109/ACCESS.2024.3378303
Google Scholar
8 Obaideen K., Albasha L., Iqbal U., and Mir H., Wireless Power Transfer: Applications, Challenges, Barriers, and the Role of AI in Achieving Sustainable Development Goals—A Bibliometric Analysis, Energy Strategy Reviews. (2024) 53, https://doi.org/10.1016/j.esr.2024.101376, 101376.
10.1016/j.esr.2024.101376
Google Scholar
9 Sari V., Design and Implementation of a Wireless Power Transfer System for Electric Vehicles, World Electric Vehicle Journal. (2024) 15, no. 3, https://doi.org/10.3390/wevj15030110, 110.
10.3390/wevj15030110
Google Scholar
10 Vinod M., Kishan D., Kannan R., Iqbal A., and Sulthan S. M., Primary Side Control Strategies for Battery Charging Regulation in Wireless Power Transfer Systems for EV Applications, 2024, IET Power Electronics.
10.1049/pel2.12639
Google Scholar
11 Zhu L., Sheng Z., Peng F., and Yang L., Control Strategy of Half-Bridge Three-Level LLC Resonant Converters With Wide Output Voltage Range, IEEE Transactions on Plasma Science. (2022) 50, no. 11, 4381–4386, https://doi.org/10.1109/TPS.2022.3176852.
10.1109/TPS.2022.3176852
Google Scholar
12 Vu V.-B., Ramezani A., and Triviño A., et al.Operation of Inductive Charging Systems Under Misalignment Conditions: A Review for Electric Vehicles, IEEE Transactions on Transportation Electrification. (2023) 9, no. 1, 1857–1887, https://doi.org/10.1109/TTE.2022.3165465.
10.1109/TTE.2022.3165465
Web of Science® Google Scholar
13 Sagar A., Kashyap A., and Nasab M. A., et al.A Comprehensive Review of the Recent Development of Wireless Power Transfer Technologies for Electric Vehicle Charging Systems, IEEE Access. (2023) 11, 83703–83751, https://doi.org/10.1109/ACCESS.2023.3300475.
10.1109/ACCESS.2023.3300475
Web of Science® Google Scholar
14 Benalia N., Benlaloui I., and Laroussi K., et al.Enhancing Electric Vehicle Charging Performance Through Series-Series Topology Resonance-Coupled Wireless Power Transfer, PLOS ONE. (2024) 19, no. 3, e0300550.
CAS PubMed Google Scholar
15 Hidayah B. O., Suryoatmojo H., and Pamuji F. A., Wireless Power Transfer in EV Using Single Phase Matrix Converter, International Seminar on Intelligent Technology and Its Applications (ISITIA), 2023, IEEE, 744–748.
Google Scholar
16 Tasnim M. N., Riana J. M., and Shams T., et al.A Critical Review on Contemporary Power Electronics Interface Topologies to Vehicle-to-Grid Technology: Prospects, Challenges, and Directions, IET Power Electronics. (2024) 17, no. 1, 157–181, https://doi.org/10.1049/pel2.12618.
10.1049/pel2.12618
Google Scholar
17 Mathuria K., Singh A., Sandeep N., Verma A. K., Prakash P. S., and Tiwari H., Introduction to EV Charging Systems, Advanced Concepts and Technologies for EV, 2024, CRC Press, 21–40.
Google Scholar
18 Foote A., Costinett D., Kusch R., Mohammad M., and Onar O., Fourier Analysis and Loss Modeling for Inductive Wireless Electric Vehicle Charging With Reduced Stray Field, IEEE Transactions on Transportation Electrification. (2024) 10, no. 4, 8771–8789, https://doi.org/10.1109/TTE.2024.3363612.
10.1109/TTE.2024.3363612
Google Scholar
19 Jiang C. Q., Long T., and Gaona D. E., Wireless Power Transfer for Electric and Hybrid EV, Emerging Technologies for Electric and Hybrid Vehicles, 2024, Springer Nature Singapore, Singapore, 289–320.
10.1007/978-981-99-3060-9_10
Google Scholar
20 Zhang M., Deng S., Lu J., Zheng D., and Yang N., A Novel Fault-Tolerant Multilevel Inverter With Preserved Output Integrity Under Post-Fault, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2024) 12, no. 2, 1793–1802, https://doi.org/10.1109/JESTPE.2024.3358870.
10.1109/JESTPE.2024.3358870
Google Scholar
21 Zhou Z., Xue L., Li C., and Geng Q., A Spread-Spectrum Modulation Scheme for a 3×6 Indirect Matrix Converter Based on a Current Ripple Model, Energies. (2024) 17, no. 11, https://doi.org/10.3390/en17112546, 2546.
10.3390/en17112546
Google Scholar
22 Feng H., Tavakoli R., Onar O. C., and Pantic Z., Advances in High-Power Wireless Charging Systems: Overview and Design Considerations, IEEE Transactions on Transportation Electrification. (2020) 6, no. 3, 886–919, https://doi.org/10.1109/TTE.2020.3012543.
10.1109/TTE.2020.3012543
Web of Science® Google Scholar
23 Amjad M., Farooq-i-Azam M., Ni Q., Dong M., and Ansari E. A., Wireless Charging Systems for Electric Vehicles, Renewable and Sustainable Energy Reviews. (2022) 167, https://doi.org/10.1016/j.rser.2022.112730, 112730.
10.1016/j.rser.2022.112730
Web of Science® Google Scholar
24 Abbas H. H., Shafiee Q., and Bevrani H., Optimal Passive LCL Filter Design for Grid-Connected Converters in Weak Grids, Electric Power Systems Research. (2024) 235, https://doi.org/10.1016/j.epsr.2024.110896, 110896.
10.1016/j.epsr.2024.110896
Google Scholar
25 Ali R., Heydari-doostabad H., Sajedi S., and O’Donnell T., Improved Design of Passive Damping for Single Phase Grid-Connected LCL Filtered Inverter Considering Impedance Stability, 2024, IET Power Electronics.
10.1049/pel2.12666
Google Scholar
26 Mohammed S. A. and Jung J. W., A Comprehensive State-of-the-Art Review of Wired/Wireless Charging Technologies for Battery EV: Classification/Common Topologies/Future Research Issues, IEEE Access. (2021) 27, no. 9, 19572–19585.
10.1109/ACCESS.2021.3055027
Google Scholar
27 Mastoi M. S., Zhuang S., and Munir H. M., et al.An in-Depth Analysis of Electric Vehicle Charging Station Infrastructure, Policy Implications, and Future Trends, Energy Reports. (2022) 8, 11504–11529, https://doi.org/10.1016/j.egyr.2022.09.011.
10.1016/j.egyr.2022.09.011
Web of Science® Google Scholar
28 Pugi L., Reatti A., and Corti F., Application of Wireless Power Transfer to Railway Parking Functionality: Preliminary Design Considerations With Series-Series and LCC Topologies, Journal of Advanced Transportation. (2018) 2018, no. 1, 14, https://doi.org/10.1155/2018/8103140, 2-s2.0-85059962624, 8103140.
10.1155/2018/8103140
Google Scholar

Citing Literature

All articles

Novel AC–AC Converter Design for High-Efficiency Wireless Electric Vehicle Charging Systems

Abstract

1. Introduction

2. The Structure of the Proposed Wireless EV Charger

2.1. The Suggested Inverter’s Structure

2.2. Working Fashions

2.3. Working Modes of the Proposed Converter in the Positive Half Cycle of the Input

2.3.1. The First Work Mode

2.3.2. The Second Method

2.3.3. Third Operating Mode

2.3.4. Fourth Operating Mode

2.3.5. Fifth Operating Mode

2.3.6. Sixth Grade

2.4. Working Modes of the Proposed Converter in the Positive Half Cycle of the Input

2.4.1. The Initial Operational Mode

2.4.2. Second Working Mode

2.4.3. Third Working Mode

2.4.4. Fourth Grade

2.4.5. Fifth Working Mode

2.4.6. Sixth Working Mode

3. Necessary Conditions for Establishing ZVS With the External Snubber Capacitor of the Keys

3.1. LCC Compensation System

3.2. Rectifier System and Output Filter

3.3. Design of Inductor

3.4. Designing Circuit Parameters of Compensator

3.5. Proposed Converter Control System

3.6. Output Equivalent Circuit From Inverter Point of View

3.7. Winding Design

4. Simulation

4.1. Simulation Results of the Proposed Wireless Charging System

4.2. Checking the Performance of the Proposed Converter Control System

5. Laboratory Sample Results

5.1. Design and Parameters of the Converter

5.1.1. Inverter Section (Figure 1a and Table 6)

5.1.2. Compensator Section (Figure 1b and Table 7)

5.1.3. Output Section (Table 8 and Figure 1c)

5.2. Crucial Performance Findings

5.2.1. Dynamics of Voltage Waveforms (Figures 16a–d and 17a–d)

5.2.2. Charge Dynamics and System Efficiency (Figure 18a–d)

6. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information