International Journal of Energy Research
Volume 2025, Issue 1 8862345
Research Article
Open Access

Multicriteria Decision-Making Evaluation of Blade Element Momentum Theory Algorithms for Optimal Design of Small-Scale HAWT Blades

Belayneh Yitayew Kassa, 

Belayneh Yitayew Kassa

Department of Mechanical Engineering , Addis Ababa Science and Technology University , P.O Box 16417 , Addis Ababa , Ethiopia , aastu.edu.et

Sustainable Energy Center of Excellence , Addis Ababa Science and Technology University , P.O Box 16417 , Addis Ababa , Ethiopia , aastu.edu.et

Department of Automotive Engineering , Arba Minch University , P.O Box 21 , Arba Minch , Ethiopia , amu.edu.et

Search for more papers by this author
Aklilu Tesfamichael Baheta, 

Aklilu Tesfamichael Baheta

Department of Mechanical Engineering , Addis Ababa Science and Technology University , P.O Box 16417 , Addis Ababa , Ethiopia , aastu.edu.et

Sustainable Energy Center of Excellence , Addis Ababa Science and Technology University , P.O Box 16417 , Addis Ababa , Ethiopia , aastu.edu.et

Search for more papers by this author
Asfaw Beyene, 

Corresponding Author

Asfaw Beyene

Department of Mechanical Engineering , San Diego State University , San Diego , California , 92182-1323 , USA , sdsu.edu

Search for more papers by this author
First published: 20 May 2025
https://doi.org/10.1155/er/8862345
Academic Editor: Olubayo Babatunde

Abstract

Several blade element momentum theory (BEMT) algorithms have been employed for the design and analysis of wind turbine rotors with varying effectiveness in optimizing the design, weight, performance, and cost. However, the optimal selection of BEMT algorithm for small wind turbines (SWTs) remains an area of ongoing research. This study presents a comprehensive comparison of five selected BEMT algorithms, evaluating their influence on blade geometry and performance across tip-speed ratios (TSRs) ranging from 0.01 to 20. A multicriteria decision-making (MCDM) approach was employed to assess the algorithms based on criteria including power output, power coefficient (Cp), thrust coefficient (CT), manufacturability (Mnf), blade weight, and cost of material (CM). The results demonstrate that both the TSR and the chosen BEMT algorithms significantly impact wind turbine performance. The maximum Cp of 0.569 was achieved at a TSR of 5.5 using the Jha algorithm. The MCDM analysis revealed that power output, Cp, and CT were assigned weights of 0.25, 0.22, and 0.16, respectively, while Mnf, weight, and CM received weights of 0.13, 0.12, and 0.12. This indicated that power output and Cp are the more desirable criteria for selecting suitable BEMT algorithms for SWTs. Among the tested algorithms, the Jha and Manwel methods exhibited superior performance across all TSRs. The MCDM analysis further identified the Jha and Ingram algorithms as the top-ranked options, with appraisal scores of 3.27 and 2.63, respectively. These findings provide valuable insights for the design and optimization of SWT blades, potentially leading to enhanced efficiency and performance.

1. Introduction

In recent times, researchers have devoted substantial attention to large wind turbines [1]; however, these turbines present several limitations that restrict their applicability in certain contexts. Notably, large wind turbines are often unsuitable for off-grid and stand-alone applications and their efficiency tends to diminish under low wind conditions [2]. Additionally, the installation and maintenance costs associated with large turbines can be prohibitively high.

In contrast, small wind turbines (SWTs), turbines with an output power of 40 kW or less, offer a viable alternative. These smaller units can be interconnected to create a larger power output, effectively addressing the limitations faced by larger turbines. One of the primary advantages of SWTs is their suitability for residential installations, which significantly reduces energy transmission and distribution losses for consumers [3]. Furthermore, SWTs generally have a subtle appearance and generate less noise than their larger counterparts, making them more acceptable in various settings. This explains the growing global interest and justifies our research interest in the advance of SWTs.

When appropriately sized and deployed in optimal conditions, SWTs can provide a reliable energy source. They hold considerable promise as a financially viable energy solution, particularly in developing nations where access to grid power may be limited. While SWTs have the potential to provide a reliable energy source for remote areas in even developed countries, their future growth is significantly impacted by the cost of manufacturing these devices. To fully realize the potential of this promising technology, it is essential to optimize several key factors, including the power coefficient (Cp), overall system efficiency, manufacturing costs, and weight of the turbines. By addressing these aspects, the SWT sector can enhance its competitiveness and contribute significantly to sustainable energy solutions.

Recent studies have shown that wind turbines often operate at Cp between 0.2 and 0.45 [4], indicating significant room for improvement. Enhancing the efficiency of these turbines is crucial for economic viability and reducing reliance on traditional energy sources. The aerodynamic performance (ADP) of SWTs plays a pivotal role in determining their overall efficiency.

To optimize ADP, researchers have explored various design parameters and optimization techniques. Blade element momentum theory (BEMT) has emerged as a foundational tool in understanding and predicting the aerodynamic behavior of wind turbine blades (WTBs). Initially proposed by Glauert [5] in 1926, BEMT combines blade element theory and momentum theory (MT) to provide a systematic approach to analyzing blade aerodynamics. BEMT discretized WTBs into elemental sections and applied fundamental principles of fluid mechanics, including conservation of mass and momentum to solve for aerodynamic forces like lift, drag, and torque. This theory assumes steady, inviscid, and incompressible fluid flow without variations in radial or circumferential directions [6]. By understanding these aerodynamic parameters, engineers can design and optimize WTBs for improved efficiency and performance.

The elegance of BEMT lies in its ability to strike a balance between accuracy and computational efficiency. By treating each blade section as an isolated entity, BEMT allows for a detailed examination of the aerodynamic forces influencing turbine performance without resorting to computationally intensive simulations. This balance has made BEMT a go-to tool for researchers and engineers striving to predict and enhance the performance of WTBs across various scales.

The historical development of BEMT algorithms mirrors the evolution of wind energy research itself. From early conceptualizations that laid the foundation for understanding the fundamentals of wind turbine aerodynamics to contemporary algorithms that leverage computational advancements, the journey of BEMT is marked by a relentless pursuit of precision and applicability.

While BEMT has been extensively utilized for wind turbine rotor design and performance evaluation, its accuracy limitations become apparent in regions of low tip-speed ratios (TSRs) and high angle of attack (AOA), where stalls occur. The presence of blade surface wakes further hinders the data reliability in these operating conditions [7]. To address these shortcomings, researchers have proposed various improvements to BEMT [8, 9].

One common approach is to introduce tip loss corrections to incorporate the effect of vortices generated at the blade tips. Prandtl [10], Glauert [5], Wood et al. [11], Zhong et al. [12], Maniac and Schimtz [13], and others have implemented tip loss models in their BEMT formulations. Sun et al. [14] further refined the model by considering the effects of wake rotation and radial velocity.

Beyond tip loss, other corrections have been explored to improve BEMT accuracy. Glauert [5], Shen et al. [15], Spera [16], Wilson et al. [17], and Buhl [18] have proposed empirical corrections for high induction factors. Pitt and Peters’ [19] skewed wake correction addresses the influence of yaw angles, while Snel et al.’s [20] 3D correction accounts for lift augmentation due to rotation. Viterna and Corringan’s [21] poststall angle correction specifically targets the stall region.

By considering these corrections independently or in combination, researchers have developed numerous BEMT algorithms tailored for horizontal axis wind turbine design and analysis. These modifications aim to improve BEMT’s accuracy and reliability, particularly in challenging operating conditions [22, 23].

In this landscape of evolving BEMT based blade design algorithms, a critical need arises for a comprehensive comparative analysis. The plethora of algorithms available to researchers and practitioners demands a nuanced understanding of their relative strengths and weaknesses, particularly in the context of small-scale horizontal axis wind turbines (SSHAWTs). While individual studies have contributed valuable insights into specific algorithms, a holistic examination that systematically compares multiple algorithms is essential. In this regard, Batu and Lemu [24] and Oleveira et al. [25] attempted to examine how the BEMT based computation methods affect the design and performance of the WTB. The former proposed four BEMT algorithms for wind turbine application (CT). However, the study could not include additional criteria such as weight, cost, thrust coefficient, et cetera, to examine the algorithm’s effectiveness in optimal design of wind turbines. Moreover, two recent algorithms, namely: Jha [7] and Oliveira et al. [25] have not been included in the previous studies and included in this study.

Whereas the latter study compares the correction methods applied to BEMT to evaluate their accuracy in predicting the performance of different size of two bladed wind turbines (small, medium, and large) and using the literature data develop a better algorithm which has good prediction accuracy. But the model’s performance was not evaluated for three-bladed wind turbines. Furthermore, the effect of TSR, especially at low TSRs, on the geometry and ADP of SWTs has not been studied so far.

The study by Batu and Lemu [24] reported that the blade geometry and its performance is highly dependent on these algorithms. Some algorithms yield good design, weight, and performance, while others give complex shapes, large weight, and low performance. Therefore, there is a need for identifying a BEMT algorithm most suitable to grant low weight, low cost, superior performance, uncomplicated manufacturability (Mnf), et cetera.

The complexity of selecting the most suitable BEMT algorithm for SSHAWT design necessitates a more sophisticated approach than traditional algorithm selection methods. Multi-criteria decision-making (MCDM) techniques offer a structured framework for evaluating and ranking alternatives based on multiple criteria. By identifying relevant criteria, assigning weights to them, and evaluating candidate algorithms, MCDM can assist in determining the optimal choice for ensuring the highest level of design target [26–28].

Several MCDM algorithms have been successfully employed in various fields, including renewable energy [29–31]. technique for order of preference by similarity to ideal solution (TOPSIS), analytic hierarchy process (AHP), VIekriterijumsko KOmpromisno Rangiranje (VIKOR), weighted aggregates sum product assessment (WASPAS), and combined compromised solution (CoCoSo) are among the commonly used methods. CoCoSo, in particular, has gained popularity due to its user-friendly nature and straightforward computational process [32–34]. Additionally, the FUCOM method can be utilized to determine the relative importance or weights of the criteria [32–34].

While MCDM has been applied to various domains, its application to the selection of BEMT algorithms for WTB design remains relatively unexplored. This research aims to bridge this gap by comprehensively evaluating BEMT algorithms for designing, predicting and improving the ADP of three-bladed SSHAWTs. By employing a MCDM approach, this study seeks to identify the most suitable algorithm that aligns with the specific requirements of SSHAWTs, considering factors such as Mnf, weight, and material cost-effectiveness. This integrated approach has the potential to contribute to more efficient and robust design solutions for SSHAWT blades.

The rationale behind such a comparative and MCDM analysis extends beyond academic curiosity. It is rooted in the practical need to guide engineers, designers, and decision-makers towards the most effective BEMT algorithm for their specific applications. SSHAWTs, with their diverse deployment scenarios, require tailored solutions, and the choice of BEMT algorithm, plays a crucial role in shaping the efficacy of these solutions.

2. Methodology

This research employed a MCDM, a comprehensive and structured approach, to thoroughly evaluate the effectiveness of selected BEMT algorithms in optimizing the critical factors of SSHAWTs. The overall procedure of this research was guided by a systematic framework comprising five key steps, to ensure a thorough evaluation of the selected BEMT algorithms.

It begins with the selection of appropriate BEMT algorithms tailored for SWTs; second, the identification and selection of performance criteria that encompass technical, economic, and operational aspects; third, the performance evaluation of these algorithms across the selected criteria, with particular emphasis on ADP, cost, Mnf, and weight; fourth, a comparative analysis using a MCDM framework to systematically rank the algorithms; and finally, a sensitivity analysis to assess the robustness of the selected algorithms under varying criteria weights.

In this case, the performance of these algorithms over ADP criterion were evaluated at various TSRs ranging from 0.5 to 20 to explore the effect of these algorithms on the geometric (i.e., chord length and twist angle distribution) and ADP of wind turbines operating under low TSRs. Then, performance of these algorithms under six criteria was evaluated at a TSR of 5.5 due to its optimized TSR. The detailed procedures are discussed in the upcoming sections.

By adopting this multifaceted approach, the study aimed to provide a detailed understanding of the strengths and limitations of each BEMT algorithm, ultimately informing the design of efficient and effective SWTs.

2.1. Overview of BEMT and Selection of Bladed Design Algorithms

The design and performance prediction of WTBs has long been done using the BEMT [6]. This theory aims to establish mathematical relations that characterize the interaction between the flow and the turbine. It solves the aerodynamic forces acting on the blade, presented in Figure 1, along with different ADP parameters such as, CT, Cp, thrust force, and power output.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Wind velocities and forces on the airfoil in a blade section [35].
The classical BEMT model proposed by Glauert consists of a system which links together three variables a, a’, and ω associated with a ring of fluid. They are defined by the Equations (1)–(3).
(1)
(2)
(3)
where a, a′, U0, ω, Ω, φ, and λr are the axial induction factor (AIF), tangential induction factor (TIF), free stream velocity, rotational speed of the ring of fluid, angular speed, inlet flow angle, and the local TSR, respectively.
The twist angle (θ), angle between the blade’s chord line and rotational plane is utilized to calculate the AOA as described in Equation (4).
(4)
The relative wind speed (Urel) on the rotating blade can be also determined from the free stream velocity, AIF, and TIF using Equation (5).
(5)
For a given blade profile, the aerodynamic forces such as, the lift coefficient (Cl) and drag coefficients (Cd) are evaluated using Equations (6) and (7).
(6)
(7)
where dL, dD, ρa, c, and dr are the elemental lift force, elemental drag force, density of air, local chord of an airfoil, and thickness of a blade element, respectively.
According to the fundamental principle of MT, the normal force (dFn) and tangential force (dFt) acting on the WTB can be determined from the axial and angular momentum depicted in Equations (8) and (9), respectively [36].
(8)
(9)
where U, ρ, and Ω represent the free stream velocity, air density, and angular speed, respectively.
The total thrust (dT) and torque (dQ) for a B-bladed WTB can be determined from Equations (10) and (11), respectively.
(10)
(11)
The first BEMT theory utilizes the following relationships, outlined in Equations (12)–(20), to design and evaluate the ADP of a rotor.
(12)
(13)
(14)
(15)
(16)
The ADP of a wind turbine rotor, characterized by Cp and CT can be determined as:
(17)
(18)
where ρ, A, and V, respectively, denote the air density (kg/m3), rotor area (m2), and wind velocity (m/s).
The local thrust coefficient (Ct,r) and power coefficient (Cp,r) can be evaluated as follows:
(19)
(20)
where φ is the flow angle, λr is the local TSR determined using Equation (15), and σ is the local solidity determined using Equation (16).

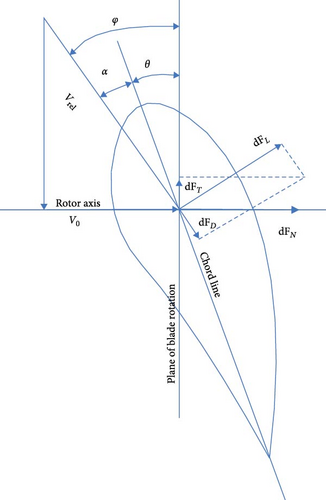
Following a classical BEMT, many scholars introduced various BEMT corrections, such as tip loss correction, poststall correction, and induction factor corrections to improve the accuracy of the BEMT. As a result, many algorithms have been introduced for the design and analysis of SWTs which are the focus of this study.

In some of the algorithms, the lift force reduction caused by airflow surrounding the blade tip was taken into account by using the Prandtl [10] tip loss correction model, F described in Equation (21).
(21)
where Fh and Ft are the hub and tip losses from vortices and can be calculated using Equations (22) and (23), respectively.
(22)
(23)
where R, rh, and r are the rotor radius, sectional radius, and hub radius, respectively.
Whereas, the high stall angle was corrected using the model proposed by Vieterna and Corringan [21] which was defined in Equations (22) and (23).
(24)
(25)
where Cds and Cls are the drag coefficient and lift coefficient at stall angle (αs). Cd,max is the maximum drag coefficient of airfoil at 90° that can be evaluated using Equation (24).
(26)
Conversely, the high induction factor, a > 1/3, was corrected using the correction model proposed by Shen et al. [15], which is calculated using the Equations provided in Equations (25) and (26).
(27)
(28)
where γ1 and γ2 are intermediate functions, which are evaluated using Equations (27) and (28), respectively.
(29)
(30)
Besides the Shen correction, Glauert’s empirical model was applied to BEMT to correct the induction factor for a CT,i > 0.96. Thus, the new values of the AIF and TIF were determined using Equations (31) and (32). This step involves a set of iterative processes and it will continue until convergent values of a and a′ are obtained. In this case, a tolerance value of 0.001 is set to check their convergence.
(31)
(32)
Furthermore, the Wilson and Walker empirical model highlighted in Equations (33) and (34) was applied to BEMT to correct the induction factor for a ai,n > ac(i.e., ac = 0.2).
(33)
(34)
where φ is the inlet flow angle, α is the AOA, β is the blade pitch angle, a is the AIF, a′ is the TIF, λr and λd are the local and design TSR, r is the sectional blade radius, B is the number of blades, n is the number of blade sections, Cld, is the design lift coefficient, Cdd is the design drag coefficient, Vd is the design flow velocity, Vw is the local angular speed, Vrel is the local resultant air velocity, Cn is the normal force coefficient of a blade, is the mass flow through the bare wind turbine, and is the mass flow through the ducted wind turbine.

Following the BEMT corrections, various formulae and algorithms have been introduced to determine the sectional chord and flow angle of the WTB to improve the performance of the rotor as discussed in [4].

Among these algorithms, a set of representative BEMT algorithms commonly employed in predicting and optimizing the ADP of WTBs were identified. Algorithms such as the Jha et al. [7], Oliveira et al. [25], Ingram [37], Manwell et al. [35], and Hansen [38] were considered based on their prevalence in the literature and industry applications. Then, these sets of algorithms that capture BEMT correction were compared to rank the alternatives based on the selected criterion. The criterion includes power output, power coefficient, thrust coefficient, weight of blade, Mnf, and material cost of the blade.

In this research, the wind turbine rotor designed by Chen et al. [39] is used as a reference geometry. However, SG6043 airfoil was used instead for modeling the wind turbine due to its suitability for SWTs [40]. The detailed description of these wind turbines is summarized in Table 1.

Table 1. Blade parameters.
Parameters Values
Rated power (W) 400
Blade length (m) 0.65
Blade root radius (m) 0.07
Rated wind speed (m/s) 12
Airfoil type SD-8000 for verification and SG6043 for this research
Number of blades 3
TSR 5.5
AOA (°) 5

Once the representative BEMT algorithms and reference geometry of a wind turbine rotor are selected, the BEM algorithms are implemented to determine the shape of the selected WTB and evaluate its performance. Then, we compared the algorithmic effectiveness with established criteria in designing a SSHAWT.

2.1.1. Ingram [37] Algorithm

The first algorithm was proposed by Ingram [37] and the algorithm utilized the Prandtl’s [10] loss correction factor described in Equation (22) to correct the BEMT model. According to this algorithm, the design lift coefficient (Cld) was taken as 80% of max(Cl). But other algorithms take the value of Cld as the Cl at corresponding optimum AOA. The drag induced to the airfoil and wake behind the turbine were not also considered in this algorithm. Moreover, the inlet flow angle (φ) at initial condition is determined using Equation (35) and later updated using Equation (38). Then the induction factors were initially determined using Equation (37) and finally updated using Equation (39). The sectional chord was evaluated using Equation (36). These make the algorithm to be odd from other algorithms. Specifically, the detailed procedures used for the design and performance analysis of a WTB can be referred to in [37].
(35)
(36)
(37)
(38)
(39)

2.1.2. The Hansen [38] Algorithm

The Hansen [38] algorithm on the other hand has been modified by incorporating the Prandtl’s [10] tip loss and Glauert’s [5] correction factor defined in Equations (22), (33), and (34) to correct the assumption of infinite number of blades and the high AIF (a > 1/3), respectively. Following these corrections, the Hansen algorithm modified the formula that calculates the sectional twist angle (ϕ) and chord (C) as illustrated in Equations (40) and (41). The detailed algorithm used for the design and performance analysis of a WTB is discussed in [38].
(40)
(41)

2.1.3. Manwell et al. [35] Algorithm

The third algorithm was Manwell et al. [35] algorithm. The algorithm incorporated Prandtl’s tip loss correction factor and Glauert’s IF correction method to improve the BEMT model. According to this algorithm, the design lift coefficient (Cld) was taken as the Cl at corresponding optimum AOA. Moreover, the AIF and TIF were assumed to be 1/3 and 0, respectively, to determine the inlet flow angle (φ) at initial condition using Equation (36). Then, the induction factors were updated using Equation (43). The sectional chord was also evaluated using Equation (42). These make the algorithm to be odd from other algorithms. Specifically, the detailed procedures used for the design and performance analysis of a WTB can be referred to in [35].
(42)
(43)

2.1.4. Jha et al. [7] Algorithm

Similar to Algorithm 3, the algorithm proposed by Jha et al. [7] combines the correction of Prandtl’s tip loss and Glauert’s induction factor to design and analyze the WT. Unlike Algorithms 1–3, in this algorithm, the formulae used to calculate the induction factors, chord length, and inlet flow angle were unique. For example, the initial inlet flow angle at each section of the blade was determined using Equation (44). The AIF and TIF were initially calculated from the inlet flow angle using Equation (46) and updated using Equations (31) and (32) following the Prandtl’s tip loss and Glauert’s correction model were applied in the model. Whereas the sectional chord was evaluated using Equation (42). These make the algorithm to be odd from other algorithms. Specifically, the detailed procedures used for the design and performance analysis of a WTB can be referred to in [7].
(44)
(45)
Then, the ith section flow angle of the blade at the nth iteration, φi,n was evaluated using the new induction factors based on Equation (46).
(46)

2.1.5. Oliveira et al. [25] Algorithm

The algorithm proposed by Oliveira et al. [25] improved the classical BEMT algorithm by integrating the Prandtl’s correction of tip loss, Shen et al. [15] correction of induction factor, and Viterna with Corrigon’s correction of high stall angle [21] to design and analyze the WT. Specifically, the detailed procedures used for the design and performance analysis of a WTB can be referred to in [25].

In this algorithm, the sectional flow angle (φi) and sectional chord (Ci) can be calculated using Equations (42) and (46). This step involves a set of iterative processes and it will continue until convergent values of a′ and a′ are obtained. In this case, a tolerance value of 0.001 is set to check their convergence. In this case, for α > αs, the Cl,i and Cd,i were corrected using the model proposed by Viterna and Corrigan [21] which was defined in Equations (22) and (23).

2.2. MCDM for Selecting Suitable Blade Design Algorithms for SWT

Following the algorithm identification, this research applied a MCDM approach to determine the criteria weights and evaluate the various BEMT algorithms across the selected criteria. In this specific study, six criteria were selected to compare the BEMT algorithms and assess their suitability for WTB design. These criteria include power output, power coefficient, thrust coefficient, blade weight, Mnf, and material cost. These criteria were chosen based on their relevance and significance in WTB design, as they provide a holistic view of the blade’s performance, structure, cost, and feasibility.

The turbine’s power coefficient (Cp), thrust coefficient (CT) were calculated based on Equations (17)–(20) using MATLAB, a widely used programming language in engineering and scientific computations. The Pout was evaluated using QBlade, an open-source wind turbine simulation software, at a wind speed of 12 m/s. This wind speed was chosen as it is typical rated wind speed for modern wind turbines and provides a realistic and relevant scenario for the analysis.

The blade weight (W) was calculated using the formula provided in Equation (47), which considers the density of the blade material (ρm = 1280 kg/m3), assumed to be epoxy fiberglass, and the blade volume (VolB). The material cost for each blade was computed by multiplying the blade mass (mB) with the price of glass fiber (P = $0.5/kg), providing an estimate of the cost-effectiveness of the different algorithms.
(47)

Mnf, being a qualitative term, was evaluated using a seven-point Likert scale, ranging from 1 (Extremely Difficult) to 7 (Extremely Easy) to manufacture. This scale was chosen as it provides a simple and intuitive way to assess the Mnf of the blade designs, a widely used approach in engineering and design practice. Additionally, root mean square error (RMSE) analysis was employed to gain insights into the complexity of the geometries associated with these algorithms. The RMSE analysis is a statistical method that measures the difference between predicted and actual values, commonly used to evaluate the accuracy and precision of models and simulations. The RMSE values offer a quantitative measure to evaluate how closely the fitted linear equations, obtained using the curve fitting toolbox in MATLAB, align with the actual chord distributions derived from various BEMT algorithms at 5.5 TSR. In this study, lower RMSE values indicate simpler geometries, which are easier and more cost-effective to manufacture, while higher values suggest increased complexity and variability.

2.2.1. Determining Criteria Weight Using FUCOM Method

After identifying the evaluation criteria, the FUCOM was employed to establish their relative importance and weights. This method was selected for its ability to validate the model through the calculation of the deviation from full consistency (DFC) metric. FUCOM is a subjective-based MCDM procedure that relies on pairwise comparisons and ensures consistency in the assigned weights. This widely recognized approach is well-suited for determining the weights of criteria in complex decision-making scenarios. By systematically evaluating each criterion against a set of predefined indicators, FUCOM provides a comprehensive assessment of their relevance to the overall decision [41]. It offers several advantages over other methods, including the requirement of fewer pairwise comparisons and its ability to accurately calculate weight coefficients, enhancing the validity of decision-making [42, 43]. The following steps outline the procedures for determining the criteria weights using FUCOM.

2.2.1.1. Step 1: Criteria Ranking and Comparative Priority Assessment

The evaluation criteria (C1, C2, C3, …, Cn) were ranked based on their relative importance, as depicted in Equation (48).
(48)

In this paper, after gathering information from the experts on the relative importance of each criterion for wind turbines, the criteria were ranked as depicted in Table 2.

Table 2. Ranking and comparative priority assessment of criteria weights.
Criterion C1 C2 C3 C4 C5 C6
Pout Cp CT Mnf W CM
Rank 1 2 3 4 5 5
Comparative priority 2 2.35 3.18 4.15 5.4 5.4
The comparative priority of each criterion (φ(k/k + 1)) was evaluated using Equation (49), where k is the rank of the criterion.
(49)

2.2.1.2. Step 2: Weight Coefficient Determination

The weight coefficients (ωj) for each criterion were determined by ensuring they satisfy the conditions of proportionality and mathematical transitivity presented in Equations (50) and (51), respectively. So that full consistency, that is, DFC(x) = 0 is satisfied.
(50)
(51)

These conditions can be fulfilled if the value of the weight coefficients meet the condition of and with the minimization of x.

2.2.1.3. Step 3: Solving Optimization Problem

To determine the optimal criteria weights, the following optimization problem highlighted in Equation (52) was solved.
(52)
When substituting the comparative priority values, Equation (52) can be reduced to Equation (53):
(53)
where ωj is the weight for the jth criterion, Xij is the normalized score of the ith airfoil for the jth criterion.

2.2.2. Selecting BEMT Algorithms Using the CoCoSo Method

Once the weights of each criterion were determined, the CoCoSo method, developed by Yazdani et al. [44] in 2018 was employed to select suitable BEMT algorithms for WTB design. This method integrates simple additive weighting and exponentially weighted product model (WPM) approaches to identify compromise solutions that effectively balance the trade-offs among various criteria [45]. The steps for applying the CoCoSo method are as follows:
  • a

    Formulating the initial decision matrix Xij as follows:

The initial decision matrix Xij was formulated as described in Equation (54).
(54)
where Xij is the performance value of ith alternative with jth criteria and m and n are the number of alternatives and criterion, respectively.

  • b. Normalize the criteria values

The criteria values were normalized according to Zelany’s [46] compromise normalization method (i.e., Equations (55) and (56)) to make the elements of the decision matrix dimensionless and comparable.
(55)
(56)
where rij and xij, respectively, represents the normalized and original value of the performance of alternative i with respect to criterion j.

  • c. Evaluate performance indices

The performance indices Si and Pi for each alternative are calculated using the weighted sum method (WSM) and WPM, as illustrated in Equations (57) and (58).
(57)
(58)

  • d. Determine three different appraisal scores

Three different appraisal scores (Kia, Kib, and Kic) for the alternatives were determined based on different aggregation strategies highlighted in Equations (59)–(61).
(59)
(60)
(61)
where Kia represents the arithmetic mean of WSM and WPM scores. Kib represents the sum of relative scores compared to the best alternative. Whereas, Kic represents the balanced compromise score. The Kic score balances the influence of summation-based and product-based aggregation methods using a weighting parameter (λ), which was set to 0.5 to achieve a trade-off between the two approaches.

  • e. Evaluate the ranking of alternatives

Finally, the ranking of alternatives ki was evaluated using the formula provided in Equation (62).
(62)

2.3. Sensitivity Analysis

To ensure the robustness and reliability of the results, a sensitivity analysis was conducted. This involved systematically varying the weight ratios (WRs) assigned to different criteria and observing the impact on the final selection outcome. By examining how changes in weights influence the decision, sensitivity analysis provides valuable insights into the stability and robustness of the proposed methodology. It also helps to identify potential areas of sensitivity and to assess the trade-offs between competing criteria.

2.4. Model Validation

To complement the numerical simulations, experimental data was extracted from existing literature on the performance data of SSHAWTs [39] (Figure 2). The experimental data served as a benchmark for validating the predictions made by the implemented BEMT algorithms. This validation approach aims to enhance the robustness of the comparative analysis and provide a comprehensive understanding of the algorithms’ performance.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Validation of the numerical model using experimental data [39].

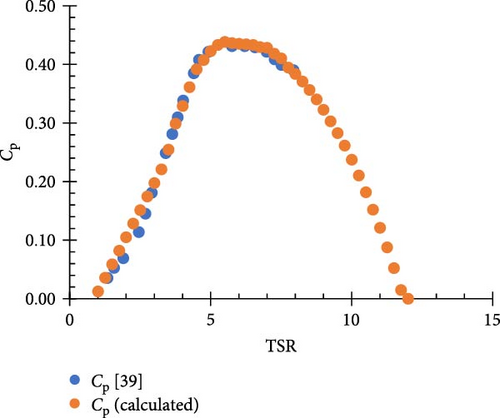
3. Results and Discussions

3.1. Comparison of BEMT Algorithms on the Geometrical and ADP Characteristics of SWTs

This section presents a comparative analysis of five BEMT algorithms: Ingram [37], Hansen [38], Manwell et al. [35], Jha [7], and Olievera [25]. The focus is on their effects on the geometrical and aerodynamic characteristics of a WTB at various TSRs. The findings reveal significant insights into how these algorithms influence chord length and twist angle distributions, which are critical for optimizing turbine performance.

3.1.1. Chord Length and Twist Angle Distribution of a WTB

The findings presented in Figure 3 highlighted the geometrical characteristics of each algorithm at various TSRs. Notably, the algorithms were evaluated based on parameters such as chord length, twist angle, and blade profile variations as depicted in Figure 3. The results highlighted that the geometry of the wind turbine was sensitive to the selected BEMT algorithm and TSR. The performance of each algorithm was also sensitive to the TSR.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The effect of BEMT algorithms on the chord distribution of WTB at various TSRs.

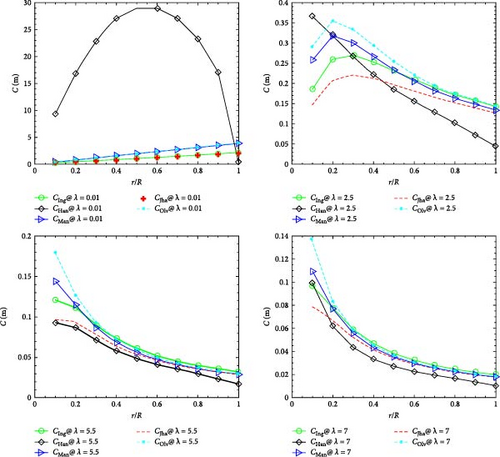
The results illustrated in Figure 3 depicted the chord length distribution against the relative radial position (r/R) along the blade length for different design methodologies, represented by CIng, CHan, CMan, CJha, and COlv. It showed that the chord length distribution along the span length was different in each λ and BEMT algorithms.

For instance, at lower TSR (λ < 1), all the BEMT algorithms except Hansen [38] and Manwell et al. [35] exhibited a minimum chord at the root section and maximum chord at the tip section of the blade. This is not common in the design of wind turbines. These findings suggest that the design TSR should be greater than 1 for getting a better shape of the WTB. The findings are aligned with Wood et al. [11] findings.

However, for λ = 2.5, each BEMT algorithm provides a better chord length distribution than their low λ counterparts. This improvement is characterized by a reduction in chord variation from the root to the tip of the blade, resulting in a more linear distribution. Such a linear distribution is advantageous as it contributes to enhanced structural integrity and Mnf. But the chord length distribution is different in each BEMT algorithm. For instance, in the case of Jha et al. [7] algorithm, the chord varies from 0.15 m at the tip section to 0.13 m at the root section. Whereas, in the case of Hansen [38], C decreased from 0.37 m at the root to 0.04 m at the blade tip. On the other hand, CIng and CJha first increased from the blade root to r/R = 0.3 and then decreased along the blade tip. This showed that Jha and Ingrams algorithm yields a favorable chord distribution as the difference between the chord at the root and tip section of blade is minimal compared to other algorithms and the lowest chord is needed to decrease the weight and cost of WTB. The findings are aligned with the findings highlighted in [47], which demonstrated that the chord and twist distribution of the wind turbine are almost linear in the low wind areas.

Conversely at a TSR of 5.5, the CHan method exhibits the lowest chord length along the blade length. Similarly, Jha’s algorithm exhibited similar trends with the Han algorithms. Whereas the Olievera [25] method showed higher chord at the root (Colv = 0.18) but is less pronounced compared to the lower TSRs. On the other hand, when the TSR was increased to 7 the chord length distribution along the blade span was decreasing in all algorithms. Among these algorithms, the Jha algorithm showed the lowest chord near the root section (r/R < 0.18) and the Han algorithm exhibited the lowest chord in the remaining blade section. In contrast, the Ingram [37] algorithm, while effective at lower TSRs, produces longer chord lengths that may hinder performance at higher speeds due to increased drag. These inconsistent trends showed that the performance of each algorithm was dependent on the TSR. Moreover, the algorithms yield a low chord blade as the TSR increases which is vital for designing low weight and cost-effective WTB. This reduction in chord length is crucial for minimizing drag and enhancing overall turbine efficiency. This observation is consistent with the design principles of WTBs, where a larger chord length near the root of the blade is necessary to provide the required structural support and ADP at lower radii.

Generally, different design methods exhibit distinct chord length distributions, indicating varied approaches to balance aerodynamic efficiency and structural integrity. Methods like Olviera [25] with higher initial chord lengths may prioritize structural strength near the root, whereas more uniform distributions aim for consistent ADP. As TSR increases, the chord length distribution becomes more uniform and reduced, reflecting the need for less surface area to maintain efficiency at higher rotational speeds. This insight underscores the importance of tailoring blade designs to specific operational TSRs. By understanding the variations among design methods and the impact of TSR, designers can make informed decisions to optimize blade performance for specific operational conditions. The findings highlight the need for a balanced approach that considers aerodynamic theories, structural requirements, and practical performance considerations to enhance the overall efficiency and effectiveness of wind turbines.

Twist angle distribution is another critical factor influenced by the chosen BEMT algorithm and the TSR. Figure 4 depicted that at lower TSRs (TSR < 1), the angles were distributed linearly along the radial position. Conversely, as TSR increases, the twist angles across all algorithms except Ingram [37] generally decrease and the twist angle distribution becomes nonlinear. This decrease helps to maintain aerodynamic efficiency by ensuring each blade section operates at its optimal AOA, which in turn enhances the turbine’s performance at low to high TSR. Maintaining lower twist angles helps to ensure structural integrity and aerodynamic efficiency, as reducing aerodynamic drag and centrifugal stresses is vital for high-speed turbine operation. These findings emphasize the need for continuous innovation in aerodynamic optimization, incorporating advanced materials, and control systems to dynamically adjust blade configurations for optimal performance. The BEMT theory supports these algorithms, indicating that optimized twist angles can significantly enhance ADP under these conditions.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The effect of BEMT algorithms on the twist angle distribution of WTB at various TSRs.

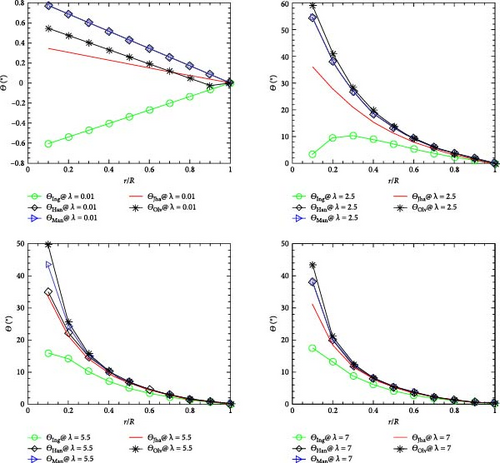
The comparative analysis of the BEMT algorithms highlights key insights regarding the trade-offs between simplicity and performance. For instance, the Ingram [37] and Jha [7] algorithms demonstrated favorable twist angle distributions, providing a balance between aerodynamic efficiency and simplicity. It results in effective twist angles that contribute positively to the turbine’s overall performance. In comparison, the Olievera [25] and Manwell et al. [35] algorithms exhibited a more complex twist angle profile at all TSRs, potentially complicating manufacturing and leading to performance inconsistencies. The Hansen [38] algorithm strikes a middle ground, producing effective twist angles without excessive complexity.

The chord length and twist angle distribution results revealed that algorithms like Jha [7] and Ingram [37] and Hansen [38] provide relatively simpler chord shapes and more favorable twist angle distributions, enhancing aerodynamic efficiency across various TSRs. The consistent patterns in chord lengths and twist angles across these algorithms suggest their robustness in design, particularly at higher TSRs. These findings were similar to the findings presented in [24].

In contrast, the Manwell et al. [35] and Olievera [25] algorithms result in more complex geometries that may hinder performance at higher speeds. The Olievera algorithm’s chord profiles, particularly at higher TSRs, exhibited complexity that could challenge Mnf, as evidenced by its high chord length at all TSRs.

Overall, these findings emphasize the critical role of algorithm selection in wind turbine design. The choice of BEMT algorithm significantly impacts both chord lengths and twist angles, ultimately influencing the turbine’s performance and efficiency. Future work should aim to refine these algorithms to enhance performance while simplifying blade geometries, ensuring that wind turbine designs are both efficient and manufacturable. Integrating quantitative results into this analysis strengthens the conclusions drawn and provides a clearer framework for future research in this field.

The observed distributions of chord length and twist angle align with established aerodynamic theories and literature on WTB design. The variations in chord length and twist angle for different TSRs underscore the necessity of optimizing blade design for efficiency and performance across diverse wind speeds. These results are consistent with the Betz limit and BEMT, emphasizing the significance of optimizing the AOA and chord length to maximize aerodynamic efficiency. Additionally, structural considerations, such as increased loads at low TSRs and potential cost savings at high TSRs, underscore the importance of balancing ADP with structural integrity. These new insights provide valuable information for optimizing blade design to enhance ADP and energy production efficiency in wind turbines.

3.1.2. Estimating Geometry Complexity Based on RMSE Values

The RMSE values offer a quantitative measure to evaluate how closely the fitted linear equations align with the actual chord distributions derived from various BEMT algorithms at 5.5 TSR. This analysis provides insights into the complexity of the geometries associated with these algorithms, where lower RMSE values indicate simpler, more predictable geometries, and higher values suggest increased complexity and variability.

The RMSE analysis showed that the Manwell et al. [35], Ingram [37], Hansen [38], Jha [7], and Olievera [25] algorithm has an RMSE of 0.013387, 0.0080774, 0.0043346, 0.0056897, and 0.019643, respectively. The RMSE analysis reveals that simpler geometries, characterized by lower RMSE values, are generally preferable for wind turbine designs, as they enhance Mnf and performance consistency. Specifically, the Hansen [38] and Jha [7] algorithm emerge as efficient options, while the Olievera [25] algorithm presents significant challenges for manufacturing due to its complex contour. On the other hand, the moderate RMSE value of Manwell et al. [35] and Ingram [37] algorithms suggests that these algorithms yield a less complex geometry which in turn reduces the challenges in manufacturing the WTB.

3.1.3. ADP Analysis of SWTs

The analysis of the power coefficient (Cp) of SSHAWTs across various BEMT algorithms illustrated in Figure 5 reveals notable differences in turbine performance as a function of TSR. The data, illustrated in Figure 5, clearly indicate the Cp values achieved by each algorithm at varying TSRs, highlighting critical trends in performance.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Performance of BEMT algorithms at various TSRs.

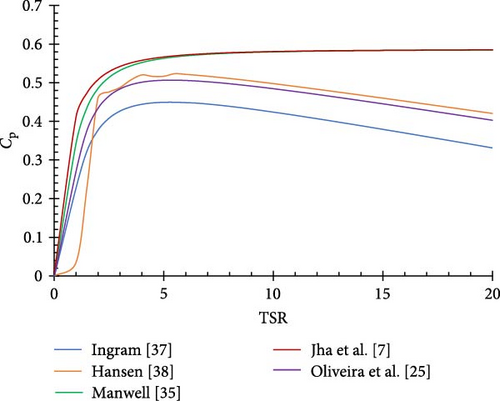
The results demonstrate that the Jha [7] algorithm consistently produces the highest Cp values at all TSRs. This suggests superior aerodynamic modeling capabilities compared to other algorithms. The Manwell et al. [35] algorithm follows closely, except at low TSR (TSR < 2.5). In contrast, Hansen [38], Olievera [25], and Ingram [37] algorithms exhibit diminishing Cp values after a TSR of 5.5, indicating their relatively lower effectiveness in capturing turbine performance.

The Ingram [37] algorithm displays the lowest performance, with a maximum Cp of 0.45, suggesting significant limitations in its performance. Across the given TSR range, the Cp values for each algorithm are shown in Figure 5, illustrating the differences in performance.

Overall, the findings suggest that higher TSRs generally correlate with increased Cp, peaking at their respective optimal points before declining. This trend underscores the importance of selecting an appropriate BEMT algorithm for accurately predicting turbine performance under various operational conditions.

The findings from this study provide significant insights into the performance of SSHAWTs as modeled by different BEMT algorithms. The consistent superiority of the Jha [7] algorithm in achieving higher Cp values emphasizes its effectiveness in capturing the aerodynamic characteristics of turbine blades. This aligns with previous studies that advocate for the use of robust models to enhance energy extraction from wind [7].

Conversely, the lower performance of the Ingram [37], Hansen [38], and Olievera [25] algorithms raise questions about their applicability in real-world scenarios. Especially, the Olievera [25] algorithm with a maximum Cp of 0.45 at TSR = 5.5, it is notably less competitive, indicating potential limitations in its modeling assumptions.

The observed relationship between TSR and Cp, where an initial increase in Cp is followed by a decline, reflects the inherent characteristics of wind turbine operation. For instance, the peak Cp values occur at TSRs of 5.5 for Ingram, Hansen, and Olievera demonstrating that maintaining optimal operating conditions is crucial to minimizing aerodynamic losses. This finding is consistent with existing literature that emphasizes the importance of optimal TSR for maximizing energy capture [48].

The implications of this research extend beyond theoretical understanding. By identifying the most effective BEMT algorithms, turbine designers can optimize wind turbine performance, leading to enhanced energy yields and reduced operational costs. Moreover, the study highlights the need for continuous refinement of predictive models, encouraging further exploration of advanced algorithms that can better accommodate the complexities of wind turbine aerodynamics.

Generally, the findings underscore the critical role of BEMT algorithms in predicting the performance of SSHAWTs. As the demand for renewable energy increases, understanding and optimizing these models will be essential for advancing wind energy technology and maximizing its potential. Future research should focus on refining these algorithms and exploring new methodologies to further enhance turbine efficiency.

3.2. MCDM Analysis of BEMT Algorithms

The results from the FUCOM analysis, summarized in the first row of Table 3, indicate that the most influential criteria for selecting appropriate BEMT algorithms for SWT are output power and power coefficient, assigned weights of 25% and 22%, respectively. In contrast, the thrust coefficient (CT), Mnf, weight, and material cost received lower weights of 16%, 13%, 12%, and 12%. These findings highlight the critical importance of aerodynamic efficiency in optimizing WTB design, as prioritizing output power and power coefficient directly contributes to enhancing energy generation capabilities [49].

Table 3. MCDM results of BEMT algorithm selection.
Criteria weights/BEMT algorithm 0.25 0.22 0.16 0.13 0.12 0.12 Ki Rank by Ki
P (W) Cp CT Mnf W (kg) CM ($)
Jha 834 0.569 0.8 5 2.031 1.035 3.27 1
Ingram 884 0.4484 0.94 4 2.769 1.411 2.63 2
Manwell 819 0.5669 0.75 3 2.822 1.438 2.27 3
Hansen 779 0.5193 0.69 5 1.975 1.007 2.17 4
Olivera 802 0.5292 0.8 3 3.495 1.782 1.31 5
DFC (X) 1.38778e−17

The diminished weights assigned to Mnf, weight, and material cost reflect the evolving landscape of small WTB design, where advancements in manufacturing techniques and the availability of lightweight, cost-effective materials have reduced traditional constraints [40]. By emphasizing ADP, this approach facilitates the development of WTBs that achieve optimal functionality.

The DFC (X) value of 1.38778E−17, which is close to zero, further confirms the consistency of the criteria weights and supports the suitability of the FUCOM method for evaluating the selection criteria of BEM algorithms.

The ranking of alternatives (Ki), calculated using the CoCoSo method, is presented in the eighth column of Table 3. The highest Ki value of 3.27 was obtained for the Jha [7] algorithm, while the lowest value of 1.31 was assigned to the Oliveira [25] algorithm. The analysis indicates that the Jha [7] and Ingram [37] algorithms are the top-ranked options for optimal design of SSHAWT applications, as demonstrated in column nine of Table 3. Both algorithms exhibit a favorable balance of essential characteristics, including high power output, power coefficient, thrust coefficient, good Mnf, low weight, and minimal material costs.

While other algorithms also displayed commendable performance, they did not achieve the same level of balance as the top-ranked options. For instance, the Hansen algorithm is noted for its low cost and weight, along with simpler geometries that facilitate manufacturing; however, it exhibited relatively lower thrust coefficients and turbine power. Conversely, the Manwell algorithm demonstrated excellent power coefficients and output, but fell short in terms of thrust coefficient and Mnf. This suggests that the optimal BEM algorithm selection is contingent on the specific requirements of the application.

The comparative analysis of the BEM algorithms further reveals that the Jha and Manwell algorithms yield wind turbines with superior ADP compared to their counterparts. In contrast, the Hansen and Jha algorithms excel in Mnf, weight, and cost considerations. When assessing thrust coefficients, the Ingram, Oliveira, and Jha algorithms outperform the others. Overall, the Jha algorithm consistently demonstrates superior suitability for the design of small WTBs, making it the preferred choice in this analysis.

3.3. Sensitivity Analysis

This study performed a sensitivity analysis to assess the robustness of the MCDM method used to select BEMT algorithms for SSHAWTs. The analysis focused on the impact of varying the WRs assigned to the selection criteria on the final ranking of the BEMT algorithms. The results demonstrated consistent algorithm rankings across a range of WR scenarios, indicating that the selection process is reliable and not overly sensitive to minor variations in criterion weights. This consistency underscores the robustness of the MCDM approach and the strength of the conclusions drawn regarding the preferred BEMT algorithms for SSHAWT design.

When equal WRs were assigned to all six criteria, among those compared, the Jha, Ingram, and Hansen algorithms emerged as the most suitable BEM algorithms, achieving Ki scores of 3.57, 2.72, and 2.51, respectively. This outcome indicates that these algorithms exhibit a balanced performance across all criteria, making them well-suited for SWT applications.

In another scenario, assigning equal weights of 0.2 to both power output and power coefficient (Cp) and 0.15 to the other four criteria, resulted in the Jha, Ingram, and Manwel algorithms being identified as the top three suitable BEM algorithms, with Ki scores of 3.44, 2.64, and 2.36. Conversely, when equal weights of 0.35 were assigned to power output and thrust coefficient (CT), while the remaining four criteria received a weight of 0.075, the Ingram, Jha, and Manwel algorithms were ranked as the top three suitable options, with Ki scores of 3.11, 3.07, and 2.10, respectively.

Furthermore, assigning a weight of 0.35 to Cp and 0.13 to the other five criteria led to Jha, Manwel, and Ingram being recognized as the top three suitable BEM algorithms, achieving Ki scores of 3.17, 2.27, and 2.10. Conversely, when higher weights (0.3) were assigned to cost of materials (CMs) and W, with 0.1 allocated to the other four criteria, the Ingram, Hansen, and Ingram algorithms were identified as the top three suitable BEM algorithms, with Ki scores of 4.67, 3.67, and 3.19.

These results illustrate a critical trade-off between maximizing power output and minimizing cost in wind turbine design. Assigning a higher weight to power output favors algorithms that prioritize high power generation, while emphasizing CM highlights algorithms that effectively reduce turbine costs. Moreover, prioritizing power output, Cp, and CT underscores the importance of efficient energy conversion, while lower weights assigned to Mnf, W, and CM indicate that these factors are less crucial for SSHAWTs.

Overall, the analysis indicates that power output, power coefficient, and thrust coefficient play significant roles in the selection of BEM algorithms. The preference for Jha and Ingram’s algorithms suggests their superior performance in energy conversion efficiency, aerodynamic characteristics, Mnf, and cost-effectiveness.

The sensitivity analysis underscores the robustness and reliability of the MCDM approach for selecting BEM algorithms in SSHAWT applications. The consistent identification of certain algorithms, particularly Jha and Ingram, across varied scenarios suggests their exceptional aerodynamic attributes for SSHAWTs. These findings provide valuable insights into the impact of WR variations and criteria selection on the decision-making process, empowering designers to make informed choices tailored to specific performance requirements.

4. Conclusions

This study provides a comprehensive comparative analysis of five selected BEMT algorithms, focusing on their influence on the geometrical characteristics and performance of wind turbines across varying TSRs. By employing a MCDM approach, this research identifies algorithms that best meet the specific requirements of SWTs. The findings indicate that both the TSR and the choice of algorithm significantly affect wind turbine performance. Notably, the Jha algorithm consistently demonstrated superior ADP across all TSRs, suggesting it is particularly effective for optimizing WTB designs. The aerodynamic analysis conducted reveals that the optimization of chord length and twist angle is crucial for maximizing the efficiency and performance of SWTs at different TSRs. The FUCOM analysis provided insight into the relative importance of various criteria in algorithm selection, with power output, power coefficient (Cp), and thrust coefficient (CT) receiving weights of 0.25, 0.22, and 0.16, respectively. In contrast, Mnf, blade weight (W), and CM were assigned lower weights of 0.13, 0.12, and 0.12, respectively. This underscores the significance of power output and Cp as primary considerations when selecting suitable BEM algorithms for SWT applications. Moreover, the MCDM analysis established Jha’s technique as a promising BEM algorithm for SSHAWT blades, particularly in low wind conditions. The sensitivity analysis confirmed the robustness and reliability of the MCDM approach in selecting BEM algorithms for SSHAWTs. The consistent performance of the Jha algorithm across various scenarios indicates its capacity to yield superior aerodynamic characteristics, alongside benefits such as low cost, reduced weight, and simplified geometries, which are critical for SWTs. This study contributes significantly to the existing literature on optimal wind turbine design, providing a solid foundation for future research aimed at optimizing wind turbine configurations for specific operational contexts. The insights gained from this analysis will enable designers to make informed decisions that align with performance requirements, ultimately enhancing the efficiency and viability of SWT technologies. While the study offers valuable insights for optimal design of WTB, it can be extended by validating findings with experimental data; incorporating additional criteria, such as acoustic performance, structural strength (e.g., structural strength and fatigue resistance), and esthetics, into the MCDM framework; and conducting comparative analyses with other MCDM methods to assess CoCoSo’s robustness.

Nomenclature

  • AOA:
  • Angle of attack (°)
  • ρ:
  • Air density (kg/m3)
  • ρm:
  • Density of the blade material (kg/m3)
  • τ:
  • Shear stress (N/m2)
  • α:
  • Angle of attack (Figure 1)
  • θ:
  • Twist angle (Figure 1)
  • φ:
  • Inflow angle (Figure 1)
  • σ:
  • Solidity
  • ω:
  • Criteria weight
  • λ, TSR:
  • Tip-speed ratio
  • a, AIF:
  • Axial induction factor
  • a′, TIF:
  • Tangential induction factor
  • ADP:
  • Aerodynamic performance
  • BEMT:
  • Blade element momentum theory
  • C:
  • Chord (m), criteria
  • Cd:
  • Drag coefficient
  • Cl:
  • Lift coefficient
  • CoCoSo:
  • Combined compromised solution
  • CM:
  • Cost of material ($)
  • Cp:
  • Power coefficient
  • CT:
  • Thrust coefficient
  • DFC:
  • Deviation from full consistency
  • F:
  • Tip loss factor
  • Fd:
  • Drag force (N)
  • Fl:
  • Lift force (N)
  • FUCOM:
  • Full consistency method
  • g:
  • Acceleration due to gravity (m/s2)
  • Ki:
  • Appraisal score
  • LDR:
  • Lift to drag ratio
  • MCDM:
  • Multicriteria decision-making
  • Mnf:
  • Manufacturability
  • P:
  • Power (w)
  • R:
  • Rotor radius (m)
  • Re:
  • Reynolds number
  • SWTs:
  • Small wind turbines
  • SSHAWT:
  • Small-scale horizontal axis wind turbine
  • SST:
  • Shear stress transport
  • Urel:
  • Relative wind speed (m/s)
  • U0, V:
  • Wind speed, free wind speed (m/s)
  • VolB:
  • Volume of blade (m3)
  • W:
  • Blade weight (Kg)
  • WTB:
  • Wind turbine blade.

    • Conflicts of Interest

    The authors declare no conflicts of interest.

    Author Contributions

    Belayneh Yitayew Kassa conceptualized the study, developed the methodology, implemented the software, validated the results, curated the data, conducted the formal analysis, and wrote the original manuscript. Asfaw Beyene and Aklilu Tesfamichael Baheta supervised the research, curated the data, and provided critical review and edited the manuscript. All co-authors have reviewed and approved the manuscript.

    Funding

    This research was financially supported by the Sustainable Energy Center of Excellence at Addis Ababa Science and Technology University under Grant IGP 015/2023 and Arba Minch University.

    Data Availability Statement

    The data that support the findings of this study are available from the corresponding author upon reasonable request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.