DFT-Based Investigation of Electronic, Optical, and Thermoelectric Properties of TaCu3X4 (X = S, Se, Te) Chalcogenides for Optoelectronic and Energy Applications
Abstract
In this investigation, the electronic, optical, and thermoelectric (TE) characteristics of the chalcogenide compound TaCu3X4 (X = S, Se, Te) were examined through first-principles calculations employing density functional theory (DFT). The exchange-correlation potential was determined using the generalized gradient approximation Perdew-Burke-Ernzerhof for solids (GGA-PBEsol). Analysis of the band structures indicated the semiconducting nature of all investigated compounds, with direct band gaps measured at 2.4, 2.2, and 2 eV for TaCu3X4 (X = S, Se, Te), respectively. Notably, strong absorption within the visible and low ultraviolet spectra was observed. Optical dispersion analyses, encompassing complex dielectric function, energy loss function, refractive index, extinction coefficient, reflectivity, and optical conductivity, were conducted within the energy range of 0–14 eV, revealing anisotropic polarization across all compounds, making them promising candidates for optoelectronic applications. Furthermore, the transport properties of the chalcogenide compounds were assessed, indicating noteworthy electrical conductivity, electronic thermal conductivity, and Seebeck coefficient, attributable to the majority electron carriers with semiconductor characteristics. Effective masses of electrons and holes were determined through dispersion curve fitting, highlighting promising TE behavior, as evidenced by the calculated figure of merit for TaCu3X4 (X = S, Se, Te), positioning it as a prospective candidate for renewable energy device implementations.
1. Introduction
Recently, interest in narrow and wide bandgap semiconductors has significantly shifted toward chalcogenide materials due to their fascinating physical properties. This class of materials is widely used in optoelectronic and thermoelectric (TE) applications. In addition to their low cost of synthesis and availability, ternary chalcogenides are more efficient narrow bandgap semiconductors compared to traditional semiconductors. Alkaline-earth chalcogenides, which belong to the II–VI group elements, crystallize in a sixfold NaCl-type structure with a closed-shell system [1–8]. It has been observed that these chalcogenides exhibit good metallization and phase structure under high-pressure conditions. The key feature of these materials lies in their applications in light-emitting diodes [9–11], magneto-optical devices [12], laser diodes [13], and microelectronic devices [14, 15], as well as in TE applications [16].
Several research groups have conducted investigations on chalcogenide materials [17]. Yang et al. [18] studied the structural properties of barium cadmium chalcogenides Ba2CdX3 (X = S, Se, Te). They observed that Ba2CdS3 and Ba2CdSe3 are formed by heating a mixture of 2BaS and CdS between 700 and 800°C. The synthesis of Ge-based materials was performed by solid-state reaction followed by spark plasma sintering, as reported by Perumal et al. [19] and Yan et al. [20]. This phenomenon is further highlighted through the comparative analysis of several isoelectronic pairs, such as GeTe and GeSe, or Bi2Se3 and Bi2S3 [21]. The results reveal that while GeTe exhibits a maximum ZT of 1.0 at 673 K, GeSe shows a ZT of 0.05 at 710 K. A similar disparity is observed between Bi2Se3 and Bi2S3, where their ZT values differ by more than a factor of 10. Such pronounced differences among isoelectronic materials are striking and warrant further explanation [22–24]. A notable example is the family of Sn chalcogenides, SnX (X = Te, Se, S), which has shown high ZT values, with ~1.6 at about 923 K for Sn0.86Mn0.14Te (Cu2Te) and ~2.6 at about 920 K for single crystal SnSe. The high performance of these materials is attributed to intrinsic features, such as high anharmonicity leading to low lattice thermal conductivity in SnSe and SnS and multiple valley bands contributing to a high Seebeck coefficient in SnTe and SnSe [25–30].
Beyond binary chalcogenides, recent studies have explored ternary chalcogenide compounds due to their potential in optoelectronic and TE applications. Notably, Al2HgS4 and Al2MgS4 cubic spinels have been investigated for their direct bandgaps of 2.11 eV and 3.69 eV, respectively, at the Γ-point, with optical absorption extending from the visible to ultraviolet region, making them promising candidates for optoelectronic devices [31]. Similarly, the X2CdS4 (X = Dy, Tm) spinels exhibit strong photon absorption in the ultraviolet range, supporting their use in sensors, optical filters, and optoelectronic applications [32]. Additionally, these materials display significant TE potential, with the figure of merit (ZT) values of 0.78 and 0.74 for Al2HgS4 and Al2MgS4, respectively, confirming their suitability for energy conversion technologies [31].
Since Petrov et al. [33] presented the applications of phase-matching and optical parametric amplification in AgGaGeS4 single crystals, there has been a growing body of research focused on second harmonic generation (SHG) and difference frequency generation (DFG). AgGaGeS4 has been regarded as a highly promising candidate to replace AgGaS2 crystals for these applications. However, significant challenges in the material’s preparation have severely limited its development. The AgGaGeS4 crystal was first synthesized in 1980, but progress in both the synthesis of AgGaGeS4 polycrystals and the growth of single crystals remained slow, with few additional details published until 1991 [34–40].
From an optical perspective, numerous experimental investigations have highlighted the crucial role of chalcogenide compounds in solar cell technology, emphasizing their optical properties and high-temperature stability, which are essential for photovoltaic applications [41–45]. Notably, NaSbS2 has gained attention for its exceptional electronic band structure, featuring regions within the Brillouin zone with both high and low dispersion, indicative of varied electronic characteristics. These attributes give rise to multi-valley features at the conduction band minimum (CBM), which are believed to significantly enhance TE efficiency. Additionally, the strong interaction between acoustic and optical phonons plays a pivotal role in thermal conductivity, further underscoring the potential of NaSbS2 as an outstanding material for TE devices [46–49].
In economic and environmental point of view, the cost of ternary chalcogenides materials is largely influenced by the availability of their components [50]. For example, tantalum (Ta), tellurium (Te), and indium (In) are relatively rare and expensive, with supply concerns due to ethical sourcing and price volatility [51]. In contrast, sulfur (S), selenium (Se), and tin (Sn) are more abundant and cost effective, while others as copper (Cu) and zinc (Zn) are widely available and inexpensive [52]. These factors significantly impact the economic feasibility of using these materials for TE and optoelectronic applications [53]. Additionally, the synthesis method plays a crucial role in the cost-effectiveness and scalability of these materials. While high-performance methods may offer excellent results, they are costly and not suitable for large-scale production. In contrast, solution processing methods provide more affordable and scalable alternatives. Balancing cost and scalability are essential to determine the practical viability of these materials for real-world applications [54]. Furthermore, the discussed materials exhibit strong industrial feasibility and environmental stability, making them promising for sustainable technological applications [55]. The use of nontoxic elements enhances environmental friendliness, particularly in Ta-series compounds, which align with energy demands while minimizing ecological impact. Their relatively small bandgaps make them excellent candidates for TE applications, supporting efficient energy conversion and industrial scalability. Additionally, their stability positions them as viable materials for optoelectronic and TE technologies, ensuring long-term functionality and cost-effectiveness [56]. Furthermore, Cu3TaX4 (X = S, Se, and Te) compounds have been confirmed for use in ion synaptic transistors, advancing neuromorphic computing for energy-efficient AI systems [57]. However, the stability and ecological impact of TaCu3X4 compounds depend on both chemical durability and degradation effects under different working conditions. While tellurides offer better stability, their toxicity raises concerns, whereas sulfides and selenides face oxidation and ion leaching issues, leading to potential environmental contamination. Studies by Baghel and Kumar [58] and Wang et al. [59] highlight these challenges, emphasizing the need to balance material performance with sustainability. Future applications, particularly in energy and industrial sectors, must consider both stability and ecological risks to develop materials that offer high performance without long-term environmental harm.
In this paper, we investigate the electronic, optical, and TE properties of quaternary chalcogenides TaCu3X4 (X = S, Se, Te) using ab-initio calculations. The second section of the manuscript elaborates on the crystal structure and computational methodology employed in the study. Section 3 presents a detailed analysis of the results obtained from the computational investigations. Finally, Section 4 summarizes the key findings and overarching conclusions drawn from the study.
2. Materials and Methods
To elucidate the electronic, optical, and transport properties of the chalcogenide materials TaCu3X4 (X = S, Se, Te), we employed the sophisticated density functional theory (DFT) framework, operationalized through the WIEN2K package. Our investigations leveraged the full-potential linearized augmented plane wave (FP-LAPW) method, renowned for its precision in capturing intricate quantum phenomena. Structural optimization was meticulously conducted using the generalized gradient approximation (GGA) within the Perdew–Burke-Ernzerhof for solids (PBEsol) formalism, recognized for its effectiveness in modeling diverse material systems with high fidelity. The electronic properties were computed using the modified Becke-Johnson (mBJ) approximation. The choice of GGA-PBEsol is based on its well-established ability to accurately refine structural parameters, which are crucial for electronic structure calculations. While PBEsol tends to underestimate absolute bandgaps, it effectively captures the systematic trends observed in more advanced functionals such as HSE06 and many-body perturbation methods like GW. This makes PBEsol a reliable tool for qualitative and comparative studies of electronic structures [60, 61]. Additionally, PBEsol’s computational efficiency makes it especially useful for large-scale simulations, particularly when studying novel materials, where hybrid functionals like HSE06 or GW are computationally prohibitive [62]. Previous studies on transition metal and chalcogenide semiconductors have shown that PBEsol can serve as a strong starting point for electronic structure calculations, with corrective methodologies applied later for more accurate band gap predictions [63, 64]. The angular momentum parameters were set to LMAX = 10 and GMAX = 12 (a.u.)−1, ensuring reliable wavefunction expansions. The plane-wave cutoff energy parameter, defined as the product of the atomic radius and wave vector (muffin-tin radii [RMT] × KMAX), was chosen to be 9.0 based on a systematic convergence test, ensuring that the plane-wave expansion was sufficient to accurately represent wavefunctions while avoiding numerical instability. For the Brillouin zone integration, we employed a 1000 k-point mesh in the density of states (DOS) calculations to achieve high-resolution spectral features. This selection was made after performing k-point convergence tests, where we observed that further increasing resulted in negligible changes in total energy (variations below 0.1 mRy) and charge deviations less than 0.0001 e per unit cell. For the transport properties, the semi-classical Boltzmann transport theory was applied using the BoltzTrap simulation code, which employs Fourier expansions of band structures and is widely recognized for its accuracy in predicting TE properties [65, 66].
TaCu3X4 (X = S, Se, Te) adopts a sulvanite-type crystal structure and crystallizes in the cubic P-43m (No. 215) space group. The atomic positions in the unit cell are as follows: Ta cations occupy (0, 0, 0), Cu cations are positioned at (0, 0, 0.5), and the chalcogen anions are located at (0.242853, 0.757147, 0.757147) for S, (0.24884, 0.24884, 0.24884) for Se, and (0.256477, 0.743523, 0.743523) for Te. Alternative atomic configurations were considered, where Ta cations remained at (0,0,0), and Cu cations were positioned at (0.5,0,0) or (0,0.5,0), depending on the specific chalcogen element.
To prevent charge leakage from the core, the RMT were carefully selected for each element (Table 1). The structural optimization was carried out to obtain the equilibrium lattice parameters, ensuring that the forces acting on the atoms were minimized.
| Compounds | RMT (Bohr) | Calc. Lattice parameters optimization (Å) | ||||
|---|---|---|---|---|---|---|
| Present work | Related work [67] | Present work | Related work [67] | Experimental | ||
| TaCu3S4 | Ta | 1.91 | 1.92 | 5.493 | 5.558 | 5.520 [68] |
| Cu | 1.96 | 1.97 | ||||
| S | 1.56 | 1.57 | ||||
| TaCu3Se4 | Ta | 1.90 | 1.89 | 5.699 | 5.732 | 5.670 [68] |
| Cu | 1.90 | 1.91 | ||||
| Se | 1.81 | 1.80 | ||||
| TaCu3Te4 | Ta | 2 | 2.00 | 5.871 | 6.009 | 5.928 [69] |
| Cu | 1.96 | 1.56 | ||||
| Te | 1.96 | 1.96 | ||||
For the calculation of the electronic structure, the Kohn–Sham (KS) wavefunctions were expanded with RMT × KMAX = 9.0, where RMT represents the RMT of the ions, and KMAX is the maximum wavevector in the plane-wave expansion. The valence orbitals considered for each element were as follows: Ta: [Xe] 4 f14 5d3 6 s2, Cu: [Ar] 4 s1 3d10, S: [Ne] 3 s2 3 p4, Se: [Ar] 3d10 4 s2 4 p4, and Te: [Kr] 4d10 5 s2 5 p4. These configurations were used to ensure accurate electronic structure calculations and provide a reliable basis for investigating the optoelectronic and transport properties of the TaCu3X4 compounds.
Table 1 presents a comparison of the computed RMT and optimized lattice parameters for TaCu3X4 (X = S, Se, Te), alongside values from related work and available experimental data. The RMT values for TaCu3S4, TaCu3Se4, and TaCu3Te4 are very close to those reported in Related Work [67], with minor variations, particularly for Ta and Cu, where the differences are around ~0.01 Bohr. These slight differences can be attributed to numerical precision and optimization choices during the computational calculations. The chalcogen (S, Se, and Te) radii align well with those in Related Work [67], ensuring consistency in structural modeling. The computed lattice constants in the present work are 5.493, 5.699, and 5.871 Å for TaCu3S4, TaCu3Se4, and TaCu3Te4, respectively. Compared to related work [67], our values are slightly lower, by about ~ 0.06 Å for TaCu3S4 and ~0.03 Å for TaCu3Se4, but still within an acceptable range of computational variation. The experimental lattice constants (5.520, 5.670, and 5.928 Å) are slightly higher than our computed values, which is consistent with DFT’s tendency to underestimate lattice parameters [68, 69].
All the investigated materials exhibit cubic symmetry, as depicted in Figure 1. In this study, DFT was employed to analyze the properties of these materials. DFT is a widely used tool in both industrial and academic research due to its ability to numerically (though approximately) solve complex quantum mechanical problems. It provides insights into total energies and bulk modulus for a given atomic arrangement within a material. The asymmetric unit cell of TaCu3X4 (X = S, Se, Te) chalcogenide crystals is illustrated in Figure 1, visualized using VESTA software (Visualization for Electronic and Structural Analysis). The structures were relaxed according to Murnaghan’s equation of state.
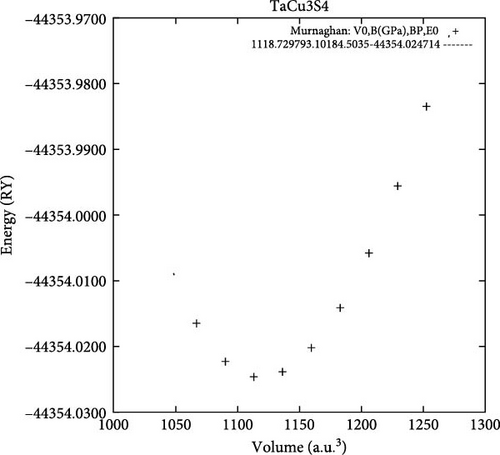
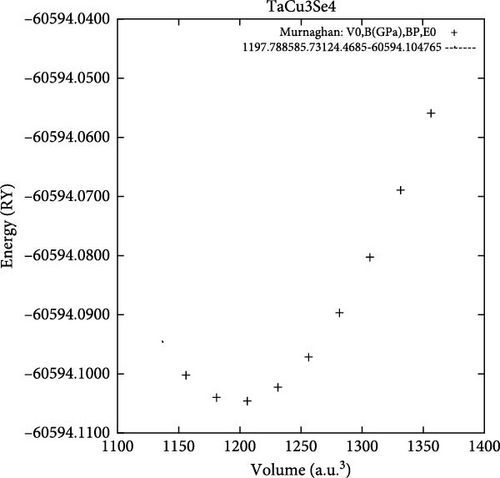
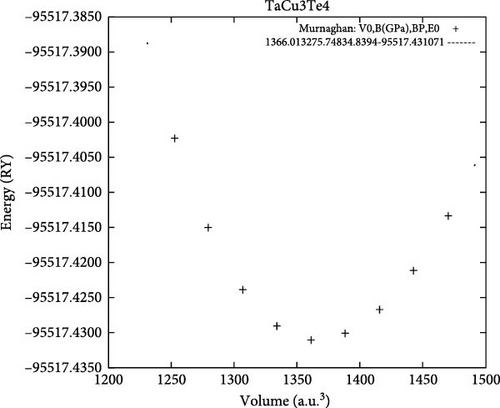
In this context, E0 represents the equilibrium total energy at absolute zero temperature, while B0 and B’0 denote the bulk modulus and its pressure derivative, respectively. Figure 2a–c vividly illustrates the equilibrium volume, which serves as a crucial indicator of material stability. The observations in Figure 2 reveal that the investigated chalcogenide crystal exhibits a notably higher degree of stability compared to other materials.
3. Results and Discussions
3.1. Electronic Band Structure
A deeper understanding of chalcogenide materials has been attained through energy minimization techniques. Figure 3 illustrates the electronic band structures of TaCu3X4 (X = S, Se, Te), resolved along the high-symmetry directions in the Brillouin zone: W, L, Γ, X, and K, using the mBJ approximations. It is evident that all these materials exhibit semiconducting characteristics. The bandgap values for TaCu3S4, TaCu3Se4, and TaCu3Te4 are relatively modest, calculated to be 2.04 eV, 1.78 eV, and 1.25 eV, respectively. The valence band maxima (VBM) and CBM converge at the Γ point, indicating a direct band gap configuration for these materials. Direct bandgap materials are generally considered superior semiconductors compared to their indirect counterparts due to their stronger optical excitations [70]. The Fermi level, positioned at zero energy, demarcates the boundary between the conduction band (CB) (above) and the valence band (below). The electronic configurations of Ta, Cu, S, Se, and Te are [Xe] 4 f14 5d3 6 s2, [Ar] 3d10 4 s1, [Ne] 3 s2 3p4, [Ar] 3d10 4 s2 4 p4, and [Kr] 4d10 5 s2 5 p4, respectively.
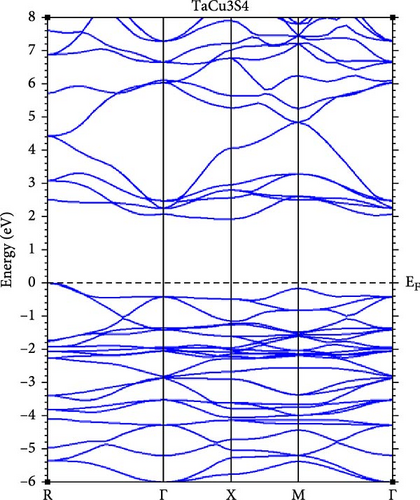
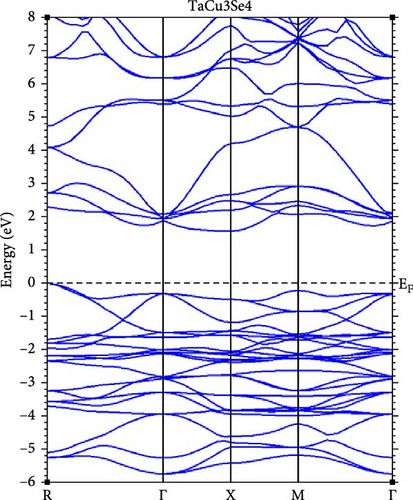
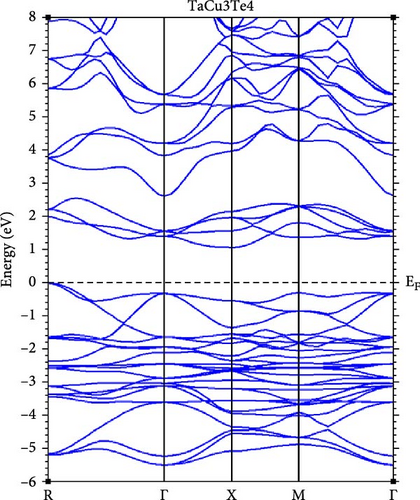
Table 2 presents a comparative analysis of the bandgap values for TaCu3S4, TaCu3Se4, and TaCu3Te4, obtained using various computational methods (GGA-PBEsol, GGA-PBE, GGA-PBEsol+U, HSE06, and G0W0) alongside experimental data. In general, the GGA-PBE and GGA-PBEsol functionals systematically underestimate the band gaps, which aligns with the known limitations of standard DFT approximations. The GGA-PBEsol+U method provides slight improvements, suggesting that on-site Coulomb corrections enhance accuracy. More advanced methods, such as HSE06 and G0W0, show significantly better agreement with experimental results, particularly for TaCu3S4 and TaCu3Se4. For TaCu3S4, the experimental bandgap of 2.70 eV is best approximated by HSE06 (2.94 eV) and G0W0 (3.94 eV), while GGA-based methods predict lower values. Similarly, in TaCu3Se4, the experimental bandgap of 2.35 eV is closely matched by HSE06 (2.47 eV) and G0W0 (2.38 eV), confirming the necessity of hybrid functionals or many-body perturbation theory for reliable predictions. However, for TaCu3Te4, there is a significant discrepancy, as GGA-PBE predicts a nearly metallic state (0.14 eV), while GGA-PBEsol+U provides a more reasonable estimate (1.11 eV). The absence of HSE06 and G0W0 results for this compound, coupled with the lack of experimental validation, limits a comprehensive assessment. Overall, the results indicate that standard GGA functionals are inadequate for accurate band gap predictions, while HSE06 and G0W0 yield significantly improved agreement with experimental values. The substantial deviations in TaCu3Te4 further highlight the necessity for higher-level theoretical treatments and experimental confirmation.
From another standpoint, the bandgap of TaCu3X4 (X = S, Se, Te) is notably influenced by compositional variations and the inherent properties of these materials. One major shortcoming is that substituting chalcogen elements (S → Se → Te) results in a gradual bandgap reduction. This decrease arises from the lower electronegativity of heavier chalcogens, which enhances covalent bonding and modifies the electronic structure. Consequently, this shift can lead to diminished optical performance in certain applications and reduced carrier mobility in Te-rich compounds, potentially hindering TE efficiency [75].
3.2. Density of States
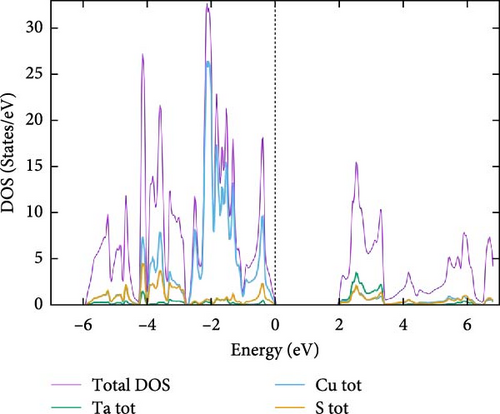
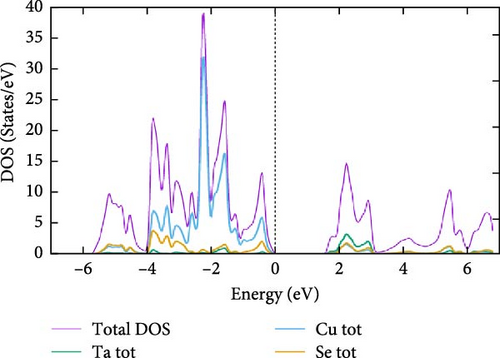
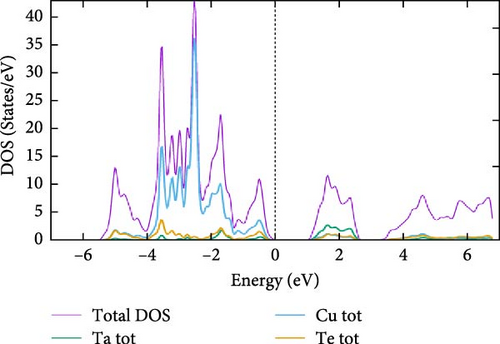
For a more comprehensive analysis of the electronic band structures, Figure 4a–c presents the combined total and partial DOS for TaCu3X4 (X = S, Se, Te), calculated using the mBJ formalism, spanning from −6.0 to 6.0 eV. It is evident that all the materials under investigation display a semiconductor gap, within which the contributions to the total density of states (TDOS) from individual elements are discernible. The DOS reveals that the upper valence band, ranging from 0 to −4.0 eV, is predominantly composed of S–p, Se–p, and Te–p orbitals, with additional minor contributions from other elements. The electronic states within the −4.0 to −6.0 eV range are primarily attributed to S–s states. In the higher energy regions of the CB, the electronic densities are derived from the hybridization of Ta-d states with minor contributions from other orbitals. Additionally, the DOS analysis highlights significant hybridization near the Fermi level, predominantly due to the interaction of Ta, Cu, S, Se, and Te–p states in the valence band. This suggests that materials with wider bandgaps are more likely to exhibit superior optical properties [76].
3.3. Effective Masses
To obtain accurate effective masses, new values of k-points originating from the valence band maximum and CBM were explored. These k-points were sampled up to 100, covering the high-symmetry points within the Brillouin zone with a length of 2π/a0. These sets were applied within the FP-LAPW method, utilizing analytical parabolic curve fitting. Notably, the nature of the bands transitioned from direct to indirect at an inflection point of 0.6 for the chalcogenides TaCu3X4 (X = S, Se, Te) [78, 79]. Consequently, a minor increase in the hole masses was observed compared to the electron masses, as detailed in Table 3. From the same perspective, the increasing ionic radius from S to Te also contributes to a higher effective mass of carriers, which reduces the charge transport efficiency, especially in Te-rich materials. This limitation is particularly relevant for TE applications, where high carrier mobility is essential for efficient energy conversion [80].
| Compounds | Hole effective masse (LVB) / | Hole effective masse (UVB) | Electron effective masse (CB) |
|---|---|---|---|
| TaCu3S4 | 1.81 | 1.78 | 1.92 |
| TaCu3Se4 | 1.85 | 1.89 | 1.93 |
| TaCu3Te4 | 0.95 | 0.94 | 1.86 |
3.4. Optical Properties
Before delving into our analyses, it is crucial to highlight the isotropic nature of the scrutinized chalcogenides, where their responses are independent of the direction of excitation. Consequently, their optical properties remain invariant regardless of the orientation of the incident electric field.
Beginning with an exploration of the absorption coefficient α (ω) (Figure 5a), it is noteworthy that the onset of the spectrum reveals a series of distinct peaks. These peaks represent electron transitions from the VBM to the CBM. Upon examining the curves of the three compounds, a clear trend emerges: the absorption coefficients progressively increase, reach their peaks, and then decline. Notably, the lowest energy point of this ascent corresponds to tellurium (Te), while for sulfur (S) and selenium (Se), it shifts to higher energy levels. These critical inflection points align precisely with the energy gaps intrinsic to each compound. When focusing on their respective maxima, sulfur exhibits the highest value, followed by tellurium, and then selenium [84–86].
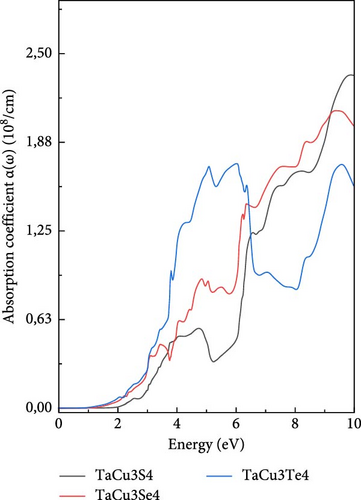
The broad absorption range underscores the versatility and suitability of these materials for various optoelectronic applications, particularly in the realm of solar cells. These findings align with the results illustrated in Figure 4.
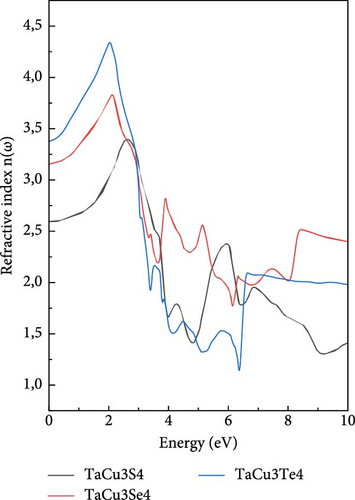
Examining the refractive index depicted in Figure 5b, it is clear that the curves follow a trend similar to that of reflectivity. The indices gradually increase, reaching peak values within the visible spectrum, and then decline. However, the sulfur compound exhibits a distinct behavior by maintaining a significant value at higher energies, unlike the other compounds. Notably, the static refractive index values, denoted as n (0), decrease as one transitions from tellurium to sulfur within the chalcogenide elements [87, 88].
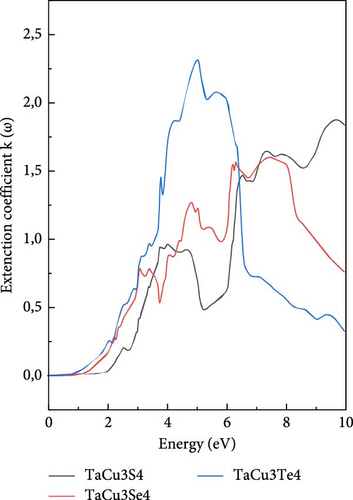
Conversely, the extinction coefficient k(ω) shown in Figure 5c rapidly escalates to its peak before gradually diminishing. As with other optical parameters, the sulfur compound exhibits the lowest k (ω) value, followed by selenium, with tellurium displaying the highest value [89].
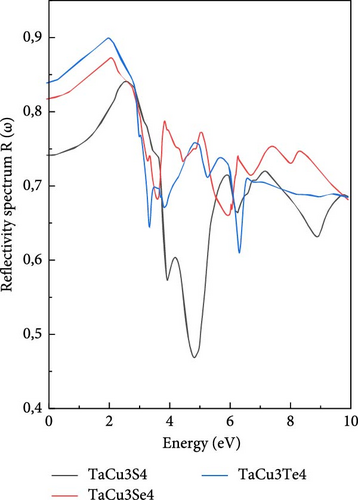
Regarding the reflectivity spectra R(ω) depicted in Figure 5d, it is observed that reflectivity increases at lower energy levels, reaching a peak at ~2.5 eV, before declining. Selenium and tellurium display similar behaviors, while sulfur diverges by showing a lower reflectivity at lower energies but the highest at higher energies. The initial reflectivity value, R (0), decreases as one transitions from tellurium to sulfur through selenium. Moreover, the maximum reflectivity for these compounds occurs at lower energies within the visible spectrum. These observations suggest that sulfur is more transparent compared to selenium and tellurium [90].
The impact of the different chalcogenide atoms on the bandgap energy, as illustrated in Figure 6, is significant. The lowest bandgap, 2.1 eV, corresponds to tellurium, the heaviest chalcogen. This bandgap increases to 2.2 eV when tellurium is replaced by selenium, and further to 2.4 eV with sulfur. This trend can be explained by the availability of free electrons in the CB and the presence of vacancies near the Fermi level. These findings indicate the potential for tuning the band gaps of these materials by varying the chalcogenide elements. In the same context, the compositional variations in TaCu3X4 (X = S, Se, Te) introduce mid-gap states that reduce optical transparency, potentially limiting their suitability for photovoltaic applications [91].
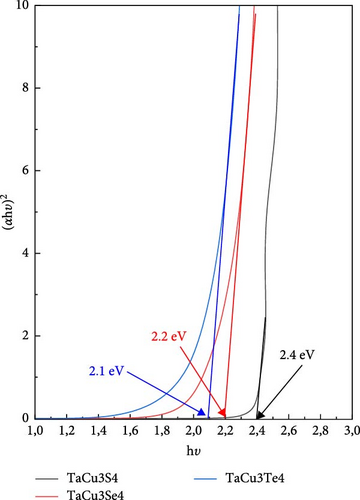
Table 4 presents a comparative analysis of the optical properties of TaCu3X4 (X = S, Se, Te) from the present work with previously reported ternary chalcogenides. It includes key parameters such as the dielectric functions, absorption coefficient, refractive index, and reflectivity spectrum.
| Compounds | TaCu3S4 | TaCu3Se4 | TaCu3Te4 | |
|---|---|---|---|---|
| Absorption coefficient (cm−1) | Present work α (ω) max | 2.30 | 2.03 | 1.72 |
| Related work α (ω) max | ||||
| Refractive index | Present work n (0) | 2.59 | 3.12 | 3.36 |
| Related work n (0) | ||||
| Reflectivity spectrum | Present work R (0) | 0.74 | 0.81 | 0.84 |
| Related work R (0) | ||||
| Extinction coefficient | Present work k (ω) max | 1.8 | 1.6 | 2.4 |
| Related work k (ω) max | ||||
Our results demonstrate that the static dielectric constant ε1 (0) values obtained in this study, 6.7, 8.2, and 11.22 for TaCu3S4, TaCu3Se4, and TaCu3Te4, respectively, are generally comparable to or slightly lower than previously reported values. The imaginary dielectric function ε2, which corresponds to optical absorption strength, shows a significantly high value in the present work, 10.13 (S4), 11.2 (Se4), and 16.1 (Te4), indicating strong electronic transitions in these materials.
The absorption coefficient in the present study is significantly higher (2.3 × 108 cm−1 for TaCu3S4, 2.03 × 108 cm−1 for TaCu3Se4, and 1.72 × 108 cm−1 for TaCu3Te4) than the related works, which report much lower values in the order of 104 cm−1. This indicates that TaCu3X4 materials have a stronger optical absorption, making them more efficient for optoelectronic and photovoltaic applications [94].
The static refractive index n (0) values in this study (2.59, 3.12, and 3.36) are higher compared to previously reported values (mostly below 2.5). This suggests enhanced optical confinement in TaCu3X4, which can be beneficial for photonic applications requiring strong light–matter interactions [95].
The reflectivity values in the present work (0.74, 0.81, and 0.84) are significantly higher than those of previously reported compounds, which generally show much lower reflectivity (below 0.2). This confirms that TaCu3X4 (X = S, Se, Te) materials exhibit a stronger optical response and lower transparency, which is essential for applications in optical coatings and photonic devices [96].
The comparison highlights that the studied compounds exhibit superior optical properties compared to previously studied ternary chalcogenides. Their higher dielectric constant, stronger absorption, higher refractive index, and greater reflectivity suggest excellent potential for UV detectors [93], optoelectronic devices [97], and next-generation photovoltaic materials [92]. These findings reinforce the significance of TaCu3X4 (X = S, Se, Te) in the development of high-performance optical materials [98].
4. TE Properties
To calculate the transport properties of TaCu3X4 (X = S, Se, Te), we utilized the BoltzTrap code, which is based on semiclassical Boltzmann theory. A material is considered more efficient if it exhibits a high electrical conductivity, a substantial Seebeck coefficient, and low electronic thermal conductivity. In this study, we investigated the TE parameters across a temperature range from 200 to 1000 K. Specifically, we computed the electrical conductivity (σ/τ), where τ represents the relaxation time, electronic thermal conductivity (κe/τ), Seebeck coefficient (S), power factor (PF), and the figure of merit (ZT) of TaCu3X4 (X = S, Se, Te).
Leveraging the WIEN2k software in conjunction with the BoltzTraP code, which utilizes the constant relaxation time approximation (CRTA) to estimate electronic conductivity and the Seebeck coefficient [65, 99], we performed a comprehensive first-principles investigation into the TE characteristics of TaCu3X (X = S, Se, Te) compounds. The BoltzTraP framework allowed for the precise computation of fundamental transport coefficients, including the Seebeck coefficient (S), electrical conductivity (σ), PF, electronic thermal conductivity (κ), and figure of merit (ZT), within a non-spin-polarized formalism over a broad temperature range from 25 to 1000 K. To ensure high numerical accuracy and convergence, a dense k-point mesh (10 × 10 × 10) was employed alongside the mBJ exchange-correlation potential, which enhances the fidelity of band structure and transport property predictions. This rigorous computational approach establishes a solid theoretical foundation for investigating the TE efficiency of these materials and assessing their potential for energy conversion applications [100–103].
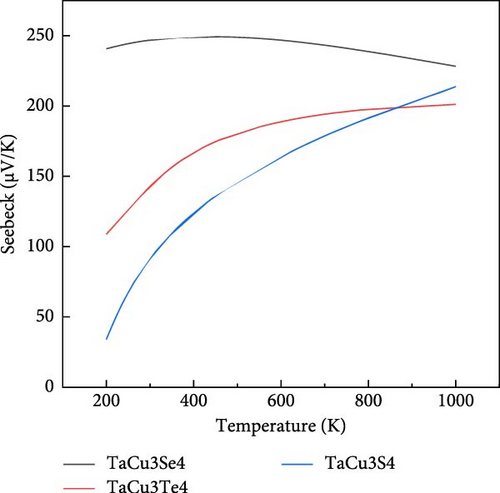
The TE potential of TaCu3X4 (X = S, Se, Te) is primarily driven by its high Seebeck coefficient, which plays a crucial role in achieving efficient TE performance. As shown in Figure 7a, the Seebeck coefficient exhibits a positive correlation with increasing temperature in both TaCu3Te4 and TaCu3S4, with computed values remaining positive across the entire temperature range for all the studied compounds. This indicates that holes are the majority charge carriers, confirming their p-type conduction behavior [92, 93]. The Seebeck coefficient increases as the X-site anion changes from S to Se to Te, suggesting that larger ions reduce carrier mobility during thermal agitation, which enhances the TE voltage. However, in TaCu3Se4, the Seebeck coefficient initially rises with temperature up to 400°C, after which a slight decrease is observed. The significant upward trend observed in TaCu3S4 highlights its greater sensitivity to temperature variations [104, 105].
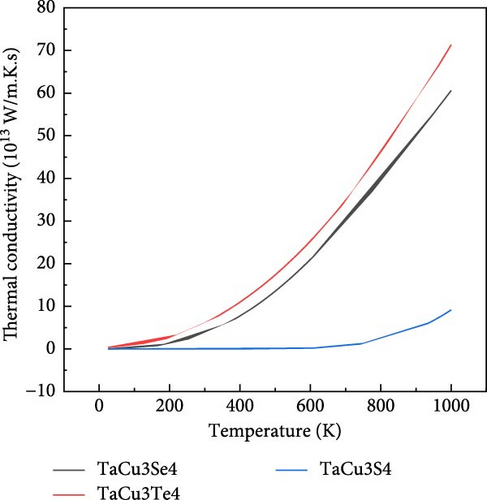
The variation in electronic thermal conductivity (κe) is directly linked to the electronic structure, influencing the heat transport mechanism in these materials. The observed positive temperature coefficient of resistivity further supports their potential as efficient TE materials. As shown in Figure 7b, the electronic thermal conductivity (κe/τ) of TaCu3X4 (X = S, Se, Te) is presented as a function of temperature, using a CRTA of τ = 10−14 s [106]. It is observed that κe/τ gradually increases with rising temperature across all examined materials, with tellurium and selenium showing a significant upward trend. In contrast, sulfur exhibits a more modest increase up to 700°C, after which the rate of increase becomes more pronounced [81].
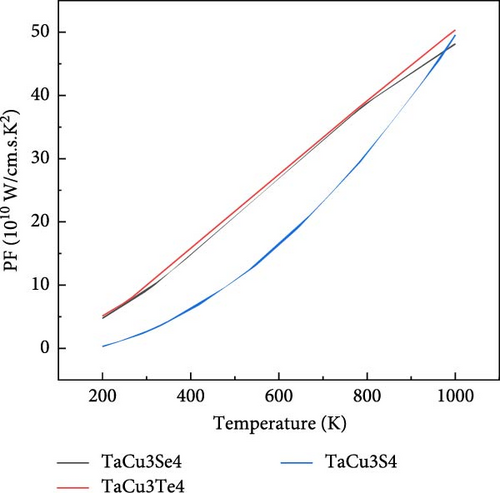
The efficiency of a TE material is often reflected by its PF, which is the product of electrical conductivity and the Seebeck coefficient. Figure 7c shows the variation of PF with temperature. It is evident that all materials display a similar trend, particularly tellurium and selenium, which exhibit nearly identical behavior. These characteristics suggest that tellurium and selenium possess favorable attributes for use in waste heat management applications [107, 108]. Sulfur also demonstrates a notable sensitivity to temperature, especially at elevated temperatures compared to other elements.
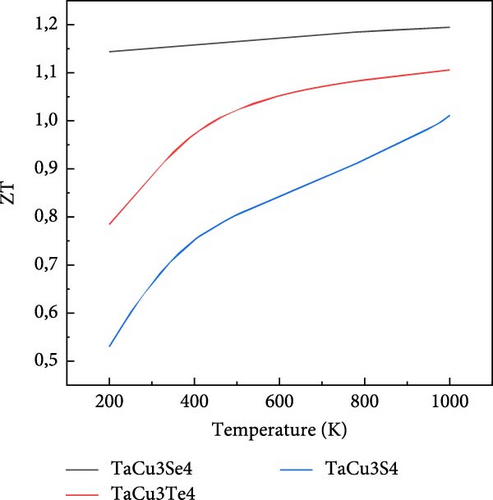
Another important transport parameter that measures the efficiency of TE materials is the figure of merit (ZT) [109, 110]. A material is considered more suitable for TE applications if its ZT value is high, which occurs with a combination of high electrical conductivity, a strong Seebeck coefficient, and low thermal conductivity, as depicted in Figure 7d. The variation of ZT with respect to temperature is observed and analyzed in Table 5.
| Compounds | Seebeck coefficient (μV/K) | Thermal conductivity (W/Kms) | Power factor (1010 W/mK2s) | Figure of merit (ZT) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 300 K | 1000 K | 300 K | 1000 K | 300 K | 1000 K | 300 K | 1000 K | ||
| TaCu3S4 | 73 | 209 | 1.04 | 0.45 x 10 (14) | 2.11 | 47 | 0.65 | 0.96 | |
| TaCu3Se4 | 247 | 224 | 3.66 | 6.06 x 10 (14) | 7.32 | 46 | 1.12 | 1.19 | |
| TaCu3Te4 | 126 | 193 | 6.04 | 7.13 x 10 (14) | 8.13 | 50 | 0.75 | 1.07 | |
Furthermore, the structural robustness, optimized chemical composition ratios, and mechanical stability of Ta-series compounds contribute to their suitability for TE energy conversion and refrigeration devices. Their environmental sustainability, owing to the use of nontoxic elements, makes them an attractive choice for next-generation energy applications [71]. These findings align with previous studies on similar chalcopyrite and Li-based TE materials, reinforcing the potential of TaCu3X4 compounds in sustainable energy solutions.
The variation of S, κe/τ, PF, and ZT at two significant temperatures, 300 and 1000 K, is presented in Table 5, which highlights the TE properties of TaCu3S4, TaCu3Se4, and TaCu3Te4. The results indicate that TaCu3Se4 and TaCu3Te4 exhibit elevated Seebeck coefficients, suggesting superior TE performance. Notably, TaCu3Te4 demonstrates the highest PF and ZT at both temperatures, underscoring its exceptional efficiency in converting thermal energy into electrical energy. Furthermore, the thermal conductivity of all compounds decreases significantly at higher temperatures, with TaCu3S4 showing the lowest value at 1000 K. These combined attributes position TaCu3Se4 and TaCu3Te4 as the most promising materials for TE applications.
5. Conclusion
In essence, the electronic, optical, and TE properties of the chalcogenide materials TaCu3X4 (X = S, Se, Te) have been meticulously scrutinized using DFT and semi-classical Boltzmann theory. Our investigation reveals that these compounds exhibit clear semiconductor characteristics, defined by a direct bandgap. Additionally, optical analyses demonstrate a significant absorption coefficient, nearing 108cm−1 within the visible spectrum, positioning these materials as strong candidates for nano-optoelectronic applications. The TE investigation further shows that TaCu3X4 (X = S, Se, Te) materials possess commendable and consistent electronic figure of merit values across a wide temperature range, with TaCu3Se4 standing out for its particularly promising ZT efficiency. Consequently, our findings highlight the significant potential of TaCu3X4 (X = S, Se, Te) materials in advancing both optoelectronic and TE technologies. The investigated materials demonstrated potential for TE and optoelectronic applications, especially due to their low cost and use of nontoxic elements. However, their efficiency is still developing compared to more established materials such as Bi2Te3 and PbTe. Despite this, their scalability makes them an attractive alternative for sustainable energy solutions, provided their efficiency can be enhanced through further material optimization. Future research will be crucial in determining whether these materials can achieve competitive ZT values and performance on par with state-of-the-art TEs. Nonetheless, while TaCu3X4 (X = S, Se, Te) materials demonstrate promising properties, shortcomings related to carrier transport, optical performance, and material stability need to be carefully managed for real-life applications. The challenge lies in balancing these limitations while optimizing the materials for TE and optoelectronic technologies, ensuring that their properties align with specific application requirements.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Conceptualization: Issam El Bakkali, Abdelali Talbi, Amina Lemnawar. Formal analysis: Issam El Bakkali, Abdelali Talbi. Investigation: Issam El Bakkali, Abdelali Talbi. Methodology: Mohamed Louzazni, Issam El Bakkali, Abdelali Talbi. Project administration: Mohamed Louzazni, Khalid Nouneh. Resources: Abdelali Talbi, Amina Lemnawar. Supervision: Mohamed Louzazni, Khalid Nouneh. Validation: Mohamed Louzazni, Khalid Nouneh. Writing – original draft: Issam El Bakkali, Abdelali Talbi. Writing – review and editing: Mohamed Louzazni, Khalid Nouneh. All authors approved the final version for submission and agree to be accountable for all aspects of the work.
Funding
The research was supported by the Moroccan Ministry of Higher Education and Research and CNRST in the PPR/37/2015 project framework.
Open Research
Data Availability Statement
The data used to support the findings of this study are included within the article.




