In this study, two distinct approaches were proposed for recovering heat from the exhaust gases of electric arc furnaces (EAFs)—the steam cycle and the organic Rankine cycle (ORC). These methods were evaluated based on various criteria, including energy and exergy efficiency, economic feasibility, and environmental impacts. To identify optimal performance parameters, the effects of different working fluids in the ORC were examined, revealing significant variations in cycle behavior depending on the fluid used. Consequently, the most effective operational conditions for each specific fluid were identified and recorded based on temperature and pressure fluctuations. The analysis led to the selection of acetone as the optimal working fluid due to its favorable performance despite its high flammability, characterized by its isentropic nature. The energy and exergy efficiencies of the cycle using this fluid reached 21% and 61%, respectively, with a power output of 597.4 kW under maximum conditions. Additionally, the study demonstrated that, given the high temperature of the heat source, the steam cycle is more justifiable than the combined steam and ORC with the proposed configuration. The exergy efficiency of the steam cycle reached a maximum of 57%, with a net power output of 2897 kW and a total cost rate of $0.041/s under these conditions. Finally, by optimizing the steam cycle using a genetic algorithm, the ideal values for exergy efficiency were slightly reduced to 53%, with a significant decrease in the total cost rate to $0.036/s.

1. Introduction

Over time, industrial development and increased human activities have led to a higher increase in energy consumption than before. To meet this growing energy demand, a larger amount of fossil fuels are consumed daily [1]. The use of fossil fuels poses various health and environmental hazards for both humans and ecosystems. Additionally, fossil fuel reserves are limited, and their utilization results in the emission of greenhouse gases (GHGs), contributing to global warming [2]. On the other hand, energy sectors contribute significantly to GHG emissions. Large and energy-intensive industries play a significant role in carbon dioxide emissions [3]; steel and cement industries can be mentioned among these industries [4]. The steel industry is considered one of the largest energy-intensive industries. Steel production annually consumes 21% of the total energy produced and ranks second among the most energy-intensive industries [5]. Global crude steel production for 63 countries was reported to be 152.6 million tons (Mt) in August 2023, representing a 2.2% increase compared to August 2022, according to the World Steel Association. Additionally, global steel demand is expected to grow by more than one-third by the year 2050 [6]. Therefore, recovering wasted energy in these industries can enhance their performance and reduce their emissions [7].

Over the past decades, the steel industry has experienced significant advancements in developing new techniques for energy efficiency [8]. There are ample opportunities throughout the steelmaking process to implement energy-efficient technologies [9]. The largest potential for waste heat in steel plants pertains to the electric arc furnace (EAF) and the reheating furnace (RHF), which are primary processes [10]. Here, we focus on analyzing waste heat from the EAF as the largest source of heat loss in a steel plant. However, besides these primary sources, there are several other sources of wasted heat in a steel plant, such as slag pits, roller tables, or cooling lines in the rolling mill. Although they only provide radiative heat, they can be utilized as small-scale recovery solutions in a heat exchanger (HEX) [11].

Numerous studies have been conducted regarding EAFs, which are commonly used in steel plants. Energy balance studies on EAFs indicate that energy input to these furnaces is wasted in various ways, including exhaust gases, furnace walls, losses due to roof opening, water cooling, radiation losses, and other inefficiencies, with exhaust gases from the furnace accounting for the largest share. Therefore, heat recovery studies from EAFs have primarily focused on recovering heat from this part. Generally, various studies have been conducted on different methods of heat recovery from hot exhaust gases in industries such as steel, cement, glass, and others, involving both high and low-temperature levels. One of the primary methods of heat recovery from exhaust gases in various industries is the utilization of organic Rankine cycles (ORCs). Hoang [12] has investigated ORCs for heat recovery, especially in diesel engines. The results show up to 10% fuel savings, with an overall thermal efficiency of 60%–90% for two or multiloop ORC compared to 10%–25% thermal efficiency for single-loop ORC systems. Liu et al. [13] aimed to enhance marine engine performance and reduce GHG emissions by introducing a new waste heat recovery (WHR) system combining steam and ORCs. Their results show that the new system reduces fuel consumption by up to 9322 tons per year at 100% engine load and increases thermal efficiency by 4.42%. In comparison, a WHR system based on a single steam RC and dual pressure ORC only improves thermal efficiency by 2.68% and 3.42%, respectively. Liao et al. [14] proposed and explored integrated systems based on the ORC as potential solutions for harnessing waste heat from low-to-moderate-temperature flue gases, employing both energy and exergy analysis techniques. The findings of the study showed that compared to ORC systems that solely rely on supercritical carbon dioxide (sCO₂), the incorporation of R601a as the working fluid led to significant improvements in thermal and exergetic efficiency, achieving improvements of 16.37% and 45.54%, respectively.

ORC units offer a promising solution for transforming existing industrial plants into carbon-neutral facilities [15]. Bălănescu and Homutescu [16] investigated the addition of an ORC unit downstream of a combined cycle power plant to increase its efficiency. The combined cycle power plant was based on an Orenda OGT15000 gas turbine with a simple cycle output of 16.5 megawatts. This study demonstrated that by adding the ORC unit, the efficiency of the power plant increased by approximately1.1%. Ghoreishi et al. [17] undertook modeling of ORC with various configurations and working fluids, presenting the results in their optimal state. Ultimately, ORCs utilizing n-heptane and toluene were recommended due to their highest efficiencies. Following optimization aimed at making the system more cost-effective, the second law efficiency increased by 5% to reach 20.6%, while the Net Financial Index (NFI) increased by 44.2%.

Holik et al. [18] addressed the heat recovery from exhaust gases in a combined cycle through the RC and ORC, optimizing the proposed system based on the minimum payback period (PBP) and maximum economic output power. The results indicated that the overall energy and electrical efficiencies of the system would reach 66.7% and 42.1%, respectively. After optimization, it was determined that, ultimately, the steam cycle is more economically viable than the ORC, with a total power plant efficiency increase of 2.97%. Kizilkan [19] studied heat recovery from a Brayton closed-cycle power plant, comparing a sCO₂ ORC with a simple RC. The results showed higher exergy and energy efficiencies for the ORC compared to the steam cycle. Subsequently, different supercritical working fluids were analyzed, and CO₂ was recommended for its energy efficiency of 27.9%.

Khater et al. [20] investigated heat recovery in a cement plant using RC, ORC, and their combination. They proposed six RC schemes and selected cyclopentane as the optimal working fluid for its availability, low cost, and short PBP despite isopropyl pentane showing higher net power and thermal efficiency. The combined steam-ORC was found to be the most effective for high-temperature WHR. Ja’fari et al. [21] studied design criteria, achievable performance, and component costs for ORCs. Various working fluids for the ORC were considered in this research. Additionally, attention was paid to balancing the energy of the EAF as one of the main sources of waste heat generation in the steel production industry.

EAF exhaust gases constitute an intermittent heat source. Therefore, the adaptation of power recovery systems to these temperature fluctuations is a matter of significant importance. Yu et al. [22] propose and investigate integrating an ORC with a latent thermal energy storage (LTES) system to enhance engine WHR, addressing intermittent and fluctuating conditions in-vehicle applications. A melting-solidification model analyzed 12 phase change materials (PCMs), identifying LiNO₃-KCl-NaNO₃ as the optimal PCM for engine exhaust heat recovery. Comparing three LTES-ORC scenarios revealed that combining ORC with double LTES yields 17.2% more total power output than a single LTES (100 L) under similar conditions. Yu et al. [23] investigated the ORC for low-grade WHR, focusing on the effects of fluctuating thermal power from heat sources. Their study highlighted that safety limitations and efficiency of ORC systems generally decrease with increased amplitude and periods of fluctuations, while higher average temperatures of the heat source expand the allowable fluctuation range. To maintain efficient ORC operation, the allowable relative amplitude should be 25–40 K for large fluctuating periods and above 35 K for periods under 200 s.

Atashbozorg et al. [24] studied and optimized RC and ORC along with Kalina cycles using different arrangements and working fluids to design a WHRS in the steel industry. The results showed that the performance of the Kalina cycle was better than the others, and for ORCs, fluids R11 and R113 were suggested. Biondi et al. [25] conducted a technical-economic analysis of a WHRS using a closed-loop sCO₂ cycle for heavy industrial processes. They performed a parametric study on key design parameters, identifying preferred configurations from a thermodynamic standpoint, which were then analyzed economically. The optimal WHR system configuration achieved an overall efficiency of 30.4% and an output power of 21.6 kW.

As evident from the aforementioned studies, numerous research works have individually utilized steam cycles and ORC, with some also exploring these cycles in combination. However, most studies have predominantly focused on the applications of these cycles in nonfluctuating and low-temperature heat sources, lacking a comprehensive comparison between them. One of the innovations in the present study is the detailed evaluation of each of these cycles over a wide range of temperatures and pressures to assess their performance under various conditions. Additionally, a thorough comparison between the steam cycle and the proposed combined cycle has been conducted, taking into account economic and environmental parameters. Another feature of this analysis is the examination of different working fluids and the selection of the optimal fluid for the ORC, along with the bi-objective optimization of the steam cycle. This approach provides clarity and facilitates a more comprehensive comparison between the cycles under the conditions specified in the study.

In this study, the characteristics of exhaust gases from EAFs in the steel industry were introduced and identified as suitable potentials for heat recovery. Subsequently, ORC was evaluated individually and in combination with the steam cycle to assess their efficiency in recovering high-temperature and fluctuating heat sources, with detailed performance reports under various conditions. The study extends previous research by comprehensively comparing top working fluids identified in past literature under new conditions. Furthermore, the performance of the steam cycle was compared with that of the ORC and optimized from various aspects. Some of the innovations of this study are as follows:

•
A comprehensive and multifaceted comparative evaluation of ORC working fluids in a range of turbine inlet temperatures and showing the changes in their various behaviors with respect to this temperature.
•
A genetic algorithm-based optimization approach for enhancing exergy and economic performance of the final cycle: a coupled Engineering Equation Solver (EES)-MATLAB framework.
•
A comprehensive analysis of energy, exergy, economic, and enviroeconomic considerations for system evaluation.

2. System Description

This study aims to design a WHRS for exhaust gases from EAFs. For this purpose, two separate power generation cycles have been utilized, as illustrated in Figure 1, including Figure 1a: a simple cycle consisting of the RC, and Figure 1b: a combined cycle consisting of the RC and ORC. Finally, by examining the performance of the two cycles in optimal conditions in terms of energy, exergy, economy, and environmental aspects, the two cycles were compared with each other. It is worth mentioning that the EES software was used for simulating the cycles, and the system optimization was performed by the genetic algorithm of MATLAB software.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Overview of two thermal recovery cycle scenarios: (a) conventional steam cycle and (b) combined steam and organic Rankine cycle.

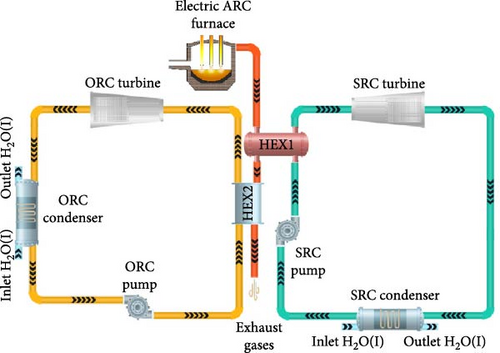
2.1. Methods and Material

In this section, some of the assumptions considered during the various stages are presented.

•
All processes have been considered as steady-state.
•
Pressure drop and gravitational effects have been ignored in all sections.
•
The ambient temperature and pressure are considered to be 298 K and 101.325 kPa, respectively.
•
The chemical composition of the exhaust gases is considered as follows: 0.25 CO₂, 0.25 CO, 0.50 N₂, where the coefficients represent the volume percentages of each component [26].

To better understand the potential of EAFs and obtain accurate values for the flow rate and energy of the exhaust gases from these furnaces, a number of these furnaces from previous studies listed in Table 1 have been used in the energy balance. The furnace specifications used in this study are derived from the average values presented in Table 1. Based on Table 1, a selected furnace capacity of 100 tons per hour has been considered, which is approximately equivalent to the average capacity of EAFs in previous studies and various factories (96.56 tons per hour). The exhaust gas energy is also estimated at 155 kWh per ton, obtained by multiplying the selected furnace capacity by the ratio of average gas energy to furnace capacity.

Table 1. Energy balance of EAFs [27–30].

Furnace capacity (t)	Off-gas energy (kWh/t)	Total energy (kWh/t)	EAF-electric energy (kWh/t)	Percent of off-gas energy (%)	Off-gas energy/furnace capacity
55	100	726	571	13.77	1.82
55	317	832	347	38.10	5.28
60	109	683	408	15.95	1.82
60	150	715	465	20.97	2.5
60	150	715	429	20.97	2.14
70	96	664	477	14.45	1.28
75	90	696	459	12.93	1.2
75	105	659	422	15.93	1.31
80	81	678	560	11.94	1.01
80	85	590	380	14.40	0.85
100	33	732	577	4.50	0.33
100	68	628	91	10.82	0.68
100	97	606	287	16.00	0.97
100	110	625	365	17.60	1.10
100	138	754	459	18.30	1.38
100	140	791	413	17.69	1.40
100	141	798	401	17.66	1.41
100	141	786	445	17.93	1.41
100	141	809	423	17.42	1.41
100	158	810	557	19.50	1.58
100	168	798	541	21.05	1.46
115	127	704	487	18.03	1.02
125	48	660	462	7.27	0.32
150	102	649	450	15.71	0.68
150	229	678	312	33.77	1.53
150	232	775	300	29.93	3.31
70	194	757	415	25.62	1.62
120	226	720	356	31.38	1.51
150	244	732	357	33.33	2.53
Average	Average	Average	Average	Average	Average
96.56	138.62	716.20	421.24	19.10	1.55

Abbreviation: EAFs, electric arc furnaces.

Another important characteristic of the exhaust gases from EAFs is their temperature. Regarding the temperature of these gases, it should be noted that this temperature varies depending on the different stages of the furnace cycle during the melting process, such as the start of melting, charging, slag tapping phase, and burner opening phase, as shown in Figure 2. For this reason, in most previous studies, an average temperature has been used for calculations. Based on Figure 2, this temperature can be considered to be 600°C [32].

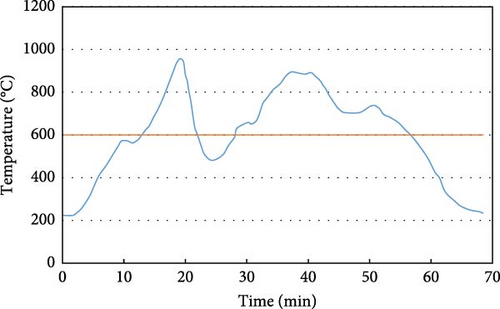
Now, with the temperature and constituents of the exhaust gases, the enthalpy of these gases, equal to 808.9 kJ/kg, has been determined. Moreover, knowing the enthalpy of these gases along with their energy, the mass flow rate can be calculated by dividing the energy by the enthalpy, resulting in a value of 19.12 kg/s.

The remaining computational parameters used for the investigated system are listed in Table 2.

Table 2. The computational parameters used.

Parameters	Value	Parameters	Value
Isentropic efficiency of ORC turbine	0.85	Isentropic efficiency of SRC turbine	0.9
Isentropic efficiency of ORC pump	0.85	Isentropic efficiency of the SRC pump	0.8
Exhaust gas temperature	873 K	Exhaust gas flow rate	19.2 kg/s
Heat exchanger pinch point temperature difference	10 K	Condenser pinch point temperature difference	5 K

Abbreviations: ORC, organic Rankine cycle; SRC, steam Rankine cycle.

2.2. System Modeling

As mentioned, the system studied in this research consists of two RCs: a steam Rankine cycle (SRC) and an ORC. The general thermodynamic equations for modeling these cycles are as follows:

Mass continuity equation:

(1)

Energy continuity equation:

(2)

This equation states that the energy input and output of a device undergoing a thermodynamic process must be equal.

Entropy and exergy balance equation:

(3)

(4)

Among other important and necessary equations in Rankine vapor and organic cycles, we can mention the energy and exergy efficiencies of these cycles, which are defined as follows.

(5)

(6)

In the above equations,

and

represent the heat and exergy input to the cycle, respectively, and the network of the cycle is equal to the following:

(7)

For energy and exergy efficiencies in the combined cycle, we also have the following:

(8)

(9)

2.3. Enviroeconomic Analyses

In this section, the aim is to determine the amount of carbon dioxide that can be prevented from being emitted per unit of recovered power. Considering that the average carbon dioxide emission intensity per kilowatt-hour of energy produced in the United States is reported to be 0.364 kgCO₂/kWh [33]. The following formula can be used for this purpose [34]:

(10)

On the other hand, to calculate the economic value of reducing the emission of each ton of carbon dioxide, one can utilize the parameter carbon credits gain (CCG) as follows [35]:

(11)

The trade cost of CO₂ in the above formula is currently set at $40 per ton.

2.4. Economic Analysis

The equations used to calculate the price related to each component of the system in both scenarios are presented in Table 3 [36, 37].

Table 3. Cost functions of system components [36–38].

Components	Cost function
RC condenser
RC turbine
RC pump
ORC turbine
ORC pump
ORC condenser

Abbreviations: ORC, organic Rankine cycle; RC, Rankine cycle.

To calculate the total initial capital (Z_tot) and operations and maintenance capital (Z_O&M), we have [39] the following:

(12)

(13)

Also, the real interest rate is defined as follows [40]:

(14)

where i and r represent the nominal interest rate and the inflation rate, respectively.

Finally, the parameter levelized cost of energy (LCOE) will be calculated as follows [41]:

(15)

While AEP represents the annual energy production, and n equals the project’s lifetime.

The net present value (NPV) of the project [40]:

(16)

Detailed calculations related to this section can be found in Appendix A.

The PBP [40]:

(17)

The EUAB represents the equivalent uniform annual benefit, and the electricity selling price in the calculations above is assumed to be 0.023 $/kWh.

2.5. Working Fluids

The thermodynamic behavior of working fluids can be identified based on the slope of their thermodynamic curves [42]. Working fluids are categorized into three groups based on the slope of their saturation vapor curve (dT/dS): dry fluids with dT/dS > 0, wet fluids with dT/dS < 0, and isentropic fluids with dT/dS ≈ 0 [43]. The T–s diagrams corresponding to each category are shown in Figure 3. Since there is no significant working fluid available, some fluids whose saturation vapor curve slope is approximately in the range between −0.5 and 0.5 can be considered isentropic fluids [44]. In systems with low inlet turbine temperatures and high inlet pressures, moist working fluids with a negative slope on the diagram may have lower efficiency due to compression and significant quality drop at the turbine outlet, leading to potential damage to the blades and system inefficiency. On the other hand, dry and isentropic working fluids demonstrate good performance because these fluids will approach isentropic expansion in the superheated region [45]. In general, the selection of a suitable working fluid plays a vital role in the performance of an organic cycle. Depending on the temperature and operational conditions of the organic cycle, the proper selection of the working fluid can lead to increased efficiency and reduced initial costs and system inefficiencies [46–48]. Therefore, the working fluid should have optimal properties at suitable states, considering numerous criteria such as economic viability, nontoxicity, nonflammability, environmental compatibility, and safety [49]. Furthermore, crossing the maximum temperature limit of the working fluid’s chemical decomposition can lead to sudden changes in its properties, which may result in instability within the system [50]. Mago et al. [51] and Hung et al. [52] concluded that wet fluids experience a decrease in efficiency with increasing temperature. Additionally, the study by Köse et al. [53] showed that isentropic fluids perform better than dry fluids under conditions similar to those in the present study.

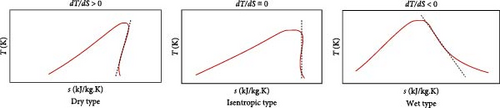
In the present study, considering the mentioned standards and the high temperature of the waste heat sources used, it was concluded that isentropic fluids, which have shown better performance in previous studies, along with some dry fluids, would be used. These fluids include R113, R141b, acetone, R600, R245fa, and R123, and they are examined in Table 4. As indicated in Table 4, each of these fluids has its advantages and disadvantages compared to others. Some fluids may perform better, but they might pose serious environmental and safety risks. Therefore, all aspects need to be considered when evaluating these fluids. Regarding the parameters of ozone depletion potential (ODP) and global warming potential (GWP) [59].

Table 4. Properties of the working fluids [14, 53–58].

Working fluids	Type	T_crit ( °C)	P_crit (MPa)	T_Max ( °C)	Flammability	Toxicity	GWP	ODP	Safety group
R113	Dry	252	3.392	214	Low	None	6130	0.85	A1
R141b	Isentropic	227	4.212	204	Medium	Low	717	0.12	A2
Acetone	Isentropic	276	4.7	234	High	Low	0.5	0	A3
R600	Dry	302	3.8	152	High	Low	20	0	A3
R245fa	Isentropic	167	3.651	154	None	High	1050	0	B1
R123	Dry/Isentropic	327	3.668	183	None	High	77	0.02	B1

Abbreviations: GWP, global warming potential; ODP, ozone depletion potential.

3. Results and Discussion

In this section, the performance of the first scenario, namely the RC, was initially evaluated parametrically from various perspectives, and the results were discussed. Subsequently, by examining the RC, the performance of different selected working fluids was demonstrated in various ways, and the working fluid that exhibited the best performance was introduced. In the next section, the second scenario, which includes a combined cycle of RC and ORC, was investigated. Finally, the RC was optimized using a genetic algorithm, and by applying the optimal parameters, the performance of the two scenarios was compared from four perspectives: energy, exergy, economic, and environmental, in the most optimal conditions.

3.1. SRC Cycle

To analyze the parametric performance of the steam cycle, the performance of the cycle was evaluated against changes in the inlet turbine temperature and pressure, ranging from 473 to 753 K and 1–10 megapascals, respectively. The variations in parameters such as energy efficiency, exergy, net power output, fluid flow rate, and steam quality at the turbine outlet can be observed in Figure 4.

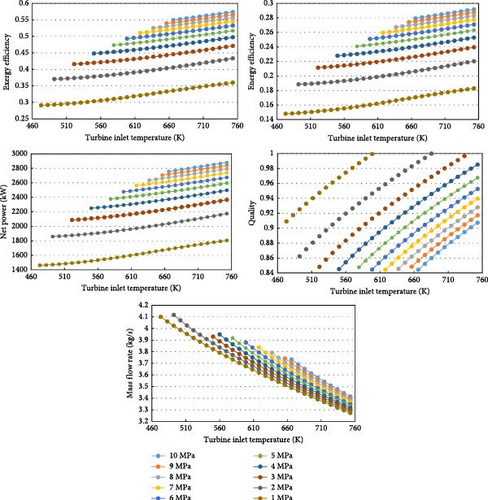
Based on the results presented in Figure 4, it is evident that the system performance improves with an increase in the turbine inlet temperature and pressure. At the lowest turbine inlet temperature and pressure of 473 K and 1 MPa, respectively, the energy efficiency, exergy, and net power output are 0.148, 0.291, and 1461 kW. These values increase to 0.2917, 0.5736, and 2879 kW, respectively, at a temperature and pressure of 753 K and 10 MPa. Additionally, the trend of changes in steam flow rate throughout this range of temperature and pressure variations is completely inverse. The steam flow rate decreases from 4.1 to 3.415 kg/s with an increase in temperature and pressure. The trend of changes in the steam flow rate is such that it decreases with an increase in temperature and increases with an increase in pressure.

As depicted in Figure 4, the steam quality at the turbine outlet exhibits a decreasing trend with increasing pressure, while it increases with temperature. It is noteworthy that in this study, all parameters and variations have been considered to ensure that the steam quality at the turbine outlet remains above 0.8.

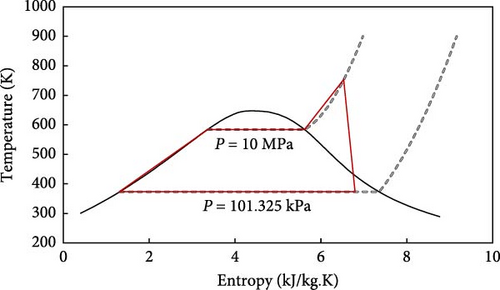
Based on the obtained results for the RC, the best performance of this cycle is observed at a temperature and pressure of 753 K and 10 MPa. Therefore, the temperature-entropy diagram of the steam cycle in this state is presented in Figure 5. Although this study employs a condensing pressure of 101.325 kPa for simplicity, exploring lower condensing pressures, such as 5 kPa, in conjunction with advanced cooling systems and multipressure evaporation strategies could significantly improve the thermodynamic performance of the system. These advanced configurations require further investigation in future studies to optimize cycle efficiency and assess their practical feasibility.

3.2. ORC Cycle

In this section, to facilitate a fair comparison between the selected working fluids, similar to the previous section, variations in parameters such as net cycle power, energy efficiency, and exergy, along with fluid mass flow rate for each fluid, are presented as functions of changes in turbine inlet temperature and pressure.

It’s worth noting that the range of temperature and pressure variations differs for each fluid and is based on the properties reported in Table 4. Specifically, the pressure range for each fluid starts from 1 MPa and continues up to its critical pressure. Similarly, the temperature variations start from the saturation temperature of the fluid at 1 MPa pressure and continue up to the maximum temperature reported for each fluid in Table 4.

The term “maximum temperature” refers to the highest temperature at which the chemical composition of the fluid remains intact. Beyond this temperature, chemical degradation occurs, leading to sudden changes in fluid properties. It should be emphasized that in this section, all parameters and variations have been considered in such a way that the steam quality at the turbine outlet remains above 0.9. Additionally, the condenser pressure in these cycles is assumed to be equal to atmospheric pressure, similar to the steam cycle.

The variations of net cycle power concerning turbine inlet temperature and pressure are depicted in Figure 6. According to the results presented in Figure 6, the net cycle power for different fluids exhibits different behaviors depending on the type of fluid (dry, moist, or isentropic). For instance, at high pressures, an increase in turbine inlet temperature results in an increase in net cycle power for the isentropic fluids, such as R141b, R245fa, and acetone. Conversely, for dry fluids like R113, R123, and R600, the net cycle power initially increases up to a certain pressure and then decreases. At lower pressures, we observe a different trend where, as we move from higher to lower pressures, the net cycle power decreases with an increase in temperature for R600 and R113. This trend is also observed with less intensity for R141b, R245fa, and R123, while for acetone, although the trend remains ascending, its intensity is reduced. Regarding the variations of net cycle power at constant temperature, it can be observed that, except for R141b and acetone, the net cycle power increases with an increase in turbine inlet pressure for all fluids. However, for these two fluids, the overall trend is similar to other fluids, but it reverses at higher pressures.

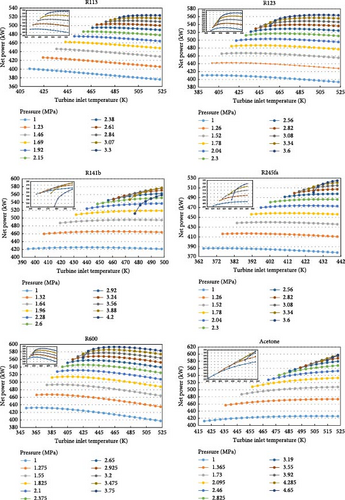
As depicted in Figure 6, the highest net cycle power is associated with acetone, occurring at a temperature of 523 K and a pressure of 4.285 MPa, yielding a value of 597.4 kW. Conversely, the lowest value is related to R113, occurring at a temperature of 523 K and a pressure of 1 MPa, resulting in a value of 376.1 kW.

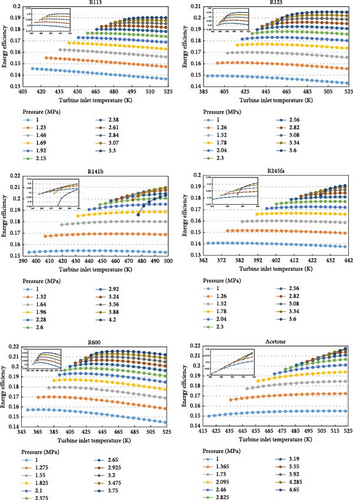
Another important parameter that has been investigated is the energy efficiency of the cycle, whose variations for each fluid are shown as a function of turbine inlet temperature and pressure in Figure 7. Considering the provided relationship for energy efficiency, it can be observed that the behavior of energy efficiency and net power output is similar, as shown in Figure 7 because they have a direct relationship with each other. As depicted in Figure 7, except for specific cases, the system’s efficiency has increased with the increase in turbine inlet temperature and pressure. The highest energy efficiency is equal to 0.2174, corresponding to acetone fluid at a temperature and pressure of 523 K and 4.285 MPa. Similarly, the lowest efficiency value is 0.1368, attributed to the R113 fluid under conditions of 523 K and 1 MPa.

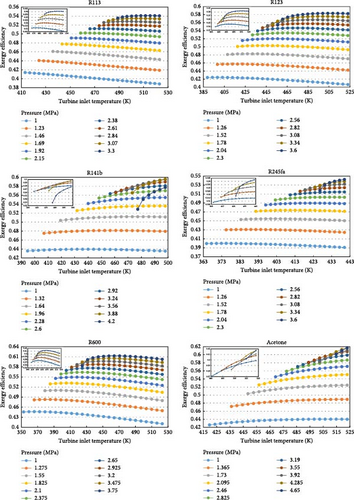
Another parameter is the exergy efficiency of the system, which exhibits a behavior similar to the previous two parameters and can be observed in Figure 8. As depicted in Figure 8, the highest exergy efficiency, like the previous parameters, occurs under similar conditions and is equal to 0.6173. Similarly, the lowest value of this parameter is 0.3886.

Finally, the mass flow rate of the fluid is examined as the last influential parameter, and the results are presented in Figure 9. According to Figure 9, the mass flow rate of fluids decreases with an increase in turbine inlet temperature, a trend observed in all fluids. Additionally, with an increase in turbine pressure, the mass flow rate exhibits a decreasing trend for all fluids as well. The lowest mass flow rate is 3.021 kg/s, observed for R600 under conditions of 523 K and 1 MPa, while the highest mass flow rate is 13.85 kg/s, observed for R113 under conditions of 413 K and 1 MPa. Furthermore, the mass flow rate for acetone under conditions of 523 K and 4.285 MPa, which had the highest energy efficiency, exergy efficiency, and net power output of the system, is 3.895 kg/s.

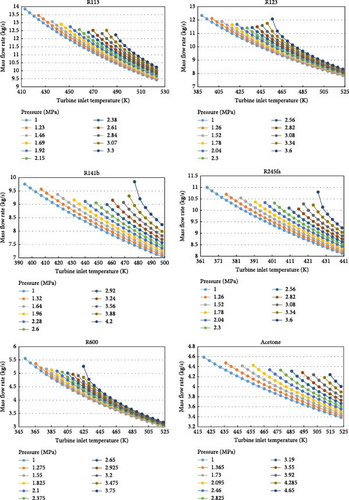
It is important to note that as the required fluid flow rate decreases in the cycle, the power required by the pump will also decrease. Considering this point, it can be expected that the power required by the pump will exhibit a behavior similar to the mass flow rate in response to changes in temperature and pressure. Therefore, the required mass flow rate of the fluid is significant, and having a lower value for the required mass flow rate can be considered an advantage. Now, to better understand and compare the selected fluids, the conditions corresponding to the best performance of each fluid are listed in Table 5.

Table 5. Characteristics of the best performance points of working fluids.

Working fluids	η_Max	φ_Max			T_tur(K)	P_tur(MPa)
R113	0.1904	0.5408	523.3	10.72	511.6	3.3
R141b	0.2099	0.5962	577	7.987	498	3.88
Acetone	0.2174	0.6173	597.4	3.895	523	4.285
R600	0.2157	0.6127	593	3.971	464	3.75
R245fa	0.191	0.5425	524.9	9.235	440	3.6
R123	0.2053	0.5832	564.3	8.927	503.8	3.6

According to Table 5, the order of fluids based on the best performance they demonstrated from strongest to weakest will be acetone, R600, R141b, R123, R245fa, and R113. It is clear that acetone, which is an isentropic fluid, performs best under the conditions of 523 K and 4.285 MPa.

While acetone is the best-performing fluid for ORC, its flammability poses significant environmental and safety risks. However, acetone has a lower GWP of 0.5 and ODP of 0, making it environmentally preferable. To mitigate flammability risks, an intermediate heat transfer circuit can prevent direct contact with heat sources. Using flame-resistant materials, installing fire and leak detection systems, and conducting regular safety training and emergency drills are essential. These strategies significantly improve the safety and environmental impact of using acetone in ORC systems. The temperature-entropy diagram corresponding to each fluid under the conditions specified in Table 5 can be observed in Figure 10. The potential safety hazards associated with the flammability of some organic working fluids warrant further investigation. Future research should explore the implementation of an intermediate heat transfer circuit, carefully considering its impact on system efficiency, cost-effectiveness, and overall system performance.

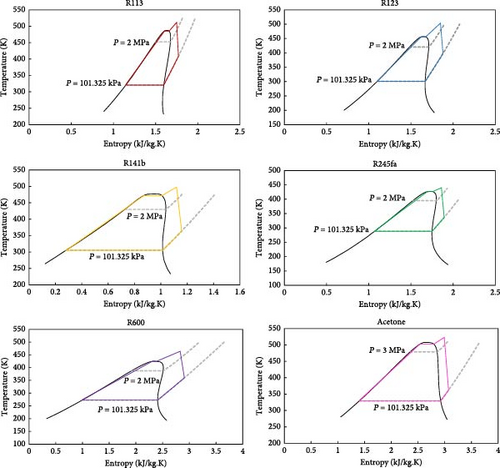
In previous studies, some examples support the results obtained in this study with acceptable accuracy. Köse et al. [53] examined organic cycles with six different working fluids, four of which include acetone, R141b, R113, and R245fa. By reviewing the reported ranges of energy and exergy efficiency for these four fluids, it is evident that the results obtained overlap with the present study. Additionally, Ghoreishi et al. [17] reported the energy efficiency for the working fluid R-245fa at a turbine inlet temperature and pressure of 373 K and 1.275 MPa to be 13.54%. In the present study, this energy efficiency at a turbine inlet temperature and pressure of 375 K and 1.26 MPa was calculated to be 15.15%, which aligns with their research with acceptable accuracy.

3.3. SRC–ORC Combined Cycle

In this section, the second scenario involving the combined SRC–ORC cycle, which consists of an RC and an ORC with acetone as the working fluid in their best operational conditions, has been examined. The results obtained from this scenario have been compared with the previous section and the SRC cycle in terms of energy, exergy, economics, and environmental aspects. To compare the two scenarios in terms of energy and exergy, parameters such as energy efficiency, exergy efficiency, and net power generation have been utilized. For the economic and environmental comparison of the two scenarios, parameters including total cost, NPV, PBP, and capital due to carbon emission reduction have been considered. The results of each scenario comparison can be found in Table 6.

Table 6. Performance results of two scenarios in different aspects.

Scenarios		η	φ	CCG ($/year)	Z_tot ($)	NPV ($)	PBP (year)
SRC	2879	0.29	0.57	335,391	1.196 × 10⁶	6.142 × 10⁶	2.714
SRC–ORC	2675	0.27	0.53	311,583	1.595 × 10⁶	4.755 × 10⁶	4.259

Abbreviations: CCG, carbon credits gain; NPV, net present value; ORC, organic Rankine cycle; PBP, payback period; SRC, steam Rankine cycle.

Based on the results presented in Table 6, it is evident that in this study, the SRC cycle and the first scenario generally exhibit better performance, with higher net power output, lower initial cost, and shorter PBP. In this study, due to the high temperature of the heat source (exhaust gases) and the greater temperature difference with the working fluids in the ORC compared to low-temperature sources, the ORC loses its efficiency advantage relative to steam cycles. Consequently, the combined cycle’s overall efficiency decreases. However, alternative configurations can still be effective. For example, the waste heat from the steam cycle’s condenser can be used as the heat source for the ORC, or higher-temperature working fluids can be employed to reduce the temperature difference, leading to improved efficiency. These adjustments can make the combined cycles more cost-effective and efficient within optimal temperature ranges. Moreover, advancements in this field continue to enhance their economic viability and flexibility in energy supply compared to steam cycles. Furthermore, to improve the system’s performance and find the optimal operating point in these cycles under the conditions provided in the present study, steam cycle optimization using a genetic algorithm has been conducted.

3.4. Optimization

The genetic algorithm is a type of computational model based on evolution, and for every problem, possible solutions are encoded in chromosome-like structures [60]. In many cases, genetic algorithms are used to optimize objective functions for various problems. A Rankine steam cycle can be analyzed from two perspectives using two main criteria. The first perspective is to assess the system in terms of improving its performance, which is well covered by the criterion of exergy efficiency (φ).

The second perspective is the feasibility of implementation and execution, which can be addressed by the criterion of system cost rate. By selecting these two criteria as the main outputs of the system, the key influential parameters need to be identified. Among the various parameters of the RC in this study, five parameters were considered as decision variables: turbine pressure (P_tur), turbine temperature (T_tur), condenser pressure (P_cond), isentropic efficiency of the turbine, and pump.

Figure 11 illustrates the optimization process steps. As mentioned, in this study, we have two main outputs: exergy efficiency and cost rate. We aim to find the maximum value for the former and the minimum value for the latter based on certain variations of the five decision variables specified in Table 7.

Table 7. Decision variables in the optimization process of thermal power recovery cycles.

Decision variable	Lower band	Upper band
T_ture,SRC(K)	673	753
P_ture,SRC(kPa)	5000	10,000
P_cond,SRC(kPa)	100	180
η_isture,SRC(% )	80	95
η_ispump,SRC(% )	80	95

Abbreviation: SRC, steam Rankine cycle.

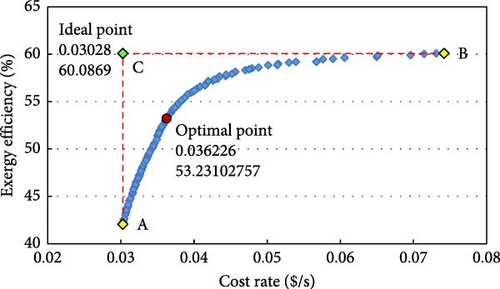
The optimization curve is depicted in Figure 12. Based on Figure 12, the characteristics of the ideal point, which aims for the lowest cost and highest efficiency, are visible in the upper-left part of the chart, marked with green. The main optimal point, which should have the least distance from the ideal point, is indicated in red on the graph, and its specifications are reported. Additionally, the specifications of points A and B, along with the ideal point corresponding to all decision variables and objective functions, are provided in Table 8.

Table 8. The results for decision variables and objective functions at the optimal point.

Parameters	A	B	Optimal
T_ture,SRC(K)	673	741	741
P_ture,SRC(kPa)	5083	9780	9653
P_cond,SRC(kPa)	139.3	103.6	102.6
η_isture,SRC(% )	80	95	84
η_ispump,SRC(% )	80	93	83
Cost rate ($/s)	0.030	0.074	0.036
η_exergy(% )	42	60	53.2

Abbreviation: SRC, steam Rankine cycle.

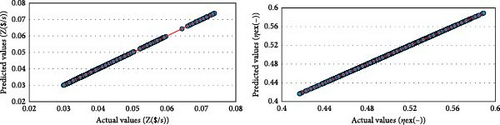
Figure 13 illustrates the validation curves for the neural network model developed for the two objective functions selected in this study. These curves demonstrate the acceptable accuracy of the neural network model in predicting the performance of the power cycle.

The scatter plots of optimal points corresponding to the five decision variables are also provided in Figure 14. The clustering pattern of these points is influenced by the location of the main optimal point. Increasing the pressure in the steam cycle leads to improved efficiency and net power of the cycle. However, it also increases the turbine cost. Considering the selected range for this parameter and the clustering of points in the upper range and around the maximum pressure of 10,000 kPa, it can be concluded that the favorable effect of increasing efficiency and power output outweighs the increase in cost.

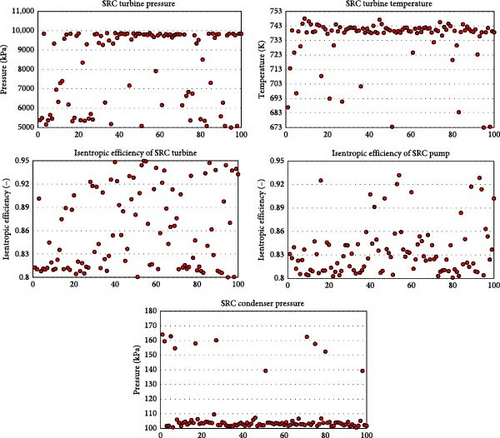
Regarding the turbine inlet temperature, similar to the previous parameter of inlet fluid pressure, increasing this parameter improves system performance while simultaneously increasing the cost. Observing the scatter plot related to this parameter, it can be seen that most points are located in the upper range and around the temperature of 743 K. The next parameter is the low pressure of the steam cycle or the condenser pressure. The scatter plot of optimal points in this parameter indicates that most points are in the lower range and around 100 kPa because increasing this parameter leads to a decrease in the net power of the cycle.

The remaining two parameters are the isentropic efficiency of the turbine and pump. As evident, increasing these two parameters also increases the overall system efficiency. However, these parameters are influential factors in the price of the turbine and pump. Therefore, as observed in the scatter plot related to them, the clustering of optimal points for both of these parameters, especially the isentropic efficiency of the pump, has occurred in the lower range of the considered interval to prevent the final price of the system from exceeding a reasonable limit.

The results related to the analysis of the systems, this time after optimization and at the primary optimum point, are presented in Table 9.

Table 9. The results of two scenarios at the main optimal point.

Scenario		η	φ	CCG ($/year)	Cost rate ($/s)	NPV ($)	PBP (year)
SRC	2672	0.27	0.53	311,288	0.036	5.803 × 10⁶	2.563
SRC–ORC	2526	0.25	0.50	294,192	0.0515	4.531 × 10⁶	4.181

Abbreviations: CCG, carbon credits gain; NPV, net present value; ORC, organic Rankine cycle; PBP, payback period; SRC, steam Rankine cycle.

Finally, the effects of variations in the exhaust gas temperatures, as one of the important and influential parameters on the exergy efficiency and net power generation in heat recovery systems, have been investigated. The results obtained are shown in Figure 15 for reference.

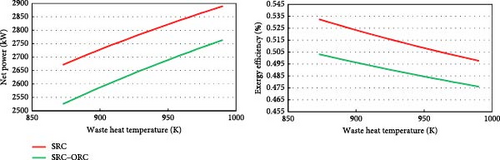
As expected, with an increase in the temperature of these gases, the net power generation has increased due to the increase in the input exergy to the heat recovery cycles. However, due to the widening temperature difference between the fluid entering the turbine in the steam cycle and the hot exhaust gases, the exergy efficiency of these cycles has decreased. This phenomenon has led to a reduction in the overall exergy efficiency in all three heat recovery systems.

4. Conclusion

In this study, the potential of exhaust gases from EAFs, commonly used in industries such as steel production, was investigated as a heat source for recovery cycles. Two scenarios involving the RC and a combination of RC and ORC were proposed and optimized using a genetic algorithm, considering energy, exergy, economic, and environmental aspects. Additionally, the efficiency of ORCs was examined using various working fluids. Key findings include:

•
Upon analyzing the first scenario, which involves using the RC for heat recovery with varying turbine inlet temperature and pressure, it was found that the optimal performance occurs at 753 K and 10 MPa. At these conditions, the cycle’s energy efficiency is 29%, exergy efficiency is 57%, and the net power reaches 2897 kW.
•
Examining the effect of variations in temperature and pressure at the turbine inlet on ORC performance revealed that cycle behavior varies with different working fluids. Based on these variations, the investigation identified and reported the optimal operational state for each fluid.
•
Acetone exhibited the best performance as an isentropic fluid among the selected working fluids for the ORC. At maximum conditions, the cycle’s energy efficiency and exergy efficiency for acetone reached 21% and 61%, respectively, with a generated power of 597.4 units. The turbine inlet temperature and pressure were 523 K and 4285 kPa. Acetone also required the least mass flow rate and had favorable environmental conditions with low ODP and GWP. However, its flammability is a drawback. Overall, considering all factors, acetone can be introduced as a suitable working fluid among the selected ones.
•
Examining the combined cycle and the second scenario revealed that the maximum energy efficiency is 27%, and the exergy efficiency is 53%. The net power output is 2675 kW.
•
By optimizing the RC to minimize total cost and maximize exergy efficiency, the optimal turbine inlet temperature and pressure were found to be 741.43 K and 9653 kPa. At these conditions, the energy and exergy efficiencies were 27% and 53%, and the net power output and total cost rate were 2672 kW and $0.036/s. When these optimal parameters were applied to the combined cycle, the energy efficiency and exergy efficiency decreased to 25% and 50%, respectively, with a net power output of 2526 kW and a total cost rate of $0.051/s.

Nomenclature

ex:: Exergy (kJ/kg)
h:: Specific enthalpy (kJ/kg)
s:: Specific entropy (kJ/kg⋅K)
P:: Pressure (kPa)
T:: Temperature (K)
M:: Molecular weight (kg/kmol)
:: Mass flow rate (kg/s)
W:: Power (kW)
Q:: Heat (kW)
Z:: Cost function ($/s)

Abbreviations

HEX:: Heat exchanger
LCOE:: Levelized cost of energy
ODP:: Ozone depletion potential
LMTD:: Logarithmic mean temperature difference
NPV:: Net present value
ORC:: Organic Rankine cycle
SRC:: Steam Rankine cycle

Subscripts

ch:: Chemical
cond:: Condenser
in:: Inlet
is:: Isentropic
out:: Outlet
ph:: Physical
ref:: Reference
tot:: Total

Greek Letter

η:: Energy efficiency
φ:: Exergy efficiency
ρ:: Density (kg/m³).

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Mahdi Mehrpour: conceptualization, data reduction, formal analysis, investigation, methodology, validation, writing–original draft. Ehsan Houshfar: conceptualization, methodology, project administration, supervision, validation, visualization, writing–review and editing. Mehdi Ashjaee: methodology, resources, supervision, writing–review and editing.

Funding

The authors declare this research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Appendix A

Exergy Components:

(A.1)

Physical Exergy:

(A.2)

Chemical Exergy:

(A.3)

Exergy of Heat Transfer:

(A.4)

Exergy Destruction:

(A.5)

Net Present Value (NPV) Components:

(A.6)

(A.7)

Equivalent Uniform Annual Benefit (EUAB):

(A.8)

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 IEA, Key World Energy Statistics 2019, 2019.
Google Scholar
2 Kong L. B., Li T., Hng H. H., Boey F., Zhang T., and Li S., Waste Energy Harvesting: Mechanical and Thermal Energies, 2014, Springer, Berlin, Germany, Berlin Heidelberg.
10.1007/978-3-642-54634-1
Google Scholar
3 Abdel-Basset M., Gamal A., Sallam K. M., Hezam I. M., and Alshamrani A. M., Sustainable Flue Gas Treatment System Assessment for Iron and Steel Sector: Spherical Fuzzy MCDM-Based Innovative Multistage Approach, International Journal of Energy Research. (2023) 2023, 25, https://doi.org/10.1155/2023/6645065, 6645065.
10.1155/2023/6645065
Web of Science® Google Scholar
4 de Bruyn J., Jongsma C., Kampman B., Görlach B., and Thie J.-E., Energy-Intensive Industries | Think Tank | European Parliament, 2020, https://www.europarl.europa.eu/thinktank/en/document/IPOL_STU(2020)652717.
Google Scholar
5 Brückner S., Liu S., Miró L., Radspieler M., Cabeza L. F., and Lävemann E., Industrial Waste Heat Recovery Technologies: An Economic Analysis of Heat Transformation Technologies, Applied Energy. (2015) 151, 157–167, https://doi.org/10.1016/j.apenergy.2015.01.147, 2-s2.0-84928716801.
10.1016/j.apenergy.2015.01.147
Web of Science® Google Scholar
6 Forder B., August 2023 Crude Steel Production - Worldsteel, 2023, https://worldsteel.org/media-centre/press-releases/2023/august-2023-crude-steel-production/.
Google Scholar
7 Dashtizadeh E., Mehrpour Darestani M., Rostami S., Ashjaee M., and Houshfar E., Comparative Optimization Study and 4E Analysis of Hybrid Hydrogen Production Systems Based on PEM, and VCl Methods Utilizing Steel Industry Waste Heat, Energy Conversion and Management. (2024) 303, https://doi.org/10.1016/j.enconman.2024.118141, 118141.
10.1016/j.enconman.2024.118141
CAS Web of Science® Google Scholar
8 Na H., Du T., and Sun W., et al.Review of Evaluation Methodologies and Influencing Factors for Energy Efficiency of the Iron and Steel Industry, International Journal of Energy Research. (2019) 43, no. 11, 5659–5677, https://doi.org/10.1002/er.4623, 2-s2.0-85067037485.
10.1002/er.4623
Web of Science® Google Scholar
9 Zhang L., Zhou M., and Yang C., et al.Evaluation and Optimization of Water Source Heat Pump for District Heating: A Case Study in Steel Plant, International Journal of Energy Research. (2020) 44, no. 12, 9399–9413, https://doi.org/10.1002/er.4955.
10.1002/er.4955
Web of Science® Google Scholar
10 Mehrpour M., Ashjaee M., and Houshfar E., Harnessing Waste Heat from Electric Arc Furnaces for Efficient Hydrogen Production: A Comparative 4E Analysis of Innovative Schemes, International Journal of Hydrogen Energy. (2025) https://doi.org/10.1016/j.ijhydene.2024.12.521.
10.1016/j.ijhydene.2024.12.521
Google Scholar
11 Manariti R., Urbano G., and Faraci E., et al. Waste Heat Recovery for Power Valorisation With Organic Rankine Cycle Technology in Energy Intensive Industries, 2019.
Google Scholar
12 Hoang A. T., Waste Heat Recovery From Diesel Engines Based on Organic Rankine Cycle, Applied Energy. (2018) 231, 138–166, https://doi.org/10.1016/j.apenergy.2018.09.022, 2-s2.0-85053381056.
10.1016/j.apenergy.2018.09.022
CAS Web of Science® Google Scholar
13 Liu X., Nguyen M. Q., Chu J., Lan T., and He M., A Novel Waste Heat Recovery System Combing Steam Rankine Cycle and Organic Rankine Cycle for Marine Engine, Journal of Cleaner Production. (2020) 265, https://doi.org/10.1016/j.jclepro.2020.121502, 121502.
10.1016/j.jclepro.2020.121502
Web of Science® Google Scholar
14 Liao G., E J., Zhang F., Chen J., and Leng E., Advanced Exergy Analysis for Organic Rankine Cycle-Based Layout to Recover Waste Heat of Flue Gas, Applied Energy. (2020) 266, https://doi.org/10.1016/j.apenergy.2020.114891, 114891.
10.1016/j.apenergy.2020.114891
CAS Web of Science® Google Scholar
15 Choi M., Lim J., Lee I., and Kim J., Carbon Neutral Design of Waste Energy Recovery System for LNG Power Plant Using Organic Rankine Cycle, International Journal of Energy Research. (2024) 2024, no. 1, 12, https://doi.org/10.1155/2024/7895267, 7895267.
10.1155/2024/7895267
Web of Science® Google Scholar
16 Bălănescu D.-T. and Homutescu V.-M., Performance Analysis of a Gas Turbine Combined Cycle Power Plant With Waste Heat Recovery in Organic Rankine Cycle, Procedia Manufacturing. (2019) 32, 520–528, https://doi.org/10.1016/j.promfg.2019.02.248, 2-s2.0-85065657272.
10.1016/j.promfg.2019.02.248
Google Scholar
17 Ghoreishi S. M. S., Vakilabadi M. A., and Bidi M., et al.Analysis, Economical and Technical Enhancement of an Organic Rankine Cycle Recovering Waste Heat from an Exhaust Gas Stream, Energy Science & Engineering. (2019) 7, no. 1, 230–254, https://doi.org/10.1002/ese3.274, 2-s2.0-85060527209.
10.1002/ese3.274
Web of Science® Google Scholar
18 Holik M., Živić M., Virag Z., Barac A., Vujanović M., and Avsec J., Thermo-Economic Optimization of a Rankine Cycle Used for Waste-Heat Recovery in Biogas Cogeneration Plants, Energy Conversion and Management. (2021) 232, https://doi.org/10.1016/j.enconman.2021.113897, 113897.
10.1016/j.enconman.2021.113897
Web of Science® Google Scholar
19 Kizilkan O., Performance Assessment of Steam Rankine Cycle and sCO2 Brayton Cycle for Waste Heat Recovery in a Cement Plant: A Comparative Study for Supercritical Fluids, International Journal of Energy Research. (2020) 44, no. 15, 12329–12343, https://doi.org/10.1002/er.5138.
10.1002/er.5138
CAS Web of Science® Google Scholar
20 Khater A. M., Soliman A., Ahmed T. S., and Ismail I. M., Power Generation in White Cement Plants From Waste Heat Recovery Using Steam-Organic Combined Rankine Cycle, Case Studies in Chemical and Environmental Engineering. (2021) 4, https://doi.org/10.1016/j.cscee.2021.100138, 100138.
10.1016/j.cscee.2021.100138
CAS Google Scholar
21 Ja’fari M., Khan M. I., Al-Ghamdi S. G., Jaworski A. J., and Asfand F., Waste Heat Recovery in Iron and Steel Industry Using Organic Rankine Cycles, Chemical Engineering Journal. (2023) 477, https://doi.org/10.1016/j.cej.2023.146925, 146925.
10.1016/j.cej.2023.146925
Web of Science® Google Scholar
22 Yu X., Li Z., Lu Y., Huang R., and Roskilly A. P., Investigation of Organic Rankine Cycle Integrated With Double Latent Thermal Energy Storage for Engine Waste Heat Recovery, Energy. (2019) 170, 1098–1112, https://doi.org/10.1016/j.energy.2018.12.196, 2-s2.0-85060061084.
10.1016/j.energy.2018.12.196
CAS Web of Science® Google Scholar
23 Yu X., Huang Y., Li Z., Huang R., Chang J., and Wang L., Characterization Analysis of Dynamic Behavior of Basic ORC Under Fluctuating Heat Source, Applied Thermal Engineering. (2021) 189, https://doi.org/10.1016/j.applthermaleng.2021.116695, 116695.
10.1016/j.applthermaleng.2021.116695
Web of Science® Google Scholar
24 Atashbozorg D., Arasteh A. M., Salehi G., and Azad M. T., Analysis of Different Organic Rankine and Kalina Cycles for Waste Heat Recovery in the Iron and Steel Industry, ACS Omega. (2022) 7, no. 50, 46099–46117, https://doi.org/10.1021/acsomega.2c03922.
10.1021/acsomega.2c03922
CAS PubMed Web of Science® Google Scholar
25 Biondi M., Giovannelli A., Di Lorenzo G., and Salvini C., Techno-Economic Analysis of a sCO2 Power Plant for Waste Heat Recovery in Steel Industry, Energy Reports. (2020) 6, 298–304, https://doi.org/10.1016/j.egyr.2020.11.147.
10.1016/j.egyr.2020.11.147
Web of Science® Google Scholar
26 Pfeiffer H. and Kirschen M., Thermodynamic Analysis of EAF Energy Efficiency and Comparison With a Statistical Model of Electric Energy Demand, 7th European Electric Steelmaking Conference2002, Associazione Italiana di Metallurgia, 1.413–411.428.
Google Scholar
27 Kirschen M., Risonarta V., and Pfeifer H., Energy Efficiency and the Influence of Gas Burners to the Energy Related Carbon Dioxide Emissions of Electric Arc Furnaces in Steel Industry, Energy. (2009) 34, no. 9, 1065–1072, https://doi.org/10.1016/j.energy.2009.04.015, 2-s2.0-68349155840.
10.1016/j.energy.2009.04.015
CAS Web of Science® Google Scholar
28 Santangelo N., Tomadin L., and Arrigo B., CHR® - Clean Heat Recovering From EAF Hot Fumes Into Electric Energy, With Consequent Fuel Saving and Reduction of Green-House Gas Emission, Proceedings of the Seminar on Steelmaking, Casting and Non-Ferrous Metallurgy. (2013) 44, 320–327.
Google Scholar
29 Kapothanillath A. N., Negative Emission From Electric Arc Furnace Using a Combination of Carbon Capture and Bio-Coal, 2023, KTH Royal Institute of Technology, Energy Technology, Master Thesis.
Google Scholar
30 Keplinger T., Haider M., Steinparzer T., Trunner P., Patrejko A., and Haselgrübler M., Modeling, Simulation, and Validation With Measurements of a Heat Recovery Hot Gas Cooling Line for Electric Arc Furnaces, Steel Research International. (2018) 89, no. 6, https://doi.org/10.1002/srin.201800009, 2-s2.0-85043677423, 1800009.
10.1002/srin.201800009
Web of Science® Google Scholar
31 Dal Magro F., Energy Recovery Systems Based on High Temperature Phase Change Materials, 2017, University of Udine, Polytechnic Department of Engineering and Architecture - DPIA 2017, Ph. D. thesis.
Google Scholar
32 Hartfuß G., Schmid M., and Scheffknecht G., Off-Gas Waste Heat Recovery for Electric Arc Furnace Steelmaking Using Calcium Hydroxide (Ca (OH) 2) Dehydration, Steel Research International. (2020) 91, no. 11, https://doi.org/10.1002/srin.202000048, 2000048.
10.1002/srin.202000048
CAS Web of Science® Google Scholar
33 Tiseo I., Power Sector Carbon Intensity in the United States in 2022, by State (in Pounds of CO₂ per Megawatt Hour), https://www.statista.com/statistics/1133295/electric-sector-carbon-dioxide-emission-rate-by-state-united-states/.
Google Scholar
34 Nasser M. and Hassan H., Assessment of Hydrogen Production from Waste Heat Using Hybrid Systems of Rankine Cycle With Proton Exchange Membrane/Solid Oxide Electrolyzer, International Journal of Hydrogen Energy. (2023) 48, no. 20, 7135–7153, https://doi.org/10.1016/j.ijhydene.2022.11.187.
10.1016/j.ijhydene.2022.11.187
CAS Web of Science® Google Scholar
35 Nasser M., Megahed T. F., Ookawara S., and Hassan H., Performance Evaluation of PV Panels/Wind Turbines Hybrid System for Green Hydrogen Generation and Storage: Energy, Exergy, Economic, and Enviroeconomic, Energy Conversion and Management. (2022) 267, https://doi.org/10.1016/j.enconman.2022.115870, 115870.
10.1016/j.enconman.2022.115870
CAS Web of Science® Google Scholar
36 Mohebali Nejadian M., Ahmadi P., and Houshfar E., Comparative Optimization Study of Three Novel Integrated Hydrogen Production Systems With SOEC, PEM, and Alkaline Electrolyzer, Fuel. (2023) 336, https://doi.org/10.1016/j.fuel.2022.126835, 126835.
10.1016/j.fuel.2022.126835
CAS Web of Science® Google Scholar
37 Izadi A., Ahmadi P., Bashiri Mousavi S., and Fakhari I., A Comparative Optimization of a Trigeneration System With an Innovative Integration of Solar Heliostat Towers and Hydrogen Production Unit, Sustainable Energy Technologies and Assessments. (2021) 47, https://doi.org/10.1016/j.seta.2021.101522, 101522.
10.1016/j.seta.2021.101522
Web of Science® Google Scholar
38 Vojdani M., Fakhari I., and Ahmadi P., A Novel Triple Pressure HRSG Integrated With MED/SOFC/GT for Cogeneration of Electricity and Freshwater: Techno-Economic-Environmental Assessment, and Multi-Objective Optimization, Energy Conversion and Management. (2021) 233, https://doi.org/10.1016/j.enconman.2021.113876, 113876.
10.1016/j.enconman.2021.113876
Web of Science® Google Scholar
39 Zarnoush M., Golaki P. P., Soltani M., Yamini E., Esmaeilion F., and Nathwani J., Comparative Evaluation of Advanced Adiabatic Compressed Gas Energy Storage Systems, Journal of Energy Storage. (2023) 73, https://doi.org/10.1016/j.est.2023.108831, 108831.
10.1016/j.est.2023.108831
Web of Science® Google Scholar
40 Mathew S., Wind Energy: Fundamentals, Resource Analysis and Economics, 2006, Springer, Meppel, The Netherlands.
10.1007/3-540-30906-3
Google Scholar
41 McKenna R., Hollnaicher S., and Fichtner W., Cost-Potential Curves for Onshore Wind Energy: A High-Resolution Analysis for Germany, Applied Energy. (2014) 115, 103–115, https://doi.org/10.1016/j.apenergy.2013.10.030, 2-s2.0-84888399952.
10.1016/j.apenergy.2013.10.030
Web of Science® Google Scholar
42 Groniewsky A., Györke Gábor, and Imre A. R., Description of Wet-to-Dry Transition in Model ORC Working Fluids, Applied Thermal Engineering. (2017) 125, 963–971, https://doi.org/10.1016/j.applthermaleng.2017.07.074, 2-s2.0-85024829810.
10.1016/j.applthermaleng.2017.07.074
CAS Web of Science® Google Scholar
43 Quoilin S., Van Den Broek M., Declaye S., Dewallef P., and Lemort V., Techno-Economic Survey of Organic Rankine Cycle (ORC) Systems, Renewable and Sustainable Energy Reviews. (2013) 22, 168–186, https://doi.org/10.1016/j.rser.2013.01.028, 2-s2.0-84874884347.
10.1016/j.rser.2013.01.028
CAS Web of Science® Google Scholar
44 Yan C., Yang A., Chien I.-L., Shen W., and Ren J., Advanced Exergy Analysis of Organic Rankine Cycles for Fischer-Tropsch Syngas Production With Parallel Dry and Steam Methane Reforming, Energy Conversion and Management. (2019) 199, https://doi.org/10.1016/j.enconman.2019.111963, 2-s2.0-85071123892, 111963.
10.1016/j.enconman.2019.111963
CAS Web of Science® Google Scholar
45 Minea V., Power Generation With ORC Machines Using Low-Grade Waste Heat or Renewable Energy, Applied Thermal Engineering. (2014) 69, no. 1-2, 1–154, https://doi.org/10.1016/j.applthermaleng.2014.04.054, 2-s2.0-84901018726.
10.1016/j.applthermaleng.2014.04.054
Web of Science® Google Scholar
46 Andersen W. C. and Bruno T. J., Rapid Screening of Fluids for Chemical Stability in Organic Rankine Cycle Applications, Industrial & Engineering Chemistry Research. (2005) 44, no. 15, 5560–5566, https://doi.org/10.1021/ie050351s, 2-s2.0-22944433472.
10.1021/ie050351s
CAS Web of Science® Google Scholar
47 Pethurajan V., Sivan S., and Joy G. C., Issues, Comparisons, Turbine Selections and Applications-An Overview in Organic Rankine Cycle, Energy Conversion and Management. (2018) 166, 474–488, https://doi.org/10.1016/j.enconman.2018.04.058, 2-s2.0-85045768612.
10.1016/j.enconman.2018.04.058
CAS Web of Science® Google Scholar
48 Vélez F., Segovia J. J., Martín M. C., Antolín G., Chejne F., and Quijano A., A Technical, Economical and Market Review of Organic Rankine Cycles for the Conversion of Low-Grade Heat for Power Generation, Renewable and Sustainable Energy Reviews. (2012) 16, no. 6, 4175–4189, https://doi.org/10.1016/j.rser.2012.03.022, 2-s2.0-84860224290.
10.1016/j.rser.2012.03.022
Web of Science® Google Scholar
49 Yang A., Su Y., Shen W., Chien I.-L., and Ren J., Multi-Objective Optimization of Organic Rankine Cycle System for the Waste Heat Recovery in the Heat Pump Assisted Reactive Dividing Wall Column, Energy Conversion and Management. (2019) 199, https://doi.org/10.1016/j.enconman.2019.112041, 2-s2.0-85072228508, 112041.
10.1016/j.enconman.2019.112041
CAS Web of Science® Google Scholar
50 Delgado-Torres A.M. and García-Rodríguez L., Preliminary Assessment of Solar Organic Rankine Cycles for Driving a Desalination System, Desalination. (2007) 216, no. 1–3, 1–275, https://doi.org/10.1016/j.desal.2006.12.011, 2-s2.0-34748879351.
10.1016/j.desal.2006.12.011
Web of Science® Google Scholar
51 Mago P. J., Chamra L. M., Srinivasan K., and Somayaji C., An Examination of Regenerative Organic Rankine Cycles Using Dry Fluids, Applied Thermal Engineering. (2008) 28, no. 8-9, 8–1007, https://doi.org/10.1016/j.applthermaleng.2007.06.025, 2-s2.0-39749161631.
10.1016/j.applthermaleng.2007.06.025
Web of Science® Google Scholar
52 Hung T. C., Wang S. K., Kuo C. H., Pei B. S., and Tsai K. F., A Study of Organic Working Fluids on System Efficiency of an ORC Using Low-Grade Energy Sources, Energy. (2010) 35, no. 3, 1403–1411, https://doi.org/10.1016/j.energy.2009.11.025, 2-s2.0-76049095519.
10.1016/j.energy.2009.11.025
CAS Web of Science® Google Scholar
53 Köse Ö., Koç Y., and Yağlı H., Performance Improvement of the Bottoming Steam Rankine Cycle (SRC) and Organic Rankine Cycle (ORC) Systems for a Triple Combined System Using Gas Turbine (GT) as Topping Cycle, Energy Conversion and Management. (2020) 211, https://doi.org/10.1016/j.enconman.2020.112745, 112745.
10.1016/j.enconman.2020.112745
CAS Web of Science® Google Scholar
54 Braimakis K. and Karellas S., Energetic Optimization of Regenerative Organic Rankine Cycle (ORC) Configurations, Energy Conversion and Management. (2018) 159, 353–370, https://doi.org/10.1016/j.enconman.2017.12.093, 2-s2.0-85044681182.
10.1016/j.enconman.2017.12.093
CAS Web of Science® Google Scholar
55 Douvartzides S. and Karmalis I., Working Fluid Selection for the Organic Rankine Cycle (ORC) Exhaust Heat Recovery of an Internal Combustion Engine Power Plant, IOP Conference Series: Materials Science and Engineering. (2016) 161, https://doi.org/10.1088/1757-899X/161/1/012087, 2-s2.0-85012981904, 012087.
10.1088/1757-899X/161/1/012087
Google Scholar
56 Ordaz-Flores A., García-Valladares O., and Gómez V., Findings to Improve the Performance of a Two-Phase Flat Plate Solar System, Using Acetone and Methanol as Working Fluids, Solar Energy. (2012) 86, no. 4, 1089–1098, https://doi.org/10.1016/j.solener.2011.10.031, 2-s2.0-84858149642.
10.1016/j.solener.2011.10.031
CAS Web of Science® Google Scholar
57 Castelli A. F., Elsido C., Scaccabarozzi R., Nord L. O., and Martelli E., Optimization of Organic Rankine Cycles for Waste Heat Recovery From Aluminum Production Plants, Frontiers in Energy Research. (2019) 7, https://doi.org/10.3389/fenrg.2019.00044, 2-s2.0-85069055295, 44.
10.3389/fenrg.2019.00044
Web of Science® Google Scholar
58 Zhang H.-H., Li M.-J., Feng Y.-Q., Xi H., and Hung T.-C., Assessment and Working Fluid Comparison of Steam Rankine Cycle -Organic Rankine Cycle Combined System for Severe Cold Territories, Case Studies in Thermal Engineering. (2021) 28, https://doi.org/10.1016/j.csite.2021.101601, 101601.
10.1016/j.csite.2021.101601
Web of Science® Google Scholar
59 Agromayor R. and Nord L. O., Fluid Selection and Thermodynamic Optimization of Organic Rankine Cycles for Waste Heat Recovery Applications, Energy Procedia. (2017) 129, 527–534, https://doi.org/10.1016/j.egypro.2017.09.180, 2-s2.0-85029744814.
10.1016/j.egypro.2017.09.180
CAS Google Scholar
60 Mitchell M., An Introduction to Genetic Algorithms, 1998, MIT Press, Cambridge, MA, USA.
10.7551/mitpress/3927.001.0001
Google Scholar

All articles

Enhanced Heat Recovery From Electric Arc Furnaces: Optimization and Comparative Analysis of Steam and Organic Rankine Cycles

Abstract

1. Introduction