1. Introduction

The leading causes of greenhouse effect are the emissions of harmful gases and oxides of carbon (CO and CO₂). The carbon dioxide (CO₂) global emissions have reached 37 GtCO₂e in 2023 rising 60% since 1990 according to EDGAR [1]. Therefore, clean and sustainable energy is an essential demand worldwide to secure environmental sustainability goals for the future [2]. Towards this goal, researchers are putting efforts to improve existing processes and develop new techniques to produce clean and sustainable energy. Substitution of fossil fuels with biofuels is one of the significant areas of research due to rising oil/gas prices and global warming. Biogas production from biomass and agricultural residues is a widespread and straightforward option for biofuel production, however, to obtain pure methane (CH₄) and to limit CO₂ in biogas is a primary challenge in biogas refining. The purified CH₄ can be fed to the natural gas grid, utilized for the synthesis of chemicals, or used as vehicle fuel [3].

Several CH₄/CO₂ separation processes are available, such as adsorption, membrane separation, or absorption, etc. Struk et al. [4] reported that removing CO₂ by chemical absorption was the most competitive among other available methods. Kapoor et al. [5] reported chemical absorption-based biogas up-gradation advantages: lower methane loss, high CO₂ removal efficiency, and high biomethane quality. Several studies have related to the development of processes for removing CO₂ from exhaust gases resulting from burning fossil fuels [6, 7]. Several solvents such as amine-based, organic, and inorganic, are used to remove CO₂ during pre or post-combustion. Commercially, the most important solvent used in the absorption of CO₂ on a large scale is the monoethanolamine (MEA) or comparable amines [7]. However, these solvents are not economically feasible for CO₂ removal in small-scale biogas facilities. Therefore, other solvents have been suggested, for example, pressurized water and or cold potassium carbonate solution. Unfortunately, potassium carbonate has a low CO₂ absorption rate at low temperatures; however, the rate of absorption can be enhanced by an activator [2]. Several promoters, such as, ammonia, MEA, and diethanolamine (DEA) have been studied to investigate their capability to increase the absorption rate of CO₂. However, researchers are still working on characterizing the absorption capacity, solubility, and amine volatility of these solvents. Recently piperazine (PZ) has been suggested as a potential effective promoter for enhancing the CO₂ absorption [8]. PZ is a cyclic diamine reacting with CO₂ twice, forming carbamate and di-carbamate. Several studies investigated the effect of PZ on the solubility of CO₂ for mixtures with other amines like methyldiethanolamine (MDEA) [9, 10]. The effect of PZ on MDEA, was reported to cause a low heat of reaction making regeneration energy-efficient [11, 12]. PZ and MDEA blend was also investigated by Bishnoi and Rochelle [13], and Dang [14], the rate constant was found to be greater than MEA. Further, PZ was also studied as an effective promoter with a blend of potassium carbonate and was reported to enhance CO₂ absorption rates [2, 6]. Pashei et al. [15] evaluated and studied the optimization of CO₂ absorption for the PZ–H₂O–CO₂ system, reporting a CO₂ removal efficiency of 97.9% and a loading of 0.25 mol/mol with an absorption rate of 3.12 g/min. According to Kadam and Panwar [16], PZ can be used as an activator because it rapidly forms carbonates with CO₂ while Stephanie et al. [17] demonstrated the absorption rate of CO₂ using PZ is more than double that of 7 m MEA due to the presence of primary and secondary amines. More than 90% efficiencies and CO₂ purity of more than 99% were reported by Baena-Moreno et al. [18] using MEA or PZ in chemical scrubbing. Akinpelumi et al. [19] studied PZ and its aerosol mitigation during absorption with less than 1 ppm PZ emissions. Borhani et al. [20] presented a model for a mixture of PZ and potassium carbonate in a packed bed column. The authors reported that increased resistance to thermal degradation and oxidation are the additional benefits for using PZ with MDEA. Privalova et al. [21] reported that the efficiency of CO₂ removal could be increased by up to 30% by adding PZ in small concentrations. To summarize, this is obvious that PZ has mostly been studied as an activator and blended with a solvent of high capacity; however, it has rarely been studied as a stand-alone absorbent. Furthermore, numerous researchers worked on the removal of CO₂ from natural gas, but this work focuses on investigating PZ as solvent for removing CO₂ during small scale biogas upgradation. Moreover, PZ has not been explored previously to assess its potential as a stand-alone absorbent for its comparison with an industrial standard, for example, pressurized water scrubbing.

Different concentrations of aqueous PZ solutions may be useful to simulate for evaluating biogas upgradation performance under viable representation of dynamic equilibria. For model development, proper representation of equilibrium is necessary to know the influence on absorption capacity. Before development and design of a dedicated absorption-desorption cycle for small scale biogas upgradation, in a first step, equilibrium studies are performed in this work to investigate the solubility of CO₂ in PZ. Based on previous experimental investigations and available literature data, simulation studies are presented using commercial simulation environment Aspen Plus software at equilibrium conditions in this work. A comparative simulation study of PZ solvent to that of a benchmark process was performed to evaluate it as a potential alternative, in terms of its capacity and performance. The results are promising, suggesting the use of PZ as a potential solvent for CO₂ absorption.

2. Material and Methods

2.1. Aqueous PZ Solvent

PZ is an organic compound with a cyclohexane basis consisting of two nitrogen atoms at opposite ends in the ring (see Figure 1), also known by the names hexahydropyrazine, piperazidine, or diethylenediamine. A broad class of chemical compounds of piperazine (PZs) exists, which contain a core PZ functional group, and many have important pharmacological properties.

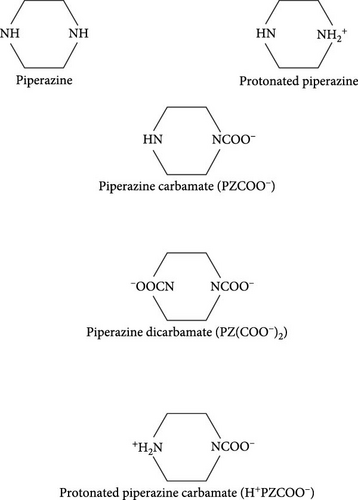
PZ has been explored as a promoter with potassium carbonate under various concentrations of 0.1–4 molal solutions by Cullinane and Rochelle [2], Chen [22], Oexmann and Kather [7], Oexmann et al. [23], and Hilliard [6]. The German based company, BASF A.G., has used PZ commercially as a promoter blended with MDEA to sweeten the natural gas. PZ is a cyclic diamine has a boiling point of 146°C–148°C and a molecular weight of 86.14 g/mol. It has a saline taste, and an amine odor and exists as small alkaline deliquescent crystals. It is hygroscopic in nature and freely soluble in ethylene glycol and water. Its solubility in water at 20°C is 15 g/100 mL and has a melting point of 106°C. It is a weak base that has two Pkb values of 9.73 and 5.35 at 25°C. A 10% aqueous solution of PZ has a pH value between 10.8 and 11.8, has high absorptivity for carbon dioxide and water, and absorbs them readily from the air. Many PZ derivatives occur naturally as illustrated in Figure 1, however, PZ can also be synthesized by a reaction of 1,2-dichloroethane and alcoholic ammonia, by reducing pyrazine with sodium in ethanol, or by the action of ethylene glycol and sodium on ethylene diamine hydrochloride [24]. Commercially PZ is produced as a coproduct from ammoniation of ethanolamine or 1,2-dichloroethane. From the product stream, it is separated which contains diethylenetriamine, ethylenediamine, and other cyclic and linear chemicals of this type. Commercially available PZ is as hexahydrate, C₄H₁₀N₂ · 6H₂O, its applications include use in the manufacture of resins, pesticides, plastics, and other industrial materials [24]. A widespread application has been found for adding primary or secondary amine to tertiary amine in absorbing CO₂ from the process gas [2, 6, 22, 23]. Therefore, a high absorption rate is seen during absorption, and low regeneration heat is required in the regeneration unit/stripper if a small amount of primary or secondary amine is added [25, 26].

Equilibrium reactions of aqueous PZ with CO₂ have been described by Bougie and Iliuta [28], Derks et al. [29], and Hilliard [6]. The electrolyte system is represented by the following equilibrium reactions [30].

Bicarbonate formation:

$$ (1)

Carbonate formation:

$$ (2)

Water dissociation:

$$ (3)

PZ protonation:

$$ (4)

PZ diprotonation:

$$ (5)

Hydrolysis of PZ monocarbamate:

$$ (6)

Hydrolysis of PZ dicarbamate:

$$ (7)

Monocarbamate protonation:

$$ (8)

2.2. Model Development

Solubility data were obtained for different ranges of partial pressure and CO₂ loading in the rich solution. The CO₂ solubility for 0.1–4 molal PZ solution at a temperature range of 298–353 K and a partial pressure up to 10,000 kPa was compared and the most reliable data from the literature was used for validation of the simulation model developed on the simulation software Aspen Plus (v7.3.2, AspenTech) in this work. The data for vapor–liquid equilibrium was calculated using the vapor and liquid compositions in aqueous solutions as a function of temperature and concentration. Vapor-liquid equilibrium of represented components can be given by Henry’s law. The following general equation for absorption represents the equilibrium for CO₂ solubility between H₂O and CO₂ [6].

$$ (9)

where, $$ is Henry’s law constant for CO₂ in H₂O, $$ is unsymmetric activity coefficient of CO₂, $$ is mole fraction of CO₂ in vapor, and $$is mole fraction of CO₂ in liquid.

The CO₂ solubility system for PZ is described by Equations (1)–(8). In Aspen plus, the j number of the equation’s equilibrium constant is expressed in terms of activity coefficient [6].

$$ (10)

where, v_i,j is stoichiometric coefficient of reaction for component i, K_j is chemical equilibrium constant and a_i is activity coefficient of component i.

Equilibrium constants for the reactions were not defined as temperature-dependent functions in the example [30] used in this case as a base. Instead, they were defined in terms of reference state free energy of the system and can be given by the following equation [6].

$$ (11)

where, $$ is component i standard free energy of formation.

The electrolyte non-random two liquid (ENRTL) model accounts for contributions from local interactions and those associated with long-range ion–ion interactions. This is given by Equations (12) and (13) [6].

$$ (12)

The excess Gibbs free energy part is given as [31].

$$ (13)

where, l_c is contribution of local for short-range interactions. Symbol Born stands for correction by Born for change in mixed solvent reference state and PDH is contribution by Pitzer-Debije-Hückel for long range ion–ion interaction.

The ENRTL model, in theory, reduces to the non-random two liquid (NRTL) model of Renon and Prausnitz [32], as the concentration of ions in electrolyte solution approach zero. Physical properties calculation routes for ENRTL and NRTL property models are different. In Equation (14), excess Gibbs energy and activity coefficients relation through model parameters can be seen [6].

$$ (14)

where, $$ = infinite dilution activity coefficient of component 2.

The definition of molar excess Gibbs free energy and molar Gibbs free energy is done with asymmetrical reference state as infinite dilute in pure solvent. For ionic and molecular solutes, the reference state follows an unsymmetrical convention defined as infinite dilution in water. The term j refers to any component in ideal mixing term calculation. Ideal gas contribution is calculated to calculate pure water’s molar Gibbs free energy. The term k refers to an ion or molecular solute in calculating aqueous infinite dilution chemical potential from the infinite dilution aqueous phase heat capacity polynomial model, which is given by Equation (15) [6].

$$ (15)

where, $$ is infinite dilution chemical potential of an ion (mole fraction based), $$ is standard change of reaction in Gibbs energy (molality scale based), and $$ is change in enthalpy of formation (molality scale based).

Henry’s law is used to calculate aqueous infinite dilution chemical potential for molecular solutes and is given by Equation (16) [6].

$$ (16)

where, $$ is infinite dilution chemical potential of an ion, T_o is reference temperature (298.15 K), and p^refis reference pressure (1 atm).

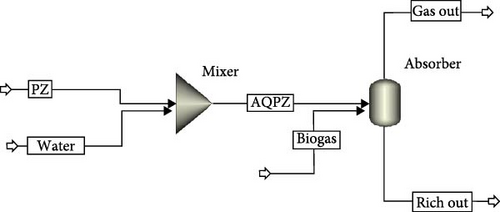
Therefore, the system satisfies the condition of thermodynamic equilibrium when the Gibbs free energy derivative at constant pressure and temperature reaches a minimum for a closed homogeneous system. The model from the example [30] described the dissociation chemistry of PZ quite accurately. Henry’s law was the basis for the equilibrium calculation of CO₂ solubility. The complicated electrolyte system is described by crucial dissociation reactions in the model. Dissociation and equilibrium constants are described as a temperature function or obtained from reference state free energy [30]. ENRTL model calculated activity coefficients in the electrolyte system. Specific parameters are adjusted to preset values using design specs without influencing other settings. To avoid the effects of condensation and evaporation, concentrations were maintained constant, and to calculate loading on specific partial pressure, partial pressure of CO₂ was kept constant. A flash column was used to calculate the vapor–liquid phase equilibrium (Figure 2). The apparent component approach was used for the models. The specific parameters like temperature, partial pressure, and solvent concentration were adjusted to defined values without affecting other settings to maintain equilibrium conditions. The temperature was kept constant to prevent system effects owing to the heat of absorption and heat of evaporation. Concentration also needed to be kept constant to avoid the effects caused by condensation and evaporation. The model was modified to include design specifications to ensure a constant concentration of PZ. Additional water, solvent, or nitrogen streams were added to maintain a constant concentration of PZ. In addition, design specifications were added to maintain a constant partial pressure of CO₂ in the system. Depending on the requirements, the total pressure of the column or nitrogen stream flowrate variable/s were chosen to either maintain or achieve a certain partial pressure of CO₂. CO₂ loadings were obtained by analyzing concentrations of CO₂ in the liquid stream. The partial pressure of CO₂ was varied at a constant temperature to calculate CO₂ loading in aqueous PZ for a specific solvent concentration. Moreover, the temperature was varied at constant pressure to observe the effect on CO₂ loading for a particular solvent concentration. This procedure was repeated for each concentration of solvent. Salt formation and precipitation were not considered in the development of this model. Convergence of the simulation model was the main issue at lower partial pressures of CO₂. This needed to be handled carefully, adjusting variables range, number of iterations, and convergence methods. The secant method was used as a default convergence method as the model included design specs.

2.2.1. H₂O–CO₂ System

The reactions described below (Equations 17–21) describe the CO₂ absorption system for water [33]. Water chemistry and dissociations in electrolyte systems are essential to the study. The Absorption system consists mainly of the dissociation of water in hydronium ion and hydroxyl ion given by the following Equation (17).

$$ (17)

CO₂ dissolves in water, forming a complex electrolyte system, equilibrium is formed between carbonic acid and CO₂.

$$ (18)

CO₂ further reacts with water to form carbonic acid. Equilibrium is formed then between carbonic acid and CO₂:

$$ (19)

Carbonic acid dissociates in two steps as it is a weak acid:

$$ (20)

$$ (21)

We can describe the reactions with the following Equations (22)–(25).

$$ (22)

$$ (23)

$$ (24)

$$ (25)

where $$, $$, $$, $$, $$, $$, $$, $$ are the concentrations of hydrogen ion, hydroxyl ion, water, carbonic acid, carbon dioxide, bicarbonate ion, hydronium ion, and carbonate ion respectively.

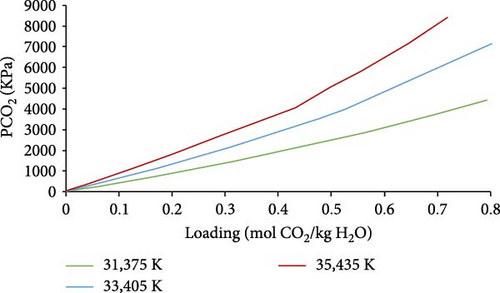
Aspen Plus calculations were done for the H₂O–CO₂ system to report the CO₂ solubility calculations at different temperatures of 313.75, 334.05, and 354.35 K to varying temperatures.

2.2.2. PZ–H₂O–CO₂ System

The thermodynamic model extends from binary to the ternary system of aqueous PZ with electrolyte–electrolyte; molecule–molecule and molecule-electrolyte interactions, for example, as water-ionic species interaction. The following equilibrium reactions represent the dissociation of PZ:

$$ (26)

$$ (27)

Equilibrium reactions of PZ with CO₂ can be described by the mechanism already described in Equations (1)–(8) [30].

3. Results

3.1. H₂O–CO₂ System Simulations

The simulations were performed on the validated model described by Equations (1)–(3) based on data from the literature [36–46]. The results of H₂O–CO₂ system simulations are shown in Figure 3, in which we can observe the effect of temperature rise on CO₂ loading. Higher loading was obtained at low CO₂ partial pressure for low temperatures. Nearly linear behavior of equilibrium loading with a varying partial pressure of CO₂ was observed (Figure 3).

3.2. PZ–H₂O–CO₂ System

3.2.1. CO₂ Solubility Model Validation

The Aspen Plus model developed for the system PZ–H₂O–CO₂ described by the Equations (1)–(8) was validated with literature data. In Figure 4a,b, the results are shown for 0.6 and 0.2 molal aqueous PZ solution at different temperatures. Literature data from Derks et al. [29] and Bishnoi and Rochelle [13] match calculated data from Aspen calculations except for a few outliers which might be due to experimental errors. At very low partial pressures of CO₂, the deviation can be observed, for example, at 0.063 and 0.13 kPa. That might be due to convergence problems caused during calculations at very low partial pressures. When the partial pressure of CO₂ is not very low, it can be observed that literature data matches better with Aspen Plus calculations at low partial pressures. In addition, the effects of temperature on loading was examined. The lower the temperature, the higher the loading of CO₂ in rich solution at any given partial pressure of CO₂ in the vapor phase. Figure 4a illustrates that CO₂ stoichiometric loading of around 1 can be achieved at partial pressures of CO₂ lower than 100 kPa.

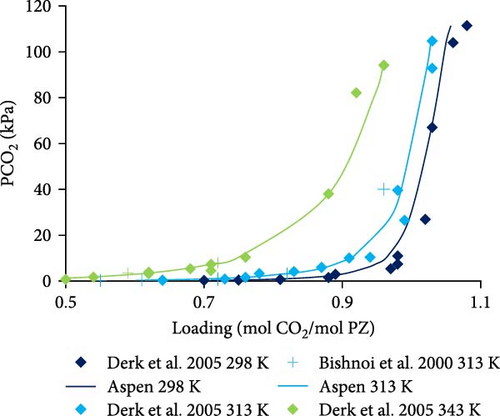
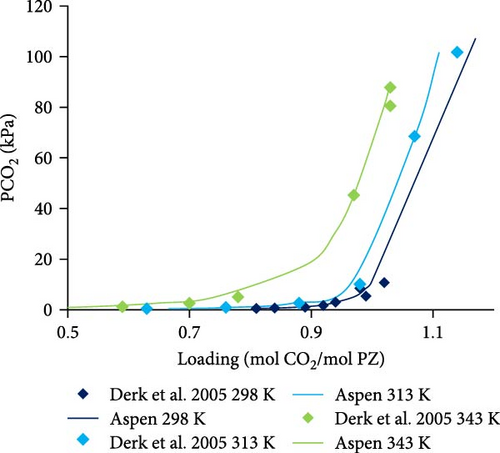
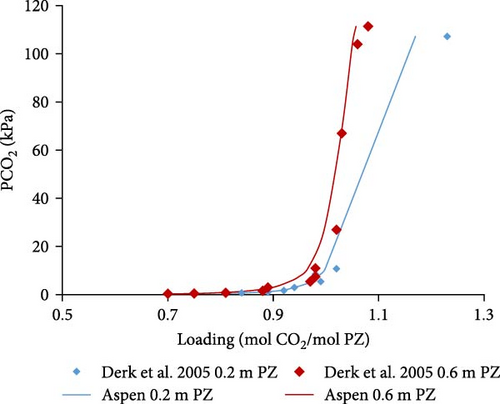
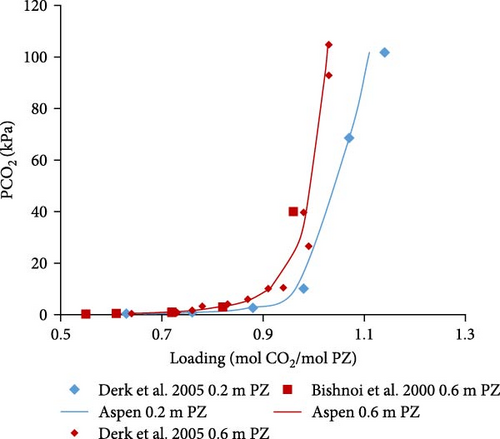
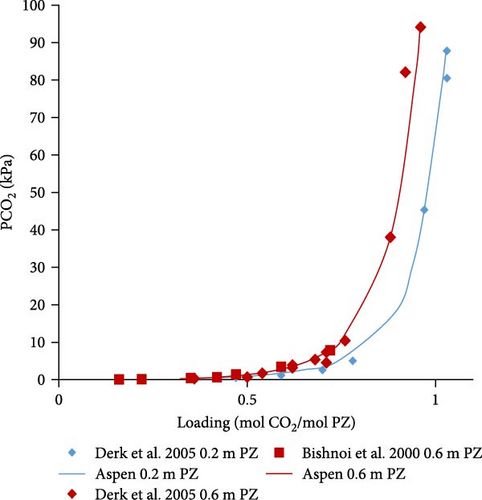
In Figure 4c–e, the Aspen calculated equilibrium data are compared with literature data from Derks et al. [29] and Bishnoi and Rochelle [13] for 0.2 and 0.6 molal PZ at specific constant temperatures (298, 313,  and 343 K). It was noticed that the calculated data fits well with the literature data. There are a few outliers but with little deviations at very low partial pressures due to convergence reasons discussed before. Apart from those outliers, the data matches perfectly.

3.2.2. Speciation Model Validation

Figure 5a shows the comparison of Aspen calculated data with literature data obtained from Ermatchkov et al. [34] for 1 molal aqueous PZ at 283.15 K. The calculated data matches quite well with the literature data except for some deviations at higher loadings. Figure 5b shows the comparison data for 1.45 molal aqueous PZ at 283.15 K. Apart from a few outliers, especially for the sum of PZCOO⁻ and HPZCOO at higher loadings, calculated data shows a reasonable match. Trends in calculations, in general, follow experimental speciation results from Ermatchkov et al. [34]. In Figure 5c, the comparison is shown for 1 m aqueous PZ this time at 298.15 K, here again the similarity of trends is observed as earlier for each species set. In Figure 5d, a comparison for 1.45 molal aqueous PZ at 298.15 K is shown, it is obvious that the sum of species sets remains equal to the molality of PZ confirming that the balance is right for a specific loading. Figure 5a–d shows moles of the set of species formed at different maximum loadings of CO₂ in the liquid. It can be seen at different loadings the extent of dissociation that takes place and the concentrations of species changing as CO₂ is absorbed. At a loading of around 0.5, the sum of PZ/PZH⁺/PZH⁺² decreases to less than half of the initial concentration, whereas concentrations of HPZCOO/PZCOO⁻ increase more than half of the initial concentration absorbing CO₂. Most of the Aspen Plus calculated data shows reasonable comparability with literature data except for slight deviations at higher loadings. As a general observation, it can be seen that the deviations are the highest for 1.45 m PZ at higher loadings.

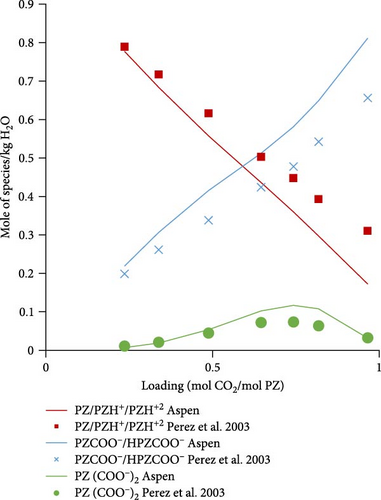
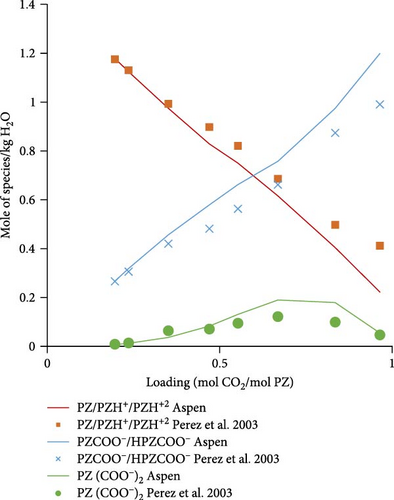
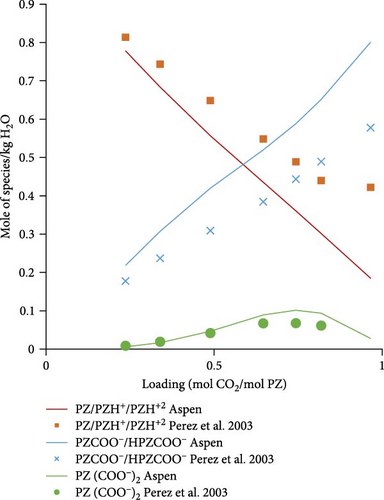
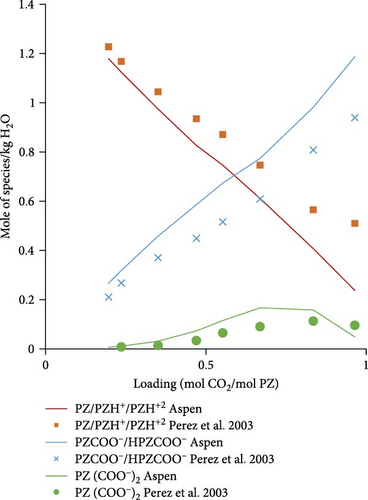
3.2.3. Simulation Studies on the Validated Model

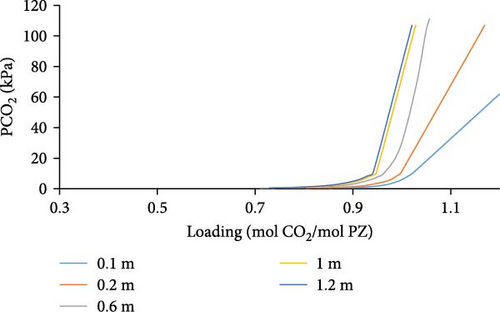
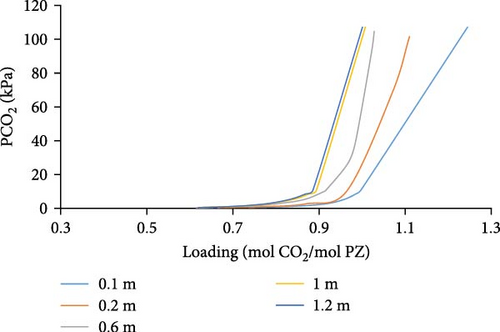
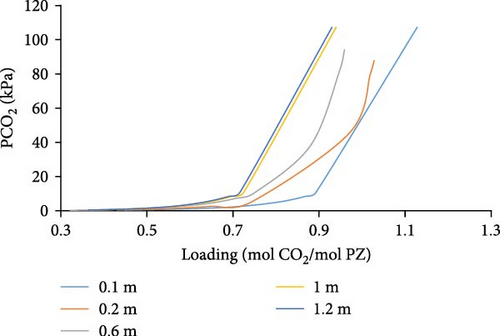
Aspen Simulations were carried out and are presented in Figure 6, at a temperature of 298, 313,  and 343K showing absorption loading curves for a range of different PZ molalities, that is, 0.1–1.2 m PZ concentrations. We observed in (Figure 6a–c) that we have higher absorption loading of CO₂ per mole of PZ for lower concentrations of PZ. That is due to the fact, that PZ only acts as an activator, an absorption rate enhancer, and does not have a high absorption capacity. Moreover, low loading of CO₂ can be observed at higher temperatures for a given partial pressure of CO₂.

3.3. Comparison of PZ With Water Scrubbing

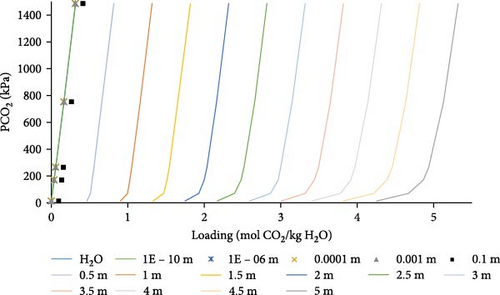
In Figure 7, different aqueous PZ concentrations were used for the comparison, starting with a concentration of about 5 molal PZ, the aqueous PZ was diluted until it reached a very low concentration. This was done to evaluate the influence of decreasing PZ concentration until it approaches water and to compare loading for each concentration to that obtained by water. As the concentration of PZ is decreased (Figure 7), a lower absorption loading was obtained at the same partial pressure of CO₂. Very diluted systems act almost like pure water, little or no difference in absorption loading can be observed for solvent with the concentration of PZ lower than 0.001 molal as compared to water. Moreover, a very little difference was observed in loading for partial pressure of CO₂ higher than 200 kPa, so increasing the partial pressure of CO₂ has little effect on loading above 200 kPa. It was observed that around 1 mol of CO₂ is absorbed per mole of PZ. An absorption loading of higher than 1 mol CO₂ per mole of PZ can be obtained at higher partial pressures of CO₂.

4. Discussion

The results matched very well with the literature data [13, 29] with less than 4% deviation. Speciation results showed dissociation species also in agreement with the literature data [34]. PZ as a stand-alone solvent performed very well even at smaller concentrations of 0.5 m aqueous PZ showing 120% higher absorption loading of CO₂ than water at the same temperature and partial pressure. Higher concentrations of PZ reported further higher absorption loading, however considering economic viability the 0.5 m PZ may be chosen for further economic evaluation. In conclusion, PZ solubility of CO₂ is a much better solvent as compared to pressurized water. Around 1 mol of CO₂ is absorbed per mole of PZ below 200 kpa. The optimum partial pressure of CO₂ was 200 kPa, above which there was no significant influence on CO₂ loading. PZ concentrations above 0.1 molal should be used for significant change in CO₂ loading as witnessed in the results obtained. In addition, the efficiency of CO₂ removal obtained was higher while we know that the CO₂ absorption rate in primary and secondary amines such as PZ is generally higher [46]. The model developed can now be extended to rate-based model development for finding optimized parameters for CO₂ solubility using the PZ–CO₂–H₂O system. The economic valuation of the rate-based model may let the solvent be employed for biogas upgradation.

5. Conclusions

This work aimed to develop an equilibrium model within Aspen Plus (v7.3.2, AspenTech) simulation environment to enable the calculation of CO₂ absorption in aqueous PZ solutions. From experimental data of CO₂ solubility in PZ, up to 4 molal PZ concentration and 10,000 kPa partial pressure of CO₂, reliable literature data was selected after rigorous comparison for model validation. To generate reliable results, simulations were performed on a validated model using PZ concentration from 0.1 to 1.2 molal for the temperature range of 298–343K and partial pressure of CO₂ up to 120 kPa. Specific parameters are adjusted to preset values using design specs without influencing other settings. The temperature was kept constant to prevent system effects owing to the heat of absorption and heat of evaporation. To avoid the effects of condensation and evaporation, concentrations were maintained constant, and to calculate loading on specific partial pressure, the partial pressure of CO₂ was kept constant. The model was validated for the PZ solvent system at different temperatures and partial pressures of CO₂ for various concentrations of PZ through extensive comparisons with literature data. Detailed analysis of electrolyte system for aqueous PZ was studied by speciation studies on Aspen Plus and validated by speciation literature data. Aspen Plus calculations matched very well with literature data for CO₂ solubility in PZ solution with less than a 4% deviation. Deviations can be observed at very low partial pressures of CO₂, probably related to convergence problems. The model created on Aspen Plus was shown to provide appropriate results that may be used to predict CO₂ absorption at equilibrium in the PZ solvent system. It was observed that the highest CO₂ loading per mole of PZ was obtained at lower temperatures, higher partial pressures of CO₂, and higher concentrations of PZ. Since pressurized water scrubbing is an industrial standard for biogas purification, maximum loadings of different concentrations of PZ solvent were compared to CO₂ solubility in water. The simulations demonstrated that the PZ system has greater CO₂ absorption capability than water; therefore, it is a potential solvent for CO₂ removal from biogas. PZ shows 120% higher absorption loading of CO₂ as compared to water for 0.5 m aqueous PZ at the same temperature and partial pressure. The acquired results may be used in future to design comprehensive absorption and desorption phases in the biogas upgrading process with aqueous PZ solutions using rate-based absorption studies in Aspen Plus. The study forms the basis for using PZ as a promoter in blend with other potential solvents with high CO₂ absorption capacity.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Muazzam Arshad: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing–original draft, visualization. Walter Wukovits: conceptualization, methodology, software, validation, resources, supervision. Anton Friedl: conceptualization, project administration, resources, supervision, validation and project administration. Hayat Khan: writing–original draft & editing, data analysis, investigation & funding. Khan Muhammad: writing–original draft. Mansoor Ul Hassan Shah: writing–review & editing. Muzammil Arshad: writing–review & editing.

Funding

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU251726].