Physical Aspects of Heat Transfer in Ternary Hybrid Nanofluid Flow Subject to Induced Magnetic Field and Cattaneo–Christov Heat Flux
Abstract
Ternary hybrid nanofluids (THNFs) offer superior heat transfer due to their multifunctional properties and adaptability compared to dihybrid nanofluids. Their ability to improve thermal performance, combined with their versatility in terms of chemical and physical properties, makes them an important innovation in fields such as renewable energy, electronics, automotive cooling, and industrial heat exchangers. Due to improved thermal performance and diverse usages of the THNFs, the goal of this paper is to examine the dynamics of THNF flow by a curved surface. The Cattaneo–Christov heat flux model is implemented instead of the classical Fourier principle for heat conduction. The nanoparticles of magnesium oxide (MgO) and copper (Cu), together with multiwalled carbon nanotubes (MWCNTs), are utilized for the formation of THNF. The effects of the induced magnetic field are further conceded. Flow-governing coupled nonlinear partial differential equations (PDEs) are acquired with the implementation of boundary layer restrictions. Suitable similarity alterations are adopted to transform the PDEs into ordinary differential equations (ODEs). The transformed system is solved numerically by implementing the NDSolve built-in function of the Mathematica package. Velocity, temperature, and the induced magnetic field have been graphically investigated under the influence of multiple aspects. The variation in skin friction force and Nusselt quantity is examined numerically. Results show that magnetic and curvature variables diminish the induced magnetic field; however, it escalates when the material variable is elevated. The suction variable decays the magnitude of heat transfer, but an opposite impact of curvature and reciprocal parameters is noticed.
1. Introduction
Ternary hybrid nanofluids (THNFs) are advanced hybrid nanoliquids that consist of three different types of nanoparticles immersed in a base fluid. These nanosized particles typically include a mixture of metal oxides, metals, or carbon-based materials like graphene, each chosen for its unique properties that improve the overall performance of the nanofluid. The base fluid can be water, ethylene glycol, oil, or other liquids commonly used in heat transfer applications. TNHFs show superior thermal conductivity enhancements compared to hybrid and dihybrid nanofluids. This improvement is mainly attributed to the synergistic effects among the three different nanoparticles, which lead to more efficient heat transfer pathways, increased surface area for energy exchange, and improved stability of the suspension. The presence of three nanoparticles also facilitates better clustering and bridging mechanisms, reducing thermal resistance within the fluid. As a result, THNFs significantly outperform hybrid and dihybrid nanofluids in thermal conductivity, making them more effective for advanced cooling and heat transfer applications. Theoretical and numerical studies [1–4] show quantitative improvement in thermal conductivity compared to hybrid and dihybrid nanofluids. The widespread use of nanofluids in industrial technologies such as paper production, pharmaceuticals, and the medical industry has gained significant attention over the last few years [5, 6]. Elnaqeeb et al. [7] and Wang et al. [8] described nanofluids as fluids that contain nanoparticles dispersed within them, which can enhance thermal conductivity and heat transfer properties. Xiu et al. [9] noted that the nanoparticles found in nanofluids are typically composed of metallic elements, metal oxides, or carbon-based materials. Oke et al. [10] noted that carbon nanotubes (CNTs) exhibit great potential as catalysts and are utilized as nanofibers that are exceptionally stiff and strong, making them ideal components in various electrical and thermal devices. Shao et al. [11] studied the natural convection flow of THNF configured within a pair of movable warm baffles, which are placed inside a permeable prismatic enclosure. Algehyne et al. [12] adopted an improved version of Fourier’s heat conduction principle to examine the heat transportation performance in THNF flow. Cao et al. [13] analyzed the physical aspects of convection transport of type free, force, and mixed in the flow of THNF, considering diverse slip effects. Noreen et al. [14] scrutinized the mass and heat transport features of THNF configured between a pair of permeable disks with the implementation of an upgraded version of Fourier’s principle accounting the influence of thermal radiation. Some recent studies on THNF are listed in [15–20].
Magnesium oxide (MgO) is a white, odorless, crystalline substance made up of magnesium and oxygen. Its high melting point, thermal stability, and electrical insulating qualities make it useful in industries such as cement manufacture, refractory materials, and pharmaceuticals. It is also used in nanotechnology, particularly to improve heat transfer qualities in nanofluids. The performance of MgO nanoparticles in mixed convection magnetized flow of hybrid nanofluid flow across a revolving disk is examined by Raju et al. [21]. Ahmadian et al. [22] performed a computational analysis for HNF (Ag − MgO/H2O) flow induced by a wavy revolving and stretching disk with radiation effects. Stability analysis with entropy generation for water-based micropolar fluid flow caused by stretching/shrinking Riga surface, submerged MgO and silver nanoparticles is explored by Mandal and Pal [23]. Hanif et al. [24] used MgO, CuO, and TiO2 nanoparticles to examine the dynamics of THNF flow induced by concentric cylinders accounting the effects of the magnetic field and entropy generation. A comparative study of wavy rotating and flat disk for heat transmission enhancement in HNF (MgO − Ag/H2O) is probed by Alrabaiah et al. [25]. A numerical investigation for HNF flow containing tiny particles of MgO and silver, caused by a porous stretchable sheet was presented by Anuar et al. [26].
Multiwalled CNTs (MWCNTs) are a subclass of CNT consisting of multiple concentric layers (walls) of graphene cylinders. These layers are nested one inside the other, forming a tubular structure. MWCNTs have exceptional thermal conductivity (up to 3000 W/m·K), which is much higher than that of conventional metals like copper (Cu). When added to nanofluids, even in small concentrations, MWCNTs can significantly upsurge the thermal conductivity of the fluid. MWCNTs are crucial for enhancing the performance of nanofluids, particularly in terms of thermal conductivity and heat transfer. Their unique properties enable MWCNT-based nanofluids to be used in a wide range of applications, from industrial cooling systems to renewable energy devices. A comparative study for thermal improvement using diverse CNTs submerged into a fluid that is configured inside a radiative channel is performed by Seyedi et al. [27]. Improvement in the thermal conductivity of THNF flow of carbonate nanomaterials in the presence of CNTs for solar power usage is reported by Sang et al. [28]. Considering the impact of thermal radiation and magnetic dipole, Kumar et al. [29] examined the significance of MWCNTs in Maxwell fluid flow. Idrees et al. [30] investigated the heat transfer characteristics of water-ethylene glycol in the suspension of SWCNT–MWCNT flow, taking into account factors such as magnetic fields, thermal radiation, and suction/injection. In the context of magnetohydrodynamics, Ramesh et al. [31] investigated the behavior of MWCNT suspended in pure water, considering the flow through the vertical microchannel.
Cu is a reddish-orange metal with high electrical and thermal conductivity. Cu nanoparticles, when suspended in fluid flows, significantly improve lubrication, modify viscosity, and bring antimicrobial properties, making them highly valuable in industries such as energy, electronics cooling, biomedical, and lubrication engineering. In fluid dynamics, where precise control of fluid movement is critical, the high thermal and electrical conductivity of Cu nanoparticles helps in maintaining desired performance for sensors, cooling systems, and reactors. Hayat et al. [32] reported the characteristics of convective and dissipative flow submerged nano-sized particles of Cu and silver with variable thickness and Joule heating. The suspension of alumina and Cu nanoparticles in pure water is utilized to examine the rheological properties of mixed convection flow, considering a convectively heated surface, was reported by Song et al. [33]. Adnan et al. [34] studied the thermal efficiency of a radiated THNF flow over a vertically aligned cylinder, taking into account the effects of permeability, magnetic field, and coupled convection. A comparative study between single-phase (CuO–water) and double-phase (Cu/Cuo–water) was conducted by Rehman et al. [35] to optimize the mass and heat transport in the presence of Coriolis force. Umadevi et al. [36] consider an axisymmetric and incompressible flow of blood diversified with Cu tiny particles to examine the behavior of velocity, flow resistance, and pressure drop. Tuncer et al. [37] and Noreen et al. [38] used multiple effects like heat absorption, Lorentz force, and natural convection in peristaltic flow, which contains Cu nanoparticles. Many researchers have investigated Cu’s properties, applications, and prospective advances in a variety of sectors, including nanofluids, composites, and thermal management systems [39–43].
- •
What will be the impact of curvature, magnetic, and suction parameters on the THNF velocity profile?
- •
How does the temperature distribution change when the suction and magnetic variables are increased?
- •
What will the surface drag force rate trend be in relation to porosity, curvature, and material parameters?
- •
How does the heat transfer vary against improved estimations of magnetic, suction, and surface curvature variables?
2. Mathematical Formulation
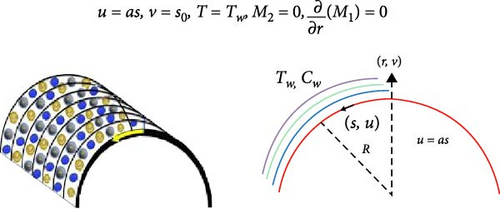
Here, two-dimensional MHD flow of an incompressible THNF through a nonporous curved surface with radius (R) and the stretching velocity Uw(s) is considered. Here, (s, r) signifies the curvilinear coordinates, where s is the coordinate for the arc length and r is normal to the tangent on the s− axis. s0 > 0 signifies the suction at the boundary of the surface. Consequences of induced magnetic field M are conceded. The parallel and normal elements of induced magnetic field are, respectively, considered M1 and M2 while at free stream the intensity of induced magnetic field is taken as Me(s). The physical domain and boundaries of the considered flow are illustrated in Figure 1. Thermophysical values and mathematical relations of solid nanoparticles and base fluid are labeled in Tables 1 and 2, respectively. For a viscous fluid in a curved geometric structure, the steady flow field equations are given as follows [42, 45]:
| Thermophysical properties | Density (ρ) | Specific heat (cp) | Thermal conductivity (k) |
|---|---|---|---|
| Copper (Cu) | 8933 | 385 | 0.613 |
| Magnesium oxide (MgO) | 3580 | 1003 | 33.6 |
| MWCNTs | 1600 | 796 | 3000 |
| Water (H2O) | 997.1 | 4179 | 0.613 |
| Dynamic viscosity of THNF | |
| Density of THNF | |
| Heat dissipation of THNF | |
| Heat capacitance of THNF |
Here, the first term signifies the stretching velocity of the curved surface with rate a, the second term means there is suction, the third term indicates the wall temperature at the surface, and the fourth and the last terms, respectively, represent the magnetic components in both directions. In addition, the first term at ambient specifies the free stream velocity, the second term shows that there is no flow along the s− component, the third term is ambient temperature, and last term signifies the strength of the magnetic field at the free stream.
2.1. Physical Quantities
3. Research Methodology
The transformed system (Equations (9)–(11)) representing the flow phenomenon and boundary restrictions defined in Equation (12) is solved by the NDSolve built-in function of the Mathematica platform. NDSolve in Mathematica is a powerful built-in function used to numerically solve differential equations. It supports both initial and boundary value problems, making it versatile for many scientific and engineering applications. NDSolve uses adaptive step size control, automatically adjusting step sizes based on the local error estimates, which improves accuracy and computational efficiency. This feature allows NDSolve to balance between accuracy and speed, especially for problems with regions of rapid change or slow dynamics [46, 47]. The accuracy of the current numerical scheme is validated in Table 3. The computational outcomes of surface drag force are compared with already established results of Roşca and Pop [48] for diverse approximations of the curvature variable while taking the remaining variables as zero. A good agreement between current and established results is observed in Table 3. The nature of THNF velocity (f′(η)), induced magnetic field (N′(η)), and thermal profile(θ (η)) against rising estimations of dimensionless magnetic parameter (β), curvature (κ), suction variable (Sw), reciprocal magnetic number (ϒ), dimensionless material parameter (Γ), thermal time relaxation (γcc), and Prandtl number (Pr) is discussed through plots. Current numerical study relies on theoretical facts, so constant values are assigned to the dimensionless variable as κ = 0.01, β = 1.0, Γ = 0.3, ϒ = Sw = 1.5, ϕ1 = ϕ2 = ϕ3 = 0.05, Pr = 8.0, and γcc = 0.2.
| κ | −Cfs | |
|---|---|---|
| Present study (NDSolve results) | Roşca and Pop [48] (bvp4c results) | |
| 5.0 | 1.15077 | 1.15076 |
| 10.0 | 1.07171 | 1.07172 |
| 20.0 | 1.03502 | 1.03501 |
| 30.0 | 1.02316 | 1.02315 |
| 40.0 | 1.01729 | 1.01729 |
| 50.0 | 1.01381 | 1.01380 |
| 100 | 1.00687 | 1.00687 |
| 200 | 1.00343 | 1.00342 |
4. Theoretical Evaluation of Outcomes
The aim of this section is to examine the nature of f′(η), N′(η), and θ(η) against rising estimations of dimensionless magnetic parameter (β), curvature (κ), suction variable (Sw), reciprocal magnetic number (ϒ), dimensionless material parameter (Γ), thermal time relaxation (γcc), and Prandtl number (Pr).
4.1. Fluctuations in Velocity
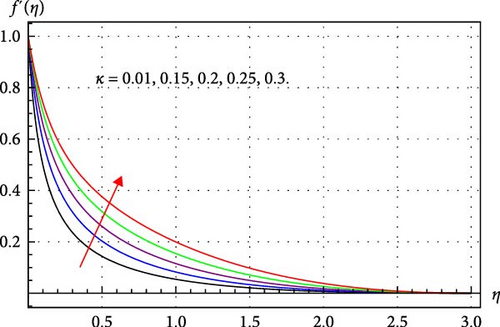
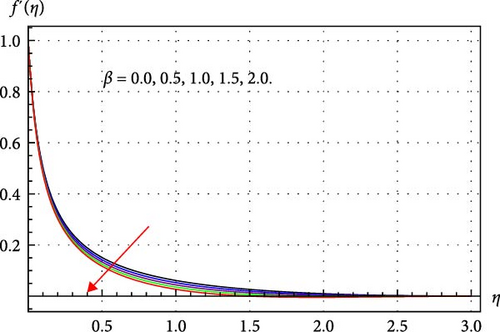
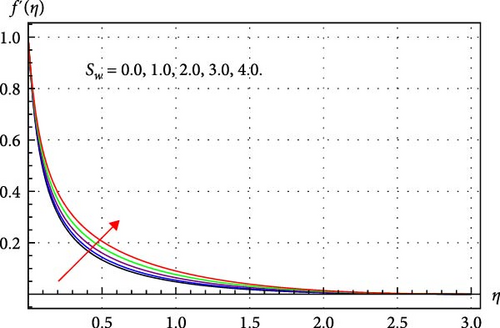
Figures 2–4 illustrate how THNF flow changes in response to rising estimations of β, κ, and Sw. Figure 2 explores the impression of curvature of the surface on the velocity profile (f′(η)). It is discovered that the curvature of the surface significantly affects fluid flow, and it is found that this effect accelerates through higher curvature parameters. Physically, higher κ reduces the radius of the curved surface, and thus, the fluid contact area decays; as a result, less resistance from the surface to the THNF is offered. Consequently, the THNF velocity profile upsurges. The consequences of β on the THNF velocity field are depicted in Figure 3. Through improvements to the magnetic parameter, it is observed that the velocity profile shrinks. The resistive force (Lorentz force) is enhanced through higher β and, which is responsible for diminishing the velocity field of THNF. The significance of the suction parameter in the velocity profile can be observed in Figure 4. Here, velocity curves degrade when the suction parameter Sw rises. Physically, through higher suction values, surface stretching velocity enhances, and thus, THNF velocity profile upsurges accelerate.
4.2. Fluctuations in Induced Magnetic Field
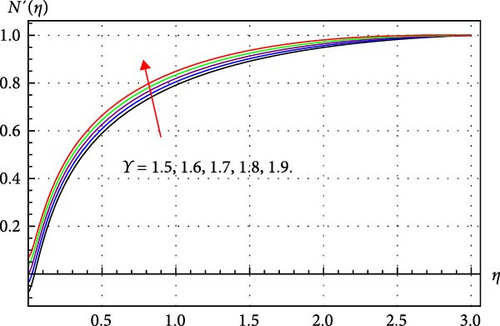
The variation in N′(η) distributions through Γ, κ, and ϒ are shown in Figures 5–7. Figure 5 explores the influence of ϒ on N′(η) field. Here, N′(η) escalates gradually for ascending amounts of ϒ. Since amplification in ϒ diminishes the kinematic viscosity of THNF and thus induced magnetic profile increases. Figure 6 exhibits the role of material variable Γ in N′(η) profile. It is observed from this figure that there exists an inverse relation between the induced magnetic field and Γ. Since Γ describes the ratio of the suction coefficient and the surface stretching constant. So improvement in Γ reduces the stretching rate while increasing the suction coefficient and thus induces magnetic field decay versus higher Γ. The implications of the curve parameter on the induced magnetic profile are portrayed in Figure 7. Following this graph, we noticed that rising κ improved N′(η). Physically, higher κ decays the THNF contact region by reducing the curvature of the curved surface, and thus fluid velocity escalates. Therefore, the induced magnetic field decays via rising κ.


4.3. Fluctuations in Temperature
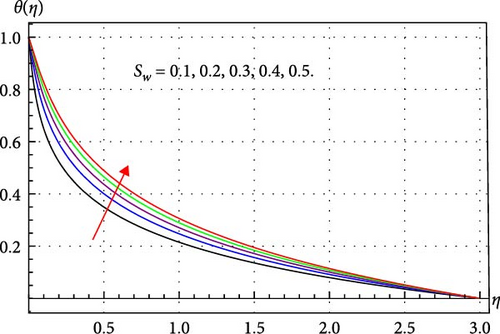
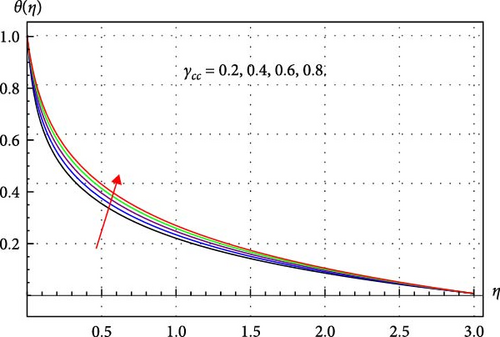
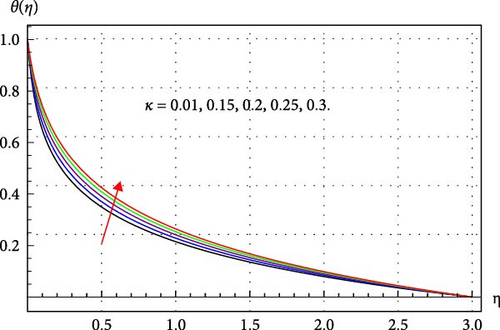
Figures 8–14 clarify how changes in several parameters like γcc, κ, β, ϕ1, ϕ2, and ϕ3 have a consequential effect on θ(η). For multiple values of Sw, the variation in θ(η) is displayed in Figure 8. An amplification in θ(η) is observed in Figure 8. When suction is applied, the pressure of the fluid decreases. In an adiabatic process, the reduction in pressure allows the fluid to expand. During expansion, the fluid does work on its surroundings, which consumes internal energy. This decrease in internal energy and consequently, the temperature field of THNF improves. Figure 9 demonstrates that when γcc rises, the fluid temperature grows. Physically, higher γcc enhances the thermal relaxation time, and thus fluid particles require more time to transmit energy to their neighboring particles. Therefore, the thermal field of the THNF profile upsurges. The surface curvature κ and temperature θ(η) relationship is depicted in Figure 10. It has been found that fluid temperature expands through rising surface curvature. The application of higher curvature variables enhances the velocity of the THNF by minimizing the contact area with the fluid. This reduction subsequently improves the thermal profile of the THNF. Figure 11 explores the relation between magnetic parameter β and θ(η). Here, θ(η) escalates through improved β estimations. Since more Lorentz force is offered due to higher β and thus the THNF thermal field becomes stronger. Figures 12–14 clarify the consequences of the volume fraction of nanoparticles on the THNF thermal field. From Figures 12–14, one can observe that the thermal profile of THNF decays. Physically, more heat is generated with the increment of volume fraction of nanoparticles and thus THNF thermal field upsurges versus higher ϕ1, ϕ2, and ϕ3.
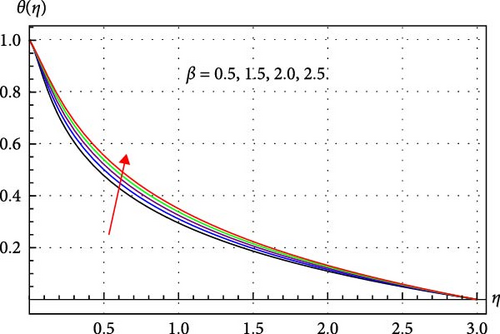
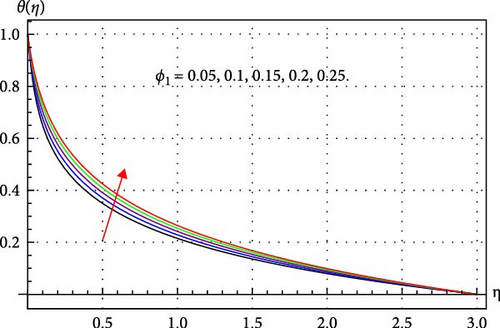
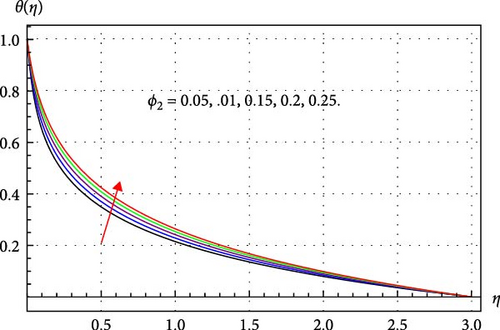
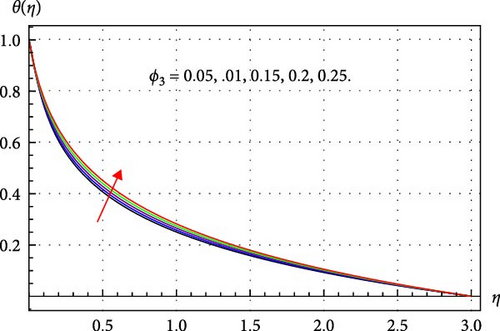
4.4. Skin Friction and Nusselt Factors
This subsection is devoted to examine the influence of diverse variables on THNF skin friction and Nusselt number . As a result of modifications in various parameters like β, κ, Γ, Sw, and ϒ, the outcomes of THNF for skin friction factor have been computed in Table 4. Through a positive change in κ, Γ, Sw, and ϒ an improved tendency in the intensity of skin friction factor has been noticed, while a negative impact β is visualized in Table 4. Table 5 has been organized by carrying out numerical calculations for the Nusselt quantity versus various variables. A diminishing tendency in the magnitude of Nusselt quantity is observed when Sw improves, whereas it upsurges through rising β, κ, Γ, and ϒ.
| β | κ | Γ | ϒ | Sw | |
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.3 | 1.5 | 1.5 | 5.3435 |
| 5.0 | — | — | — | — | 5.1468 |
| — | 0.2 | — | — | — | 6.0264 |
| — | 0.3 | — | — | — | 7.4537 |
| — | — | 0.3 | — | — | 7.1459 |
| — | — | 0.4 | — | — | 7.7132 |
| — | — | — | 2.0 | — | 6.5620 |
| — | — | — | 2.5 | — | 6.6785 |
| — | — | — | — | 5.0 | 6.5763 |
| — | — | — | — | 10.0 | 7.0630 |
| β | κ | Γ | ϒ | Sw | |
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.3 | 1.5 | 1.5 | 2.1357 |
| 5.0 | — | — | — | — | 2.3145 |
| — | 0.2 | — | — | — | 2.6136 |
| — | 0.3 | — | — | — | 2.9367 |
| — | — | 0.4 | — | — | 3.9426 |
| — | — | 0.5 | — | — | 4.0528 |
| — | — | — | 2.0 | — | 2.9158 |
| — | — | — | 2.5 | — | 3.0578 |
| — | — | — | — | 5.0 | 1.5792 |
| — | — | — | — | 10.0 | 0.9563 |
5. Concluding Statements
- •
For improved levels of curvature and suction variable, the velocity profile of THNF shows increasing behavior.
- •
Improved estimations of the variables magnetic, curvature, suction, and thermal relaxation improve the THNF thermal profile.
- •
Rising reciprocal magnetic and curvature variables diminish the induced magnetic field; however, it escalates when the material variable is elevated.
- •
The intensity of skin friction force upsurges via higher reciprocal, magnetic, material, and curvature variables, while an opposite impact of suction parameters is observed.
- •
The suction variable decays the magnitude of heat transfer, but an opposite impact of curvature and reciprocal parameters is noticed.
5.1. Future Research Directions
The current study could be extended by considering the effects of surface porosity, Darcy Forchheimer, thermal radiation, and heat generation or absorption. Exploring various geometries, such as stretching cylinders and rotating disks, may be significant future work in this area.
Nomenclature
-
- f′:
-
- Nondimensional velocity of a fluid
-
- N′:
-
- Induced magnetic field
-
- P:
-
- Pressure (Nm−2)
-
- κ:
-
- Curvature variable
-
- (u, v):
-
- Components of velocity (m/s)
-
- Nu:
-
- Nusselt number
-
- β:
-
- Nondimensional magnetic variable
-
- ν:
-
- Kinematic viscosity of the fluid (m2/s)
-
- T∞:
-
- Ambient fluid temperature (K)
-
- (M1, M2):
-
- Parallel and normal elements of induced magnetic field (kg/s2/A)
-
- knf:
-
- Thermal conductivity (W/mK)
-
- Pr:
-
- Prandtl number
-
- γcc:
-
- Thermal relaxation time variable
-
- Sw:
-
- Suction variable
-
- O:
-
- Center of curved surface
-
- ϕ:
-
- Solid volume fraction of nanoparticles
-
- (r, s):
-
- Cartesian coordinates (m)
-
- Γ:
-
- Dimensionless factor
-
- λ:
-
- Thermal relaxation time (K)
-
- T :
-
- Fluid temperature (K)
-
- Cp:
-
- Specific heat (J/kg/K)
-
- Tw :
-
- Fluid temperature at the surface (K)
-
- η:
-
- Dimensionless variable
-
- R:
-
- Radius of curved surface (m)
-
- θ:
-
- Dimensionless temperature
-
- Me(s):
-
- Strength of induced magnetic field at free stream (kg/s2/A)
-
- ϒ:
-
- Reciprocal magnetic number
-
- μ:
-
- Dynamic viscosity (kg/m/s)
-
- N:
-
- Dimensionless induced magnetic field
-
- uw(s):
-
- Surface stretching velocity (m/s)
-
- Cf:
-
- Skin friction
Subscripts
-
- nf:
-
- Dihybrid nanofluid
-
- thnf:
-
- Ternary hybrid nanofluid
-
- (1, 2, 3) MgO, Cu:
-
- MWCNTs
-
- f:
-
- Base fluid.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Kiran Batool and Saima Zainab conceptualized, designed the analysis, and wrote the text paper. Ghada A. Khouqeer and Naglaa AbdelAll interpreted and analyzed the data. Mohammed Sallah contributed to methodology and validation. Fazal Haq reviewed, edited, and supervised overall activities.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (Grant IMSIU-DDRSP2503).
Acknowledgments
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (Grant IMSIU-DDRSP2503).
Open Research
Data Availability Statement
All data generated or analyzed during this study are included in this published article.




