International Journal of Energy Research

Volume 2025, Issue 1 5377974

Research Article

Open Access

Development and Verification of a Spatial Dynamics Code RESTA-3D for Light Water Reactors

Yong Cui,

Yong Cui

orcid.org/0000-0002-0748-8980

Shanghai Institute of Applied Physics , Chinese Academy of Sciences , Shanghai , 201800 , China , cas.cn

Search for more papers by this author

Jing Shang,

Corresponding Author

Jing Shang

[email protected]

orcid.org/0009-0005-9191-9083

State Key Laboratory of Nuclear Power Safety Technology and Equipment , China Nuclear Power Engineering Co. Ltd. , Shenzhen , 518172 , Guangdong , China

Search for more papers by this author

Longwei Mei,

Longwei Mei

Institute of High Energy Physics , Chinese Academy of Sciences , Beijing , 100049 , China , cas.cn

China Spallation Neutron Source Science Center , Chinese Academy of Sciences , Dongguan , 523803 , Guangdong , China , cas.cn

Search for more papers by this author

Jianfei Tong,

Jianfei Tong

orcid.org/0000-0003-2555-9583

Institute of High Energy Physics , Chinese Academy of Sciences , Beijing , 100049 , China , cas.cn

China Spallation Neutron Source Science Center , Chinese Academy of Sciences , Dongguan , 523803 , Guangdong , China , cas.cn

Search for more papers by this author

Yong Cui,

Yong Cui

orcid.org/0000-0002-0748-8980

Shanghai Institute of Applied Physics , Chinese Academy of Sciences , Shanghai , 201800 , China , cas.cn

Search for more papers by this author

Jing Shang,

Corresponding Author

Jing Shang

[email protected]

orcid.org/0009-0005-9191-9083

State Key Laboratory of Nuclear Power Safety Technology and Equipment , China Nuclear Power Engineering Co. Ltd. , Shenzhen , 518172 , Guangdong , China

Search for more papers by this author

Longwei Mei,

Longwei Mei

Institute of High Energy Physics , Chinese Academy of Sciences , Beijing , 100049 , China , cas.cn

China Spallation Neutron Source Science Center , Chinese Academy of Sciences , Dongguan , 523803 , Guangdong , China , cas.cn

Search for more papers by this author

Jianfei Tong,

Jianfei Tong

orcid.org/0000-0003-2555-9583

Institute of High Energy Physics , Chinese Academy of Sciences , Beijing , 100049 , China , cas.cn

China Spallation Neutron Source Science Center , Chinese Academy of Sciences , Dongguan , 523803 , Guangdong , China , cas.cn

Search for more papers by this author

First published: 07 January 2025

https://doi.org/10.1155/er/5377974

Academic Editor: Yashwant Sawle

Share a link

Email
Wechat
Bluesky

Abstract

A neutronics/thermal-hydraulics (TH) coupled spatial dynamics code, reactor system transient analysis-three dimensional (RESTA-3D), has been developed for both static and transient analysis of large advanced light water reactors (LWRs), with a focus on control rod (CR) ejection accidents. The code is based on a neutron diffusion model, employing the widely used “two-step” strategy in 3D Cartesian coordinates. A polynomial nodal expansion method (NEM) is used to handle spatial variables, while the neutron kinetics solver applies the exponential transformation technique. Additionally, the code integrates a single-channel TH module and a steam table set at 15.5 MPa. The accuracy of the code has been validated against three transient benchmarks: the 3D-LRA benchmark for boiling water reactors (BWRs), the NEACRP 3D benchmark, and the mixed oxide (MOX)/UO2 core benchmark for pressurized water reactors (PWRs). These benchmarks address both static and transient behaviors, and the results have been thoroughly analyzed. The close agreement between the RESTA-3D results and reference data, as well as other codes, confirms its reliability, making it a promising tool for future dynamic analyses of large-scale advanced PWRs.

1. Introduction

Reducing the volume of nuclear waste per unit of energy, extending reactor lifetimes, and achieving deeper burnup are three practical approaches for enhancing the economic competitiveness of existing light water reactors (LWRs), while maintaining nuclear safety [1]. However, these efforts face a range of industry challenges, including fuel clad creep and growth [2], Chalk River unidentified deposits (CRUD) formation, localized corrosion, and power shift [3], among others. These phenomena are expected [4–6], which enable coupled neutronics, thermal-hydraulics (TH), nuclides burnup, thermomechanics, and radiochemistry calculations. During the multiphysical simulations of nuclear reactors, spatial dynamics analysis based on neutronics/TH coupling [7] is a fundamental and crucial aspect [8].

With the continuous advancements in numerical reactor core physics models and state-of-the-art parallel computing, considerable attention has been directed towards integrating the “one-step” strategy for full-core neutron transport with high-fidelity TH models in recent years. In 2010, the U.S. Department of Energy launched the Consortium for the Advanced Simulation of Light Water Reactors (CASL), which resulted in the development of the full-core neutron transport code system MPACT and the TH module CTF, based on the subchannel model. These two tools were integrated to perform fully coupled neutronics/TH simulations for entire reactor cores [1]. The high-precision 3D neutronics/TH coupling code NECP-X/SUBSC [8], developed and validated by Xi’an Jiaotong University, is similar to MPACT/CTF and exhibits comparable accuracy. It includes a neutron transport module based on the one-dimensional (1D) S_N method and the 2D method of characteristics (MOC), along with a subchannel TH model. Seoul National University combined the MATRA subchannel TH module with an enhanced version of the neutron transport code DeCART to perform core transient simulations [9]. Compared to computational fluid dynamics (CFD) software, the subchannel TH model is more efficient for neutronics/TH coupling. However, in terms of neutronics, the full-core neutron transport methods (e.g., MOC and SP_n based on the finite element method) require large parallel computing resources, and their computational burden remains unacceptable in nuclear engineering practice. Instead, the fast-running, assembly-wise “two-step” approach, which involves fuel assembly homogenization followed by core diffusion, is still widely used in the global nuclear power industry. Recently, Zhang et al. [10] investigated the propagation of uncertainties from the fundamental nuclear library to key reactor startup parameters in CPR1000 with initial fuel loading. These parameters include temperature coefficients, critical boron concentrations, power distributions, and the integral worth of the rod cluster CA (RCCA). The analyses were performed using the “two-step” code system Bamboo-C [10]; Jeon et al. [11] developed the GPU-accelerated code system VANGARD, which integrated the source expansion nodal method (SENM) with a highly parallelized depletion simulation and solution model based on the Chebyshev rational approximation method (CRAM). The performance of the code was evaluated using realistic AP1000 core problems, demonstrating its excellent efficiency and accuracy [11]. Hegyi, Maráczy, and Temesvári [12] conducted transient simulations of xenon behavior in a VVER-type reactor using the enhanced “two-step” code system KARATE, with the results showing good agreement with experimental measurements.

TMSR3D [7] is a 3D spatial dynamics code system specifically designed for molten salt reactors (MSRs). It comprises four modules: (1) TMSR-LINK, a code for producing and functionalizing assembly few group parameters based on the lattice code DRAGON5 [13]; (2) a neutronics model utilizing the standard polynomial nodal expansion method (NEM) [14] for spatial variables and an exponential transformation model for time-dependent term discretization; (3) a time-dependent multichannel TH module for determining core temperature profiles, fuel velocity, and pressure drop distributions in molten salt; and (4) a postprocessing module for data collection, analysis, and visualization [15]. In this study, a simple single-channel module with an integrated steam table was newly developed to enhance the applicability of this code for simulating the dynamic behavior of LWRs. Using this model, together with the NEM neutronics module, a critical boron concentration search model, and a feedback model of macroscopic cross-sections distinct from those in MSRs, a spatial dynamics code reactor system transient analysis-three dimensional (RESTA-3D) was developed for LWR simulations. To validate the accuracy of the RESTA-3D code, three international benchmarks 3D-LRA [7], NEACRP 3D [16], and mixed oxide (MOX)/UO2 core [17] were modeled and simulated, to capture both static and transient behaviors of the benchmark cores. Detailed analyses of these characteristics revealed that the RESTA-3D code can reliably predict the dynamic responses of LWRs.

The structure of this paper is as follows: Section 2 reviews the methodology adopted in the RESTA-3D code. Section 3 presents the simulation results and discussions. Finally, Section 4 concludes the study.

2. Numerical Model and Solution Method

2.1. Brief Description of the Neutronics Model

Since all nodes are homogenized in advance for modern nodal methods, the neutron current conservation equation for node k and energy group g in Cartesian geometry can be expressed using the standard neutronics notations:

()

where

, and the whole volume of a node could be written as V^k =

, as depicted in Figure 1a; g stands for the index of energy group (g = 1, 2,…, G); k denotes the index of node (k = 1, 2, …, N);

stands for the size (cm) of homogenized node k in u-direction (u = x, y, z);

and

represent the node-averaged flux (cm⁻²⋅s⁻¹) and the node surface-averaged net currents (cm⁻²⋅s⁻¹), respectively, as displayed in Figure 1b; χ_g denotes the fission energy spectrum;

denotes the macroscopic total neutron cross-section (cm⁻¹);

and

are the scattering matrix (cm⁻¹) and the production cross-section (cm⁻¹), respectively; k_eff stands for the effective multiplication factor.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Schematic view of node (a) and neutron current (b).

In most nodal methods, transverse integration typically involves performing the integration of the 3D equation along the two axes orthogonal to each coordinate direction. This procedure decomposes the original 3D equation into three separate 1D equations, which are coupled through transverse leakage terms. For instance, the 1D equation along the u-axis is expressed as follows:

()

where

is the diffusion coefficient (cm). The 1D transverse integrated partial flux can be described as follows:

()

and the integration term for transverse leakage is written in an analogous manner:

()

In the RESTA-3D code, the 1D partial neutron fluxes from Equation (3) are approximated using an orthogonal polynomial expansion method. In the NEM, these fluxes are represented by polynomials up to the fourth order:

()

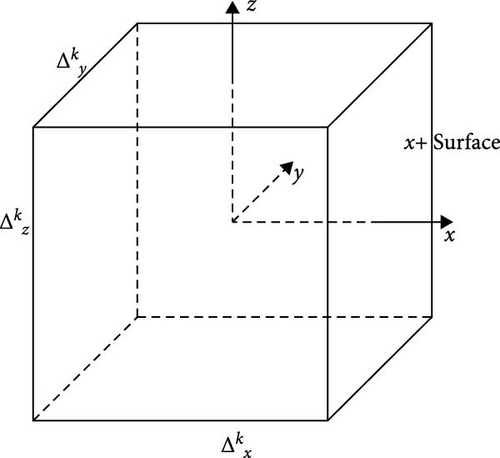
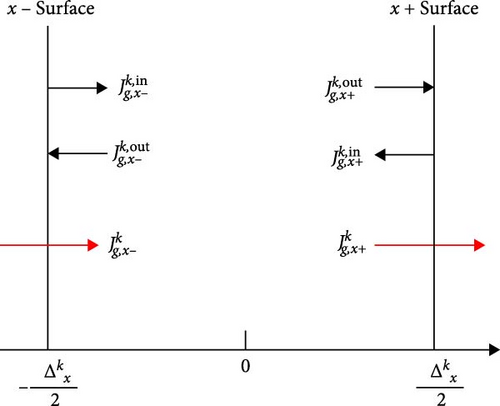
Here, represents the expansion coefficients of the 1D partial fluxes, and the orthogonal Legendre polynomials are chosen as basis functions [14].

The coefficients for the lower-order terms, and , can be determined based on the node-averaged neutron flux , and the incoming/outgoing partial neutron currents across the node boundaries, and , by applying corresponding neutronics boundary conditions at the edges of the nodes. To derive the higher-order coefficients, and , a weighted residual method is applied to Equation (2), ensuring that these terms are systematically obtained.

After addressing the transverse leakage terms using a 2nd order polynomial approximation [14], the final coupling equations for the partial neutron currents can be expressed as follows:

()

where

and

represent the incoming and outgoing partial neutron currents, respectively;

and

correspond to the leakage and source terms, respectively;

and

denote the response matrices that encapsulate the nodal coupling coefficients. A detailed derivation of the spatial discretization in RESTA-3D can be found in the literature [14, 18].

Compared to the traditional point kinetic approximation, the 3D spatial dynamics based on the coupled neutronics/TH model can explicitly simulate localized reactor perturbation and capture the core response to unintended reactivity insertion, which is essential for reactor safety analysis [19]. In general, the 3D multigroup spatial-kinetic equations for node k are given by:

()

and concentration balance equations of the delayed neutron precursor (DNP):

()

Here v_g represents the average velocity of neutrons (cm⋅s⁻¹) in energy group g; denotes the removal cross-section (cm⁻¹). The index i identifies the DNP group; denotes the DNP concentration (cm⁻³); indicates the yield of prompt neutrons released in group g, while represents the probability of delayed neutrons decaying from the ith-group DNP and depositing in neutron energy group g; β_i refers to the yield of delayed neutrons in group i, with β being the total yield across all groups. Finally, λ_i is the decay constant (s⁻¹) of delayed neutrons in the ith-group.

In RESTA-3D, the time derivative terms in Equation (7) are addressed using the exponential transformation of the neutron flux [19], as this approach enhances simulation accuracy for transients expected to exhibit exponential variation [20]:

()

The term () represents an intermediate variable in the exponential transformation method (ETM). It, evolves gradually over time, assuming that the exponential transformation factors, (t), are appropriately chosen.

By systematically organizing Equations (7)– (9) and applying the fully implicit backward difference scheme (FIBDS) to the time derivative terms (the detailed theoretical derivation of this procedure can be found in references [14, 19]), the original 3D multigroup spatial-kinetic equations for node k can be derived and simplified as follows:

()

The index n denotes the current time point, and n + 1 corresponds to the next time point, with Δt_n representing the time step.

and F^k,n + 1 are related to the scattering and fission sources terms, respectively, and their definitions can be found in the literature [14, 19]. The generalized removal cross-section

is defined as follows:

()

The exponential transformation factors

, derived from the solutions in the previous step [21]:

()

For the DNP equations, applying FIBDS to Equation (8) yields:

()

It is important to note that Equation (10) shares a similar structure with the static nodal equation. In this formulation, all source terms, except the neutron fluxes from previous calculations, are updated in each neutronics/TH iteration based on the corresponding core parameters at a given time. Therefore, the static solver remains valid for solving transient problems.

2.2. Single-Channel TH Model

To model and simulate the transient phenomena, such as the reactivity-initiated accident (RIA), for LWRs with TH feedback, a simplified single-channel model has been newly implemented into the RESTA-3D code. This model is characterized by single-phase flow, no cross-flow between channels, constant mass flow rate, and constant pressure, with the steam table set at 15.5 MPa [22].

Under these assumptions, the total coolant flow rate is uniformly distributed to the inlet of each channel adjacent to the fuel pins. The temperature profile of the coolant is first determined during the TH calculations using an axial 1D energy conservation equation:

()

where ρ_c and h are density (kg⋅m⁻³) and specific enthalpy (J⋅kg⁻¹) of the coolant, respectively; s and w denote flow area (m²) and its mass flow rate (kg⋅s⁻¹), respectively; q_l is the linear power density of coolant (W⋅m⁻¹), which characterizes the heat convected from fuel pin cladding.

The spatial partial derivative of specific enthalpy in Equation (14) can be approximated by the following discretization scheme [19]:

()

Here, index j represents the axial node j, which coincides with the neutronics module; Δz denotes the node height. The inlet specific enthalpy of node j, denoted as

, can be approximated using linear interpolation [23]:

()

Multiplying Equation (16) by the node height Δz_j and simultaneously applying FIBDS, yields the discretized equation for the coolant specific enthalpy:

()

Equation (17) could be further simplified as:

()

where

()

Subsequently, the coolant temperature and density at each node can be calculated from the steam table by linear interpolation based on the obtained specific enthalpy.

Preventing fuel pin meltdown is the primary safeguard for the safe operation of LWRs under both normal and accident conditions. This requirement dictates that the maximum centerline temperature of the fuel pin should not exceed its melting point. In the RESTA-3D code, a 1D radial heat transfer simulation model is employed to calculate the heat transfer from the pin cladding to the moderator and determine the fuel centerline temperature. The heat conduction equation governing the fuel pin is expressed as follows:

()

with the heat flux being zero at the fuel pellet center [19], where C_P, ρ, and k denote heat capacity (J⋅kg⁻¹⋅K⁻¹), density (kg⋅m⁻³) and thermal conductivity (W⋅m⁻¹⋅K⁻¹) of the fuel pin material, respectively; Q_v represents the volumetric source of heat (W⋅m⁻³); T stands for fuel pin temperature (K).

The time-dependent term in Equation (20) can also be discretized by FIBDS:

()

The spatial mesh used to solve Equation (21) is shown in Figure 2, where the fuel pin is divided into N + 2 meshes, and the dashed lines represent the mesh centerlines. Integrating Equation (21) over the interval [r_i−1/2, r_i + 1/2] results in the discretized form:

()

where

()

The heat transfer equations describing conduction across the gas gap and convection from the cladding to the coolant are expressed as follows:

()

and

()

respectively. Here, q denotes the heat flux (W⋅m⁻²);

and

represent inner and outer radii (m) of the cladding, respectively; H_g and h(t) denote the equivalent gap conductance (W⋅m⁻²⋅K⁻¹) and the convection heat transfer coefficient (W⋅m⁻²⋅K⁻¹) on the cladding surface, respectively; R_f is the fuel pellet radius (m); T_col stands for the coolant temperature (K).

2.3. Coupling Scheme

In RESTA-3D, the macroscopic cross-section Σ under the realistic operating conditions can be calculated using the following formula:

()

where ρ is water density; c is the boron concentration in ppm; T_M is the moderator temperature; T_F is Doppler temperature, defined as the sum of the centerline temperature T_f,c and the surface temperature T_f,s of the fuel pellet, weighted accordingly. It can be obtained from the relation in [24]:

()

In Equation (26), the subscript zero denotes the macroscopic cross sections generated at the reference point (ρ₀, c₀, T_F0, and T_M0).

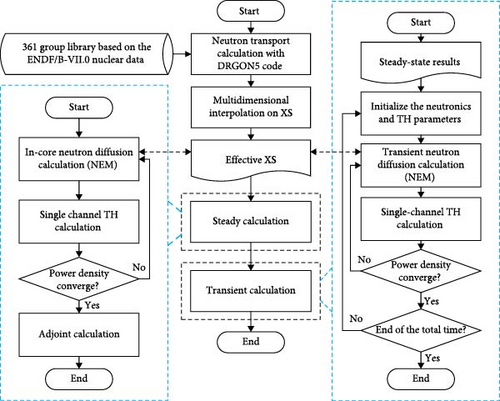
In addition to the abovementioned coupling scheme, RESTA-3D can also handle multidimensional tabular cross-section libraries, where the feedback parameters include boron concentration, moderator density, and core temperature. As shown in Figure 3, during static or transient simulations, the group constants and kinetics parameters are updated either according to Equation (26) or through multidimensional linear surface interpolation. This process accounts for the variation in cross sections caused by control rod (CR) movement during each time step or iteration, thereby, coupling the TH and neutronics modules and considering the local feedback of core variables on group constants and kinetic parameters.

3. Results and Discussion

3.1. 3D-LRA Benchmark

The 3D-LRA benchmark focuses on a prompt supercritical transient scenario, specifically modeling and simulating a cruciform control assembly (CA) drop accident in a boiling water reactor (BWR). This event involves a significant reactivity insertion and a marked negative temperature feedback. As shown in Figure 4, the active core contains four distinct types of fuel assemblies (materials 1, 2, 3, and 4), each measuring 15 cm × 15 cm × 300 cm. The axial and radial reflectors are modeled using material 5, with a width of 15 cm. Neutron energy and DNP are divided into two groups. At the beginning of the transient, the cruciform CA descends from the upper to the lower region of the reactor core over a 2-s period, with a velocity of 150 cm/s. Detailed information on the group constants and kinetic parameters for this problem can be found in the existing literature [25].

A Doppler feedback model and an adiabatic heating model are incorporated into the 3D-LRA simulation, as expressed by:

()

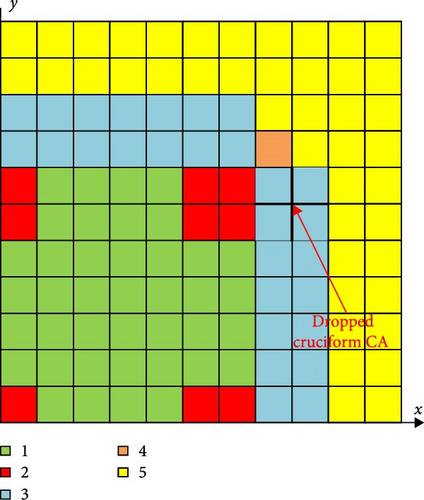
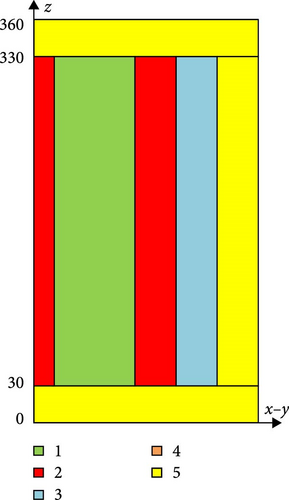
The parameters are α₁ = 3.83 × 10⁻¹¹ K⋅cm³ and α₂ = 3.034 × 10⁻³ K^−0.5. t₀ denotes the start time, and the original core average temperature is set to 300 K. During the calculation, the initial neutron fluxes are normalized based on a preset power density of 1.0 × 10⁻⁶ W⋅cm⁻³, and the energy released per fission is taken as 3.204 × 10⁻¹¹ J/fission. The flux–volume weighted method, used to calculate group constants and kinetics parameters in nodes with partially inserted CRs, reduces the CR cusping effect [7]. Additionally, Equation (28) is iteratively solved using the Crank–Nicholson semi-implicit scheme to determine the core-averaged temperature.

Figure 5 compares the power density and core temperature profiles simulated by RESTA-3D with those obtained from the reference code TNGFM [26]. Following the introduction of the perturbation, the normalized power density rapidly increases by a factor of 10 within a short time, peaking at 5717 W⋅cm⁻³ around 0.9 s, indicating the occurrence of a prompt supercritical event with minimal influence from delayed neutrons on reactivity. Almost simultaneously, negative temperature feedback from the Doppler effect begins to take effect as the core temperature starts to rise at 0.82 s, leading to a subsequent decrease in power density. As the CA continues to drop, its relatively large differential worth at the core center causes the inserted reactivity to surpass the negative temperature feedback, resulting in a second power density peak of 362 W⋅cm⁻³ at approximately 1.5 s. The CA is fully inserted after 2.0 s, making the reactor core subcritical. Consequently, the normalized power density gradually decreases, while the core temperature continues to rise, reaching around 1000 K at 3 s due to the absence of a heat sink.

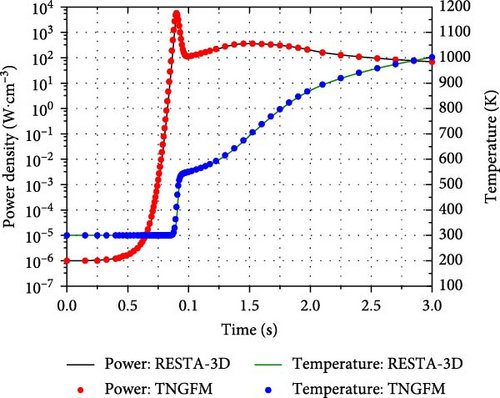
As shown in Figure 5, the maximal percent errors in power density and core temperature are 3.7% and 5.6%, respectively, both occurring near the first power peak. Despite these relatively small discrepancies, the RESTA-3D solutions during the RIA show good agreement with those from the reference code, indicating that the neutron kinetics model proposed in this paper is accurate and suitable for preliminary neutronics/TH calculations.

3.2. NEACRP 3D Pressurized Water Reactor (PWR) Benchmark

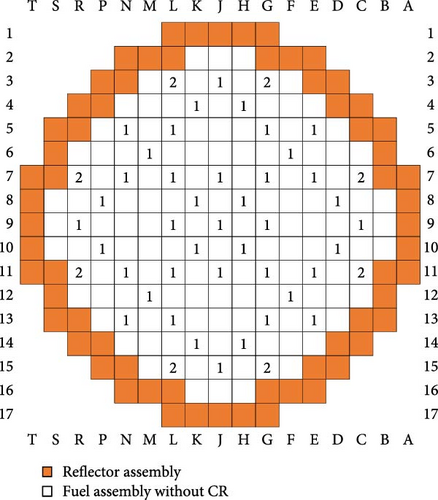
The core configuration and operational data of the NEACRP 3D PWR benchmark, including geometry, physical properties, and few-group parameters, are extracted from a realistic PWR. An additional CR is placed at the center of core to address the issue of single CR ejection with complete rotational symmetry during the verification process. As described in the benchmark, CR ejection events may result from the failure of the CR drive mechanism casing located above the reactor pressure vessel in a PWR. Such an event could cause a rapid, localized disturbance in core safety parameters, posing a significant challenge to the accuracy of any neutronics/TH coupling code based on the nodal method.

The radial core layout of the NEACRP 3D PWR benchmark is shown in Figure 6, where the size of each fuel assembly is 21.606 cm × 21.606 cm. In this study, a quarter core model is used in the radial direction, with each fuel assembly consisting of 2 × 2 nodes. Vertically, the reactor core is divided into 18 layers. The 1st and 18th layers, starting from the bottom, represent the axial reflector, each with a height of 30 cm. The remaining 16 layers form the reactor active core, which has a height of 367.3 cm. Table 1 lists the primary design parameters for the benchmark core. Detailed information on cross-section data, thermal relations, and properties can be found in the related literature [24]. The accident scenarios in this study are initiated by the rapid ejection of the CR at hot zero power (HZP) and hot full power (HFP). These scenarios include six cases, labeled A, B, and C under both HZP and HFP conditions, as summarized in Table 2.

Table 1. Primary core parameters for the NEACRP 3D pressurized water reactor (PWR) benchmark.

Parameters	Values
Steady state operation data
Core power (MWth)	2775
Inlet temperature (°C)	286
Core pressure (MPa)	15.5
Inlet mass flow rate (kg·s⁻¹)	12,893
Fraction of heat deposited in coolant (%)	1.9
Fuel assembly geometry
Pellet diameter (mm)	8.239
Clad outer diameter (mm)	9.517
Clad wall thickness (mm)	0.571
Fuel rod pitch (mm)	12.655
Inner diameter of guide tube (mm)	11.448
Outer diameter of guide tube (mm)	12.259
Number of fuel pins	264
Number of guide tubes	25

Table 2. Operation data for the rod ejection transients ^∗.

Case	Condition	Number of ejected CR	Position of ejected rod (in steps)
Case	Condition	Number of ejected CR	Initial	Final
A1	HZP	1 (central)	0	228
A2	HFP	1 (central)	100	228
B1	HZP	4 (peripheral)	0	228
B2	HFP	4 (peripheral)	150	228
C1	HZP	1 (Full core)	0	228
C2	HFP	1 (Full core)	100	228

Abbreviations: CR, control rod; HFP, hot full power; HZP, hot zero power.
^∗The maximal number of steps is 228, 0 means the CR is fully inserted.

Table 3 lists the steady state results obtained by RESTA-3D including the maximal power peaking factor, critical boron concentration, and the reactivity introduced by rod ejection compared with the refined PANTHER solutions [27]. It shows that the maximum discrepancy in critical boron concentration is −0.119%, occurring in Case A1. This indicates that the critical boron concentration search model and the coupling scheme, which updates the few-group parameters using their derivatives, are effectively and correctly implemented in the respective modules. The maximum discrepancies in the maximum power peaking factor and reactivity introduced by rod ejection are −2.468% and −5.370%, respectively. These discrepancies may be attributed to the different spatial and temporal discretization schemes used in the two nodal methods. In general, the static results from the RESTA-3D align well with the revised reference solutions and can be used as initial conditions for further transient analyses.

Table 3. RESTA-3D results for the NEACRP 3D PWR at steady state compared against benchmark results.

Cases	A1	A2	B1	B2	C1	C2
Core conditions	HZP	HFP	HZP	HFP	HZP	HFP
Critical boron concentration (ppm)
PANTHER	561.20	1156.63	1247.98	1183.83	1128.29	1156.63
RESTA-3D	560.53	1156.14	1247.38	1184.54	1127.69	1156.06
Relative error (%)	−0.119	−0.042	−0.048	0.060	−0.053	−0.049
Maximal power peaking factor
PANTHER	2.8792	2.2073	1.9330	2.0954	2.1867	2.2073
RESTA-3D	2.8467	2.2171	1.8853	2.0688	2.1729	2.2690
Relative error (%)	−1.129	0.444	−2.468	−1.269	−0.631	2.795
Reactivity introduced by CR ejection (pcm)
PANTHER	824.31	91.58	826.18	99.45	949.09	79.23
RESTA-3D	820.12	91.32	822.97	94.11	944.10	80.93
Relative error (%)	−0.508	−0.284	−0.389	−5.370	−0.526	2.146

Abbreviations: CR, control rod; HFP, hot full power; HZP, hot zero power; PWR, pressurized water reactor; RESTA-3D, reactor system transient analysis-three dimensional.

For Cases A2 and B2, before the transient processes begin, the reactor operates under static conditions with a full power of 2775 MWth, and the average fuel and coolant temperatures are 538°C and 310°C, respectively. As shown in Figure 7b,d, with reactivities of 91.58 and 99.45 pcm inserted into the core over 0.1 s for Cases A2 and B2, respectively, the relative power increases for both cases are less than 10%. This suggests that delayed-critical transient conditions occur, and the effect of delayed neutrons on core reactivity is significant.

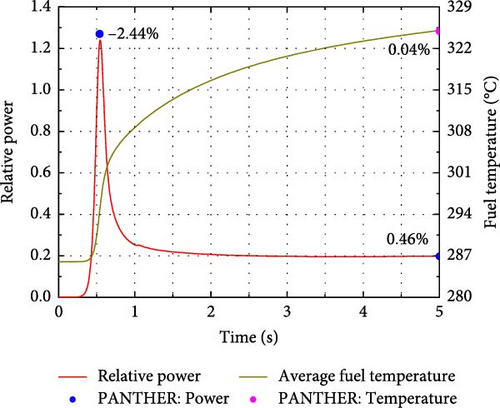
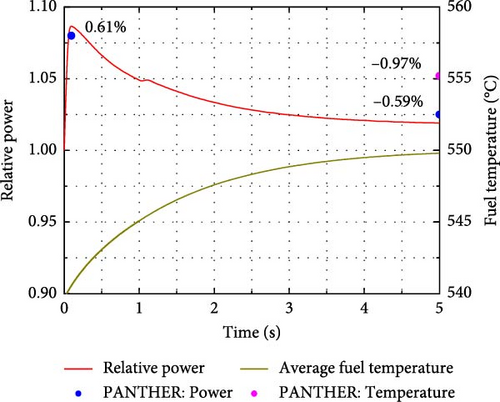
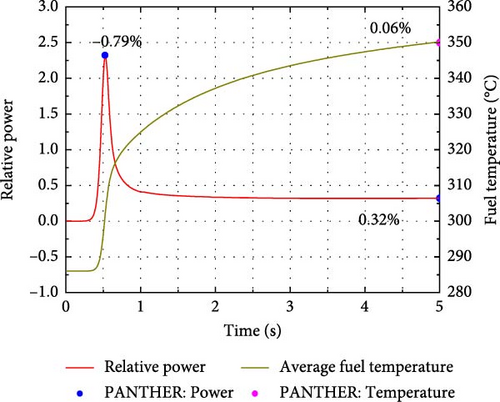
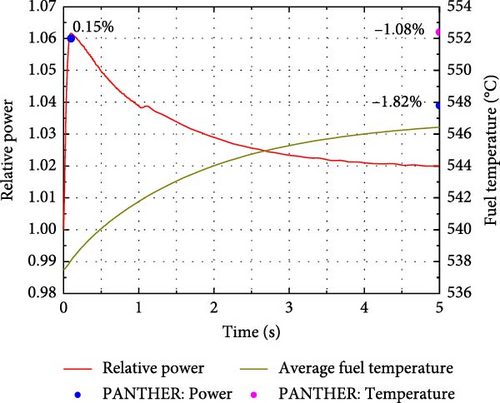
Compared to Cases A1 and B1, the core parameters, including relative power and average fuel temperature, in Cases A2 and B2 exhibit a faster response to the perturbation. This is because the initial relative power in Cases A1 and B1 is 10⁻⁶, and the fuel temperature is uniformly distributed, equal to the inlet coolant temperature of 286°C. A significant increase in power is observed after 0.3 s, while the delayed rise in fuel temperature results from the lag effect of heat transfer. In Cases A2 and B2, the timely increases in fuel and coolant temperatures lead to a balance between the induced negative reactivities and inserted reactivity. As a result, the relative power drops sharply after reaching its peak within 0.1 s. Eventually, the reactor core reaches a new steady state without the implementation of any safety strategy. As shown in Figure 7, the solutions obtained from the RESTA-3D, including peak power, final power, and fuel temperature, are compared with those from the PANTHER code for all four cases. The maximum deviations of the calculated power peak, final power, and final fuel temperature are −2.44%, −1.82%, and 1.08%, respectively, indicating good agreement. Therefore, the developed scheme for handling the neutronics/TH coupling problem in the RESTA-3D code is both correct and effective. These benchmark problems are likely to be particularly sensitive, especially with regard to CR reactivity. Thus, a sensitivity analysis should be conducted to better understand the source of the deviations.

To provide a more intuitive representation of the localized perturbations in core parameters, the initial and final fuel temperature distributions for Case C2 are shown in Figure 8. As observed in Figure 8a, under the HFP condition, the static fuel temperature distribution is axisymmetric, and the peak temperature values shift to the lower half of the reactor core with coolant cooling and the insertion of different types of CRs. The transient is perturbed by a 128 cm CR ejection during the first 0.1 s, which introduces a 79.23 pcm reactivity into the core. Similar to Cases A2 and B2, reactor self-regulation at HFP is much more effective than that at HZP. A stable state is reached within 5 s, with the average fuel temperature increasing by only 8.81°C. The localized perturbations are clearly visible in Figure 8b. In the region near the assembly where the CR is ejected, the local fuel temperature increases significantly during the transient, and the peak temperature on the left side of the reactor core also rises sharply. This results in an asymmetric fuel temperature distribution.

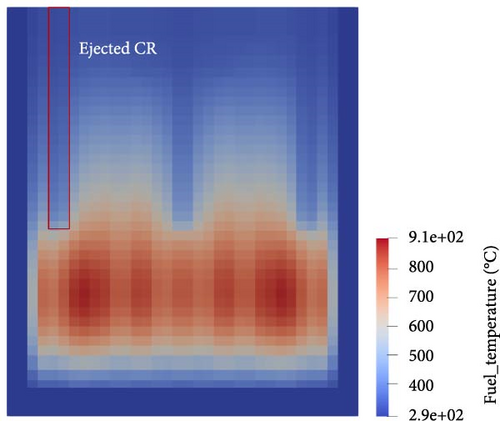
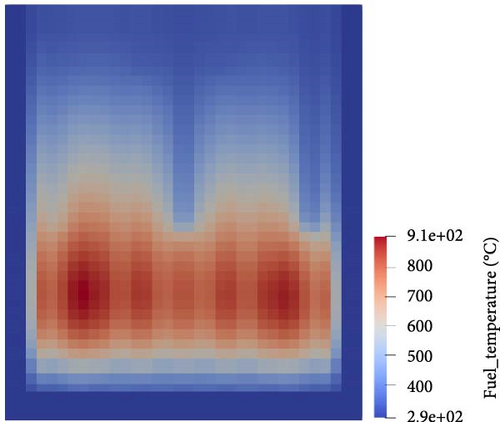
3.3. PWR MOX/UO2 Core Benchmark

In this section, the PWR MOX/UO2 core benchmark [28] is selected to assess the precision and stability of the RESTA-3D code. This benchmark is based on a realistic Westinghouse PWR with four thermal loops, featuring partial loading of weapons-grade MOX fuel. The use of MOX, a blend of Pu and U in oxide form, along with burnup variations within the core, results in a substantial neutron flux gradient across the fuel assemblies [19]. This presents challenges for neutronics/TH coupling codes that employ nodal methods.

The quarter-core configuration of this benchmark problem is shown in Figure 9, and the primary design and TH parameters of the active core are displayed in Table 4. Detailed neutronics and TH parameters can be found in the literature [28]. This benchmark consists of four parts: (1) 2D steady-state neutronics calculations with fixed TH parameters; (2) 3D boron concentration search under HFP condition with TH feedback; (3) 3D boron concentration search under HZP condition with TH feedback; (4) CR ejection accident simulation under HZP conditions. In this study, Part 3 is omitted for brevity, while the remaining three parts are simulated and analyzed in detail to validate the RESTA-3D code. The two-group assembly homogenization parameters for this benchmark, including macroscopic cross-sections, neutron diffusion coefficients, assembly discontinuity factors (ADFs), kinetic parameters at different burnup points, moderator density, fuel and moderator temperatures, and boron concentrations, are generated using DRAGON5 [13], leveraging the nuclear library in SHEM-361 format based on the ENDF/B-VII.0 data.

Table 4. Primary design parameters of the mixed oxide (MOX)/UO2 core.

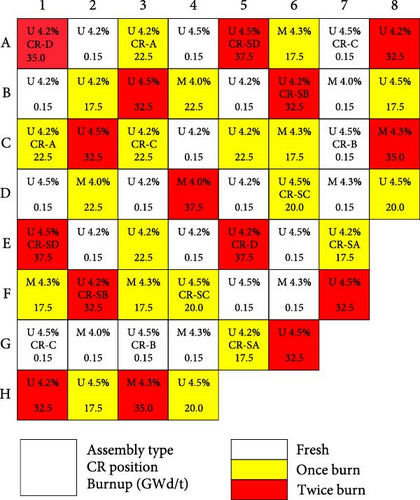
Parameters	Values
Core power (MWth)	3565
Inlet temperature (°C)	286.85
Core pressure (MPa)	15.5
Inlet mass flow rate (kg/s)	15,849.4
Number of fuel assemblies	193
Fuel lattice, fuel rods per assembly	17 × 17 square, 264
Guide tubes per assembly	25
Active fuel length (cm)	365.76
Assembly pitch (cm)	21.42
Pin pitch (cm)	1.26

In Part 1, the fuel temperature, moderator density, and boron concentration are set to 560 K, 752.06 kg/m³, and 1000 ppm, respectively. During the calculation, two layers of nodes are modeled along the axial direction to simulate a 2D problem. In the radial direction, a 2 × 2 node division is applied for each fuel assembly to improve the solution accuracy. The values of k_eff in both all rods out (ARO) and all rods in (ARI) conditions, along with the total CR worth calculated using the RESTA-3D, are shown in Table 5. These results are compared with those from the reference codes DeCART [29], PARCS [30], and CITATION [31], as stored in the benchmark book [28]. Among the three codes, DeCART, a heterogeneous high-order multigroup neutron transport code using the MOC, is selected as the reference. PARCS employs both the analytic nodal method (ANM) and the NEM, while CITATION utilizes the finite difference method (FDM). Table 5 indicates that, compared to DeCART, k_eff values obtained from the RESTA-3D in ARO and ARI conditions differ by 0.5% and 0.42%, respectively. The relative error in the total CR worth is only 0.706%, which is in good agreement with the reference solutions. Additionally, the solutions from PARCS are closer to those from the RESTA-3D than those from the other two codes, as both use nodal methods.

Table 5. k_eff and total CR worth ^∗.

Code	k_eff		Total rod worth (pcm)	Error (%)
Code	ARO	ARI	Total rod worth (pcm)	Error (%)
DeCART	1.058520	0.987430	6801	—
PARCS 2G	1.063786	0.991536	6850	0.710
CITATION	1.060337	0.988785	6825	0.339
RESTA-3D	1.063782	0.991535	6849	0.706

Abbreviations: ARI, all rods in; ARO, all rods out; CR, control rod; RESTA-3D, reactor system transient analysis-three dimensional.
^∗PARCS 2G means PARCS code with 2 neutron energy groups, similarly hereinafter.

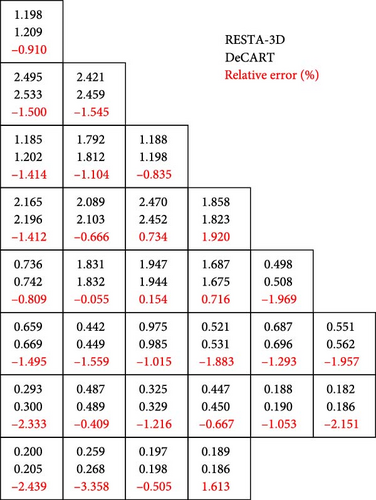
The radial power peaking factor is an important reactor variable that characterizes the intensity and profile of heat production. It is defined as the ratio of the maximum heat production within a fuel assembly to the average heat production throughout the reactor core in the radial plane. Figures 10 and 11 present the power profile normalized by the average value in the radial direction, along with the relative deviation between the RESTA-3D and DeCART under ARO and ARI conditions, respectively. For the ARO condition, the maximal difference of −3.755% occurs at position (C, 2), while for the assembly with the highest radial power peaking factor, (B, 1), the relative error is −2.421%. For the ARI condition, the maximal difference of −3.358% occurs at position (H, 2), while the highest radial power peaking factor of 2.495 is still located at (B, 1), with a difference of −1.5%. Overall, the static solutions from RESTA-3D static solutions are very close to the heterogeneous solution from the DeCART neutron transport code, despite the slightly higher errors in local areas, mainly due to the loading of MOX fuel, CR insertion, and the burnup variation of the fuel assemblies.

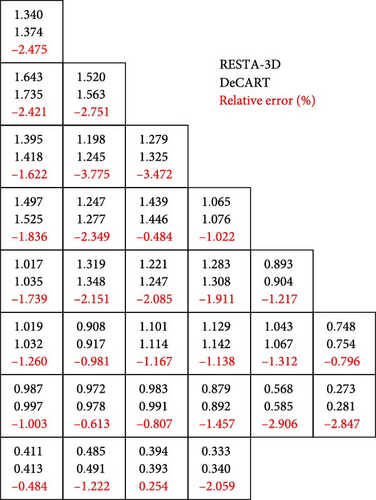
In Part 2, critical boron concentration search is conducted under HFP conditions with TH feedback. In this section, the SKETCH code utilizing ANM is incorporated into the reference codes. After obtaining the critical boron concentration, a coupled neutronics/TH steady-state calculation is performed. Table 6 indicates that the final critical boron concentration and core-averaged TH parameters are in good agreement with the results from reference codes, further validating the accuracy and applicability of the proposed boron concentration search model as well as the single-channel TH model, including the steam table at 15.5 MPa, implemented in the RESTA-3D.

Table 6. Comparison of core averaged TH parameters and critical boron concentration.

Code	Critical boron concent. (ppm)	Core average T/H properties
Code	Critical boron concent. (ppm)	Fuel temp. (°C)	Coolant density (g/cm³)	Coolant temp. (°C)	Outlet cool. density (g/cm³)	Outlet cool. temp. (°C)
PARCS 2G	1679	562.9	0.7061	308.2	0.6621	325.7
PARCS 4G	1674	563.0	0.7061	308.2	0.6621	325.7
PARCS 8G	1672	563.1	0.7061	308.2	0.6621	325.7
SKETCH	1675	563.5	0.7055	307.8	0.6596	325.8
RESTA-3D	1673	562.8	0.7057	308.1	0.6615	325.5

Abbreviations: RESTA-3D, reactor system transient analysis-three dimensional; TH, thermal-hydraulics.

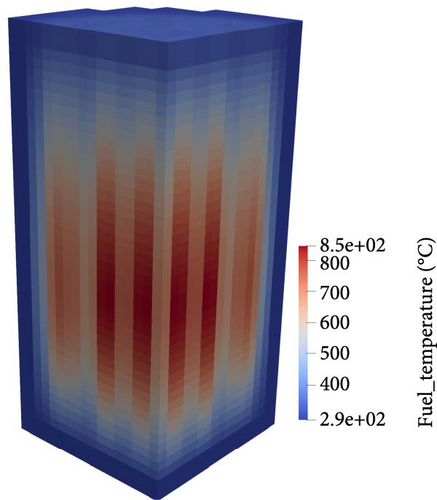
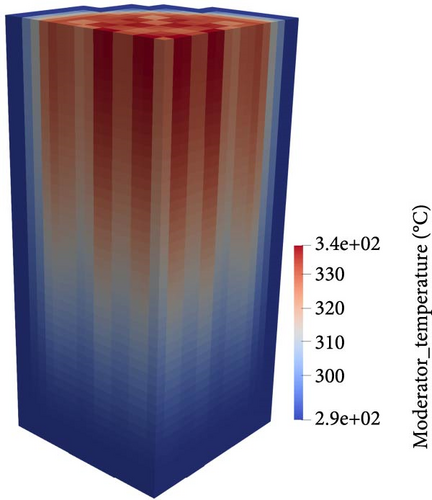
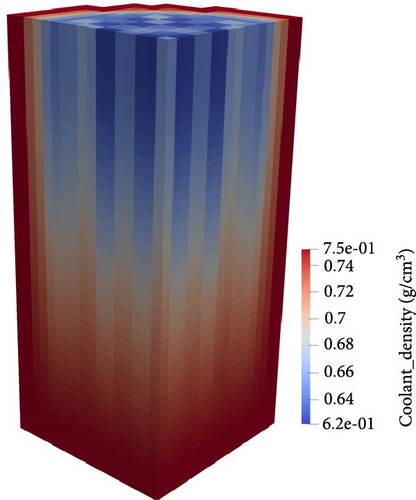
Additionally, the 3D steady-state distributions of fuel temperature, moderator temperature, and moderator density under HFP conditions, calculated by the RESTA-3D, are shown in Figure 12. From these, the effect of CR insertion on core parameters is clearly observed. The fuel temperature profile exhibits a symmetrical distribution, similar to the nuclear heat distribution in fuel pins. The moderator (water) enters the reactor core with an average temperature of 286.85°C and gradually heats up as it flows through the active core, due to heat convection from the fuel pins and the deposition of a small amount of nuclear heat in the moderator. Ultimately, the moderator exits the active core with an average temperature of 308.1°C. In contrast, the moderator density decreases as it flows from the reactor core inlet to the outlet, with the mean outlet density of the moderator being 0.6615 g/cm³. Multi-phase flow may occur during this process, which will be further investigated in future work using a subchannel TH model.

In Part 4, the reactor is operated under steady-state HZP condition with a critical boron concentration of 1341 ppm. A perturbation is then introduced by ejecting (E, 5) from the bottom to the top of the reactor core within 0.1 s. A comparison of the calculated β_eff, peak time, peak power, and peak reactivity during the transient between the RESTA-3D and the reference codes is displayed in Table 7. The results show that the peak time, peak reactivity, and β_eff from these codes are consistent. However, significant discrepancies are observed in the peak power. Notably, the PARCS 8G solution results in a 30% increase in transient peak power compared to the 2G solution, while the group effect in PARCS has minimal influence on the other parameters. Overall, since the PARCS 8G solution is closer to the results from RESTA-3D, it is selected as the reference code in the subsequent verification process.

Table 7. Peak power, time, reactivity, and β_eff obtained from the reactor system transient analysis-three dimensional (RESTA-3D) in comparison to those from reference codes.

Code	Peak time (s)	Peak power (%)	Peak reactivity ($)	β_eff (pcm)
PARCS 2G	0.34	142	1.12	579
PARCS 4G	0.33	152	1.12	579
PARCS 8G	0.32	172	1.14	580
SKETCH	0.34	144	1.12	579
RESTA-3D	0.35	173	1.12	580

The power profile and reactivity evolution from the RESTA-3D compared to the reference are depicted in Figure 13. It can be observed that, with the introduction of CR ejection, the reactivity rises to 1.12$ (649.6 pcm) in the first 0.1 s, leading to a prompt supercritical state. The core power initially increases sharply from 0.0001% to 173% of the full power (3565 MWth) and then rapidly decreases as negative reactivity from the rising coolant and fuel temperatures is gradually introduced into the core, as seen in Figure 14. Eventually, the core power stabilizes at 20% of full power, with the corresponding reactivity at 0.57$. Therefore, the moderator and fuel temperatures increase slowly over 1 s.

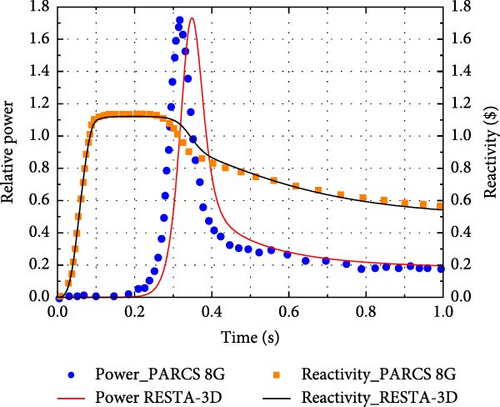
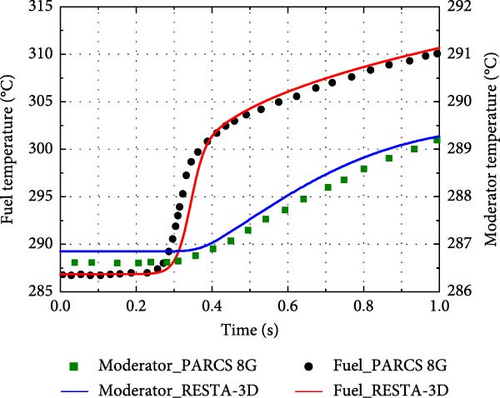
The RESTA-3D results agree well with the reference in terms of curve trends and values at special points, such as the start, peak, and end points. However, there are still some nonnegligible discrepancies. For example, the relative power peak from RESTA-3D occurs 0.02 s later than that from PARCS 8G, and the moderator temperature from RESTA-3D is consistently higher than the reference result throughout the transient. In fact, while the 8G solution is expected to reduce energy discretization errors in PARCS, it introduces a more significant spatial discretization error due to the more complex spatial distribution of neutron flux. This is especially noticeable in the low-energy groups, where interactions between groups are more pronounced. The impact of increasing neutron energy groups on core parameters under both static and transient conditions depends on the competing effects of group and spatial discretization [28]. Furthermore, the use of different discretization methods for spatial and time-dependent terms, node sizes, time steps, and TH properties may also contribute to the discrepancies. Within acceptable computational errors, the RESTA-3D results are in good agreement with those from PARCS 8G, further validating the correctness and availability of the kinetics and TH models implemented in the RESTA-3D.

4. Conclusions

In this study, the 3D spatial dynamics code TMSR3D, originally designed for MSRs using the neutronics/TH method, has been extended to a new code RESTA-3D for simulating LWRs. The neutronics module incorporates the 4th-order NEM for spatial discretization and the ETM to handle the time derivative terms in the 3D neutron kinetics equations, both of which are adopted from the original TMSR3D without DNP flow. A simplified single-channel TH model, including a steam table at 15.5 MPa, has been newly developed to account for thermal feedback. Additionally, a critical boron concentration search model has been introduced specifically for LWRs. A comprehensive discussion of the numerical models and solution methods adopted in the extended code is provided.

To verify the theoretical models and solution methods implemented in the RESTA-3D code, the 3D-LRA benchmark problem is first used to test its performance in addressing BWR problems. Subsequently, two PWR benchmarks, NEACRP 3D and MOX/UO2 cores, are simulated, with both steady-state characteristics and transient behaviors thoroughly analyzed. The numerical solutions demonstrate that the RESTA-3D code is an effective tool for the dynamic analysis of large-scale advanced PWRs, such as the CPR1000, CAP1400, and HPR1000 (Hualong Pressurized Reactor).

Future developments for the code aim to replace the current NEM neutronics module with a more advanced nodal method, such as the semi-ANM (SANM), incorporating nonlinear iterations and GPU acceleration. Additionally, further extensions could include a subchannel TH model that accounts for cross-flow, multiphase flow, and flow distribution at the core inlet.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Yong Cui: writing–original draft preparation, software, conceptualization, validation. Jing Shang: writing–review and editing, supervision. Longwei Mei: methodology, data curation, project administration. Jianfei Tong: validation, formal analysis. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the Young Potential Program of Shanghai Institute of Applied Physics, Chinese Academy of Sciences (Grant SINAP-YXJH-202204), National Natural Science Foundation of China (Grant 11805033), and State Key Laboratory of Nuclear Power Safety Monitoring Technology and Equipment (Grant K-A2019.418).

Acknowledgments

The first author would like to acknowledge Dr. Muhammad Imron from Abu Dhabi Polytechnic for his helpful remarks and suggestions.

Open Research

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Turinsky P. J. and Douglas B. K., Modeling and Simulation Challenges Pursued by the Consortium for Advanced Simulation of Light Water Reactors (CASL), Journal of Computational Physics. (2016) 313, 367–376.
10.1016/j.jcp.2016.02.043
CAS Google Scholar
2 He Y. N., Chen P., Wu Y. W., Su G. H., Tian W. X., and Qiu S. Z., Preliminary Evaluation of U₃Si₂-FeCrAl Fuel Performance in Light Water Reactors Through a Multi-Physics Coupled Way, Nuclear Engineering and Design. (2018) 328, 27–35.
10.1016/j.nucengdes.2017.12.019
CAS Web of Science® Google Scholar
3 Short M. P., Hussey D., Kendrick B. K., Besmann T. M., Stanek C. R., and Yip S., Multiphysics Modeling of Porous CRUD Deposits in Nuclear Reactors, Journal of Nuclear Materials. (2013) 443, no. 1–3, 579–587.
10.1016/j.jnucmat.2013.08.014
CAS Web of Science® Google Scholar
4 Gaston D., Newman C., Hansen G., and Damien L.-G., MOOSE: A Parallel Computational Framework for Coupled Systems of Nonlinear Equations, Nuclear Engineering and Design. (2009) 239, no. 10, 1768–1778.
10.1016/j.nucengdes.2009.05.021
CAS Web of Science® Google Scholar
5 Cammi A., Marcello V. D., Luzzi L., Memoli V., and Ricotti M. E., A Multi-Physics Modelling Approach to the Dynamics of Molten Salt Reactors, Annals of Nuclear Energy. (2011) 38, no. 6, 1356–1372.
10.1016/j.anucene.2011.01.037
CAS Web of Science® Google Scholar
6 Yang G., Jaradat M. K., Yang W. S., and Lee C., Development of Coupled PROTEUS-NODAL and SAM Code System for Multiphysics Analysis of Molten Salt Reactors, Annals of Nuclear Energy. (2022) 168, https://doi.org/10.1016/j.anucene.2021.108889, 108889.
10.1016/j.anucene.2021.108889
CAS Google Scholar
7 Cui Y., Chen J. G., and Wu J. H., et al.Development and Verification of a Three-Dimensional Spatial Dynamics Code for Molten Salt Reactors, Annals of Nuclear Energy. (2022) 171, https://doi.org/10.1016/j.anucene.2022.109040, 109040.
10.1016/j.anucene.2022.109040
CAS Google Scholar
8 Liu Z., Chen J., Cao L., Zhao C., He Q., and Wu H., Development and Verification of the High-Fidelity Neutronics and Thermal-Hydraulic Coupling Code System NECP-X/SUBSC, Progress in Nuclear Energy. (2018) 103, 114–125, https://doi.org/10.1016/j.pnucene.2017.11.010, 2-s2.0-85036457305.
10.1016/j.pnucene.2017.11.010
CAS Google Scholar
9 Jung Y. S., Shim C. B., Lim C. H., and Joo H. G., Practical Numerical Reactor Employing Direct Whole Core Neutron Transport and Subchannel Thermal/Hydraulic Solvers, Annals of Nuclear Energy. (2013) 62, 357–374, https://doi.org/10.1016/j.anucene.2013.06.031, 2-s2.0-84880869700.
10.1016/j.anucene.2013.06.031
CAS Google Scholar
10 Zhang L., Xie H., Mao W., and Ping J., Nuclear-Data Uncertainty Analysis for the Start-up Physics Test of CPR1000 Reactor, Annals of Nuclear Energy. (2021) 156, https://doi.org/10.1016/j.anucene.2021.108197, 108197.
10.1016/j.anucene.2021.108197
CAS Google Scholar
11 Jeon S., Hong H., Choi N., and Joo H. G., Methods and Performance of a GPU-Based Pinwise Two-Step Nodal Code VANGARD, Progress in Nuclear Energy. (2023) 156, https://doi.org/10.1016/j.pnucene.2022.104528, 104528.
10.1016/j.pnucene.2022.104528
CAS Google Scholar
12 Hegyi G., Maráczy C., and Temesvári E., Simulation of Xenon Transients in the VVER-1200 NPP Using the KARATE Code System, Annals of Nuclear Energy. (2022) 176, https://doi.org/10.1016/j.anucene.2022.109258, 109258.
10.1016/j.anucene.2022.109258
CAS Google Scholar
13 Marleau G., Hébert A., and Roy R., A User Guide for DRAGON Version, 5, Institut De Génie Nucléaire, Département de Génie Mécanique, École Polytechnique de Montréal, 2012.
Google Scholar
14 Cui Y., Chen J. G., Dai M., and Cai X. Z., Development of a Steady State Analysis Code for Molten Salt Reactor Based on Nodal Expansion Method, Annals of Nuclear Energy. (2021) 151, https://doi.org/10.1016/j.anucene.2020.107950, 107950.
10.1016/j.anucene.2020.107950
CAS Google Scholar
15 Ayachit U., The ParaView Guide, 2019, Kitware, Inc., New York.
Google Scholar
16 Pinem S., Sembiring T. M., and Liem P. H., NODAL3 Sensitivity Analysis for NEACRP 3D LWR Core Transient Benchmark (PWR), Science and Technology of Nuclear Installations. (2016) 2016, 11, https://doi.org/10.1155/2016/7538681, 2-s2.0-84979670918, 7538681.
10.1155/2016/7538681
Web of Science® Google Scholar
17 Biery M. and Avramova M., Investigations on Coupled Code PWR Simulations Using COBRA-TF With Soluble Boron Tracking Model, Progress in Nuclear Energy. (2014) 77, 72–83, https://doi.org/10.1016/j.pnucene.2014.06.005, 2-s2.0-84904005712.
10.1016/j.pnucene.2014.06.005
CAS Google Scholar
18 Lawrence R. D., Progress in Nodal Methods for the Solution of the Neutron Diffusion and Transport Equations, Progress in Nuclear Energy. (1986) 17, no. 3, 271–301, https://doi.org/10.1016/0149-1970(86)90034-X, 2-s2.0-0022902897.
10.1016/0149-1970(86)90034-X
CAS Web of Science® Google Scholar
19 Muhammad I., Development and Verification of Open Reactor Simulator ADPRES, Annals of Nuclear Energy. (2019) 133, 580–588, https://doi.org/10.1016/j.anucene.2019.06.049, 2-s2.0-85068542053.
10.1016/j.anucene.2019.06.049
Google Scholar
20 Hendricks J., Finite Difference Solution of the Time-Dependent Neutron Group Diffusion Equations, 1975, Massachusetts Institute of Technology.
10.2172/4140727
Google Scholar
21 Kim D. S. and Cho N. Z., Kinetics Calculation Under Space-Dependent Feedback in Analytic Function Expansion Nodal Method via Solution Decomposition and Galerkin Scheme, Nuclear Science and Engineering. (2002) 140, no. 3, 267–284, https://doi.org/10.13182/NSE02-A2260, 2-s2.0-0036496777.
10.13182/NSE02-A2260
CAS Google Scholar
22 Wagner W. and Kretzschmar H., International Steam Tables: Properties of Water and Steam Based on the Industrial Formulation IAPWSIF97, 2008, Springer-Verlag, Berlin Heidelberg.
10.1007/978-3-540-74234-0
Google Scholar
23 Liem P. H., Pinem S., Sembiring T. M., and Tran H. N., Status on Development and Verification of Reactivity Initiated Accident Analysis Code for PWR (NODAL3), Nuclear Science and Technology. (2016) 6, no. 1, 1–13, https://doi.org/10.53747/jnst.v6i1.139.
10.53747/jnst.v6i1.139
Google Scholar
24 Finnemann H. and Galati A., NEACRP 3-D LWR Core Transient Benchmark-Final Specifications (NEACRP-L-335), 1991, OECD Nuclear Energy Agency.
Google Scholar
25 Ban Y., Endo T., and Yamamoto A., A Unified Approach for Numerical Calculation of Space-Dependent Kinetic Equation, Journal of Nuclear Science and Technology. (2012) 49, no. 5, 496–515, https://doi.org/10.1080/00223131.2012.677126, 2-s2.0-84862840403.
10.1080/00223131.2012.677126
CAS Google Scholar
26 Institute of Nuclear and New Energy Technology, Verification Report of the TNGFM Code, 2009, Tsinghua University, Beijing.
Google Scholar
27 Kinght M. P. and Bryce P., Derivation of a Refined PANTHER Solution to the NEACRP PWR Rod-Ejection Transient, Proceedings of the Joint International Conference on Mathematical Method Applications, Saratoga Springs. (1997) 1, no. 302.
Google Scholar
28 Kozlowski T. and Downar T., PWR MOX/UO2 Core Transient Benchmark Final Report, 2007, Purdue University.
Google Scholar
29 Joo H. G., Cho J. Y., Kim Y., Zee S. Q., and Chang M. H., Dynamic Implementation of the Equivalence Theory in the Heterogeneous Whole Core Transport Calculation, Proceedings of the International Conference on Physics of Reactors (PHYSOR 2002), 2002, Seoul, Korea, American Nuclear Society.
Google Scholar
30 Downar T. J., Barber D. A., and Miller R. M., et al. PARCS: Purdue Advanced Reactor Core Simulator, Proceedings of the International Conference on Physics of Reactors (PHYSOR 2002), 2002, Seoul, Korea, American Nuclear Society.
Google Scholar
31 Luthfi W. and Pinem S., Calculation of 2-Dimensional PWR MOX/UO2 Core Benchmark OECD NEA, 6048 With SRAC Code, Jurnal Teknologi Reaktor Nuklir Tri Dasa Mega. (2020) 22, no. 3, 89–96, https://doi.org/10.17146/tdm.2020.22.3.5955.
10.17146/tdm.2020.22.3.5955
Google Scholar

All articles

Development and Verification of a Spatial Dynamics Code RESTA-3D for Light Water Reactors

Abstract

1. Introduction

2. Numerical Model and Solution Method