International Journal of Energy Research

Volume 2025, Issue 1 4099569

Research Article

Open Access

Load Frequency Control of Power Systems Integrated With Heterogeneous Controllable Loads: A Hybrid MPC Approach

Chongxin Huang,

Corresponding Author

Chongxin Huang

[email protected]

orcid.org/0000-0003-0498-8100

College of Automation , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Chen Jin,

Chen Jin

College of Automation , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Song Deng,

Song Deng

Institute of Advanced Technology , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Hui Ge,

Hui Ge

College of Automation , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Chongxin Huang,

Corresponding Author

Chongxin Huang

[email protected]

orcid.org/0000-0003-0498-8100

College of Automation , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Chen Jin,

Chen Jin

College of Automation , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Song Deng,

Song Deng

Institute of Advanced Technology , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

Hui Ge,

Hui Ge

College of Automation , Nanjing University of Posts and Telecommunications , Nanjing , Jiangsu , China , njupt.edu.cn

Search for more papers by this author

First published: 14 July 2025

https://doi.org/10.1155/er/4099569

Academic Editor: Próspero Acevedo-Peña

Share a link

Email
Wechat
Bluesky

Abstract

With the increasing participation of flexible loads in power grid regulation, the heterogeneity of flexible loads poses a critical challenge in load frequency control (LFC) of power systems. This paper proposes a novel hybrid model predictive control (HMPC)-based LFC strategy for power systems with heterogeneous controllable loads (HCLs), comprising continuous-type controllable loads (CCLs) and discrete-type controllable loads (DCLs). To the best of our knowledge, this is the first paper to introduce discrete-type controllable resources into the LFC framework and formulate a hybrid predictive model incorporating both continuous and discrete control inputs. Due to the hybrid predictive model involving both continuous and integer decision variables, we employ a mixed-integer linear quadratic programing (MILQP) algorithm to solve the problem and obtain the optimal LFC strategy. Simulation results on a three-area interconnected power system demonstrate that the proposed HMPC-based LFC achieves improved performance over traditional PI-based LFC in terms of overshoot (OS) reduction, oscillation damping, and regulation speed. The effectiveness of the proposed approach depends on the accuracy of the LFC model, which may present challenges in scenarios with significant system uncertainties. Nonetheless, this research contributes an innovative control paradigm for LFC design in power systems with heterogeneous regulation resources.

1. Introduction

1.1. Article Motivation

Frequency stability represents a balance between power supply and demand in an entire power grid, while load frequency control (LFC) is crucial for keeping this balance. Therefore, the LFC plays a key role in ensuring frequency stability and system security [1–3]. In recent decades, large-scale renewable energies have been developed and integrated into power grids to reduce greenhouse gas emissions [4, 5]. The low inertia, intermittency, and uncertainty of these renewable energies pose significant challenges on power system LFC. In addition, high-proportion renewable energy integration has led to a sharp decrease in the proportion of traditional energies. Thus, the capacity of conventional generators which can be used for LFC regulation has been compressed. Consequently, it is unable and uneconomical to rely solely on the traditional generation units for LFC regulation [6–8]. In this context, much attention has been turned to flexible controllable loads at the demand side since the controllable loads can participate in the LFC with the help of advanced information and communication technology and advanced measurement techniques [9, 10].

In a deregulated electricity market, flexibly controllable loads at the demand side are diverse and exhibit heterogeneous characteristics [7, 11]. Regarding the power output characteristics of controllable loads, some can be controlled continuously, while others can only be controlled discretely (e.g., switch-controlled loads). When these heterogeneous controllable loads (HCLs) participate in the LFC through the real-time electricity market, independent system operators (ISOs) have to redesign the corresponding LFC strategy. However, rare relevant research work has been conducted on this issue.

1.2. Literature Review and Research Gaps

1.2.1. LFC Approach Review

1.2.1.1. Improved PID Approaches

In order to improve the performance of traditional PID-based LFC strategy, researchers have proposed some advanced PID control strategies. To deal with the information staleness caused by communication time delay, an age-of-information-aware PI controller was used for LFC design in [12]. Similarly, to address the issue of communication time delay, a robust proportional integral derivative double derivative (PIDD2) controller was introduced for the interconnected power system LFC [13]. To endow the controller with a higher degree of parameter freedom, a new cascaded fractional-order PID (FOI-FOPIDD2) was adopted to design the LFC, where the controller gains were optimized by a squid game optimizer [14]. To support the system inertia against the attenuation caused by renewable energies, the authors in [15] provided a solution combining virtual inertia control with conventional LFC, and developed a fractional-order PID algorithm. In addition, a Kalman-filter PI-based control approach was proposed to formulate the LFC strategy for observing the unmeasurable system states and compensating the original PI controller [16]. Despite the widespread adoption of PID controllers in the industry due to the simplicity of concept and ease of implementation, they exhibit a large limitation when applied to the multi-input multi-output systems.

1.2.1.2. Robust Approaches

The uncertainties in system parameters, information communication, load disturbances, etc., may degrade the performance of the control system. Consequently, numerical studies have been conducted to enhance the robustness of LFC system. For instance, the authors in [17] utilized a feedforward control loop and an integral sliding mode control loop to suppress the disturbances as by loads and renewable energies. In light of the uncertainties of time-varying delay in communication channels, the authors in [18] presented a PI-type robust H-infinity LFC design method via the reciprocally convex inequality. Similarly, to address the issue of time delays, the authors in [19] designed an adaptive delay compensator to compensate the communication delay in the control loop. In response to the potential threat of cyberattacks on communication networks, the authors in [20] proposed a decentralized event-triggered mechanism-based algorithm for updating LFC scheme to fortify the robustness against the cyberattacks. However, since these methods primarily rely on conventional LFC models for controller design, their direct application to hybrid LFC controller design is challenging.

1.2.1.3. Data-Driven Approaches

The data-driven control methodology, which does not depend on accurate mathematical models, has undergone swift advancement in recent years, and its application in the power systems LFC has also begun to be investigated. For example, the authors in [8] proposed a data-driven LFC model via learning from the input–output trajectory instead of the accurate LFC model. For preventing the system frequency from running out of control due to sudden off-grid faults, the authors in [21] developed a fault-tolerant LFC scheme based on the deep meta-reinforcement learning algorithm for islanded microgrids. In addition, the deep reinforcement learning algorithm was also applied to the power system LFC against renewable energy uncertainties [22]. Unlike machine learning-based methods, a data-driven LFC scheme relying on the input and output data of the power system instead of the dynamic model of power systems was proposed in [23], where an event-triggered strategy was used to reduce the communication and computation burden. The authors in [24] introduced a model-free adaptive dynamic programing algorithm for the LFC design via utilizing measured data to learn the optimal gain without relying on model parameters. The aforementioned data-driven methods typically necessitate a considerable investment of time for model training, and the decision-making process of these models can be challenging to be interpreted, potentially leading to certain limitations in their practical application.

1.2.1.4. Model Predictive Control (MPC)-Based Approaches

The MPC approach has been effectively applied across various engineering fields, including process industries, power electronics, and energy systems. Recently, researchers have begun to study its application in the LFC of power systems. For instance, to enhance the disturbance rejection capability and improve the control performance of the LFC, the adaptive MPC approaches were employed to design the LFC controller for hybrid power systems integrated with multiple energies [25, 26]. To reduce the frequency regulation burden of conventional generators, various adjustable resources have been introduced into power systems. In [27], a diverse mix of energy storage was used for LFC performance enhancement, and a new MPC approach is proposed to design the load frequency controller of microgrids. In [28], battery energy storage systems were introduced to participate in the power system LFC, and a two-layer MPC algorithm was developed to generate the optimal control signals. Towards a multiarea power system with hybrid renewable generators and storage devices, the authors in [29] established the predictive model of the system, and utilized a transient search optimization algorithm to optimize the MPC-based LFC scheme. With the help of vehicle-to-grid technology, electric vehicles (EVs) supported by some advanced control technologies can provide auxiliary frequency regulation service [30]. For instance, an optimal MPC was applied for the LFC of the islanded power grid with EVs [31]. To track the LFC signal from an ISO, an MPC method was proposed to coordinate plug-in hybrid EVs, controllable loads, and cogeneration units [32]. To keep the SoC balance of hybrid energy storage systems and reduce the computational burden of controllers, a distributed MPC method was utilized to design the LFC strategy for multiarea power systems [33]. The above reported studies mainly focus on using the conventional MPC or the improved MPC to design the LFC for the power systems integrated renewable energies and energy storage units. However, the LFC predictive models established in the reported studies mathematically fall under the category of linear quadratic programing (LQP) models, as both the decision variables and state variables of these models are continuous. When hybrid HCLs participate in the LFC of power systems, the corresponding model decision variables may simultaneously include both continuous variables and discrete variables (such as binary variables, integer variables, etc.). At this point, there is still a lack of related research on how to design the LFC for power systems.

1.2.1.5. Improved PID+MPC Approaches

To address the adverse effects of fluctuations in renewable energy sources like PVs and wind power on frequency stability, a new class of LFC strategies have been developed in recent years. These strategies combined the enhanced PID algorithms with MPC techniques to design LFC controllers for complex power systems. The LFC controllers were implemented in two configurations: series-connected [34–37] and parallel-connected [38]. In the series-connected configuration, the MPC cascaded with enhanced PID (i.e., FOPID and PIDN) or the enhanced PID cascaded with MPC approaches were proposed to improve frequency regulation performance of multiarea power systems. Some intelligent optimization algorithms, such as the grasshopper optimization algorithm, sooty tern optimization algorithm, and salp swarm algorithm, were employed to determine the optimal parameters for the controllers. While in the parallel-connected configuration, the MPC in parallel with FOPID were used to design the LFC controller for multiarea interconnected power systems. Benchmark tests confirmed the superior frequency regulation capabilities of these methods over conventional PID and MPC algorithms in the LFC of complex power systems. However, the aforementioned research has exclusively considered continuously adjustable power sources for the power system LFC, while neglecting potential contributions from flexible loads (particularly switch-controlled adjustable loads) in frequency regulation.

1.2.2. Flexible Loads Participating in LFC

In recent years, flexible controllable loads have played an important role in the LFC, and related research has been carried out successively. The authors in [39] proposed a general framework for introducing demand response (DR) into the LFC model and analyze the impact of the DR communication delay on the LFC performances. Considering communication delay and sampling effect, the authors in [40] designed an optimal LFC scheme to regulate DR and generation units. Recently, much attention has been paid to the heterogeneous properties of flexible controllable loads. For instance, in [41], a two-level control framework was proposed to coordinate the energy consumption of heterogeneous loads. In [42], a distributed optimization framework was introduced to control large-scale heterogeneous loads. In [43–45] different control technologies were adopted to coordinate heterogeneous thermostatically-controlled loads (TCLs) at the aggregator’s level. While the aforementioned studies have extensively explored the involvement of heterogeneous loads in power system frequency regulation, the adopted load models are almost continuous in their mathematical formulation, failing to account for cases where the load models are discrete.

1.2.3. Hybrid Model Predictive Control (HMPC) Application

In recent decays, the HMPC theory has been developed to address the controller design for hybrid industrial systems, where control variables include discontinuous components, such as on/off switches, gears, speed selectors, etc. [46]. The application fields of HMPC cover control systems of behavioral medical devices [47], production inventory systems [48], HVAC systems [49], power electronic converters [50], and more, demonstrating exceptional control performances. The power system LFC with numerous HCLs also exhibits the aforementioned hybrid characteristics, and thus the HMPC theory can also provide a theoretical foundation for the corresponding LFC design. However, to the best of our knowledge, the existing research has hardly addressed how to utilize this theory for LFC design.

1.2.4. Current Research Gaps

Based on a comprehensive review of existing literature, the key differences between this study and existing typical work are highlighted in Table 1 and the main research gaps and motivations are identified as follows:

Table 1. Comparison between this study and previous typical work.

References	Research focus	Regulation resources	Constraints	Model type	Control methodology
[13]	Time delay	Conventional generators	Neglect	Continuous	Robust PIDD2
[16]	Model uncertainties	Conventional generators	Neglect	Continuous	KF-PI control
[19]	Time delay	Conventional generators, DRs	Neglect	Continuous	Robust control
[23]	Model uncertainties	Conventional generators, DGs	Neglect	Continuous	Data-driven approach
[24]	Model uncertainties	Conventional generators	Neglect	Continuous	Zero-sum game and ADP
[26]	Disturbance rejection	Conventional generators, DGs	Neglect	Continuous	Adaptive MPC
[28]	Model uncertainties	Conventional generators, ESs	Neglect	Continuous	Robust MPC
[29]	LFC parameter optimization	Conventional generators, ESs	Consider	Continuous	TSO-MPC
[34]	New-type LFC	Conventional generators, DGs	Neglect	Continuous	Cascaded MPC and FOPID
[35]	New-type LFC	Conventional generators, DGs	Neglect	Continuous	Cascaded MPC and FOPID
[37]	New-type LFC	Conventional generators, DGs	Neglect	Continuous	MPC- (1+PID)
This study	New LFC model and approach	Conventional generators, HCLs	Consider	Hybrid	Hybrid MPC

•
The existing studies on the power system LFC predominantly rely on continuous mathematical models of power system dynamics. However, when HCLs (e.g., thermostatically controlled loads and on/off loads) participate in the LFC, their discrete nature (binary/integer variables) introduces a new challenge for controller design. The current MPC-based LFC schemes fail to adequately address the co-optimization of continuous and discrete decision variables in LFC predictive models, limiting practical applicability.
•
Since existing LFC designs seldom consider control inputs with both continuous and discrete variables, this paper presents a novel method accounting for HCLs that comprise continuous-type controllable loads (CCLs) and discrete-type controllable loads (DCLs).

1.3. Article Contributions and Organization

From the literature review, it can be concluded that the existing research rarely considers the heterogeneous characteristics of loads, and there are few studies on the controller design for HCLs participating in power system LFC. This article presents a novel HMPC-based LFC design method for the power system integrated with HCLs. The main contributions are given as follows:

1.
The models of the HCLs are formulated in the power system LFC framework. The HCLs are categorized into CCLs and DCLs. The former are represented by first-order continuous dynamics, and the latter are expressed as integer variables.
2.
A novel hybrid predictive model is established for the LFC design of the power systems integrated with the HCLs. The heterogeneous characteristics of controllable loads, the system operation constraints, and the LFC objective are fully considered in this model.
3.
A rolling optimization algorithm is proposed to solve the hybrid predictive model of the LFC. Given that the hybrid predictive model is a typical mixed-integer LQP (MILQP) problem, a rolling interactive iterative solving process is provided for calculating the optimal LFC command based on the MILQP method.
4.
The proposed HMPC algorithm overcomes key limitations of conventional MPC-based LFC schemes in discrete control variable handling, while offering a unified approach for LFC systems with mixed continuous-discrete control inputs.

The rest of this article is organized as follows: Section 2 introduces the framework and model of HCLs participating in the LFC. Section 3 formulates the LFC model of the HCL-integrated power systems. Section 4 designs the LFC strategy based on the HMPC algorithm. Section 5 conducts the simulations. Finally, Section 6 draws a conclusion for this article.

2. Framework and Model of HCLs Participating in LFC

The diagram of HCLs participating in the LFC of a power system area is shown in Figure 1. As the figure shows, a power system area includes conventional generators, renewable energies, and controllable and uncontrollable loads, and it is connected to its neighboring areas through some tie lines. This article states that renewable energies and uncontrollable loads in the LFC framework are deemed as power disturbance sources. The control center assigns the LFC commands to the regulation resources (i.e., conventional generators and controllable loads) to keep the system frequency stable and maintain the tie-line power at its scheduled value.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Diagram of HCLs participating in LFC.

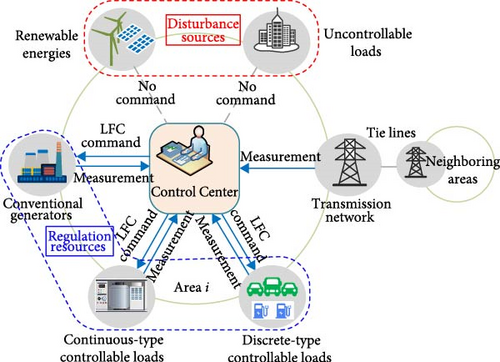
The controllable loads are the energy-intensive load aggregators under contract with the power system operator, and they can be categorized into CCLs and DCLs according to the power output characteristics. The power of CCLs can be adjusted continuously in a specific range. The TCLs (e.g., heaters, chillers, and central air conditioners) are typically CCLs. The DCLs include interruptible and laddered loads (e.g., none-V2G EVs), and their power response is significantly discontinuous and stepwise.

The model of the CCL is usually represented by a first-order inertial element as follows:

()

where ΔP_{CCL, c} is the power increment of the c^th CCL; T_{CCL, c} is the time constant of the c^th CCL;

(

denotes the set of real numbers) is the control input of the c^th CCL;

is the total power increment of CCLs; and n is the number of CCLs.

Assuming that a DCL has several control gears and each gear corresponds to the load power

, its power response model can be formulated as

()

where ΔP_{DCL, d} is the power increment of the d^th DCL;

is the total power increment of DCLs; m is the number of DCLs; and

(

denotes the set of integers) is the control input (or gear position) of the d^thDCL. The control input Δu_DCL,d is defined as:

()

where

, and

denote an integer set, a positive integer set, and a negative integer set, respectively.

3. Model of Power System Integrated With HCLs

3.1. LFC Model Structure

This paper presents the HMPC-based LFC framework of an HCL-integrated power system area shown in Figure 2. Under this framework, the control center of the i^th area measures the system frequency deviation and tie-line power deviation to calculate the area control error (ACE) first. Then, a PI regulator determines the area regulation requirement (ARR) based on the ACE. Subsequently, the ARR is distributed to the frequency regulation participants (e.g., the conventional generators and the controllable loads) according to the HMPC scheme. Finally, the participants respond to the frequency regulation command from the control center by adjusting their power output. The variables and parameters in Figure 2 are defined in the nomenclature part.

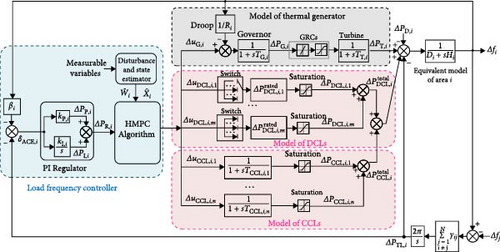
3.2. Hybrid State-Space Model

According to the LFC model illustrated in Figure 2, leaving aside the regulation limitations, we can deduce the corresponding dynamic equations of the ith area as follows [2, 23, 33]:

()

where Δf_i is the frequency deviation; ΔP_T,i is the power increment of the turbine; ΔP_G,i is the power increment of the governor; ΔP_TL,i is the tie-line power deviation; ΔP_I,i is the integral outputs of the PI regulator; ΔP_D,i is power disturbance of loads and renewable energies; Δu_G,i is the control input of the thermal generator; Δu_{CCL, i, c} is the control input of the c^th CCL; Δu_{CCL, i, d} is the control input of the d^th DCL; T_G,i is the time constant of the governor; T_T,i is the time constant of the turbine; R_i is the droop coefficient of the thermal generator; H_i is the inertia constant, D_i is the damping constant; β_i is the frequency bias coefficient; γ_ij is tie-line synchronizing coefficient between area i and j; k_I,i is the integral coefficients of the PI regulator; N is the number of the neighboring areas; n is the number of the CCLs; m is the number of the DCLs.

Since the control inputs in the model (4) include continuous and discrete variables, this model is a hybrid dynamic model. Utilizing X_i, U_C,i, U_D,i, Y_i, and W_i to denote the state vector, the continuous control input vector, the discrete control input vector, the output vector, and the disturbance variable, we can obtain a hybrid state-space model as follows:

()

where

, and

are given as

()

where A_i, B_C,i, B_D,i, F_i, C_i, and A_ij denote the state matrix, the continuous control input matrix, the discrete control input matrix, the disturbance input matrix, the system output matrix, and the interaction matrix between area i and j, respectively.

It should be noted that the power disturbances and partial states in the model (5) cannot be measured directly. Usually, the measurable variables include the frequency deviation Δf_i, the tie-line power deviation ΔP_TL,i, the power of CCLs ΔP_CCL,i,c, the ACE δ_ACE,i, and the ARR ΔP_R,i. Choosing

as the measured output vector, we can prove the following conditions.

1.
(A_i, (B_C,i B_D,i)) is controllable.
2.
(A_i, C_M,i) is observable.
3.
has full rank.

Since the above conditions (2) and 3) hold, we can easily estimate the states X_i and the disturbances W_i according to the method provided by James et al. [51]. Thus, this paper directly use X_i and W_i to replace their estimated values and for brevity.

4. LFC Strategy Design Based on HMPC

4.1. Hybrid Predictive Model

4.1.1. Discrete Hybrid State-Space Model

Given an appropriate sampling period T_s, we obtain the discrete hybrid state-space model of the system (5) as follows:

()

where

, and

4.1.2. LFC Objective Function

As far as a multiarea power system is concerned, the main objective of the LFC for each area is to make the frequency deviation Δf_i, the ACE δ_ACE,i, and the tie-line power ΔP_TL,i as small as possible after load disturbance occurs. It can be known from the Figure 2 that the ARR ΔP_R,i is the output of the PI controller based on the ACE δ_ACE,i = −(β_iΔf_i + ΔP_TL,i). If the objective of minimizing ΔP_R,i is achieved, then the LFC purposes for minimizing Δf_i, δ_ACE,i, and ΔP_TL,i will be attained. In addition, another goal of the LFC is to minimize energy consumption. Therefore, the quadratic objective function for the LFC is designed as

()

where Q_Y,i, R_C,i, R_D,i are positive-definite symmetric, and denote the weighting matrixes of the output, the continuous input, and the discrete input, respectively; N_Y and N_C (N_Y ≥ N_C) denote the prediction and control horizons, respectively.

4.1.3. Operational Limitations

The conventional thermal power generators must satisfy their ramp rate and upper–lower bound constraints (associated with the generation rate constraints (GRCs) block in Figure 2). Thus, the control commands to the thermal power generators should meet the following conditions:

()

where

and

denote the minimum and maximum ramp rates of the thermal generator, respectively;

and

denote the minimum and maximum adjustable power of the thermal generator, respectively.

The CCLs are constrained by their minimum and maximum regulation capacity (associated with the saturation block in Figure 2) when participating in the LFC. Thus, the control commands to the CCLs cannot exceed their capacity, i.e.,

()

where

and

denote the minimum and maximum regulation power of the cth CCL, respectively.

The control commands to the DCLs are integer variables and meet the following constraints (associated with the switch and saturation blocks in Figure 2):

()

where

and

denote the minimum and maximum values of Δu_{DCL, i, d}(k), respectively.

For the given prediction horizon N_P and control horizon N_C, by utilizing the variable definition in (5), we rewrite the constraints (9–11) in a compact form as follows:

()

At instant k, the optimal LFC problem for each power system area can be formulated to be a hybrid predictive model, that is,

()

The hybrid predictive model (13) is a typical MILQP problem since the objective function is quadratic, the constraints are linear, and the decision vector (control input vector) includes both continuous and integer variables.

Assuming that the optimal solution

of the optimal control problem (13) exists at time k, the control input at time k can be obtained by disregarding the optimal control inputs

, ⋯,

after time k, that is,

()

According to the receding horizon principle, by repeating the entire optimization procedure at time k + 1, the control law of the LFC model (7) will be updated based on the optimal predictive control law obtained from solving the hybrid predictive model (13).

Remark 1. The system stability can be analyzed using Lyapunov stability theory. Bemporad and Morari [46] proposed a theorem to ensure the stability of the HMPC-based closed-loop system, supported by rigorous theoretical proof. Since the stability proof is not the primary focus of this paper, it is omitted here. As noted in Subsection 3.2, the LFC model (7) is controllable and observable. According to the theorem proposed in [46], by appropriately selecting prediction N_Y and control horizon N_C as well as positive definite weighting matrices Q_Y,i, R_C,i, and R_D,i, the existence of a feasible solution for model (13) and the system stability can be well guaranteed.

4.2. LFC Strategy Based on MILQP Algorithm

To obtain the optimal LFC strategy for each power system area at instant k, it is necessary to solve the hybrid predictive model (13) based on the measured (or estimated) states and disturbances. The solution procedures are summarized below:

1.
Compute the discrete system matrixes , , , , , and according to the system parameters, and preset the weight matrixes Q_Y,i, R_C,i, and R_D,i, the predictive horizon N_Y, and the control horizon N_C.
2.
Estimate all the states X_i and disturbances W_i in area i, receive the frequency deviation Δf_j from the neighboring areas and transmit its own Δf_i to the neighboring areas.
3.
Solve the hybrid predictive model (13) by the MILQP algorithm to calculate the optimal continuous control command sequence and the optimal discrete control command sequence .
4.
Choose the first values in the above two sequences as the control commands if the hybrid predictive model (13) is feasible at instant k,that is, and . Otherwise, remain the control command at the previous instant, that is, U_C,i(k) = U_C,i(k − 1) and U_D,i(k) = U_D,i(k − 1).

Remark 2. The coupled component in the state-space equation is only related to the frequency deviation Δf_j, not all the states X_j. This can be seen from the LFC framework shown in Figure 2. Therefore, two adjacent areas only need to exchange the frequency deviation signal with each other. Since Δf_j is the first element of the vector X_j, we use to denote Δf_j for ease of description.

The solution process of the HMPC-based LFC strategy for each power system area is described in Algorithm 1.

Algorithm 1: HMPC algorithm for the ith area.

Input: Q_Y,i, R_C,i, R_D,i, N_Y,i, N_C,i, and system parameters in model (13);
Output:U_C,i(k) and U_D,i(k);
Formulate LFC problem as MILQP model (13); while time
k ≤ k_maxdo
Estimate X_i(k) and W_i(k), receive from neighboring areas, and transmit to neighboring areas;
Employ Gurobi optimizer to solve model (13);
if model (13) is feasible then
;
;
else
U_C,i(k) = U_C,i(k − 1);
U_D,i(k) = U_D,i(k − 1);
end
k ← k + 1;
end

5. Case Studies

5.1. Parameters of Test System

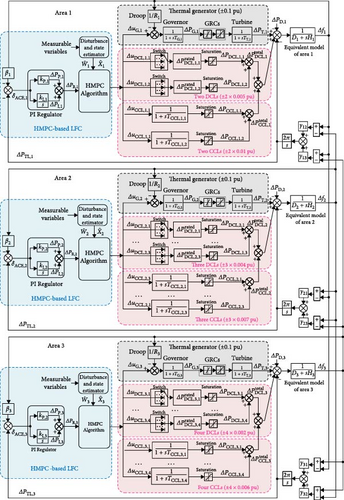
Based on a three-area power system benchmark [25], we develop a simulation model (as Figure 3 shown) to validate the proposed HMPC-based LFC strategy. Each power system area in this model incorporates both CCLs and DCLs. The system parameters are provided in Table 2, while the HCL parameters are detailed in Table 3.

Table 2. Parameters of three-area power system.

Area	D_i (pu/Hz)	H_i (s)	R_i (Hz/pu)	T_G,i (s)	T_T,i (s)	β_i (pu/Hz)	γ_ij (pu/Hz)	(pu)	(pu/s)
1	0.015	0.1667	3.00	0.08	0.40	0.3483	γ₁₂ = 0.20 γ₁₃ = 0.25	(−0.1, 0.1)	(−0.001, 0.001)

2	0.016	0.2017	2.73	0.06	0.43	0.3827	γ₂₁ = 0.20 γ₂₃ = 0.12	(−0.1, 0.1)	(−0.001, 0.001)

3	0.015	0.1247	2.82	0.07	0.30	0.3692	γ₃₁ = 0.25 γ₃₂ = 0.12	(−0.1, 0.1)	(−0.001, 0.001)

Table 3. Parameters of HCLs in case studies.

Area	n	T_CCL,i (s)	(pu)	m	(pu)
1	2	0.5	(−0.010, 0.010)	2	0.001	(−5, −4, −3, −2, −1, 0, 1, 2, 2, 3, 4, 5)
2	3	0.35	(−0.007, 0.007)	3	0.001	(−4, −3, −2, −1, 0, 1, 2, 2, 3, 4)
3	4	0.2	(−0.006, 0.006)	4	0.001	(−2, −1, 0, 1, 2)

In our test system, we define the power rating of conventional generators and CCLs by their operational limits (minimum and maximum active power output in per-unit (pu) values, 1 pu = 1 GW). For DCLs, the power rating corresponds to their available operating gears. The specific limits for each frequency regulation resource are enumerated in Tables 2 and 3.

In the case studies, the parameters of the proposed HMPC-based load frequency controller are empirically tuned through extensive simulation studies to achieve satisfactory performance under various operating conditions(Table 4 for detailed values). Although this experimental approach produces practically viable results, we recognize that systematic parameter optimization (e.g., the optimization-based methods proposed in [14, 29]) could potentially improve control performance. Nevertheless, since controller parameter optimization falls beyond the scope of this study, we defer this investigation to future work.

Table 4. Parameters of the proposed controllers in case studies.

Area	PI parameters		HMPC parameters
Area	k_P,i	k_I,i	N_Y	N_C	Q_Y,i	R_C,i	R_D,i
1	0	0.3	5	2	1.65	diag{0.2, 0.8, 0.8}	diag{2, 6} × 10⁻⁶
2	0	0.2	5	2	2.8	diag{0.15, 0.85, 0.85}	diag{2, 4, 8} × 10⁻⁶
3	0	0.4	5	2	0.45	diag{0.18, 0.8, 0.8, 0.8, 0.8, 0.8}	diag{3, 5, 6, 6} × 10⁻⁶

5.2. Simulation and Analysis

The simulation tests are carried out on a PC with an 8-core Intel i7-6700K CPU (4.0 GHz) and 16 GB RAM, using MATLAB/Simulink. The MILQP model was solved with Gurobi optimization software. The average computation time per control decision ranges from 0.03 to 0.06 s, which is well within the 0.1 second sampling period, ensuring real-time feasibility.

5.2.1. Simulation Results Under Step Load Disturbance

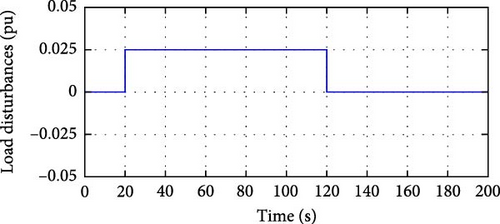
For simplicity, we assume that the same step load disturbance occurs in the three areas. The step load disturbance is set as: in the initial period, the load disturbance ΔP_D = 0; at 20 s, ΔP_D = 0.0025 pu; at 120 s, ΔP_D = 0. The step load disturbance in three areas is given by Figure 4, and the system responses to the disturbance are show in Figures 5–7.

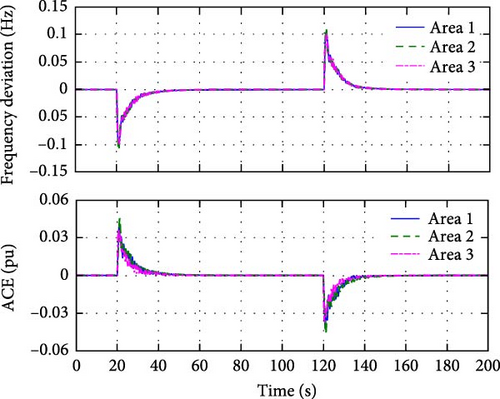
From the frequency deviation and ACE curves in Figure 5 we can see that the frequency deviation and ACE in the three regions are quickly restored to zero. The maximum frequency deviation and the maximum ACE are 0.115 Hz and 0.045 pu, respectively, and the adjustment time is about 20 s.

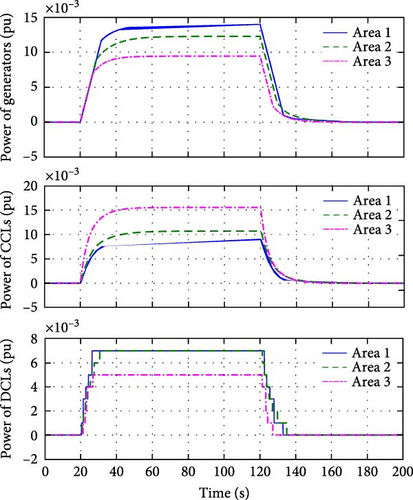
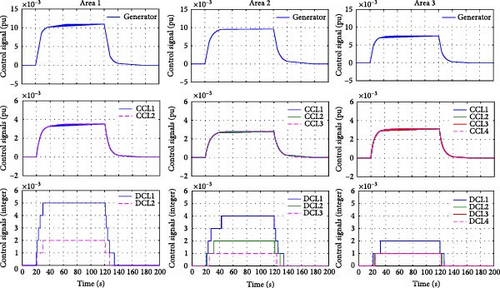
Figures 6 and 7 illustrate the power outputs and the control signals of the generators, the CCLs, and the DCLs, respectively. We can see that after the step load disturbances occur, the generators, the CCLs, and the DCLs quickly adjust their power in response to the LFC commands of each area, while satisfying their output constraints. The results also show that the power output curves of the generators and the CCLs are continuous, while those of DCLs are discrete. It should be noted that the power output level and adjustment time are determined by the HMPC algorithm based on the corresponding hybrid predictive model, and the main reason for the slightly longer adjustment time given by the HMPC algorithm is to minimize the overshoots (OSs) of the frequency and ACE.

5.2.2. Simulation Results Under Ramp Load Disturbance

In this case, we test the performances of the proposed LFC strategy under ramp load disturbances. The profiles of the ramp load disturbances are shown in Figure 8. The results under ramp load disturbances are shown in Figures 9–11.

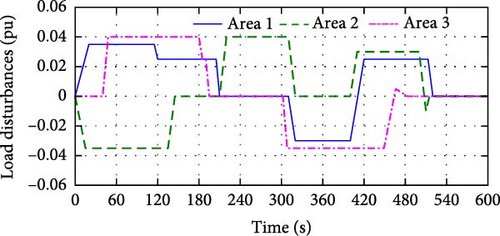
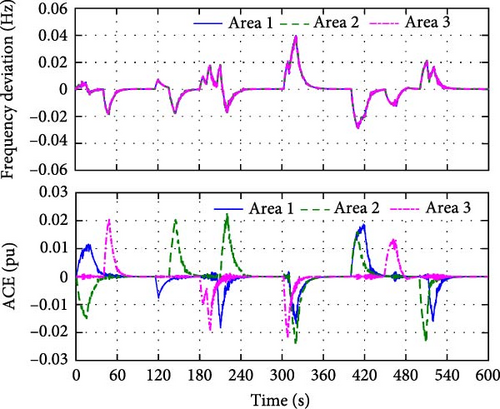
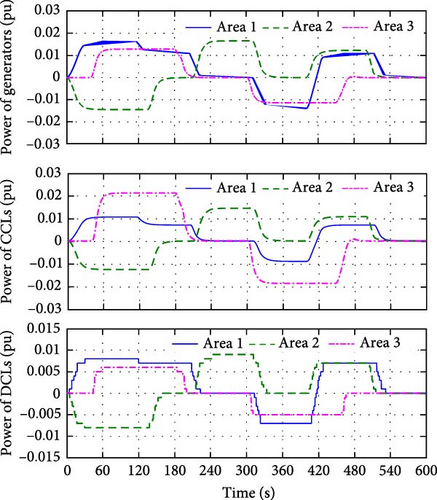
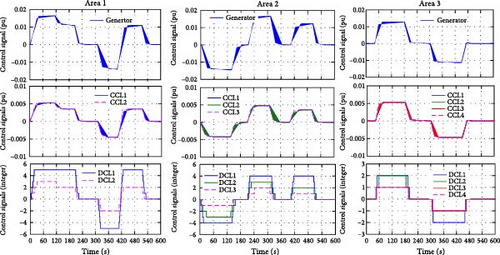
Figure 9 illustrates that the proposed LFC strategy can drive the system frequency deviation and the ACE convergence to zero under the frequent load fluctuations. Under the given load disturbances, the maximum frequency deviation and the maximum ACE are only 0.04 Hz and 0.025 pu, respectively. Furthermore, there is no overshoot (OS) in both frequency deviation and ACE response curves.

The power outputs and the control signals of the generators, the CCLs, and DCLs are shown in Figures 10 and 11. It can be seen that the generators, the CCLs, and the DCLs quickly adjust their power to respond to the LFC demand under their physical constraints. The load disturbance curves in Figure 8, the power output curves in Figure 10 and the control signals curves in Figure 11 illustrate that the total power increment matches the load deviation in each area. This indicates that under normal load disturbance conditions, each area is responsible for its power balance to reduce the cross-regional power support, which can help to alleviate the tie-line power fluctuations.

5.2.3. Performance Comparison Analysis

Since existing MPC-based LFC strategies in [26, 28, 34–37] primarily address controller design for power systems with continuous control variables, they cannot be directly applied to the hybrid power system with mix continuous-discrete control variables considered in this study. For comparison purposes, we adapt the conventional PI-based LFC approach. The PI parameters remain identical to those listed in Table 4, and the modified power allocation algorithm is presented below:

()

where round (⋅) denotes the rounding function.

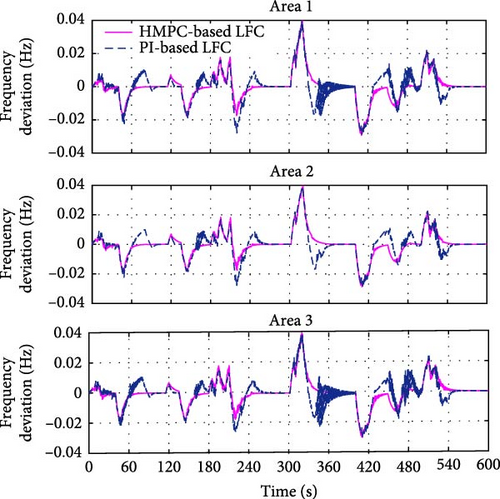
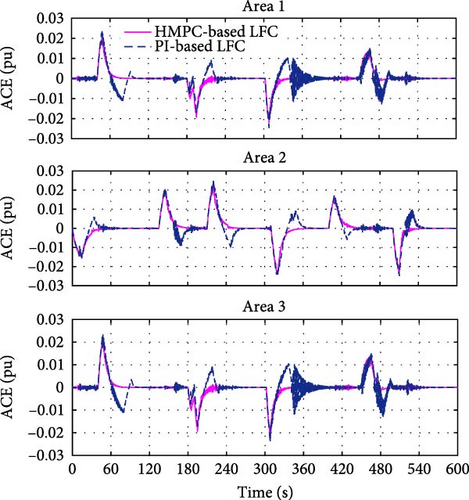
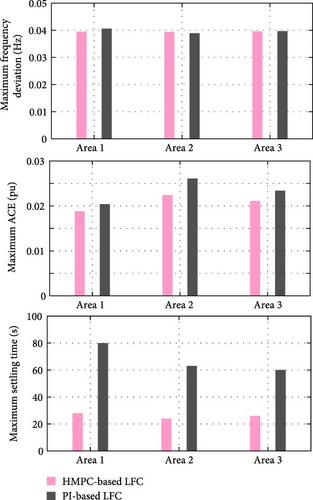
A comparative analysis of the proposed HMPC and conventional PI-based LFC schemes under identical ramp disturbances (as Figure 8 shown) is presented in Figures 12 and 13, and the corresponding quantitative performance metrics of the two schemes are summarized in Figure 14. The comparative results in Figure 14 demonstrate that under identical load disturbances, the HMPC-based LFC and the PI-based LFC yield comparable magnitudes of maximum frequency deviation and ACE. However, the HMPC-based LFC achieves 2.5 times faster settling time (ST), the oscillation-free monotonic convergence without OS, and the superior convergence stability compared to the PI-based LFC.

5.2.4. Parameter Sensitivity Analysis

Considering that the LFC controller design is usually based on a simplified equivalent model of the power system, this study selects two key parameters (the system inertia constant [H_i] and the damping constant [D_i]) for sensitivity analysis to evaluate the impact of model parameter uncertainties on control performances. In the tests, these two parameters are varied by gradients of ±10%, ±20%, and ±30%, and a step load disturbance (0.05 pu) is applied. We observe the system frequency response and focus on three dynamic performance indicators: OS, undershoot (US), and ST. The parameter sensitivity test results shown in Table 5, where the bolded row represents the case with normal system parameters. The results indicate that: (1) the proposed controller can maintain system stability within ±30% parameter variation range, but the ST tends to increase as parameters deviate from their nominal values; (2) the OS is unaffected by the changes in H_i and D_i; and (3) the US shows a negative correlation with system parameters, decreasing as H_i and D_i increase.

Table 5. Impact of parameter changes on control performances.

System parameters (H_i and D_i)	Area 1			Area 2			Area 3
System parameters (H_i and D_i)	OS (Hz)	US (Hz)	ST (s)	OS (Hz)	US (Hz)	ST (s)	OS (Hz)	US (Hz)	ST (s)
↑+30%	0	−0.141	16.5 ↑	0	−0.160	16.9 ↑	0	−0.149	16.7 ↑
↑+20%	0	−0.145	16.6 ↑	0	−0.166	16.5 ↑	0	−0.154	16.8 ↑
↑+10%	0	−0.150	16.6 ↑	0	−0.171	16.9 ↑	0	−0.156	16.6 ↑
Normal values	0	−0.165	15.4	0	−0.184	14.6	0	−0.166	15.3
↓−10%	0	−0.165	16.1 ↑	0	−0.189	16.6 ↑	0	−0.167	16.3 ↑
↓−20%	0	−0.179	16.2 ↑	0	−0.199	16.9 ↑	0	−0.175	16.5 ↑
↓−30%	0	−0.190	18.3 ↑	0	−0.213	16.8 ↑	0	−0.186	17.0 ↑

6. Conclusion

For the problem of both CCLs and DCLs participating in the LFC, this article provides an HMPC algorithm to design the LFC strategy of power systems. The CCLs and the DCLs are modeled with first-order continuous dynamics and integer variables. The hybrid predictive model used for the LFC design is formulated to be an MILQP model. The real-time LFC strategy is obtained by solving the MILQP model in a rolling fashion. Simulation results illustrate that the proposed HMPC-based LFC can optimally coordinate the CCLs, the DCLs, and the conventional generators to satisfy the frequency regulation demands, and both the frequency deviation and the ACE can be restored to zero with small OSs after load disturbances occur. In addition, the proposed HMPC-based LFC performs better in overshoot, regulation speed, and oscillation suppression than the PI-based LFC.

Future research should focus on optimizing controller parameters using advanced optimization algorithms and enhancing the robustness of the proposed HMPC-based LFC system against parameter uncertainties via disturbance rejection design. In addition, since the solution time for the MILQP problem grows exponentially with the system size, how to reduce the model solution time to meet the real-time requirements of the LFC in large-scale power systems remains a challenge. Scaling down model size through model reduction techniques, enhancing solution efficiency via advanced heuristic algorithms (e.g., genetic algorithms, simulated annealing algorithms, and other AI-driven algorithms), and alleviating computational load with distributed algorithmic architectures (e.g., distributed HMPC) are all potential solutions.

Nomenclature

ACE:: Area control error
ARR:: Area regulation requirement
CCL:: Continuous-type controllable load
DCL:: Discrete-type controllable load
DR:: Demand response
GRC:: Generation rate constraint
EV:: Electric vehicle
HCL:: Heterogeneous controllable load
MPC:: Model predictive control
HMPC:: Hybrid MPC
LFC:: Load frequency control
MILQP:: Mixed-integer linear quadratic programing
PID:: Proportional integral derivative
TCL:: Thermostatically-controlled load
pu:: Per unit
s.t:: subject to

Indices and Sets

i:: Index of power system area
N:: Number of neighboring areas
c:: Index of CCL
n:: Number of CCLs
d:: Index of DCL
m:: Number of DCLs
:: Real number set
:: Integer set
k:: Index of time step
Superscript ^min:: Minimum value of corresponding variable
Superscript ^max:: maximum value of corresponding variable

Variables

Δf_i:: Frequency deviation (Hz)
ΔP_T,i:: Power increment of the turbine (pu)
ΔP_G,i:: Power increment of the governor (pu)
ΔP_TL,i:: Tie-line power deviation (pu)
δ_ACE,i:: Area control error (pu)
ΔP_P,i:: Proportional output of the PI regulator (pu)
ΔP_I,i:: Integral output of the PI regulator (pu)
ΔP_R,i:: Area regulation requirement (pu)
Δu_G,i:: Control input of the thermal generator (pu)
ΔP_D,i:: Power disturbance of loads and renewable energies (pu)
ΔP_{CCL, c}:: Power increment of the cth CCL (pu)
:: Total power increment of CCLs (pu)
ΔP_{DCL, d}:: Power increment of the dth DCL (pu)
:: Total power increment of DCLs (pu)
Δu_{CCL, c}:: Control input of the cth CCL (pu)
Δu_{DCL, d}:: Control input of the dth DCL
X_i:: State vector
W_i:: Variable
U_C,i:: Continuous control input vector
:: Optimal value of U_C,i
U_D,i:: Continuous control input vector
:: Optimal value of U_D,i
Y_i:: Output vector
:: The estimated state vector
:: The estimated disturbance variable

Parameters and Matrixes

T_G,i:: Time constant of the governor (s)
T_T,i:: Time constant of the turbine (s)
T_CCL,i:: Time constant of the CCL (s)
R_i:: Droop coefficient of the thermal generator (Hz/pu)
H_i:: Inertia constant (s)
D_i:: Damping constant (pu/Hz)
β_i:: Frequency bias coefficient (pu/Hz)
γ_ij:: Tie-line synchronizing coefficient between area i and j (pu/Hz)
k_P,i:: Proportional coefficients of the PI regulator
k_I,i:: Integral coefficients of the PI regulator
N_Y:: Prediction horizon
N_C:: Control horizon
A_i:: State matrix
A_ij:: Interaction matrix between area i and j
B_C,i:: Continuous control input matrix
B_D,i:: Discrete control input matrix
F_i:: Disturbance input matrix
C_i:: Output matrix
Q_Y,i:: Weighting matrix of output vector
R_C,i:: Weighting matrix of continuous input vector
R_D,i:: Weighting matrix of discrete input vector.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

There are no research data available to be shared.

References

1 Bevrani H., Robust Power System Frequency Control, 2014, Springer, New York.
10.1007/978-3-319-07278-4
Google Scholar
2 Liao K. and Xu Y., A Robust Load Frequency Control Scheme for Power Systems Based on Second-Order Sliding Mode and Extended Disturbance Observer, IEEE Transactions on Industrial Informatics. (2018) 14, no. 7, 3076–3086, https://doi.org/10.1109/TII.2017.2771487, 2-s2.0-85033725474.
10.1109/TII.2017.2771487
Web of Science® Google Scholar
3 Gulzar M. M., Sibtain D., Alqahtani M., Alismail F., and Khalid M., Load Frequency Control Progress: A Comprehensive Review on Recent Development and Challenges of Modern Power Systems, Energy Strategy Reviews. (2025) 57, https://doi.org/10.1016/j.esr.2024.101604, 101604.
10.1016/j.esr.2024.101604
Web of Science® Google Scholar
4 Li X., Wang W., and Ye L., et al.Improving Frequency Regulation Ability for a Wind-Thermal Power System by Multi-Objective Optimized Sliding Mode Control Design, Energy. (2024) 300, https://doi.org/10.1016/j.energy.2024.131535, 131535.
10.1016/j.energy.2024.131535
Web of Science® Google Scholar
5 El-Ela A. A. A., El-Sehiemy R. A., Shaheen A. M., and Diab A. E.-G., Design of Cascaded Controller Based on Coyote Optimizer for Load Frequency Control in Multi-Area Power Systems With Renewable Sources, Control Engineering Practice. (2022) 121, 105–058.
Google Scholar
6 Mohandes B., Moursi M. S. E., Hatziargyriou N., and Khatib S. E., A Review of Power System Flexibility With High Penetration of Renewables, IEEE Transactions on Power Systems. (2019) 34, no. 4, 3140–3155, https://doi.org/10.1109/TPWRS.2019.2897727, 2-s2.0-85067786829.
10.1109/TPWRS.2019.2897727
Web of Science® Google Scholar
7 Wu X., Yao L., Yu Y., Jiang X., Wu R., and Gong G., Heterogeneous Aggregation and Control Modeling for Electric Vehicles With Random Charging Behaviors, IEEE Transactions on Sustainable Energy. (2023) 14, no. 1, 525–536, https://doi.org/10.1109/TSTE.2022.3219343.
10.1109/TSTE.2022.3219343
Web of Science® Google Scholar
8 Cai G., Jiang C., and Yang D., et al.Data-Driven Predictive Based Load Frequency Robust Control of Power System With Renewables, International Journal of Electrical Power & Energy Systems. (2023) 154, https://doi.org/10.1016/j.ijepes.2023.109429, 109429.
10.1016/j.ijepes.2023.109429
Web of Science® Google Scholar
9 Lund P. D., Lindgren J., Mikkola J., and Salpakari J., Review of Energy System Flexibility Measures to Enable High Levels of Variable Renewable Electricity, Renewable and Sustainable Energy Reviews. (2015) 45, 785–807, https://doi.org/10.1016/j.rser.2015.01.057, 2-s2.0-84923800917.
10.1016/j.rser.2015.01.057
Web of Science® Google Scholar
10 Villar J., Bessa R., and Matos M., Flexibility Products and Markets: Literature Review, Electric Power Systems Research. (2018) 154, 329–340, https://doi.org/10.1016/j.epsr.2017.09.005, 2-s2.0-85029391307.
10.1016/j.epsr.2017.09.005
Web of Science® Google Scholar
11 Liu M., Shi Y., and Liu X., Distributed MPC of Aggregated Heterogeneous Thermostatically Controlled Loads in Smart Grid, IEEE Transactions on Industrial Electronics. (2016) 63, no. 2, 1120–1129, https://doi.org/10.1109/TIE.2015.2492946, 2-s2.0-84962423497.
10.1109/TIE.2015.2492946
Web of Science® Google Scholar
12 Jiao D., Shao C., Hu B., Xie K., Lin C., and Ju Z., Age-of-Information-Aware PI Controller for Load Frequency Control, Protection and Control of Modern Power Systems. (2023) 8, no. 1, 1–15, https://doi.org/10.1186/s41601-023-00311-z.
10.1186/s41601-023-00311-z
Web of Science® Google Scholar
13 Kumar M. and Hote Y. V., Robust PIDD2 Controller Design for Perturbed Load Frequency Control of an Interconnected Time-Delayed Power Systems, IEEE Transactions on Control Systems Technology. (2021) 29, no. 6, 2662–2669, https://doi.org/10.1109/TCST.2020.3043447.
10.1109/TCST.2020.3043447
Web of Science® Google Scholar
14 Ye Y., Daraz A., Basit A., Khan I. A., and AlQahtani S. A., Cascaded Fractional-Order Controller-Based Load Frequency Regulation for Diverse Multigeneration Sources Incorporated With Nuclear Power Plant, International Journal of Energy Research. (2024) 2024, no. 1, https://doi.org/10.1155/2024/7939416, 7939416.
10.1155/2024/7939416
Web of Science® Google Scholar
15 Ragab A., Allam D., and Attia H. A., Supporting Load Frequency Control Process by Using Adaptive Model Reference Virtual Inertia Controller When Connecting Renewable Energy Plants, Computers and Electrical Engineering. (2024) 117, https://doi.org/10.1016/j.compeleceng.2024.109295, 109295.
10.1016/j.compeleceng.2024.109295
Web of Science® Google Scholar
16 Shangguan X.-C., Wei C.-G., Zhang C.-K., He Y., and Jiang L., Performance Enhancing Control of Frequency for Future Power Systems With Strong Uncertainties, IEEE Transactions on Industrial Informatics. (2024) 20, no. 10, 12439–12449, https://doi.org/10.1109/TII.2024.3424288.
10.1109/TII.2024.3424288
Web of Science® Google Scholar
17 Mi Y., Ma Y., and He X., et al.Robust Load Frequency Control for Isolated Microgrids Based on Double-Loop Compensation, CSEE Journal of Power and Energy Systems. (2021) 9, no. 4, 1359–1369.
Google Scholar
18 Guo W., Liu F., Zou R., and Liu K., H∞ Load Frequency Control of Power Systems With Multiple Time-Varying Delays via Improved Reciprocally Convex Inequality, Journal of the Franklin Institute. (2023) 360, no. 12, 7933–7957.
10.1016/j.jfranklin.2023.06.017
Web of Science® Google Scholar
19 Hosseini S. A., Toulabi M., Dobakhshari A. S., Ashouri-Zadeh A., and Ranjbar A. M., Delay Compensation of Demand Response and Adaptive Disturbance Rejection Applied to Power System Frequency Control, IEEE Transactions on Power Systems. (2020) 35, no. 3, 2037–2046, https://doi.org/10.1109/TPWRS.2019.2957125.
10.1109/TPWRS.2019.2957125
Web of Science® Google Scholar
20 Zhang Z., Chen H., Liu B., Zhang H., and Zhong S., An Effective Updating Scheme Based DETM Robust LFC Under Non-Ideal Communication Network, Automatica. (2024) 167, https://doi.org/10.1016/j.automatica.2024.111786, 111786.
10.1016/j.automatica.2024.111786
Web of Science® Google Scholar
21 Li J. and Cheng Y., Deep Meta-Reinforcement Learning-Based Data-Driven Active Fault Tolerance Load Frequency Control for Islanded Microgrids Considering Internet of Things, IEEE Internet of Things Journal. (2024) 11, no. 6, 10295–10303, https://doi.org/10.1109/JIOT.2023.3325482.
10.1109/JIOT.2023.3325482
Web of Science® Google Scholar
22 Yan Z. and Xu Y., Data-Driven Load Frequency Control for Stochastic Power Systems: A Deep Reinforcement Learning Method With Continuous Action Search, IEEE Transactions on Power Systems. (2019) 34, no. 2, 1653–1656, https://doi.org/10.1109/TPWRS.2018.2881359, 2-s2.0-85056584019.
10.1109/TPWRS.2018.2881359
Web of Science® Google Scholar
23 Bu X., Yu W., Cui L., Hou Z., and Chen Z., Event-Triggered Data-Driven Load Frequency Control for Multiarea Power Systems, IEEE Transactions on Industrial Informatics. (2022) 18, no. 9, 5982–5991, https://doi.org/10.1109/TII.2021.3130415.
10.1109/TII.2021.3130415
Web of Science® Google Scholar
24 Hu S., Luo Y., Xie X., and Zhang H., H ∞ Optimal Load Frequency Control of Power System: A Novel Model-Free Approach, IEEE Transactions on Circuits and Systems II: Express Briefs. (2024) 72, no. 1, 228–232.
Google Scholar
25 Wang W., Yorino N., Sasaki Y., Zoka Y., Bedawy A., and Kawauchi S., A Novel Adaptive Model Predictive Frequency Control Using Unscented Kalman Filter, Electric Power Systems Research. (2022) 213, https://doi.org/10.1016/j.epsr.2022.108721, 108721.
10.1016/j.epsr.2022.108721
Web of Science® Google Scholar
26 Gulzar M. M., Sibtain D., and Ahmad A., et al.An Efficient Design of Adaptive Model Predictive Controller for Load Frequency Control in Hybrid Power System, International Transactions on Electrical Energy Systems. (2022) 2022, 7894264.
10.1155/2022/7894264
Web of Science® Google Scholar
27 Khokhar B. and Parmar K. P. S., Utilizing Diverse Mix of Energy Storage for LFC Performance Enhancement of a Microgrid: A Novel MPC Approach, Applied Energy. (2023) 333, https://doi.org/10.1016/j.apenergy.2023.120639, 120639.
10.1016/j.apenergy.2023.120639
Web of Science® Google Scholar
28 Oshnoei A., Kheradmandi M., and Muyeen S. M., Robust Control Scheme for Distributed Battery Energy Storage Systems in Load Frequency Control, IEEE Transactions on Power Systems. (2020) 35, no. 6, 4781–4791, https://doi.org/10.1109/TPWRS.2020.2997950.
10.1109/TPWRS.2020.2997950
Web of Science® Google Scholar
29 Taher A. M., Hasanien H. M., and Aleem S. H. A., et al.Optimal Model Predictive Control of Energy Storage Devices for Frequency Stability of Modern Power Systems, Journal of Energy Storage. (2023) 57, https://doi.org/10.1016/j.est.2022.106310, 106310.
10.1016/j.est.2022.106310
Web of Science® Google Scholar
30 Nguyen H. N. T., Zhang C., and Zhang J., Dynamic Demand Control of Electric Vehicles to Support Power Grid With High Penetration Level of Renewable Energy, IEEE Transactions on Transportation Electrification. (2016) 2, no. 1, 66–75, https://doi.org/10.1109/TTE.2016.2519821, 2-s2.0-85029907567.
10.1109/TTE.2016.2519821
Web of Science® Google Scholar
31 Khooban M. H., An Optimal Non-Integer Model Predictive Virtual Inertia Control in Inverter-Based Modern AC Power Grids-Based V2G Technology, IEEE Transactions on Energy Conversion. (2021) 36, no. 2, 1336–1346, https://doi.org/10.1109/TEC.2020.3030655.
10.1109/TEC.2020.3030655
Web of Science® Google Scholar
32 Galus M. D., Koch S., and Andersson G., Provision of Load Frequency Control by PHEVs, Controllable Loads, and a Cogeneration Unit, IEEE Transactions on Industrial Electronics. (2011) 58, no. 10, 4568–4582, https://doi.org/10.1109/TIE.2011.2107715, 2-s2.0-80052363501.
10.1109/TIE.2011.2107715
Web of Science® Google Scholar
33 Huang C., Yang M., Ge H., Deng S., and Chen C., DMPC-Based Load Frequency Control of Multi-Area Power Systems With Heterogeneous Energy Storage System considering SoC Consensus, Electric Power Systems Research. (2024) 228, https://doi.org/10.1016/j.epsr.2023.110064, 110064.
10.1016/j.epsr.2023.110064
Web of Science® Google Scholar
34 Sibtain D., Rafiq T., Bhatti M. H., Shahzad S., and Kilic H., Frequency Stabilization for Interconnected Renewable Based Power System Using Cascaded Model Predictive Controller With Fractional Order PID Controller, IET Renewable Power Generation. (2023) 17, no. 16, 3836–3855, https://doi.org/10.1049/rpg2.12885.
10.1049/rpg2.12885
Web of Science® Google Scholar
35 Gulzar M. M., Sibtain D., and Khalid M., Cascaded Fractional Model Predictive Controller for Load Frequency Control in Multiarea Hybrid Renewable Energy System With Uncertainties, International Journal of Energy Research. (2023) 2023, 5999997.
10.1155/2023/5999997
Web of Science® Google Scholar
36 Iqbal M. and Gulzar M. M., Master-Slave Design for Frequency Regulation in Hybrid Power System Under Complex Environment, IET Renewable Power Generation. (2022) 16, no. 14, 3041–3057, https://doi.org/10.1049/rpg2.12553.
10.1049/rpg2.12553
Web of Science® Google Scholar
37 Gulzar M. M., Designing of Robust Frequency Stabilization Using Optimized MPC-(1 + PID) Controller for High Order Interconnected Renewable Energy Based Power Systems, Protection and Control of Modern Power Systems. (2023) 8, no. 1, 1–14.
10.1186/s41601-023-00286-x
Google Scholar
38 Gulzar M. M., Umar M. M., and Al-Dhaifallah M. M., Robust Load Frequency Control of Hybrid Power System, 2023 International Conference on Control, Automation and Diagnosis (ICCAD), 2023, IEEE, 1–8.
Google Scholar
39 Pourmousavi S. A. and Nehrir M. H., Introducing Dynamic Demand Response in the LFC Model, IEEE Transactions on Power Systems. (2014) 29, no. 4, 1562–1572, https://doi.org/10.1109/TPWRS.2013.2296696, 2-s2.0-84903266390.
10.1109/TPWRS.2013.2296696
Web of Science® Google Scholar
40 Lin C., Hu B., Shao C., Li W., Li C., and Xie K., Delay-Dependent Optimal Load Frequency Control for Sampling Systems With Demand Response, IEEE Transactions on Power Systems. (2022) 37, no. 6, 4310–4324, https://doi.org/10.1109/TPWRS.2022.3154429.
10.1109/TPWRS.2022.3154429
Web of Science® Google Scholar
41 Xu Z., Callaway D. S., Hu Z., and Song Y., Hierarchical Coordination of Heterogeneous Flexible Loads, IEEE Transactions on Power Systems. (2016) 31, no. 6, 4206–4216, https://doi.org/10.1109/TPWRS.2016.2516992, 2-s2.0-84961327128.
10.1109/TPWRS.2016.2516992
Web of Science® Google Scholar
42 Ghaemi R., Abbaszadeh M., and Bonanni P. G., Optimal Flexibility Control of Large-Scale Distributed Heterogeneous Loads in the Power Grid, IEEE Transactions on Control of Network Systems. (2019) 6, no. 3, 1256–1268, https://doi.org/10.1109/TCNS.2019.2933945, 2-s2.0-85070668889.
10.1109/TCNS.2019.2933945
Web of Science® Google Scholar
43 Zheng J., Laparra G., Zhu G., and Li M., Aggregate Power Control of Heterogeneous TCL Populations Governed by Fokker–Planck Equations, IEEE Transactions on Control Systems Technology. (2020) 28, no. 5, 1915–1927, https://doi.org/10.1109/TCST.2020.2968873.
10.1109/TCST.2020.2968873
Web of Science® Google Scholar
44 Hu J., Cao J., and Chen M. Z., et al.Load Following of Multiple Heterogeneous TCL Aggregators by Centralized Control, IEEE Transactions on Power Systems. (2017) 32, no. 4, 3157–3167, https://doi.org/10.1109/TPWRS.2016.2626315, 2-s2.0-85021296208.
10.1109/TPWRS.2016.2626315
Web of Science® Google Scholar
45 Yao Y. and Zhang P., Unified Control Strategy of Heterogeneous Thermostatically Controlled Loads With Market-Based Mechanism, Journal of Modern Power Systems and Clean Energy. (2020) 8, no. 6, 1231–1239, https://doi.org/10.35833/MPCE.2018.000828.
10.35833/MPCE.2018.000828
Web of Science® Google Scholar
46 Bemporad A. and Morari M., Control of Systems Integrating Logic, Dynamics, and Constraints, Automatica. (1999) 35, no. 3, 407–427, https://doi.org/10.1016/S0005-1098(98)00178-2, 2-s2.0-0033097938.
10.1016/S0005-1098(98)00178-2
Web of Science® Google Scholar
47 El Mistiri M., Khan O., Martin C. A., Hekler E., and Rivera D. E., Data-Driven Mobile Health: System Identification and Hybrid Model Predictive Control to Deliver Personalized Physical Activity Interventions, IEEE Open Journal of Control Systems. (2025) 4, 83–102, https://doi.org/10.1109/OJCSYS.2025.3538263.
10.1109/OJCSYS.2025.3538263
PubMed Web of Science® Google Scholar
48 Nandola N. N. and Rivera D. E., An Improved Formulation of Hybrid Model Predictive Control With Application to Production-Inventory Systems, IEEE Transactions on Control Systems Technology. (2013) 21, no. 1, 121–135, https://doi.org/10.1109/TCST.2011.2177525, 2-s2.0-84871741531.
10.1109/TCST.2011.2177525
Web of Science® Google Scholar
49 Jeong C., Brastein O. M., Skeie N.-O., and Sharma R., Hybrid Model Predictive Control Scheme for Controlling Temperature in Building Under Uncertainties, IEEE Access. (2023) 11, 116820–116832, https://doi.org/10.1109/ACCESS.2023.3324691.
10.1109/ACCESS.2023.3324691
Web of Science® Google Scholar
50 Karami Z., Shafiee Q., Sahoo S., Yaribeygi M., Bevrani H., and Dragicevic T., Hybrid Model Predictive Control of DC–DC Boost Converters With Constant Power Load, IEEE Transactions on Energy Conversion. (2021) 36, no. 2, 1347–1356, https://doi.org/10.1109/TEC.2020.3047754.
10.1109/TEC.2020.3047754
Web of Science® Google Scholar
51 James B. R., David Q. M., and Moritz M. D., Model Predictive Control: Theory, Computation, and Design, 2017, Nob Hill Publishing, Albuquerque.
Google Scholar

All articles

Load Frequency Control of Power Systems Integrated With Heterogeneous Controllable Loads: A Hybrid MPC Approach

Abstract

1. Introduction

1.1. Article Motivation

1.2. Literature Review and Research Gaps

1.2.1. LFC Approach Review

1.2.1.1. Improved PID Approaches

1.2.1.2. Robust Approaches

1.2.1.3. Data-Driven Approaches

1.2.1.4. Model Predictive Control (MPC)-Based Approaches

1.2.1.5. Improved PID+MPC Approaches

1.2.2. Flexible Loads Participating in LFC

1.2.3. Hybrid Model Predictive Control (HMPC) Application

1.2.4. Current Research Gaps

1.3. Article Contributions and Organization

2. Framework and Model of HCLs Participating in LFC

3. Model of Power System Integrated With HCLs

3.1. LFC Model Structure

3.2. Hybrid State-Space Model

4. LFC Strategy Design Based on HMPC

4.1. Hybrid Predictive Model

4.1.1. Discrete Hybrid State-Space Model

4.1.2. LFC Objective Function

4.1.3. Operational Limitations

4.2. LFC Strategy Based on MILQP Algorithm

5. Case Studies

5.1. Parameters of Test System

5.2. Simulation and Analysis

5.2.1. Simulation Results Under Step Load Disturbance

5.2.2. Simulation Results Under Ramp Load Disturbance

5.2.3. Performance Comparison Analysis

5.2.4. Parameter Sensitivity Analysis

6. Conclusion

Nomenclature

Nomenclature

Indices and Sets

Variables

Parameters and Matrixes

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information