This paper addresses the distributed filter design issue of nonlinear systems in sensor networks. Furthermore, by considering the synthesized filter gain fluctuations, the nonfragile design scheme is developed to improve the implementation robustness and applicableness. Since the nonlinear system model is more practical and general to describe the real-world dynamical systems, the nonlinear objective system measured by a sensor network grouped by sensor nodes is investigated. Moreover, in order to solve this theoretical filtering problem, the control theory and system theory are applied with control model transformation. More precisely, all the filters are supposed to be designed with the measurement of each sensor in the sensor network. Firstly, the distributed filtering problem is converted to the stability of filtering error system. Then, sufficient convex optimization conditions are accordingly established to ensure the desired H_∞ disturbance attenuation level with the desired guaranteed cost performance. Then, distributed filter gains can be derived by means of convex optimization method. Finally, the illustrative simulation of a nonlinear system with four sensor nodes is given to demonstrate the usefulness and correctness of our filter design.

1. Introduction

The last decades have witnessed a rapid development of sensor technologies, where numerous theoretical researches and practical applications can be found in industrial processes, medical services, engineering electronics, and other information collection scenarios [1–5]. In particular, increasing attentions have been paid to the sensor networks, which means that a large number of sensor nodes are grouped and the data fusion is achieved by network communication. Since a single sensor commonly has limited communication capability and constrained computational ability, significant advances can be obtained by sensor networks, such as high efficiency, high robustness, and high reliability [6–9]. However, as a fundamental topic of sensor measurement, the filtering problem is more complicated for the sensor networks due to the multiple sensors and intergraded data communications. Furthermore, as certain centralized signal processing over large sensor networks is impractical or very expensive, it is reasonable and effective to develop distributed framework and algorithms by each sensor node. Under this context, each sensor node can perform local information processing and information exchanges collectively [10–12].

For the distributed filtering problem of sensor networks, the consensus-based methods have been proved to be useful in many circumstances. As a result, some remarkable results and well-known approaches can be found in the literature [13–16]. Meanwhile, it should be noticed that the filter gain fluctuations should not be neglected, which may lead to undesirable filtering performance or even filtering failures. Moreover, there always exist parameter uncertainties and environment interruptions in practical filter implementation. In order to deal with practical applications of filters, the nonfragile filtering strategy should be designed accordingly [17–19]. In fact, the nonfragile control issues have been extensively studied for control systems and many effective methods are reported with controller or estimator gain fluctuations. However, it is worth mentioning that the distributed filtering analysis and synthesis are more challenging with nonfragile designs. On the other hand, by taking into account the practical cost of sensors networks, the guaranteed cost performance should be addressed, where an upper bound of the prescribed performance should be satisfied and minimized during the distributed filtering [20–22]. Unfortunately, until now, the distributed nonfragile guaranteed cost filtering problems of nonlinear systems via sensor networks have not been fully studied under the H_∞ framework and remain opening areas, which motives us for this research.

In our work, the distributed filtering issue of sensor networks is discussed for a sort of nonlinear systems with external disturbances. Compared with most existing results, the main contributions can be listed as the following aspects. (1) Firstly, the distributed nonfragile filter design problem is investigated in the presence of the practical gain fluctuations, and a unified framework for sensor networks is proposed to estimate the true states. With this strategy, the distributed filters are more applicable for practical sensor network implementations. (2) Secondly, the quadratic guaranteed cost performance is introduced on the basis of sensor networks, where sampled data are utilized by the sensors. (3) Thirdly, the computational distributed filter design method is established based on the linear matrix inequality convex optimization, such that the desired filter gains can be designed with feasible solutions effectively.

The remainder parts of our work are presented as follows. In Section 2, the distributed filter model is formulated based on sensor networks and the model transformation with essential preliminaries is presented later. In Section 3, sufficient conditions are derived by filter error model and distributed filter gains are designed accordingly. In Section 4, our proposed filtering approach is applied to simulation for efficiency demonstration. In Section 5, the paper is concluded with some further remarks.

1.1. Notations

ℝⁿ denotes n dimensional Euclidean space. ℝ^m×n represents the set of m × n real matrices. A matrix M > 0 means that M is positive definite. ⊗ stands for the Kronecker product. ^∗ denotes the ellipsis terms in symmetry matrices.

2. Preliminaries and Problem Formulation

Consider the following class of nonlinear system with external disturbance:

()

where x(t) ∈ ℝⁿ denotes the system state, w(t) ∈ ℝⁿ represents the external disturbance, f(x(t)) is a Lipschitz nonlinear function satisfying ‖f(α(t)) − f(β(t))‖ ≤ κ‖α(t) − β(t)‖, κ > 0, ∀α(t), β(t) ∈ ℝⁿ, z(t) ∈ ℝ^l stands for the system output measurement to be estimated. All A, B, and L denote the constant system matrix of the nonlinear dynamical system, respectively.

Remark 1. The nonlinear system models have been widely utilized to model the practical dynamical systems. In this paper, the Lipschitz nonlinear function is adopted to describe the nonlinear dynamics, which would lead to more challenging issues for control system analysis and synthesis

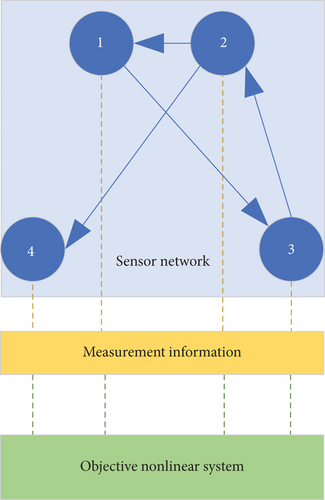
In order to enhance the filter design for output estimation, a sensor network consisting of N sensor nodes is constructed under distributed communication network. Under this framework, the network topology of this sensor network is described by a directed graph , , with and being the sets of nodes and edges, and is the weighted adjacency matrix and presents the local neighbors of sensor i. More precisely, assume that a_ij > 0 when sensor i receives information from sensor j with a_ii = 1, and a_ij = 0 when there is no communication between sensor i and sensor j [23]. Without loss of generality, all the sensors in the sensor network share a unified sampling sequel with time-varying sampling period defined by t_k+1 − t_k = h(t) > 0, k = 0, 1, 2, ⋯. In addition, it is assumed that , where is a known constant.

Consequently, the sampled-data measurement for sensor i can be represented as follows [24]:

()

where y_i(t) denotes the ith sensor measurement output and C_i and D_i denote the constant system matrix, respectively.

Consequently, on the basis of above sensor network, the distributed filters in sensor network can be designed as follows:

()

where

denotes the estimation of x(t) based on sensor i and K_ij represents the distributed filter gain to be determined. Furthermore, certain filter gain fluctuation ΔK_ij is taken into account for more practical implementations, which satisfies that ΔK_ij = M_ijΩ(t)N with Ω^T(t)Ω(t) ≤ I, M_ij and N being known constant matrices. Then, the distributed filter model is modified by

()

Based on the above model, we can define the following distributed filter errors:

()

As a result, the dynamics of distributed filter errors can be deduced as follows:

()

which can be further reformulated in the form of Kronecker product by

()

with

Eventually, we can formulate the following augmented filtering dynamical system:

()

where

and

Then, the following definition can be presented for the distributed filters, such that the augmented filtering dynamical system can effectively achieve desired H_∞ disturbance attenuation performance with desired guaranteed cost.

Definition 1 (see [25], [26].)The H_∞ disturbance attenuation performance is defined by

and the cost performance is described by

Then, the H_∞ performance with desired guaranteed cost is said to be satisfied for the augmented filtering system under zero initial conditions, if there exist parameters γ > 0 and for all nonzero w(t), such that it holds that J_∞ < 0 and

Remark 2. Compared with common H_∞ performance, the guaranteed cost H_∞ performance for filtering problems is more general, where the prescribed cost can be ensured while dealing with the disturbance affections. On the other hand, some practical applications focus more on the optimal control performance, such that it is necessary to design the optimal guaranteed cost control strategies. When the guaranteed cost performance is introduced into the distributed filter design procedure, it means that an upper bound on the closed-loop value of quadratic cost function can be established.

To this end, the purpose of this paper is to design desired distributed filter gains to achieve the above guaranteed cost H_∞ performance in sensor network [27, 28]. Before proceeding further, some important lemmas are introduced for deriving the main results.

Lemma 1 (see [29].)For matrices M₁, M₂, and M₃, where and , then it holds that if and only if

Lemma 2 (see [30].)For matrix M^T = M, and F₁ and F₂ being real matrices of appropriate dimensions with O(t) satisfying O^T(t)O(t) ≤ I, it holds that , if and only if there exists a scalar ε > 0 such that , or equivalently

3. Distributed Filter Gain Design

In this section, we will derive sufficient convex optimization conditions to design the distributed filter gains with detailed proofs.

Theorem 1. With parameter , the augmented filtering error system can achieve guaranteed cost H_∞ performance with distributed filter gains K_ij, i, j = 1, 2, ⋯N, if there exist matrices ℙ > 0, ℚ > 0, and ℝ > 0, such that the following convex optimization condition Θ < 0 can hold, where

Furthermore, the cost performance J_c can be guaranteed by

Proof 1. By applying the virtual delay method, one can obtain that

()

where

Choose the following Lyapunov–Krasovskii function for augmented filtering system (9)

()

where

Then, it can be derived along with evolution of V(t) by

From the plant model nonlinear function, it yields that

where

Subsequently, it can be derived that

where

Furthermore, it holds that

Considering the external disturbances, one has that

where

Therefore, it follows by Schur complement lemma that when Θ < 0 holds, then . Furthermore, under zero initial conditions and for all nonzero w(t), it can be verified that

which means that J_∞ < 0 can be ensured accordingly.

Meanwhile, one can derive that when w(t) = 0, one has that

such that by integrating both sides of the above inequality from 0 to ∞, it follows that

In the end, from Definition 1, one can verify that the guaranteed cost and H_∞ performance can be achieved, which completes the proof.

Remark 3. The novel sufficient convex optimization is utilized in this paper based on the linear matrix inequality method, which has been widely used for control system analysis and synthesis. The feasible solutions of the convex optimization conditions can be easily solved by Matlab or other mathematical software [31].

By the above established theorem, the following theorem is presented for solving the optimized filter gains.

Theorem 2. With parameter , the augmented filtering error system can achieve guaranteed cost H_∞ performance, if there exist matrices with , , , and , such that the following convex optimization condition Ψ < 0 can hold, where

With above feasible solutions, the desired distributed filter gains K_ij, i, j = 1, 2, ⋯N, can be calculated as follows:

and the distributed filter gains K_ij in sensor network are obtained by matrix

Furthermore, the cost performance J_c can be guaranteed by

Proof 2. Let and one has where

Then, by employing Lemma 2 to the above condition, the rest of the proof can be easily completed by matrix manipulation.

Remark 4. In this work, the time-varying sampling period is considered, which is more general for practical sensor network implementation. Furthermore, the maximum value of can also be optimized by solving the above convex conditions as

Remark 5. The established results are in the form of strict linear matrix inequality convex optimization. It should be pointed out that as the number of sensor nodes in the sensor network increases, the number of matrix variables of linear matrix inequality would increase accordingly. This implies that there is a computational complex tradeoff between the sensor nodes and the feasible filter design solutions.

4. Illustrative Example

In this section, we will perform an illustrative example to show the effectiveness of our distributed filter design.

Consider the nonlinear dynamical system as (1), whose system parameters are assumed to be

In order to obtain the true state of nonlinear system, a sensor network consisting of four sensors is constructed, where Nodes 1, 2, 3, and 4 are grouped as a sensor network with information communications. In this sensor network, each sensor node can measure the objective nonlinear system state with measurement output and the corresponding network topology is depicted in Figure 1 and the time-varying sampling period is assumed to be h = 0.2 s and h = 0.15 s [32, 33].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Illustration of sensor network topology for nonlinear system.

In addition, the sensor system parameters are supposed to be

By considering the possible filter gain fluctuations, it is assumed that

Furthermore, the H_∞ performance index γ is set by 2. Based on the above simulation parameters, the desired distributed filter gains K_ij can be acquired by solving the convex optimization condition in Theorem 2 as follows:

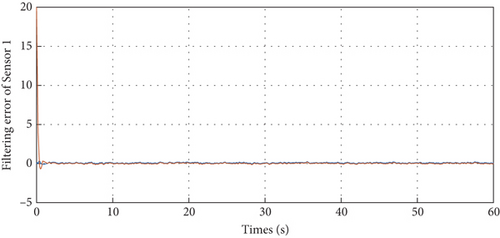
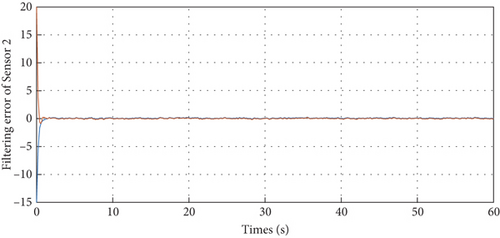
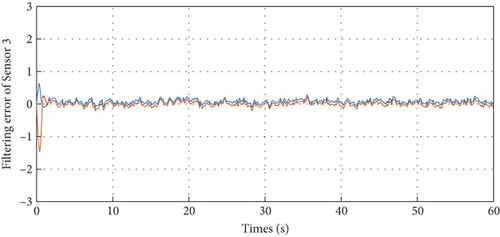
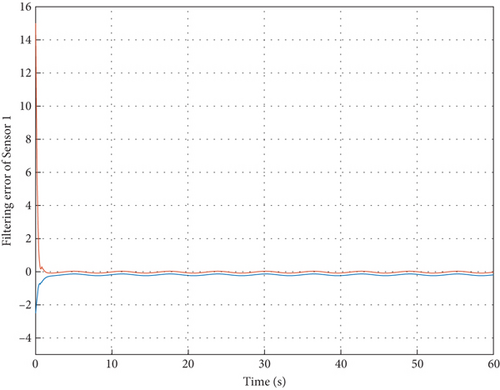
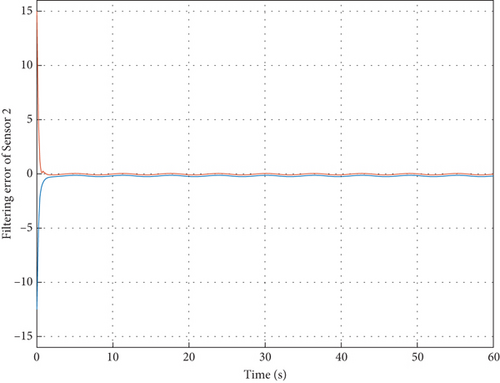
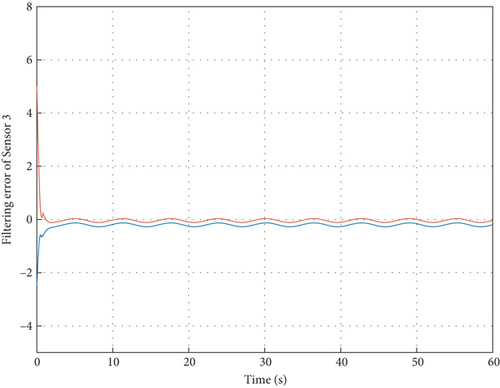
With the above parameters, the external disturbance w(t) is assumed to be a band-limited white noise with power 0.01; the corresponding filtering error dynamics in the sensor network are depicted in Figures 2, 3, 4, and 5, such that the designed filters can well obtain the true states despite external disturbances. These simulation results can support our theoretical findings.

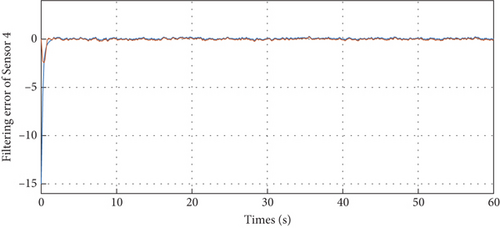
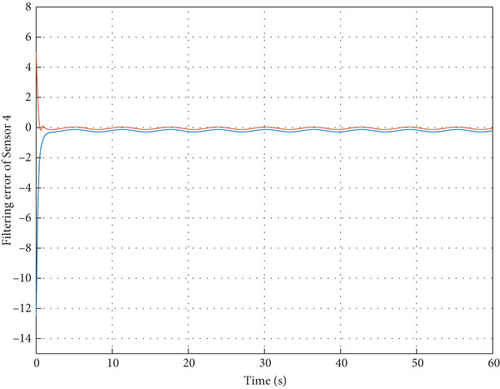
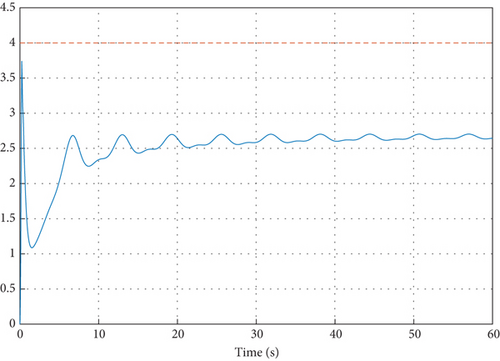
In addition, when the external disturbance is assumed to be w(t) = 0.2sin(t), the filtering error dynamics in the sensor network are shown in Figures 6, 7, 8, and 9, from which one can see the filters can also well obtain the true states despite external disturbances. Furthermore, according to the linear matrix inequality convex optimization, the maximum value of can also be optimized as 0.57 s and the cost performance can be calculated by Theorem 2 as 1221. Meanwhile, it is noted from Figure 10 that under zero initial condition, the ratio to , which means that H_∞ disturbance attenuation level is less than the prescribed value and the H_∞ performance can be then satisfied. These simulation results can well demonstrate the filtering performance as expected.

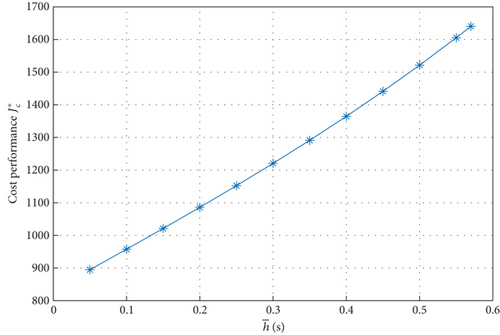
Moreover, Figure 11 depicts the relation between the chosen value of and the cost performance . As a result, it can be found that choosing bigger value of would lead to higher cost performance, which implies that the sampling period of sensor network should be chosen properly.

5. Conclusions

The guaranteed cost H_∞ distributed filtering problem for nonlinear system has been studied based on sensor network in our paper. In particular, we have considered the possible distributed filter gain fluctuations to improve the robustness of filter design. Based on the formulated augmented filtering system, sufficient conditions have been established by using the Lyapunov–Krasovskii method to ensure the guaranteed cost H_∞ performance. Furthermore, the distributed filter gains have been calculated by solving the convex optimization problem. In the end, an illustrative example has been given for validating the correctness of our established design results. In the future, one interesting topic toward current researches would be the fault detection filter design issues, which is also important for sensor networks.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the National Natural Science Foundation of China under Grant 52174352.

Acknowledgments

The authors are grateful to the editor and reviewers for their valuable suggestions which improved this article.

Open Research

Data Availability Statement

All data supporting the findings of this study are available within the article.

References

1 Xu N., A survey on sensor networks, IEEE Communications Magazine. (2002) 40, no. 8, 102–114, https://doi.org/10.1109/MCOM.2002.1024422, 2-s2.0-0036688074.
10.1109/MCOM.2002.1024422
Web of Science® Google Scholar
2 Yick J., Mukherjee B., and Ghosal D., Wireless sensor network survey, Computer Networks. (2008) 52, no. 12, 2292–2330, https://doi.org/10.1016/j.comnet.2008.04.002, 2-s2.0-46449122114.
10.1016/j.comnet.2008.04.002
Web of Science® Google Scholar
3 Li J. and Gao H., Survey on sensor network research, Journal of Computer Research and Development. (2008) 45, no. 1.
Google Scholar
4 Patel H., Rajput D. S., Reddy G. T., Iwendi C., Bashir A. K., and Jo O., A review on classification of imbalanced data for wireless sensor networks, International Journal of Distributed Sensor Networks. (2020) 16, no. 4, 155014772091640, https://doi.org/10.1177/1550147720916404.
10.1177/1550147720916404
Web of Science® Google Scholar
5 Lilhore U. K., Khalaf O. I., Simaiya S., Romero T., Andrés C., Abdulsahib G. M., and Kumar D., A depth-controlled and energy-efficient routing protocol for underwater wireless sensor networks, International Journal of Distributed Sensor Networks. (2022) 18, no. 9, 155013292211171, https://doi.org/10.1177/15501329221117118.
10.1177/15501329221117118
Web of Science® Google Scholar
6 Wang Y.-A., Shen B., Zou L., and Han Q.-L., A survey on recent advances in distributed filtering over sensor networks subject to communication constraints, International Journal of Network Dynamics and Intelligence. (2023) 2, no. 2, 100007–100007, https://doi.org/10.53941/ijndi0201007.
10.53941/ijndi0201007
Google Scholar
7 Rullán-Lara J.-L., Salazar S., and Lozano R., Real-time localization of an uav using Kalman filter and a wireless sensor network, Journal of Intelligent & Robotic Systems. (2012) 65, no. 1-4, 283–293, https://doi.org/10.1007/s10846-011-9599-8, 2-s2.0-84855442850.
10.1007/s10846-011-9599-8
Google Scholar
8 He S., Shin H.-S., Xu S., and Tsourdos A., Distributed estimation over a low-cost sensor network: a review of state-of-the-art, Information Fusion. (2020) 54, 21–43, https://doi.org/10.1016/j.inffus.2019.06.026.
10.1016/j.inffus.2019.06.026
Web of Science® Google Scholar
9 Felemban E., Shaikh F. K., Qureshi U. M., Sheikh A. A., and Qaisar S. B., Underwater sensor network applications: a comprehensive survey, International Journal of Distributed Sensor Networks. (2015) 11, no. 11, 896832, https://doi.org/10.1155/2015/896832, 2-s2.0-84947444382.
10.1155/2015/896832
Web of Science® Google Scholar
10 Liang Y., Dong X., Han L., Li Q., and Ren Z., Globally optimal distributed time-varying weight information filter of mobile sensor network, Journal of the Franklin Institute. (2020) 357, no. 11, 7308–7326, https://doi.org/10.1016/j.jfranklin.2020.04.030.
10.1016/j.jfranklin.2020.04.030
Google Scholar
11 He X., Xue W., and Fang H., Consistent distributed state estimation with global observability over sensor network, Automatica. (2018) 92, 162–172, https://doi.org/10.1016/j.automatica.2018.03.029, 2-s2.0-85044465437.
10.1016/j.automatica.2018.03.029
Web of Science® Google Scholar
12 Li C., Dong H., Li J., and Wang F., Distributed Kalman filtering for sensor network with balanced topology, Systems & Control Letters. (2019) 131, article 104500, https://doi.org/10.1016/j.sysconle.2019.104500, 2-s2.0-85073707000.
10.1016/j.sysconle.2019.104500
Google Scholar
13 Yu W., Chen G., Wang Z., and Yang W., Distributed consensus filtering in sensor networks, IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics). (2009) 39, no. 6, 1568–1577, https://doi.org/10.1109/TSMCB.2009.2021254, 2-s2.0-70349618998, 19447730.
10.1109/TSMCB.2009.2021254
PubMed Web of Science® Google Scholar
14 Zhu S., Chen C., Li W., Yang B., and Guan X., Distributed optimal consensus filter for target tracking in heterogeneous sensor networks, IEEE Transactions on Cybernetics. (2013) 43, no. 6, 1963–1976, https://doi.org/10.1109/TSMCB.2012.2236647, 2-s2.0-84890072663, 23757586.
10.1109/TSMCB.2012.2236647
PubMed Web of Science® Google Scholar
15 Battistelli G., Chisci L., Mugnai G., Farina A., and Graziano A., Consensus-based linear and nonlinear filtering, IEEE Transactions on Automatic Control. (2015) 60, no. 5, 1410–1415, https://doi.org/10.1109/TAC.2014.2357135, 2-s2.0-84928502344.
10.1109/TAC.2014.2357135
Web of Science® Google Scholar
16 Li W. and Jia Y., Distributed consensus filtering for discrete-time nonlinear systems with non-Gaussian noise, Signal Processing. (2012) 92, no. 10, 2464–2470, https://doi.org/10.1016/j.sigpro.2012.03.009, 2-s2.0-84860749272.
10.1016/j.sigpro.2012.03.009
Web of Science® Google Scholar
17 He S. and Xu H., Non-fragile finite-time filter design for time-delayed Markovian jumping systems via t–s fuzzy model approach, Nonlinear Dynamics. (2015) 80, no. 3, 1159–1171, https://doi.org/10.1007/s11071-015-1933-4, 2-s2.0-84940005896.
10.1007/s11071-015-1933-4
Web of Science® Google Scholar
18 Nithya V., Sakthivel R., and Alzahrani F., Dissipative-based non-fragile filtering for fuzzy networked control systems with switching communication channels, Applied Mathematics and Computation. (2020) 373, article 125011, https://doi.org/10.1016/j.amc.2019.125011.
10.1016/j.amc.2019.125011
Google Scholar
19 Xu Z., Su H., Lu R., and Wu Z.-G., Non-fragile dissipative filtering for 2-d switched systems, Journal of the Franklin Institute. (2017) 354, no. 14, 6234–6246, https://doi.org/10.1016/j.jfranklin.2017.07.021, 2-s2.0-85026457858.
10.1016/j.jfranklin.2017.07.021
Web of Science® Google Scholar
20 Yang H., Xia Y., Shi P., and Liu B., Guaranteed cost control of networked control systems based on delta operator Kalman filter, International Journal of Adaptive Control and Signal Processing. (2013) 27, no. 8, 701–717, https://doi.org/10.1002/acs.2345, 2-s2.0-84880328157.
10.1002/acs.2345
CAS Web of Science® Google Scholar
21 Zhao Y. and Yang C., Information fusion robust guaranteed cost Kalman estimators with uncertain noise variances and missing measurements, International Journal of Systems Science. (2019) 50, no. 15, 2853–2869, https://doi.org/10.1080/00207721.2019.1690719.
10.1080/00207721.2019.1690719
Web of Science® Google Scholar
22 Shen B., Wang Z., and Tan H., Guaranteed cost control for uncertain nonlinear systems with mixed time-delays: the discrete-time case, European Journal of Control. (2018) 40, 62–67, https://doi.org/10.1016/j.ejcon.2017.11.006, 2-s2.0-85039720091.
10.1016/j.ejcon.2017.11.006
Web of Science® Google Scholar
23 Dong H., Wang Z., and Gao H., Distributed filtering for a class of time-varying systems over sensor networks with quantization errors and successive packet dropouts, IEEE Transactions on Signal Processing. (2012) 60, no. 6, 3164–3173, https://doi.org/10.1109/TSP.2012.2190599, 2-s2.0-84861171805.
10.1109/TSP.2012.2190599
Web of Science® Google Scholar
24 Tian S. and Xu K., Distributed non-fragile state estimation of nonlinear systems over sensor networks, 2022 37th Youth Academic Annual Conference of Chinese Association of Automation (YAC), 2022, Beijing, China, IEEE, 1028–1032, https://doi.org/10.1109/YAC57282.2022.10023685.
10.1109/YAC57282.2022.10023685
Google Scholar
25 Wang J., Wang D., Yan H., and Shen H., Composite Antidisturbance Control for Hidden Markov Jump Systems With Multi-Sensor Against Replay Attacks, IEEE Transactions on Automatic Control. (2024) 69, no. 3, 1760–1766, https://doi.org/10.1109/TAC.2023.3326861.
10.1109/TAC.2023.3326861
Google Scholar
26 Shen H., Xing M., Yan H., and Cao J., Observer-based l2−l∞ control for singularly perturbed semi-Markov jump systems with an improved weighted TOD protocol, Science China Information Sciences. (2022) 65, no. 9, article 199204, https://doi.org/10.1007/s11432-021-3345-1.
10.1007/s11432-021-3345-1
Google Scholar
27 Yu J., Dong X., Li Q., and Ren Z., Robust H_∞ guaranteed cost time-varying formation tracking for high-order multiagent systems with time-varying delays, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2020) 50, no. 4, 1465–1475.
10.1109/TSMC.2018.2883516
Web of Science® Google Scholar
28 Sun S., Zhang H., Qin Z., and Xi R., Delay-dependent H_∞ guaranteed cost control for uncertain switched t–s fuzzy systems with multiple interval time-varying delays, IEEE Transactions on Fuzzy Systems. (2021) 29, no. 5, 1065–1080.
10.1109/TFUZZ.2020.2968877
Web of Science® Google Scholar
29 Reciprocally convex approach to stability of systems with time-varying delays, Automatica. (2011) 47, no. 1, 235–238, https://doi.org/10.1016/j.automatica.2010.10.014, 2-s2.0-78650807125.
10.1016/j.automatica.2010.10.014
Web of Science® Google Scholar
30 Geromel J. C., de Oliveira M. C., and Hsu L., Lmi characterization of structural and robust stability, Linear Algebra and its Applications. (1998) 285, no. 1-3, 69–80, https://doi.org/10.1016/S0024-3795(98)10123-4, 2-s2.0-0004992230.
10.1016/S0024-3795(98)10123-4
Web of Science® Google Scholar
31 Jiang G.-P. and Zheng W. X., An lmi criterion for linear-state-feedback based chaos synchronization of a class of chaotic systems, Chaos, Solitons & Fractals. (2005) 26, no. 2, 437–443, https://doi.org/10.1016/j.chaos.2005.01.012, 2-s2.0-18544367821.
10.1016/j.chaos.2005.01.012
Web of Science® Google Scholar
32 Liang J., Shen B., Dong H., and Lam J., Robust distributed state estimation for sensor networks with multiple stochastic communication delays, International Journal of Systems Science. (2011) 42, no. 9, 1459–1471, https://doi.org/10.1080/00207721.2010.550402, 2-s2.0-79960490958.
10.1080/00207721.2010.550402
Web of Science® Google Scholar
33 Liu Y., Wang Z., Zou L., Hu J., and Dong H., Distributed filtering for complex networks under multiple event-triggered transmissions within node-wise communications, IEEE Transactions on Network Science and Engineering. (2022) 9, no. 4, 2521–2534, https://doi.org/10.1109/TNSE.2022.3164833.
10.1109/TNSE.2022.3164833
Google Scholar

All articles

Distributed Nonfragile Guaranteed Cost Filter Design for Nonlinear Systems With Sensor Networks

Abstract

1. Introduction

1.1. Notations

2. Preliminaries and Problem Formulation

3. Distributed Filter Gain Design

4. Illustrative Example

5. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Distributed Nonfragile Guaranteed Cost Filter Design for Nonlinear Systems With Sensor Networks

Abstract

1. Introduction

1.1. Notations

2. Preliminaries and Problem Formulation

3. Distributed Filter Gain Design

4. Illustrative Example

5. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information