An Optimal Control Study for a Two-Strain SEIR Epidemic Model With Saturated Incidence Rates and Treatment
Abstract
This work will study an optimal control problem describing the two-strain SEIR epidemic model. The model studied is in the form of six nonlinear differential equations illustrating the dynamics of the susceptible and the exposed, the infected, and the recovered individuals. The exposed and the infected compartments are each divided into two subclasses representing the first and the second strains. The model includes two saturated rates and two treatments for each strain. We begin our study by showing the well posedness of our problem. The basic reproduction number is calculated and depends mainly on the reproduction numbers of the first and second strains. The global stability of the disease-free equilibrium is fulfilled. The optimal control study is achieved by using the Pontryagin minimum principle. Numerical simulations have shown the importance of therapy in minimizing the infection’s effect. By administrating suitable therapies, the disease’s severity decreases considerably. The estimation of parameters as well as a comparison study with COVID-19 clinical data is fulfilled. It was shown that the mathematical model results fit well the clinical data. In order to eradicate the infection, it is very important that the first and second strain reproduction numbers must be less than unity.
1. Introduction
The SIR pioneer work of Kermack and McKendric in 1927 [1] has inaugurated most mathematical modeling in epidemiology. SIR abbreviation stands for susceptible-infected-recovered compartments. Those classes were sufficient to study many infectious diseases. However, after the infection occurs, the individual is first exposed to the virus and will be infectious. Therefore, another compartment must be added to the classical SIR one, and the new abbreviation will be SEIR, which means susceptible-exposed-infected-recovered configuration. Many papers have used the SEIR model to study many infectious diseases such as coronavirus disease 2019 (COVID-19) [2, 3], hepatitis B infection (HBV) [4], and human immunodeficiency virus (HIV) [5]. It is worthy to notice that the late COVID-19 has attracted the attention of many researchers [6]. Different treatments of infectious diseases have been considered and studied in many works [7–9]. The optimal control of many infectious diseases has been studied [10–12].
The organization of this present paper will take the following form. First, Section 2 will be devoted to our two-strain SEIR epidemic model with two saturated incidence rates and two treatments. Next, Section 3 will investigate the disease-free equilibrium global stability. The optimal control study of our problem using the Pontryagin minimum principle is fulfilled in Section 4. Section 5 is dedicated to several numerical solutions showing the importance of the control strategy. Concluding remarks are given in Section 6. The parameters estimation is given in the Appendix section.
2. The Problem Well Posedness
In this section, we will focus attention on the problem’s well posedness. More precisely, we will show that Problem (1) admits a positive and bounded solution.
2.1. Positivity Results
Our problem describes population dynamics; therefore, all the acting variables must be nonnegative. Hence, we have the following result of positive invariance.
Theorem 1. For any initial data , the variables (S(t), E1(t), E2(t), I1(t), I2(t), R(t)) to Model (1) will remain also positive ∀ t > 0.
Proof 1. First, assume that tf = sup{ζ ≥ 0 | ∀t ∈ [0, ζ] we have S(t) ≥ 0, E1(t) ≥ 0, E2(t) ≥ 0, I1(t) ≥ 0, I2(t) ≥ 0and R(t) ≥ 0}. Let us now prove that tf = +∞.
Suppose that 0 < tf < +∞, then from the solutions continuity fact, we have S(tf) = 0 or E1(tf) = 0 or E2(tf) = 0 or I1(tf) = 0 or I2(tf) = 0 or R(tf) = 0.
However, from System (1) first equation, we have (dS(tf)/dt) = Λ > 0, which contradicts (2). Similar remark for the other variables E1(t), E2(t), I1(t), I2(t), and R(t). We conclude that tf could not be finite. This concludes the demonstration.
2.2. Boundedness Result
Proposition 1. The following closed set
Proof 2. Let the total population be
We conclude that is a positively invariant set. All solutions to Problem (1) remain bounded.
The positivity and boundedness results ensure the existence of solution.
3. Analysis of the Problem
This section will be devoted to providing the basic reproduction number and the disease-free equilibrium stability result.
3.1. Basic Reproduction Number
is called the strain-1 reproduction number, while is nemad the strain-2 reproduction number.
3.2. Global Stability of the Disease-free Equilibrium
We obtain the global stability of the disease-free equilibrium using the Lyapunov method. More precisely, we have the following result.
Theorem 2. The disease-free equilibrium is globally asymptotically stable when the basic reproduction number is less than unity.
Proof 3. First, let us consider the following Lyapunov function:
Finally, when and .
We conclude that the negativity of the Lyapunov function will be achieved when the basic reproduction number is less than unity.
The disease-free equilibrium is globally asymptotically stable when .
4. The Optimal Control Study
4.1. The Infection Optimization Problem
4.2. Existence of Trajectories
Theorem 3. f satisfies the following equation:
Proof 4. Since f(t, x, u) is at least C1 with respect to t, x, u and x, u belong to the bounded set and U, respectively, then (12) is satisfied (see [21, 22]).
Theorem 4. For any control u(·) ∈ [0, 1]2, the ODE System (22) has a unique solution.
Proof 6. We exploit the existence theorem in [22] (Theorem III.4.1 p68-69).
By Theorem 3, we have that (27) is satisfied.
The set is clearly not empty by Theorem 4.
The set [0, 1]2 is convex and closed.
Hence, L(t, x, u) ≥ c1∥u∥β − c2, with c1 = C, c2 = Λ/δ and β = 2.
4.3. The Infection Optimality System
The optimality system to Problem (22) is given by the following result.
Theorem 6. There exist six adjoint equations to Problem (22) given by
Proof 7. The six adjoint equations can be obtained via Pontryagin principle [23] such that
5. Numerical Simulations
In this section, we will provide some numerical simulations to highlight the role of control strategies in combating the infection. We use Gekko Optimization Suite [24] in Python [25]. Fitting data of the cumulative cases of Senegal country estimate the model’s parameters. For more details, see the Appendix. We consider T = 16743927 the total population of Senegal. We have two tests: Test 1 and Test 2. The values of the parameters are shown in Table 1.
| Parameters | Test 1 | Test 2 | |
|---|---|---|---|
| Λ | 0.0914T/100 | 0.0914T/100 | Fixed |
| k1 | 0.05 | 0.2 | Fixed |
| k2 | 0.04 | 0.15 | Fixed |
| δ | 0.000219 | 0.000219 | Fixed |
| ξ1 | 10 | 0.08 | Fixed |
| ξ2 | 12 | 0.9 | Fixed |
| μ1 | 0.00012 | 0.003 | Fitted |
| μ2 | 0.001 | 4.896·10−5 | Fitted |
| β1 | 7.71·10−7 | 1.52·10−6 | Fitted |
| β2 | 7.92·10−7 | 4.6·10−6 | Fitted |
| γ1 | 5.57·10−5 | 0.0009 | Fitted |
| γ2 | 0.000515 | 0.0002 | Fitted |
| C1 | 100/β2 | 100/β2 | Fixed |
| C2 | 100/β1 | 100/β1 | Fixed |
Table 2 gives the initial conditions.
| Initial conditions | S(0) | E1(0) | E2(0) | I1(0) | I2(0) | R(0) |
|---|---|---|---|---|---|---|
| Test 1 | 16660213 | 20212 | 24254 | 17065 | 22184 | 0 |
| Test 2 | 16661290 | 8085 | 40424 | 6826 | 27303 | 0 |
The parameters Λ, k1, k2, δ, ξ1, and ξ2 are fixed. By inserting them into the formulas in the Appendix, obtained by fitting the model to the COVID-19 data, we obtain the values of the other parameters as well as the initial conditions. Since for both tests, we choose different values of k1 and k2, we obtain different values of the fitted parameters and the initial conditions.
Figures 2, 3, 4, and 5 show the dynamic of two-strain infection model with and without controls. We clearly observe that with control, the number of susceptible individuals is higher than that without control. Hence, controls have played an essential role in maximizing susceptible individuals. Moreover, in both strains, infected and exposed individuals are reduced with control, while without the control, they remain at a strictly positive level. The convergence toward the free endemic equilibrium with control is observed. More precisely, all the states converge toward the endemic-free equilibrium (Λ/δ, 0, 0, 0, 0, 0), which means that the infection can be eradicated.
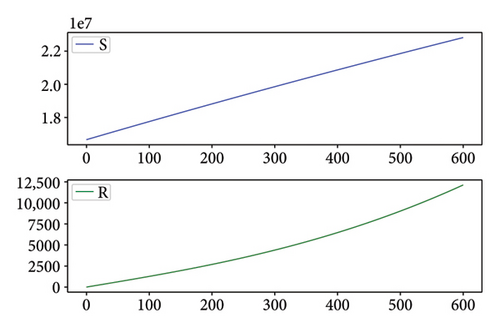
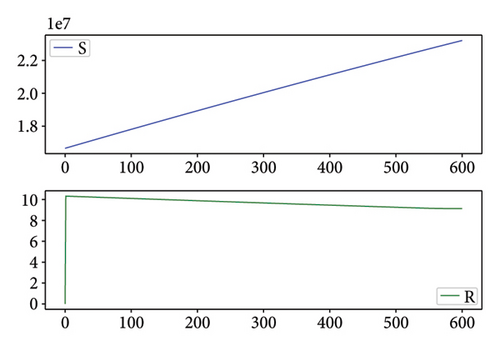
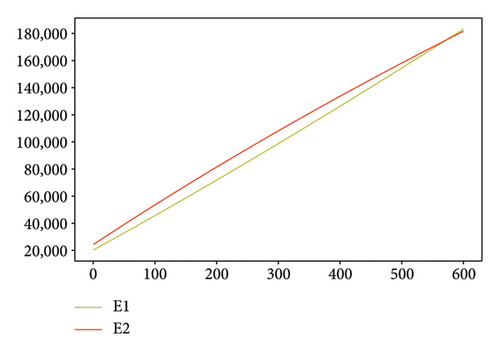
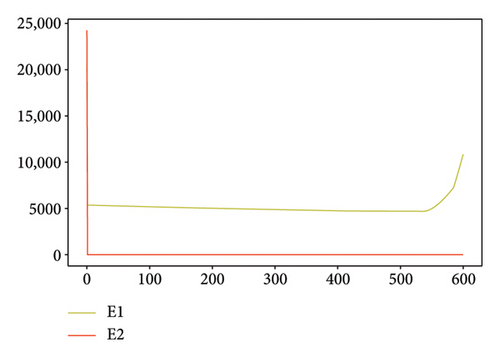
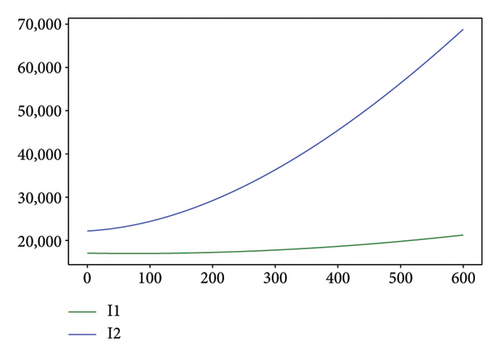
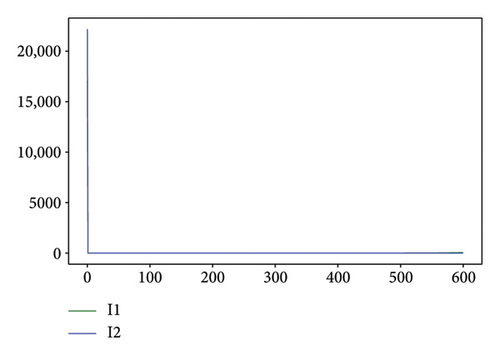
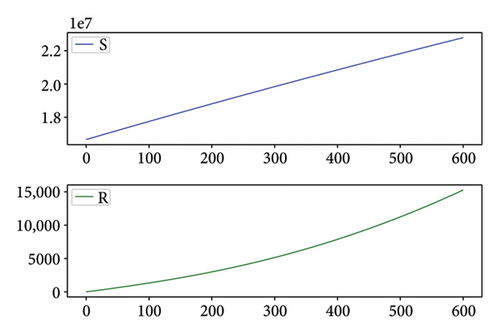
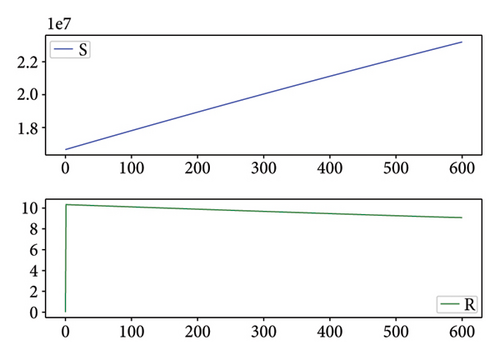
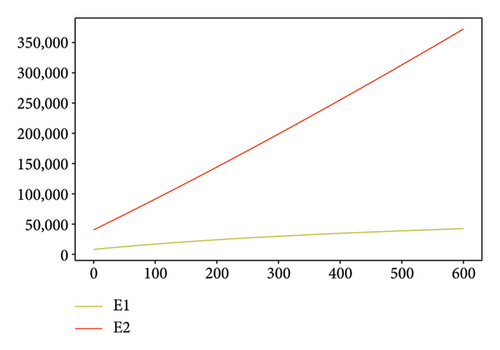
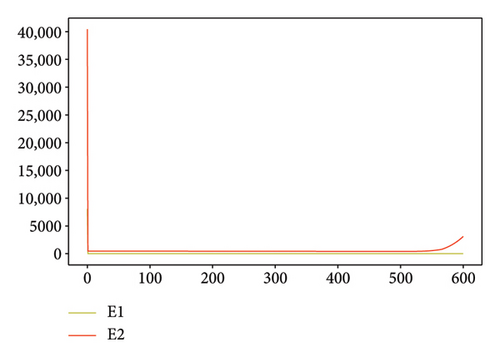
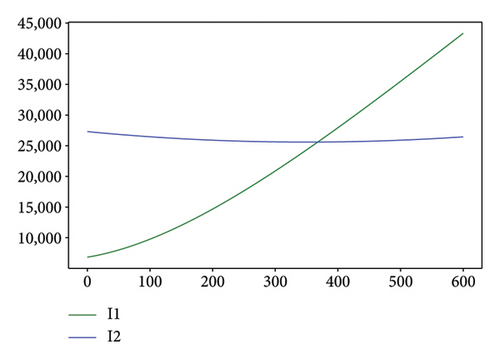
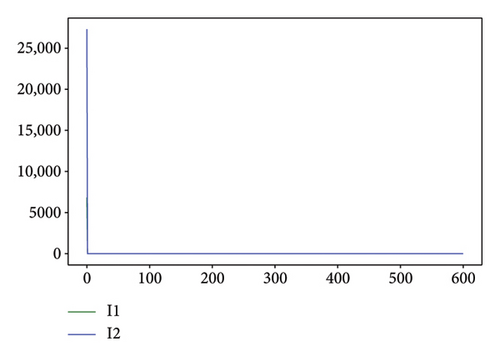
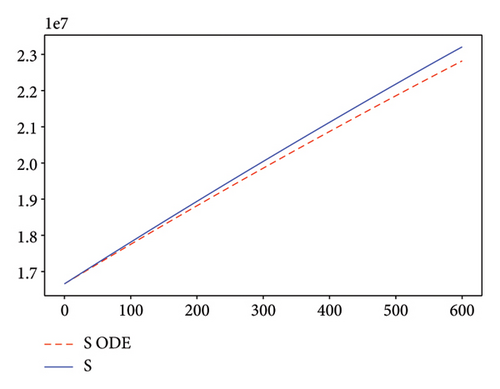
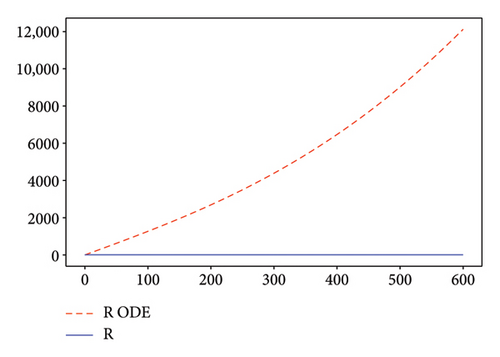
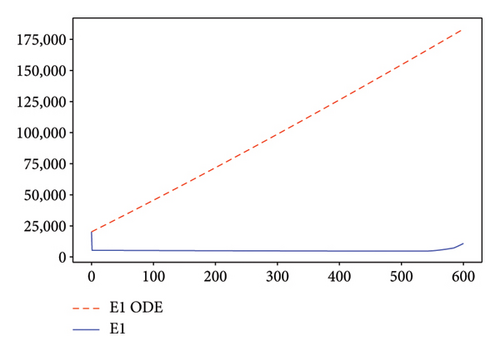
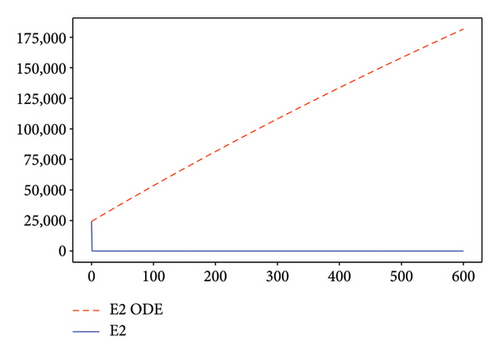
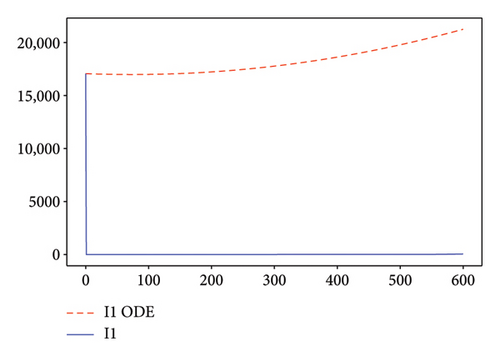
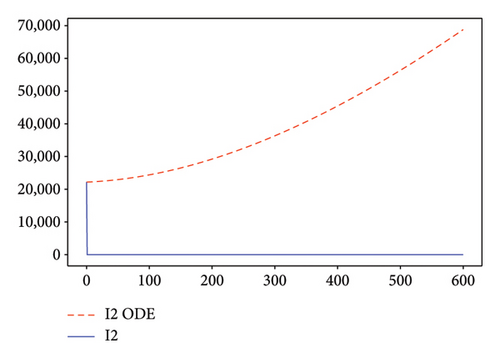
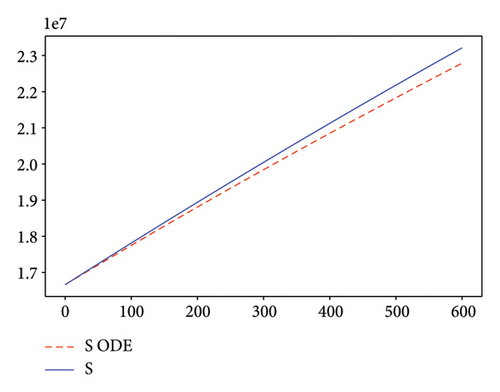
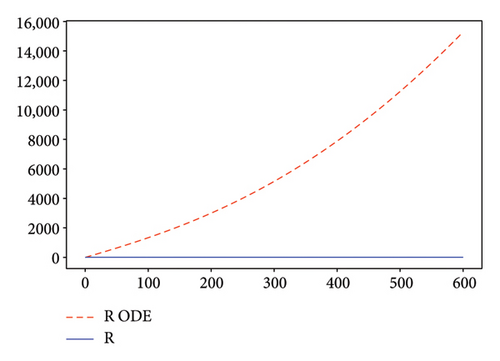
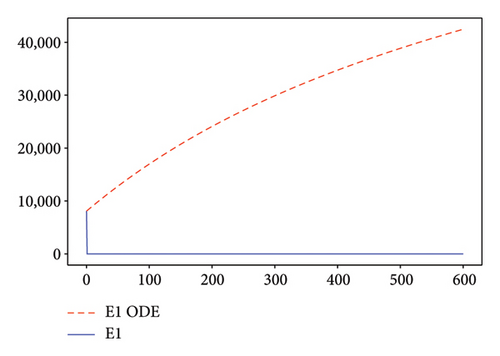
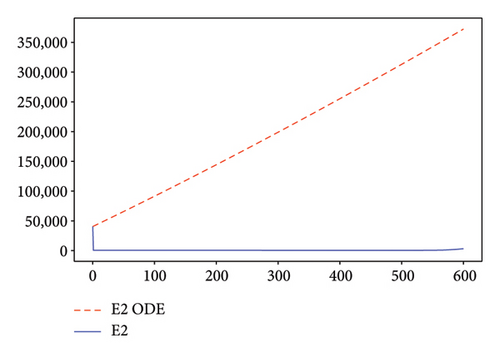
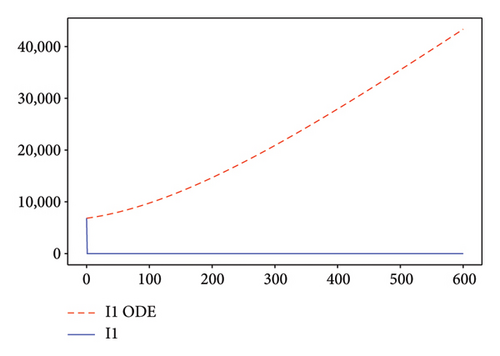
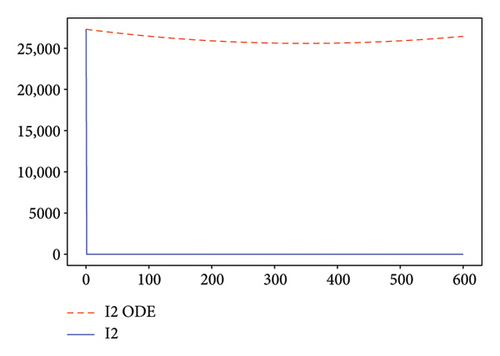
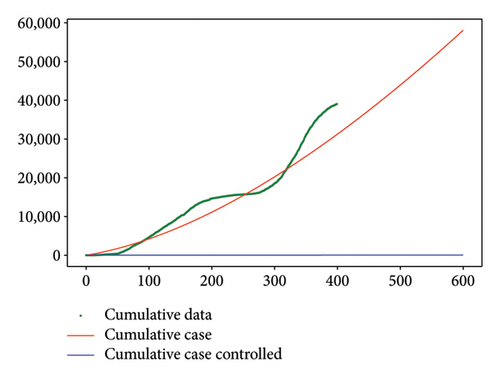
Figure 6 shows a comparison of cumulative case data, the cumulative case with and without controls.
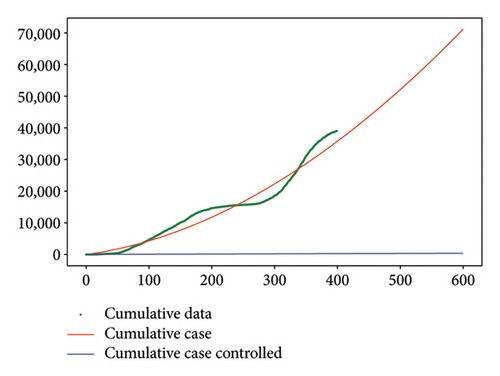
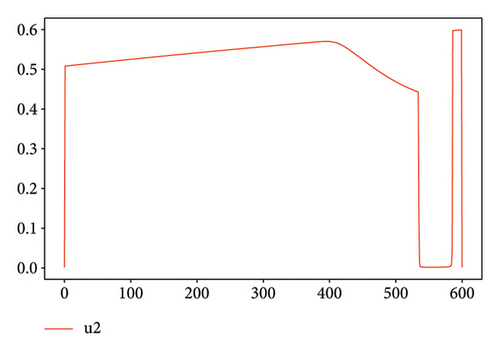
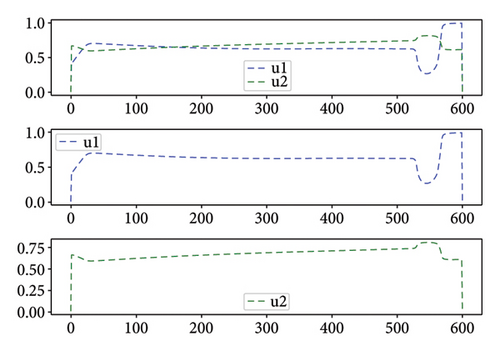
For Test 1, we see that from 0 to 400, the control u1 is zero unlike the control u2, which is at an average level over the period from 0 to 500 as is shown in Figure 7, while the trends are reversed in the period from 500 to 600. Thus, in the first period, the priority is given to the treatment of Strain 2 and the situation is reversed in other periods. This has made it possible to reduce the cumulative cases of infection as depicted in Figure 6(a).
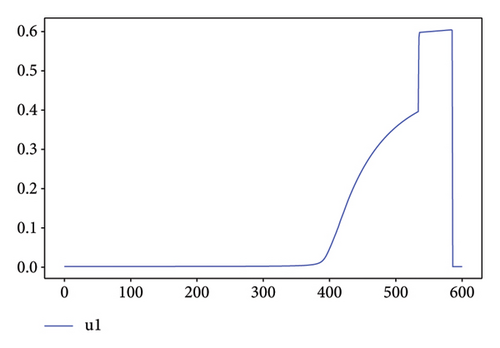
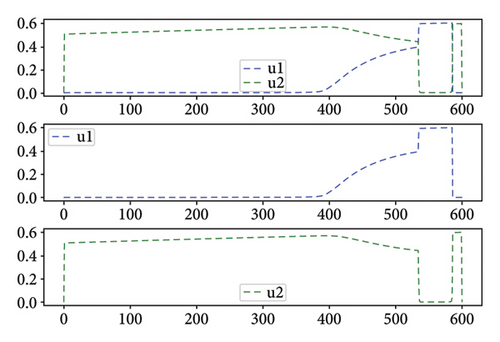
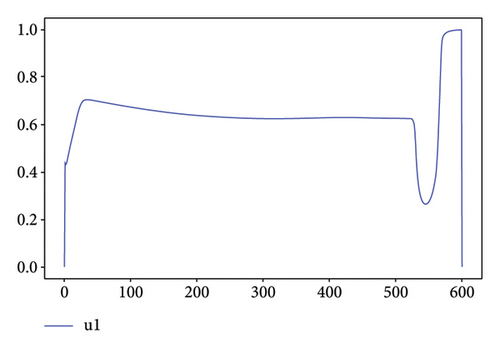
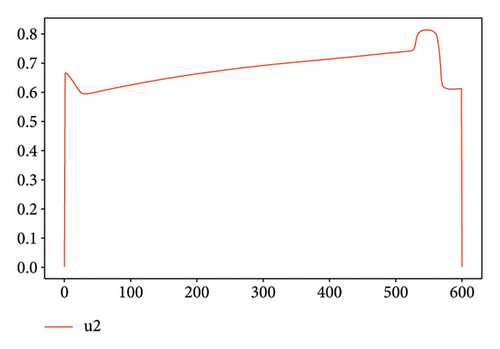
As shown in Figure 8 for Test 2, the controls u1 and u2 are at a high level, varying between 0.6 and 1 over most of the study period from 0 to 600. Indeed, control u1 has a level lower than 0.5 over the period from 525 to 575. Thus, over the periods from 0 to 20 and from 150 to 575, the priority is given to the treatment of Strain 2 unlike the other periods. We see that the cumulative case of infection is reduced over the entire study period as shown in Figure 6(b).
6. Conclusion
In this work, we have studied numerically and theoretically a mathematical model describing the dynamics of a two-strain SEIR epidemic model. The model contains a system of nonlinear differential equations describing the interaction between the susceptible, the first, and the second strain exposed individuals, the first and the second strain infected individuals and the recovered ones. Two saturated rates and two treatments were incorporated into the model. The well posedness of the model was established in terms of positivity and boundedness of solutions. The basic reproduction number was calculated as a function of the reproduction numbers of the first and second strains. The global stability of the disease-free equilibrium was fulfilled. We have performed an estimation study of the problem parameters. In addition, the model numerical simulation was compared with COVID-19 clinical data. The optimal control study was achieved by using the Pontryagin minimum principle. Numerical simulations have shown the importance of therapy in minimizing the infection’s effect. It was shown that the disease severity decreased remarkably when good therapies were administrated. As future directions of the present work, one can consider more than two strains or include the birth logistic growth rate.
Disclosure
A preprint of this paper was shared in Arxiv on April 26, 2024 [29].
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
No funding was received for this work.
Acknowledgments
Karam Allali is grateful to the support from the Laboratory Mathematics, Computer Science and Applications, University Hassan II of Casablanca and the hospitality of Babacar Mbaye Ndiaye at LMDAN in the University Cheikh Anta Diop of Dakar during the research collaboration visit.
Appendix A: Estimation of Parameters
The estimation of the parameters of Model (1) is done by using the techniques in [21, 26, 27]. Generally, pandemic data fit with an exponential type of function. Analyzing the Senegal COVID − 19 data, we see that the function does not follow exponential curve.
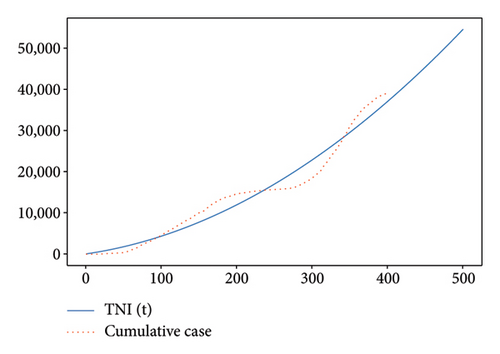
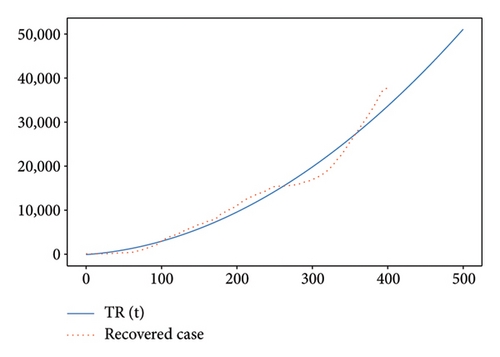
We fit, respectively, the cumulative and recovered case data of COVID − 19 in Senegal, from 2020 March 02 to 2021 April 04, with the two polynomial functions TNI(t) = at2 + bt + c and TR(t) = et2 + ft + g, see Figure A1. In addition, we assume that these functions can be given in integral form as and .
We use 32.9% of year 2018 for the birth rate from [28]. Then, the recruitment is Λ = 32.9%T/365 by day. The death rate is 7.9% by the year 2018.
Now, we will discuss the coefficients C1 and C2. We simulated two tests. For both tests, the values of the coefficients are related to the infection rate. We consider that if the infection rate is such that β1 < β2, then the propagation of Strain 2 is more than that of Strain 1. The more the infection spreads through the population, the greater the treatment expenses. Then, we set C1 = 100/β2 and C2 = 100/β1.
Open Research
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.




