Discrete Dynamics in Nature and Society
Volume 2025, Issue 1 8384630
Research Article
Open Access

Fractals and Chaotic Solitons Phenomena in Conformable Coupled Higgs System

Naveed Iqbal, 

Naveed Iqbal

Department of Mathematics , College of Science , University of Ha’il , Ha’il , 2440 , Saudi Arabia , uoh.edu.sa

Search for more papers by this author
Wael W. Mohammed, 

Wael W. Mohammed

Department of Mathematics , College of Science , University of Ha’il , Ha’il , 2440 , Saudi Arabia , uoh.edu.sa

Search for more papers by this author
Amjad E. Hamza, 

Amjad E. Hamza

Department of Mathematics , College of Science , University of Ha’il , Ha’il , 2440 , Saudi Arabia , uoh.edu.sa

Search for more papers by this author
Shah Hussain, 

Shah Hussain

Department of Mathematics , College of Science , University of Ha’il , Ha’il , 2440 , Saudi Arabia , uoh.edu.sa

Search for more papers by this author
Yousef Jawarneh, 

Yousef Jawarneh

Department of Mathematics , College of Science , University of Ha’il , Ha’il , 2440 , Saudi Arabia , uoh.edu.sa

Search for more papers by this author
Rasool Shah, 

Corresponding Author

Rasool Shah

Department of Computer Science and Mathematics , Lebanese American University , Beirut , Lebanon , lau.edu.lb

Search for more papers by this author
First published: 29 April 2025
https://doi.org/10.1155/ddns/8384630
Academic Editor: Ahmed Ezzat Matouk

Abstract

The current study aims to construct and examine a new plethora of soliton solutions for the conformable coupled Higgs system (CCHS), a system of nonlinear fractional partial differential equations (NFPDEs) which was initially presented utilize a systematic structure to consider the responsive mechanism of the Higgs system in the electroweak theory perspective, within the framework of the standard model of physics. To achieve our goal, we utilize a transformation-based analytical technique, namely, the generalized Bernoulli equation method (gBEM), which reduces CCHS to nonlinear ordinary differential equations (NODEs) via a fractional complex transformation. The fresh assortment of soliton solutions is produced when the resultant NODEs are tackled using the Maple tool. We employ 3D and contour visualizations to graphically represent the behavior of acquired solitons, which prominently reveal that these soliton solutions show axial, chaotic, and periodic perturbations which induce instabilities in soliton and may lead to the formation of fractals. The results appear groundbreaking, showcasing diverse families of soliton solutions with intricate interrelations and dynamics. These findings not only advance our theoretical understanding of CCHS dynamics but they may also have implications in NFPDE–related fields.

1. Introduction

Fractional partial differential equations (FPDEs) are a significant broadening of traditional partial differential equations (PDEs) which enfold nonlocal derivatives noticed in a spectrum of cosmic events and analytical models. Particularly, nonlinear FPDEs (NFPDEs) are extensively applied across various disciplines, such as industry, plasma dynamics, life science, applied science, and economics, to quantitatively capture complicated systems that qualitatively describe intricate such unexplained diffusion, viscoelasticity, and fractional Brownian motion [1–5]. The confluence of non-Markovian properties and nonlocality in FPDEs gives rise to their rich and complex dynamics, posing significant challenges to their solution. Researchers have developed numerical techniques such as radial basis function (RBF) [6], singular boundary method (SBM) [7, 8], finite element methods [9] and spectral radial point interpolation method (SRPIM) [10] to overcome this obstacle. However, without advanced mathematical expertise, these approaches can lead to significant errors. Regardless, the application of analytical methods has been instrumental in resolving FPDEs. They facilitate enhanced comprehension of the underlying analytical framework and allow researchers to gain a better understanding of the system’s behavior. Furthermore, analytical methods serve as a vital benchmark for assessing numerical accuracy, generating scenario-specific approximations and providing efficient solutions. They also facilitate the development of closed-form solutions by illuminating the underlying dynamics of the problem [11–16].

Researchers are therefore intensifying their focus on mathematical methods for solving FPDEs, resulting in the establishment of several frameworks for addressing these issues. For instance, Wu and Baleanu implemented the variational iteration method (VIM) to obtain the approximate solutions for Burgers’ flow equation with fractional order [17], while Duan et al. presented a comprehensive analysis of the Adomian decomposition method (ADM) and its variations, i.e., the multistage ADM, for FPDEs with defined boundary conditions [18]. Xu et al. extended the homotopy perturbation method (HPM) to accommodate FPDEs with fractal order [19]. Similarly, Raslan et al. used the employed tanh technique to get traveling wave solutions for fractional-order equal width wave (EWW) and modified EWW (MEWW) equations [20]. In [21], Jafari et al. used the fractional subequation method to obtain the exact solutions of the fractional Sharma–Tasso–Olver (STO) equations and extended reaction Duffing models. In addition, mathematicians have also explored other solution techniques for PDEs and FPDEs such as the elliptic expansion technique [22], the fractional reduced differential transform method (FRDTM) [23], the exp-function approach [24], the Bäcklund transformation bilinear method [25, 26], the (G′/G) expansion method [27, 28], the Hirota bilinear method [29], the fractional Fourier transform method [30], the separation of the variable method [31], and the generalized Bernoulli equation method (gBEM) [32, 33].

Among these techniques, the gBEM has proven to be a valuable tool for researchers to construct precise soliton solutions for NFPDEs. Via a variable transformation, this gBEM transforms a NFPDE into an integer-indexed node. The proposed method involves formulation of a finite series form solution with arbitrary parameters for nonlinear ordinary differential equations (NODEs), which, upon substitution into the equation, yields an algebraic system of equations that admits soliton solutions for the focused NFPDE, as verified using Maple.

This work focuses on applying the gBEM to investigate the soliton solutions for the conformable coupled Higgs system (CCHS), a fractional extension of the CHS, a nonlinear PDE system that describes the dynamic behaviors of complex and real scalar fields’ framework. The coupling of these fields with a gauge field is enabled by the covariant derivative. The CHS was initially formulated as a theoretical framework to elucidate the underlying dynamics of the Higgs mechanism, especially in the context of electroweak symmetry breaking within the standard model. The CHS is conceptually expressed as [34–38]
()
where w ≡ w(x, t) and z ≡ z(x, t). The CHS provides a description of the soliton behavior, where these waves maintain their structure and integrity during propagation. The system’s fist equation governs the background fields’ evolution, while the second equation accounts for the solitons amplitude and phase modifications. Notably, the system exhibits nonlinearity leading to several complex phenomena including the generation, formation, and scattering of solitons. The CHS significance in particle physics lies in its capacity to describe the dynamics of particle behavior, mass, and interactions. Notably, the system’s nontrivial scattering, topological solitons, amplitude, and symmetry breakdown present a rich landscape for exploration in both experiment and theory.
To develop the CCHS, conformable derivatives are substituted for conventional derivatives in the CHS, facilitating a more comprehensive analysis of the mathematical model. The key advantage of conformable derivatives in the CHS is that it allows for the inclusion of long-range memory effects, which is not present in the traditional derivative. This leads to a more accurate and realistic representation of the system’s dynamics, particularly when dealing with noisy and disturbed systems. In addition, the application of conformable derivatives can give rise to the emergence of unique solution types, including fractal and conformable solitons, which have been observed in numerous physical systems. These unconventional solutions may exhibit unique characteristics that challenge conventional understanding, offering a new novel perspective on the system dynamics. To gain insight into CCHS, it is characterized mathematically by [37]
()
where 0 < α, β ≤ 1. The conformable fractional derivatives and allow for the inclusion of nonlocal effects that are essential for accurately modeling the behavior of solitons in the system. The key aspect of CCHS is to provide a comprehensive mathematical framework for understanding the relationship between gauge field and real scalar field. Beyond its origin in the particle physics, the CHS has emerged as a theoretical tool for the Higgs mechanism and expanded to encompass applications in electroweak theory as well. The CHS has been investigated by researchers, as a theoretical framework for modeling diverse nonlinear physical systems, including intricate nonlinear behavior in various fields and superconductor dynamics. In addition, the fractional model’s incorporation of conformable derivatives facilitates a more detailed understanding of systems with nuanced temporal dynamics, thus expanding its relevance to systems exhibiting intricate dynamics.

Before this research work, a number of authors have previously investigated the CHS in both integer and fractional orders using various analytical techniques. Rezazadeh et al. in [5] solved the CHS in time-fractional form using the Sin–Gorden approach. Jabbari et al. obtained exact solutions to the CHS using He’s semi-inverse approach and a simple (G′/G)-expansion method [34]. Likewise, Atas et al. in [35] found invariant optical soliton solutions for CHS. The exp-expansion approach was utilized by Seadawy et al. in [36] to get traveling wave solutions for the targeted system. Mu and Qin offered a rogue waves solution for CHS in [37], using the Hirota technique. Based on the existing literature, numerous scholars have investigated solitonic phenomena in CCMS. Nevertheless, perturbed and fractal soliton solutions have not been investigated and examined within the framework of the targeted model using gBEM. This assertion highlights a significant gap in the body of current research. Our study fills this gap by offering a thorough analysis of the model and outlining the suggested gBEM. In order to do this, we employed the suggested transformation-based gBEM, which uses a fractional complex transformation to convert CCHS to NODEs. When the resulting NODEs are solved with the Maple tool, some new plethora of soliton solutions is generated. To visually depict the behavior of acquired solitons, we use 3D and contour visualizations. These visualizations clearly indicate that the soliton solutions exhibit axial, chaotic, and periodic perturbations, which cause instabilities in the soliton and may result in the production of fractals. The findings, which display several families of soliton solutions with complex dynamics and interrelations, seem revolutionary. These results contribute to our theoretical knowledge of CCHS dynamics and might have applications in domains connected to NFPDEs. Chaos is integral to many technological and scientific applications, such as biological systems, fluid dynamics, plasma physics, and optical communications, where nonlinear interactions result in ordered yet unexpected behaviors. The study of chaos in this work is motivated by the fundamental importance of chaos in understanding pattern formation, nonlinear wave behavior, and instability in complex systems. By studying chaotic disturbances in soliton solutions, we want to improve our knowledge of the long-term dynamics and self-organization of nonlinear systems. This information might be useful for developing dependable soliton-based technologies, signal processing, and encrypted communication.

The remaining sections of the paper are arranged as follows. Section 2 outlines the description of conformable fractional derivatives and gBEM’s methodology. Section 3 provides soliton solutions for CCHS. A discussion and numerous illustrations are included in Section 4. Our research is summarized in Section 5.

2. Methods and Materials

2.1. Conformable Fractional Derivative

The concept of CFDs is solely dependent on how the classical derivative limit is defined and several results such as the sum rule, power rule, product rule, and quotient rule in [39–44] are obtained. By taking advantage of the advantages of CFDs unlike other fractional derivative operators, NFPDEs can be explicitly addressed. Surprisingly, since it defies the chain rule, many fractional derivative representations for equations do not lead to traveling wave and soliton solutions [45, 46]. For this reason, CFDs were added to equation (1). The definition and other theorems that specify essential characteristics of the integrated CFDs are given in this part as follows:
()
demonstrated the limits’ exits, keeping in mind that the derivative is Dθ(f)(t) = t1−θf′(t) if f is fully differentiable at t. Furthermore, we provide a new definition and derive a number of outcomes, including the sum rule, power rule, constant rule, product rule, and chain rule. Starting with a generalization of the conformable fractional derivative, we have the following definition.

Definition 1. Given a function with 0 ≤ α < b. Then, the “α-conformable fractional derivative” of f of order ϑ is defined by

()

If f is (ϑ, α)-differentiable in some exist, then we define that
()

If the α-conformable fractional derivative of f of order ϑ exists, then we simplify and say that f is (ϑ, α)-differentiable.

Theorem 1. Let h(t) and g(t) be the (α, ϑ)-differentiable functions on (ϑ, b), and let . Then, the function ζ(t) = Ω1h(t) + Ω2g(t) is (α, ϑ)-differentiable on (ϑ, b), and its (α, ϑ)-conformable fractional derivative is given by

()

Theorem 2. Let ζ(t) = tΩ, where , and ζ is defined on (ϑ, b). The (α, ϑ)-conformable fractional derivative of ζ is given by

()

Theorem 3. Let ζ(t) = Ω, where Ω is a constant. The (α, ϑ)-conformable fractional derivative of ζ is zero, which is defined as

()

Theorem 4. Let h(t) and g(t) be (α, ϑ)-differentiable functions on (ϑ, b). Then, the product ζ(t) = h(t)g(t) is (α, ϑ)-differentiable on (ϑ, b), and its (α, ϑ)-conformable fractional derivative is given by

()

Having these definitions in hand, we can present the following properties for (ϑ, α)-differentiable functions. Regarding the conformable fractional derivative, Khalil et al. [38] defines further properties such as the Laplace transformation, Taylor’s series expansion, Gronwall’s inequality, and several integration techniques. However, the main result which we use here is the chain rule which we discuss in the following theorem.

Theorem 5. Let f(t) and h(t) be arbitrary differentiable functions, then

()

Proof 1. If the function h is a constant in a neighborhood t0, then . However, we make the following assumption about the nonconstant function h in the vicinity of t0. Here, we are able to find an κ > 0∋h(t1) ≠ h(t2) for any t1, t2 ∈ (t0 − κ0, t0 + κ0). Thus, since the function h is continuous at t0, for t0 > α, (where α ≥ 0), we acquire

()

Theorem 6. Let 0 ≤ α < b and ϑ ∈ (0, 1]. If a function is (ϑ, α)− differentiable at , then f is continuous at t0.

Proof 2. Since

()
we have
()
let . Then, we get , which implies that f is continuous at t0.

2.2. The Working Methodology of gBEM

In the following section, we present the operational procedure of gBEM, an elegant technique for solving nonlinear FPDEs. The basic structure of FPDEs [23] is summarized as follows:
()
where u represents an unknown function which depends upon x, y, z, and t, and , , , and are conformable fractional derivative operators. To solve equation (11), we shall perform the following:
  •  

    Step 1: We begin our adventure by applying a variable transformation in the following manner:

    ()

  •  

    By using several definitions of the function ξ, we design a transformation that transforms equation (11) into the next NODE.

    ()

  •  

    Step 2: Following that, we consider a solution to equation (13) derived using a series-based technique. This technique not only speeds our study but also shows an orderly and visually appealing solution to the equation as follows:

    ()

  •  

    where Bi represents nonzero constants, while H(ξ) is the solution for the following ordinary differential equation (ODE):

    ()

  •  

    Step 3: The nonlinear component and highest order derivative of equation (13) are then balanced homogeneously to get the positive integer M, as shown in equation (14). This balancing technique is crucial because it ensures that the resulting equation may be effectively handled using the analytical approaches outlined as follows.

  •  

    Step 4: By inserting equation (14) into equation (13), we establish an algebraic system of equations by grouping all terms with the same power of H(ξ) and putting them equal to zero.

  •  

    Step 5: Following that, the established system is handled using Maple, which generates the computed values for the relevant parameters.

  •  

    Step 6: The sets of soliton solutions are then produced by combining the values of parameters in equation (14) with the suitable solution in (15). In addition, the many soliton solutions for equation (15) applied to the various conditions are presented as follows.

Family 1. For any nonzero real numbers ϖ and ν with the conditions ϖ2 > 0 and ν ≠ 0, respectively, equation (15) generates the following families of solutions:

()
()
()
()
()
()
()
where M1 and M2 are such nonzero real constants that satisfies .
()
()
()
where M1 and M2 are such nonzero real constants that satisfies .
()
()
where ρ is an arbitrary unknown constant.

Family 2. If ϖ = 0 and ν ≠ 0, the solution of equation (15) is

()

3. Execution of the gBEM

In this specific section, we utilize our proposed gBEM for addressing the CCHS presented in equation (2). The following transformation is applied in order to extend this technique to handle equation (2):
()
with
()
where ϱ(x, t) is the phase component of the soliton, η is the velocity of the soliton, and τ is the wavenumber. We substitute the required parameters, from equations (32) and (33), into equation (2) to get
()
In the above system of equation, prime represents differentiation with respect to ξ. Furthermore, by integrating the second equation in an above system with respect to ξ, twice and putting the constant to be zero, we acquire
()
Substituting equation (35) into the first equation of system (34), we obtain
()
Now, by applying the balancing principle in equation (36), we get M = 1, and by plugin equation (17), we get the following series form solutions:
()
By putting (37) in (36) and collecting all the terms with the same power of H(ξ) yields an expression in H(ξ). Upon equating each coefficient of the expression to zero, we get a system of algebraic equations. Using Maple and solving the resultant system provides the following three cases of solution for the involved parameters:
  •  

    Case 1:

    ()

  •  

    Case 2:

()

Assuming Case 1, we get the subsequent following family of soliton solutions for equation (2).

Family 3. For any nonzero real numbers ϖ and τ with the conditions ϖ2 > 0 and τ ≠ 0, respectively, equation (36) for Case 1 generates the following family of solutions:

()
()
()
()
()
()
()
where M1 and M2 are such nonzero real constants that satisfies .
()
()
()
where M1 and M2 are such nonzero real constants that satisfies .
()
()
where ρ is an arbitrary unknown constant.

Family 4. If ϖ = 0 and τ ≠ 0, the solution of equation (38) for Case 1 is

()

Assuming Case 1, we get the subsequent following family of soliton solutions for equation (2).

Family 5. For any nonzero real numbers ϖ and τ with the conditions ϖ2 > 0 and τ ≠ 0, respectively, equation (36) for Case 2 generates the following family of solutions:

()
()
()
()
()
()
()
where M1 and M2 are such nonzero real constants that satisfies .
()
()
()
where M1 and M2 are such nonzero real constants that satisfies .
()
()
where ρ is an arbitrary unknown constant.

Family 6. If ϖ = 0 and τ ≠ 0, the solution of equation (38) for Case 2 is

()

4. Discussion and Graphs

The preliminary goal of the present study was to incorporate gBEM in order to address CCHS which provided a number of soliton solutions’ families. Moreover, our current approach can be regarded as a decent generalization of the basic BEM (in turn), which leads to an extensive tool for the treatment of various nonlinear problems. Our proposed fractional-order solutions reveal significant results, unlike those obtained for the old traditional previously used integer-order solutions, which are not able to represent properly all physical phenomena. With our presented technique, one can obtain the exact solution of nonlinear problems in physical sciences without any need to linearize the equation which is demanded by some other previously-published approaches. Furthermore, the gBEM approaches used in this research are solid tools that have proven successful in a variety of physical phenomena, highlighting their usefulness and adaptability in solving challenging nonlinear models.

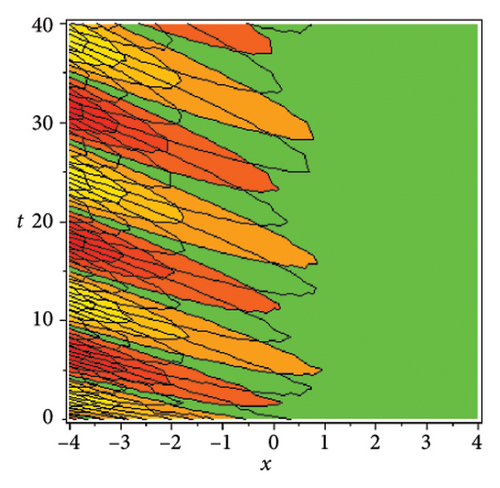
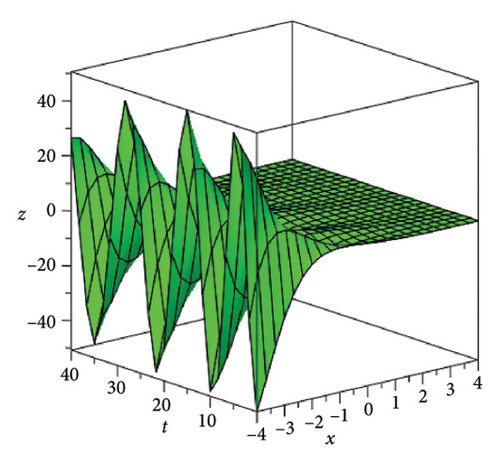
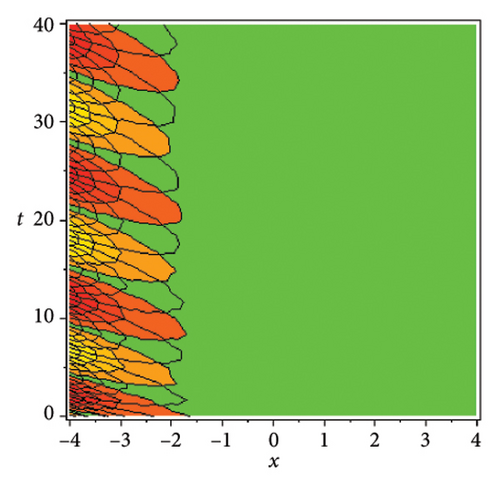
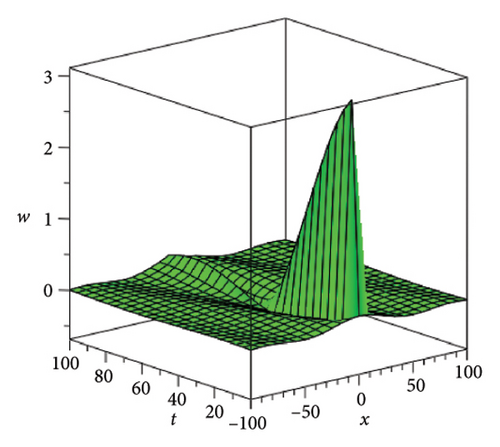
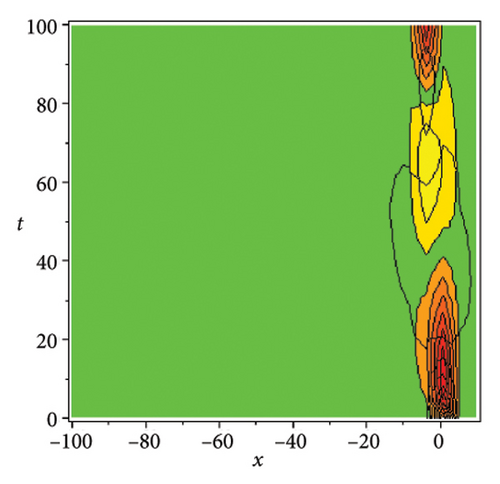
In the CCHS domain, we found chaotic solitons with predominantly axial and periodic disturbances. Within the context of CCHS, complex behaviors and patterns might result from the interactions and dynamics between the scaler fields. The disruption that happens along the system’s axis or direction is known as an axial perturbation. Conversely, periodic perturbation is a kind of regular, repeating disruption that is applied to the system of the model. All things considered, these disturbances cause more intracity, which causes the solitons to behave chaotically. On the other hand, our investigation showed that the dispersion of nonlinearity and the addition of external input caused axial and periodic disturbances in the produced solitons, resulting in the production of optical fractals. Fractal structures are produced by the solitons’ instabilities caused by these perturbations. Complex geometric structures and self-similarities with repetitions at different scales are characteristics of these systems. Recent developments in soliton theory have created exciting new avenues for mathematical research, especially fractal soliton theory [47–49], which examines the complex relationship between fractals and solitons. A fractal soliton is a stable, limited wave packet that possesses both a fractal and a solitonic structure. Nonuniform-bordered solitons with complex geometric patterns at different sizes that self-replicate gradually are called fractal solitons. Solitons and fractal geometry can be linked to gaining an understanding of nonlinear processes in physics, engineering, and biology [50–52]. As a result, the fractal soliton concept has several real-world uses across numerous fields. Due to its unique property, which helps us comprehend the dynamics and robustness of chaotic systems, fractal solitons are helpful in the study of chaos theory. The growing interest in fractal soliton research in modern mathematics should stimulate new ideas in both theoretical and practical mathematics. Moreover, Figure 1 is drawn for the axially perturbed lump-type kink solition solutions w1,1(t, x) and z1,1(t, x) in equation (40). Figure 2 is drawn for the perturbed periodic-axially perturbed solition solutions w1,4(t, x) and z1,4(t, x) in equation (43). Figure 3 is drawn for the chaotic perturbed lump-type kink solition solutions w1,8(t, x) and z1,8(t, x) in equation (47). Figure 4 is drawn for the periodic-axially perturbed solition solutions w1,11(t, x) and z1,11(t, x) in equation (50). Figure 5 is drawn for the chaotic perturbed bright kink solition solution w2,3(t, x) and chaotic dark kink soliton solution R2,3(t, x) in equation (55). Figure 6 is drawn for the perturbed chaotic kink solition solutions w2,6(t, x) and z2,6(t, x) in equation (58). Figure 7 is drawn for the perturbed chaotic lump-type kink solition solutions w2,7(t, x) and z2,7(t, x) in equation (59). Figure 8 is drawn for the axially perturbed chaotic solition solutions w2,13(t, x) and z2,13(t, x) in equation (65).

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed lump-type kink solition solutions w1,1(t, x) and z1,1(t, x) in equation (40) are depicted for G−1 = 10, G0 = 5, G1 = 20, τ = 0.02, η = τ, σ = 1, ϖ = 15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed lump-type kink solition solutions w1,1(t, x) and z1,1(t, x) in equation (40) are depicted for G−1 = 10, G0 = 5, G1 = 20, τ = 0.02, η = τ, σ = 1, ϖ = 15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed lump-type kink solition solutions w1,1(t, x) and z1,1(t, x) in equation (40) are depicted for G−1 = 10, G0 = 5, G1 = 20, τ = 0.02, η = τ, σ = 1, ϖ = 15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 1 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed lump-type kink solition solutions w1,1(t, x) and z1,1(t, x) in equation (40) are depicted for G−1 = 10, G0 = 5, G1 = 20, τ = 0.02, η = τ, σ = 1, ϖ = 15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed periodic-axially perturbed solition solutions w1,4(t, x) and z1,4(t, x) in equation (43) are depicted for G−1 = 10, G0 = 50, G1 = 20, τ = 0.009, η = τ, σ = 1, ϖ = 0.15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed periodic-axially perturbed solition solutions w1,4(t, x) and z1,4(t, x) in equation (43) are depicted for G−1 = 10, G0 = 50, G1 = 20, τ = 0.009, η = τ, σ = 1, ϖ = 0.15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed periodic-axially perturbed solition solutions w1,4(t, x) and z1,4(t, x) in equation (43) are depicted for G−1 = 10, G0 = 50, G1 = 20, τ = 0.009, η = τ, σ = 1, ϖ = 0.15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 2 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed periodic-axially perturbed solition solutions w1,4(t, x) and z1,4(t, x) in equation (43) are depicted for G−1 = 10, G0 = 50, G1 = 20, τ = 0.009, η = τ, σ = 1, ϖ = 0.15, ν = 1.9, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed lump-type kink solition solutions w1,8(t, x) and z1,8(t, x) in equation (47) are depicted for G−1 = 100, G0 = 50, G1 = −200, τ = 0.0090, η = τ, σ = 1, ϖ = 0.5, ν = 0.90, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed lump-type kink solition solutions w1,8(t, x) and z1,8(t, x) in equation (47) are depicted for G−1 = 100, G0 = 50, G1 = −200, τ = 0.0090, η = τ, σ = 1, ϖ = 0.5, ν = 0.90, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed lump-type kink solition solutions w1,8(t, x) and z1,8(t, x) in equation (47) are depicted for G−1 = 100, G0 = 50, G1 = −200, τ = 0.0090, η = τ, σ = 1, ϖ = 0.5, ν = 0.90, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed lump-type kink solition solutions w1,8(t, x) and z1,8(t, x) in equation (47) are depicted for G−1 = 100, G0 = 50, G1 = −200, τ = 0.0090, η = τ, σ = 1, ϖ = 0.5, ν = 0.90, α = 0.2, β = 0.4.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the periodic-axially perturbed solition solutions w1,11(t, x) and z1,11(t, x) in equation (50) are depicted for G−1 = 10, G0 = 95, G1 = 27, τ = 0.090, η = τ, σ = 1, ϖ = 5, ν = 0.90, α = 0.2, β = 0.4. In this profile, the fractal pattern is formed due to the axial perturbation of the system along the t-axis.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the periodic-axially perturbed solition solutions w1,11(t, x) and z1,11(t, x) in equation (50) are depicted for G−1 = 10, G0 = 95, G1 = 27, τ = 0.090, η = τ, σ = 1, ϖ = 5, ν = 0.90, α = 0.2, β = 0.4. In this profile, the fractal pattern is formed due to the axial perturbation of the system along the t-axis.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the periodic-axially perturbed solition solutions w1,11(t, x) and z1,11(t, x) in equation (50) are depicted for G−1 = 10, G0 = 95, G1 = 27, τ = 0.090, η = τ, σ = 1, ϖ = 5, ν = 0.90, α = 0.2, β = 0.4. In this profile, the fractal pattern is formed due to the axial perturbation of the system along the t-axis.
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the periodic-axially perturbed solition solutions w1,11(t, x) and z1,11(t, x) in equation (50) are depicted for G−1 = 10, G0 = 95, G1 = 27, τ = 0.090, η = τ, σ = 1, ϖ = 5, ν = 0.90, α = 0.2, β = 0.4. In this profile, the fractal pattern is formed due to the axial perturbation of the system along the t-axis.
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed bright kink solition solution w2,3(t, x) and chaotic dark kink soliton solution R2,3(t, x) in equation (55) are depicted for τ = 0.09, σ = 0.04,  aϖ = 0.005, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed bright kink solition solution w2,3(t, x) and chaotic dark kink soliton solution R2,3(t, x) in equation (55) are depicted for τ = 0.09, σ = 0.04,  aϖ = 0.005, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed bright kink solition solution w2,3(t, x) and chaotic dark kink soliton solution R2,3(t, x) in equation (55) are depicted for τ = 0.09, σ = 0.04,  aϖ = 0.005, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the chaotic perturbed bright kink solition solution w2,3(t, x) and chaotic dark kink soliton solution R2,3(t, x) in equation (55) are depicted for τ = 0.09, σ = 0.04,  aϖ = 0.005, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic kink solition solutions w2,6(t, x) and z2,6(t, x) in equation (58) are depicted for τ = 0.09, σ = 0.04, ϖ = 5, ν = 0.70, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic kink solition solutions w2,6(t, x) and z2,6(t, x) in equation (58) are depicted for τ = 0.09, σ = 0.04, ϖ = 5, ν = 0.70, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic kink solition solutions w2,6(t, x) and z2,6(t, x) in equation (58) are depicted for τ = 0.09, σ = 0.04, ϖ = 5, ν = 0.70, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic kink solition solutions w2,6(t, x) and z2,6(t, x) in equation (58) are depicted for τ = 0.09, σ = 0.04, ϖ = 5, ν = 0.70, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic lump-type kink solition solutions w2,7(t, x) and z2,7(t, x) in equation (59) are depicted for τ = 0.09, σ = 0.04, ϖ = 0.5, ν = 0.90, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic lump-type kink solition solutions w2,7(t, x) and z2,7(t, x) in equation (59) are depicted for τ = 0.09, σ = 0.04, ϖ = 0.5, ν = 0.90, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 7 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic lump-type kink solition solutions w2,7(t, x) and z2,7(t, x) in equation (59) are depicted for τ = 0.09, σ = 0.04, ϖ = 0.5, ν = 0.90, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 7 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the perturbed chaotic lump-type kink solition solutions w2,7(t, x) and z2,7(t, x) in equation (59) are depicted for τ = 0.09, σ = 0.04, ϖ = 0.5, ν = 0.90, , , α = 0.2, β = 0.4, M1 = 8, M2 = 3.
Details are in the caption following the image
Figure 8 (a)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed chaotic solition solutions w2,13(t, x) and z2,13(t, x) in equation (65) are depicted for , , .
Details are in the caption following the image
Figure 8 (b)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed chaotic solition solutions w2,13(t, x) and z2,13(t, x) in equation (65) are depicted for , , .
Details are in the caption following the image
Figure 8 (c)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed chaotic solition solutions w2,13(t, x) and z2,13(t, x) in equation (65) are depicted for , , .
Details are in the caption following the image
Figure 8 (d)
Open in figure viewerPowerPoint
The above 3D and contour plots of the axially perturbed chaotic solition solutions w2,13(t, x) and z2,13(t, x) in equation (65) are depicted for , , .

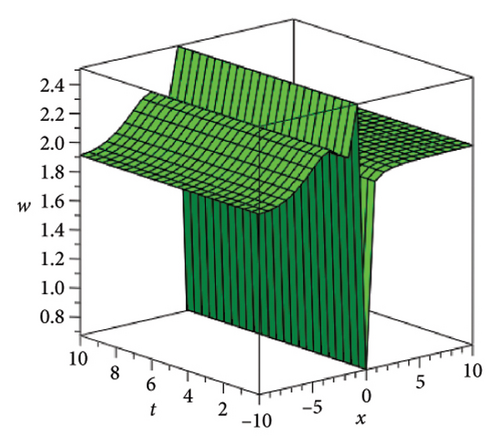
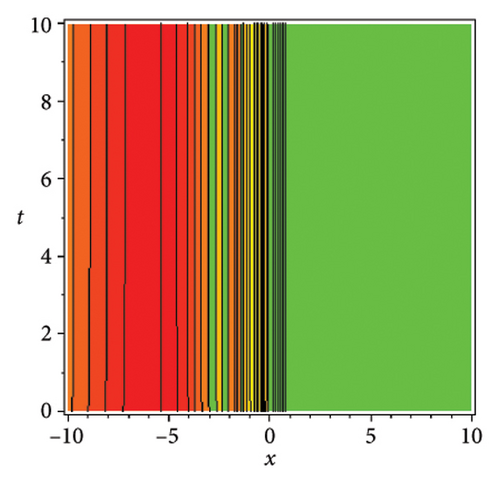
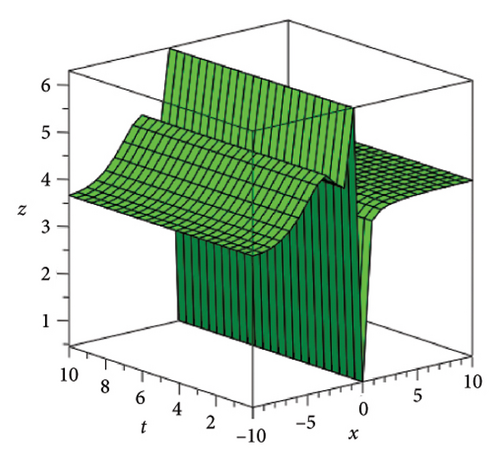
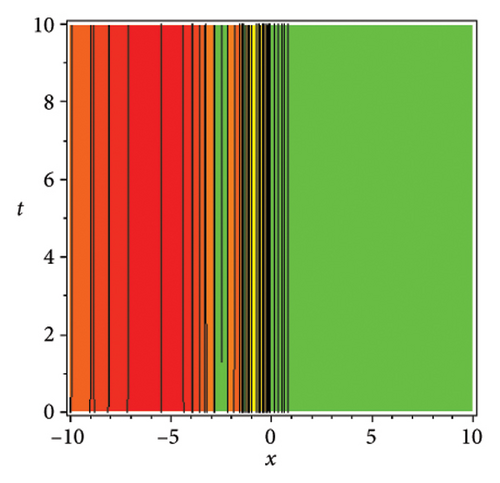
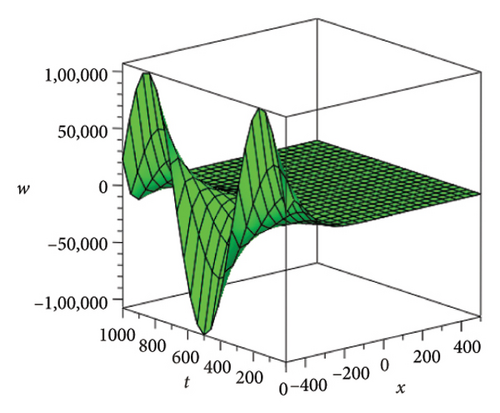
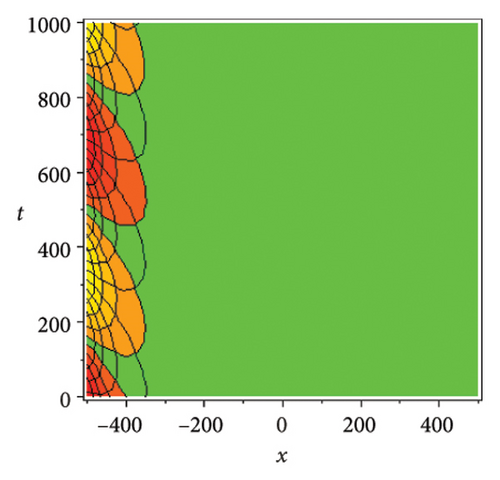
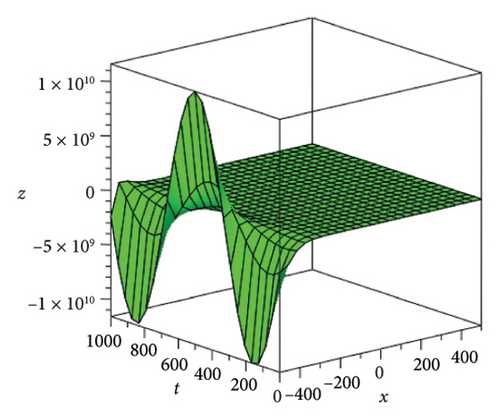
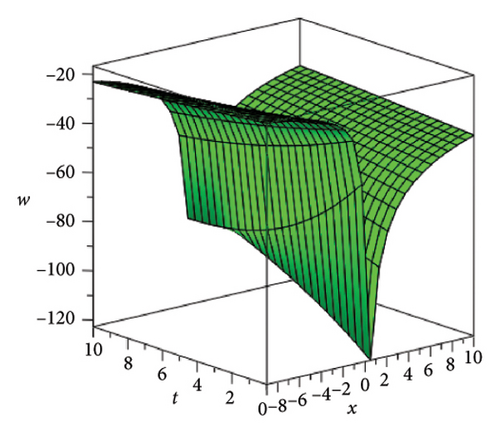
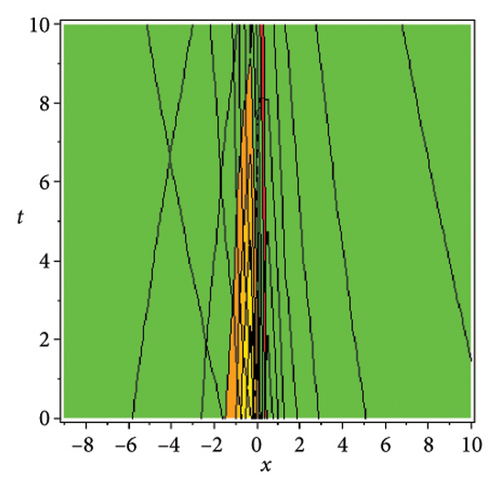
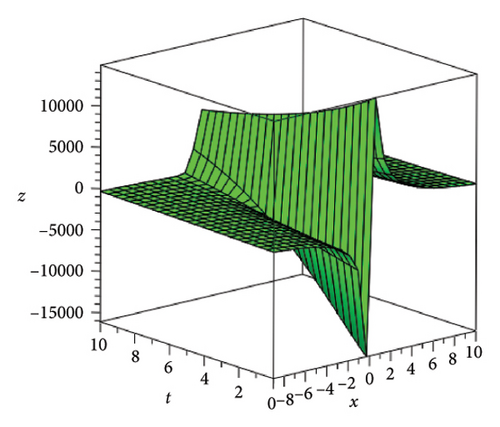
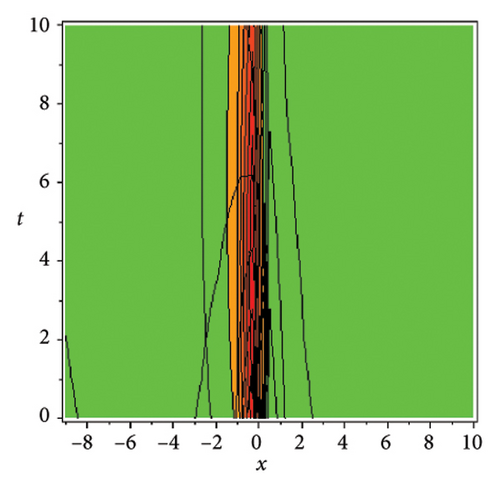
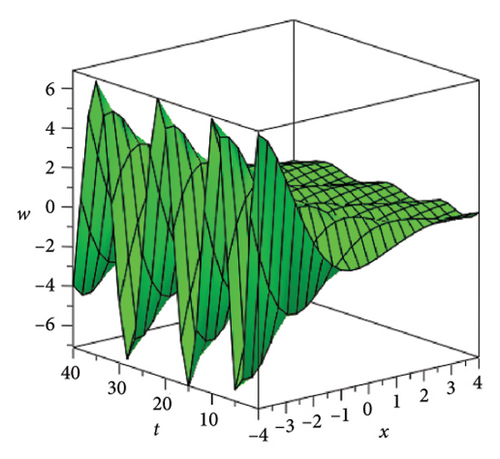
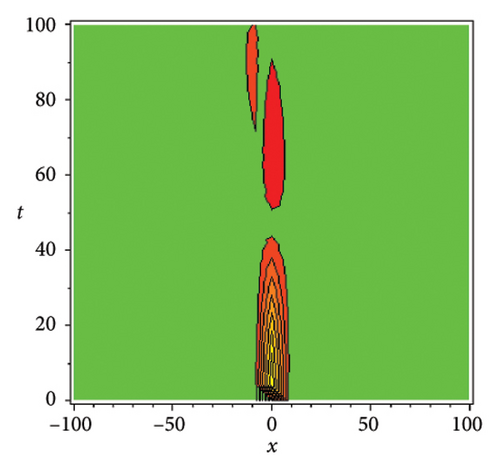
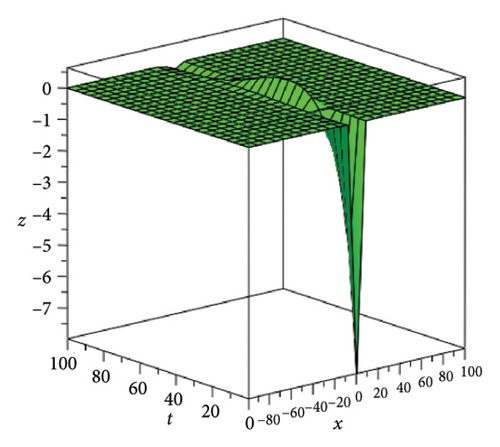
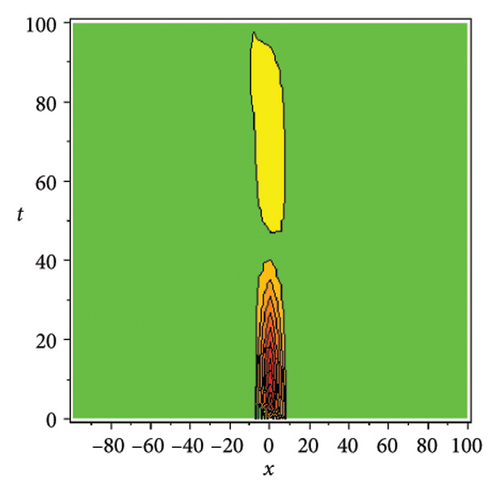
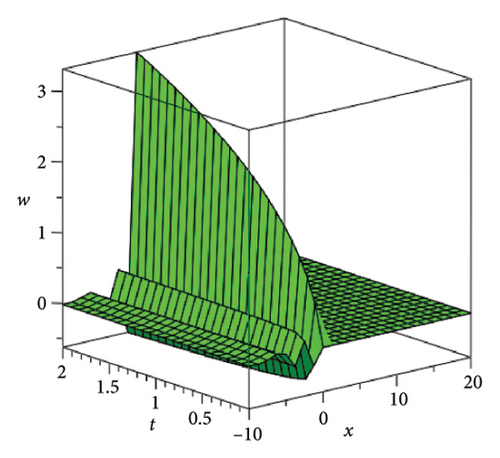
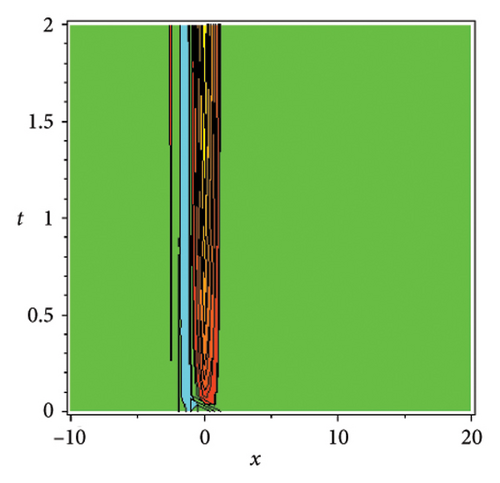
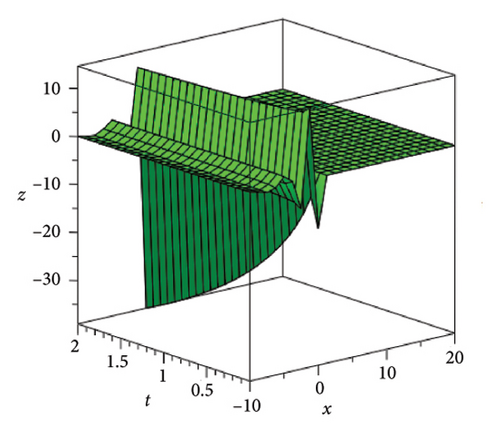
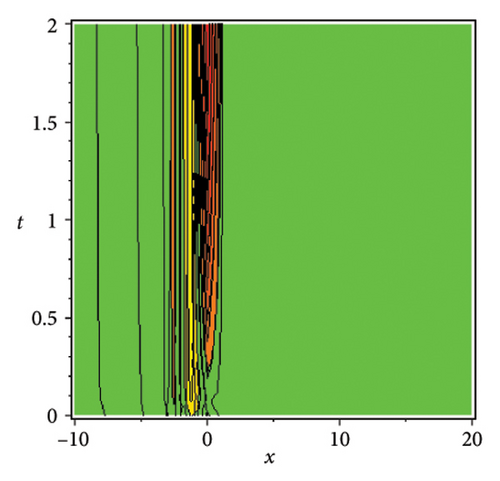
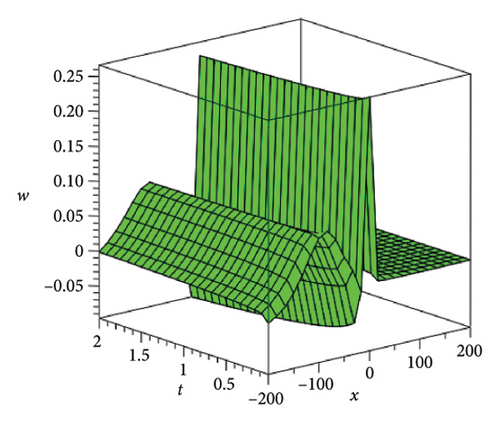
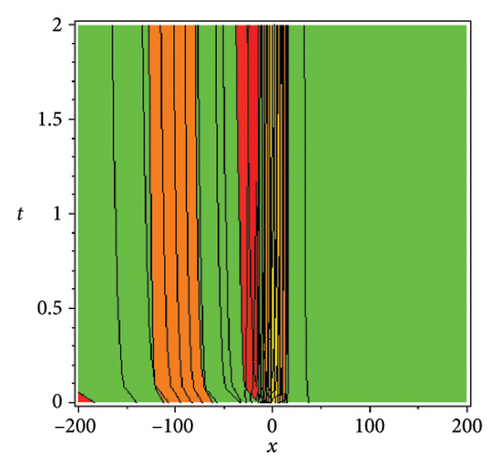
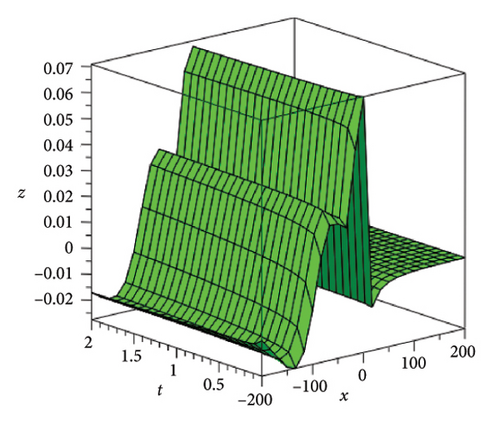
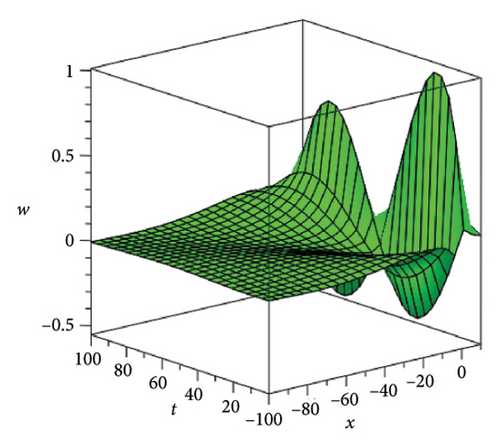
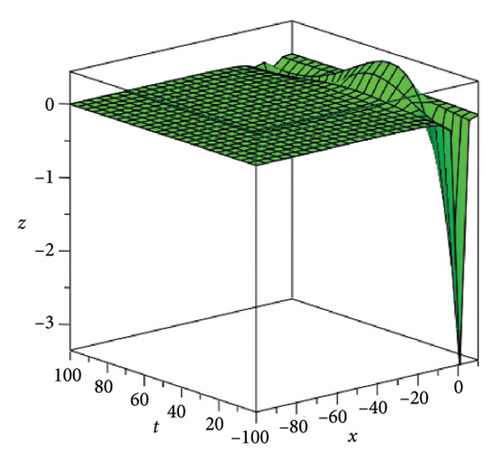
5. Conclusion

In conclusion, we used gBEM to construct and analyze chaotic soliton solutions in the CCHS, a system of NFPDEs that was initially put up as a theoretical framework to explain the dynamics of the Higgs mechanism within the context of electroweak theory, a part of the standard model of particle physics. In order to accomplish this, we utilized gBEM, which extracted NODEs from the CCHS via a fractional complex transformation. A fresh set of soliton solutions was produced when the resultant NODEs were processed using the Maple tool. We were able to graphically represent the behavior of the acquired solitons by using 3D and contour visualizations. Notably, these soliton solutions displayed axial, chaotic, and periodic disturbance, causing instabilities within the soliton and potentially resulting in the construction of fractal environments. The acquired results also indicate many families of soliton solutions with complex dynamics and interrelationships, which is a breakthrough discovery. Our theoretical knowledge of CCHS dynamics is improved by these discoveries, which may possibly have ramifications in domains connected to NFPDEs. Even while the gBEM has significantly improved our understanding of soliton dynamics and how they are applied to the model’s field, it is important to understand its limitations, particularly the proposed gBEM, which fails when the highest derivative term and nonlinear component are not homogenously balanced, as in this case, the soliton cannot be produced due to the imbalance between dispersion and nonlinearity. Notwithstanding this limitation, the present investigation demonstrates that the methodology employed in this work is very effective, reliable, and flexible for nonlinear problems in a variety of natural scientific domains. Moreover, the future objective of this study is to analyze bifurcating and chaotic behavior of the governing model using time series, Lyapunov exponent, phase portrait, and Poincaré map approaches.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

The authors contributed equally and approved the final manuscript.

Funding

This research was funded by the Scientific Research Deanship at the University of Ha’il, Saudi Arabia, through the project number: RG-23 059.

Acknowledgments

This research was funded by the Scientific Research Deanship at the University of Ha’il, Saudi Arabia, through the project number: RG-23 059.

    Data Availability Statement

    All data generated or analyzed during this study are included in this published article.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.