A Robust Biobjective Model for Designing Resilient Supply Chain Networks for Hospitals With Integrated Financial and Physical Flows
Abstract
In today’s volatile environment, supply chain networks, particularly those in hospitals, are increasingly vulnerable to disruptions, emphasizing the need for integrating resilience strategies into their design. However, the implementation of these strategies introduces financial challenges that must be carefully managed. This study addresses gaps in the existing literature by developing a biobjective optimization model that integrates both financial and physical flows to design resilient supply chain networks under demand uncertainty. The proposed three-level network includes primary and backup suppliers, a factory, and distribution centers. Financial resources such as existing capital, bank loans, and trade credit are considered to improve working capital and ensure operational stability. Trade credit terms and repayment schedules are explicitly modeled across all levels of the supply chain. A proactive fuzzy goal programming approach is employed, and the model is solved using the CPLEX solver. Computational experiments using synthetic data are conducted to evaluate the model’s performance. To illustrate the practical application of the model, a case study based on the hospital equipment supply chain at Nantong First People’s Hospital is used. The results show that the selection of backup suppliers is influenced by financial feasibility, and trade credit plays a crucial role in supporting resilience across multiple levels. This study emphasizes the importance of incorporating financial considerations into the design of resilient hospital supply chains and offers valuable insights for policymakers and practitioners seeking to balance resilience with financial performance.
1. Introduction
Designing supply chain networks is a core aspect of management, involving strategic and operational decisions [1]. Given the increasing frequency of uncertainties and disruptions, redesigning supply chain networks to ensure customer demand fulfillment has become a necessity [2]. In the face of fluctuating customer demand and unstable resource supply, effective risk management strategies must be implemented to align disruptions with organizational capabilities and objectives [3]. Supply chain disruptions typically arise from three primary sources: natural disasters, human-induced destructive activities, and widespread pandemics, all of which threaten operational stability [4]. Among the various approaches to managing such disruptions, resilience stands out as a key strategy. Resilience in supply chains refers to the ability to sustain operations and meet customer demands efficiently, cost-effectively, and equitably, even during crises [5].
To enhance resilience, it is crucial to assess the supply chain’s actual and potential capacities, enabling companies to prepare for and respond to disruptions effectively [6, 7]. Proactively anticipating disruptive events, including financial crises, is vital to supply chain network design [8]. Given their vulnerability to such crises, companies must adopt tailored strategies to counter uncertainties and bolster resilience. However, selecting resilience strategies is challenging due to the significant financial implications they impose [9]. The resilience and performance of small and medium-sized enterprises, in particular, are strongly influenced by their financial management capabilities [10]. Achieving sustainable and long-term development of supply chains requires balanced growth across economic, environmental, and social dimensions, along with seamless integration of financial and physical flows [11].
Financial flow, along with the flow of goods and information, is crucial and influential in any supply chain [12]. Therefore, financial flows must be considered in addition to physical flows in supply chain network design. Financial flow exists similarly to physical flow but in the opposite direction. Financial operations complement the physical product flow and ensure financing from supply to customer [13]. Since adopting a resilience approach imposes financial burdens, financing in a resilient supply chain is highly significant. Moreover, integrating financial and logistical decisions improves overall network performance [14].
In the theoretical foundations of the research, financial and physical flows have been modeled separately. Due to their mutual effectiveness, simultaneous optimization of these flows enhances supply chain efficiency [15]. Proper working capital management is vital for SMEs as it reduces the need for external financial resources, such as trade credit and loans. Supplier trade credit for producers and producer trade credit for customers, and considering delays in these payments, ensure proper use of working capital [16].
Material and information flows have been extensively studied in supply chain network design, but financial flows have rarely been addressed. Furthermore, while resilience strategies have been employed in supply chains, their financial burden has not been considered in modeling. Financial resources are essential today for improving supply chains and dealing with disruptions. Companies face the challenge of financing and limited financial resources. Given the above, simultaneous attention to financial and physical flows in supply chain financial planning and financing strategies enhances supply chain resilience against disruptions.
This research addresses the critical issue of designing resilient supply chain networks that balance financial and operational performance under demand uncertainty. The main contribution is the development of a comprehensive biobjective optimization model that integrates financial and physical flows, bridging a significant gap in the literature. Specifically, this study introduces trade credit and financing strategies into the modeling framework to explicitly account for the financial burdens associated with resilience strategies. By focusing on maximizing net present value (NPV) and demand fulfillment, the model provides a holistic approach to decision-making in supply chain network design. This work offers theoretical advancements by incorporating financial constraints and repayment schedules, as well as practical insights for companies dealing with financial constraints and operational uncertainties. The findings contribute to both academic research and industry practices, offering actionable strategies for enhancing supply chain resilience.
2. Literature Review
Despite numerous studies on resilient supply chains, research that simultaneously examines physical and financial flows is scarce. Adopting resilience strategies imposes financial burdens on companies, and integrating financial and physical flows in such models ensures the financing of these strategies. The existing research related to this study can be categorized into resilient supply chains and supply chain financing.
2.1. Resilience Strategy Impacts
In the realm of resilient supply chains, several fundamental studies have made significant contributions. Meena and Sarmah [17] utilized a multisourcing strategy to address the problem of producer allocation among multiple suppliers, taking into account the risk of disruptions. Zahiri et al. [18] examined resilience and sustainability in their multiobjective hybrid model design, using strategies such as multisourcing and node complexity management as resilience strategies. Jabbarzadeh et al. [5] developed a resilient and sustainable supply chain using strategies such as excess production capacity, emergency inventory, and supplier support.
Gholami-Zanjani et al. [19] created a biobjective stochastic model to cover specific features of meat inventory planning. Hasani et al. [20] considered economic, environmental, and reduction strategies for designing a resilient and green supply chain network for medical device manufacturing. Foroozesh et al. [9] explored the design of a resilient green supply chain network for perishable products under disruption risks and cognitive uncertainties, aiming to minimize the impacts of disruptions by employing new strategies, including multisourcing, financial suppliers, horizon collaboration, risk paths, and coverage radius. Habib et al. [8] applied a robust possibilistic programming approach for designing a biodiesel supply chain network. Juan and Li [21] examined the financial performance of companies in supply chains, focusing on dynamic capabilities and supply chain resilience. Li et al. [22] empirically investigated the relationship between business model design, supply chain resilience, and supply chain performance using blockchain technology and data from Chinese companies. Nguyen et al. [10] studied the impact of supply chain financing on supply chain risk, resilience against risk, and the performance of small and medium enterprises in Vietnam’s global supply chains. Taleizadeh et al. [23] designed an optimal sustainable supply chain system considering pricing decisions and resilience factors. Vali-Siar and Roghanian [24] examined the design of a responsive, resilient, and sustainable hybrid supply chain network under uncertainty. Erken et al. [25] investigated how additive manufacturing can contribute to the resilience, profitability, and competitiveness of e-commerce supply chains. Arabi and Alikhani [3] conducted research based on the resource dependence theory to select the best combination of various resilience strategies, examining the positive and negative impacts of these strategies and the dynamics of supply chains.
2.2. Financial Flow Modeling
The integration of financial and physical flows in supply chains has been a subject of growing interest in the literature, particularly in light of the increasing complexity and uncertainty in global supply chains. In the early stages of this research, Nickel et al. [26] laid the foundation for a comprehensive approach to supply chain network design by emphasizing the critical role of financial decisions. They introduced the concept of concurrently planning both financial and physical flows within the supply chain, a challenge that had not been fully addressed by earlier network design models that typically focused on just the physical flow of goods. This shift toward incorporating financial flows was pivotal, as it acknowledged that financial decisions are integral to overall supply chain optimization.
Building on this foundation, Nobil et al. [27] expanded the scope of financial considerations in supply chain design by introducing the role of loans and stakeholder capital in financing factory construction. Their work highlighted the importance of securing appropriate funding sources for supply chain infrastructure, noting that the strategic deployment of financial capital can significantly influence both the operational efficiency and the scalability of supply chains. This shift toward financial integration was further explored by Arani and Torabi [15], who integrated tactical, financial, and physical plans under fuzzy uncertainty conditions. They created a model that captured the interactions between financial resources, production processes, and demand fulfillment, providing a more holistic view of the supply chain. Their work was one of the early attempts to model the uncertainty inherent in financial flows, anticipating the challenges faced by modern supply chains exposed to fluctuating costs and uncertain demand patterns.
As the literature on financial supply chain management evolved, scholars such as Devalkar and Krishnan [28] began exploring the role of trade credit in improving supply chain coordination. Their research demonstrated that trade credit not only serves as a mechanism for financing purchases but also fosters collaboration between suppliers and buyers, thereby enhancing overall supply chain efficiency. The role of financial strategies in managing supply chain costs was further emphasized by Wang and Huang [29], who discussed the importance of budgeting funds for necessary supply chain costs, particularly in the context of capital constraints. Their research illustrated that effective financial planning, including the use of trade credit and loans, could help optimize the flow of goods and capital within a supply chain, ensuring that sufficient resources are available to meet demand and maintain operational continuity.
In addressing supply chain uncertainties, Goli et al. [30, 31] examined the impact of both demand uncertainties and product return rates on supply chain financing. Their work added an important dimension to the financial flow discussion by incorporating the complexities of demand volatility and the challenges associated with managing returned goods, which are critical factors for maintaining liquidity in supply chains. The effect of payment schemes on network design was explored by Tsao et al. [32], who focused on the interactions between external suppliers, distribution centers, and retailers. They demonstrated that payment schemes, specifically timing and terms of payment, have a direct impact on the design and operational efficiency of the supply chain, influencing both supplier relationships and the financial stability of the entire network.
The literature continued to evolve, particularly with the advent of the COVID-19 pandemic, which brought financial and operational disruptions to the forefront of supply chain management. In this context, Sama et al. [33] analyzed the financial and physical flows within supply chains, focusing on optimizing working capital during the pandemic. Their study highlighted the need for supply chains to be adaptable and flexible in their financial planning to cope with unexpected disruptions. Concurrently, Bigler et al. [34] addressed the design of supply chain networks through a mathematical model that maximizes shareholder value by considering both product flows and financial resources. Their approach linked financial decision-making with supply chain network design, underscoring the importance of an integrated approach to supply chain management.
The impact of financial instruments on fresh product supply chains under uncertainty was further studied by Guan et al. [35], who integrated trade credit and loans into a unified optimization model. Their work revealed that combining financial instruments can significantly improve supply chain resilience and performance, particularly when dealing with the inherent uncertainties of fresh product supply chains. A similar approach was taken by Bigler et al. [36], who proposed a mixed-integer nonlinear programming model that incorporated both financial and operational decisions into supply chain network design. Their model explored complex elements such as bank loans, debt repayment, and shareholder capital utilization, providing a comprehensive tool for balancing financial sustainability with operational efficiency.
The use of digital twin frameworks to enhance supply chain resilience was introduced by Badakhshan and Ball [37], who showed that digital twins can be leveraged to reduce the impact of disruptions on both financial and physical flows. Their work demonstrated that a digital twin approach can significantly decrease the cash conversion cycle for upstream supply chain members, improving liquidity and enhancing the overall performance of the supply chain. Rahmanzadeh et al. [13] further expanded this idea by exploring the role of open innovation in integrating financial and physical flows, proposing new pricing mechanisms and innovation-driven product design processes. This approach emphasized the importance of incorporating external innovations into supply chain strategies to boost operational efficiency and financial sustainability.
As resilience became an increasingly critical focus, Razavian et al. [38] proposed a model for resilient and risk-averse supply chains that combined financial and physical strategies to mitigate the impact of disruptions. They introduced several resilience strategies, including multisourcing, emergency inventory, and excess production capacity, and used probabilistic programming to model disruption risks. This work paved the way for future research into combining financial resilience with operational strategies to ensure supply chain stability during crises. More recently, Abbasi et al. [39] advanced the field by proposing a framework for evaluating eco-friendly supply chains and dynamic capabilities that ensure performance amid disruptions. Their findings support the growing need for supply chains to be sustainable and adaptable, integrating financial and operational strategies to mitigate risks and enhance resilience.
Lastly, Umar and Wilson [40] examined the resilience sources for food supply chains, focusing on logistics responses during disruptions caused by natural disasters. Their case studies in South Asia demonstrated the critical role of logistics in enhancing supply chain resilience. Similarly, Jabbarzadeh and Shamsi [41] developed an optimization model that integrates strategic and tactical decisions to plan for resilient and sustainable supply chains, showing that robust optimization methods can result in significant cost savings, demonstrating their superior performance compared to deterministic approaches.
2.3. Research Gaps and Contributions
Despite the significant body of literature on supply chain resilience, financial integration, and trade credit, a critical gap remains in understanding the financial burden imposed by implementing resilience strategies in the supply chain. While existing models often focus on one-sided trade credit, they fail to fully capture the complexities and advantages of a two-sided trade credit model under uncertainty. Devalkar and Krishnan [28] and Guan et al. [35] explored trade credit’s role in improving coordination and resilience, but these studies predominantly use single-sided trade credit, which may not reflect real-world practices where suppliers and buyers play a more active role in financing. By incorporating two-sided trade credit, this study provides a more realistic and comprehensive approach to managing financial flows in supply chains.
Moreover, while prior research has acknowledged using backup suppliers as a key strategy for enhancing supply chain resilience, studies like [15, 32] primarily focus on operational strategies and financial flows separately. The integration of backup suppliers as a strategic component for risk mitigation, alongside primary suppliers, has not been adequately explored. This study uniquely combines operational and financial strategies, proposing an integrated model that includes trade credit for raw material purchases, credit sales of products, and the simultaneous selection of primary and backup suppliers. This approach is designed to provide greater flexibility and risk coverage within the supply chain, particularly during disruptions, and has the potential to deliver more robust outcomes compared to previous models that did not account for these interdependencies.
Additionally, while many studies have employed exact methods or metaheuristic algorithms to optimize supply chain networks (e.g., [26, 38]), there is limited research on the application of fuzzy goal programming (GP) to handle the inherent uncertainties in supply chain operations. Exact methods (e.g., Benders decomposition) often struggle with large, complex problems due to their computational intensity, while heuristic and metaheuristic methods (e.g., Lagrangian relaxation and genetic algorithm) may lack precision when dealing with uncertainties in financial decisions. The use of fuzzy GP in this study allows for the flexible incorporation of multiobjective optimization, considering financial and operational goals under uncertain conditions.
The innovative contribution of this study lies in integrating two-sided trade credit and backup supplier selection in a three-level supply chain network while incorporating budget constraints and trade credit repayment schedules for factories and distribution centers. This model introduces a more nuanced understanding of financial resilience, defined as maintaining operational continuity and meeting demand despite disruptions by ensuring that necessary financial resources are available. Compared to existing approaches, this study provides a more comprehensive and flexible solution, addressing both trade-offs between maximizing demand fulfillment and profitability, which is a challenge not sufficiently tackled in the literature.
3. Methodology
In this section, the research problem and the mathematical model are first outlined. Following a detailed explanation of the solution method, the mathematical model will be examined under uncertainty conditions. To validate the mathematical model, a sample example is provided and solved using GAMS software.
3.1. Problem Definition
Adopting a resilient approach in supply chains and all production systems and businesses is paramount today. Resilience ensures that systems can always meet customer needs in the event of disruptions. Major disruptions typically occur at the primary level of the supply chain, i.e., the suppliers. If a supplier experiences disruptions in providing raw materials to manufacturers, it can destabilize the entire network, resulting in unfulfilled customer demands and significant dissatisfaction within the supply chain. This is because all decision-making processes are based on customer demand.
While resilience has been explored in various studies, the financial burden imposed by resilience strategies to counteract disruptions has often been overlooked. This research addresses this issue by incorporating financial considerations into resilience strategies.
The problem addressed in this study involves the design of a resilient and financially viable supply chain network that can effectively respond to disruptions and uncertainties in demand. The goal is to simultaneously optimize the physical flow of materials (raw materials, products) and the financial flow (trade credit, loans) in a supply chain while considering real-world constraints, such as operational capacities, financial limits, and supplier disruptions.
The supply chain consists of several key elements, including suppliers, factories, distribution centers, and trade credit providers. Suppliers provide raw materials to the factory, which manufactures products that are then distributed to customers via distribution centers. Trade credit, an essential financial resource in supply chains, facilitates purchases of raw materials from suppliers and products from the factory.
The mathematical formulation is designed to capture the trade-off between demand fulfillment and financial sustainability. Specifically, it integrates operational decisions (such as supplier selection and product manufacturing) with financial decisions (including trade credit allocation and repayment). The objective is to maximize the NPV of the supply chain while ensuring that demand is met under uncertainty. Furthermore, the model incorporates resilience strategies, such as the selection of backup suppliers to mitigate disruptions in the supply of raw materials.
Figure 1 depicts the schematic of the modeled supply chain, which is inspired by [42]. The mathematical model is multiperiod and multiproduct, and the Bertsimas and Sim method is used to model demand uncertainty.
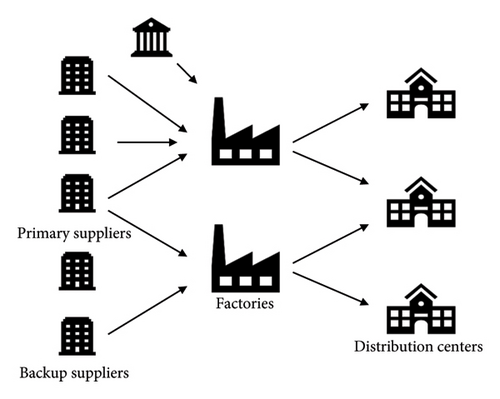
3.1.1. Model Assumptions
- •
Demand in the model is considered uncertain.
- •
All decisions are executable instantly.
- •
Primary suppliers may experience disruptions, but backup suppliers remain unaffected.
- •
Suppliers and factories allocate trade credit for purchasing raw materials and products for factories and distribution centers.
- •
Trade credit is modeled according to the open account or net period financing method, which sets an allowable delay period for trade credit repayment. If repayment occurs before this period ends, no penalty is incurred; if the allowable period is exceeded, repayment must include a specified penalty.
- •
Each operational period is divided into three stages.
- •
Any established factory can take out a loan in the first period (this loan can be made available to the factory at the end of the first stage of the first time period).
- •
Each established factory is considered a fixed asset throughout the planning horizon, with depreciation calculated using the sum-of-years-digits method.
- •
The inventory of raw materials and the value of remaining raw materials are not considered.
- •
The supply chain network design model accounts for tax rates and inflation rates.
- •
Loan capital can be paid without cost, but it must be repaid before the end of the planning horizon.
These assumptions reflect practical considerations for real-world applications. Fixed factory depreciation methods, such as the sum-of-years-digits approach, provide a systematic and accelerated allocation of asset costs, aligning with financial reporting standards and tax regulations. Zero inventory assumptions simplify the model while emphasizing the need for just-in-time practices, which are widely adopted in modern supply chain systems to reduce holding costs and improve efficiency. These assumptions create a realistic foundation for analyzing financial and operational trade-offs in supply chain resilience.
3.2. Proposed Mathematical Model
In the following, first, the sets, parameters, and variables are used in the mathematical model of the problem. Next, the objective functions and constraints of the proposed mathematical model are provided.
3.2.1. Sets and Indices
- •
S Set of suppliers with index s = 1, …, S s ∈ S
- •
J Set of distribution centers with index j = 1, …, J j ∈ J
- •
I Set of raw materials with indexes i = 1, …, I i ∈ I
- •
V Set of products with index v = 1, …, V v ∈ V
- •
T Set of periods with index t = 1, …, T t ∈ T
- •
L Set of backup suppliers with index l = 1, …, L l ∈ L
- •
F Set of specifying the type of purchase (cash or credit) with index f ∈ F
- •
N Set of potential factory locations with index n = 1, …, N n ∈ N
3.2.2. Parameters
- •
dvjt: Demand of product v by the distribution center j during period t (units of product per period)
- •
asst: Supplier capacity s during period t (units of raw material per period)
- •
αvnvnt: Production capacity for product v in factory n during period t (units of product per period)
- •
: Backup supplier capacity l of raw materials i during period t (units of raw material per period)
- •
α: Continuous compound interest rate to calculate NPV (in decimal form)
- •
R: Loan interest rate (in decimal form)
- •
θ: Inflation (in decimal form)
- •
Tax: Tax rate (in decimal form)
- •
icc: Initial capital available in the first period for building factories and carrying out production operations (monetary units)
- •
L: The maximum loan amount available in the first period for building factories and carrying out production operations (monetary units)
- •
Rsis Interest rate for late repayment of commercial credit that the supplier s has paid and for the purchase of raw materials i (in decimal form)
- •
Rlil: Interest rate for late repayment of commercial credit that the supplier l has paid for the purchase of raw materials i (in decimal form)
- •
IN − nvnv: Penalty interest rate for late repayment of trade credit that factory n has paid for product v (in decimal form)
- •
Ois: The maximum amount of commercial credit that the supplier s has played to buy raw materials i (monetary units)
- •
OLilt: The maximum amount of commercial credit that the supplier l has paid during the t to buy materials i (monetary units)
- •
Zvnt: The maximum amount of commercial credit that the factory n has paid during period t to sell the product i (monetary units)
- •
φis: Allowed delay in repayment of trade of supplier s for material i (time periods)
- •
φlls: Allowable delay in refunding trade credit to supplier s which is for the purchase of raw materials i (time periods)
- •
βnv: Allowable delay in repaying trade credit to factory n for the purchase of the product v (time periods)
- •
γn: The life time of the factory n (time periods)
- •
δn: Factory scrap value in place n (monetary units)
- •
pisn: The price of raw materials i that factory n pays to supplier s (monetary units)
- •
ppvnj: Price of product v which the distribution center j pays to the factory n (monetary units)
- •
pliln: Price of raw materials i that factory n pays to supplier l (monetary units)
- •
cnn: Fixed cost for setting up a factory on factory n (monetary units)
- •
: Production cost for a unit of product v (monetary units)
- •
: Inventory holding cost for a unit of product v (monetary units)
- •
: Shipping cost of product v from factory n to the distribution center j (monetary units)
- •
aiviv: The amount of raw materials i which to consumed to produce a product v (units of raw material)
- •
deltsst: The percentage that the main supplier s cannot supply raw materials in period t (in decimal form)
- •
Gsst: Disruption for the main supplier in the period t (in decimal form)
- •
ICnt: The amount of money left in the factory n at the end of period t
- •
B: A large number
3.2.3. Decision Variables
- •
Yn: A binary variable and equal to 1 if a factory is established at location n; otherwise 0
- •
xss: A binary variable and equal to 1 if the supplier s is selected; otherwise 0
- •
ICOn: The amount of initial capital to the factory n that is allocated at the beginning of the first period.
- •
xll: A binary variable and equal to 1 if the supplier l is selected; otherwise 0
- •
QMisntf: Amount of raw materials i that supplier s buys from factory n during period t in the form of f (cash/credit)
- •
TCisnt: The amount of trade credit that the supplier s gives to factory n to buy raw materials i during period t
- •
PTisnψt: The amount of trade credit repayment to the supplier s has paid in period ψ to the factory n to buy raw materials i in period t
- •
Qlnlnfit: Amount of raw materials i that supplier l buys for the factory n during period t in the form of f (cash/credit)
- •
TRilnt: The amount of trade credit that the supplier l gives to factory n to buy raw materials i during period t
- •
PRilnt: The amount of trade credit repayment to the supplier l in period ψ to pay to the factory n in period t.
- •
: Quantity of product v that factory n produces during period t
- •
: Level of inventory of product v in factory n at the end of period t
- •
SCvnjt: The amount of trade credit that factory n gives to the distribution center j to buy the product v during period t
- •
L − Kn: Amount of loan to the factory n in the first period
- •
STvnjψt: Amount of trade credit repayment to the factory n during period ψ to pay to distribution center j in period t
- •
: Operating cost for the factory n during period t
- •
: Tax cost for the factory n during period t
- •
Πnt: Taxable income for the factory n during the t
- •
PRnt: A payment for the principal of the loan received by the factory n in the first period
- •
IIn: A payment for the loan interest received by the factory n in the first period
- •
: Quantity of product v which distribution center j buys from the factory n during period t in the form of f (cash/credit).
The objective functions of the mathematical model are presented in Constraints (1) and (2). The first objective function aims to maximize the NPV of shareholders’ equity at the end of the planning horizon, and the second objective function aims to maximize demand fulfillment.
- 1.
Cash Remaining in Factories: This component represents the cash left in factories at the end of the planning horizon. Given that the model spans multiple periods, the cash remaining in the factories at the end of the final period is the sum of the remaining cash from the previous period, cash revenue from sales, repayment of trade credit received by the factory, minus the total repayment of trade credit obtained from the primary and backup suppliers, operational costs, taxes, and the principal and interest of loans.
- 2.
Value of Finished Goods Inventory: This component represents the value of the inventory of finished goods at the end of the planning horizon. For simplicity, the inventory value is calculated by multiplying the inventory of finished goods by the unit production cost, which is a model parameter. The unit production cost is thus considered the value of one unit of finished goods inventory.
- 3.
Cost of Establishing a Factory Minus Depreciation: This component represents the cost incurred in establishing a factory minus the total depreciation of the factories over the planning horizon, calculated using the sum-of-years-digits method. The cost of establishing the factory is considered the factory’s value, from which depreciation is subtracted, and the remaining value of the established factory is maximized in the objective function.
- •
Stage 1: Incoming Cash Flow: Cash carried over from the previous period and loans.
- •
Stage 2: Incoming Cash Flow: Cash revenue from sales and repayment of trade credit by distribution centers to the factories.
- •
Outgoing Cash Flow: Costs for establishing the factory (only in the first period), production costs, inventory, transportation, and repayment of trade credit to suppliers.
- •
Stage 3: Outgoing Cash Flow: Payments for loan principal and interest, as well as tax payments.
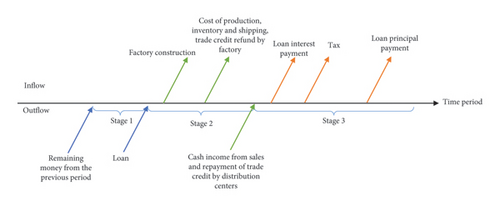
4. Solution Method
GP is widely used to address multiobjective optimization problems. In traditional GP, decision-makers set specific aspiration levels or goals for each objective function and seek to minimize deviations from these goals. However, in practical scenarios, uncertainty often makes it challenging to establish fixed target values. The fuzzy set theory has been effectively applied to decision-making in uncertain circumstances to address this issue. Combining fuzzy set theory with GP results in fuzzy goal programming (FGP), which is a more adaptable approach for dealing with uncertain goals.
A recent advancement in this area is preventive fuzzy goal programming (PFGP), introduced by Mirzace et al. [43]. This method builds upon FGP by incorporating varying levels of importance and priority for different goals. Unlike earlier methods that required a fixed lower bound for goal achievement, PFGP allows for a more nuanced approach by prioritizing goals. This means that achieving a minimum degree of success for a less critical goal does not compromise the overall achievement of more important goals. PFGP integrates these priorities into the model through priority constraints, making it suitable for multiobjective problems where goals vary in importance and are subject to uncertainty.
- •
μ0: Degree of goal achievement
- •
U0: Upper bound of resilience for the goal
- •
L0: Lower bound of resilience for the goal
- •
: Positive deviations from the expected level
- •
: Negative deviations from the expected level
- •
go0: Expected goal of the objective function.
Equations (35)–(42) represent the system constraints, and fo denotes the objective function o.
4.1. Evaluating the Model Under Uncertainty
Recent developments in robust optimization techniques have provided effective solutions for managing data uncertainty. These methodologies focus on identifying solutions that balance optimal performance with feasibility under fluctuating conditions. Robust optimization prioritizes solutions that maintain stability and reliability by allowing slight deviations in objective values to handle uncertainties effectively [44].
Robust optimization models generally fall into two categories. The first category targets optimizing performance under worst-case scenarios, ensuring acceptable outcomes even in extreme conditions. The second category defines robustness through predefined criteria, evaluating whether solutions meet these criteria under different scenarios [45, 46].
In the robust optimization framework, the uncertain parameters are assumed to belong to a specified uncertainty set. The Bertsimas and Sim approach introduces a parameter Γ, which controls the solution’s conservatism level [45].
In the mathematical model of this research, the parameters for demand and disruption levels in the primary supplier are subject to uncertainty, which is addressed using the Bertsimas and Sim method to formulate their robust equivalents. Considering that these parameters impact constraints (11), (2), and (28), the robust counterparts are formulated in equations (56)–(59).
The robust optimization method by Bertsimas and Sim allows for the control of uncertainty through the introduction of specific variables and parameters. This methodology ensures that the solutions remain viable even under uncertain conditions.
- •
μ: Dual variables associated with the initial linear optimization constraints.
- •
Γ: The number of uncertain coefficients deviating from their nominal values.
- •
λ: Dual variables associated with the initial linear optimization constraints.
- •
p: The percentage of disruption affecting the parameters.
The robust optimization framework is particularly advantageous in scenarios characterized by high levels of uncertainty. By employing the Bertsimas and Sim method, the mo32del accounts for potential variations in demand and supplier disruptions, ensuring that the solutions are resilient and reliable. This approach is essential for practical decision-making in supply chain management, where parameters can often be unpredictable.
The use of robust optimization techniques in this research highlights the importance of addressing uncertainty in mathematical modeling. It provides a structured way to ensure that the solutions are optimal and robust against potential disruptions and fluctuations in key parameters.
5. Numerical Results
This section presents the numerical results and validation of the mathematical model through a case study based on the hospital equipment supply chain at Nantong First People’s Hospital. The supply chain under consideration includes two suppliers, two backup suppliers, two potential factory locations, and two distribution centers, spanning a planning horizon of five periods. The demand at the distribution centers ranges from 25 to 40 units per period. Based on historical data and prior experience, the average demand is allocated to the factories and suppliers to determine their capacity parameters. Specifically, supplier capacities range from 100 to 110 units, while factory capacities vary from 120 to 130 units.
The fixed costs associated with establishing factories are calculated based on their respective capacities using ∑v∈V αvnvnt, where γ0 and γ1 are set to 5000 and 25, respectively. These fixed costs are then averaged and denoted as U0, representing the average fixed cost for factory establishment. The transportation cost is calculated by multiplying the distance between suppliers and factories, as well as between factories and distribution centers, by 5% of U0, reflecting the cost of transporting goods within the network.
The problem is solved using GAMS software and the CPLEX solver, applying PFGP method. The model assumes that μ1 ≥ μ2, with the first objective achieving a value of 264.959873 and the second objective reaching 0.809. The deviation values for the first objective are and . Based on these results, Backup Supplier 2 and Primary Suppliers 1 and 2 are selected to fulfill the factory’s production needs, and Factory n2 is established within the supply chain network.
To effectively address the problem, it is crucial to determine the boundaries of the objective functions and assess any potential conflicts between them. This analysis in Table 1 provides valuable insights into the trade-offs involved in optimizing multiple objectives simultaneously. In particular, the trade-off between maximizing demand fulfillment and profitability becomes evident. As the demand fulfillment level increases, additional costs are incurred, such as repayments on trade credit obtained from suppliers, operational expenses, taxes, and interest payments on loans. Consequently, unless the additional revenue from meeting increased demand outweighs these rising costs, profitability declines. Therefore, careful consideration of these competing objectives is essential for achieving an optimal balance in the supply chain.
| ENPV optimization | EFR optimization | |
|---|---|---|
| ENPV value | 977,545 | 619,771 |
| EFR value | 805 | 835 |
Table 2 shows the amount of raw materials transferred from the backup supplier l2 to factory n2. The first row of this table indicates the total amount of raw material i2 transferred from supplier s1 to factory n2 in Period 3.
| Type of purchase | Period | Factory | Backup suppliers | Raw materials | ||||
|---|---|---|---|---|---|---|---|---|
| Credit | Cash | n2 | n1 | l2 | l1 | i2 | i1 | |
| 138 | 0 | 3 | ✓ | ✓ | ✓ | |||
| 140 | 0 | 4 | ✓ | ✓ | ✓ | |||
Table 3 presents the quantity of raw materials transferred from suppliers to the factory. The first row of this table shows the total amount of raw material i1 transferred from supplier s2 to factory n1 in all periods.
| Type of purchase | Period | Factory | Backup suppliers | Raw materials | ||||
|---|---|---|---|---|---|---|---|---|
| Credit | Cash | n2 | n1 | Credit | Cash | n2 | ||
| 3.1 | 315.2 | 1 | ✓ | ✓ | ✓ | |||
| 9.2 | 117 | 2 | ✓ | ✓ | ✓ | |||
| 6.1 | 0 | 3 | ✓ | ✓ | ✓ | |||
| 3.1 | 201.3 | 4 | ✓ | ✓ | ✓ | |||
Table 4 presents the quantities of products that are transferred from the factory to distribution centers. The first row of this table indicates the total amount of product v1 that is transported from factory n2 to distribution center j1 across all periods.
| Type of purchase | Period | Distribution centers | Factories | Product | ||||
|---|---|---|---|---|---|---|---|---|
| Credit | Cash | j2 | j1 | n2 | n1 | v2 | v1 | |
| 0 | 134 | 1 | ✓ | ✓ | ✓ | |||
| 32.7 | 103.6 | 2 | ✓ | ✓ | ✓ | |||
| 0 | 120 | 3 | ✓ | ✓ | ✓ | |||
| 38.1 | 105.2 | 4 | ✓ | ✓ | ✓ | |||
Table 5 encompasses the amounts related to trade credits and the repayments of these credits, which the factories received from suppliers for purchasing raw materials. Regarding the scheduling of trade credit repayments between the backup supplier and the factory, it can be noted that in Period 3, an amount of 138 units was received, and the repayment was made one period later without incurring any penalties. Similarly, in Period 4, an amount of 140 units was received, and the repayment was also made in the following period. Since the allowable delay period for repaying trade credits received from suppliers is set to one period, most repayments were made after one period without any late payment penalties being applied. However, rows 2, 1, and 7 of Table 5 include penalties.
| TC | PT | Period | Factory | Supplier | Raw material | ||||
|---|---|---|---|---|---|---|---|---|---|
| Payment | Refund | n2 | n1 | s2 | s1 | i2 | i1 | ||
| 30.3 | 42.3 | 1 | 3 | ✓ | ✓ | ✓ | |||
| 36.4 | 51.2 | 1 | 3 | ✓ | |||||
| 32.8 | 34.1 | 2 | 3 | ✓ | ✓ | ||||
| 32.5 | 31.7 | 4 | 5 | ||||||
| 30.3 | 30.4 | 1 | 2 | ✓ | ✓ | ||||
| 34.7 | 37.7 | 2 | 3 | ✓ | |||||
| 36.2 | 48.3 | 1 | 3 | ✓ | ✓ | ✓ | |||
Table 6 presents the amounts related to trade credits and their repayments, which distribution centers received for purchasing products from suppliers. The schedule for repaying these trade credits is provided in Table 6. Since the allowable delay period for repaying the trade credits received from the factories is set to one period, all repayments were made in the final period. Given that part of the model’s objective function is to maximize cash on hand at the end of the planning horizon in the factories, this repayment schedule aligns with the goal of maximizing the model’s objective function. Finally, an illustrative form of the results of the mathematical model is provided in Figure 3.
| SC | ST | Period | Distribution center | Factory | Product | ||||
|---|---|---|---|---|---|---|---|---|---|
| Payment | Refund | j2 | j1 | n2 | n1 | v2 | v1 | ||
| 101,705 | 17,053 | 2 | 5 | ||||||
| 10,764 | 14,013 | 3 | 5 | ✓ | ✓ | ✓ | |||
| 10,211 | 10,211 | 4 | 5 | ||||||
| 11,570 | 19,670 | 2 | 5 | ||||||
| 11,870 | 15,490 | 3 | 5 | ✓ | ✓ | ✓ | |||
| 11,128 | 11,128 | 4 | 5 | ||||||
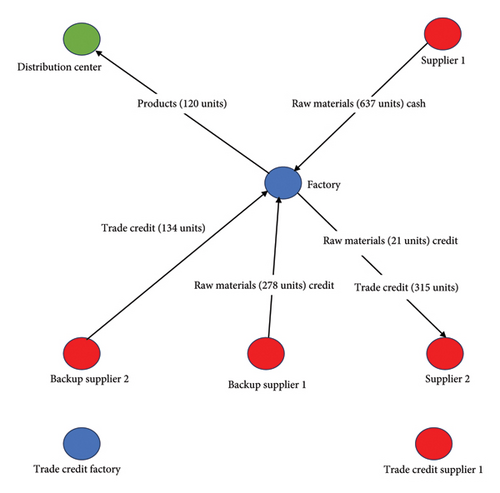
Figure 3 visualizes the supply chain model, showing the flow of raw materials, products, and trade credit among key components such as suppliers, factories, and distribution centers. The arrows in the diagram represent the direction of flow, with labeled quantities indicating the amounts being shipped between the entities. Specifically, it shows that 637 units of raw materials are shipped from Supplier 2 to Factory in cash, 21 units are shipped from Supplier 1 to Factory on credit, and 278 units are shipped from Backup Supplier 1 to Factory on credit. Additionally, the Factory to Distribution Center flow includes 120 units of products. The diagram also highlights the financial flows, such as 315 units of trade credit from Trade Credit Supplier 1 to Factory and 134 units of trade credit from Factory to Distribution Center. This visualization helps trace the quantities of materials and products being transported, as well as the associated financial transactions, providing insights into the optimal decision-making process for managing supply chain operations.
5.1. Sensitivity Analysis
In this section, the parameters under uncertainty conditions are analyzed. The percentage changes in demand are between 0 and 1, and the uncertainty control parameter is also between 0 and 1. According to Table 7, as the impact of uncertainty increases, the objective function values deteriorate. In the proposed model, various parameters Γ directly influence the decision variables. One method to determine the value of these parameters is to solve the model multiple times for each Γ value and select the best option that offers better consistency and fit. Another method for selecting these parameters is the stochastic programming approach. In this study, the first method was employed, and the different values of Γ were obtained, as shown in Table 7.
| Γd − ΓGS | 0.0 | 0.2 | 0.3 | 0.4 | 0.5 |
|---|---|---|---|---|---|
| Γd − ΓGS | 0.0 | 0.2 | 0.3 | 0.4 | 0.5 |
| Per | Z2 | ||||
| 0.0 | 0.819 | 0.829 | 0.83 | 0.245 | 0.83 |
| 0.1 | 0.819 | 0.795 | 0.776 | 0.762 | 0.745 |
| 0.2 | 0.819 | 0.762 | 0.735 | 0.703 | 0.765 |
| 0.3 | 0.819 | 0.730 | 0.691 | 0.431 | 0.609 |
| 0.4 | 0.819 | 0.693 | 0.679 | 0.583 | 0.532 |
| 0.5 | 0.819 | 0.667 | 0.604 | 0.523 | 0.452 |
| 0.6 | 0.819 | 0.637 | 0.562 | 0.461 | 0.385 |
| 0.7 | 0.819 | 0.603 | 0.517 | 0.409 | 0.304 |
| 0.8 | 0.819 | 0.573 | 0.472 | 0.341 | 0.239 |
| 0.9 | 0.819 | 0.531 | 0.432 | 0.284 | 0.169 |
| 1 | 0.819 | 0.521 | 0.38 | 0.231 | 0.089 |
| Γd − ΓGS | 0.0 | 0.2 | 0.3 | 0.4 | 0.5 |
| Per | Z1 | ||||
| 0.01 | 959,292 | 959,292 | 959,292 | 959,292 | 959,292 |
| 0.1 | 951,044 | 942,792 | 934,549 | 926,302 | 918,054 |
| 0.2 | 942,797 | 926,302 | 909,807 | 893,312 | 876,817 |
| 0.3 | 934,549 | 909,807 | 885,064 | 860,321 | 835,579 |
| 0.4 | 926,302 | 893,312 | 860,321 | 827,331 | 794,341 |
| 0.5 | 918,054 | 876,817 | 835,579 | 794,341 | 753,104 |
| 0.6 | 909,807 | 860,321 | 810,836 | 761,351 | 711,866 |
| 0.7 | 901,559 | 843,826 | 786,094 | 728,361 | 670,628 |
| 0.8 | 893,312 | 827,331 | 761,351 | 695,371 | 629,391 |
| 0.9 | 885,064 | 810,836 | 736,609 | 662,381 | 588,153 |
| 1.0 | 876,817 | 794,341 | 711,866 | 629,391 | 546,915 |
As shown in Figure 4, the deterioration of the results (a decrease in the values of the first and second objectives) occurs with an increase in the uncertainty budget. This deterioration exceeds the percentage of the allowable deviation from the nominal value (Per), as a larger range for the uncertain parameter results in higher penalties being applied, ultimately leading to worse outcomes.
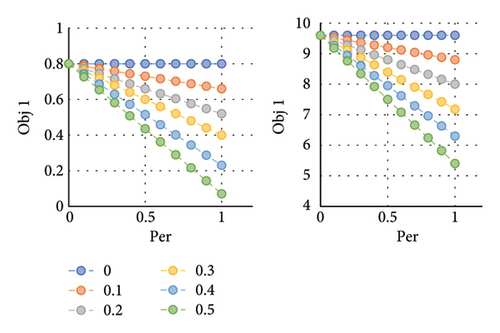
Figure 5 clearly illustrates the deterioration of results as the uncertainty budget and the percentage deviation from the nominal value increase. In this context, supply chain network management plays a crucial role, particularly in decision-making related to the level of risk and the consideration of uncertainty. If a manager chooses to partially or entirely disregard uncertainty, they are essentially accepting the associated risk. The extent to which uncertainty is disregarded and the level of risk assumed varies depending on the management approach and risk tolerance.
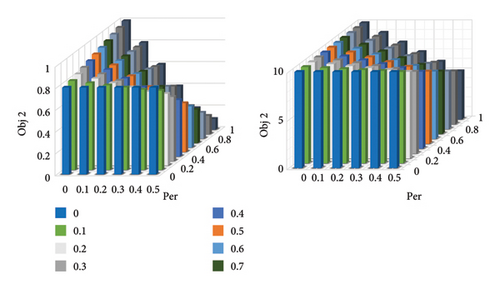
Based on the results in Table 7 and the corresponding graphs, if the level of uncertainty is at its maximum, the outcome using the Bertsimas and Sim method is at its minimum. Conversely, if one of these values is zero, the result matches the deterministic model. For example, according to Table 7, if the allowable deviation (Per) is 20%, the uncertainty level (Γ) is reduced from 0.3 to 0.2, the second objective increases from 0.777 to 0.792, and the first objective increases from 934,549.21 to 942,796.73. However, this increase occurs at the cost of disregarding some level of uncertainty. Similarly, as the level of uncertainty decreases, customer demand satisfaction and profit margins increase.
In this scenario, the manager must make a final decision regarding the acceptance of the level of uncertainty and the costs associated with risk-taking based on supply chain network strategies. This decision ultimately allows for an accurate estimation of the objective function related to profit and system demand. Therefore, as uncertainty increases, the information needed to estimate the objective functions accurately is lost, leading to better results. However, these results are more detached from reality and involve higher risk.
In the design of supply chain networks, demand is one of the key parameters in the mathematical model. This section increases the demand parameter by 10%–30% of the initial value. The results of this analysis are shown in Figure 6.
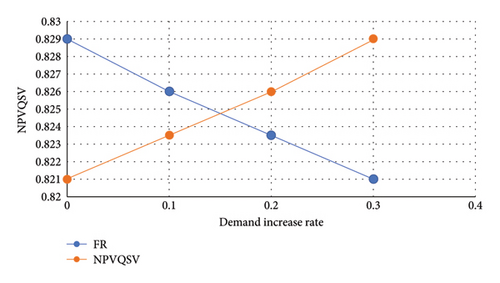
As shown in Figure 6, with an increase in demand within the defined range, the value of the objective function representing the NPV of shareholders’ equity at the end of the planning horizon (NPVQSV) increases, while the objective function related to demand estimation for customer satisfaction decreases. Since the supply chain network in this study is designed with limited capital, the objective function for demand estimation to satisfy customers was initially met at a level of 0.824 due to the shortage of financial resources. With the increase in demand, while keeping other model parameters constant, the available financial resources can satisfy an even smaller portion of customer demand.
To assess the impact of the backup supplier’s trade credit as an internal financing source for product manufacturing, the trade credit parameter from the backup supplier was increased from 10% to 60% of its initial value. The results of this analysis are presented in Figure 7.

As shown in Figure 7, increasing the trade credit provided by the backup supplier to the factory for purchasing raw materials frees up the existing financial resources previously allocated for raw material procurement, allowing them to be redirected toward other production costs. Consequently, production levels and the objective function related to demand estimation increase. However, the increase in costs leads to a reduction in profits. Meeting demand and maintaining market share are critical for businesses operating within the supply chain. Effective supply chain management aims to ensure profitability for all members, achieved through coordination and collaboration among them.
In the present study, the demand estimation achieved is 0.824, indicating that part of the demand was not met, potentially leading to customer dissatisfaction. If demand increases, supply chain managers must coordinate with suppliers to ensure its fulfillment, a necessity that hinges on securing adequate financing. As a financial resource, trade credit fosters coordination among supply chain members by linking their financial positions, thus preventing financial shortages. Given that financial flows support the physical flows and operations of the supply chain, using trade credit and loans, along with involving a backup supplier, helps address the budget constraints faced by the supply chain.
The results indicate that the quantity of raw materials provided to the factory by the backup supplier was zero in cash but 278 units on credit. This amount would not have been supplied without the backup supplier, leading to shortages and customer dissatisfaction. On the other hand, 21 units were supplied on credit and 637 units in cash by the primary supplier to the factory. This demonstrates the significance of considering financial flows alongside physical flows when making decisions about transferring physical goods from one tier to another.
Moreover, uncertainty in today’s business environment is inevitable, and managers must secure their businesses by adopting a supply chain perspective and utilizing appropriate financial and operational strategies. Employing a robust approach allows managers to realistically assess the impact of risk and uncertainty on the objective functions and manage risk coverage accordingly. The results show that managers who disregard uncertainty are essentially accepting the associated risk. The degree to which uncertainty and risk are disregarded will vary depending on the management style and risk tolerance. If the level of uncertainty is at its highest, the outcome of the Bertsimas and Sim method is at its lowest, and if any of these values is zero, the result matches that of the deterministic model. When the primary supplier faces disruptions, the backup supplier is utilized to meet the objective functions, with the financial burden being covered through credit purchases of raw materials. Additionally, the analysis shows that the factory’s trade credit decreases with delays in repayment, and with an increase in interest rates, the penalty for delays increases.
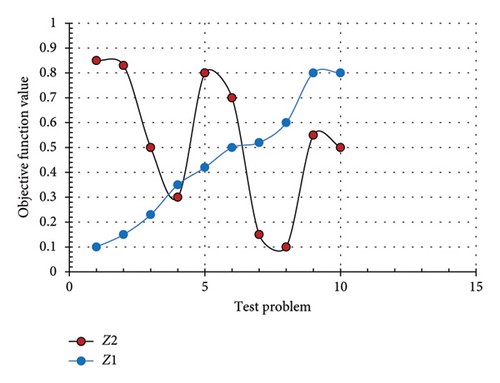
Subsequently, 10 sample problems are examined. The dimensions of these problems are presented in Table 8, detailing the specifications for the primary and backup suppliers, ranging from 2 to 10; potential factory locations, ranging from 2 to 12; distribution centers, ranging from 2 to 35; raw materials and products, ranging from 2 to 7; and the planning horizon, ranging from 5 to 6 periods. In six problems, the second objective is prioritized over the first, while in the remaining four, the first objective takes precedence over the second.
| Test problem | Suppliers | Factory | Distribution center | Raw material | Product | Period | Z1 | Z2 | Execution time | |
|---|---|---|---|---|---|---|---|---|---|---|
| μ2 ≥ μ1 | 1 | 2 | 2 | 2 | 2 | 2 | 5 | 9,521,431 | 0.84 | 1 |
| 2 | 2 | 3 | 2 | 2 | 2 | 5 | 1,350,227 | 0.81 | 2 | |
| μ1 ≥ μ2 | 3 | 2 | 3 | 5 | 3 | 3 | 5 | 2,209,743 | 0.54 | 3.1 |
| 4 | 2 | 4 | 8 | 3 | 3 | 6 | 3,249,751 | 0.34 | 9.1 | |
| μ2 ≥ μ1 | 5 | 3 | 5 | 10 | 4 | 4 | 6 | 4,151,671 | 0.79 | 14.3 |
| 6 | 4 | 6 | 15 | 4 | 4 | 6 | 5,007,342 | 0.68 | 17.4 | |
| μ1 ≥ μ2 | 7 | 5 | 8 | 20 | 5 | 5 | 6 | 5,304,762 | 0.14 | 23.2 |
| 8 | 6 | 10 | 25 | 6 | 6 | 6 | 6,165,874 | 0.11 | 30.1 | |
| μ2 ≥ μ1 | 9 | 7 | 12 | 30 | 7 | 7 | 6 | 7,554,823 | 0.59 | 99.3 |
| 10 | 7 | 12 | 35 | 7 | 7 | 6 | 7,645,921 | 0.59 | 0.125 | |
Table 8 indicates that, overall, the value of the first objective function in this study has increased progressively. Additionally, in problems where the second objective was prioritized, the value of the second objective also exhibited an upward trend. For instance, the results from solving problems 1, 2, 5, 6, 9, and 10 can be compared with those from problems 3, 4, 7, and 8. This trend is attributed to the nature of the preventive fuzzy GP method utilized in this study. Figure 8 illustrates the examination of the model across different dimensions.
5.2. Performance Evaluation of Proposed Mathematical Model
In this section, a comparison of the proposed model, which incorporates two-sided trade credit in a resilient supply chain, is provided with existing models in the literature, such as Goli et al. [30], Zhao and You [47], and Wang et al. [48]. As shown in Table 9, the use of two-sided trade credit enhances the resilience of the supply chain, leading to better demand fulfillment even in the face of disruptions. Specifically, compared to the traditional financial flow optimization model of Goli et al. [30], our approach results in an NPV of $9521431, which is higher than the $7531780 achieved by the traditional financial flow optimization model. Additionally, our model achieves a demand fulfillment rate of 95%, which is 10% higher than the 85% demand fulfillment of the single-sided trade credit model. The sensitivity analysis also shows that our model is more robust to variations in demand and supplier disruptions than the robust optimization model of Zhao and You [47], offering superior financial stability and operational resilience. The numerical results demonstrate that our approach significantly improves financial and operational performance under demand uncertainty.
| Model | Trade credit type | Performance metrics | Financial performance (NPV) | Demand fulfillment | Resilience to demand uncertainty | Key advantage |
|---|---|---|---|---|---|---|
| Proposed model | Two-sided trade credit | Balances financial and operational performance under demand uncertainty. | $9,521,431 | 84% | Robust to variations in demand and supplier disruptions | Enhanced resilience, better financial stability, and demand fulfillment. |
| Goli et al. [30] | Financial flow optimization without trade credit | Focuses on operational efficiency without considering financial performance in detail. | $7,531,780 | 73% | Less resilient to demand fluctuations | — |
| Zhao and You [47] | Robust optimization | Designed to handle disruptions but does not explicitly consider trade credit effects. | — | — | Less resilient to demand fluctuations | — |
| Wang et al. [48] | No trade credit | Traditional supply chain model. | — | — | Limited resilience to disruptions | — |
5.3. Performance Evaluation of Proposed Solution Method
In this section, we evaluate the performance of the proposed PFGP method by comparing it with other solution methods in the literature. Specifically, the comparison is made with exact methods, heuristic approaches, and metaheuristic algorithms. The comparison focuses on key performance indicators such as NPV, demand fulfillment, computational time, and robustness to supply chain disruptions.
The exact methods like Benders decomposition [31] guarantee optimal solutions but are often computationally expensive, especially for large-scale problems. The heuristic methods, such as Lagrangian relaxation [49], are faster but might sacrifice solution quality and robustness. Metaheuristic methods, such as Nondominated Sorting Genetic Algorithm-II (NSGA-II) [50], offer flexibility and can handle multiobjective optimization problems. However, they may struggle with convergence and may not always provide the best solution in terms of NPV or demand fulfillment. Table 10 presents the comparison of the proposed FGP method with these three types of solution methods.
The performance evaluation presented in Table 10 shows that the proposed PFGP method outperforms both exact methods and metaheuristic approaches in terms of solution quality, computational efficiency, and robustness to supply chain disruptions. The PFGP model achieves an NPV of $9,521,431 and a demand fulfillment rate of 84%, outperforming the Benders decomposition, which achieves a lower NPV of $9,350,000. Benders decomposition suffers from high computational costs, making it less practical for larger scale problems. Furthermore, the PFGP approach demonstrates greater robustness to disruptions, maintaining performance even under varying demand conditions, whereas the exact method shows moderate robustness.
In comparison with heuristic and metaheuristic methods, the PFGP model also shows superior performance. The heuristic method requires 134 s to find a solution, achieving a slightly lower NPV of $9,300,000 and demand fulfillment of 80%. NSGA-II performs similarly, with an NPV of $9,200,000 and 40 s of computation time, but struggles with lower demand fulfillment (79%) and reduced robustness. Although the heuristic and metaheuristic methods are faster than the PFGP approach, they fail to match the high-quality solution and the resilience to disruptions that the PFGP method provides. Overall, the PFGP method offers the best trade-off between solution quality, computational efficiency, and robustness in resilient supply chain optimization.
6. Discussion
The results of this study highlight the critical role of integrating financial and operational flows in supply chain resilience, particularly under uncertainty and financial constraints. By incorporating two-sided trade credit, the proposed model effectively enhances financial performance (NPV of $9,521,431) and demand fulfillment (84%), outperforming traditional single-sided trade credit approaches and robust optimization models. These findings underscore the importance of credit-based financing mechanisms in supply chain operations, demonstrating that strategic financial planning can significantly improve operational robustness while maintaining profitability. The trade-off between maximizing demand fulfillment and ensuring financial stability remains a key challenge, as higher demand fulfillment often leads to increased financial obligations, such as trade credit repayments and operational expenses.
One of the notable contributions of this research is the use of PFGP, which balances computational efficiency and solution quality. Compared to exact methods like Benders decomposition (which suffers from high computational costs) and metaheuristic approaches like NSGA-II, the PFGP method reduces computational time to 40 s while maintaining a superior NPV and demand fulfillment rate. This balance is crucial for decision-makers who need scalable and computationally efficient methods to optimize large-scale supply chains. Additionally, including backup suppliers in the model provides a risk-mitigation strategy, ensuring continuity in raw material procurement when primary suppliers face disruptions. The analysis also reveals that delays in trade credit repayment affect cash flow stability, with increased interest rates imposing penalties on late repayments, further reinforcing the need for strategic financial planning.
Another significant insight from the results is the sensitivity of supply chain performance to uncertainty levels. The findings demonstrate that as demand variability increases, financial stability becomes a key determinant of resilience, reinforcing the need for adaptable financial policies. The trade credit parameter adjustments further highlight that higher trade credit allowances improve production capacity but reduce profit margins due to increasing financial obligations. Thus, supply chain managers must carefully balance liquidity, credit terms, and resilience strategies to optimize financial and operational outcomes. This study provides a framework for integrating financial considerations into resilient supply chain models, offering practical implications for industries managing supply chain risks through credit-based financing and supplier diversification.
7. Conclusion
This study proposes a robust biobjective model for designing resilient supply chain networks that integrate financial and physical flows under demand uncertainty. By incorporating trade credit, bank loans, and capital resources, the model addresses the financial constraints imposed by resilience strategies, offering a comprehensive framework for decision-making in supply chain design. The findings emphasize the importance of financial feasibility in selecting backup suppliers and highlight the role of trade credit as a mechanism to improve both operational and financial performance.
The scientific value added by this research lies in its integration of financial and physical flows, bridging a critical gap in the literature. Unlike existing models that focus solely on physical flows, this approach accounts for financial constraints, repayment schedules, and trade credit policies, enabling companies to align resilience strategies with financial stability. The proposed model provides actionable insights for practitioners, helping organizations optimize their financial resources while improving resilience.
In practical terms, the results demonstrate that trade credit and financing strategies enhance NPV and demand fulfillment, particularly under financial constraints. Companies can leverage these findings to prioritize investments in resilience strategies, ensuring sustainable growth and operational stability. Moreover, the ability to release financial resources through trade credit agreements supports production efficiency and flexibility.
However, this study has certain limitations that provide avenues for future research. First, the model assumes deterministic repayment schedules, which may not fully capture real-world variability in financial markets. Future studies can explore stochastic approaches to incorporate uncertainties in repayment terms and interest rates. Second, the computational experiments were based on synthetic data; extending the analysis to real-world case studies would validate the model’s applicability further. Third, integrating environmental and social sustainability dimensions into the financial framework would offer a more holistic perspective on resilient supply chain design.
Future research directions could include expanding the model to incorporate dynamic and multiperiod decision-making processes, enabling a more realistic representation of supply chain evolution over time. Investigating the impact of different financing mechanisms, such as government subsidies and venture capital, on resilience strategies would provide further insights. Additionally, exploring decentralized decision-making approaches, where supply chain partners make collaborative financial and operational decisions, could enhance flexibility and adaptability in dynamic environments.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
Dan Wu is grateful for the following project: China Medical Equipment Association Operation and Performance Branch “Research on high-quality development path of public hospitals under the background of DRG payment” (CMOP-3-2023-9).
Acknowledgments
Dan Wu is grateful for the following project: China Medical Equipment Association Operation and Performance Branch “Research on high-quality development path of public hospitals under the background of DRG payment” (CMOP-3-2023-9).
Open Research
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon request.




