1. Introduction

Mpox (also known as monkeypox) is a disease originally present in animals, notably rodents in Africa, and now circulating in humans, making it an emerging zoonosis. The disease appears as an attenuated form of human smallpox, with less severe symptoms and a lower lethality (number of deaths out of the number of people affected) [1]. Monkeypox is caused by the virus of the monkey’s name.

Since May 2022, thousands of cases of Mpox have been reported in nonendemic countries (regions where the disease does not exist permanently) [2]. Studies are underway to better understand the epidemiology, sources of infection, and modes of transmission of this disease. As of September 1, 2022, there were several tens of thousands of diagnosed cases. Various models have been proposed to define the dynamics of disease transmission and estimate the monkey’s evolution or variol.

The resurgence of Mpox in Africa, affecting the Democratic Republic of Congo (DRC) and other countries on the continent (including Burundi, Kenya, Rwanda and Uganda), and the appearance of a new variant (1b) prompted the World Health Organization (WHO) to trigger its highest level of global health alert on 14 August 2024. The WHO has therefore announced the arrival of the first vaccines against Mpox in September 2024 in the DRC, one of the African countries hardest hit by the epidemic.

Several studies on Mpox vaccination models have been recently carried out. [3] studied the transmission of monkeypox during pregnancy and highlighted the high risk among African women. Some treatment recommendations applicable to women infected with the virus during their pregnancy can be found in [4, 5]. Reference [6] found that Mpox is controllable and can be eradicated in a semiendemic equilibrium by vaccination. However, in a fully endemic equilibrium, Mpox cannot be eradicated by vaccination alone. To understand the relative effects of changes in sexual behaviour and vaccination-induced immunity on cases of smallpox. Reference [7] studied the potential role of behavioural changes or vaccination in the trajectory of the epidemic. Reference [8] studied the impact of combined vaccination and treatment interventions as control strategies to study the transmission dynamics of MPXV. Reference [9] developed a deterministic model for the transmission dynamics of a disease subject to quarantine, isolation and an imperfect vaccine, and proved that the imperfect vaccine could have either a positive or negative impact dependent on a certain threshold value.

To assess the feasibility of managing and eliminating Mpox through voluntary vaccination and treatment [10], developed a model of monkeypox virus vaccination and transmission without lifelong immunity. They demonstrated the importance of treatment, vaccination and public understanding as exclusive preventive measures in the context of monkeypox. A paper by [8] developed a model of human-to-human transmission of monkeypox virus with post-exposure vaccination. They showed that the combination of a public awareness campaign, postexposure vaccination and isolation is the best way to eradicate the monkeypox virus from society, given the lack of vaccines to cover the large susceptible population. The impact of smallpox vaccines on Mpox epidemics was investigated in [11]. In [12], the impact of vaccination and raising awareness among high-risk groups on the smallpox epidemic in the United States, 2022–2023 was studied. Their models suggest that the smallpox epidemic of 2022–2023 in the United States was controlled by a combination of a two-dose smallpox vaccination campaign, awareness-raising among high-risk groups and sexual risk reduction. To show how vaccination considerably slows the spread of the disease [13], we have used a practical application of complex fractional techniques in epidemiology. In their model [14], they showed that not vaccinating is often an optimal solution from the point of view of the individual. They also showed that, for certain values of the parameters in their model, there are several equilibria in the vaccination game. For example, in the absence of government-imposed minimum vaccination rates, the population could easily revert to a nonvaccination scenario. Furthermore, the authors in [8] studied the dynamics of the transmission of monkeypox virus infection in the context of interventions combining vaccine and treatment. Their analysis shows that baseline reproductive numbers, which have been used as a threshold to measure new infections in host populations, decrease as vaccination and treatment control parameters increase. The role of vaccination and public awareness in predicting the incidence of smallpox in the UK is examined in [15]. They predicted that targeted vaccination of high-risk groups prevented resurgence in cases due to a reversal of behaviour. Recent studies have explored the combined impact of vaccination and treatment strategies on epidemic control using compartmental models, such as the work by [16], which analyzed the interplay between vaccines and treatment in the context of dengue dynamics.

After reviewing several studies on the monkeypox virus and its transmission pathways, we found that no study considered a compartmental model with vaccination in a complex network with a heterogeneous component population. Our aim is to study the different parameters that could reduce the transmission of the disease and the effects of these parameters on the number of basic reproductions.

In this work, we are motivated by the Mpox cases recorded in Central Africa, particularly in the DRC [17]. With this in mind, we develop a model that incorporates complex networks on the transmission dynamics of monkeypox virus, taking into account the fact that the vaccination campaign against the virus is imperfect.

We also evaluate sensitivity analysis to find the parameters that influence disease transmission. Our research highlights the importance of treatment, vaccination and public understanding as the sole preventive measures in the context of monkeypox. In addition, our analysis shows that the disease can only be managed and controlled if vaccine efficacy is greater than 70%. If vaccine efficacy is low, treatment alone will not provide lasting control of the disease.

The structure of the paper is as follows. Section 1 presents a general description of the model and some dynamic behaviors. Section 2 identifies the model parameters that significantly influence the number of basic reproductions through a global sensitivity analysis. Section 3 presents the numerical simulations performed to support the theoretical results of the reference values for the model parameters. Finally, we conclude with a discussion.

2. Materials and Methods

2.1. The Model’s Description

We propose a compartmental SEIHRV-SIR epidemic model on a heterogeneous network of monkeypox transmission dynamics, composed of two populations, namely humans and rodents. The human compartment is denoted h, while the rodent compartment is denoted r. We divided the status of N individuals in the human population into several categories: susceptible, exposed, infected, hospitalized and eliminated. Susceptible individuals are healthy and easily infected. Exposed individuals are infected, but show no symptoms of infection and have no capacity to infect others. Infected individuals have been contaminated by an outbreak and present some degree of contagion. Hospitalized people are those with severe symptoms who are being treated in hospital. Recovered persons are those who have acquired immunity after an illness, or those who have died after an illness. The rodent population is subdivided into three compartments: susceptible rodents S^r(t), infected rodents I^r(t) and recovered rodents R^r.

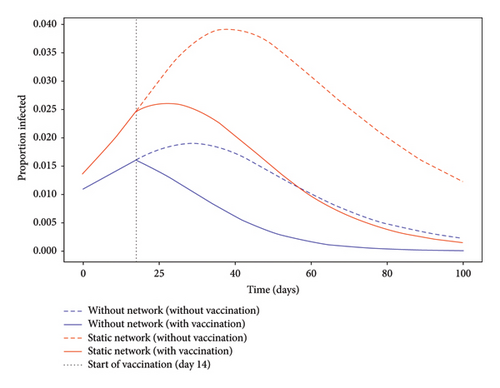
Human interactions are represented by a static Barabási-Albert (BA) network. This type of network accounts for contact heterogeneity, especially the presence of highly connected individuals (super-spreaders). The network remains fixed over time to simplify the mathematical analysis and simulations. While this is a useful first approximation, it does not capture time-varying behaviors or contact changes. Figure 1 illustrates the evolution of the epidemic in a static complex network scenario and in a simple model. We discuss these limitations in the following sections.

Each individual in the community can be considered a vertex of the network, and each contact between two contacts is represented by an edge connecting the vertices. The number of edges coming from a vertex, that is the number of contacts a person has, is called the vertex’s degree. In addition, we define S_k as the fraction of susceptible individuals among individuals of degree k. Similarly, E_k, I_k, H_k and R_k represent the fraction of exposed, infected, hospitalized and eliminated individuals of degree k, respectively. Clearly, $$ view proof 1 and $$, N = N₁ + N₂ + ⋯+N_k is the population size and P(k) = N_k/N is the degree distributions of the network(the probability that a uniformly chosen individual has contacts). The features of transmission are illustrated in Figure 2, and the Mpox propagation process can be described as follows:

$$ ()

where

$$ ()

and $$. So the probability that any edge of the network contains the infected individual is equal to the proportion of the total number of edges connected by the infected individuals to the total number of edges in the network. <k> represents the average degree of the network.

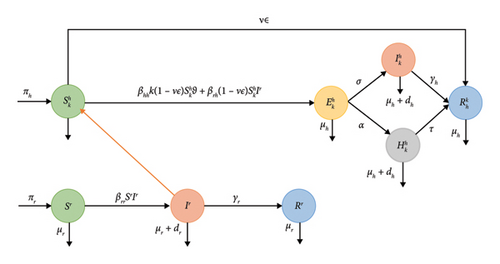
The parameters used in our model are summarised in Table 1, together with their numerical values and associated sources or assumptions. The choice of values is based on data from the literature [18], estimates or standard assumptions in similar epidemiological models. For example, the human recruitment rate (π_h) and natural mortality (μ_h) are directly derived from reference [18], which ensures a realistic basis for human demographic dynamics. Similarly, the equivalent rates for rodents (π_r, μ_r) are also obtained from [18]. Transmission probabilities (β_hh, β_rr) were estimated to reflect levels of infectivity compatible with the available biological data, while ensuring a realistic dynamic regime. The average number of daily contacts k is a value typically used in other similar diseases, and adopted here as a reasonable assumption. Recovery rates for infected individuals are also based on [18], and represent average infection times of the order of 1–2 days (depending on the inverse of the rate). Vaccination rates (ν), vaccine efficacy (ϵ) and treatment rates (α) are assumptions but reasonable, and provide a basis for exploring different control strategies. Lastly, the mortality rates (d_h) induced by the disease in humans and rodents (d_r) are taken from [18], as is the recovery rate of those hospitalised (τ), and make it possible to represent the severity of the infection in the two hosts.

Table 1. Values of parameters used in the model, and the sources used for the numerical values.

Parameter	Definition	Value	Source
πh	Recruitment rate of human	2.9	[18]
k	Number of contact per day	12	Assumed
βrh	Probability of rodent infectiousness	0.64	Estimated
βrr	Probability of rodent infection	0.78	Estimated
γh	Recovery rate of infected humans.	0.83	[18]
γr	Recovery rate of infected rodent.	0.6	[18]
ν	Vaccination rate	0.25	Assumed
μh	Natural mortality rate of humans	1.5	[18]
ϵ	Vaccine efficacy	0.5	Assumed
α	Treatment rate of infectious humans	0.5	Assumed
τ	Recovery rate of hospitalized individuals	0.4	Estimated
dh	Disease-induced mortality rate of humans	0.01	[18]
πr	Recruitment rate of rodent	0.2	[18]
μr	Recovery rate of infected rodent.	0.6	[18]
dr	Death rate of rodent due to infection.	0.4	[18]

These choices guarantee both the biological coherence and the stability of the dynamic system, by ensuring realistic simulation trajectories. The definitions of the parameters are given in Table 1.

Let $$ with f ∈ {s, e, i, h, r} and g_r(t) = G_r(t)/N with g ∈ {s, i, r}. Using the normalization theory our model reduces to the following:

$$ ()

2.4. Global Asymptotic Stability of the DFE

For the elimination of Mpox to be independent of the initial sizes of the subpopulations in the model, the overall asymptotic stability of the DFE must be established. This is what we now examine. Consider the feasible region

$$ ()

Lemma 3. It is a positively invariant set for the model (3) with non-negative initial condition in $$.

The proof of this lemma is provided in Appendix (available here).

Lemma 4. Let $$ such that $$ is a globally stable equilibrium. If G(X₁, X₂) satisfies the following two conditions given in [20], namely

$$ ()

the DFE is globally asymptotically stable.

Theorem 5 (Global asymptotic stability of the DFE). The DFE Γ of model (3) is globally asymptotically stable if R₀ < 1:

A complete proof of the global asymptotic stability of the DFE is given in Appendix (available here).

In this section, we validated the considered Mpox model (3). The data used to calibrate the model correspond to cumulative confirmed cases of Mpox in the DRC. These data come from the official Our World in Data database, updated in April 2025 [21]. The period covered runs from April 2022 to April 2025. Only data validated by the national health authorities and consolidated by the WHO has been retained, thus guaranteeing rigorous quality control. Parameters were estimated using nonlinear least squares by fitting log (I + R) to the cumulative case data. This is to better capture the initial dynamics of the epidemic, where data are often less plentiful and more sensitive to fluctuations. The uncertainty around the predictions was assessed using a bootstrap procedure with 200 replications, providing 95% confidence intervals. The results (Figure 3) show good concordance between the model and the observations while accounting for the potential variability around the fitted curve.

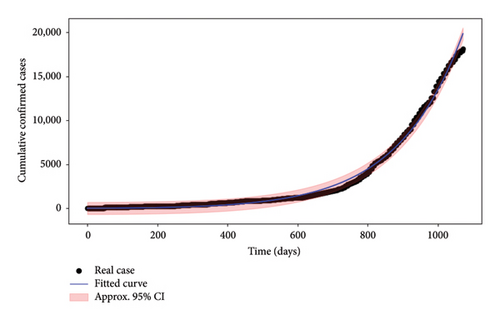
The model was initially calibrated using data from the DRC, making it highly relevant to this region. However, its generic structure—including the dynamics between humans and reservoir hosts, direct and indirect transmission, and interventions—can be adapted to other regions, subject to certain modifications. Specific adjustments to the model’s parameters and structure may therefore be required for relevant application in other contexts. In the long term, the model’s flexibility could allow it to be used as a decision-support tool in a variety of environments, provided it is properly recalibrated with local data.

2.5. Global Sensitivity Analysis

The input parameters determine the results of the compartmental mathematical models, which may be subject to uncertainty. A global sensitivity analysis is therefore carried out to examine the effect of uncertainty and the sensitivity of numerical simulation results to changes in each parameter of our model. Therefore, a global sensitivity analysis is performed to determine the most influential model parameters using a combination of Latin Hypercube Sampling (LHS) and Partial Rank Coefficient (PRCC).

Figure 4 shows that the probability of human-to-human transmission (β_hh), the probability of human-to-rodent transmission (β_rh), vaccine efficacy (ϵ) and the vaccination rate (ν) are the parameters with the greatest influence on the increase in the number of infected individuals. The first two parameters have positive relationships and the last two have negative relationships. This means that an increase in the vaccination rate and vaccine efficacy leads to a reduction in the number of people infected. In addition, a reduction in the probability of transmission leads to a reduction in the number of cases of monkey pox.

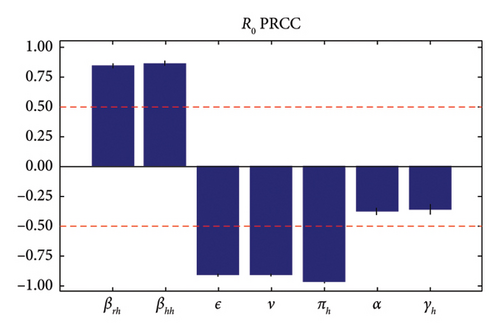
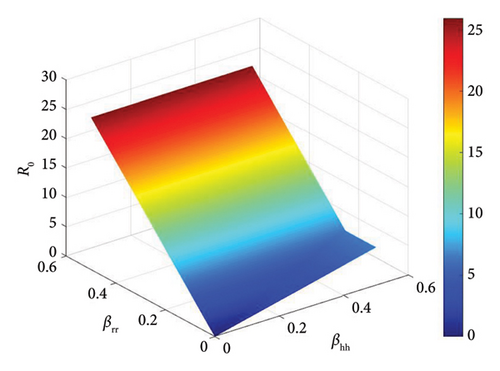
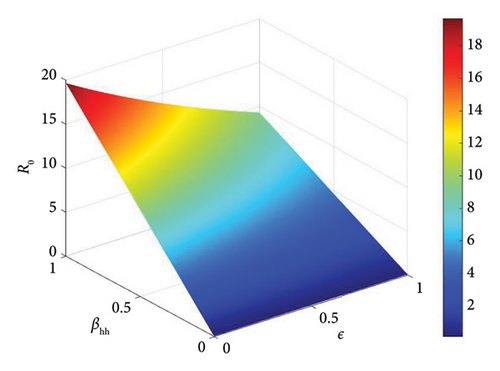
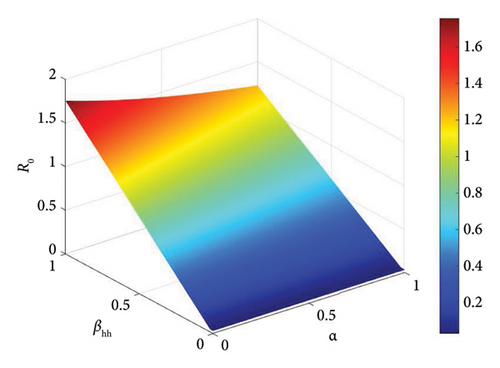
The basic reproduction number is a crucial parameter in disease dynamics, giving us key information about the disease. To better understand the effect of various disease transmission parameters on the basic reproduction number, we obtained surface plots showing the variation in R₀ as a function of sensitive parameters. Figure 5 shows that increasing the intra-human transmission value leads to an increase in disease transmission. Similarly, Figures 6 and 7 show that the efficacy of the affected vaccine and the treatment rate directly reduce monkeypox transmission. This supports the results observed in Figure 4.

2.6. Numerical Simulations

In this section, we conduct a numerical analysis of Mpox transmission through vaccination and treatment using several distinct scenarios. The model simulations were conducted under an epidemic scenario, without assuming a pre-existing endemic equilibrium. The total population was set to N = 105, 800, 000, based on recent demographic estimates for the DRC. Initial conditions were specified as proportions of the total population: $$, $$, $$, $$, $$, $$, $$, and $$. Simulations were carried out over a 1000-day period, ending on April 6, 2025, which corresponds to the last available date in the dataset. This duration captures both the early and peak phases of the epidemic, allowing for a comprehensive analysis of the transmission dynamics. In the figures, model outputs are presented as proportions of the total population to facilitate comparison across compartments and enhance graphical interpretability. The model’s parameter values are listed in Table 1.

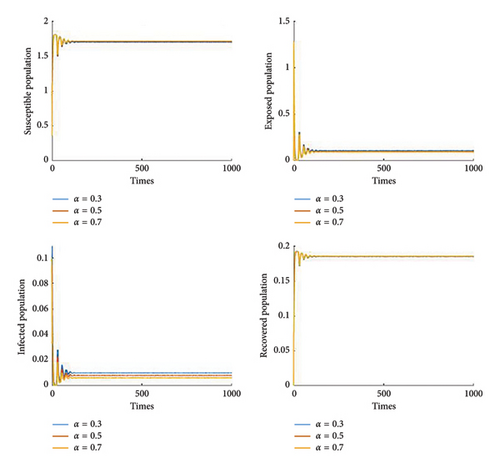
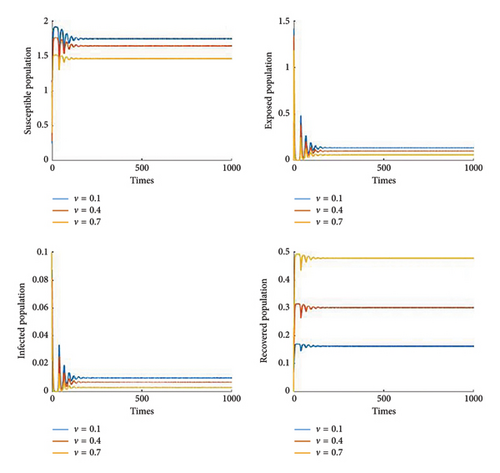
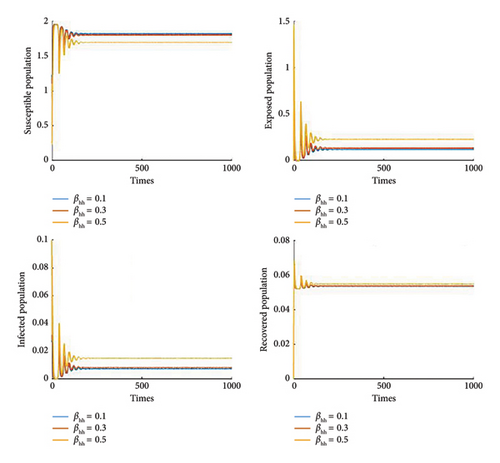
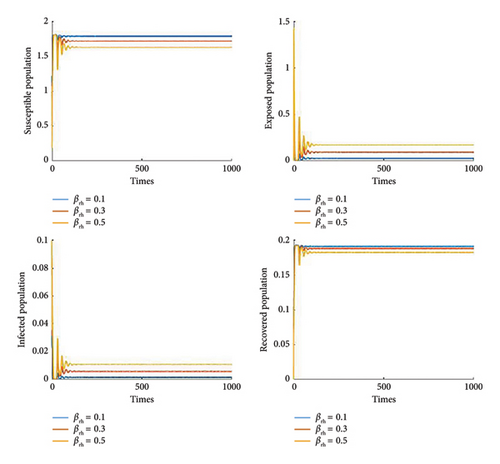
Figure 8 shows the effect of the cure rate on disease transmission dynamics. As the treatment strategy increases, the susceptible population and the recovered human population increase, while the exposed population and the infected population decrease. Furthermore, Figure 9 illustrates that, in general, vaccination programmes help to establish high levels of immunity in populations and reduce the number of people susceptible to the disease. Furthermore, it is noted that if the efficacy of the vaccine reaches 70%, then we can control the disease Figures 10 and 11 show the effect of transmission probabilities. As these transmissions increase, the susceptible population decreases and the infected population increase.

3. Discussion

In this paper, a complex network SEIHRV-SIR model with therapeutic interventions and vaccination is proposed for monkeypox variol disease. The model is used to simulate the dynamics of the virus, to better understand the complexity of infectious diseases and to develop effective prevention measures. The model’s equilibrium points were calculated, and detailed global stability tests were performed to better understand the system’s stability in different conditions. The basic reproduction number was determined and numerical simulations were carried out to validate the results. The global sensitivity analysis of the proposed model revealed that vaccine efficacy and transmission rates are the most influential parameters, implying that if vaccination is perfect, the number of immunized individuals who can resist the disease is considerably reduced as vaccination imperfection rates increase. In this way, vaccination programs are shown to help establish high levels of immunity in populations and reduce the number of individuals susceptible to disease. The theoretical and numerical study presented also confirms that to stop the disease spreading, infection rates need to be maintained as low as possible through appropriate control measures. Furthermore, by implementing better health conditions and treatment strategies, and increasing cure rates, we can stabilise the DFE point and eventually eliminate the incidence of infection. In order to ensure that the simulations and results are founded on complex predictive epidemiology models, the study employs real data to estimate model parameters. This method improves the model’s relevance and application to actual situations, producing reliable data for public health initiatives.

The model considers that human interactions follow a static BA type network, characterised by a scale-free structure with a few highly connected nodes. This choice is based on two main considerations: on the one hand, the ability of the BA model to reproduce properties empirically observed in human contact networks, in particular the presence of superspreaders; on the other hand, its simplicity of algorithmic generation and its computational robustness in a large-scale simulation framework.

However, we recognise that this approach has certain limitations. In particular, the static nature of the network may miss important temporal variations in social behaviour, containment policies or spontaneous changes in contact patterns. This hypothesis could therefore, depending on the context, underestimate or overestimate the effectiveness of targeted interventions.

With this in mind, future extensions to the model could incorporate dynamic or temporal networks, capable of capturing structural changes in interactions (e.g., confinement, school closures and teleworking). The use of empirical proximity or mobility data (such as anonymised GPS or Bluetooth recordings) would also make it possible to refine the network structure over time. However, using a static network is a major limitation. To better reflect real-world dynamics, future models should include time-varying or dynamic networks. This would help design more accurate and effective public health strategies for managing future outbreaks.

Altogether, the model is a contribution to the infectious disease modelling field and can be a valuable resource for government and public health authorities in designing effective disease control strategies. By identifying the key factors in the spread of monkeypox virus, we can develop effective, targeted interventions to prevent and control future epidemics. In conclusion, this study offers important new understandings of the dynamics of SEIHRV-SIR epidemiological trends in a network that incorporates immunization. The study’s assumptions and simplifications make it necessary for us to take the results cautiously, even though they emphasize the significance of vaccination campaigns. Understanding the study’s scope and possible consequences for practical public health strategies—especially in light of emerging infectious diseases like Mpox requires acknowledging these limitations.

This model was initially calibrated using data from the DRC, giving it strong contextual relevance for this region. However, its generic structure, including direct and indirect transmission, as well as interventions, can be adapted to other regions, subject to certain modifications.

Specific adjustments to the model’s parameters and structure may therefore be required for relevant application in other contexts. In the long term, the model’s flexibility could allow it to be used as a decision-support tool in a variety of different contexts, provided that it is correctly recalibrated with local data.

Furthermore, mobility has an impact on the dynamics of disease transmission; thus, its impacts also need to be considered. Age-related impacts on the efficacy of an intervention for a specific vaccine have not been considered. Subsequent research will address these questions.

4. Conclusion

In this study, we developed a SEIHRV-SIR model structured on a heterogeneous contact network to simulate the transmission dynamics of monkeypox, including human-to-human and animal-to-human interactions. The model integrates vaccination and treatment strategies and was calibrated using real epidemiological data from the DRC.

The results confirm that vaccine efficacy and transmission rates are key determinants of outbreak size and persistence. Our findings highlight the importance of targeted vaccination campaigns and treatment strategies, especially in contexts where contact patterns are heterogeneous and superspreaders may exist. Despite the simplifying assumption of a static network, the model reproduces observed trends and supports the use of sensitivity analysis to inform public health decisions.

Future work should incorporate time-varying contact networks and mobility data to improve realism and guide more precise intervention planning. Overall, this model provides a valuable framework for anticipating the spread of zoonotic diseases and optimizing resource allocation during emerging outbreaks.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Abdoulaye Sow, Cherif Diallo, Hocine Cherifi contributed equally to this work.

Funding

No funding was received for this manuscript.

Supporting Information

The detailed proofs of the aforementioned computations are provided in the Appendix.