Volume 2025, Issue 1 6402353

Research Article

Open Access

Harmonic–Arithmetic Index for the Generalized Mycielskian Graphs and Graphenes With Curvilinear Regression Models of Benzenoid Hydrocarbons

Pooja Danushri Namidass

orcid.org/0009-0007-9537-4775

Department of Mathematics , College of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , Tamil Nadu , India , srmist.edu.in

Search for more papers by this author

Shobana Loganathan,

Corresponding Author

Shobana Loganathan

[email protected]

orcid.org/0000-0002-6401-6533

Department of Mathematics , College of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , Tamil Nadu , India , srmist.edu.in

Search for more papers by this author

Pooja Danushri Namidass,

Pooja Danushri Namidass

orcid.org/0009-0007-9537-4775

Department of Mathematics , College of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , Tamil Nadu , India , srmist.edu.in

Search for more papers by this author

Shobana Loganathan,

Corresponding Author

Shobana Loganathan

[email protected]

orcid.org/0000-0002-6401-6533

Department of Mathematics , College of Engineering and Technology , SRM Institute of Science and Technology , Kattankulathur , Tamil Nadu , India , srmist.edu.in

Search for more papers by this author

First published: 01 May 2025

https://doi.org/10.1155/cmm4/6402353

Academic Editor: Pramita Mishra

Share a link

Email
Wechat
Bluesky

Abstract

The generalized Mycielskian graphs are known for their advantageous properties employed in interconnection networks in parallel computing to provide efficient and optimized network solutions. This paper focuses on investigating the bounds and computation of the harmonic–arithmetic index of the generalized Mycielskian graph of path graph, cycle graph, complete graph, and circulant graph. Furthermore, exploring the harmonic–arithmetic index of graphene provides insights into its structural properties, aiding in material design, predictive modeling, and understanding its behavior in various applications. Additionally, the study delves into analyzing the harmonic–arithmetic index of the curvilinear regression model concerning elucidating specific properties of benzenoid hydrocarbons, offering insights into their structural characteristics.

1. Introduction

Chemical graph theory is a branch of mathematics that focuses on understanding the properties and behaviors of chemical compounds using graphs. Molecules are represented as graphs, with atoms being the vertices and chemical bonds being the edges. These graphs can be used to represent the structure and connectivity of molecules, allowing one to analyze and predict their properties. Topological indices are numerical descriptors derived from the molecular graph structure that provide insights into various chemical properties, determined solely by their topology or connectivity arrangement, without regard to bond lengths or angles. They are key mathematical descriptors in chemical graph theory and hold considerable importance due to their utility in quantitative structure–property relationship (QSPR) and quantitative structure–activity relationship (QSAR). These indices offer an efficient means to translate chemical composition into numerical values, facilitating correlation with physical properties. Over the years, numerous topological indices have been explored, with those based on distance or molecular degree proving most beneficial. QSPR models use topological indices to predict various physicochemical, biological, and pharmacological properties of molecules. These properties include boiling points (BPs), solubility, toxicity, and biological activity. In drug design, topological indices help identify potential drug candidates by predicting their interaction with biological targets. This can streamline the drug discovery process by reducing the number of compounds that need to be synthesized and tested [1]. The authors in [2–5] have studied the QSPR analysis using several distance- and degree-based topological indices for antidrugs and chemical compounds.

The graphs considered in this paper are simple graphs. The idea of valency in chemistry and the degree concept in graph theory are quite similar. The degree of the vertex is the number of edge incident to that vertex, d_G(v) denoted the degree of the vertex v, where δ is the minimum degree and Δ is the maximum degree. Two vertices are adjacent if there is an edge between those vertices. In 1975, Randic introduced an index [6] which is one of the most extensively studied. This index is defined as

where d_u and d_v are the degrees of the vertices u and v, respectively. In this contest, a different variant of the Randic index [7], called the harmonic index, is defined as follows:

As far as the literature indicates, this index first appeared in [8]. The geometric–arithmetic index is based on ratios of geometrical and arithmetical means of end vertex degrees of edges, which was evaluated by Vukičević and Furtula [9] in 2009 as follows:

Similarly to that, the harmonic–arithmetic (HA) index, a recent addition to the topological indices proposed by Albalahi et al. [10], quantifies the relationship between the harmonic and arithmetic means based on the degrees of the endpoints of edges, which is defined as

()

More extensive research on the HA index is detailed in [11].

The Mycielskian graph, coined after Jan Mycielski [12], is a technique in graph theory where a new graph is formed from an existing one by systematically introducing extra vertices and edges while maintaining its triangle-free nature and clique number. Stiebitz introduced the generalized Mycielskian graph in [13], which represents natural extensions of the Mycielskian graph. These graphs have useful applications in graph coloring and network design. De in [14] has calculated various topological indices of the generalized Mycielskian graphs, and Chanda and Iyer in [15] have determined the Sombor index for the Mycielskian graphs.

Computational analysis of indices for different chemical and nanostructures has also been an active area of research. Recent interest in graphene-based nanotubes and nanomaterials has stimulated further interest in the study of polycyclic benzenoids. Porous two-dimensional (2D) nanographene structures hold great potential across various research fields, offering diverse applications including nanochemistry, metal ion sequestration, and enhanced electrical properties, with topological descriptors aiding in structural characterization and property prediction. Their porous nature facilitates the fabrication of highly efficient electrodes, promising significant advancements in battery and energy storage technologies [16]. In the realm of chemistry, graphene finds diverse applications due to its large surface area, chemical stability, and unique electronic structure. The authors in [17, 18] have derived various topological indices of graphene.

Benzenoid hydrocarbons are a specific type of polycyclic aromatic hydrocarbons (PAHs) composed of six-membered rings containing only carbon and hydrogen atoms. Also known as condensed polycyclic unsaturated conjugated hydrocarbons, these compounds are typically planar because of the geometry of their six-membered rings. Their planar structure contributes to their relative stability compared to other PAHs. To establish the relationship between the variables under investigation, a statistical technique known as curvilinear regression is employed [19]. This method can be utilized to explore the association between the chemical structures of molecules and topological indices, aiding in the analysis of chemical and biological activity. In [20], Arockiaraj et al. introduce an innovative method that employs generalized reverse-degree parameters and conducts a QSPR investigation employing both the linear and cubic regression models to evaluate the efficacy of recent drugs against multiple coronavirus variants.

Motivated by the preceding literatures, this paper investigates the bounds and computational methods for determining the HA index of the generalized Mycielskian graph applied for P_n, C_n, K_n, and . It also calculates the HA index for graphene and analyzes and predicts the chemical application of the HA index in framing the curvilinear regression models for the six physiochemical properties using SPSS software.

2. Generalized Mycielskian Graph

The generalized Mycielskian graph is an interesting construction in graph theory that increases the number of vertices and edges while preserving its triangle-free property.

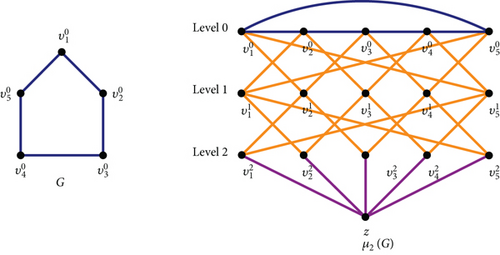
Definition 1 ([15]). Let G be any graph with vertex set, V(G) = {v₁, v₂, ⋯, v_n}, and edge set E(G). Let m be any positive integer. For each integer k(0 ≤ k ≤ m), let V^k be the k^th copy of vertices in V, that is, . The generalized Mycielskian graph of G denoted by μ_m(G) is the graph with the vertex set V(μ_m(G)) = V⁰ ∪ V¹ ∪ V² ⋯ ∪V^m ∪ {z} and the edge set The vertex is at level k, and so the vertices of V^k are called as vertices of level k.The identification of for 1 ≤ i ≤ n and thus refers to the vertices at level 0 as original vertices, the vertices at level k ≥ 1 as shadow vertices at level m, and the vertex z as the universal vertex (root). The root is only adjacent to the shadow vertices at level m. It is observed from the structure that

•
For m = 0, μ₀(G) is the graph obtained from G by adding a universal vertex.
•
For m = 1, μ₁(G) = μ(G).

An illustration of the generalized Mycielskian graph constructed from C₅ is provided in Figure 1.

Proposition 1 ([15]). Let μ_m(G) be the m -Mycielskian graph of a G with n vertices. Then, for each v ∈ V(μ_m(G))

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Generalized Mycielskian graph of C₅.

2.1. Bounds for HA Index of the Generalized Mycielskian Graph

The following subsection provides bounds for the HA index of the generalized Mycielskian graphs.

Theorem 1. Given that a graph G with a vertex set V = {u₁, u₂, u₃, ⋯, u_n} of size n and edges of size m, then

where t represents the levels in the μ_t(G). Equality holds if and only if G is isomorphic to regular graph.

Proof 1. Utilizing the vertex set and edge set from Definition 1 in Equation (1) and replacing m = t in Proposition 1

From Proposition 1

We infer

and

Also

Therefore, combining the above equations

When δ = Δ = r

2.2. HA Index of the Generalized Mycielskian Graph

In this section, HA index of the generalized Mycielskian graphs of m levels for P_n, C_n, K_n, and are computed using edge contribution method.

Theorem 2. For a graph G with n vertices and m levels in μ_m(G)

1.
HA(μ_m(P_n)) = n(2m − 1) − 6m(32m/9) + 123/25 + (96(n − 3)/49) + (16n/(2 + n)²) + (12n(n − 2)/(3 + n)²),
2.
HA(μ_m(C_n)) = n(2m − 1) + (145n/49) + (12n²/(3 + n)²),
3.
HA(μ_m(K_n)) = nm(n − 1) − n(n − 2) + (n(n − 1)/2) + (8n²(n − 1)²/(3n − 2)²),
4.

Proof 2. For a graph G with n vertices, the graph μ_m(G) is constructed with vertices across m levels. The analysis focuses on the degrees of the endpoints of the edges within the graph. The edge distribution is partitioned into four levels, as indicated in Table 1, that displays the number of edges where the endpoints have the same degree.

Table 1. Edge contribution of μ_m(P_n).

Level in μ_m(P_n)	(d_u, d_v)	\|(d_u, d_v)\|
Level 0	(2, 4)	2
Level 0	(4, 4)	(n − 3)

Between levels p − 1 and p: 1 ≤ p ≤ m − 1	(2, 4)	(m − 1)4
Between levels p − 1 and p: 1 ≤ p ≤ m − 1	(4, 4)	(m − 1)2(n − 3)

Between levels m − 1 and m	(2, 3)	2
	(2, 4)	2
	(3, 4)	2(n − 3)

Between levels m and z	(2, n)	2
Between levels m and z	(3, n)	n − 2

From Table 1

Table 2 gives the edge distribution of the graph μ_m(C_n).

Table 2. Edge contribution of μ_m(C_n).

Level in μ_m(C_n)	(d_u, d_v)	\|(d_u, d_v)\|
Level 0	(4, 4)	n
Between levels p − 1 and p: 1 ≤ p ≤ m − 1	(4, 4)	2n(m − 1)
Between levels m − 1 and m	(4, 3)	2n
Between levels m and z	(3, n)	n

Hence

Table 3 gives the edge distribution of the graph μ_m(K_n).

Table 3. Edge contribution of μ_m(K_n).

Level in μ_m(K_n)	(d_u, d_v)	\|(d_u, d_v)\|
Level 0	(2(n − 1), 2(n − 1))
Between levels p − 1 and p: 1 ≤ p ≤ m − 1	(2(n − 1), 2(n − 1))	n(n − 1)(m − 1)
Between levels m − 1 and m	(2(n − 1), n)	n(n − 1)
Between levels m and z	(n, n)	n

From Table 3

Figure 2 illustrates the generalized Mycielskian graph of a path graph with m levels.

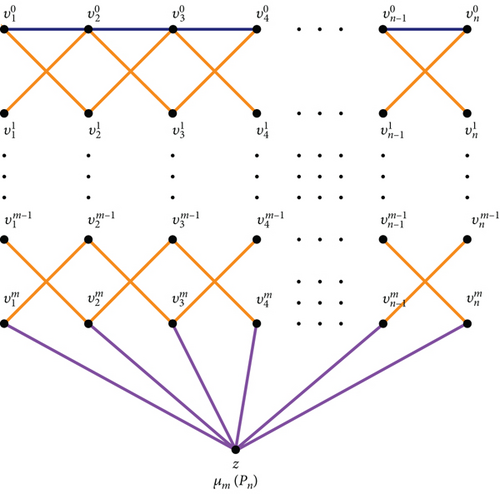
Table 4 gives the edge distribution of the graph .

Table 4. Edge contribution of

Level in	(d_u, d_v)	\|(d_u, d_v)\|
Level 0	(8, 8)	2n
Between levels p − 1 and p: 1 ≤ p ≤ m − 1	(8, 8)	4n(m − 1)
Between levels m − 1 and m	(8, 5)	4n
Between levels m and z	(5, n)	n

From Table 4

3. HA Index of Graphene

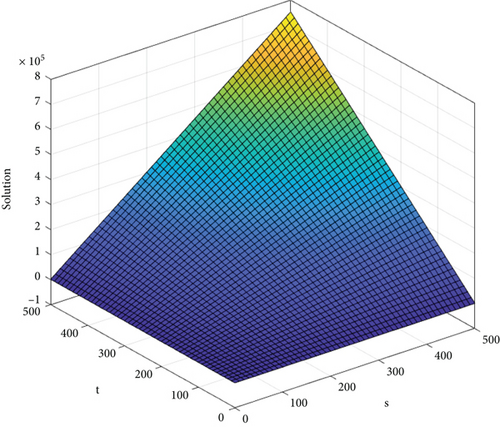
Graphene was first isolated from graphite in 2004 by Andre Geim and Konstantin Novoselov. It can exist in several different forms, each with its own unique properties and structures. The paper focuses on monolayer graphene, the most renowned form characterized by a single layer of carbon atoms arranged in a hexagonal lattice. Understanding the topological properties of benzenoid systems is crucial in the context of graphene because these properties play a significant role in determining the chemical and biological properties of polycyclic benzenoids [21]. The following result is on deriving the HA index of graphene, and a 3D model of the same is represented.

Theorem 3. Given the “t” and “s” benzene rings in each row, the HA index of graphene is given by

Proof 3. The graphene structure composed of “t” and “s” benzene rings in each row, let the edge, e = (d_u, d_v), represent the number of edges connecting vertices with degrees d_u and d_v. Within this 2D arrangement of graphene as depicted in the figure, only the edges (2,2), (2,3), and (3,3) are present. In Figures 3 and 4, the edges (2,2), (2,3), and (3,3) are distinguished by green, red, and black coloring, respectively.

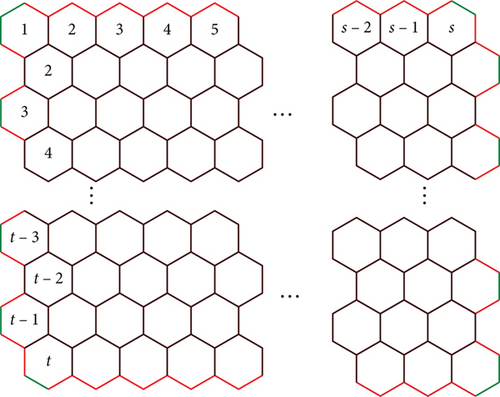
Case (i) For t = 1

Table 5 gives the edge contribution for Figure 3.

Table 5. t = 1, s > 1.

(d_u, d_v)	e = \|(d_u, d_v)\|
(2, 2)	6
(2, 3)	4s − 4
(3, 3)	s − 1

From Table 5

Case (ii) For t > 1 and s ≥ 1

The cardinality of the edges with the end degree vertices is mentioned in Table 6.

Table 6. Edge contribution of graphene when t > 1, s ≥ 1.

(d_u, d_v)	e = \|d_u, d_v\|
(2, 2)	t + 4
(2, 3)	4s + 2t − 4
(3, 3)	3ts − 2s − t − 1

From Table 5

In Figure 5, the HA index of graphene when t > 1 and s ≥ 1 is graphically represented in 3D.

4. Curvilinear Regression Model

The practical use of the HA index in the curvilinear regression models for benzenoid hydrocarbon’s properties, such as BP, π-electron, molecular weight (MW), polarizability (PO), molar volume (MV), and molar refractivity (MR), is examined in this section. The regression models show that the properties that are being studied have a substantial link with the HA index. The following regression models have been examined:

()

In this regression equation, Y stands for the dependent variable, A represents the regression constant, and B_i where i = 1, 2, 3 are the regression coefficients associated with independent variables X_i where i = 1, 2, 3. The parameter n indicates the sample size used for constructing the regression equation, while r denotes the correlation coefficient, SE represents the standard error of the estimates, MSE indicates mean square error, RMSE is the root-mean-square error, and F signifies Fisher’s statistic. It is obvious that the optimal prediction model will minimize the error. The structures of 22 benzenoid hydrocarbons considered for this study are illustrated in Figure 6.

Table 7 displays the experimental values of the physicochemical properties of 22 benzenoid hydrocarbons alongside their corresponding HA index values.

Table 7. Experimental values of benzenoid hydrocarbons and HA index.

Derivatives of benzene	HA	BP	π -elec	MW	PO	MV	MR
Benzene	6	78.8	8	78.11	10.4	89.4	26.3
Naphthalene	10.84	221.5	13.683	128.17	17.5	123.5	44.1
Phenanthrene	15.76	337.4	19.448	178.23	24.6	157.7	61.9
Anthracene	15.68	337.4	19.314	178.23	24.6	157.7	61.9
Chrysene	20.68	448	25.192	228.3	31.6	191.8	79.8
Benzo[a]anthracene	20.6	436.7	25.101	228.3	31.6	191.8	79.8
Triphenylene	20.76	425	25.275	228.3	31.6	191.8	79.8
Tetracene	20.52	436.7	25.188	228.3	31.6	191.8	79.8
Benzo[a]pyrene	22.6	495	28.222	252.3	35.8	196.1	90.3
Benzo[e]pyrene	24.36	467.5	28.336	252.3	35.8	196.1	90.3
Perylene	23.68	467.5	28.245	252.3	35.8	196.1	90.3
Anthanthrene	26.52	497.1	31.253	276.3	40	200.4	100.8
Benzo[ghi]perylene	23.68	501	31.425	276.3	40	200.4	100.8
Dibenz[a.c]anthracene	25.6	518	30.942	278.3	38.7	225.9	97.6
Dibenz[a.h]anthracene	25.52	524.7	30.881	278.3	38.7	225.9	97.6
Dibenz[a.j]anthracene	25.52	524.7	30.88	278.3	38.7	225.9	97.6
Picene	25.6	519	30.43	278.3	38.7	225.9	97.6
Coronene	29.52	525.6	34.572	300.4	44.1	204.7	111.4
Dibenzo[a.h]pyrene	28.52	552.3	33.928	302.4	42.9	230.2	108.1
Dibenzo[a.i]pyrene	28.52	552.3	33.954	302.4	42.9	230.2	108.1
Dibenzo[a.l]pyrene	27.6	552.3	34.031	302.4	42.9	230.2	108.1
Pyrene	18.86	404	22.506	202.25	28.7	162	72.5

The curvilinear regression model yields correlation coefficients (denoted as r) between the HA index and physicochemical properties of benzenoid hydrocarbons.

From Figure 7, it is clear that π-electron, MV, PO, and MR have the best correlation coefficient in the linear, quadratic, and cubic models.

Linear regression equations: The following is a consideration of the linear regression models for the HA Index using Equation (2):

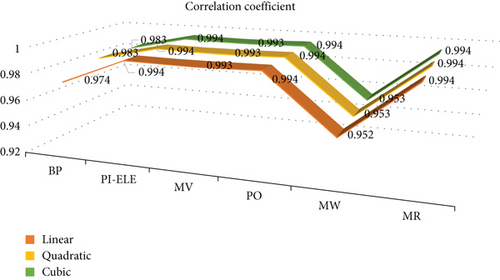
Table 8 provides the metrics utilized in linear regression analysis.

Table 8. Metrics of the linear regression model.

Properties	r²	F	SE	MSE	RMSE
BP	0.948	364.917	27.129	735.998	27.129
π -elec	0.988	160.782	0.783	0.613	0.783
MW	0.986	1420.804	7.097	80.356	7.096
PO	0.987	1525.917	1.007	1.013	1.006
MV	0.905	191.483	11.461	131.351	11.460
MR	0.987	1856.649	2.513	6.315	2.513

Quadratic regression equations: The following is a consideration of the quadratic regression models for the HA Index using Equation (3):

Table 9 provides the metric used in a quadratic regression analysis.

Table 9. Metrics of the quadratic regression model.

Properties	r²	F	SE	MSE	RMSE
BP	0.984	569.017	15.648	244.849	15.648
π -elec	0.988	791.701	0.788	0.620	0.787
MW	0.987	745.003	6.935	48.090	6.935
PO	0.987	733.076	1.027	1.055	1.027
MV	0.920	109.874	10.787	116.351	10.787
MR	0.987	748.379	2.563	6.569	2.563

Cubic regression equations: The following is a consideration of the cubic regression models for the HA index using Equation (4):

Table 10 presents the metrics employed in cubic regression analysis.

Table 10. Metrics of the cubic regression model.

Properties	r²	F	SE	MSE	s
BP	0.984	368.777	15.874	251.971	15.874
π -elec	0.989	530.830	0.786	0.617	0.786
MW	0.988	512.821	6.828	46.623	6.828
PO	0.988	474.546	1.042	1.087	1.043
MV	0.927	76.438	10.598	112.321	10.598
MR	0.988	486.166	2.597	6.744	2.597

The aforementioned curvilinear regressions were calculated with a significance level of 0.0001. As evident from the calculated values, the π-electron exhibits the minimum error, followed by PO and MR. Figures 8, 9, 10, 11, 12, and 13 show the linear, quadratic, and cubic regression graph models and compares them with the HA index and physical and chemical properties.

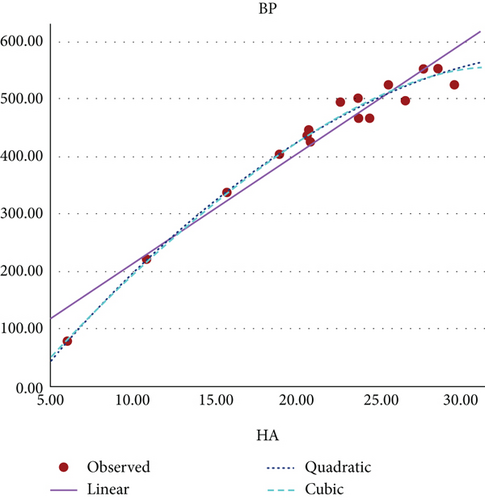
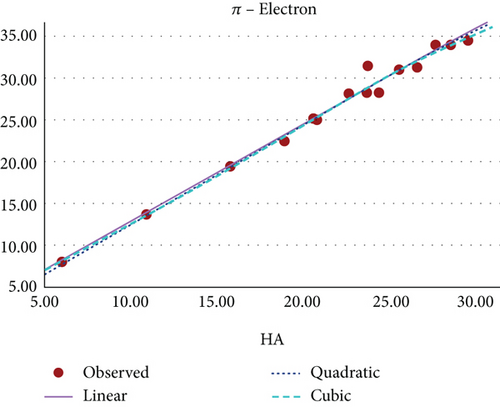
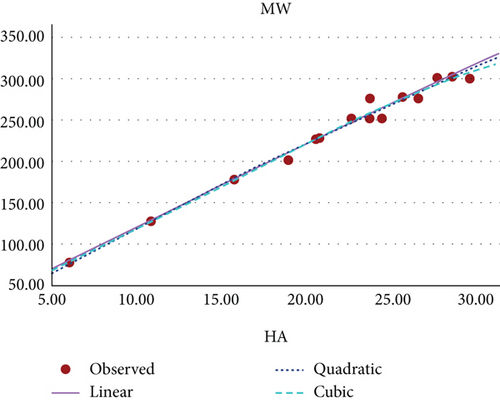
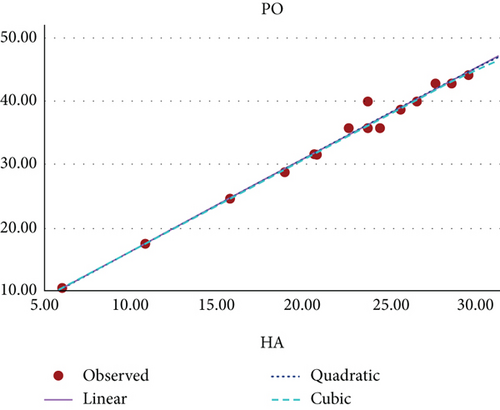
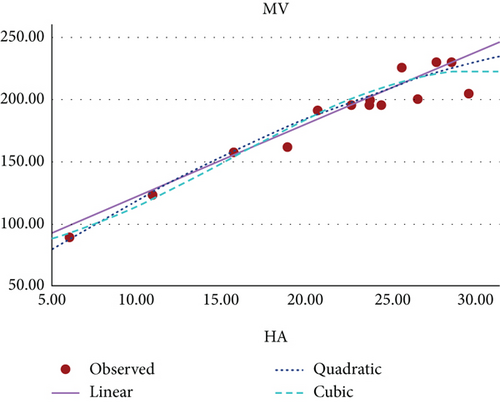
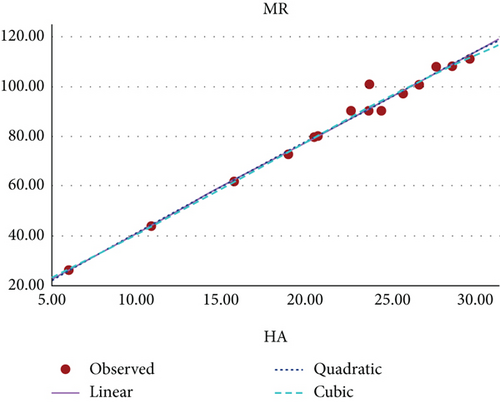
Figure 8 shows the scatter plot for the curvilinear regression model of BP and HA index of benzenoid hydrocarbons.

Figure 9 shows the scatter plot for the curvilinear regression model of π-electron and HA index of benzenoid hydrocarbons.

Figure 10 shows the scatter plot for the curvilinear regression model of MW and HA index of benzenoid hydrocarbons.

Figure 11 shows the scatter plot for the curvilinear regression model of PO and HA index of benzenoid hydrocarbons.

Figure 12 shows the scatter plot for the curvilinear regression model of MV and HA index of benzenoid hydrocarbons.

Figure 13 shows the scatter plot for the curvilinear regression model of MR and HA index of benzenoid hydrocarbons.

The curvilinear models suggests that the HA index demonstrates the highest potential as a predictive index for π-electron energy, with benzenoid hydrocarbon’s MR and PO following closely behind. Figures 8, 9, 10, 11, 12, and 13 present a visual representation in the form of scatter diagrams, illustrating the variations in each model with respect to the HA index.

In [22], the authors have evaluated the effectiveness of multiplicative and scalar multiplicative descriptors in predicting four physicochemical properties BP, log P, retention index, and enthalpy of 22 benzenoid hydrocarbons using the QSAR/QSPR models. The study proposes that scalar multiplicative descriptors offer a superior alternative to multiplicative descriptors, analyzing their predictive capabilities using entropy measures. In this paper, we also explore the chemical applicability of the HA index for some benzenoid hydrocarbons in predicting six properties that are BP, π-elec, MW, PO, MV, and MR using a curvilinear regression model. Among these, three properties such as π-electron energy, MR, and PO show high predictability.

5. Conclusion

The exploration of the HA index for the Mycielskian graphs unveils significant insights into their structural properties, offering a new perspective on their behavior in various contexts. This qualitative analysis highlights the importance of the HA index in understanding the intricate molecular structure of graphene. Through the study of benzenoid hydrocarbons, curvilinear regression models encompassing linear, quadratic, and cubic equations demonstrate promising trends and patterns. These models suggest that the HA index is a highly effective predictor of π-electron energy, MR, and PO. The findings underscore the critical role of topological indices in the field of chemistry, especially in the realm of drug design and development. This study provides researchers with valuable insights into the practical applications of the HA index across a variety of chemical compounds.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this manuscript.

Open Research

Data Availability Statement

The data used have been included in the manuscript.

References

1 Arockiaraj M., Campena F. J. H., Greeni A. B., Ghani M. U., Gajavalli S., Tchier F., and Jan A. Z., QSPR Analysis of Distance-Based Structural Indices for Drug Compounds in Tuberculosis Treatment, Heliyon. (2024) 10, no. 2, e23981, https://doi.org/10.1016/j.heliyon.2024.e23981, 38293487.
10.1016/j.heliyon.2024.e23981
CAS PubMed Web of Science® Google Scholar
2 Arockiaraj M., Paul D., Clement J., Tigga S., Jacob K., and Balasubramanian K., Novel Molecular Hybrid Geometric-Harmonic-Zagreb Degree Based Descriptors and their Efficacy in Qspr Studies of Polycyclic Aromatic Hydrocarbons, SAR and QSAR in Environmental Research. (2023) 34, no. 7, 569–589, https://doi.org/10.1080/1062936X.2023.2239149, 37538006.
10.1080/1062936X.2023.2239149
CAS PubMed Web of Science® Google Scholar
3 Awan N. H., Ghaffar A., Tawfiq F. M., Mustafa G., Bilal M., and Inc M., QSPR Analysis for Physiochemical Properties of New Potential Antimalarial Compounds Involving Topological Indices, International Journal of Quantum Chemistry. (2024) 124, no. 11, e27391, https://doi.org/10.1002/qua.27391.
10.1002/qua.27391
CAS Web of Science® Google Scholar
4 Rasheed M. W., Mahboob A., and Hanif I., Uses of Degree-Based Topological Indices in Qspr Analysis of Alkaloids With Poisonous and Healthful Nature, Frontiers in Physics. (2024) 12, 1–18.
10.3389/fphy.2024.1381887
Web of Science® Google Scholar
5 Zaman S., Yaqoob H. S. A., Ullah A., and Sheikh M., QSPR Analysis of Some Novel Drugs Used in Blood Cancer Treatment Via Degree Based Topological Indices and Regression Models, Polycyclic Aromatic Compounds. (2024) 44, no. 4, 2458–2474, https://doi.org/10.1080/10406638.2023.2217990.
10.1080/10406638.2023.2217990
CAS Web of Science® Google Scholar
6 Randic M., Characterization of Molecular Branching, Journal of the American Chemical Society. (1975) 97, no. 23, 6609–6615, https://doi.org/10.1021/ja00856a001, 2-s2.0-8644280181.
10.1021/ja00856a001
CAS Web of Science® Google Scholar
7 Zhong L., The Harmonic Index for Graphs, Applied Mathematics Letters. (2012) 25, no. 3, 561–566, https://doi.org/10.1016/j.aml.2011.09.059, 2-s2.0-80955166259.
10.1016/j.aml.2011.09.059
Web of Science® Google Scholar
8 Fajtlowicz S., On Conjectures of Graffiti-II, Congressus Numerantium. (1987) 60, 187–197.
Google Scholar
9 Vukičević D. and Furtula B., Topological Index Based on the Ratios of Geometrical and Arithmetical Means of End-Vertex Degrees of Edges, Journal of Mathematical Chemistry. (2009) 46, no. 4, 1369–1376, https://doi.org/10.1007/s10910-009-9520-x, 2-s2.0-70350166990.
10.1007/s10910-009-9520-x
CAS Web of Science® Google Scholar
10 Albalahi A. M., Ali A., Alanazi A. M., Bhatti A. A., and Hamza A. E., Harmonic-Arithmetic Index of (Molecular) Trees, Contributions to Mathematics. (2022) 7, 41–47, https://doi.org/10.47443/cm.2023.008.
10.47443/cm.2023.008
Google Scholar
11 Ali A., Milovanović E., Stankov S., Matejić M., and Milovanović I., Inequalities Involving the Harmonic-Arithmetic Index, Afrika Matematika. (2024) 35, no. 2, 1–10, https://doi.org/10.1007/s13370-024-01183-8.
10.1007/s13370-024-01183-8
Web of Science® Google Scholar
12 Mycielski J., Sur le coloriage des graphs, Colloquium Mathematicae. (1955) 3, no. 2, 161–162.
10.4064/cm-3-2-161-162
Google Scholar
13 Stiebitz M., Beiträge zur Theorie der färbungskritischen Graphen, 1985, PhD diss., https://www.deutsche-digitale-bibliothek.de/item/PG2LN6GYMPMTW6GAM7T33VNNZZTJKEDO.
Google Scholar
14 De N., Computing Certain Topological Indices of Generalised Mycielskian Graphs, International Journal of Discrete Mathematics. (2017) 2, no. 3, 112–118.
Google Scholar
15 Chanda S. and Iyer R. R., On the Sombor Index of Sierpiński and Mycielskian Graphs, Communications in Combinatorics and Optimization. (2025) 10, no. 1, 20–56.
Web of Science® Google Scholar
16 Arockiaraj M., Raza Z., Fiona J. C., Abraham J., Shalini A. J., and Balasubramanian K., Topological Descriptors, Entropy Measures and NMR Spectral Predictions for Nanoporous Graphenes With [14] Annulene Pores, International Journal of Quantum Chemistry. (2024) 124, no. 1, e27284, https://doi.org/10.1002/qua.27284.
10.1002/qua.27284
Web of Science® Google Scholar
17 Ravi V. and Desikan K., Neighbourhood Degree-Based Topological Indices of Graphene Structure, Biointerface Research in Applied Chemistry. (2021) 11, no. 5, 13681–13694.
10.33263/BRIAC115.1368113694
CAS Web of Science® Google Scholar
18 Shigehalli V. S. and Kanabur R., Computation of New Degree-Based Topological Indices of Graphene, Journal of Mathematics. (2016) 2016, no. 1, 4341919, https://doi.org/10.1155/2016/4341919, 2-s2.0-85014082987.
10.1155/2016/4341919
Google Scholar
19 Shanmukha M. C., Usha A., Kulli V. R., and Shilpa K. C., Chemical Applicability and Curvilinear Regression Models of Vertex-Degree-Based Topological Index: Elliptic Sombor Index, International Journal of Quantum Chemistry. (2024) 124, no. 9, e27376, https://doi.org/10.1002/qua.27376.
10.1002/qua.27376
CAS Web of Science® Google Scholar
20 Arockiaraj M., Greeni A. B., and Kalaam A. R. A., Linear Versus Cubic Regression Models for Analyzing Generalized Reverse Degree Based Topological Indices of Certain Latest Corona Treatment Drug Molecules, International Journal of Quantum Chemistry. (2023) 123, no. 16, e27136, https://doi.org/10.1002/qua.27136.
10.1002/qua.27136
CAS Web of Science® Google Scholar
21 Arockiaraj M., Clement J., and Balasubramanian K., Analytical Expressions for Topological Properties of Polycyclic Benzenoid Networks, Journal of Chemometrics. (2016) 30, no. 11, 682–697, https://doi.org/10.1002/cem.2851, 2-s2.0-84991728152.
10.1002/cem.2851
CAS Web of Science® Google Scholar
22 Paul D., Arockiaraj M., Jacob K., and Clement J., Multiplicative Versus Scalar Multiplicative Degree Based Descriptors in QSAR/QSPR Studies and Their Comparative Analysis in Entropy Measures, European Physical Journal Plus. (2023) 138, no. 4, https://doi.org/10.1140/epjp/s13360-023-03920-7.
10.1140/epjp/s13360-023-03920-7
Web of Science® Google Scholar

All articles

Harmonic–Arithmetic Index for the Generalized Mycielskian Graphs and Graphenes With Curvilinear Regression Models of Benzenoid Hydrocarbons

Abstract

1. Introduction

2. Generalized Mycielskian Graph

2.1. Bounds for HA Index of the Generalized Mycielskian Graph

2.2. HA Index of the Generalized Mycielskian Graph

3. HA Index of Graphene

4. Curvilinear Regression Model

5. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Harmonic–Arithmetic Index for the Generalized Mycielskian Graphs and Graphenes With Curvilinear Regression Models of Benzenoid Hydrocarbons

Abstract

1. Introduction

2. Generalized Mycielskian Graph

2.1. Bounds for HA Index of the Generalized Mycielskian Graph

2.2. HA Index of the Generalized Mycielskian Graph

3. HA Index of Graphene

4. Curvilinear Regression Model

5. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information