Within the framework of China’s “Dual Carbon” strategy, numerous cities have articulated visions and objectives for optimizing the travel structure of transport to further urban sustainable development goals. A critical challenge lies in minimizing CO₂ emissions from road networks while meeting diverse transport demands. However, at present the mode shares are set arbitrarily and may not be realistically achievable. When government officials establish travel structure targets, they may not adequately consider the intricate balance between residents’ travel demands and low-carbon development objectives. To address this issue, this paper presents a dual-layer optimal allocation model for transport modes, which simultaneously addresses travel demand management and carbon emission control. The upper-layer model evaluates carbon emissions with the help of speed-dependent emission factors for various transport modes, and the lower-layer model leverages the logit Stochastic User Equilibrium (logitSUE) model to yield the velocities of road segments under a diverse array of travel structures. A sophisticated fusion algorithm, integrating the Dial_MSA algorithm with a genetic algorithm (GA), is developed to solve the model. The proposed model and algorithm are tested on a large-scale real network and show its robustness and scalability. The optimal travel structure derived from this study can provide a theoretical foundation and empirical support for policymakers and urban planners in setting transport infrastructure goals and strategies.

1. Introduction

“Transport mode optimization” is an indispensable choice for low-carbon development of urban road transport. In recent years, many cities have established objectives for modal split to align with urban sustainable development goals. In Europe, 36 cities including Brussels, Milan, Munich, and Edinburgh collectively signed the “Brussels Charter” pledging to attain a minimum 15% share of bicycle commuting by 2020 [1]. As early as 2009, Copenhagen set an ambitious target to become the world’s first carbon-neutral city by 2025 [2]. Within its carbon neutrality roadmap, a clear goal was articulated to achieve a modal split in which active and public transport modes account for more than 75% of all travel. Thus, it is evident that optimizing the urban transport modal split is crucial for advancing low-carbon development in road transport.

In the context of China’s “Dual Carbon” strategy, the “modal shift” in transport has emerged as a crucial pathway to achieving the goals of peaking carbon emissions and achieving carbon neutrality. Numerous cities have, accordingly, outlined visions and targets for the optimization of their transport modalities. The Wuhan Urban Master Plan (2016–2030) set forth a target composition for future transport development: “40% public transport, 40% nonmotorized modes, and 20% private motorized vehicles [3].” The 14th Five-Year Plan of Hunan Province stipulates that, by 2025, the share of green travel in cities with a resident urban population exceeding one million should surpass 50% [4]. In parallel, Nanjing’s 14th Five-Year Plan proposes that the contribution of public transport to motorized travel should reach 65% by 2030 [5]. These objectives underscore the aspirations of major Chinese cities to optimize travel modes, amidst the pressing need for carbon control, and to transition toward zero or low-carbon mobility solutions.

However, at present the mode shares are set arbitrarily and may not be realistically achievable. When government officials establish these aforementioned targets, they often lack a solid theoretical foundation and may not adequately consider the intricate balance between residents’ travel demands and low-carbon development objectives. This deficiency implies that they might not be able to fully and judiciously contemplate the exceedingly intricate and nuanced equilibrium that exists between the travel requisites of the populace and the aims of low-carbon progression.

Most existing research on transport structure allocation has focused on maximizing the potential for carbon emission reduction, while neglecting the analysis of residents’ travel choice behaviors and travel demands, resulting in outcomes that deviate from actual requirements. On the other hand, previous studies have established emission models with simplified assumptions about constant travel speeds and emission factors despite changes in travel modes. However, these assumptions may lead to increased carbon emissions, as the operational state of road traffic flow would undergo notable changes following alterations in travel patterns.

To overcome the abovementioned limitations, the primary aim of this study is to ascertain the ideal proportion of different transport modes that simultaneously satisfies travel demand and investigate the maximum potential for reducing emissions through modal shift. It introduces a carbon emission model with dynamic emission factors that captures the impact of changes in travel structure on emissions. The findings could offer empirical data support for governmental agencies and transport planners.

The main contributions of this paper are as follows. First, a dual-layer optimal allocation model for transport modes is established that considers both travel demand and carbon emissions. The model effectively captures the impact of changes in travel structure on traffic flow conditions and subsequently on vehicle speeds and emissions. Second, a sophisticated fusion algorithm that seamlessly integrates Dial_MSA with GA id is designed based on the characteristics of the problem. Third, through the experiments on algorithm performance and sensitivity analysis, the effectiveness of the model and algorithm is verified, and some insights are provided for carbon emission reduction.

The rest of the paper is organized as follows. Section 2 reviews related works. Section 3 describes the problem and presents the model. Section 4 elaborates the solution algorithm. Section 5 shows the results of computational experiments and Section 6 presents scenario analysis and results. Section 7 concludes the paper and points out the directions for future research and provides some policy recommendations.

2. Literature Review

In recent years, the carbon reduction benefits resulting from optimized travel patterns have received considerable attention and have been the subject of numerous scholarly investigations. In terms of model construction, many scholars investigate the relationship between transport modes and the environment by establishing objective functions or constraints that take into account fuel consumption or emission metrics. Model analysis and construction range from macroaggregation models to microanalysis models.

2.1. Macroaggregation Modeling

Aggregate models typically represent modal shifts using exogenous assumptions on mode shares or using mode share elasticities which only depend on cost. Salvucci and his colleagues [6] incorporated substitution elasticities, and Daly et al. [7] imposed constraints on travel time expenditures and infrastructure investments into an integrated energy optimization model, which utilizes linear programming techniques to determine the most cost-effective transport configurations. Mocanu, Joshi, and Winkler [8] considered the poorer accessibility to workplaces caused by the shift from cars to public buses and adopted a data-driven approach to investigate the potential for a modal shift from car to public transport for German commuters. Using scenario analysis, Ngoc et al. [9] projected that improving public transport could reduce Hanoi’s traffic emissions by 21.11% by 2030. O’Riordan et al. [10] devised an Irish Passenger Transport Emissions and Mobility (IPTEM) model to quantify the energy consumption and emission intensity of passenger transport in Ireland, considering the shift toward low-carbon modalities.

2.2. Discrete Choice Modeling

Due to the inability of macroaggregate models to analyze deeper factors influencing mode choice, such as travel time budgets and infrastructure availability, many scholars have attempted to construct discrete choice models to analyze the potential for carbon emission reduction through modal shifts. Those disaggregate local studies containing data about individual trips, typically obtained from surveys and location data, can comprehensively consider the factors that impact mode choice. Thomas and Serrenho [11] used a discrete choice model to evaluate potential modal shifts against factors that influence mode choice, considering constraints that determine which modes of transport are suitable for making a trip, such as passenger characteristics, trip characteristics, and public transport capacity. After analyzing the commuting behavior at the Technical University of Madrid and its impact on climate change, Sobrino and Arce [12] proposed a set of policy interventions such as promoting shared commuting initiatives, economic incentives for public transport, and integrated parking management. Tiwari, Jain, and Rao [13] considered several important aspects (including mobility, safety, and built environment) in determining travel modes and emphasized that the maximized reduction in CO₂ emissions could be achieved when the infrastructure for public and nonmotorized transport is enhanced. Bantis and Haworth [14] explored the possibility to include both elements of the environment and individual characteristics of travelers in the task of transportation mode transition detecting using dynamic Bayesian Networks. Izdebski et al. [15] utilized the discrete choice (ordinal logit) model to explore the possibility of using short sea shipping (SSS) as a sustainable freight modal alternative from four aspects: leadership buy-in, emergency logistics, public policy, and sustainability. Chen et al. [16] have developed a green policy design model for coastal transportation systems, incorporating factors such as transportation costs and carbon emission taxes.

2.3. Mathematical Optimization Model

To more intuitively analyze the relationship between transport modes and the environment, as well as to explore the carbon reduction benefits of various factors, some scholars have attempted to conduct relevant research directly from a mathematical modeling perspective, using some linear or nonlinear mathematical optimization models. Zhang [17] developed an urban transport mode optimization model under carbon reduction objectives. This model, considering four facets—transport management, resources, technology, and land use, provides paths for optimizing urban travel structure and methods for policy formulation. Lu et al. [18] introduced model of public transit mode proportion (MPMP) with the goal of minimizing CO₂ emissions in road networks through the optimization of the public transport share. Filom and Razavi [19] discussed the relationship between transport modalities and environmental concerns and proposed an optimization model using mixed integer linear programming (MILP), incorporating carbon tax as a surrogate measure for environmental costs. The results of this study illustrate the considerable potential for increasing the utilization of more environmentally. Eslamippor [20] developed a two-objective mathematical model to investigate the routing of hybrid vehicles, minimizing facility establishment, vehicles, fuel costs, and customer waiting time. The proposed model was solved by multiobjective particle swarm optimization (MPSO) and NSGA-II in large scale.

2.4. Summary

Table 1 summarizes the studies reviewed where modal shift has been explicitly included in modeling and analyzed as a strategy for reducing emissions and energy use. The aforementioned studies underscore the importance of demand-side reduction and modal shift in achieving our climate goals. However, based on the analysis and summary of the aforementioned literature, we can identify two clear gaps in the literature.

Table 1. Comparison of different transport modal shift methodologies.

Authors	Feasible modes constraints	Travel behavior constraints	Dynamic emission factors	Modes considered	Model type
Salvucci et al. [6]	Yes	No	No	ALL	Linear programming
Daly et al. [7]	Yes	No	No	ALL	Linear programming
Mocanu, Joshi, and Winkler [8]	No	No	No	Public transport	Macroaggregation model
Ngoc et al. [9]	No	No	No	Urban modes	Macroaggregation model
O’Riordan et al. [10]	No	No	No	Road transport	Macroaggregation model
Thomas and Serrenho [11]	Yes	Yes	No	ALL	Discrete choice model
Sobrino and Arce [12]	No	Yes	No	Urban modes	Discrete choice model
Tiwari, Jain, and Rao [13]	No	Yes	No	Public transport	Discrete choice model
Bantis and Haworth [14]	No	Yes	No	ALL	Multiple logistic regression
Izdebski et al. [15]	Yes	Yes	No	SSS	Ordinal logit
Chen et al. [16]	No	Yes	No	Water carrier	Nonlinear programming
Zhang [17]	No	Yes	No	Public transport	Multiobjective programming
Lu et al. [18]	Yes	Yes	No	Rail transit, bus, and taxi	Linear programming
Filom and Razavi [19]	No	No	No	ALL	MILP
Eslamippor [20]	Yes	No	No	Hybrid vehicle	Biobjective model

First, the mode shares applied in the aforementioned scenario analyses are set arbitrarily and may not be realistically achievable. These models have not thoroughly taken into account the travel demands of residents, such as requirements for travel time, comfort, and convenience. In reality, as the living standards of city dwellers continually rise, the demand for superior travel quality has been escalating. Assurances of minimized travel time, enhanced comfort, and increased infrastructure availability are pivotal factors that influence residents’ choices of transport modes. However, the systematic assessment of the prospects for modal shift, considering the constraints imposed by trip characteristics, passenger preferences, and infrastructure availability, remains unclear. Furthermore, some studies have overlooked the constraints on the feasibility of travel models, such as the travel distance and coverage area of various modes of transportation.

Second, there is a lack of analysis and modeling regarding the correlation between travel structure shifts, network service levels, and network carbon emissions. These models do not capture the alterations in traffic flow states induced by changes in travel structures, nor do they reflect the modifications in vehicular emissions resulting from changes in traffic flow states. Motor vehicle activity data and emission factors are the two main elements for estimating carbon emissions. In the modeling processes of the aforementioned papers, the estimation of carbon emissions in the objective functions typically employs a macro-level estimation approach based on fixed emission factors. This means that, regardless of changes in travel structure, the emission factors for various modes of travel remain constant (i.e., they are independent of speed). The emission factors are sourced from static databases that provide average carbon emission factors for motor vehicles. These are static emission factors that do not consider variations in vehicular emissions under disparate traffic flow conditions. For example, Mocanu, Joshi, and Winkler [8] estimated the overall emissions by multiplying the distance traveled using each transport mode with emissions and energy conversion factors. O’Riordan et al. [10] adopted fuel consumption and fuel emission factors to calculate passenger transport CO₂ emissions. Lu et al. [18] estimated carbon emissions by multiplying the emission factors per unit travel distance for each mode of transport by the corresponding activity parameters.

The allocation of transport modes constitutes the third phase in the four-step transport planning process, which defines the proportion of different transport means chosen by commuters. The predictive outcomes of this phase are the origin–destination (OD) distribution volumes for various transport modes, which underpin traffic distribution. Hence, given the same OD travel demand, divergent travel structures will yield different OD volumes for each mode of transport, and subsequently, posttraffic distribution, the volume and average velocity on different road sections will alter [21]. Essentially, vehicles will operate at varying speeds in different traffic flow conditions, and these different speeds consequently signify dissimilar emission rates [22–26]. Thus, modifications in the structure of travel modes can cause shifts in the total carbon emissions of the entire road network. Consequently, previous research may not have been able to accurately estimate carbon emission levels under varying road traffic flow operational conditions and hence cannot precisely assess the localized carbon emission levels related to road traffic.

Hence, to rectify the deficiencies observed in preceding studies, this paper proposes a dual-layer optimization model to describe the correlation between travel modal shift optimization, road network service level, and road network carbon emissions, subject to a set of constraints imposed by trip characteristics, passenger preferences, travel time budge, and infrastructure availability. By evaluating the varied traffic allocation outcomes and road network carbon emissions corresponding to diverse travel structures, the model ascertains the optimal urban travel structure that yields the minimum carbon emissions across the road network.

3. Modeling Strategy

Transport refers to the means of facilitating the movement of people or goods. Guided by the principles of low-carbon road transport development, the fundamental objective in optimizing the travel structure to meet carbon control demands is to harmonize environmental conservation with residents’ mobility requirements. Therefore, the core principles governing the control and optimization of the travel structure should effectively address both the travel demands of residents and the imperative to control carbon emissions. The model operates under the following assumptions:

1.
The distribution of OD demand within peak hours for the road network is known and fixed [27, 28].
2.
Travelers’ route selection behavior adheres to the principles of stochastic user equilibrium [29, 30].
3.
The scenario of multiple transfers during a single trip is not considered [31].
4.
During the process of optimizing the travel structure, the potential increase in carbon emissions resulting from energy transition or the adoption of emerging technologies (e.g., connected vehicle technology) is not taken into consideration.

A dual-layer model is proposed to optimize the travel structure, with the proportion of different travel modes serving as the decision variables. The upper-level model constitutes a carbon emissions estimation model, which seeks to minimize the CO₂ emissions from the road network while taking into account the proportions of different travel modes as decision variables. This model is utilized to compute the carbon emissions levels across the road network under varying proportions of travel modes. On the other hand, the lower-level model is a Logit Stochastic User Equilibrium (Logit SUE) traffic assignment model. It outputs the traffic flows and travel speed parameters of each road segment for the upper-level model to assess the carbon emissions for each road segment, thereby aggregating the overall carbon emissions of the entire road network.

This paper adopts the total carbon emissions as the evaluation metric, aiming to optimize the road network’s CO₂ emissions by minimizing their overall amount. In previous research, we developed a carbon emission mesoscopic model based on dynamic emission factors (emission factors that vary with speed) to estimate the overall carbon emissions of the road network under different traffic flow conditions [32]. This model can describe changes in traffic flow conditions resulting from modal shifts and subsequently evaluate the changes in overall road traffic carbon emissions. Therefore, in this study, we employ this model to assess road network carbon emissions. The basic expression of the model is as follows:

()

where E denotes the total carbon emissions from the road network (in grams, g).

denotes the traffic flow of vehicle type i powered by energy source k on road segment a (in vehicles). EF_ik(v_a) signifies the carbon emission factor of vehicle type i powered by energy source k on road segment a at speed v_a (in grams per kilometer, g/km). l_a signifies the length of road segment a (in kilometers, km).

Speed-dependent emission factors have not yet been used to address the optimization of travel structure, primarily because acquiring emission factors for different vehicle speeds was previously a laborious and time-consuming task. We previously proposed an emission factor acquisition method based on localized fuel consumption and speed correction factors (SCFs) [33]. This method is applicable for efficiently obtaining localized emission factor data for any city. The detailed methods for obtaining these two critical parameters are provided in reference [33].

()

where

represents the corresponding baseline emission factor (BEF) for the vehicle type i powered by energy source k at the average speed

. It can be derived by baseline fuel consumption (BFC) using the carbon balance method. SCF_i(v) denotes the emission factor correction coefficient for the vehicle type i at speed v.

3.1. Model’s Variables and Parameters

A brief definition of indices, parameters, decision variables, and their associated notations used in this study is presented in Table 2.

Table 2. Notations.

Indices	Definition
i	Index of travel mode, i ∈ I
a	Index of road segment, a ∈ A
k	Index of energy source, k ∈ K

Sets	Definition

I	Set of travel modes
A	Set of road segments in the road network
K	Set of energy sources

Parameters	Definition

E	Total carbon emissions from the road network (measured in grams, g)
	Traffic flow of vehicle type i powered by energy source k on road segment a (measured in vehicles)
EF_ik(v_a)	Carbon emission factor of vehicle type i powered by energy source k on road segment a at speed v_a (in grams per kilometer, g/km)
EF₅	Carbon emission factor for rail transit (in grams per passenger-kilometer, g/pkm)
l_a	Length of road segment a (in kilometers, km)
	Baseline emission factor (BEF) for the vehicle type i powered by energy source k at the average speed
SCF_i(v)	Emission factor correction coefficient for the vehicle type i at speed v
R	Total number of travel trips during peak hours in the city
	Average travel distance of the i-th travel mode (in kilometers, km)
δ_i	Proportion of the i-th travel mode in motorized travel (%)
D	Overall resident travel volume during peak hours (in passenger-kilometers, pkm)
t_i	Travel time per kilometer for the i-th travel mode (in min/km)
T	Tolerance limit for unit distance average travel time (in min/km)
C_i	Average area per person for the i-th travel mode (measured in square meters, m²)
N_i	Average passenger occupancy for the i-th travel mode (measured in persons)
C	Lower tolerance limit for residents’ comfort during travel (measured in m²/person)
J_i	Average transfer time for i-th travel mode (measured in minutes)
J	Upper tolerance limit of the average transfer time that residents can endure (measured in minutes)

Decision variable	Definition

p_i	Proportion of the i-th travel mode in total travel trips (%)

3.2. Upper-Level Formulation

3.2.1. Objective Function

Based on the above analysis, the upper-level model is formulated with the specific goal of minimizing the overall CO₂ emissions from the road network. As the carbon emission factor for rail transit remains independent of road operating conditions, this study differentiates the carbon emission estimation method for rail transit from that of road transport. A fixed carbon emission factor is adopted to assess the carbon emissions from rail transit. Furthermore, as nonmotorized transport and walking modes do not generate carbon emissions, their carbon emissions are not accounted for in the objective function. Therefore, we modify equations (1)–(3) as the carbon emission objective function in this study. The model is represented as follows:

()

where E denotes the total carbon emissions from the road network (in grams, g). R represents the total number of travel trips during peak hours in the city. p_i indicates the proportion of the i-th travel mode in total travel trips (%), serving as the decision variable. I = {1, 2, 3, 4, 5}, respectively, represent passenger cars, buses, motorcycles, nonmotorized transport (including bicycles and walking), and rail transit.

signifies the average travel distance of the i-th travel mode (in kilometers, km). EF_ik(v_a) signifies the carbon emission factor of vehicle type i powered by energy source k on road segment a at speed v_a (in grams per kilometer, g/km). The specific estimation method is referenced in equation (2). EF₅ represents the carbon emission factor for rail transit (in grams per passenger-kilometer, g/pkm).

denotes the traffic flow of vehicle type i powered by energy source k on road segment a (in vehicles). l_a signifies the length of road segment a (in kilometers, km). K denotes the set of energy sources. A denotes the set of road segments in the road network. δ_i represents the proportion of the ith travel mode in motorized travel (%), which can be derived from the decision variable p_i.

()

3.2.2. Constraints

3.2.2.1. Constraint 1: Ensuring Travel Demand

In the process of optimizing the travel structure, it is imperative to prioritize the fulfillment of residents’ essential travel demands, considering that different transport modes cater to varying travel distances and accessibility levels. To ensure the satisfaction of resident travel demands, the summation of person-kilometers for all travel modes should equate to the total demand for OD trips during peak hours in the city, as expressed by

()

where D represents the overall resident travel volume during peak hours (in passenger-kilometers, pkm).

3.2.2.2. Constraint 2: Ensuring Travel Time

During commuting hours, residents typically exhibit a higher demand for travel time when making their travel choices. At such times, the importance of travel time for residents outweighs the priority of opting for low-carbon travel options. Based on the operating speeds and reliability for each transport mode, it is evident that during morning and evening peak commuting hours, ground-level public transit experiences decreased attractiveness, while rail transit’s appeal significantly rises due to its immunity to ground traffic conditions. In certain instances, rail transit may even surpass private car transport in terms of attractiveness.

To effectively capture residents’ travel time preferences while selecting travel modes during commuting hours, this paper introduces the “tolerance limit for unit distance average travel time” as the representative metric. This metric delineates the threshold beyond which residents are less willing to tolerate travel time and can be expressed as

()

where t_i represents the travel time per kilometer for the i-th travel mode (in minutes per kilometer, min/km). T denotes the tolerance limit for unit distance average travel time (in minutes per kilometer, min/km). m indicates the number of travel mode categories.

3.2.2.3. Constraint 3: Ensuring Comfort

As urban residents’ living standards continue to improve, their expectations for travel comfort have escalated. In this study, the comfort level of various transport modes during travel is quantified using the “crowding level” metric, which represents the unit area available per person during the travel process. This constraint can be mathematically expressed as

()

where C_i denotes the average area per person for the i-th travel mode (measured in square meters, m²). N_i indicates the average passenger occupancy for the i-th travel mode (measured in persons). C denotes the lower tolerance limit for residents’ comfort during travel (measured in square meters per person, m²/person).

3.2.2.4. Constraint 4: Ensuring Convenience

For residents, travel convenience stands as a crucial determinant in their choice of travel mode, consistently outweighing the priority of reducing urban road traffic carbon emissions. Public transport, due to its fixed routes and stations, generally cannot offer point-to-point services. As a result, residents often need to walk or cycle to access public transit, which also contributes significantly to the relatively lower proportion of public transit usage in certain small to medium-sized cities with underdeveloped public transport facilities.

In this study, the metric “average transfer time per trip” is adopted to quantify the convenience level of various travel modes. Transfer time refers to the duration taken by passengers from their origin to the nearest rail transit or bus station, as well as the waiting time at the station after arrival. It is essential to note that the transfer time for private cars, motorcycles, and nonmotorized transport is negligible. Consequently, to ensure the convenience of residents’ travel, equation (8) must be satisfied.

()

where J_i denotes the average transfer time for i-th travel mode (measured in minutes). J represents the upper tolerance limit of the average transfer time that residents can endure (measured in minutes).

3.2.2.5. Constraint 5: Sum of Proportions Equal to Unity

The fundamental constraint dictates that the sum of proportions for all travel modes must be equal to 1, as represented by the following equation:

()

3.3. Lower-Level Formulation

Within the realm of static traffic assignment methodologies, the SUE traffic assignment model constitutes a variant of the probabilistic allocation model, firmly grounded on the SUE theory. This innovative model abandons the restrictive assumption of users having complete cognizance of their respective routes, thereby offering a more realistic depiction of actual road network conditions. Consequently, the SUE model has emerged as a prominent point of interest in the field. The SUE model is further classified into the Logit loading model and the Probit loading model, delineated on the basis of variations in the probability functions dictating path choice. The Logit SUE model, due to its operational simplicity and enhanced interpretability, has been the cornerstone for numerous advancements within the SUE model framework. In recent years, the Logit SUE model has been increasingly adopted across diverse domains such as road network planning and bus network scheduling, underscoring its widespread applicability and relevance [34–37].

Hence, this study opts for the Logit SUE model as the lower-layer model, which outputs the traffic flows and travel speed parameters of each road segment for the upper-level model. The primary objective of this model is to perform traffic assignment based on OD distribution and provided travel mode proportions. Subsequently, it generates the traffic flow and speed for each road segment in the entire road network. The model is outlined as follows:

()

For a detailed understanding of the specific meanings of each parameter in this model, please refer to the cited literature. Through the aforementioned Logit SUE model, we can determine the traffic flow volume q_a and travel time function t_a for road segment a. Subsequently, by considering the length l_a of road segment a, we can compute the average travel speed v_a for that specific segment. These calculated values of traffic flow volume q_a and average travel speed v_a can then be used as inputs for the upper-level carbon emissions estimation model. This allows us to obtain the total carbon emissions from the road network under different travel structure conditions.

4. Solution Algorithm

The solution algorithm employed in this study aims to optimize the travel structure while simultaneously minimizing the carbon emissions from the road network. The flowchart of the dual-layer model solution algorithm is depicted in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flowchart of the solution algorithm for the dual-level travel structure optimization model.

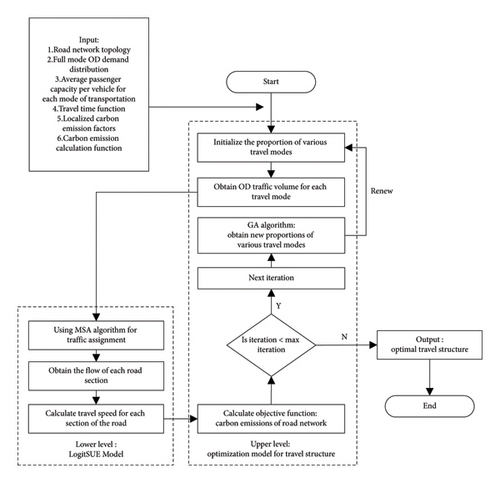
Due to a significant body of literature supporting the efficacy of genetic algorithm (GA) in solving large-scale practical network dual-layer models [38–42], this study integrates the Dial_MSA algorithm from the lower-level model into the GA to solve the upper-level travel structure optimization model.

The algorithm initiates with the lower-level model, reading all input data, including road network data, travel time functions, OD demand matrices, average passenger occupancy for each travel mode, carbon emission factors, and carbon emission calculation functions. The specific algorithm steps are as follows:

1.
Initialize the proportions of each travel mode. As the initial travel structure, this study adopts the current proportions of travel modes obtained from resident travel surveys during the transport planning process.
2.
Load flow. To carry out traffic assignment, the traffic volume attributed to rail transit and nonmotorized transport is removed since they do not belong to road traffic or occupy motorized lanes.
3.
Traffic assignment. Utilizing the initialized travel mode proportions and the average passenger occupancy for each travel mode, the OD demand in person units is converted into traffic volume for each travel mode in vehicle units. The lower-level Dial_MSA algorithm is then applied, utilizing road network data, travel time functions, and the current traffic volumes for each travel mode, to distribute the flow demand matrix to each road segment in the network, thereby obtaining the traffic volume for each segment. The specific and detailed process of the solution of the lower model is presented in Figure 2.

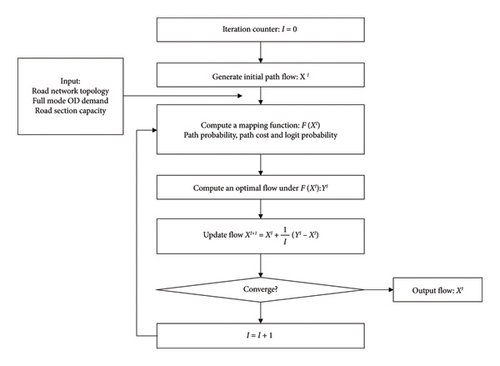
The diagram depicts an iterative process for determining traffic flow distribution in a road network, given the network topology, full mode OD demand, and road section capacity. The process begins with initializing the iteration counter I to zero and generating an initial path flow X. The next step involves computing a mapping function F(X^I), which is used to derive path probability, path cost, and logit probability. Subsequently, the optimal flow Y^I is computed under the mapping function F( X^I ). The flow X^I+1 is then updated and the convergence condition is checked. If the solution has converged, the process outputs the final path flow X^I. Otherwise, the iteration counter I is incremented by one, and the steps are repeated until convergence is achieved.

Subsequently, the Bureau of Public Roads (BPR) function and the segment lengths are used to calculate the average travel speed for each road segment. This speed is then utilized to derive emission factors for different vehicles on different road segments [33]. As the BPR function is a monotonically increasing convex function, and the travel time on segment a depends solely on the flow volume on that segment, the lower-level model can be treated as a convex optimization problem. Consequently, the model possesses a unique global solution and can be solved using any effective convex combination method (such as the MSA algorithm).

3.
Calculate the total carbon emissions for the current iteration of the upper-level model. Based on the results from Step 3, the total carbon emissions from the road network can be computed using the objective function (equation (3)). The CO₂ emission total is obtained by summing the products of road segment lengths, traffic volumes for different travel modes, and corresponding emission factors. Thus, the calculated CO₂ emissions represent the objective function value for the current iteration.
4.
Multiple iterations are conducted to seek the optimal travel structure with the lowest carbon emissions. If the current iteration count is less than the predefined maximum iteration count, the algorithm proceeds to the next iteration, employing the GA algorithm to generate the proportions of travel modes for the subsequent iteration. This iterative process continues until the current iteration count surpasses the predefined maximum iteration count, at which point the algorithm terminates, providing the optimal proportions of travel modes that correspond to the lowest total CO₂ emissions for the road network.

5. Case Study

To validate the effectiveness of the model and the designed algorithms, this study conducted a case analysis using the real urban road network of the central urban area in Changxing County.

5.1. Model Parameters

5.1.1. Changxing County Network

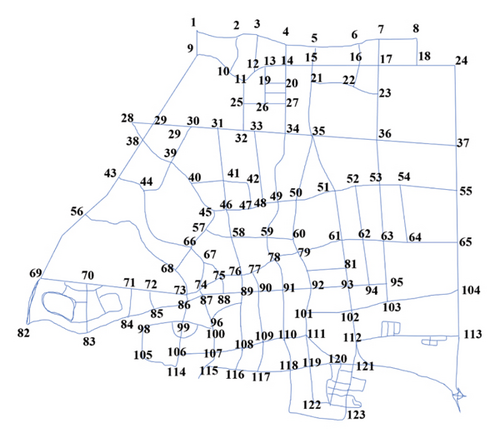
The road network of Changxing County’s central urban area was acquired from OpenStreetMap. The road network comprises a total of 123 road nodes, 26 area centers, and 380 road segments. The transport demand data include 26 OD pairs. The road network’s structure is illustrated in Figure 3.

5.1.2. Traffic Parameters

Currently, Changxing County lacks a rail transit system, and thus, it is not taken into consideration during the travel structure optimization process. Various model parameters such as T and A (upper limit for the average travel time tolerance per unit distance and maximum acceptable transfer time) were obtained from traffic surveys conducted in Changxing County. The total number of peak hour trips amounts to 70,109, with an average single trip distance of 5.5 km. The overall travel volume for residents is 3,85,599 pkm (person-kilometers). The upper limit for the average travel time tolerance per unit distance is set at 1.5 min, while the tolerable congestion limit stands at 1.5 m²/person, and the maximum acceptable transfer time is 13 min. Other transport parameters can be found in Table 3.

Table 3. The values of transport parameters in Changxing County.

Parameters	Units	Passenger car	Public bus	Motorcycle	Nonmotorized
Average travel distance	kilometers (km)	6.5	7.3	4.5	2.5
Average passenger occupancy rate	Passenger (p)	1.8	20.0	1.5	1.0
Average vehicle area	Meters squared (m²)	3.5	15.0	2.0	1.0
Unit kilometer travel time	Minute (min)	1.5	3.0	2.0	7.5
Average transfer time	Minute (min)	0.0	20.0	0.0	0.0

5.1.3. Localized Emission Factors

To assess the average fuel consumption of cars and motorcycles in Changxing County, this study adopts the method of weighted average fuel consumption as mentioned in reference [33] to quantify the fuel consumption of cars. This approach involves calculating the average fuel consumption for each car type based on various engine displacements and the corresponding proportion of vehicles with different engine displacements and then obtaining the weighted average fuel consumption for cars.

Regarding buses, the local fuel consumption data for Changxing County’s buses is obtained from the local bus operating company. According to the fuel consumption statistics provided by the Changxing County Bus Company, the diesel buses consume 22.20 L of fuel per 100 km.

Utilizing the localized CO₂ emission factor retrieval method described in equation (2), the emission factors for cars, buses, and motorcycles in Changxing County are presented in Table 4.

Table 4. Speed-dependent emission factors for various vehicle types in Changxing County.

Transport modes	Fuel type	BFC (L/100 km)	BER (g/km)	SCF
Passenger car	Gasoline	9.07	222.79	See reference [25]
Transit bus	Diesel	22.2	594.87	See reference [25]
Motorcycle	Gasoline	3.67	90.15	See reference [25]

5.2. Computation of the Model

The model parameters mentioned above were applied to the dual-layer optimization model for traffic travel structure, which was specifically designed to address carbon control requirements. By employing our designed solution algorithm, the road network structure data and OD data were inputted to solve the aforementioned model. Computation of the model for the road network in Changxing County was carried out using Intel Core [email protected] GHz with 16 GB RAM. The parameter settings for the GA are based on preliminary experiments and a literature review, aimed at balancing the algorithm’s exploration and exploitation capabilities, thereby improving convergence efficiency and solution quality. Specifically, the population size is set to 100, ensuring sufficient diversity to avoid premature convergence while balancing search capability and computational efficiency. The number of iterations is set to 50, considering the problem’s complexity, to provide adequate runtime for finding high-quality solutions. The crossover rate is set at 0.8 to facilitate gene exchange between individuals and accelerate the emergence of new features. The mutation rate is set at 0.05 to maintain genetic diversity within the population, preventing the algorithm from becoming trapped in local optima. In addition, Simulated Binary Crossover and Polynomial Mutation distributions are used for crossover and mutation distributions, respectively.

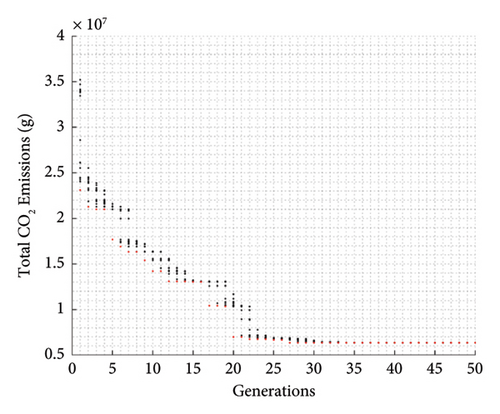
The convergence graph of the objective function during the traffic assignments execution process is depicted in Figure 4.

The ultimate optimal transport travel structure and the current one for Changxing County are depicted in Table 5.

Table 5. The optimal transport travel structure in Changxing County.

Transport modes	Travel structure (optimal) (%)	Travel structure (current) (%)
Passenger car	15.7	41.6
Transit bus	49.4	6.8
Motorcycle	—	11.8
Nonmotorized	34.9	39.8

6. Discussion

6.1. Scenario Analysis

To better understand how these parameters influence the optimal mode allocation and provide more precise and reliable recommendations for policymakers, we employed scenario analysis for key parameters in the model, such as connecting time, demand, and average occupancy rate of buses. Using Section 4 as the baseline scenario (Scenario 0), we considered factors such as urban infrastructure development, advancements in vehicle fuel technology, and policy support to establish the following three future scenarios:

Scenario 1: This scenario considers a 20% increase in demand among residents of Changxing County over the next two to 3 years. However, due to economic constraints, there is no further development in road infrastructure or public transport, meaning all other parameters remain unchanged.
Scenario 2: Building on Scenario 1, this scenario considers the optimization of the public transport network and operational scheduling, which will enhance the accessibility of public buses, reduce residents’ waiting time for buses (i.e., lower J₂), and increase the average occupancy rate of buses (i.e., higher N₂). Simultaneously, residents may face higher travel costs and reduced comfort (i.e., lower A) in this scenario.
Scenario 3: In addition to the conditions of Scenario 2, this scenario considers the significant development of nonmotorized transport. This includes increased urban infrastructure for slow traffic, improved right-of-way protection, and greater convenience for residents to travel by bicycle. Consequently, the travel time per kilometer for nonmotorized trips decreases (i.e., t₄ decreases).

The values of the indicators corresponding to each scenario are presented in Table 6. Using the algorithm proposed in the section, the optimum ratios of passenger cars, public buses, and nonmotorized modes, along with the lowest CO₂ emissions for all the scenarios, are shown in Figure 5.

Table 6. Parameter value changes in different scenarios.

Indicators	Scenario 0	Scenario 1	Scenario 2	Scenario 3
D	385599	462719	462719	462719
J₂	20	20	10	10
N₂	20	20	30	30
t₄	7.5	7.5	7.5	5.5
T	4.5	4.5	4.5	4.5
A	1	1	0.8	0.8
L₃	2.5	2.5	2.5	3.5

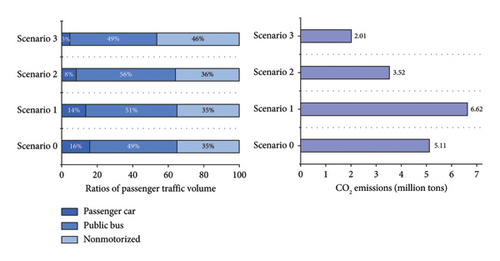
Compared to the base scenario, Scenario 1, with all other external conditions and constraints unchanged, yields higher carbon emissions due to increased travel demand, even though the proportion of bus usage increases. This is because limitations on travel comfort and travel time assurance remain unchanged, restricting the proportion of public transport and nonmotorized travel. Despite potential improvements in the attractiveness of the public transport system through measures such as route optimization, issues such as congestion during peak hours, the inconvenience of transfers, and longer travel times compared to private cars continue to pose significant barriers to widespread public transport usage. These factors collectively limit the extent to which public transport and nonmotorized modes (such as walking and cycling) can increase their share in the overall travel structure, thereby failing to offset the carbon emissions increase resulting from the growth in travel demand.

Scenario 2 builds on Scenario 1 by reducing the waiting time for public transport and increasing the average occupancy rate of buses, resulting in the lowest CO₂ emissions of 3.52 million tons. On the one hand, enhanced public transport services and optimized stops and schedules reduce the waiting time cost for residents, encouraging more people to choose public transport. On the other hand, the increased average occupancy rate of buses significantly improves the service level of the urban road network. As buses are used more effectively, traffic flow becomes smoother, and the average vehicle speed increases. This change is crucial for reducing carbon emissions, as it reduces idle time during traffic congestion, decreases fuel consumption, and dramatically lowers CO₂ emissions.

Scenario 3 further enhances the infrastructure for nonmotorized transport beyond Scenario 2 and implements a series of innovative measures to ensure the rights and safety of nonmotorized users, creating a more friendly, convenient, and low-carbon travel environment. In this scenario, for short-distance travel, the public’s behavior shifts positively, with more people opting for nonmotorized modes for trips within 3.5 km. This includes, but is not limited to, electric bicycles and shared bikes, which are favored by many citizens for their high flexibility, low cost, and eco-friendliness. As a result, the proportion of nonmotorized modes in the optimal travel ratio further increases, with significant environmental benefits. The most direct impact is the continued reduction in CO₂ emissions, which is crucial for improving urban air quality and promoting ecological balance. In addition, the widespread adoption of nonmotorized travel fosters social interaction and community vitality, enhances physical health, and contributes to a more harmonious and sustainable urban lifestyle.

Through the aforementioned scenario analysis, we can discern that various factors, including differing residential travel demands, the layout and accessibility of public facilities, as well as service quality encompassing punctuality, comfort, and safety of transportation modes, exert profound impacts on shaping the optimal travel structure to varying degrees. These intricate and intertwined factors necessitate a holistic consideration of residents’ actual needs, the optimization of urban spatial layout, and the continuous enhancement of service quality when planning urban transportation systems, aiming to achieve a dual improvement in travel efficiency and residents’ satisfaction. However, in previous studies, travel demand has often been overlooked and not included in the consideration [6–10]. This oversight may lead to an underestimation of the maximum carbon benefits associated with shifts in travel modes. Neglecting travel demand may also result in significant deviations between model analysis results and real-world situations, impacting the comprehensive understanding and accurate assessment of the environmental benefits of travel structure optimization measures. Therefore, when discussing the impact of travel mode shifts on carbon emissions reduction, it is crucial to comprehensively consider both travel demand and carbon reduction needs. This is also the reason why this paper proposes that the constraint conditions of travel demand must be considered when modeling the optimization of travel structure.

On the other hand, from Scenario 2, it can be observed that when efforts are focused on optimizing and improving the quality of public transportation services to attract more users to choose public transit as their primary mode of travel, thereby significantly increasing the average occupancy rate of buses, the carbon reduction effect becomes highly significant and measurable. This impact is not only evident in the direct reduction of CO₂ emissions but also profoundly highlights the crucial role of enhanced public transportation system efficiency in alleviating urban traffic congestion and promoting environmental sustainability.

Notably, the carbon reduction effect resulting from this modal shift is often inadequately captured and accurately characterized by conventional static emission factor models [11–16] or analytical frameworks. These models typically rely on fixed traffic flow and emission factors, neglecting the dynamic influence of service quality improvements on passenger choices and vehicle operating efficiency in real-world transportation systems, thus underestimating the potential carbon benefits of public transportation optimization measures.

6.2. Computational Complexity and Scalability of the Algorithm

In this paper, we proposed a GA algorithm incorporating the MSA algorithm for handling small- to medium-sized road networks. In the actual case study, which involved 123 road nodes, 26 area centers, and 380 road segments, we demonstrated the effectiveness of the algorithm in managing small- to medium-sized road networks. The computation time for finding the optimal capacity expansion was 2 h for 50 generations. It was observed that total emissions showed a drastic reduction in the first 20 generations, and then the objective function value stabilized, indicating a converged solution. The runtime and memory usage met expectations and can effectively address mode optimization in many county-level cities in China.

While this model algorithm can indeed handle larger-scale networks, the computation time and memory requirements will increase linearly with the network scale. In extremely large networks, such as those in megacity road networks, computational resources, and time may become bottlenecks. For larger urban road networks, future work could explore parallel computing techniques to further optimize the algorithm, significantly enhancing efficiency and scalability to handle larger and more complex networks. In the context of this study, achieving a globally optimal solution is not the primary goal. Instead, large-scale networks can be partitioned into multiple small- to medium-sized networks based on administrative regions. By applying the algorithm proposed in this paper to these partitioned networks, a trade-off can be made between the quality of the solution and the efficiency, allowing for some degradation in solution quality in exchange for improved efficiency.

6.3. Potential Limitations of Assumptions

Before constructing the model, we made several conditional assumptions. While these assumptions are intended to simplify complex realities and enhance the model’s operability and interpretability, they may also limit the model’s comprehensiveness and accuracy to some extent. The potential limitations or implications of these assumptions on the results are discussed as follows:

1.
We adopted the assumption that the OD patterns of trips are known and fixed, primarily based on observations that travel demand within our study area remains relatively stable over specific time periods. The OD data are crucial for the scientific distribution of subsequent travel mode shares. However, obtaining high-quality OD data is not an easy task, it typically requires large-scale transport surveys, including questionnaires, GPS tracking, mobile phone signaling analysis, and the integration of various technological methods. This process is not only time-consuming and labor-intensive but also demands substantial human and material resources. While ignoring the dynamic changes in travel demand may lead to inaccuracies in predicting future traffic flows or assessing the impacts of transport policies, in most cases, especially during periods without significant external disruptions, general travel patterns tend to be relatively stable. This stability means that models based on the assumption of fixed OD patterns still hold significant practical value and provide meaningful insights when describing and analyzing daily traffic conditions.
2.
The assumption that residents’ route choice behavior follows the SUE was adopted to simulate travelers’ decision-making processes when faced with incomplete traffic information. This assumption reflects the characteristics of travelers’ behavior in the real world to a certain extent, allowing us to more accurately portray the operational state of the transport network. However, while the SUE assumption is reasonable, it also has significant limitations. Firstly, it overlooks the interactions and social influences among travelers, which can significantly impact route choices in actual traffic conditions. Secondly, there is uncertainty regarding the deviation between perceived and actual travel times, which may result in inaccuracies in the model’s predictions. To mitigate these limitations, we plan to collect more comprehensive traffic data in future research to more accurately estimate the distribution of perceived time deviations and consider incorporating additional factors that influence travelers’ route choice behavior into the model.
3.
The assumption of “no transfers required for a single trip” in the model is based on considerations of simplifying the model’s complexity and focusing on the specific research area of county-level cities in China. Given the relatively small size of these cities and the simpler structure of their transport networks, residents’ daily travel often allows them to reach their destinations directly without frequent transfers. This real-world context provides a reasonable basis for the model’s assumption. However, this simplification inevitably introduces certain limitations and potential impacts:
Firstly, in actual urban transport systems, transfers are a common phenomenon, especially in larger or more complex urban structures. Ignoring transfers means our model may not fully capture real-world travel behavior patterns, thereby limiting its applicability in guiding actual transport planning and policymaking. Secondly, transfers usually come with increased time and economic costs (such as waiting times and transfer fees), as well as potential declines in comfort. Therefore, not considering transfers may underestimate overall travel costs, potentially leading to inaccurate predictions of traveler behavior (inconvenient transfers or long transfer times are likely to decrease the probability of choosing public transport, increasing the proportion of trips made by private cars). In future research, we plan to explore multilayer network models or multimodal transport assignment models to explicitly consider the factors associated with transfers.
4.
The optimization of travel modes, the enhancement of energy structures, and improvements in vehicle emission technologies are three complementary pillars that together form the core strategic framework for reducing carbon emissions in the transport sector and promoting green mobility. Each of these elements holds significant potential for emission reductions, which is invaluable for achieving global climate goals. In this paper, we specifically focus on the dimension of travel mode optimization, aiming to explore the substantial potential for reducing carbon emissions through adjusting and optimizing travel behavior patterns, enhancing the efficiency of public transport systems, and encouraging nonmotorized and shared transport modes. To this end, we have developed a theoretical model and conducted a series of analyses based on it. However, to simplify the problem and concentrate on the core issues, we made a specific assumption in the modeling process: We temporarily do not consider the carbon reduction benefits that may arise from energy structure optimization and improvements in vehicle emission technologies.

The introduction of this assumption does not imply that we disregard the importance of energy structure and vehicle technologies. Rather, it is intended to precisely align with the current research topic and objectives, allowing for a more focused examination of the direct impact and contribution of travel mode optimization in reducing carbon emissions within the transport sector. This provides valuable insights and references for policymakers, urban planners, and professionals in the transport industry.

Of course, we fully recognize the limitations of this assumption. In practical applications, optimizing energy structures (such as increasing the share of clean energy and reducing reliance on fossil fuels) and improving vehicle emission technologies (such as enhancing engine efficiency and developing low-emission vehicles) may increase the proportion of private car usage (as private cars offer the most convenient and comfortable mode of travel), further boost public transport usage, and potentially decrease the share of nonmotorized travel, given its limited range. Therefore, in future research, we plan to incorporate energy structure optimization and vehicle emission technology improvements into the analytical framework to develop a more comprehensive and integrated system for evaluating emission reduction strategies.

7. Conclusions

This paper presents a dual-layer optimal allocation model for transport modes that considers both travel demand and carbon emissions, and we engineer a sophisticated fusion algorithm that seamlessly integrates Dial_MSA with GA to solve this model. This approach is tested on a large real network and shows its robustness and scalability.

Regarding findings, the model effectively captures the impact of changes in travel structure on vehicle emissions. By employing this model, optimal proportions of different transport modes can be derived, minimizing the total carbon dioxide emissions from the road network while meeting transport demands. This optimal travel structure could serve as valuable theoretical and decision-making support for planners, aiding them in obtaining reasonable proportions of public and private vehicle transport demands while implementing measures to promote sustainable and low-carbon transport development.

However, on the other hand, the research presented in this paper exhibits certain limitations. While the current algorithm has achieved certain results in addressing urban road network issues, its practical application effectiveness needs to be further enhanced in terms of algorithm validity when confronted with larger-scale urban road networks, particularly complex and vast traffic networks such as those in megacities. In future research, we aim to further improve the algorithm’s operational efficiency and robustness by optimizing the algorithm and employing parallel computing techniques, in order to better accommodate the complexity and scale of megacity road networks.

To effectively promote modal shifts in transport, traffic managers need to develop and implement a series of comprehensive measures that encompass infrastructure investment, policy measures, and public participation.

7.1. Infrastructure Investment

Investment in transport infrastructure is fundamental to achieving modal shifts. Governments and urban managers should prioritize the construction and improvement of public transport networks, optimizing the connectivity of bus and metro lines. Efforts are required to enhance public transport infrastructure, improve the construction of dedicated public transport lanes, and promote the development of stations through comprehensive land use planning. Tailored measures should be implemented in various locations to prioritize public transport, such as establishing bus-exclusive lanes and implementing a priority system for public transport signals along major bus corridors, thereby achieving large-scale and networked development of public transport in city centers and densely populated areas. Simultaneously, safe and convenient bicycle and pedestrian paths should be developed to ensure the safety and comfort of walkers and cyclists. Reasonable traffic island, pedestrian crossings, and physical separation should be established to ensure the right-of-way, priority, and exclusivity of slow traffic, thereby ensuring the safety of slow transport. Meanwhile, traffic calming measures should be implemented (e.g., raised intersections, roundabouts, speed bumps, and pedestrian safety islands) to reduce the negative effects of motorized vehicles on the traffic environment and create a comfortable local atmosphere.

7.2. Policy Incentives

Policy measures are effective tools for promoting modal shifts. Measures such as implementing reasonable controls on private car ownership, such as license plate restrictions, and prioritizing public transport in city centers, are needed. In addition, speed limits can be imposed in “low-carbon transport demonstration areas,” and the allocation of parking resources in traffic-congested areas can be carefully managed. Furthermore, the number of parking spaces can be limited in densely populated and mixed-use areas in the city center to reduce the frequency of car usage in areas with limited road resources. Subsidies for public transport can also reduce travel costs for passengers, incentivizing more people to choose public transport. In addition, incentives for active transport, such as allowances for employees commuting by bicycle, are also effective policy measures.

7.3. Public Engagement

Public recognition and participation are crucial for achieving modal shifts. Traffic managers should conduct public awareness and education campaigns through various channels to enhance public awareness of low-carbon travel options. For example, they can use social media, community events, and educational programs to inform the public about the benefits of low-carbon travel for the environment and personal health. Moreover, managers should encourage public involvement in the transport planning process, gathering their feedback and suggestions to improve the acceptance and effectiveness of policies and measures.

Overall, within the context of the “dual-carbon” strategy, by implementing these measures, traffic managers can fully harness the power of technology and innovation to promote modal shifts, achieving low-carbon emission reduction goals. This will not only help protect the environment but also enhance the quality of life for urban residents and promote sustainable urban development.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Jing Gan: writing–review and editing, software. Dongmei Yan: writing–review and editing, validation. Linheng Li: conceptualization, methodology, writing–original draft, and writing–review and editing.

Funding

This study was carried out with the support of the Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications (Grant No. NY222030).

Acknowledgments

This study was carried out with the support of the Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications (Grant No. NY222030).

Open Research

Data Availability Statement

Data are available on request.

References

1 European Cyclists’ Federation, 2009.
Google Scholar
2 Urban Development, CPH 2025 Clim. Plan, 2016.
Google Scholar
3 Report on the Preliminary Work of Wuhan Comprehensive Planning (2016–2030), https://Max.Book118.Com/html/2020/0630/7046153133002144.Shtm.
Google Scholar
4 Outline of Hunan Province’s 14th Five Year Plan, http://www.Hunan.Gov.Cn/Topic/Hnsswghgy/Index.Html.
Google Scholar
5 Nanjing City’s 14th Five Year Plan for Urban Public Transport Development, http://Td.Jiangsu.Gov.Cn/Art/2022/2/23/Art_41651_10356804.Html.
Google Scholar
6 Salvucci R., Tattini J., Gargiulo M., Lehtilä A., and Karlsson K., Modelling Transport Modal Shift in TIMES Models Through Elasticities of Substitution, Applied Energy. (2018) 232, 740–751, https://doi.org/10.1016/j.apenergy.2018.09.083, 2-s2.0-85053196829.
10.1016/j.apenergy.2018.09.083
Google Scholar
7 Daly H. E., Ramea K., Chiodi A., Yeh S., Gargiulo M., and Gallachóir B. O., Incorporating Travel Behaviour and Travel Time Into TIMES Energy System Models, Applied Energy. (2014) 135, 429–439, https://doi.org/10.1016/j.apenergy.2014.08.051, 2-s2.0-84907185159.
10.1016/j.apenergy.2014.08.051
Web of Science® Google Scholar
8 Mocanu T., Joshi J., and Winkler C., A Data-Driven Analysis of the Potential of Public Transport for German Commuters Using Accessibility Indicators, European Transport Research Review. (2021) 13, https://doi.org/10.1186/s12544-021-00507-0.
10.1186/s12544-021-00507-0
PubMed Google Scholar
9 Ngoc A. M., Nishiuchi H., Van Truong N., and Huyen L. T., A Comparative Study on Travel Mode Share, Emission, and Safety in Five Vietnamese Cities, International Journal of Intelligent Transportation Systems Research. (2022) .
10.1007/s13177-021-00283-0
Google Scholar
10 O’Riordan V., Rogan F., Gallachóir B., Mac Uidhir T., and Daly H., How and Why We Travel—Mobility Demand and Emissions from Passenger Transport, Transportation Research Part D: Transport and Environment. (2022) 104.
10.1016/j.trd.2022.103195
Google Scholar
11 Thomas H. and Serrenho A. C., Using Different Transport Modes: An Opportunity to Reduce UK Passenger Transport Emissions?, Transportation Research Part D: Transport and Environment. (2024) 126, https://doi.org/10.1016/j.trd.2023.103989.
10.1016/j.trd.2023.103989
Google Scholar
12 Sobrino N. and Arce R., Understanding Per-Trip Commuting CO2 Emissions: A Case Study of the Technical University of Madrid, Transportation Research Part D: Transport and Environment. (2021) 96.
10.1016/j.trd.2021.102895
Google Scholar
13 Tiwari G., Jain D., and Rao K., Ramachandra, Impact of Public Transport and Non-motorized Transport Infrastructure on Travel Mode Shares, Energy, Emissions and Safety: Case of Indian Cities, Transportation Research Part D: Transport and Environment. (2016) .
10.1016/j.trd.2015.11.004
Google Scholar
14 Bantis T. and Haworth J., Who You Are Is How You Travel: A Framework for Transportation Mode Detection Using Individual and Environmental Characteristics, Transportation Research Part C: Emerging Technologies. (2017) 80, 286–309, https://doi.org/10.1016/j.trc.2017.05.003, 2-s2.0-85019496807.
10.1016/j.trc.2017.05.003
Web of Science® Google Scholar
15 Izdebski M. J., Kalahasthi L. K., Regal-Ludowieg A., and Holguín-Veras J., Short Sea Shipping as a Sustainable Modal Alternative: Qualitative and Quantitative Perspectives, Sustainable Times. (2024) 16, 1–25, https://doi.org/10.3390/su16114515.
10.3390/su16114515
Google Scholar
16 Chen K., Su S., Gong Y., Xin X., and Zeng Q., Coastal Transportation System Green Policy Design Model Based on Shipping Network Design, International Journal of Logistics Research and Applications. (2024) 27, 428–449, https://doi.org/10.1080/13675567.2021.1940112.
10.1080/13675567.2021.1940112
Google Scholar
17 Zhang L., Long R., Chen H., and Yang T., Analysis of an Optimal Public Transport Structure under a Carbon Emission Constraint: A Case Study in Shanghai, China, Environmental Science & Pollution Research. (2018) 25, 3348–3359, https://doi.org/10.1007/s11356-017-0660-4, 2-s2.0-85034214223.
10.1007/s11356-017-0660-4
CAS PubMed Google Scholar
18 Lu L., Wang C., Deng W., and Bing X., An Optimal Allocation Model of Public Transit Mode Proportion for the Low-Carbon Transportation, Mathematical Problems in Engineering. (2015) 2015.
Google Scholar
19 Filom S. and Razavi S., Decarbonization through Modal Shift Using a Synchromodal Platform: A Case Study in the Great Lakes, Journal of Supply Chain Management. (2023) 4, 97–113, https://doi.org/10.59490/jscms.2023.7145.
10.59490/jscms.2023.7145
Google Scholar
20 Eslamipoor R., Direct and Indirect Emissions: A Bi-Objective Model for Hybrid Vehicle Routing Problem, Journal of Business Economics. (2024) 94, 413–436, https://doi.org/10.1007/s11573-023-01168-2.
10.1007/s11573-023-01168-2
Google Scholar
21 Fan W., Tang Z., Ye P., Xiao F., and Zhang J., Deep Learning-Based Dynamic Traffic Assignment with Incomplete Origin–Destination Data, Transportation Research Record. (2023) 2677, 1340–1356.
10.1177/03611981221123805
Google Scholar
22 Ma J., Xu M., and Jiang J., Mapping High-Resolution Urban Road Carbon and Pollutant Emissions Using Travel Demand Data, Energy. (2023) 263.
10.1016/j.energy.2022.126059
Google Scholar
23 Vieira J. P. B., Pereira R. H. M., and Andrade P. R., Estimating Public Transport Emissions from General Transit Feed Specification Data, Transportation Research Part D: Transport and Environment. (2023) 119.
10.1016/j.trd.2023.103757
Google Scholar
24 Lei J., Yang C., Fu Q., Chao Y., Dai J., and Yuan Q., An Approach of Localizing MOVES to Estimate Emission Factors of Trucks, International Journal of Transportation Science and Technology. (2024) 13, 229–242.
10.1016/j.ijtst.2023.02.002
Google Scholar
25 Qian J. and Eglese R., Fuel Emissions Optimization in Vehicle Routing Problems with Time-Varying Speeds, European Journal of Operational Research. (2016) 248, 840–848, https://doi.org/10.1016/j.ejor.2015.09.009, 2-s2.0-84945205458.
10.1016/j.ejor.2015.09.009
Web of Science® Google Scholar
26 Xiao J., Liu X., Zhang H., Cao Z., Kang L., and Niu Y., The Low-Carbon Vehicle Routing Problem With Dynamic Speed on Steep Roads, Computers & Operations Research. (2024) 169, https://doi.org/10.1016/j.cor.2024.106736.
10.1016/j.cor.2024.106736
Google Scholar
27 Shao H., Lam W. H. K., Sumalee A., and Hazelton M. L., Estimation of Mean and Covariance of Stochastic Multi-Class OD Demands From Classified Traffic Counts, Transportation Research Part C: Emerging Technologies. (2015) 59, 92–110, https://doi.org/10.1016/j.trc.2015.05.017, 2-s2.0-84942989782.
10.1016/j.trc.2015.05.017
Web of Science® Google Scholar
28 Wang J., Song J., Zhao C., and Jeff) Ban X., Distributionally Robust Origin–Destination Demand Estimation, Transportation Research Part C: Emerging Technologies. (2024) 165, https://doi.org/10.1016/j.trc.2024.104716.
10.1016/j.trc.2024.104716
Google Scholar
29 Sheu J. B., Mass Evacuation Planning for Disasters Management: A Household Evacuation Route Choice Behavior Analysis, Transportation Research Part E: Logistics and Transportation. (2024) 186, https://doi.org/10.1016/j.tre.2024.103544.
10.1016/j.tre.2024.103544
Google Scholar
30 Dieter P., Caron M., and Schryen G., Integrating Driver Behavior into Last-Mile Delivery Routing: Combining Machine Learning and Optimization in a Hybrid Decision Support Framework, European Journal of Operational Research. (2023) 311, 283–300, https://doi.org/10.1016/j.ejor.2023.04.043.
10.1016/j.ejor.2023.04.043
Google Scholar
31 Namdarpour F., Liu B., Kuehnel N., Zwick F., and Chow J. Y. J., On Non-myopic Internal Transfers in Large-Scale Ride-Pooling Systems, Transportation Research Part C: Emerging Technologies. (2024) 162, https://doi.org/10.1016/j.trc.2024.104597.
10.1016/j.trc.2024.104597
Google Scholar
32 Gan J., Li L., Xiang Q., and Ran B., A Prediction Method of GHG Emissions for Urban Road Transportation Planning and its Applications, Sustainable Times. (2020) 12, 1–18, https://doi.org/10.3390/su122410251.
10.3390/su122410251
PubMed Google Scholar
33 Li L., Wang C., Gan J., and Zhang D., A Fuel Consumption-Based Method for Developing Local-specific CO2 Emission Rate Database Using Open-Source Big Data, Journal of Big Data. (2024) 11, 1–25.
10.1186/s40537-024-00932-7
CAS Google Scholar
34 Liu B., Zhang Y., and Du W., A Simplified C-Logit Stochastic User Equilibrium Model on Bimodal Transportation Network, Mathematical Problems in Engineering. (2020) 2020, https://doi.org/10.1155/2020/3702965.
10.1155/2020/3702965
Google Scholar
35 Dong X., Sun X., He J., and Yan X., A Congestion Bottleneck Analysis Model for Tourist Block Street Network, International Journal of Modeling, Simulation, and Scientific Computing. (2020) 11, 1–18, https://doi.org/10.1142/S1793962320500543.
10.1142/S1793962320500543
CAS Google Scholar
36 Tan H., Du M., and Bin Yu C., A Multiple-Path Gradient Projection Method for Solving the Logit-Based Stochastic User Equilibrium Model, Journal of Transport and Land Use. (2020) 13, 539–558, https://doi.org/10.5198/jtlu.2020.1600.
10.5198/jtlu.2020.1600
Google Scholar
37 Chen A., Ryu S., Xu X., and Choi K., Computation and Application of the Paired Combinatorial Logit Stochastic User Equilibrium Problem, Computers & Operations Research. (2014) 43, 68–77, https://doi.org/10.1016/j.cor.2013.08.022, 2-s2.0-84884698410.
10.1016/j.cor.2013.08.022
Web of Science® Google Scholar
38 Guan Y., Xiang W., Wang Y., Yan X., and Zhao Y., Bi-level Optimization for Customized Bus Routing Serving Passengers with Multiple-Trips Based on State-Space-Time Network, Physica A: Statistical Mechanics and its Applications. (2023) 614.
10.1016/j.physa.2023.128517
Google Scholar
39 Chen J., Jia X., and He Q., A Novel Bi-level Multi-Objective Genetic Algorithm for Integrated Assembly Line Balancing and Part Feeding Problem, International Journal of Production Research. (2023) 61, 580–603.
10.1080/00207543.2021.2011464
Google Scholar
40 Galiana J., Rodríguez I., and Rubio F., How to Stop Undesired Propagations by Using Bi-level Genetic Algorithms, Applied Soft Computing. (2023) 136.
10.1016/j.asoc.2023.110094
Google Scholar
41 Shang J., Gao J., Jiang X., Liu M., and Liu D., Optimal Configuration of Hybrid Energy Systems Considering Power to Hydrogen and Electricity-Price Prediction: A Two-Stage Multi-Objective Bi-Level Framework, Energy. (2023) 263.
10.1016/j.energy.2022.126023
Google Scholar
42 Tan M., Dai Z., Su Y., Chen C., Wang L., and Chen J., Bi-Level Optimization of Charging Scheduling of a Battery Swap Station Based on Deep Reinforcement Learning, Engineering Applications of Artificial Intelligence. (2023) 118.
10.1016/j.engappai.2022.105557
Google Scholar

Citing Literature

All articles

Dual-Layer Dynamic Optimization Model for Carbon-Conscious Transport Mode Allocation

Abstract

1. Introduction

2. Literature Review

2.1. Macroaggregation Modeling

2.2. Discrete Choice Modeling

2.3. Mathematical Optimization Model

2.4. Summary

3. Modeling Strategy

3.1. Model’s Variables and Parameters

3.2. Upper-Level Formulation

3.2.1. Objective Function

3.2.2. Constraints

3.2.2.1. Constraint 1: Ensuring Travel Demand

3.2.2.2. Constraint 2: Ensuring Travel Time

3.2.2.3. Constraint 3: Ensuring Comfort

3.2.2.4. Constraint 4: Ensuring Convenience

3.2.2.5. Constraint 5: Sum of Proportions Equal to Unity

3.3. Lower-Level Formulation

4. Solution Algorithm

5. Case Study

5.1. Model Parameters

5.1.1. Changxing County Network

5.1.2. Traffic Parameters

5.1.3. Localized Emission Factors

5.2. Computation of the Model

6. Discussion

6.1. Scenario Analysis

6.2. Computational Complexity and Scalability of the Algorithm

6.3. Potential Limitations of Assumptions

7. Conclusions

7.1. Infrastructure Investment

7.2. Policy Incentives

7.3. Public Engagement

Conflicts of Interest

Author Contributions

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information