Volume 2025, Issue 1 9950491

Research Article

Open Access

MHD Free Convective Transport Through an Inclined Porous Sheet With Thermal Radiation Effect: An Unsteady Analysis

Mahamudul Hassan Milon,

Mahamudul Hassan Milon

Department of Mathematics , Khulna University of Engineering and Technology , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Hasanuzzaman,

Corresponding Author

Md. Hasanuzzaman

[email protected]

orcid.org/0000-0002-0724-4935

Department of Mathematics , Khulna University of Engineering and Technology , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Asaduzzaman,

Md. Asaduzzaman

Department of Mathematics , Khulna University of Engineering and Technology , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Mahamudul Hassan Milon,

Mahamudul Hassan Milon

Department of Mathematics , Khulna University of Engineering and Technology , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Hasanuzzaman,

Corresponding Author

Md. Hasanuzzaman

[email protected]

orcid.org/0000-0002-0724-4935

Department of Mathematics , Khulna University of Engineering and Technology , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Asaduzzaman,

Md. Asaduzzaman

Department of Mathematics , Khulna University of Engineering and Technology , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

First published: 20 June 2025

https://doi.org/10.1155/admp/9950491

Academic Editor: Ivan Giorgio

Share a link

Email
Wechat
Bluesky

Abstract

An analysis of an unsteady magnetohydrodynamics (MHD) natural convective transport through a uniform inclined perforated plate in the presence of thermal radiation effect has been carried out due to its potential applications in geophysics and astronomy, as well as a variety of engineering problems, such as aerodynamics, cooling towers, and nuclear reactor boundary layer control. The partial differential equations (PDEs) have been transformed into ordinary differential equations (ODEs) by considering the similarity transformation. The nondimensional ODEs have been solved by using shooting technique through MATLAB tools. The influences of the numerous nondimensional numbers or parameters like inclined angle (γ), Prandtl number (Pr), Dufour number (Df), Schmidt number (Sc), thermal radiation parameter (R), and suction parameter (v₀) on the fluid flow, concentration, and temperature are explained. For larger values of R and Df, the fluid’s temperature and velocity increased. The velocity field reduces for higher amounts of γ. The local skin friction coefficient (f′(0)) enhanced by 58% and reduced by 46% due to moving values of γ from 0° to 60° and M from 0.5 to 4.0, respectively. The values of f^′(0) enhanced by about 16% and the values of θ′(0) reduced by about 46% due to growing values of R from 0.5 to 3.5. Finally, we provided a comparison between our results with the published study. The comparison reveals good agreement.

1. Introduction

The effect of hydromagnetic (magnetohydrodynamics [MHD]) on the mass transfer and natural convective heat of an electrically conducting viscous fluid across an inclined heated plate has attracted attention due to its potential applications in geophysics and astronomy as well as a variety of engineering problems, such as aerodynamics, cooling towers, and nuclear reactor boundary layer control. In light of these applications, Umemura and Law [1] presented a universal relation for the natural convective boundary layer flow upon a vertical sheet with shifting inclination. They also observed that the flow characteristics depend not only on the distance from the main edge but also on the extent of inclination. The study of mixed effects of electric and magnetic fields in the presence of electrically conducting fluids, which is called MHD. Significant attention of MHD has diverse applications in numerous fields of biomedical sciences and engineering like missile technology, astrophysics, ionized gases, traveling wave tubes, medical sciences, and cosmology. The flow of fluid through interconnected pores is called a porous medium. It is effective in many branches, such as the study of water through oil reservoirs, underground water resources, the dying process, material science, and purification process. Thermal radiation is a type of energy that transforms heat energy by an electromagnetic photons. The effects of thermal radiation is significantly important in manufacturing industries, heating rooms and buildings, nuclear power plants and several impulsion devices for aircraft. Sharma and Gupta [2] studied MHD flow on an implanted stretching surface by perforated medium including the thermal radiation effect. An inspection of the role of radiation on combined convection flow upon a horizontal surface embedded in a perforated medium by Bakier and Gorla [3]. Swapna et al. [4] discussed the mass transfer on mixed transmission periodic flow past a perforated medium in an inclined sheet. Achogo et al. [5] investigated the MHDs convective cyclical flow by a perforated medium in an inclined passage with radiative and chemical reaction effects. Chen [6] has examined the impacts of Effect number and ohmic heating on constant MHD-free convective transport over an inclined perforated surface with varying wall concentration and temperature. The combined buoyancy roles of temperature and mass (concentration) effects were examined by Anghel et al. [7] on the steady natural convection boundary layer over the upper surface of an inclined plate. The analytic solution of convective transport upon a semi-infinite inclined sheet in a perforated medium with the effects of the heat production and radiation was discovered by Bhuvaneswari et al. [8]. Mbeledogu and Ogulu [9] have examined the time-dependent free convective heat and mass transfer flow of a rotating fluid across a permeable plate with the thermal radiation effect. Many researchers have noted the importance of free convection of thermal radiation that is effective in heating rooms and buildings using radiators. Barik and Dash [10] analyzed the important roles of chemical reaction, viscous dissipation, and thermal radiation on a time-dependent MHD flow of an incompressible and electrically conducting fluid in a perforated medium. The effects of thermal radiation and heat generation on the mass transfer and heat flow of an electrically conducting fluid moving through an infinitely perforated plate were examined by Lavanya et al. [11]. Kim [12] examined how a transverse magnetic field affected the 2D laminar flow through a porous material via a vertical permeable moving sheet in a time-dependent manner. The flow was an electrically conducting polar, incompressible, and viscous substance. Hasanuzzaman et al. [13] have examined the effects of suction and blowing on the time-dependent natural convective heat transfer flow of laminar bounar layer fluid around vertical slender bodies. To solve the ordinary differential equations (ODEs), they have also applied the shooting technique with the help of MATLAB software. Very recently, Hasanuzzaman et al. [14] discussed the influences of Dufour and thermal on an unsteady free magneto-convective heat-mass transport across a vertical porous sheet. Furthermore, by using the additional term “thermal radiation,” Hasanuzzaman et al. [15] expanded on the work of Hasanuzzaman et al. [14]. The shooting method is utilized to solve the coupled ODEs that govern the flow numerically.

The driving potentials and fluxes in a continuous fluid have a more complex connection when mass and heat transfers occur simultaneously. An energy flow can also be produced by temperature gradients in addition to composition differences. The concentration gradients may also generate the mass fluxes. The Soret effect or heat diffusion is identified with this concentration gradient. For instance, the Soret effect has been used to mix gases with extremely small molecular weights (H₂, He) and to separate isotopes. According to Eckert and Drake [16], the average molecular weight (N₂, air) of the Dufour (diffusion-thermo) influence was found to be large enough to merit study. The combined effects of Hall current and thermal radiation on mass, heat, and momentum transfer in laminar boundary-layer flow across an inclined permeable stretched sheet with changing viscosity were investigated by Shit and Haldar [17]. The combined effects of thermal radiation and chemical reaction on the MHD natural convection flow of an incompressible, viscous, and electrically conducting fluid over an inclined sheet passing in a perforated medium have been studied by Ali et al. [18]. Ismail et al. [19] analyzed a time-dependent MHD natural convective heat and mass transfer flow past an infinitely inclined plate through a porous media. Khan et al. [20] investigated the effects of mass and heat transfer on the unstable MHD Newtonian fluid flow with the impact of a wall shear stress. Khan et al. [21] investigated the analysis of the scientific and theoretical investigations of wall shear stress on dusty viscoelastic fluid and heat-absorbing an inclined upright channel. Ali et al. [22] analyzed to evaluate heat transfer research into the porous medium of a magnetic field and the unsteady MHD slip flow of a ternary hybrid Casson fluid through a nonlinear flexible disk. An examination of the flow of a sodium alginate (SA)-based Casson tetra hybrid nanofluid through a porous medium and between two parallel plates, taking into consideration the influence of couple stress, has been investigated by Khan et al. [23]. Zhang et al. [24] explored the attributes of convection and Joule heating across a MHD two-dimensional stagnation point flow of a nano liquid depending on the permeable curved stretching/shrinking surface and mass suction. The rate of heat and mass transfers in MHD Williamson nanofluid flow over an exponentially porous stretching surface subject to the heat generation/absorption and mass suction has been investigated by Li et al. [25]. A comprehensive study of the nature of micropolar fluid on an unsteady MHD-free convective transference through a perforated sheet is discussed by Azad et al. [26], considering the suction and Lorentz’s force effects. Barmon et al. [27] investigated the effects of thermal radiation and Lorentz’s force on heat and mass flow in a nanofluid with a magnetic field and free convection as it passes over a vertical permeable sheet.

The effects of the Dufour and Soret on an unsteady MHD natural convection transport past an inclined porous plate were recently described by Hasanuzzaman et al. [28]. We studied MHD free convection flow across an inclined plate embedded in a perforated media containing an electrically conducting incompressible viscous fluid. By adding the term “thermal radiation,” the current study expands on Hasanuzzaman et al. [28].

Based on the aforementioned studies, the primary goal of the current research project is to examine how radiative forces affect an unstable free magneto-convective transport past an inclined perforated plate. The novelty of this present study is to extend Hasanuzzaman et al. [21] by including the additional term thermal radiation. The impact of a number of nondimensional quantities or characteristics, including the suction parameter, Schmidt number, Prandtl number, Dufour number, and inclination angle, has been given numerical results that are graphically explained. In the tabular formations, the heat and mass transfer rates as well as the local skin-friction coefficient have been examined.

2. Mathematical Analysis

An infinitely sloped perforated sheet is considered to be traversed by a two-dimensional unstable electrically conducting, viscous, and incompressible fluid flow. Along the x-axis, the infinitely inclined permeable sheet is taken. The free-stream velocity is parallel to the inclined permeable sheet. It is also assumed that this plate is perpendicular to the y-axis. Along the flow direction, a uniform magnetic field B₀ is applied. When t > 0, the velocity of the fluid at the wall is U₀. The temperature of the fluid at the wall is T_w. The fluid concentration at the wall is C_w. Figure 1 shows the coordinate systems and the flow configuration (Hasanuzzaman et al. [21]). The body force term is assumed to represent only the effects of density changes with concentration and temperature, and the fluid’s characteristics are thought to be constant. We consider here the porous plate is infinite that is x → ∞. So, as x → ∞.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Physical model and coordinate systems.

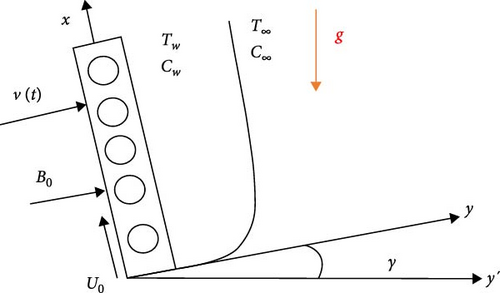
The following governing equations, which take into account Boussinesq’s approximation, are given by (Hasanuzzaman et al. [28]):

The continuity equation

()

The momentum equation

()

The energy equation

()

The mass balance equation

()

The associated boundary conditions are as follows:

()

where g = gravitational acceleration, u = velocity components across the x-axis, v = velocity components across the y-axis, γ = inclined angle, T = fluid temperature, C = fluid concentration, β = coefficient of volumetric expansion according to temperature, υ = kinematic viscosity, β^∗ = coefficient of volumetric expansion according to concentration, T_w = wall temperature, C_w = wall concentration, σ = electrical conductivity, B₀ = magnetic induction, ρ = fluid density, C_p = specific heat at constant pressure, q_r = component of radiative heat flux, T_∞ = free stream fluid temperature, T_m = mean temperature of the fluid, C_∞ = free stream fluid concentration, k_T = thermal diffusion ratio, D_m = coefficient of the mass diffusivity, C_s = concentration susceptibility, k = thermal conductivity of the sheet and t is the time.

Using σ as a similarity parameter

()

where σ represents the length scale. Time affects this length scale. Taking into account this time-dependent length scale, continuity Equation (1) can be solved as follows:

()

Here, the nondimensional normal velocity at the plate is v₀. Here, v₀ < 0 performs blowing and v₀ > 0 performs suction.

The radiative heat flux q_r, as per the Rosseland approximation (Raptis [29]), is determined by

where the symbols have their usual meaning.

Following Raptis [30], we consider that the temperature difference within the flow are small. So, it may be revealed as a linear function of the temperature.

When we ignore higher-order terms and expand T⁴ in a Taylor series around T₀, we get

We used the following similarity transformations in this paper, which are given by

()

The PDEs Equations (1)–(4) are transformed into the following dimensionless coupled ODEs using the aforementioned Equations (7)–(9).

()

subject to the boundary conditions

()

where the Prandtl number is

is the local modified Grashof number, the magnetic force parameter is

, the local Grashof number is

, thermal radiation parameter is

, the Soret number is

, the Dufour number is

, the Schmidt number is

, and

The flow parameters are provided by

()

where Nu_x represents the local Nusselt number, Sh_x indicates the local Sherwood number, and C_f is the local skin friction.

3. Numerical Technique

The nonlinear coupled partial or ODEs involving energy, momentum, and concentration are the main governing equations that govern Newtonian fluids. These nonlinear differential equations are typically nearly impossible to solve analytically, necessitating the use of numerical methods. Therefore, the system was solved as the nonlinear ODEs Equations (10)–(12) with the boundary conditions Equations (13)–(14) using the quasilinearization method (QLM). This method’s fundamental idea is to convert higher-order nonlinear differential equations into simultaneous linear differential equations of the first order, which are subsequently converted into initial value problems. The following new variables must be added to these equations to account for this observation:

Therefore, the following seven comparable first-order differential equations can be created from the higher-order differential Equations (10)–(12).

The transformed boundary conditions:

where the unknowns α₁, α₂, α₃, α₄, and α₅ have been determined such that

This technique summarizes that an initial value problem initially is obtained from the boundary value problem. A shooting technique is then adopt numerically to estimate the values of α₁, α₂, α₃, α_4, and α₅ as long as the boundary conditions are met:

Finally, these equations have been solved numerically through MATLAB software.

4. Results and Discussions

Heat and mass transmission over an inclined perforated sheet have been investigated to determine the effects of thermal radiation magneto-advection that is solely dependent on time. The coupled ODEs Equations (10)–(12) are resolved by using the QLM with the help of shooting technique through MATLAB software. To get a physical significance of this problem, the dimensionless concentration, velocity, and temperature fields are discussed for different values of the dimensionless numbers/parameters. We considered the values of the parameters/numbers which are γ = 15°, M = 0.5, R = 0.5, Df = 2.0, Sr = 2.0, Pr = 0.71, Gr = 10.0, Gm = 12.0, Sc = 0.22 in the whole simulation.

The velocity field appears for the variation of thermal radiation parameter (R) in Figure 2. We can see that the fluid velocity is upgraded for higher values of R. The skin-friction coefficient is enhanced in this case. The skin friction enhanced means the fluid velocity increases for higher values of R. The impact of R in the presence of temperature manifestation in Figure 3. It is concluded from Figure 3 that the thermal gradient becomes less at the surface for higher values of R. The heat transfer rate diminishes for uplifting values of R at the surface. The thermal boundary layer becomes thicker for liable of the thermal radiation parameter. The system is cooling because the fluid is dropping its heat energy from the flow.

The velocity profile for various magnetic force parameter (M) values is displayed in Figure 4. From Figure 4, it is observed that the fluid motion decays for higher values of M. When the magnetic force parameter increases, then an obstructive type of force, such as a drag force, is created. This is because as M increases, the Lorentz force is enhanced, which impedes the flow and slows down the fluid motion.

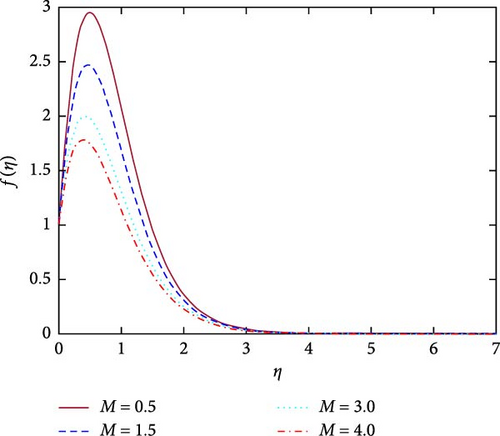
Figures 5 and 6, respectively, reveal the velocity and temperature profiles for various values of the Prandtl number (Pr). It’s important to note that, Pr is defined as the ratio of kinematic viscosity to thermal diffusivity. It is observed from the definition of Pr that the momentum diffusivity enhances for higher values of Pr. Higher values of Pr in this case result in improved fluid viscosity. So, the fluid can’t flow freely in the computational domain. Finally, the fluid velocity decreases for higher values of Pr as shown in Figure 5. Again, the thermal diffusivity reduces for higher values of Pr. A decrease in thermal diffusivity indicates an improvement in the rate of heat transmission. In this instance, as seen in Figure 6, the fluid’s temperature drops as Pr increases. Actually, the heat conduction reduces for cause of a higher Pr has lower thermal conductivity, so temperature is declining.

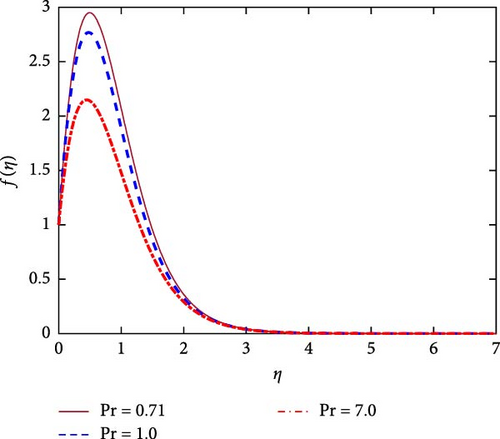
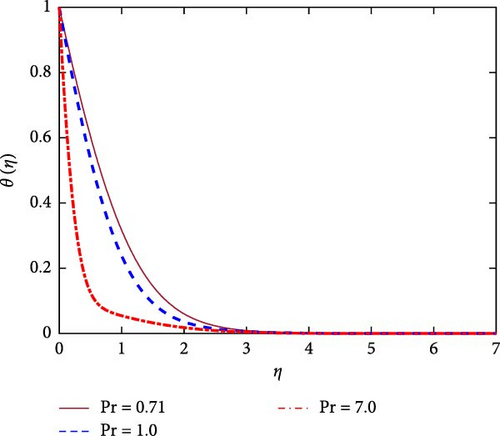
Figure 7 shows dissimilar values of Schmidt number (Sc) on the velocity field. It can be seen that escalating amounts of Sc, the velocity of fluid lessens. Because, the Schmidt number (Sc) is directly proportional to the momentum diffusivity. As a result, the fluid’s kinematic viscosity increases as Sc increases. That is the cause for the movement of fluid particles can indeed be restricted in the computational domain.

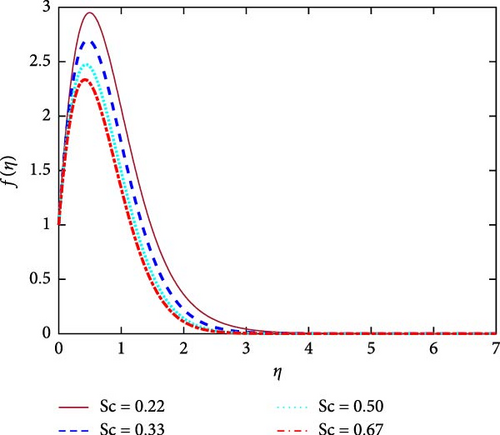
The numerous values of Schmidt number (Sc) on the concentration profile is shown in Figure 8. We realize that, molecular diffusivity is indeed inversely proportional to Sc in the context of mass transfer. So, when the Sc increases, mass diffusivity is reducing. As a result the concentration profile lessens. This is because that mass transfer, therefore, can be manipulated by applying interplay with the species field and the Schmidt number of the material’s velocity field.

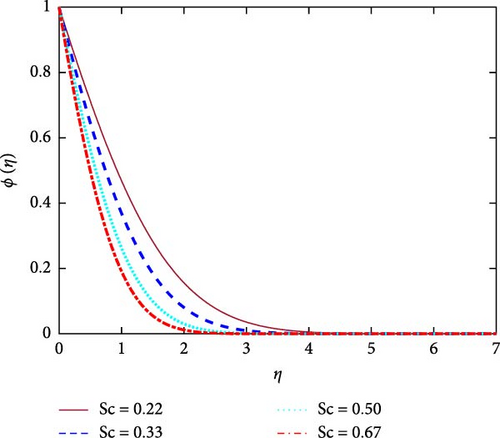
Figure 9 demonstrates the effect of inclined angle (γ) on the profile of velocity. We noticed that at increasing levels of γ, the velocity tends to decline. The buoyant force’s consequent effect decreases with increasing γ values due to the multiplication factor cos γ. Consequently, the velocity rapidly decreases as γ values increase. Furthermore, for horizontal surfaces, fluid velocity is a strictly monotonic increasing function (γ = 90°).

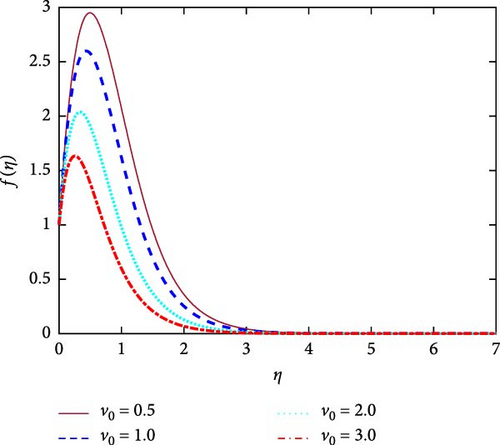
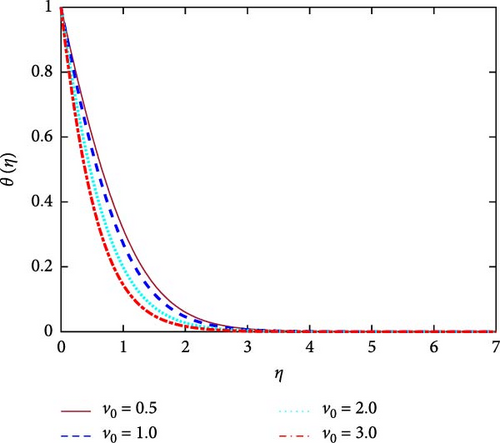
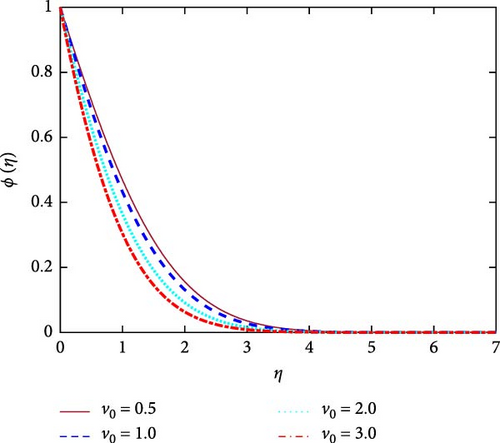
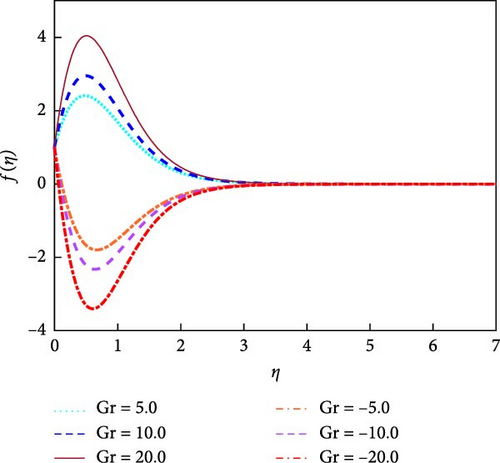
The important role of the suction parameter (v₀) on the velocity, termperature and concentration distributions are portrayed in Figures 10–12, respectively. The suction effect in the computational region exists when v₀ > 0. Figure 10 shows that when suction occurs (v₀ > 0), the volume of fluid in the computational region drops. The frictional force enhances for higher values of v₀. The fluid particle can’t move free in this domain due to increasing vals of v₀. Therefore, in order to raise the suction value, the fluid velocity reduces. The boundary layer’s growth caused by the suction effect eventually stabilizes. The velocity profile is seen to be growing, reaching its maximum value close to the porous plate’s leading edge before progressively declining to zero. With an increase of v₀, the heat transfer rate enhanced. In this instance, the thermal boundary layer becomes thinner. As shown in Figure 11, the fluid temperature decreases as the suction increases. It is seen from Figure 12 that the the concentration of the fluid reduces for growing values of the v₀. The density boundary layers thickness is reduced due to enhanceing the suction. It suggests that the fluid velocity enhances for higher values of Gr shown in Figure 13. For both positive and negative values of Gr, the velocity field creates a symmetrical structure. The upper portion of velocity profile represents heating system for Gr > 0. The lower portion of velocity field shows the cooling system for Gr < 0.

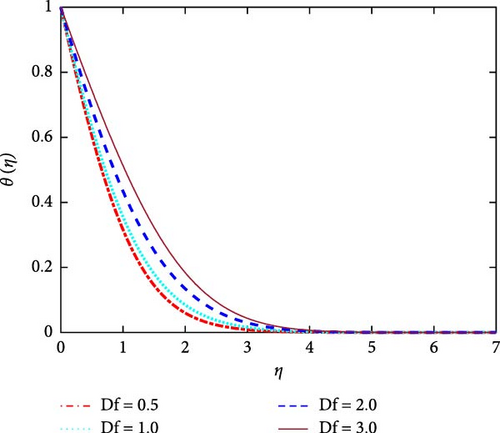
For separate values of the Dufour number (Df), the velocity of the fluid is shown in Figure 14. We can see that Df improves, the viscosity of the fluid fall off owing to the fact that Df inversely varies as the kinematic viscosity (ν). So for fluid particles can make progress candidly. The temperature profile is discussed in Figure 15 for individual values of Df.Df is proportionate to the thermal diffusion(k_T). Seeing that, the Dufour effect is high-riser to the fluid temperature because heat flow is produced by a solute gradient.

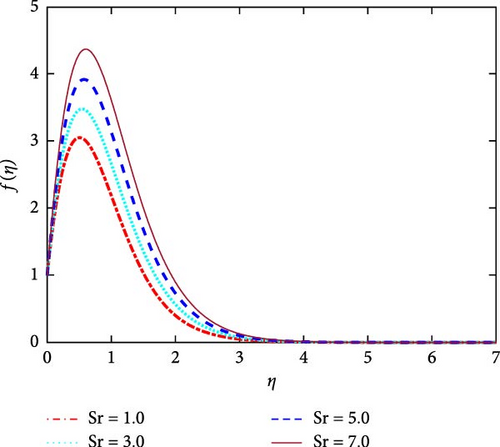
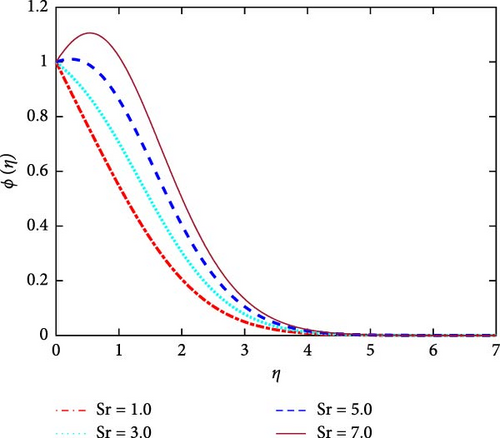
The velocity and concentration distributions for various values of the Soret number (Sr) are plotted in Figures 16 and 17. It is commonly known that Sr equals the kinematic viscosity (υ) divided by the mass diffusivity coefficient (D_m). The relation is called the mathematical formula for Sr. The Soret number (Sr) and the kinematic viscosity (υ) are inversely correlated. We can infer from Figure 16 that as the values of Sr increase, the kinematic viscosity decreases. A decrease in kinematic viscosity results in a decrease in friction force. As a result, the fluid velocity increases as Sr increases. On the other hand, There is a proportional relationship between the mass diffusivity coefficient (D_m) and the Soret number (Sr). It is observed from Figure 17 that the mass diffusivity enhances for higher values of Sr. Under a temperature gradient, the Soret effect occurs when big heavy molecules split apart from small light molecules. Growing Soret number values result in a discernible improvement in concentration profiles. As a consequence, the concentration boundary layer becomes noticeably thicker. As a result, the fluid concentration increases as Sr increases.

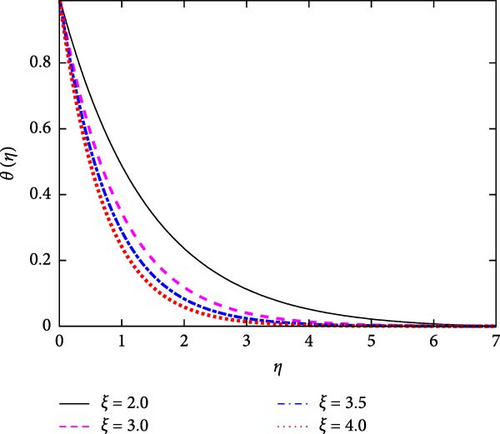
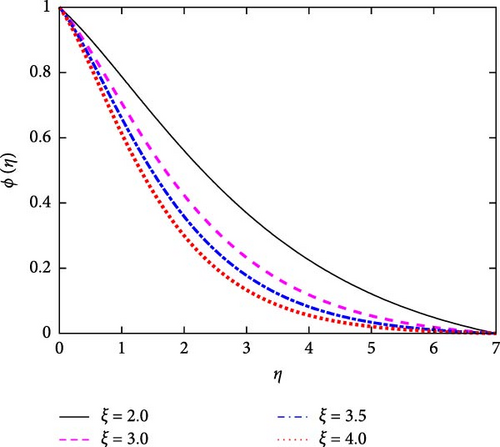
Figures 18–20 represent the effect of the time-dependent parameter (ξ) on the velocity, temperature, and concentration profiles, respectively. The above figures show that the fluid’s velocity, temperature, and concentration diminish for higher values of ξ.

Tables 1–7 provide the important roles of several nondimensional parameters or numbers on the local skin-friction coefficient (f^′(0)), mass transfer rate (−ϕ^′(0)), and heat transmission rate (−θ^′(0)) at the plate. From the above Tables, it is found that the local skin-friction coefficient enhances for higher values of the thermal radiation (R), and the local Grashof number (Gr). As the values of Gr increased from 5.0 to 20.0 and R from 0.5 to 3.5, respectively, the values of f’ (0) increased by roughly 48% and 16%. So, The fluid velocity increases in these situations as a result. Beside, the local skin friction coefficient (f′(0)) reduces for higher values of the magnetic force parameter (M), the suction parameter (v₀), the Prandtl number (Pr), the inclination (γ) and the Schmidt number (Sc). The amount of f^′(0) reduces by about 46%, 29%, 27%, 58%, and 21% because of rising M values from 0.5 to 4.0, v₀ from 0.5 to 3.0, Pr from 0.71 to 7.0, γ from 0° to 60°, and Sc from 0.22 to 0.67, respectively. Consequently, in these circumstances, the fluid motion falls rapidly. The heat transfer rate −θ^′(0) improve for higher values of the Prandtl number (Pr), and the suction parameter (v₀) but reduces for higher values of the thermal radiation (R). When R increases from 0.5 to 3.5, the heat transmission rate decreases by almost 46%. So, the temperature of the fluid enhances for R. The values of −θ^′(0) enhances by about 49%, and 77% due to moving values of v₀ from 0.5 to 3.0, Pr from 0.71 to 7.0, respectively. As a result, the fluid temperature diminishes for these cases. Finally, the mass transfer rate (−ϕ^′(0)) augments for higher values of v₀ and Sc. The values of (−θ^′(0)) improve by roughly 48% and 40%, respectively, for greater values of Sc from 0.22 to 0.67 and v₀ from 0.5 to 3.0.

Table 1. Impact of the magnetic force parameter (M) on f^′(0), −θ^′(0), and −ϕ′(0).

M	f^′(0)	−θ^′(0)	−ϕ′(0)
0.5	10.0476117851418	0.865049397235658	0.601216551513671
1.5	8.25682766816121	0.865049397235658	0.601216551513671
3.0	6.38571379908059	0.865049397235658	0.601216551513671
4.0	5.45765100881443	0.865049397235658	0.601216551513671

Table 2. Effect of the suction parameter (v₀) on f^′(0), −θ^′(0), and −ϕ′(0).

v₀	f^′(0)	−θ^′(0)	−ϕ′(0)
0.5	10.0476117851418	0.865049397235658	0.601216551513671
1.0	9.68353362183671	1.013845353345080	0.676806131865002
2.0	8.54957138297996	1.334857649386220	0.837546383804518
3.0	7.08846007068890	1.680047505772860	1.008998356177420

Table 3. Effect of the thermal radiation parameter (R) on f′(0), −θ^′(0), and −ϕ′(0).

R	f^′(0)	−θ^′(0)	−ϕ′(0)
0.5	10.0476117851418	0.865049397235658	0.601216551513671
1.5	10.8745272197712	0.648992635082552	0.601216551513671
2.5	11.4539129500399	0.540025236378924	0.601216551513671
3.5	11.9079299359829	0.471045245793566	0.601216551513671

Table 4. Effect of the Prandtl number (Pr) on f′(0), −θ^′(0), and −ϕ′(0).

Pr	f′(0)	−θ^′(0)	−ϕ′(0)
0.71	10.0476117851418	0.865049397235658	0.601216551513671
1.0	9.53611064134524	1.05476373089869	0.601216551513671
7.0	7.35726563571183	3.69020425639396	0.601216551513671

Table 5. Effect of the Schmidt number (Sc) on f′(0), −θ^′(0), and −ϕ′(0).

Sc	f′(0)	−θ^′(0)	−ϕ′(0)
0.22	10.0476117851418	0.865049397235658	0.601216551513671
0.33	9.23416134357182	0.865049397235658	0.756769634829211
0.50	8.45815840860712	0.865049397235658	0.963553979417469
0.67	7.94982517262245	0.865049397235658	1.14691830107933

Table 6. Effect of the inclination (γ) on f′(0), −θ^′(0), and −ϕ′(0).

γ (°)	f′(0)	−θ^′(0)	−ϕ′(0)
0	10.4713834953486	0.865049397235658	0.601216551513671
15	10.0476117851418	0.865049397235658	0.601216551513671
30	8.84894322552380	0.865049397235658	0.601216551513671
45	6.92380885399900	0.865049397235658	0.601216551513671
60	4.41750184201957	0.865049397235658	0.601216551513671
90	−1.63637983071561	0.865049397235658	0.601216551513671

Table 7. Effect of the local Grashof number (Gr) on f′(0), −θ^′(0), and −ϕ′(0).

Gr	f′(0)	−θ^′(0)	−ϕ′(0)
5.0	7.68217210755349	0.865049397235658	0.601216551513671
10.0	10.0476117851418	0.865049397235658	0.601216551513671
20.0	14.7784938804610	0.865049397235658	0.601216551513671
−5.0	−10.9549304121426	0.865049397235658	0.601216551513671
−10.0	−13.3203713827876	0.865049397235658	0.601216551513671
−20.0	−18.0512535386513	0.865049397235658	0.601216551513671

5. Comparable Table

The comparison of the numerical findings of the current study with those of earlier publications is shown in Table 8. To verify the validity and correctness of the result obtained, numerical data for f′(0) and the heat transfer rate (−θ^′(0)) at the sheet are compared with the results of Hasanuzzaman et al. [28] for the case of (R = 0).

Table 8. Values of −θ^′(0) and f^′(0).

f^′(0)

Hasanuzzaman et al. [21]

f^′(0)

Present study

−θ^′(0)

Hasanuzzaman et al. [21]

−θ^′(0)

Present study

0.71

6.06446

6.06445

0.70580

0.70582

7.0

4.08719

4.08717

3.60339

3.60337

6. Conclusions

This study examined how thermal radiation affects an unstable free magneto-convective transport via an inclined porous sheet. We applied the approach of similarity transformations to the system to obtain ODE’s. We solved the ODE’s by using the QLM in the shooting technique through MATLAB. Based on the current simulations, the following remarks are drawn:

•
Temperature and velocity of the fluid increase to improve the Dufour number and the thermal radiation parameter (R) levels.
•
The fluid velocity declines for increasing amounts of inclination (γ).
•
As the Prandtl number (Pr) increases, the fluid’s temperature and velocity rapidly decrease.
•
For moving values of the Schmidt (Sc), the fluid’s concentration and velocity decrease.
•
Moving the values of γ from 0° to 60° resulted in a 58% enhancement of the values of f′(0).
•
As R increased from 0.5 to 3.5, the quantity of f′(0) increased by approximately 16%, and the amount of θ^′(0) decreased by approximately 46%.
•
The improving values of M from 0.5 to 4.0 result in a 46% reduction in the values of f′(0).
•
In particular, the outcomes exhibit remarkable congruence with the previously published study.

Nomenclature

MHD:: Magnetohydrodynamics
u:: x-Direction velocity component (MS⁻¹)
T:: Fluid temperature (K)
T_∞:: Free stream temperature (K)
T_W:: Wall temperature (K)
T_m:: Fluid mean temperature (K)
C:: Fluid concentration (MolM⁻³)
C_W:: Wall concentration (MolM⁻³)
C_∞:: Free stream concentration (MolM⁻³)
k:: Thermal conductivity (WM⁻¹K⁻¹)
β^∗:: Coefficient of volumetric expansion with concentration (K⁻¹)
σ:: Similarity parameter
D_m:: Mass diffusivity coefficient
M:: Magnetic force parameter
Pr:: Prandtl number
Gm:: Modified local Grashof number
t:: Time (S)
N_u:: Nusselt number
f(η):: Dimensionless velocity
S_h:: Sherwood number
B:: Uniform magnetic field (Am⁻¹)
v:: y- Direction velocity component (MS⁻¹)
J:: Current density (Am⁻²)
U₀(t):: Uniform surface velocity (MS⁻¹)
v (t):: Suction velocity (MS⁻¹)
C_P:: Specific heat at constant pressure (Jkg⁻¹K⁻¹)
ρ:: Fluid density (KgM⁻²)
g:: Acceleration due to gravity (MS⁻²)
υ:: Kinematic viscosity (M²S⁻¹)
C_s:: Concentration susceptibility (M³kg⁻¹)
β:: Coefficient of volumetric expansion with temperature (K⁻¹)
v₀:: Suction and blowing parameter
k_T:: Thermal diffusion ratio
Gr:: Local Grashof number
Df:: Dafour number
Sr:: Soret number
S_c:: Schmidt number
τ:: Shear stress
ϕ(η):: Dimensionless concentration
θ(η):: Dimensionless temperature.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this manuscript.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Umemura A. and Law C. K., Natural-Convection Boundary-Layer Flow Over a Heated Plate With Arbitrary Inclination, Journal of Fluid Mechanics. (1990) 219, no. -1, 571–584, https://doi.org/10.1017/S0022112090003081, 2-s2.0-0025505718.
10.1017/S0022112090003081
Web of Science® Google Scholar
2 Sharma K. and Gupta S., Analytical Study of MHD Boundary Layer Flow and Heat Transfer Towards a Porous Exponentially Stretching Sheet in Presence of Thermal Radiation, International Journal of Advances in Applied Mathematics and Mechanics. (2016) 4, 1–10.
Google Scholar
3 Bakier A. Y. and Gorla R. S. R., Thermal Radiation Effect on Mixed Convection From Horizontal Surfaces in Saturated Porous Medium, Transport in Porous Medium. (1996) 23, 357–363.
CAS Google Scholar
4 Swapna Y., Raju M. C., and Sharma R. P., Mass Transfer Effects on MHD Mixed Convective Periodic Flow Through Porous Medium in an Inclined Channel With Transpiration Cooling and Thermal Radiation, Jnananbha. (2017) 47, no. 1, 195–206.
Google Scholar
5 Achogo W. H., Okereke I. C. Ofomata A. I., and Amadi O. F., Magnetohydrodynamic Convective Periodic Flow Through a Porous Medium in an Inclined Channel With Thermal Radiation and Chemical Reaction, International Journal of Innovative Science and Research Technology. (2020) 5, no. 1, 1129–1139.
Google Scholar
6 Chen C.-H., Heat and Mass Transfer in MHD Flow by Natural Convection from a Permeable, Inclined Surface With Variable Wall Temperature and Concentration, Acta Mechanica. (2004) 172, no. 3-4, 219–235, https://doi.org/10.1007/s00707-004-0155-5, 2-s2.0-10644263553.
10.1007/s00707-004-0155-5
Web of Science® Google Scholar
7 Anghel M., Hossain M. A., Zeb S., and Pop I., Combined Heat and Mass Transfer by Free Convection Past an Inclined Flat Plate, International Journal of Applied Mechanics and Engineering. (2001) 6, no. 2, 473–487.
Google Scholar
8 Bhuvaneswari M., Sivasankaran S., and Kim Y. J., Exact Analysis of Radiation Convective Flow Heat and Mass Transfer Over an Inclined Plate in a Porous Medium, World Applied Sciences Journal. (2010) 10, no. 7, 774–778.
CAS Google Scholar
9 Mbeledogu I. U. and Ogulu A., Heat and Mass Transfer of an Unsteady MHD Natural Convection Flow of a Rotating Fluid Past a Vertical Porous Flat Plate in the Presence of Radiative Heat Transfer, International Journal of Heat and Mass Transfer. (2007) 50, no. 9-10, 1902–1908, https://doi.org/10.1016/j.ijheatmasstransfer.2006.10.016, 2-s2.0-33847232508.
10.1016/j.ijheatmasstransfer.2006.10.016
Web of Science® Google Scholar
10 Barik R. N. and Dash G. C., Thermal Radiation Effect on an Unsteady Magnetohydrodynamic Flow Past Inclined Porous Heated Plate in the Presence of Chemical Reaction and Viscous Dissipation, Applied Mathematics and Computation. (2014) 226, 423–434, https://doi.org/10.1016/j.amc.2013.09.077, 2-s2.0-84888586698.
10.1016/j.amc.2013.09.077
Web of Science® Google Scholar
11 Lavanya S., Devika B., and Kesavaiah D. C., Radiation Effect on Unsteady Free Convective MHD Flow of a Viscoelastic Fluid Past a Tilted Porous Plate With Heat Source, Journal of Xidian University. (2020) 14, no. 4, 2298–2312.
Google Scholar
12 Kim Y. J., Unsteady MHD Convection Flow of Polar Fluids Past a Vertical Moving Porous Plate in a Porous Medium, International Journal of Heat and Mass Transfer. (2001) 44, no. 15, 2791–2799, https://doi.org/10.1016/S0017-9310(00)00332-X, 2-s2.0-0035827369.
10.1016/S0017-9310(00)00332-X
Web of Science® Google Scholar
13 Hasanuzzaman M., Kabir M. A., and Ahmed M. T., Transpiration Effect on Unsteady Natural Convection Boundary Layer Flows Around a Vertical Slender Body, Results in Engineering. (2021) 12, https://doi.org/10.1016/j.rineng.2021.100293, 100293.
10.1016/j.rineng.2021.100293
Google Scholar
14 Hasanuzzaman M., Azad M., Kalam A., and Hossain M., Effects of Dufour and Thermal Diffusion on Unsteady MHD Free Convection and Mass Transfer Flow Through an Infinite Vertical Permeable Sheet, SN Applied Sciences. (2021) 3, no. 12, 1–11, https://doi.org/10.1007/s42452-021-04842-8.
10.1007/s42452-021-04842-8
Web of Science® Google Scholar
15 Hasanuzzaman M., Ahamed T., and Miyara A., Thermal Radiation Effect on Unsteady Magneto-Convective Heat-Mass Transport Passing in a Vertical Permeable Sheet With Chemical Reaction, Computational and Mathematical Methods in Medicine. (2022) 2022, 11, https://doi.org/10.1155/2022/2872940, 2872940.
10.1155/2022/2872940
PubMed Web of Science® Google Scholar
16 Eckert E. R. G. and DrakeR. M.Jr, Analysis of Heat and Mass Transfer, 1972, McGraw-Hill Book Company, New York.
Google Scholar
17 Shit G. C. and Haldar R., Thermal Radiation on MHD Flow, Heat and Mass Transfer Over an Inclined Permeable Stretching Sheet, Thermal Science. (2011) 15, no. suppl. 2, 195–204, https://doi.org/10.2298/TSCI101115029S, 2-s2.0-84869765773.
10.2298/TSCI101115029S
Google Scholar
18 Ali F., Khan I., Samiulhaq, Shafie S., and Abbott D., Conjugate Effects of Heat and Mass Transfer on MHD Free Convection Flow Over an Inclined Plate Embedded in a Porous Medium, PLoS ONE. (2013) 8, no. 6, https://doi.org/10.1371/journal.pone.0065223, 2-s2.0-84879540065, e65223.
10.1371/journal.pone.0065223
CAS PubMed Web of Science® Google Scholar
19 Ismail Z., Khan I., Nasir N. M., Jusoh R., Salleh M. Z., and Shafie S., Rotation Effects on Coupled Heat and Mass Transfer by Unsteady MHD Free Convection Flow in a Porous Medium Past an Infinite Inclined Plate, AIP Conference Proceedings. (2014) 1605, 410–415.
10.1063/1.4887624
Google Scholar
20 Khan A., Khan I., Ali F., and Shafie S., Effects of Wall Shear Stress on MHD Conjugate Flow Over an Inclined Plate in a Porous Medium With Ramped Wall Temperature, Mathematical Problems in Engineering. (2014) 2014, 15, https://doi.org/10.1155/2014/861708, 2-s2.0-84899483579, 861708.
10.1155/2014/861708
Web of Science® Google Scholar
21 Khan D., Ali G., Kumam P., and Rahman A., A Scientific Outcome of Wall Shear Stress on Dusty Viscoelastic Fluid along Heat Absorbing in an Inclined Channel, Case Studies in Thermal Engineering. (2022) 30, https://doi.org/10.1016/j.csite.2022.101764, 101764.
10.1016/j.csite.2022.101764
Web of Science® Google Scholar
22 Ali G., Kumam P., Sitthithakerngkiet K., and Jarad F., Heat Transfer Analysis of Unsteady MHD Slip Flow of Ternary Hybrid Casson Fluid Through Nonlinear Stretching Disk Embedded in a Porous Medium, Ain Shams Engineering Journal. (2024) 15, no. 2, https://doi.org/10.1016/j.asej.2023.102419, 102419.
10.1016/j.asej.2023.102419
Web of Science® Google Scholar
23 Khan D., Kumam P., Suttiarporn P., and Srisurat T., Fourier’s and Fick’s Laws Analysis of Couple Stress MHD Sodium Alginate Based Casson Tetra Hybrid Nanofluid Along With Porous Medium and Two Parallel Plates, South African Journal of Chemical Engineering. (2024) 47, 279–290, https://doi.org/10.1016/j.sajce.2023.12.003.
10.1016/j.sajce.2023.12.003
Web of Science® Google Scholar
24 Zhang X. H., Abidi A., and Ahmed A. E. S., et al.MHD Stagnation Point Flow of Nanofluid Over a Curved Stretching/Shrinking Surface Subject to the Influence of Joule Heating and Convective Condition, Case Studies in Thermal Engineering. (2021) 26, https://doi.org/10.1016/j.csite.2021.101184, 101184.
10.1016/j.csite.2021.101184
Web of Science® Google Scholar
25 Li Y.-X., Alshbool M. H., Lv Y.-P., Khan I., Riaz Khan M., and Issakhov A., Heat and Mass Transfer in MHD Williamson Nanofluid Flow Over an Exponentially Porous Stretching Surface, Case Studies in Thermal Engineering. (2021) 26, https://doi.org/10.1016/j.csite.2021.100975, 100975.
10.1016/j.csite.2021.100975
Web of Science® Google Scholar
26 Azad M. A. K., Hasanuzzaman M., Hossain M. M., and Miyara A., Suction and Lorentz Force Effects on MHD Free Convective Transport of Micropolar Fluid Passing a Unsteady Analysis, Alexandria Engineering Journal. (2024) 100, 72–81, https://doi.org/10.1016/j.aej.2024.04.067.
10.1016/j.aej.2024.04.067
Web of Science® Google Scholar
27 Barmon A., Hasanuzzaman M., and Hasan M. K., Radiative and Lorentz’s Effects on MHD Free Convective Mass and Heat Transfer Time-Dependent Nanofluid Flow across Vertical Perforated Plate, Alexandria Engineering Journal. (2024) 104, 266–278, https://doi.org/10.1016/j.aej.2024.05.060.
10.1016/j.aej.2024.05.060
Web of Science® Google Scholar
28 Hasanuzzaman M., Milon M. H., Hossain M. M., and Asaduzzaman M., Dufour and Thermal Diffusion Effects on Time-Dependent Natural MHD Convective Transport Over an Inclined Porous Plate, International Journal of Thermofluids. (2024) 21, https://doi.org/10.1016/j.ijft.2024.100572, 100572.
10.1016/j.ijft.2024.100572
Google Scholar
29 Raptis A., Flow of a Micropolar Fluid Past a Continuously Moving Plate by the Presence of Radiation, International Journal of Heat and Mass Transfer. (1998) 41, no. 18, 2865–2866, https://doi.org/10.1016/S0017-9310(98)00006-4, 2-s2.0-0032171455.
10.1016/S0017-9310(98)00006-4
Web of Science® Google Scholar
30 Raptis A., Radiation and Viscoelastic Flow, International Communications in Heat and Mass Transfer. (1999) 26, no. 6, 889–895, https://doi.org/10.1016/S0735-1933(99)00077-9, 2-s2.0-0033174174.
10.1016/S0735-1933(99)00077-9
CAS Web of Science® Google Scholar

All articles

MHD Free Convective Transport Through an Inclined Porous Sheet With Thermal Radiation Effect: An Unsteady Analysis

Abstract

1. Introduction

2. Mathematical Analysis

3. Numerical Technique

4. Results and Discussions

5. Comparable Table

6. Conclusions

Nomenclature

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

MHD Free Convective Transport Through an Inclined Porous Sheet With Thermal Radiation Effect: An Unsteady Analysis

Abstract

1. Introduction

2. Mathematical Analysis

3. Numerical Technique

4. Results and Discussions

5. Comparable Table

6. Conclusions

Nomenclature

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information