Advances in Mathematical Physics
Volume 2025, Issue 1 8619224
Research Article
Open Access

Travelling Wave Solutions of a Time Regularised Long Wave Equation Associated With the Korteweg-de Viries Equation in Fluid Dynamics

Ercan Çelik, 

Corresponding Author

Ercan Çelik

Department of Applied Mathematics and Informatics , Kyrgyz-Turkish Manas University , Bishkek , Kyrgyzstan , manas.edu.kg

Department of Mathematics , Ataturk University , Erzurum , Türkiye , atauni.edu.tr

Search for more papers by this author
First published: 16 January 2025
https://doi.org/10.1155/admp/8619224
Academic Editor: Mengxin Chen

Abstract

In this paper, we investigate the physical significance of the time regularised long wave (TRLW) equation within the realm of mathematics. Other varieties of travelling wave solutions to the analysed problem in hyperbolic form are looked at using the (1/G′)-expansion method. Physically, the singular point’s shock wave structure offers the framework for asymptotic mathematics analyses. It offers a scientific perspective on the phenomenon of non-linear propagation. By giving particular values to constants in solutions, 3-D, contour, and 2-D graphs can depict the state of the wave at any given time.

1. Introduction

Numerous natural physical phenomena are clarified through non-linear science. It has been noted that developing a mathematical model of non-linear wave phenomena is frequently employed in research and engineering [1]. This indicates that research into non-linear partial differential equations (nPDEs) has recently grown significantly [2]. Many scientists have been researching the idea of a soliton for around 200 years. Researchers interest in plasma physics [3], optical fibres [4], biophysics [5], nuclear physics [6], ocean science [7], chemical kinematics [8], et cetera have studied the soliton phenomena. Recent studies show that various kinds of solitons or soliton solutions have been seen both empirically and theoretically. Some solitons that were once thought impossible are now based on modern technology.

Non-linear physical mechanisms are a fundamental concept that helps us understand the complexity of nature and achieve important scientific and technological advances. Understanding these mechanisms can help us develop more effective solutions in many fields and provide a better understanding of the natural world. In the current work, we look for travelling wave nPDE solutions using the (1/G′)-expansion method. In recent years, authors have researched analytical solutions of nPDEs using different methods. These methods are the (1/G′)-expansion method, optimal auxiliary function method, hetero-Bäcklund transformations, modified Laplace decomposition method, Laurent series expansion, Haar wavelet collocation method, generalised Darboux transformation, extended (G′/G2)-expansion method, Hirota’s simple method, N-fold Darboux transformation, auto-Bäcklund transformations and so on [9–27].

We have obtained analytic solutions of the time regularised long wave (TRLW) equation via (1/G′)-expansion method. This is the TRLW equation, one of the variants of the Korteweg-de Viries (KdV) equation put forth by Joseph and Egri [25]. The TRLW equation can be represented as [26]:
(1)
where x, t and u represent spatial coordinate, time and amplitude, respectively, and α is a non-zero constant. The aim of this study is to generate distinct form TRLW equation travelling wave solutions, which is an alternative to the KdV equation [27]. The travelling wave form to be produced for the TRLW equation is of hyperbolic type and contains a singular point. Travelling wave solutions in this form can be valuable to researchers studying the shock wave nature or asymptotic behaviour.

Travelling wave solutions of the TRLW equation were presented using (G′/G)-expansion method [25]. Analytic solutions of the TRLW equation were attained by applying the exp(−ϕ(n))-expansion method [28]. Wave solutions of the TRLW were investigated by the modified simple equation method [2]. Various soliton solutions of the TRLW equation were investigated via the extended sinh-Gordon equation expansion method [29]. Numerical works of the solitary wave solutions of the RLW equation demonstrate that they stably exhibit true soliton behaviour when interacting with other solitary waves [30]. The RLW equation is solved using finite elements in linear space with the help of Galerkin’s method [31].

Travelling wave solutions, many branches of physics use the TRLW equation, particularly when studying non-linear wave systems. Solitons, or solutions that propagate without changing shape over time, are studied using the TRLW equation, which can handle a non-linear wave system. A solution for the TRLW equation is obtained using the Adomian decomposition method [32]. It has been noted that long wave equations can be used to a wide range of variable combinations, just as they can be applied to a variety of variations of the steadily varying flow equation [33]. The TRLW equation’s starting value problem is well-posed and compatible for long waves with small amplitudes, as demonstrated by Bona and Chen [34]. Because it may be used to explain a wide range of significant physical phenomena, including ion–acoustic plasma waves and shallow water waves, the TRLW equation is crucial to the study of non-linear waves [35]. The exp (−Φ (ξ))-expansion method is proposed to generate travelling wave solutions for the TRLW equation [27].

To outline this article: Section 2 introduces the (1/G′)-expansion method for nPDEs. In Section 3, the application of the TRLW equation using the (1/G′)-expansion method is discussed. Section 4 contains conclusions and discussions. The last section contains some important results.

2. (1/G′)-Expansion Method

Take into consideration the nPDEs’ overall format:
(2)
let u(x, t) = U(ξ), ξ = x − vt, v ≠ 0 here. In Equation (2), v is velocity of the wave. We can then convert to the following non-linear ODE for U(ξ):
(3)
Let us consider the solutions for Equation (3) as follows:
(4)
where ai is constant, m is a positive integer that serves as the balancing term and the second order ODE provided by G = G(ξ) is as follows:
(5)
where A is the integral constant. A polynomial with the (1/G′) is constructed by computing the needed derivatives of Equation (4) and replacing in Equation (3). By setting the coefficients of these polynomials equal to zero, a system of algebraic equations is created. The computer program solves the equation. Thus, the solution of Equation (2) is found.

3. Analytical Solutions of TRLW Equation Using (1/G′)- Expansion Method

Let us take Equation (1). By using transform u = u(x, t) = U(ξ),  ξ = x − vt,
(6)
and by integrating Equation (6), we get:
(7)
where c is an integral constant. This integral constant customises the solution of the equation and can represent certain physical conditions or initial values. In Equation (7), we identify the equilibrium term m = 2, and using Equation (4), we get the following solution form:
(8)
When Equation (8) is substituted for Equation (7) and the necessary adjustments are performed, the following systems of equations may be produced:
(9)
Case 1: If,
(10)
substituting values in Equation (10) for Equation (8), we get the following solutions:
(11)
Case 2: If,
(12)
substituting values in Equation (12) for Equation (8), we get the following solutions:
(13)

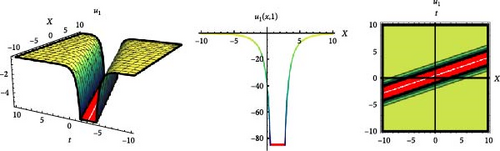
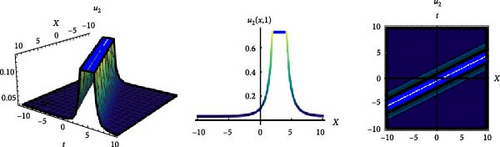
A negative time parameter t does not make any physical sense. However, it can have different meanings mathematically. Therefore, in this study, the parameter t is taken in the range of (−10,10). In addition, graphs that we can call standing waves are presented in Figures 1 and 2 by giving appropriate values to the constants in the hyperbolic form travelling wave solutions presented with Equations (11) and (13).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
3- and 2-dimensional and contour plots of Equation (11) for A = 2,  μ = 2,  λ = 0.5,  α = 1,  and v = 3.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
3- and 2-dimensional and contour plots Equation (13) for A = 3,  μ = 1,  λ = 0.8,  a2 = 1,  and v = 2.

4. Results and Discussions

The TRLW equation, which has many aspects of the KdV equation and is recognised as an alternative to the KdV problem, is solved using hyperbolic form travelling wave solutions in this paper. In the work of non-linear waves, the TRLW equation, like the KdV equation, sheds light on many physical phenomena [25]. Travelling waves play a significant role in the analysis of non-linear phenomena in applied sciences. Travelling waves, which are used as a mathematical tool in energy transport, continue to be the focus of attention for many researchers. We believe that the travelling wave solutions produced in this paper will be useful in analysing shallow water waves.

In this study, travelling wave solutions of the TRLW equation have been successfully obtained through the expansion method. The solutions obtained are different from the solutions obtained in studies [18, 21, 22, 29]. In non-linear physics, wave mechanics, non-linear wave propagation refers to the evolution of wave motion in a non-linear manner due to changing conditions in the medium. This type of wave propagation is observed in various fields, especially, in areas such as acoustics, hydrodynamics, optics and plasma physics. Both non-linear wave propagation and shock waves can be used to analyse the non-linear effects of wave motion using the travelling wave solutions produced in this work.

Equation (1) is known as the time-corrected long wave equation. α is a coefficient in the non-linear term of the equation. If α is zero, the non-linear term disappears and the equation simplifies. Physically, the fact that α is zero has a significant impact on the nature of the equation. The disappearance of the non-linear term linearises the wave behaviour. This can change the way waves propagate and interact. The fact that α is non-zero in the travelling wave solutions produced in this study may be important in modelling the non-linear dispersion phenomenon.

When the travelling wave solutions presented with Equations (11) and (13) are examined, they contain singular points.

In Equation (11), it has a singular point for A = 2,  μ = 2,  λ = 0.5,  α = 1,  v = 3,  and t = 1 at the x = 1.6137056388801092 point and exhibits asymptotic behaviour. Similarly, in Equation (13), it has a singular point for A = 3,  μ = 1,  λ = 0.8,  a2 = 1,  v = 2,  and t = 1 at the x = 3.094335921692375 point and exhibits asymptotic behaviour. The asymptotic behaviour of waves is an important instrument for non-linear physics. Asymptotic behaviour refers to a particular behaviour of a system as it approaches infinity in time or space. The asymptotic behaviour of waves is critical for understanding the long-term evolution of wave motions. Asymptotic analysis is a powerful tool for predicting the long-term behaviour of waves and predicting future events.

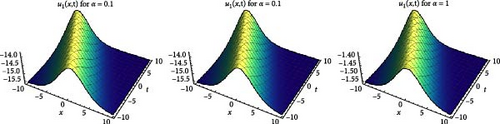
By using the travelling wave solution obtained in this study and presented with Equation (13), discussions can be made about the amplitude or height of the wave, as in the study [36]. For this discussion, the following simulation can be examined for different values of the coefficient of the non-linear term α, which affects the amplitude of the wave and is included in the mechanism of Equation (1).

When Figure 3 is carefully analysed, the wave amplitude becomes smaller as the α value increases.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The response given by Equation (13) for different values of α A = −0.5,  μ = 2,  λ = 0.5,  and v = −0.5.

Advantages of the (1/G′)-expansion method is that the solution produced by the method has a singular point. The travelling wave solution, which contains a singular point, can suggestion a varied aspect to the discussions about shock waves. It can be said that it is an effective, reliable and useful method for generating travelling wave solutions of nPDEs.

5. Conclusion

In this article, hyperbolic travelling wave solutions of the TRLW equation were successfully generated using the (1/G′)-expansion method. This well-known method is used to find analytic solutions of TRLW equation. The travelling wave solutions presented in this study contain a singular point within its structure. We consider that travelling wave solutions containing singular points are important for scientists studying asymptotic behaviour. It can also be more valuable if the free parameters in the solutions presented gain physical meaning. In the future, we can propose the (1/G′)-expansion method to attain the solution of nPDEs. For arbitrary values given to the parameters in the solutions, graphs are presented. The results found in this theoretical study can be applied to understand the properties and elastic behaviour of non-linear structures, including solitons, and also to play a significant role in a wide variety of physical applications.

Conflicts of Interest

The author declares no conflicts of interest.

Funding

There is no funding for this work.

Data Availability Statement

The data sharing is not applicable to this paper as no datasets were generated or analysed during the current study.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.