Volume 2025, Issue 1 9968037

Research Article

Open Access

Structural, Mechanical, Electronic, and Optical Properties of CsCdX₃ (X = Cl, Br, and I): A Comparative Study Using First Principle Calculation

Md. Al Momin

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Rafiqul Islam,

Md. Rafiqul Islam

Department of Electrical and Electronic Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Amran Sarker,

Corresponding Author

Md. Amran Sarker

[email protected]

orcid.org/0000-0001-8687-6940

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Solayman,

Md. Solayman

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Razia Khan Sharme,

Razia Khan Sharme

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Rasidul Islam,

Corresponding Author

Md. Rasidul Islam

[email protected]

orcid.org/0000-0002-9916-793X

Department of Electrical and Electronic Engineering , Jamalpur Science & Technology University , Jamalpur , 2012 , Bangladesh

Search for more papers by this author

Sohail Ahmad,

Sohail Ahmad

Department of Physics , College of Science , King Khalid University , P.O. Box 9004 , Abha , Saudi Arabia , kku.edu.sa

Search for more papers by this author

Md. Al Momin,

Md. Al Momin

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Rafiqul Islam,

Md. Rafiqul Islam

Department of Electrical and Electronic Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Amran Sarker,

Corresponding Author

Md. Amran Sarker

[email protected]

orcid.org/0000-0001-8687-6940

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Solayman,

Md. Solayman

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Razia Khan Sharme,

Razia Khan Sharme

Department of Materials Science and Engineering , Khulna University of Engineering and Technology (KUET) , Khulna , 9203 , Bangladesh , kuet.ac.bd

Search for more papers by this author

Md. Rasidul Islam,

Corresponding Author

Md. Rasidul Islam

[email protected]

orcid.org/0000-0002-9916-793X

Department of Electrical and Electronic Engineering , Jamalpur Science & Technology University , Jamalpur , 2012 , Bangladesh

Search for more papers by this author

Sohail Ahmad,

Sohail Ahmad

Department of Physics , College of Science , King Khalid University , P.O. Box 9004 , Abha , Saudi Arabia , kku.edu.sa

Search for more papers by this author

First published: 13 May 2025

https://doi.org/10.1155/acmp/9968037

Academic Editor: Sefer Bora Lisesivdin

Share a link

Email
Wechat
Bluesky

Abstract

This study presents a comparison of structural, optical, mechanical, and electronic characteristics of CsCdX₃ (X = Cl, Br, and I) by employing first principle calculations. We performed this calculation using the general gradient approximation (GGA) scheme within the Perdew–Berke–Ernzerhof (PBE) functional, which is carried out by the Cambridge Serial Total Energy Package (CASTEP) system. The computation’s validity is validated by a comparison of accessible mathematical and experimental findings. The computed lattice constants show excellent consistency with those obtained from the theoretical calculation and experimental techniques. The computed result explicates that when the larger halogen is substituted for the smaller one, the cell volume and lattice parameter of CsCdX₃ (X = Cl, Br, and I) increase. The obtained mechanical characteristics evidence that CsCdX₃ (X = Cl, Br, and I) compounds are ductile, and ductility increases with the replacement of Cl with Br and I, respectively, and CsCdI₃ exhibits the highest amount of ductility. Indirect bandgap semiconductor to metallic transition is found in the energy band diagrams when I occupies the X site of CsCdX₃ instead of Cl and Br. Furthermore, the absorption coefficient, the dielectric constant, conductivity, and refractive index demonstrate that when Cl is replaced by I and Br, redshift occurs in the optical spectra. Among the compounds, the reflectivity of CsCdI₃ is the highest in the IR region, making CsCdI₃ suitable as an IR reflector. But in the UV region, CsCdCl₃ could be suitable as a UV reflector.

1. Introduction

Researchers are looking for advanced materials with a wide range of applications to meet technological challenges in the future. Because of this, a variety of the material’s features have been thoroughly researched in recent years to use them effectively in cutting edge technology. Experimental and theoretical investigations may be used to examine the physical characteristics of materials [1]. Perovskites have gained significant attention from scientists and researchers in recent times due to their remarkable chemical and physical properties, including superconductivity, semiconductivity, ferroelectricity, thermoelectricity, piezoelectricity, catalytic activity, colossal magnetoresistance, half-metallic transport, and ferromagnetism [2–10]. Furthermore, their diverse range of applications, such as optoelectronic devices, photovoltaic cells, photodetectors, LEDs, etc. [11–18], has made them attractive to the scientific community. Perovskites are also considered to be significant materials in the photocatalytic sector because of their excellent stability and broad absorption spectrum, which generate electron–hole pairs that facilitate photoelectrochemical reactions [19]. Numerous experimental and theoretical techniques have been developed to investigate different properties of perovskites [20, 21]. One theoretical approach that is gaining traction and showing a lot of promise is the density functional theory (DFT) [22–26], as it gives more accurate and consistent results close to the experiments [27–31].

Owing to the unique optoelectronic characteristics, halide perovskites are gaining interest from photovoltaic researchers [32–34]. Halide perovskites are thought to originate from a parent phase with the generic formula ABX₃ (wherein X symbolizes halides, A symbolizes a cation, and B symbolizes a heavy metal cation, such as Pb, Cd, etc.). Till today, halide-based cells have the greatest possible power conversion efficiency (PCE) among all perovskites, coming in at 25.5% [32, 35–37]. Cesium (Cs)-based halide perovskites have received great attention in the photovoltaic industries because of their high absorption coefficient in the visible and ultraviolet spectrum [38]. It was demonstrated that CsSnX₃ and CsPbX₃ possess appropriate band gaps and impressive absorption coefficients [32–34], rendering them potential prospects for employment in the solar sector. Like other Cs-based halide perovskites, Cs-cadmium (Cd)-based perovskites are also promising materials for various sectors because of their remarkable properties. CsCdCl₃ has excellent thermal and electric properties, making it a viable thermoelectric material for automobile industries [39]. Also, CsCdCl₃ is a promising candidate for various optical devices, owing to their strong absorption coefficient [38]. CsCdX₃ (Cl and Br) is also found to be a potential candidate for sprintonic applications when doped with C and N because of their strong magnetic properties [40].

Like other Cs-based perovskites, multiple studies were conducted on CsCdX₃ (X = Cl and Br) [41, 42]. The mechanical, optical, electrical, and structural characteristics of CsCdCl₃ were investigated in earlier studies in both pressured and nonpressurized circumstances, and the obtained results elicited the fact that CsCdCl₃ possesses indirect band gaps [41, 42]. Further, the electronic, magnetic, and structural characteristics of CsCdBr₃ were reported with B, C, and N dopants [32, 40]. It was found that CsCdBr₃ is an indirect semiconductor and a nonmagnetic material. However, when B, C, and N were doped into the Br sites of CsCdBr₃, ferromagnetic characteristics were discovered. Apart from this, these materials have exceptional optical characteristics in the UV, making them very promising for use in optoelectronic devices in the UV range [42]. As far as we are aware, no theoretical or experimental investigations have been conducted on CsCdI₃. Furthermore, no research has yet been done on the optical and mechanical characteristics of CsCdBr₃. Therefore, employing first principles calculations, it is possible to investigate the mechanical, optical, electronic, and structural characteristics of CsCdX₃ (X = Cl, Br, and I) and compare the outcomes.

In this study, we used density functional theory to analyze the structural features, mechanical characteristics (Young’s modulus, bulk modulus, share modulus, Pugh’s ratio, Poisson’s ratio, Cauchy pressure, machinability index, Vickers hardness, and anisotropy), electronic characteristics, and different optical characteristics of CsCdX₃ while X is replaced by Cl, Br, and I, respectively, and compared these calculated results among these three materials. We also have calculated the chemical and mechanical stability, ductility, and brittle nature of these three compounds.

2. Computational Method

In this study, first principles calculations within the DFT framework have been conducted [43, 44] employing the Cambridge Serial Total Energy Package (CASTEP) [45]. To investigate the characteristics, CASTEP primarily utilizes the plane wave pseudopotential total energy approach [46]. Utilizing the Perdew–Berke–Ernzerhof (PBE) functional and the general gradient approximation (GGA), the electronic exchange-correlation energy is computed [47, 48]. Ultrasoft pseudopotentials of Vanderbilt type are used to simulate the interaction between valence electrons and ion cores [46]. The ideal crystal structure was precisely guaranteed by utilizing the Broyden–Fletcher–Goldfarb–Shanno (BFGS) technique [49], which offers a quick method to identify the building with the lowest energy. A plane wave energy cutoff of 660 eV along with a k-point mesh of 8 × 8 × 8 was employed to ensure accurate structural and characteristic estimations. The convergence tests with respect to key parameters, such as the plane wave cutoff energy and k-point sampling, to ensure that the method converges efficiently and provides reliable results, the convergence graph is displayed in Figure S1 in the supporting manuscript. To sample the Brillouin zone of the k-points, the Monkhorst–Pack method was employed [50]. The stress–strain method was applied in typical circumstances to obtain the studied model’s elastic stiffness constants [51]. The strain magnitude was adjusted to 0.003 to get the best results. The following criteria were set for convergence: total energy = 5 × 10⁻⁶eV/atom, maximum stress = 0.02 GPa, maximum force at 0.01 Å, and maximum displacement = 5.0 × 10⁻⁴Å.

3. Results and Discussions

3.1. Structural Properties

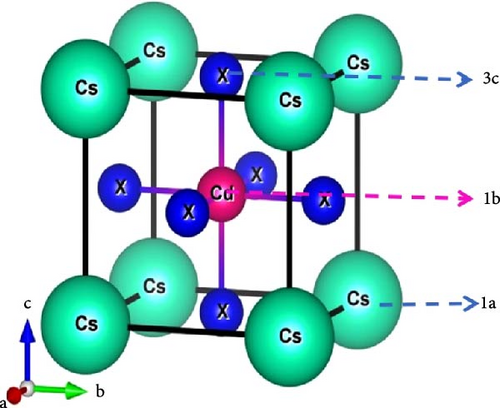
The CsCdX₃ compound, where X symbolizes Cl, Br, or I, has a cubic crystal structure having the space group Pmm (#221). The crystalline structure of CsCdX₃ was illustrated employing the VESTA software [52], as shown in Figure 1. The crystal lattice of CsCdX₃ comprises five atoms, with X representing the halogens Cl, Br, or I. The Cs atom is positioned at coordinates (0, 0, 0) and occupies Wyckoff position 1a, while the Cd atom is situated at coordinates (0.5, 0.5, 0.5) and occupies Wyckoff position 1 b. The X (X = Cl, Br, and I) atoms occupy Wyckoff position 3 c at coordinates (0.5, 0.5, 0). Together with the prior simulated and experimental data, Table 1 displays the estimated lattice constants and cell volumes of CsCdX₃. The calculated lattice constant of CsCdCl₃ deviates, respectively, by 2.36% and 0.08% from the experimental and computational work and by 0.1% for CsCdBr₃ from the theoretical work, which indicates the accuracy of the calculation of this work. A comparison table of our calculated lattice parameters and band gaps, alongside previously studied and experimental data, is provided in Table S5. As far as Table 1, when a smaller atomic size halide is replaced by a larger one, the lattice parameter of CsCdX₃ increases. When Br and I replace Cl, the lattice parameters become 5.619 Å and 6.045 Å, respectively. Table 1 also shows the cell volume of CsCdX₃, which is found to increase gradually when Cl is replaced by Br and then by I.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Optimized crystal structure of cubic CsCdX₃ (X = Cl, Br, and I).

Table 1. Calculated, theoretical as well as empirical lattice constant (Å), formation energy (Δ E_f), cell volume (V), and tolerance factor (t) of CsCdX₃.

Compound	Lattice parameter (Å)			Volume, V (Å³)	Formation energy, Δ E_f (eV/atom)	Tolerance factor, (t)
Compound	Exp.	Previous work	This work	Volume, V (Å³)	Formation energy, Δ E_f (eV/atom)	Tolerance factor, (t)
CsCdCl₃	5.210 [53 ]	5.329 [40]	5.333	151.712	−2.92	0.95
CsCdBr₃	—	5.613 [40]	5.619	177.435	−2.58	0.94
CsCdI₃	—	—	6.045	220.898	−2.20	0.92

The formation energy of CsCdX₃ is computed using Equation (1) to assess the chemical stability of the structure and obtain results listed in Table 1:

(1)

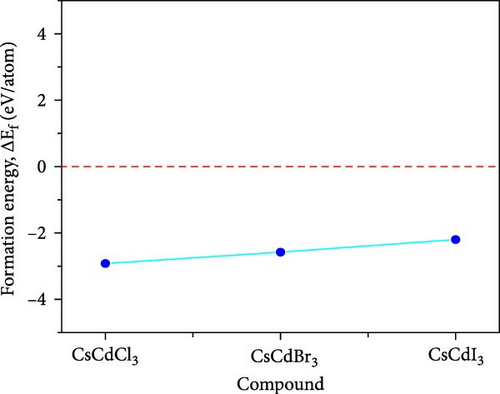
Here, E_s(X), E_s(Cs), and E_s(Cd) correspond to the energies of X (Cl, Br, and I), Cs, and Cd respectively, while E_total(CsCdX₃) specifies the system’s (unit cell) total energy. The negative value of ΔE_f(CsCdX₃) demonstrates that CsCdX₃ is chemically stable [54]. Figure 2 also visually displays the examined compounds’ negative formation energy. For structural stability, the tolerance factor (t) is calculated using the following formula:

(2)

The usual tolerance factor ranges from 0.8 to 1 for cubic perovskite. Table 1 demonstrates that the tolerance factor of CsCdCl₃, CsCdBr₃, and CsCdI₃ are 0.95, 0.93, and 0.92, respectively. So, all three compounds are structurally stable.

3.2. Mechanical Properties

Elastic and mechanical characteristics are critical for materials intended for applications in devices. These properties also help understand how a material will respond under stressed conditions. Calculating elastic constants is necessary to assess a material’s stability, stiffness, ductile-brittle nature, hardness, machinability, isotropic-anisotropic properties, and bonding nature [55, 56]. The calculated elastic constants (C_ij) for CsCdX₃ are presented in Tables S1–S4 in the supporting information. The Born stability criteria [43] are, C₁₁ > 0, C₁₁ − C₁₂ > 0, C₁₁ + 2C₁₂ > 0 and C₄₄ > 0, which is used to assess the mechanical stability of a material that is subject to the condition that the elastic constants must be greater than zero for the cubic structure. These elastic constants were obtained using the “stress–strain” premise and plotted in Figure 3. It can be observed from the plot that C₁₁, C₄₄, and C₁₂ are greater than zero, confirming the mechanical stability of all three compounds.

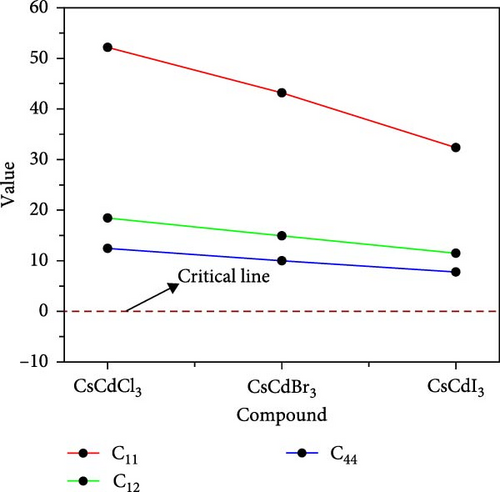
Table 2 provides an estimation and listing of various mechanical features of CsCdX₃, such as Young’s modulus (E), bulk modulus (B), shear modulus (G), Poisson’s ratio(υ), Pugh’s ratio (B/G), Machinability index (μ_M), Vicker’s hardness (H_v), universal anisotropic factor (A^U), and Zener anisotropic factor (A). These features are obtained using elastic constants. The Vigot–Reuss–Hill (VRH) method is applied to comprehend how solids behave mechanically under different circumstances [57]. For cubic lattices, the Voigt bulk modulus (B_V) and Voigt shear modulus (G_V) are defined as follows [58]:

Table 2. Measured bulk modulus, B (in GPa); shear modulus, G (in GPa); Young’s modulus, E (in GPa); Pugh’s ratio, B/G; Poisson’s ratio, υ; Vickers Hardness, H_v; Cauchy pressure, C₁₂–C₄₄; and Machinability Index,μ_M of CsCdX₃.

Properties	CsCdCl₃	CsCdBr₃	CsCdI₃
Bulk Modulus, B	29.6676	24.3384	18.8305
Shear Modulus, G	14.0519	11.5013	8.7414
Young Modulus, E	36.4078	29.8084	22.7101
Pugh’s ratio, B/G	2.11	2.12	2.15
Poisson’s ratio, υ	0.295	0.296	0.300
Vickers Hardness, H_v	1.916	1.565	1.171
Cauchy pressure, C₁₂ − C₄₄	5.9881	4.8965	4.1078
Machinability Index, μ_M	2.39	2.43	2.43

(3)

(4)

Additionally, the following formulas are used to calculate the Reuss bulk modulus (B_R) and the Reuss shear modulus (G_R) in terms of cubic lattices:

(5)

(6)

The Voigt–Reuss–Hill (VRH) technique is employed to obtain the bulk (B) and shear (G) moduli [59]:

(7)

(8)

The B is the fracture resistance, and materials with higher B values tend to be more resistant to fracture compared to those with lower B values. Table 2 revealed that CsCdCl₃ exhibits the highest B value and decreases when Br and I are used as substitutes for Cl, respectively. Thus, among the three compounds, CsCdCl₃ shows the highest fracture toughness. The G indicates the plastic deformation resistance and increases with the value of G. Table 2 demonstrates that CsCdCl₃ has the highest value of G and decreases whenever Br and I are substituted for Cl, respectively. Young’s modulus (E) assess a material’s stability or resilience against flexible distortion under load. From Table 2, it is observed that CsCdCl₃ shows greater stiffness than the other two materials.

The following formulas are used to compute Young’s modulus (E) and Poisson’s ratio (υ) [60]:

(9)

(10)

To assess the substance’s brittle-ductile characteristics, Pugh’s ratio (B/G) is utilized, and 1.75 is the borderline to separate brittleness from ductility. A material is considered ductile if its B/G ratio is more than 1.75 and brittle if it is less than that. Moreover, the material becomes more ductile as the B/G ratio rises. According to Table 2, all three compounds we studiously investigated are ductile, and that ductility increases by replacing Cl with Br and I. Among the compounds, CsCdI₃ exhibits the highest ductility. Like B/G, the brittle-ductile nature of materials is also confirmed by Poisson’s ratio ν. The borderline that separates brittleness and ductility is 0.26; in this case, any material becomes ductile if the number exceeds 0.26. The computed compounds are ductile, as shown in Table 2, with CsCdI₃ exhibiting the maximum ductility. Cauchy pressure is another parameter that is utilized to figure out the ductility or brittleness of a substance. Cauchy pressure levels that are positive indicate ductility, whereas those that are negative denote brittleness [61]. All the properties listed in Table 2 are in favor of the ductility of the compounds. The capability to withstand plastic deformation depends on the hardness of the material.

(11)

Equation (11) is employed for determining the compounds’ hardness, which is displayed in Table 2, where CsCdCl₃’s hardness is found to be 1.916. However, when Br and I are used as substitutes for Cl, the hardness reduces by 1.224 times and 1.636 times, respectively. The machinability index μ_M, which identifies a substance’s cutting capability, the most economical quantity of machine utilization, and deformation, has had a major influence on the industrial sector. By using the following formula, it may be obtained:

(12)

The μ_M is estimated to be 2.39 for CsCdCl₃ but for CsCdBr₃, and CsCdI₃ the μ_M is found to be the same and 1.02 times greater than the value of CsCdCl₃.

Elastic anisotropy is necessary to understand microscopic behavior in single as well as multicrystalline substances. The anisotropy of a material mainly resulted from C₁₁. So, identifying the elastic tensor’s directionality is essential. By analyzing the mechanical robustness and suitability of a material, we can investigate elastic anisotropy. The measure of elastic anisotropy may be expressed as [62]:

(13)

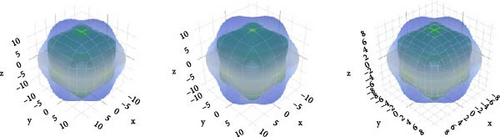
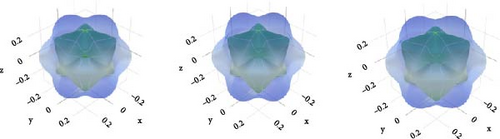
If A^U has a zero value, the substance is isotropic. The discrepancy from this value defines the corresponding level of anisotropy. All three compounds exhibit very little anisotropy, as Table 3 shows.

Table 3. Calculated Shear anisotropic factors A_i (i = 1–3), Zener’s anisotropy index (A), anisotropy in shear (A^G), anisotropy in bulk modulus (AB), universal anisotropy index (A^U), and equivalent Zener anisotropy (A^eq) of CsCdX₃.

Compound	A₁	A₂	A₃	A	A_G	A^U	A^eq
CsCdCl₃	0.737554	0.737554	0.737554	0.737554	0.011082	0.112064	1.355833
CsCdBr₃	0.707993	0.707993	0.707993	0.707993	0.014246	0.144523	1.412443
CsCdI₃	0.743068	0.743068	0.743068	0.743068	0.010548	0.106608	1.345773

The formulas that measure the proportion of the extent of anisotropy under shear (A_G) as well as in bulk or compressibility (A_B) are given below:

(14)

(15)

In this case, materials behave isotropic in nature while A_G as well as A_B has a value of zero. The data shown in Table 3 demonstrates that the measure of A_B is consistently zero for all substances, proving the isotropic nature of CsCdX₃ in compression. Nevertheless, A_G deviates a little from zero value, indicating that CsCdX₃ shows some anisotropy under shear(A_G) conditions, and among them, CsCdBr₃ exhibits the most anisotropy under shear (A_G)conditions. The following formula is used to examine the shear anisotropic components A_i (i = 1–3) to more accurately analyze shear anisotropy across various planes [63, 64].

(16)

([100] plane)

(17)

([010] plane)

(18)

([001] plane)

A₁, A₂, A₃, and A are all equal in a cubic structure, and A denotes the Zener anisotropy index, which is derived by [65]:

(19)

If A = 1, then the material exhibits isotropic behavior. Anisotropy refers to the extent of deviation from unity. As shown in Table 3, A has a value of less than one, so these compounds are not isotropic. Among the compounds, CsCdBr₃ shows the highest anisotropy, which is also supported by the equivalent anisotropy factor (A^eq). Again, the small anisotropic behavior of CsCdX₃ is confirmed in Table 3. The following formula can be used for determining the A^eq:

(20)

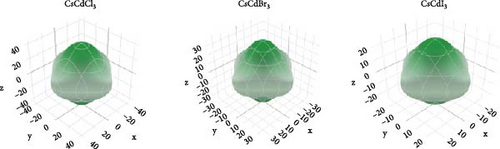
Spherical 3D images reflect the isotropy, while nonspherical images reveal the anisotropy [63]. The amount of anisotropy is quantified by measuring its divergence from the spherical form, and the anisotropy increases with the deviation. Figure 4 reflects that, in comparison to other compounds, CsCdBr₃ exhibits a slightly greater amount of anisotropy.

3.3. Electronic Properties

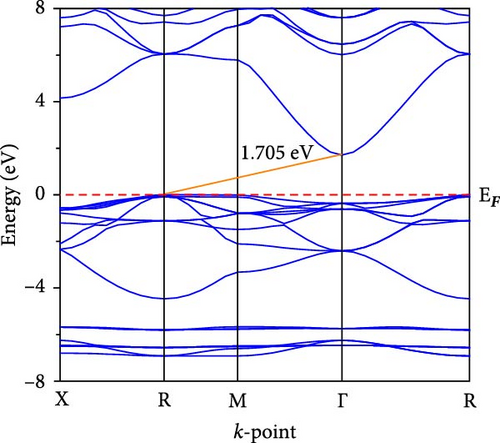
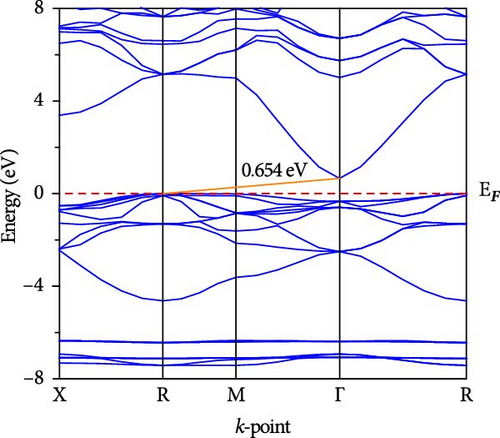
The electronic band dispersion profile is essential for understanding electron transport mechanisms in a solid. We calculated the band dispersion profile of CsCdX₃ (X = Cl, Br, and I) in the Brillouin zone’s high symmetry paths (X, R, M, Γ, and R) and plotted it in Figure 5. The red horizontal dotted line at 0 eV (E_F) symbolizes the Fermi level. The band dispersion profile of CsCdCl₃ demonstrates that it is an indirect (R- Γ) bandgap semiconductor having a bandgap of 1.705 eV. But when Br replaces Cl, the conduction band (CB) approaches the fermi level, the indirect gap at R- Γ reduces and is found to be 0.654 eV. Further, the band gap reduces to 0 eV at Γ point when I. Thus, replacing Cl, CsCdI₃ exhibits metallic behavior. For these substances, there isn’t yet an experimental band gap, so the validity of our results is confirmed by comparing them against previously published (theoretical) findings, as shown in Table 4. It is found that our calculated band has excellent consistency with the previously computed band gap. It is also found that there is an inverse relation between the bandgap and nuclear size of the halogen in halide perovskite. The band gap reduction may be connected with electronegativity, which decreases with the atomic size of the halogen atom.

Table 4. Calculated as well as the theoretical band gap of CsCdX₃.

Compound	Band gap, E_g (eV)
Compound	Previous work	This work
CsCdCl₃	1.691 [41]	1.705
CsCdBr₃	0.70 [32]	0.654
CsCdI₃	—	0

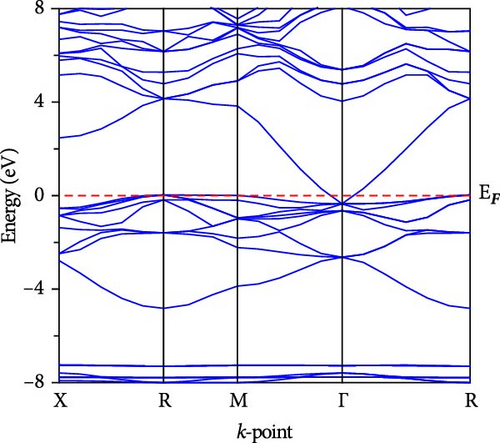
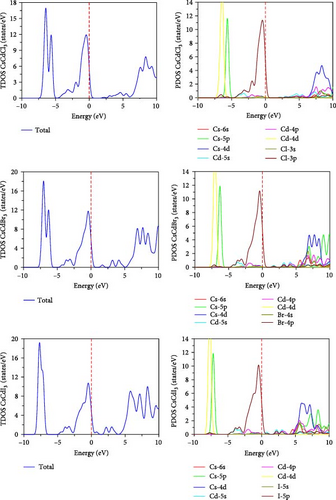
The band structures can also be explained by the total density of states (TDOS) shown in Figure 6, whereas the red horizontal dotted line at 0 eV symbolizes the Fermi level. As seen in the figure, the semiconducting behavior of CsCdCl₃ and CsCdBr₃ is indicated by their zero TDOS values being close to the Fermi level. However, TDOS exhibits a little rise close to the fermi level when I replace Cl, suggesting that the substance is metallic. Thus, TDOS justifies the statement of the band structure. The PDOS further explains this behavior. When “I” take the place of “Cl”, Cd-5s states shifted toward the Fermi level, and I-5p displays a little peak close to 0 eV. Hence, the minor peak in the TDOS near 0 eV is caused by the combination of I-5p and Cd-5s states. This indicates the metallic nature of CsCdI₃. Again, TDOS shows that when I substitute Cl, the CB peak progresses further toward the lower energy region. The presence of halogen p states is the primary cause of the valance band (VB) peak around the fermi level, as depicted in Figure 5. On the contrary, in the conduction band, Cs-4d and Cs-5p contribute the most to the CB, while there is a small contribution from Cs-6s, Cd-4p, and s states of halogens. The band gap reduction mainly occurs due to the contribution of halogens.

3.4. Optical Properties

Optical characteristics, which vary depending on the kind of substance and the incoming radiation, may be used to understand how light interacts with substances. The important optical characteristics, including conductivity, reflectivity, absorption, dielectric function, and refractive index, are measured for CsCdX₃ and plotted in Figure 7. The dielectric function can be expressed by ε(ω) = ε₁(ω) + ε₂(ω) ,where ε₁(ω) and ε₂(ω) symbolizes the real and imaginary parts of the dielectric constant, respectively. The real part of the dielectric constant is mathematically derived by the Kramers–Kronig transformation [66].

(21)

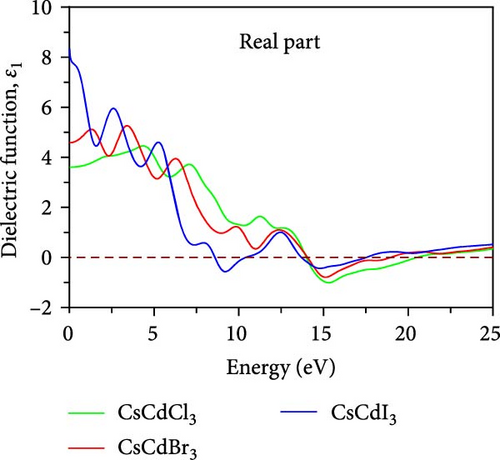
The magnitude of the static dielectric constant, ε₁(0) is evaluated to be 3.61 for CsCdCl_3, but when Br and I are used as substitutes for Cl, its values become 4.58 and 8.33, respectively. The value of ε₁(0) slightly increases in the lower energy region for CsCdBr₃ and CsCdCl_3, but it sharply decreases in the lower energy region for CsCdI₃. A vital measure for evaluating an optoelectronic device’s efficacy is the ε₁(0). The charge carrier recombination rate probability is less in the substance with the greater dielectric constant [66]. Moreover, the metallic characteristics are indicated by the negative portion of the real dielectric constant.

The imaginary dielectric constant, ε₂ can be determined from the actual transition between the unoccupied and occupied electronic states and can be written as [66]:

(22)

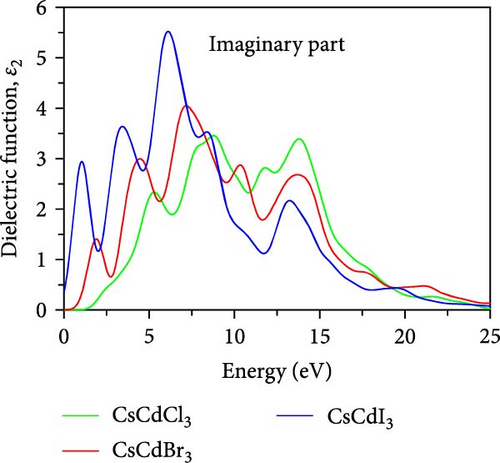
The ε₂(ω) is a very important parameter because the absorption characteristics of a material depend on it. Figure 7b shows the variation of ε₂(ω) within the energy spanning from 0 eV up to 20 eV, within this limit, three significant peaks are observed for CsCdCl₃ at about 5.3, 8.8, and 13.8 eV. In the case of CsCdBr₃ major peaks are observed at 4.4, 7.15, and 10.2 eV, with an additional peak at 1.94 eV. Similar to CsCdBr₃, major peaks appeared at 3.41, 6.03, and 8.52 eV for CsCdI_3, with an additional peak at 1.01 eV. The peaks are found to shift towards the lower energy side when Br and I are used as substitutes for Cl. It is also found that CsCdI₃ exhibits sharper peaks than the other two compounds.

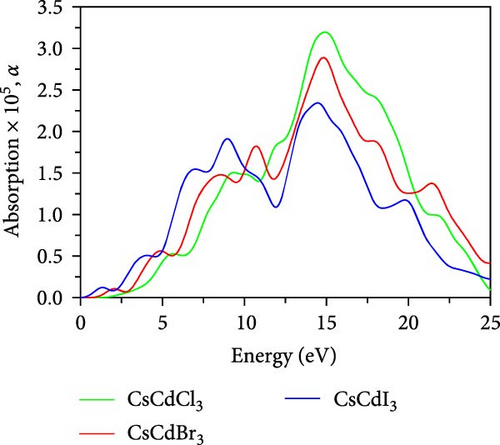
The absorption coefficient, α plays a key role in choosing a material in various optoelectronic devices as well as solar cell usage. Figure 7c illustrates the change in α with respect to photon energy, where each compound exhibits three significant peaks in the 0–20 eV energy range. The peaks appeared at 5.56, 9.06, and 14.7 eV. However, it becomes apparent that these peaks migrate towards the lower energy side when Br and I are used as substitutes for Cl. CsCdBr₃ exhibits major absorption peaks at 4.77, 8.39, and 14.7 eV, and one additional peak at 10.7 eV, whereas maximum peaks are observed in the UV region. CsCdI₃ exhibits major peaks at 3.97, 6.94, and 14.4 eV, and two additional peaks at 1.29 eV and 9.02 eV, respectively. CsCdI₃’s absorption edge begins from 0 eV, which also confirms the metallic nature of CsCdI₃.Moreover, the absorption spectra cover the whole IR and the visible region. CsCdCl₃ and CsCdBr₃ exhibit higher peaks in the UV region. So, we can predict that they are suitable as UV detectors and efficient UV absorbers [66].

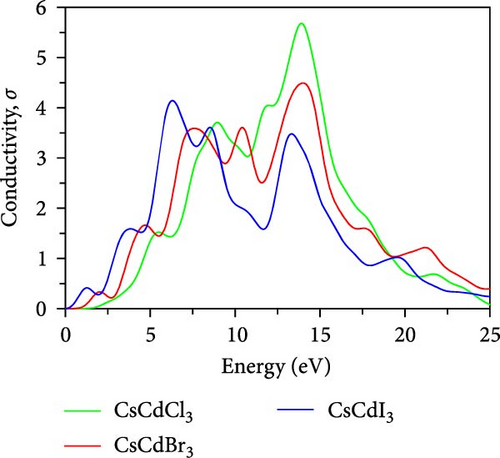
Photoconductivity, σ is a very crucial property of a material. It also refers to optical conductivity. The photoconductivity spectra of CsCdX₃ are demonstrated in Figure 7d, which exhibits a comparable absorption spectra pattern. As seen in Figure 7d, the CsCdCl₃, CsCdBr₃, and CsCdI₃ show the highest peak in the energy range of 13–14.5, 10–11.5, and 6–7 eV, respectively. The figure displays the maximum conductivity of these compounds is located within the UV area, and the peak shifted toward the lower energy area when Br and I replace Cl.

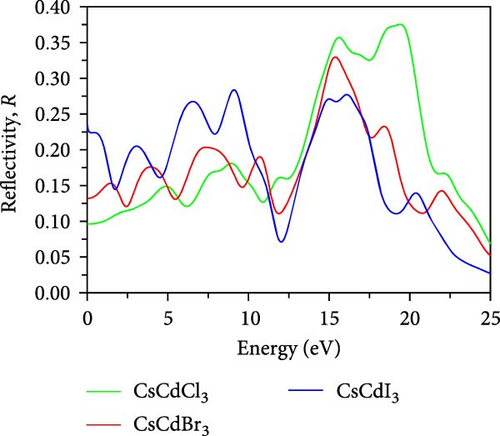
The reflectivity spectra plotted in Figure 7e demonstrate that very low reflectivity (0.096) is obtained for CsCdCl₃ at 0 eV. But when Br and I are used as substitutes for Cl, the reflectivity increases by the amounts of 0.132 and 0.236, respectively. Further, CsCdI₃ gives higher reflectivity in the IR region than CsCdCl₃ and CsCdBr₃. So, we can predict that CsCdI₃ is a more suitable material for the IR reflector and photographic technology [67]. CsCdCl₃, CsCdBr₃, and CsCdI₃ display the highest reflectivity in the energy range of 18–21 eV, 14–16 eV, and 8–10 eV, respectively. Thus, these compounds could potentially be employed as an effective covering material to minimize the effect of solar heating in the UV region [35]. Further, CsCdI₃ is predicted to be used as a UV shielding material due to having good reflectivity in the UV range [35]. This compound also has good reflectivity in the visible range; hence, it might be used in a solar cell as a form of back reflector. Another noticeable information is that the highest reflectivity is obtained in the energy range when the real dielectric component has negative values.

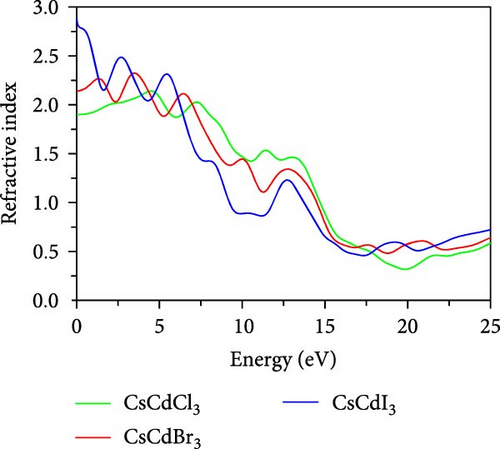
Figure 7f depicts the refractive index spectrum, which shows that the highest peak appears at 0 eV, progressively decreasing with photon energy. CsCdX₃ (X = Cl, Br, and I) exhibits the minimum refractive index value in the UV area and the highest in the IR region. Among the compounds, CsCdI₃ exhibits a greater refractive index at 0 eV, so it can be utilized as a waveguide [68]. Further, CsCdI₃ can be used as an ohmic contact in OLED and QLED [67] as it is metallic and shows a good refractive index at 0 eV.

4. Conclusion

Using DFT calculations, the optical, mechanical, electronic, and structural characteristics of CsCdX₃ are examined here. It is found that the estimated lattice constants and the previously published values coincide quite well. Because Br and I have bigger atomic sizes than Cl, it becomes apparent that replacing Cl with Br and I leads to higher cell volumes and lattice constants. Additionally, the estimated formation energy as well as elastic constants support the mechanical and chemical stability of CsCdX₃. Moreover, Poisson’s and also Pugh’s ratios validate CsCdX₃’s ductility, which increases when Br and I are used as substitutes for Cl. Apart from its enhanced ductility, CsCdI₃ has superior machinability. The band dispersion diagram further supports the metallic character of CsCdI₃, suggesting that it is a desirable material for usage as structural support in various devices. The halogen size is inversely proportionate with the bandgap, as explained by the computed band structure. The band gap shrinks as halogen atomic size rises. It would be possible to employ CsCdX₃ (Cl, Br) as UV absorbers and detectors due to its broad UV absorption coefficient. Moreover, CsCdI₃ exhibits exceptional infrared reflectivity, making them appropriate for infrared reflectors. They may be used as waveguides because of their greater refractive index in the infrared range.

Ethics Statement

All the authors declare that the manuscript does not have studies on human subjects, human data or tissue, or animals.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Md. Al Momin, Md. Rafiqul Islam, Md. Amran Sarker, Md. Solayman, Razia Khan Sharme, Md. Rasidul Islam, and Sohail Ahmad involved in conceptualization, methodology, software, validation, formal analysis, visualization, investigation, data curation, writing original draft, and review and editing.

Funding

Research supported by: Deanship of Research and Graduate Studies at King Khalid University ^∗ RGP2/415/45.

Acknowledgments

The authors extend their appreciation to the deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/415/45.

Supporting Information

Additional supporting information can be found online in the Supporting Information section.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information

References

1 Hossain K. M., Saiduzzaman M., Kumada N., Takei T., Yamane H., and Kabir Rubel M. H., Hydrothermal Synthesis and Crystal Structure of a Novel Bismuth Oxide: (K_0.2 Sr_0.8)(Na_0.01 Ca_0.25 Bi_0.74)O₃, ACS Omega. (2021) 6, no. 24, 15975–15980, https://doi.org/10.1021/acsomega.1c01694.
10.1021/acsomega.1c01694
CAS PubMed Google Scholar
2 Koonce C. S., Cohen M. L., Schooley J. F., Hosler W. R., and Pfeiffer E. R., Suyerconducting Transition Temperatures of Semiconducting SrTiOs, Physical Review Journals Archive. 163, 380.
Google Scholar
3 Samantaray C. B., Sim H., and Hwang H., The Electronic Structures and Optical Properties of BaTiO3 and SrTiO3 Using First-Principles Calculations, Microelectronics Journal. (2005) 36, no. 8, 725–728, https://doi.org/10.1016/j.mejo.2005.03.001, 2-s2.0-23744450023.
10.1016/j.mejo.2005.03.001
CAS Web of Science® Google Scholar
4 Samantaray C. B., Sim H., and Hwang H., Electronic Structure and Optical Properties of Barium Strontium Titanate (BaxSr1−xTiO3) Using First-Principles Method, Physica B: Condensed Matter. (2004) 351, no. 1-2, 158–162, https://doi.org/10.1016/j.physb.2004.05.025, 2-s2.0-3342906370.
10.1016/j.physb.2004.05.025
CAS Web of Science® Google Scholar
5 Muta H., Kurosaki K., and Yamanaka S., Thermoelectric Properties of Rare Earth Doped SrTiO3, Journal of Alloys and Compounds. (2003) 350, no. 1-2, 292–295, https://doi.org/10.1016/S0925-8388(02)00972-6, 2-s2.0-0037450317.
10.1016/S0925-8388(02)00972-6
CAS Web of Science® Google Scholar
6 Baettig P., Schelle C. F., LeSar R., Waghmare U. V., and Spaldin N. A., Theoretical Prediction of New High-Performance Lead-Free Piezoelectrics, Chemistry of Materials. (2005) 17, no. 6, 1376–1380, https://doi.org/10.1021/cm0480418, 2-s2.0-15444376436.
10.1021/cm0480418
CAS Web of Science® Google Scholar
7 Wang H., Wang B., Li Q., Zhu Z., Wang R., and Woo C. H., First-Principles Study of the Cubic Perovskites BiM O3 (M = Al, Ga, In, and Sc), Physical Review B. (2007) 75, no. 24, https://doi.org/10.1103/PhysRevB.75.245209, 2-s2.0-34347401845, 245209.
10.1103/PhysRevB.75.245209
CAS Web of Science® Google Scholar
8 Henrich V. E., The Surfaces of Metal Oxides, Reports on Progress in Physics. (1985) 48, no. 11, 1481–1541, https://doi.org/10.1088/0034-4885/48/11/001, 2-s2.0-36149037896.
10.1088/0034-4885/48/11/001
CAS Web of Science® Google Scholar
9 Millis A. J., Shraiman B. I., and Mueller R., Dynamic Jahn-Teller Effect and Colossal Magnetoresistance in La 12x Sr x MnO, American Physical Society. (1996) 77, 175.
CAS Google Scholar
10 Solayman M., Sarker M., Muntasir M., and Materials R. S. O., Pressure-Induced Investigation of Structural, Electronic, Optical, and Mechanical Properties of BaCeO₃, Optical Materials. (2024) 148, 114699.
10.1016/j.optmat.2023.114699
CAS Web of Science® Google Scholar
11 Yin W.-Jian, Shi T., and Yan Y., Unique Properties of Halide Perovskites as Possible Origins of the Superior Solar Cell Performance, Advanced Materials. (2014) 26, no. 27, 4653–4658, https://doi.org/10.1002/adma.201306281, 2-s2.0-84904562552.
10.1002/adma.201306281
CAS PubMed Web of Science® Google Scholar
12 Ramasamy P., Lim D.-H., Kim B., Lee S.-H., Lee M.-S., and Lee J.-S., All-Inorganic Cesium Lead Halide Perovskite Nanocrystals for Photodetector Applications, Chemical Communications. (2016) 52, no. 10, 2067–2070, https://doi.org/10.1039/C5CC08643D, 2-s2.0-84961299160.
10.1039/C5CC08643D
CAS PubMed Web of Science® Google Scholar
13 Krishnamoorthy T., Ding H., and Yan C., et al.Lead-Free Germanium Iodide Perovskite Materials for Photovoltaic Applications, Journal of Materials Chemistry A. (2015) 3, no. 47, 23829–23832, https://doi.org/10.1039/C5TA05741H, 2-s2.0-84948412675.
10.1039/C5TA05741H
CAS Web of Science® Google Scholar
14 Islam M. R., Mazumder A. A. M., Mojumder M. R. H., Shifat A. S. M. Z., and Hossain M. K., Strain-Induced Tunable Optoelectronic Properties of Inorganic Halide Perovskites APbCl₃ (A = K, Rb, and Cs), Japanese Journal of Applied Physics. (2023) 62, no. 1, 011002.
10.35848/1347-4065/acb09e
Web of Science® Google Scholar
15 Khalid Hossain M., Toki G. F. I., and Madan J., et al.A Comprehensive Study of the Optimization and Comparison of Cesium Halide Perovskite Solar Cells Using ZnO and Cu₂FeSnS₄ as Charge Transport Layers, Royal Society of Chemistry. (2023) 47, 8602–8624, https://doi.org/10.1039/d3nj00320e.
10.1039/d3nj00320e
Google Scholar
16 Hasan M., Sarker M., Mansur M., and Heliyon M. I., Pressure-Induced Structural, Electronic, Optical, and Mechanical Properties of Lead-Free GaGeX₃ (X = Cl, Br and, I) Perovskites: First-Principles Calculation, Cell Press. (2024) 10, no. 15, e34824.
CAS Google Scholar
17 Sarker M. A., Hasan M. M., Islam M. R., Talukder M. R., Islam M. R., and Sharif A., Investigating Pressure-Driven Semiconductor-to-Metal Transition in Lead-Free Perovskites AlGeX₃ (X = F, Cl, and Br): Insights From First-Principles Calculations, Materials Advances. (2024) 5, no. 22, 8970–8985, https://doi.org/10.1039/d4ma00611a.
10.1039/D4MA00611A
CAS Web of Science® Google Scholar
18 Sarker M. A., Muntasir M., Momin M. A., Solayman M., and Islam M. R., Pressure-Induced Structural, Electronic, and Optical Properties of Lead-Free NaGeX3 (X = F, Cl, Br, and I) Perovskites: First-Principles Calculation, Advanced Theory and Simulations. (2024) 7, no. 7, https://doi.org/10.1002/adts.202400112, 2400112.
10.1002/adts.202400112
CAS Web of Science® Google Scholar
19 Sarker M. A., Hasan M. M., Momin M. A., Irfanc A., Islam M. R., and Sharif A., Band Gap Engineering in Lead Free Halide Cubic Perovskites GaGeX₃ (X = Cl, Br, and I) Based on First-Principles Calculations, The Royal Society of Chemistry. 14, 9805–-9818.
Google Scholar
20 Islam M. R., Mojumder M. R. H., and Moshwan R., et al.Strain-Driven Optical, Electronic, and Mechanical Properties of Inorganic Halide Perovskite CsGeBr₃, ECS Journal of Solid State Science and Technology. (2022) 11, no. 3, https://doi.org/10.1149/2162-8777/ac56c2, 033001.
10.1149/2162-8777/ac56c2
CAS Web of Science® Google Scholar
21 Islam R., Liu K., and Wang Z., et al.Strain-Induced Electronic and Optical Properties of Inorganic Lead Halide Perovskites APbBr₃ (A = Rb and Cs), Materials Today Communications. (2022) 31, 103305.
10.1016/j.mtcomm.2022.103305
CAS Web of Science® Google Scholar
22 Dar S. A., Srivastava V., Sakalle U. K., Parey V., and Pagare G., DFT Investigation on Electronic, Magnetic, Mechanical and Thermodynamic Properties Under Pressure of Some EuMO3 (M = Ga, In) Perovskites, Materials Research Express. (2017) 4, no. 10, https://doi.org/10.1088/2053-1591/aa90af, 2-s2.0-85042068626, 106104.
10.1088/2053-1591/aa90af
Web of Science® Google Scholar
23 Raza H. H., Murtaza G., Umm-e-Hani, and Arif Khalil R. M., Optoelectronic and Thermal Properties of LiXH3(X = Ba, Sr and Cs) for Hydrogen Storage Materials: A First Principle Study, Solid State Communications. (2019) 299, https://doi.org/10.1016/j.ssc.2019.113659, 2-s2.0-85067613862, 113659.
10.1016/j.ssc.2019.113659
CAS Web of Science® Google Scholar
24 Khandy S. A., Islam I., Gupta D. C., and Laref A., Predicting the Electronic Structure, Magnetism, and Transport Properties of New Co-Based Heusler Alloys, International Journal of Energy Research. (2018) 42, no. 13, 4221–4228, https://doi.org/10.1002/er.4182, 2-s2.0-85052510913.
10.1002/er.4182
CAS Web of Science® Google Scholar
25 Behram R. B., Iqbal M. A., Rashid M., Atif Sattar M., Mahmood A., and Ramay S. M., Ab-Initio Investigation of AGeO3 (A = Ca, Sr) Compounds via Tran-Blaha-Modified Becke-Johnson Exchange Potential, Chinese Physics B. (2017) 26, no. 11, https://doi.org/10.1088/1674-1056/26/11/116103, 2-s2.0-85033708435, 116103.
10.1088/1674-1056/26/11/116103
Web of Science® Google Scholar
26 Ali M. A., Wahab A., Gulana, Murtaza G., and Khan A., First Principles Calculations for Structural, Elastic, Mechanical, Electronic and Optical Properties of CsYbCl3, Materials Research Express. (2019) 6, no. 6, https://doi.org/10.1088/2053-1591/ab0bb2, 2-s2.0-85064433988, 065905.
10.1088/2053-1591/ab0bb2
CAS Web of Science® Google Scholar
27 Ali M. A., Alam N., Dar S. A., Khan A., Murtaza G., and Laref A., A Theoretical Study of the Structural, Thermoelectric, and Spin-Orbit Coupling Influenced Optoelectronic Properties of CsTmCl3 Halide Perovskite, International Journal of Quantum Chemistry. (2020) 120, no. 7, https://doi.org/10.1002/qua.26141, e26141.
10.1002/qua.26141
CAS Web of Science® Google Scholar
28 Verma A. S., Kumar A., and Bhardwaj S. R., Correlation Between Ionic Charge and the Lattice Constant of Cubic Perovskite Solids, Physica Status Solidi (b). (2008) 245, no. 8, 1520–1526, https://doi.org/10.1002/pssb.200844072, 2-s2.0-55449111873.
10.1002/pssb.200844072
CAS Web of Science® Google Scholar
29 Jiang L. Q., Guo J. K., and Liu H. B., et al.Prediction of Lattice Constant in Cubic Perovskites, Journal of Physics and Chemistry of Solids. (2006) 67, no. 7, 1531–1536, https://doi.org/10.1016/j.jpcs.2006.02.004, 2-s2.0-33745822006.
10.1016/j.jpcs.2006.02.004
CAS Web of Science® Google Scholar
30 Verma A. S. and Jindal V. K., Lattice Constant of Cubic Perovskites, Journal of Alloys and Compounds. (2009) 485, no. 1-2, 514–518, https://doi.org/10.1016/j.jallcom.2009.06.001, 2-s2.0-72049107443.
10.1016/j.jallcom.2009.06.001
CAS Web of Science® Google Scholar
31 Verma A. S. and Kumar A., Bulk Modulus of Cubic Perovskites, Journal of Alloys and Compounds. (2012) 541, 210–214, https://doi.org/10.1016/j.jallcom.2012.07.027, 2-s2.0-84865057374.
10.1016/j.jallcom.2012.07.027
CAS Web of Science® Google Scholar
32 Liu D., Peng H., and Sa R., Theoretical Study of Mixed-Halide Influence on the Stability and Electronic Properties of CsCd(Cl/Br)3, Computational and Theoretical Chemistry. (2021) 1200, https://doi.org/10.1016/j.comptc.2021.113251, 113251.
10.1016/j.comptc.2021.113251
CAS Web of Science® Google Scholar
33 Hossain M. K., Toki G. F. I., and Samajdar D. P., et al.Deep Insights Into the Coupled Optoelectronic and Photovoltaic Analysis of Lead-Free CsSnI 3 Perovskite-Based Solar Cell Using DFT Calculations and SCAPS-1D Simulations, ACS Omega. (2023) 8, no. 25, 22466–22485, https://doi.org/10.1021/acsomega.3c00306.
10.1021/acsomega.3c00306
CAS PubMed Web of Science® Google Scholar
34 Islam M., Islam A., and Liu K., et al.Strain-Induced Tunability of the Optoelectronic Properties of Inorganic Lead Iodide Perovskites APbI3 (A = Rb and Cs), Physica B: Condensed Matter. (2022) 638, 413960.
10.1016/j.physb.2022.413960
CAS Web of Science® Google Scholar
35 Alam M. S., Saiduzzaman M., Biswas A., Ahmed T., Sultana A., and Hossain K. M., Tuning Band Gap and Enhancing Optical Functions of AGeF3 (A = K, Rb) Under Pressure for Improved Optoelectronic Applications, Scientific Reports. (2022) 12, no. 1, https://doi.org/10.1038/s41598-022-12713-4, 8663.
10.1038/s41598-022-12713-4
CAS PubMed Web of Science® Google Scholar
36 Hossain M., Toki G., Kuddus A., and Reports M. R. S., An Extensive Study on Multiple ETL and HTL Layers to Design and Simulation of High-performance Lead-Free CsSnCl₃-Based Perovskite Solar Cells, Scientific Reports. (2023) 13, 2521.
10.1038/s41598-023-28506-2
CAS PubMed Web of Science® Google Scholar
37 Hossain M., Bhattarai S., and Arnab A., et al.Harnessing the Potential of CsPbBr 3-Based Perovskite Solar Cells Using Efficient Charge Transport Materials and Global Optimization, The Royal Society of Chemistry. (2023) 13, 21044–-21062.
CAS Google Scholar
38 Ilyas B. M. and Elias B. H., A Theoretical Study of Perovskite CsXCl3 (X = Pb, Cd) Within First Principles Calculations, Physica B: Condensed Matter. (2017) 510, 60–73, https://doi.org/10.1016/j.physb.2016.12.019, 2-s2.0-85010689214.
10.1016/j.physb.2016.12.019
CAS Web of Science® Google Scholar
39 Agbaoye R. O., Adebambo P. O., and Adebayo G. A., First Principles Comparative Studies of Thermoelectric and Other Properties in the Cubic and Hexagonal Structure of CsCdCl3 Halide Perovskites, Computational Condensed Matter. (2019) 21, https://doi.org/10.1016/j.cocom.2019.e00388, 2-s2.0-85065126546, e00388.
10.1016/j.cocom.2019.e00388
Web of Science® Google Scholar
40 Damerdji N. O., Amrani B., Khodja K. D., and Aubert P., First-Principle Study on the Origin of Ferromagnetism in Non-Magnetic Halide Perovskite CsCdM3 (M = Cl and Br) Doped With B, Journal of Superconductivity and Novel Magnetism. (2018) 31, no. 9, 2935–2940, https://doi.org/10.1007/s10948-017-4538-y, 2-s2.0-85040704706.
10.1007/s10948-017-4538-y
CAS Web of Science® Google Scholar
41 Hayatullah, Murtaza G., and Khenata R., Structural, Elastic, Electronic and Optical Properties of CsMCl3 (M = Zn, Cd), Physica B: Condensed Matter. (2013) 420, 15–23, https://doi.org/10.1016/j.physb.2013.03.011, 2-s2.0-84877825674.
10.1016/j.physb.2013.03.011
CAS Web of Science® Google Scholar
42 Ghebouli B., Ghebouli M. A., Fatmi M., and Bouhemadou A., First-Principles Study of the Structural, Elastic, Electronic, Optical and Thermodynamic Properties of the Cubic Perovskite CsCdCl3 Under High Pressure, Solid State Communications. (2010) 150, no. 39-40, 1896–1901, https://doi.org/10.1016/j.ssc.2010.07.041, 2-s2.0-77957366046.
10.1016/j.ssc.2010.07.041
CAS Web of Science® Google Scholar
43 Mouhat F. and Coudert F. X., Necessary and Sufficient Elastic Stability Conditions in Various Crystal Systems, Physical Review B. (2014) 90, no. 22, https://doi.org/10.1103/PhysRevB.90.224104, 2-s2.0-84916210748, 224104.
10.1103/PhysRevB.90.224104
CAS Web of Science® Google Scholar
44 Kohn W., Density Functional and Density Matrix Method Scaling Linearly With the Number of Atoms, 1996.
Google Scholar
45 Clark S. J., Segall M. D., and Pickard Ii C. J., et al. First Principles Methods Using CASTEP, 2009, https://www.accelrys.com/references/castep/.
Google Scholar
46 Segall M. and Lindan P., First-Principles Simulation: Ideas, Illustrations and the CASTEP Code, Journal of Physics: Condensed Matter. (2002) 14, no. 11, 2717–2744, https://doi.org/10.1088/0953-8984/14/11/301, 2-s2.0-0037171005.
10.1088/0953-8984/14/11/301
CAS Web of Science® Google Scholar
47 Perdew J. P., Burke K., and Ernzerhof M., Generalized Gradient Approximation Made Simple, Physical Review Letters. (1996) 77, no. 18, 3865–3868, https://doi.org/10.1103/PhysRevLett.77.3865, 2-s2.0-4243943295.
10.1103/PhysRevLett.77.3865
CAS PubMed Web of Science® Google Scholar
48 Moghal B. K. and Islam M. R., Tuning the Electronic, Phonon, and Optical Properties by Strain-Induced on the Monolayer Transition Metal Dichalcogenides ASe2 (A = Mo and W), Materials Today Communications. (2022) 31, https://doi.org/10.1016/j.mtcomm.2022.103240, 103240.
10.1016/j.mtcomm.2022.103240
CAS Web of Science® Google Scholar
49 Fischer T. H. and Almlof J., General Methods for Geometry and Wave Function Optimization, The Journal of Physical Chemistry. (1992) 96, no. 24, 9768–9774, https://doi.org/10.1021/j100203a036, 2-s2.0-33749419794.
10.1021/j100203a036
CAS Web of Science® Google Scholar
50 Monkhorst H. J. and Pack J. D., Special Points for Brillonin-Zone Integrations^∗, Physical Review B. (1976) 13, 5188.
10.1103/PhysRevB.13.5188
Google Scholar
51 Kang J., Lee E.-C., and Chang K. J., First-Principles Study of the Structural Phase Transformation of Hafnia under Pressure, Physical Review B. (2003) 68, no. 5, https://doi.org/10.1103/PhysRevB.68.054106, 2-s2.0-13244267586, 054106.
10.1103/PhysRevB.68.054106
CAS Web of Science® Google Scholar
52 Momma K. and Izumi F., VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis, Journal of Applied Crystallography, 2008, 41, 653–658.
Google Scholar
53 Tran F., Blaha P., Schwarz K., and Novák P., Hybrid Exchange-Correlation Energy Functionals for Strongly Correlated Electrons: Applications to Transition-Metal Monoxides, Physical Review B. (2006) 74, no. 15, https://doi.org/10.1103/PhysRevB.74.155108, 2-s2.0-33749832261.
10.1103/PhysRevB.74.155108
Web of Science® Google Scholar
54 Pan Y. and Chen S., Influence of Alloying Elements on the Mechanical and Thermodynamic Properties of ZrB2 Boride, Vacuum. (2022) 198, https://doi.org/10.1016/j.vacuum.2022.110898, 110898.
10.1016/j.vacuum.2022.110898
CAS Web of Science® Google Scholar
55 Hasan M. Z., Rasheduzzaman M., and Monower Hossain K., Pressure-Dependent Physical Properties of Cubic SrBO3(B = Cr, Fe) Perovskites Investigated by Density Functional Theory, Chinese Physics B. (2020) 29, no. 12, https://doi.org/10.1088/1674-1056/abab7f, 123101.
10.1088/1674-1056/abab7f
CAS Web of Science® Google Scholar
56 Teli N. A. and Mohamed Sheik Sirajuddeen M., A DFT Study of the Structural, Elastic, Electronic and Magnetic Properties of New Quaternary Compounds TiHfOsX(Al, Ga, In), Physics Letters A. (2020) 384, no. 32, https://doi.org/10.1016/j.physleta.2020.126793, 126793.
10.1016/j.physleta.2020.126793
CAS Web of Science® Google Scholar
57 Hill R., The Elastic Properties of Crystalline Aggregate, Proceedings of the Physical Society. Section A. (1952) 65, 349–354.
10.1088/0370-1298/65/5/307
CAS Web of Science® Google Scholar
58 Naher M. I. and Naqib S. H., Structural, Elastic, Electronic, Bonding, and Optical Properties of Topological CaSn3 Semimetal, Journal of Alloys and Compounds. (2020) 829, https://doi.org/10.1016/j.jallcom.2020.154509, 154509.
10.1016/j.jallcom.2020.154509
CAS Web of Science® Google Scholar
59 Hill R., The Elastic Behaviour of a Crystalline Aggregate, Proceedings of the Physical Society. Section A. (1952) 65, no. 5, 349–354, https://doi.org/10.1088/0370-1298/65/5/307, 2-s2.0-33144479510.
10.1088/0370-1298/65/5/307
CAS Web of Science® Google Scholar
60 Mehl M. J., Pressure Dependence of the Elastic Moduli in Aluminum-Rich Al-Li Compounds, Physical Review B. (1993) 47, no. 5, 2493–2500, https://doi.org/10.1103/PhysRevB.47.2493, 2-s2.0-0000347941.
10.1103/PhysRevB.47.2493
CAS PubMed Web of Science® Google Scholar
61 Pettifor D. G., Theoretical Predictions of Structure and Related Properties of Intermetallics, Materials Science and Technology. (1992) 8, 345–349.
10.1179/mst.1992.8.4.345
CAS Web of Science® Google Scholar
62 Ravindran P., Fast L., Korzhavyi P. A., Johansson B., Wills J., and Eriksson O., Density Functional Theory for Calculation of Elastic Properties of Orthorhombic Crystals: Application to TiSi2, Journal of Applied Physics. (1998) 84, no. 9, 4891–4904, https://doi.org/10.1063/1.368733, 2-s2.0-0000586374.
10.1063/1.368733
CAS Web of Science® Google Scholar
63 Biswas A., Alam M. S., Sultana A., Ahmed T., Saiduzzaman M., and Hossain K. M., Effects of Bi and Mn Codoping on the Physical Properties of Barium Titanate: Investigation via DFT Method, Applied Physics A. (2021) 127, no. 12, https://doi.org/10.1007/s00339-021-05094-4, 939.
10.1007/s00339-021-05094-4
CAS Google Scholar
64 Duan Y. H., Sun Y., Peng M. J., and Zhou S. G., Anisotropic Elastic Properties of the Ca-Pb Compounds, Journal of Alloys and Compounds. (2014) 595, 14–21, https://doi.org/10.1016/j.jallcom.2014.01.108, 2-s2.0-84893834590.
10.1016/j.jallcom.2014.01.108
CAS Web of Science® Google Scholar
65 Sun Z., Li S., Ahuja R., and Schneider J. M., Calculated elastic properties of M2AlC (M = Ti, V, Cr, Nb and Ta), Solid State Communications. (2004) 129, no. 9, 589–592, https://doi.org/10.1016/j.ssc.2003.12.008, 2-s2.0-0347601678.
10.1016/j.ssc.2003.12.008
CAS Web of Science® Google Scholar
66 Ahmed T., Roknuzzaman M., and Sultana A., et al.Physical Properties of Rare Earth Perovskites CeMO3 (M = Co, Cu) in the Context of Density Functional Theory, Materials Today Communications. (2021) 29, https://doi.org/10.1016/j.mtcomm.2021.102973, 102973.
10.1016/j.mtcomm.2021.102973
CAS Web of Science® Google Scholar
67 Podder A., Solayman M., Das O., and Dujana W. A., A DFT Investigation on Optical Properties of Mg Doped SrMoO3 for Optoelectronic Applications, 2021 International Conference on Electronics, Communications and Information Technology (ICECIT), 2021, IEEE, 1–4.
Google Scholar
68 Rasheduzzaman M., Hossain K. M., Mitro S. K., Hadi M. A., Modak J. K., and Hasan M. Z., Structural, Mechanical, Thermal, and Optical Properties of Inverse-Heusler Alloys Cr2CoZ (Z = Al, In): A First-Principles Investigation, Physics Letters A. (2021) 385, https://doi.org/10.1016/j.physleta.2020.126967, 126967.
10.1016/j.physleta.2020.126967
CAS Web of Science® Google Scholar

All articles

Structural, Mechanical, Electronic, and Optical Properties of CsCdX₃ (X = Cl, Br, and I): A Comparative Study Using First Principle Calculation

Abstract

1. Introduction

2. Computational Method