Volume 2025, Issue 1 6686777

Research Article

Open Access

First-Principles Calculations to Investigate Structural, Electronic, Mechanical, Optical, and Magnetic Properties of RhNbSb Half-Heusler Compound

Adem Beriso Bejo,

Corresponding Author

Adem Beriso Bejo

[email protected]

orcid.org/0009-0005-5847-3606

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Megersa Wodajo Shura,

Megersa Wodajo Shura

orcid.org/0000-0001-7800-0789

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kumneger Tadele,

Kumneger Tadele

orcid.org/0000-0002-2777-0166

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Fekadu Tolessa Maremi,

Fekadu Tolessa Maremi

orcid.org/0000-0002-4147-5470

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Mesfin Asfaw Afrassa,

Mesfin Asfaw Afrassa

orcid.org/0000-0002-5968-2515

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kunsa Haho Habura,

Kunsa Haho Habura

orcid.org/0000-0001-7141-8998

Department of Physics , Arba Minch University , Arba Minch , Ethiopia , amu.edu.et

Search for more papers by this author

Adem Beriso Bejo,

Corresponding Author

Adem Beriso Bejo

[email protected]

orcid.org/0009-0005-5847-3606

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Megersa Wodajo Shura,

Megersa Wodajo Shura

orcid.org/0000-0001-7800-0789

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kumneger Tadele,

Kumneger Tadele

orcid.org/0000-0002-2777-0166

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Fekadu Tolessa Maremi,

Fekadu Tolessa Maremi

orcid.org/0000-0002-4147-5470

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Mesfin Asfaw Afrassa,

Mesfin Asfaw Afrassa

orcid.org/0000-0002-5968-2515

Department of Applied Physics , Adama Science and Technology University , Adama , Ethiopia , astu.edu.et

Search for more papers by this author

Kunsa Haho Habura,

Kunsa Haho Habura

orcid.org/0000-0001-7141-8998

Department of Physics , Arba Minch University , Arba Minch , Ethiopia , amu.edu.et

Search for more papers by this author

First published: 02 May 2025

https://doi.org/10.1155/acmp/6686777

Academic Editor: Sefer Bora Lisesivdin

Share a link

Email
Wechat
Bluesky

Abstract

In this work, the structural, mechanical, electronic, optical and magnetic properties of the RhNbSb half-Heusler compound were examined and analyzed using density functional theory (DFT). According to the results, type I atomic arrangement is structurally the most stable for the compound. In all three of its atomic arrangement types, the compound is mechanically stable and ductile according to the analysis of its mechanical properties. Generalized gradient approximation (GGA) + U approach was applied in addition to GGA approach, where U is Hubbard parameter, to increase the accuracy of results in electronic band structure, density of states (DOS), and magnetic moments. Therefore, electronic band structure and DOS calculations demonstrate that the compound exhibits metallic properties in both its type I and type II atomic arrangements with GGA predictions. However, under GGA + U calculations, the compound becomes half metal when in type I but it still reflects metallic nature when in type II. The compound’s half-metallic nature in type I under the GGA+U method suggests that it may be a good fit for spintronics applications in this type I of its atomic arrangement. The calculated total magnetic moment of the compound under GGA + U approach exactly fits with Slater–Pauling rule of half-metallic nature in its type I atomic arrangement, a result that supports half-metallic nature of the compound in type I atomic arrangement for electronic properties under GGA + U prediction. Furthermore, the compound might be taken into consideration for optoelectronic applications according to the results of computed optical characteristics.

1. Introduction

Since their discovery in 1903 [1], Heusler compounds’ fascinating features have attracted a lot of attention for applications in spintronic [2], optoelectronic [3, 4], and thermoelectric systems [5–7]. Half-Heusler compounds are members of the Heusler compound family with the chemical formula XYZ, where X is transition metal, Y is transition or rare earth element, and Z is a nonmagnetic element from main groups III, IV, or V [8, 9].

Half-Heusler compounds have tunable electronic band structures that can be semiconducting, insulators, metallic, or half-metallic [10], because of this, they have high potential to be considered for applications, such as optoelectronics and spintronics, where control over electron spin and charge is crucial, because their band gap can be engineered [11, 12].

Numerous theoretical predictions suggest that a variety of materials, such as ferromagnetic metallic oxides [13], diluted magnetic semiconductors [14], and Heusler compounds [15], can exhibit half-metallic properties. It has been observed that these compounds contain half-metallic elements [16].

Another characteristic of half-metallic materials is that they typically have an integer total magnetic moment. Naturally, half-metallic materials have metallic nature for the majority spin channel (spin-up) at the Fermi level (E_F), but semiconducting/insulating nature for the minority spin channel (spin down) [17]. Theoretically, materials that are half-metallic can have 100% spin polarization at the Fermi level, which makes them excellent candidates for use in spintronic devices. Magnetic random access memory (MRAM), for instance [18], in 1983, de Groot and his colleagues discovered the half-metallic property in the NiMnSb half-Heusler compound while examining the material’s electronic band structure [19]. Tailoring magnetic properties of half-Heusler compounds by either chemical substitution or by other external factors is also another approach to make them suitable for spintronics applications [20]. Furthermore, since half-Heusler compounds have high thermal stability, they can have applications in spintronic devices in extreme environments [21].

Half-Heusler compounds’ band gap tunability qualities also make them appropriate for a number of optoelectronic uses [22, 23], such as photovoltaics [24, 25], light-emitting diodes (LEDs) [26], and photodetectors [27, 28]. Optically, half-Heusler compounds have high absorption coefficient and low electron energy loss in low electromagnetic energy spectrums (visible and infrared), qualifying them appropriate for some optoelectronic applications, such as infrared detectors and solar cells [29, 30].

Numerous studies on the properties of half-Heusler compounds, such as those based on Rh families, were theoretically carried out under zero pressure [31, 32]. For instance, the structural, elastic, electronic, and vibrational properties of the LiTiAl half-Heusler compound were investigated in [33] using the first principles approach. For spintronics applications, CoMnAl, CrTiAs, and RhCrSn half-Heusler compounds were studied using the DFT approach in [34]. N. Mehmood et al. carried out an ab initio studies on the structural, elastic, mechanical, electronic, magnetic, and optical properties of RhCrZ (Z = Si, Ge) half-Heusler compounds, both of these compounds exhibited half-metallic behavior with 100% spin polarization at the Fermi level [35]. It was recently observed by I. Muhammad et al. [36] that the RhMnSb half-Heusler compound shifted from metallic to half-metallic behavior when pressure exceeded 21 Gpa. The study examined the structural, mechanical, thermal, magnetic, and electronic properties of the compound under pressure using the DFT technique.

Even with the significant advancements in our knowledge of half-Heusler materials, there are still untested candidates with possibly better qualities. To the best of our knowledge, no theoretical or experimental research has been done on RhNbSb compound. The unique elemental combination in RhNbSb, which indicates a promising interaction of structural, electronic, mechanical, optical, and magnetic properties, makes this absence of research unexpected. The capacity of Rh and Nb to contribute to half-metallicity, which is a highly desirable feature for spintronic applications is well-known, but Sb frequently plays a crucial role in stabilizing the structure.

The goal of this work is, therefore, to close this gap by thoroughly examining RhNbSb. Through first-principles computations based on DFT, we examined this compound’s structural, mechanical, electronic, magnetic, and optical properties. According to our results, RhNbSb is a half-metallic material that has a lot of potential for use in spintronics. This work expands our knowledge of this significant class of materials and establishes the foundation for further experimental and theoretical research by presenting RhNbSb as a new member of the half-Heusler family.

In order to put its performance in context and emphasize its special qualities, we also contrast its attributes with those of other thoroughly researched half-Heusler compounds. For example, our results were compared to those of closely related half-Heusler compound, like RhNbAs [37], in order to offer an alternate validation. Consistent patterns in structural, electronic, mechanical, optical, and magnetic properties are shown by this comparison, which supports the validity of our findings. Despite the fact that the lack of previous studies highlights the uniqueness and importance of our work, this work is the first theoretical investigation of RhNbSb and lays the groundwork for future experimental and theoretical research on this material.

2. Computational Details

Analyses of the structural, mechanical, electronic, optical, and magnetic properties of the RhNbSb half-Heusler compound were performed using DFT as implemented in the quantum espresso simulation software. This study treated electron exchange and correlation using projector augmented-wave (PAW) pseudopotential with GGA Perdew, Burke, and Ernzerhof (PBE) functional type. For optical properties calculations, norm conserving pseudopotential was used which is appropriate for this property prediction. In addition to the usual GGA approach, calculations were carried out utilizing the GGA+U approach to get more precise electronic band structure, density of states (DOS), and magnetic moments. This method was considered to interpret for the strong on-site Coulomb interactions in the localized d-orbitals of Rh and Nb atoms which conventional DFT approximations, such as GGA, might not be able to adequately characterize. The Hubbard parameter, U, was taken into account in the computations for greater precision because the electronic structure configurations of Niobium (Nb: [Ar]4d⁴5s) and Rhodium (Rh: [Ar]4d⁸5s) atoms contain d-orbital electrons. The electronic and magnetic property calculations utilized the values of U in types I, II, and III for Rh, which were 5.0601 eV, 4.8887 eV, and 4.7322 eV, and Nb, which were 2.6945 eV, 2.7050 eV, and 2.5850 eV, respectively, obtained through the calculations. These values were found to accurately reflect the compound’s electronic and magnetic properties, including its magnetic moments and half-metallic behavior. We further confirmed the appropriateness of these values by contrasting our findings with previous research on analogous materials. Kinetic energy cutoff, k-points and lattice parameter convergence tests were performed and optimizations were then carried out prior to the computation of structural, mechanical, electronic, optical and magnetic properties. A mesh k-point of 12 × 12 × 12 was taken in the first irreducible Brillouin zone for all three types of atomic arrangements of the compound RhNbSb; however, a denser k-point of 36 × 36 × 36 was utilized for the computation of partial density of states (PDOS). Different values of the lattice parameters were used, which were found after the convergence test, but a plane wave basis cutoff energy of 80 Ry was used for all sorts of atomic arrangements under our investigation. Energy-strain method was employed in the computation of mechanical properties. Since RhNbSb half-Heusler compound has cubic crystal structure only three independent elastic constants (C₁₁, C₁₂, and C₄₄) are sufficient for the study of mechanical property of the compound because all other mechanical parameters can be readily obtained from these elastic constants. Consequently, the lattice was stretched by 0%, ±1%, ±2%, ±3%, and ±4% for each cube lattice structure, yielding their total minimum energies, E₀ (V). As seen in the relationship below, these minimum energies and stresses were fitted to the appropriate parabolic equations of ∆E/V₀ [37],

(1)

Software tools, such as XCrySDen and VESTA, were used for crystal modeling, design, and visualization.

3. Results and Discussion

3.1. Structural Properties

This work considers the RhNbSb half-Heusler compound with space group F43m (No. 216) and face-centered cubic structure. According to certain experimental research, the atomic arrangement of half-Heusler structures affects their properties. [38]. Studying the RhNbSb half-Heusler compound in its three most prevalent atomic configurations is therefore crucial [39]. Therefore, we examined this compound’s structural properties by accounting for these three most prevalent varieties, which are type I, type II, and type III. Figure 1 depicts the atomic configurations of these three kinds of the arrangements.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Three common types of atomic arrangement for RhNbSb half-Heusler compound generated by VESTA. Type I (a), type II (b) and type III (c).

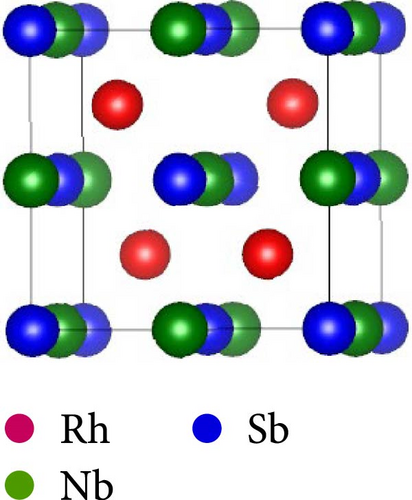
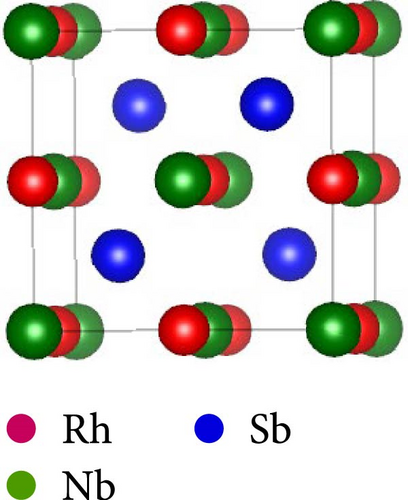
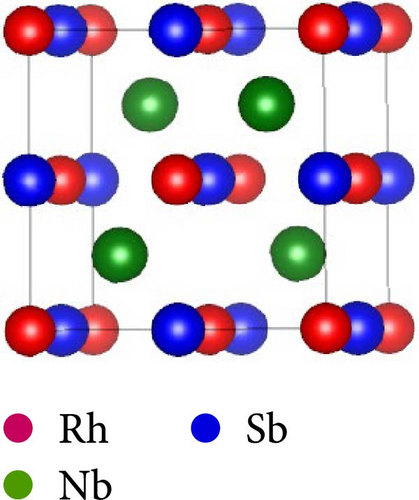
The positions of atoms in these types of atomic arrangement are illustrated in Table 1.

Table 1. Sites of atoms Rh, Nb, and Sb in three types of atomic arrangement for RhNbSb half-Heusler compound.

Types	Rh	Nb	Sb
Type I	(0.25, 0.25, 0.25)	(0.50, 0.50, 0.50)	(0.00, 0.00, 0.00)
Type II	(0.50,0.50, 0.50)	(0.00,0.00, 0.00)	(0.25,0.25, 0.25)
Type III	(0.00,0.00, 0.00)	(0.25,0.25, 0.25)	(0.50,0.50, 0.50)

For the three different types of atomic arrangements of the RhNbSb half-Heusler compound, the Birch–Murnaghan equation of state, which is given as [40],

(2)

was used to calculate the equilibrium lattice constant (a₀), equilibrium volume (V₀), equilibrium energy (E₀), bulk modulus (B), and its pressure derivative (Bʹ). We reported the values of these parameters in Table 2.

Table 2. The optimized lattice constant, the bulk modulus, and its first pressure derivative, minimum volumes, and energies of the three types of RhNbSb half-Heusler compound.

Types	(a₀) (a.u)	V₀ (a.u)³	E₀ (Ry)	B (Gpa)	B′
Type I	11.7524	405.81	−1152.19053	153.0	4.36
Type II	11.8995	421.24	−1152.07581	133.0	5.42
Type III	11.9803	429.87	−1152.10300	126.3	5.45

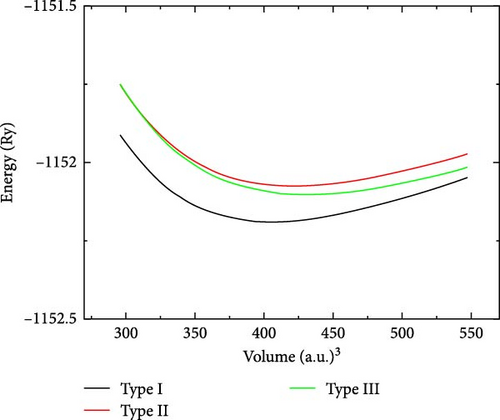
Figure 2 displays the volume against energy of the RhNbSb compound for each of the three possible atomic arrangements. Given the lowest value of minimum energy in type I atomic arrangement when compared to other types of atomic arrangement, it can be concluded from Table 2 and Figure 2 that the compound is most stable in this arrangement.

To further check the stability of the compound, we calculated its formation energy. Formation energy is used to evaluate thermodynamic stability of a given material and it gives insights into relative stability of the materials crystal structure in relation to its constituent elements. It is the difference between the total energy of the compound and the sum of the energies of its constituent elements in their stable arrangements. Its negative value indicates that the compound is thermodynamically stable compared to its constituent elements and therefore it is unlikely to break down into its component elements because energy would be needed to accomplish it. It is given by the following relation:

(3)

where E_formation, E_tot, n_i and E_i stand for the formation energy, total energy of the compound, the number of atoms of element i in the compound and energy of element i in its most stable form respectively, with i in the summation runs over all constituent elements of the compound. For this particular compound (RhNbSb), this relation becomes:

(4)

with E_RhNbSb, E_Rh, E_Nb and E_Sb for the total energy of the compound RhNbSb and energy of the elements Rh, Nb, and Sb respectively. Table 3 illustrates total energy of the compound, energy for each atom in the compound in their most stable form and formation energy of the compound in all of its three atomic configurations. From this table, we observe that the formation for all three types of atomic arrangements is negative and therefore, the compound is thermodynamically stable (cannot be decompose into its individual elements) and can be experimentally synthesized.

Table 3. Formation energies of the RhNbSb half-Heusler compound in all its three types.

Compound	Types	Total energy of the compound (Ry)	Individual elements	Energy per atom (Ry)	Formation energy (Ry)
RhNbSb	Type I	−1152.18068622	Rh	−470.17407732	−0.11803237
	Type II	−1152.06567328	Nb	−334.24603482	−0.00301943
	Type III	−1152.09614099	Sb	−347.64254171	−0.03348714

3.2. Phonon Calculation

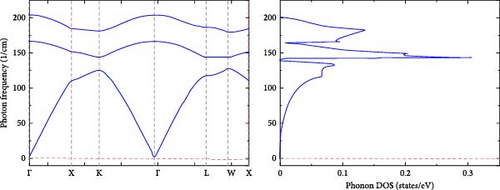
Figure 3 shows the calculated phonon band structure of RhNbSb, which offers important information about the dynamical stability and lattice vibrational properties of the compound. A system with three atoms per primitive unit cell is shown by the phonon dispersion curves (left figure), which show three acoustic and three optical branches. Interestingly, the acoustic branches start at zero frequency at the Γ-point, which is a basic prerequisite for any crystalline material’s dynamical stability. The sharp dip in the lowest acoustic branch near the Γ-point, where the frequency naturally falls to zero, is a prominent property of the phonon dispersion. Given that translational symmetry requires acoustic phonons to have zero frequency at Γ, this behavior is expected. Crucially, the RhNbSb compound’s dynamic stability is confirmed by the lack of imaginary (negative) frequencies. Furthermore, there is a noticeable phonon band gap between the optical and acoustic branches, measuring around 100 cm⁻¹. Such a gap is frequently caused by a significant variation in bond stiffness or a noticeable mass contrast between constituent atoms, both of which affect the behavior of thermal transport. The material’s vibrational properties are further clarified by the phonon DOS), which is displayed in the right figure. At low frequencies (<100 cm⁻¹), a considerable portion of the total phonon states are concentrated, suggesting that the acoustic modes primarily contribute to lattice dynamics. The optical branches can be seen in two different frequency ranges, roughly 150 cm⁻¹ and 200 cm⁻¹. A degree of phonon localization is suggested by their comparatively flat dispersion, which is probably caused by the lighter Nb atom participation in high-frequency vibrations.

3.3. Mechanical Properties

Any material’s mechanical properties must be investigated in order to determine how much the material will react to external stress [41]. Elastic constants, C_ij, and other associated mechanical parameters provide more details regarding the mechanical properties of a particular material [42]. Even if many elastic constants are required for other, more complex geometry, only three independent elastic constants, namely C₁₁, C₁₂, and C₄₄ are sufficient for cubic materials like half-Heusler compounds [43]. These three elastic constants can be used to easily derive other mechanical parameters [44]. Table 4 lists the computed values of these three elastic constants as well as other mechanical parameters for each of the three atomic arrangement types of the compound RhNbSb. The Born–Huang mechanical stability criteria is satisfied by the three elastic constants for the three types of atomic arrangements of the RhNbSb compound, which are C₁₁ + 2C₁₂ > 0, C₁₁ − C₁₂ > 0, and C₄₄ > 0 [45]. Furthermore, for all sorts of atomic arrangements, these elastic constants follow the cubic stability condition (C₁₂ < B < C₁₁) [46]. As a result, the compound exhibits mechanical stability across all three atomic arrangement types and therefore can be used in building thermoelectric devices, where materials must endure mechanical and thermal stress. In other words, for thermoelectric devices in the real world, mechanical stability guarantees toughness and reliability under mechanical and thermal stress. Mechanical stability of the compound also ensures its suitability under high pressure applications, such as in aircraft or energy technologies.

Table 4. Calculated values of elastic constants (C_ij (Gpa)), bulk modulus (B (Gpa)), Voigt mudulus (G_V (Gpa)), Reuss modulus (G_R (Gpa)), shear modulus (G (Gpa)), Pugh’s ratio (B/G), Young’s modulus (Y (Gpa)), Poisson ratio ν, hardness (H), anisotropy (A) and Cauchy’s pressure (CP) for the three types of RhNbSb half-Heusler compound.

Mechanical parameters	Type I	Type II	Type III
C₁₁	205.7	191.32	177.57
C₁₂	128.26	105.21	101.01
C₄₄	83	56.66	67.9
B	154.07	133.91	126.53
G_V	65.29	51.22	56.05
G_R	56.95	50.3	51.85
G	61.12	50.76	53.95
B/G	2.52	2.64	2.35
Y	161.95	135.2	141.71
ν	0.32	0.33	0.31
H	7.52	6.4	7.61
A	2.14	1.32	1.77
CP	45.26	48.55	33.11

Pugh’s ratio, B/G, with an equilibrium value of 1.75, is used to distinguish between ductile and brittle materials. Pugh’s ratio for the compound RhNbSb in our current study is bigger than this equilibrium value in all three of its atomic arrangement types; as a result, the compound is ductile in nature in all three of its atomic arrangement types.

The following relations yield the bulk modulus (B) and shear modulus (G) from the Voigt–Reuss and Hill [47, 48] approximation,

(5)

(6)

with,

(7)

(8)

where G_V and G_R stand for the shear modulus of Reuss and Voigt, respectively, because RhNbSb has the maximum value of B when it is in the type I atomic arrangement, it is the hardest and has a strong resistance to fracture in this configuration. Similar to this, because it has the largest value of G compared to the other two types, it has a high resistance to plastic deformation when it is in the type I atomic arrangement. There is consistency between two forms of computations as seen by the nearly identical bulk modulus obtained from elastic constants, C₁₁ and C₁₂, (Table 4) and that obtained by Birch–Murnaghan (Table 2).

The explicit values of a material’s young modulus (Y), Poission ratio (v), and hardness (H) [49] are as follows,

(9)

(10)

(11)

Since the Young modulus quantifies the stiffness or rigidity of a material, RhNbSb is at its stiffest when its atomic arrangement is in type I since in this type, Y has the highest value in relation to the other types. The Poission’s ratio, which typically runs from 0.0 to 0.5, is used to identify the type of bonding present in a material. The material is covalently bound if v = 0.1, has an ionic bond if ν = 0.25, and a metallic bond if ν = 0.33 [50]. As a result, in all three forms of its atomic arrangement, RhNbSb exhibits metallic nature. As we will see later under electronic section, this nature is also demonstrated. It is important to note that the mechanical property calculations were carried out using the GGA approximation. Consequently, the ν result needs to be compared to Figures 4 and 5.

Anisotropy (A) and Cauchy’s pressure (CP), which are used to determine the quantity of defects and the kind of bonding (brittle or ductile) in a material, respectively, are two more mechanical parameters that are helpful for mechanical property investigation. These are expressed mathematically below as [51],

(12)

(13)

Defects become more likely as A’s value rises above 1, since 1 is its equilibrium value. Therefore, in the type I atomic arrangement, RhNbSb has a significant likelihood of defects. All three of the atomic arrangement types under investigation have positive values for CP, suggesting that RhNbSb is ductile by nature in each of the three atomic arrangement types.

Theoretically, one can determine the fusion temperature, which is crucial for the materials employed in the heating system, as [52]

(14)

Table 5 displays the computed fusion temperature values for the chemical in each of its three atomic arrangement types, with type I having the highest value. This compound is stable at high temperatures because it generally has a high melting temperature in all three of its atomic arrangement types.

Table 5. The calculated density (ρ (kg/m³)), the transverse (v_t), longitudinal (v_l) and average (v_m) elastic wave velocities (in m/s), Debye temperatures θ_D (in K), and melting temperatures T_m (in K) for three types of RhNbSb compound.

Mechanical parameters	Type I	Type II	Type III
ρ	8782	8460	8291
v_m	2956.50	2747.29	2854.33
v_l	5179.72	4881.46	4892.86
v_t	2638.42	2449.49	2551.05
θ_D	324.46	297.87	307.09
T_m ± 300 K	1768.89	1683.89	1602.62

The Debye temperature, θ_D, provides information about a material’s thermal stability. It is a basic parameter that gives information on a material’s lattice vibrational properties. It is strongly associated with important mechanical and thermal qualities, like specific heat capacity, thermal conductivity, and structural stability, and represents the lattice’s greatest vibrational frequency. When evaluating a material’s viability for high-temperature applications, the Debye temperature is especially crucial for RhNbSb and similar materials.

It can be calculated mathematically using the following relation [53],

(15)

where ρ, v_m, M, n, N_A, h, and K_B represent mass density, average sound velocity, molecular weight, number of atoms in the compound, Avogadro’s number, Planck’s and Boltzmann’s constants, respectively. Strong interatomic bonds, which translate into improved thermal stability and resistance to lattice vibrations under thermal stress, are generally indicated by a high θ_D. For materials used in thermoelectric applications, where prolonged exposure to temperature gradients is typical, this characteristic is essential. Furthermore, lattice thermal conductivity, which is essential for maximizing the effectiveness of thermoelectric devices, is connected to the Debye temperature. The thermoelectric performance of materials with a well-balanced θ_D can be improved by limiting thermal conductivity and maintaining thermal stability.

RhNbSb is a good candidate for high heat applications due to its strong atomic bonding and tough lattice stability, as indicated by its predicted Debye temperature, particularly in its type I atomic arrangement. These applications include industrial heat-resistant components, thermoelectric devices, and other contexts where materials that can sustain high heat loads without degrading are needed. This study offers important new information on the thermal behavior of RhNbSb and its prospective use in high temperature settings by examining θ_D. The average sound velocity of a material is represented by the formula [54],

(16)

where v_t and v_l stand for the corresponding transverse and longitudinal sound velocities, and are respectively expressed as,

(17)

(18)

The computed values of the compound RhNbSb’s density (ρ kg/m³), transverse, longitudinal, and average velocities (m/s), Debye (θ_D) and melting temperatures (K) for the three atomic arrangements are displayed in Table 5.

The mechanical stability of this compound is consistent with the Debye temperature that is being described here (Table 5). The material’s capacity to tolerate heat stress is demonstrated by the high value of θ_D, which reflects the strong interatomic bonding indicated by the mechanical stability of the compound from elastic constants (Table 4 and Born–Huang criteria). The suitability of RhNbSb for high-temperature applications, such as thermoelectric and heat-resistant materials, is highlighted by these findings.

3.4. Electronic Properties

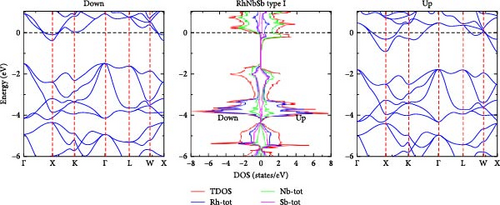
We have computed the electronic band structure, total DOS and PDOS for the RhNbSb half-Heusler compound by using both the GGA and GGA+U methods. These properties enable us to identify whether the compound is semiconductor, half-metallic or metallic. In the irreducible Brillouin zone at the equilibrium lattice parameters, the electronic band structure of the RhNbSb compound with both majority (spin-up) and minority (spin-down) spin channels are depicted in Figures 4 and 6 for type I and in Figures 5 and 7 for type II along the main symmetry directions. The GGA approach was used to compute the spin-polarized electronic band structure of the compound for the type I atomic arrangement (Figure 4). The results indicate that the bottom of the conduction band crosses the Fermi level (E_F) in both the majority and minority spin channels, indicating a metallic nature in both spin channels. That is, the GGA method indicates that the compound has a metallic property. However, under the GGA+U method, the compound’s type I atomic arrangement (Figure 6) exhibits metallic behavior for the majority spins (spin-up) due to band lines crossing E_F, but for the minority spin channel, E_F was not crossed by the electronic band structure, indicating that the compound is semiconductor. As a result, the compound exhibits half-metallic behavior under GGA+U treatment in type I atomic arrangement. Electronic band structures under the GGA and GGA+U approaches for both the majority and minority spin channels in the case of type II atomic arrangement clearly cross the Fermi level, indicating that the compound has metallic nature at its equilibrium lattice constant when it is in type II atomic arrangement.

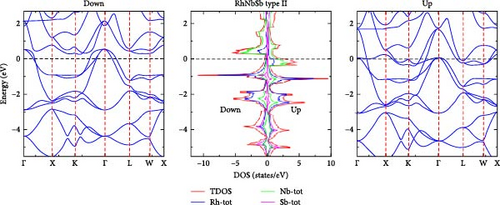
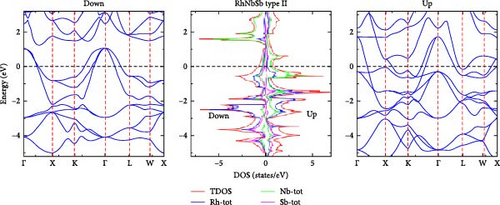
In order to gain a deeper understanding of the electronic properties of the RhNbSb half-Heusler compound, the GGA and GGA+U approaches were used to calculate the compound’s DOS and PDOS, which are shown in Figures 4 and 6 and Figures 5 and 7 for type I and type II atomic arrangements, respectively. For both majority and minority spin channels in both atomic configurations, the trend of these DOS (both PDOS and DOS) closely matches the electronic band structure. For example, under GGA+U approximation in type I atomic arrangement (Figure 6) both DOS (DOS and PDOS) did not cross the Fermi level in the case of minority channel (spin-down) indicating semiconductor property of the material but the Fermi level is well crossed by both DOS and PDOS in the majority spin channel (spin-up) that shows metallic character of the compound resulting in half-metallic behavior of the compound which well agrees with both the electronic band structures in this type atomic arrangement (Figure 6). With type II atomic arrangements, where the compound exhibits metallic character when treated by both GGA and GGA+U, the agreement between electronic band structures and DOS as well as PDOS also remains true.

Furthermore, information about the contribution of electronic properties of component atoms in the compound on their chemical bonding can be provided both by DOS and PDOS. For both type I and type II atomic arrangement below Fermi level large contribution comes from Rh PDOS whereas above Fermi level large contribution to DOS comes from Nb PDOS. Below and far from Fermi level Sb PDOS largely contributes to DOS. The overall contribution to DOS comes from Rh PDOS in both types and under both approaches.

Generally speaking, structural properties of a material have a significant impact on its electronic properties. In the RhNbSb half-Heusler combination under current research, for instance, we have found that varying atomic configurations within a particular material structure (cubic RhNbSb) can impact the electronic property of the material. Under the GGA+U technique, this material readily reflected half-metallic electronic properties in the type I atomic arrangement; nevertheless, under the GGA and GGA+U approaches, its band structure continued to reflect metallic properties in the type II atomic arrangement.

In type I atomic configuration, RhNbSb is recognized as a half-metallic material, displaying a spin-polarized band gap in one spin channel (spin down) and metallic behavior in the other (spin-up). In the semiconducting spin channel, the computed band structure reveals an indirect band gap, with the conduction band minimum at the X point and the valence band maximum at the Γ point. RhNbSb’s half-metallic nature, which is defined by 100% spin polarization at the Fermi level, emphasizes its potential for use in spintronics. Figure 6 shows the detailed electronic band structure and DOS.

3.5. Optical Properties

To find RhNbSb half-Heusler compound applications in optoelectronics, it is essential to analyze its optical properties. Using a GGA technique, we examined the optical properties of this material in a type I atomic arrangement over the photon energy range of 0–40 eV. The findings are shown in Figure 8. The complex dielectric function, ε is the fundamental optical parameter for optical response of materials and is defined as [55],

(19)

where ε₁ is the real part which relates to electromagnetic propagation properties and ε₂ is the imaginary part which is responsible for optical absorption in a given material. The real and imaginary components of the dielectric functions for the RhNbSb half-Heusler compound in the photon energy range of 0–40 eV are calculated and displayed in Figure 8a. The visible energy region is where the sharp peaks for the real and imaginary components are found, at 2.14 and 2.34 eV, respectively. In the real section, the static dielectric constant, ε₁ (0), equals 4.24. The electron transition between the valence and conduction bands is depicted by the peaks in the imaginary section, where the highest transition happens at the highest peak.

The refractive index (n (ω)) and extinction coefficient (k (ω)) which are the real and imaginary parts of complex refractive indexes, N = n + ik, can be obtained in terms of real and imaginary parts of dielectric function with the following relations [56],

(20)

(21)

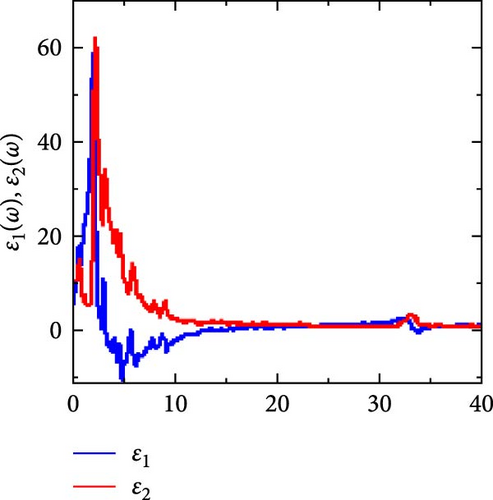
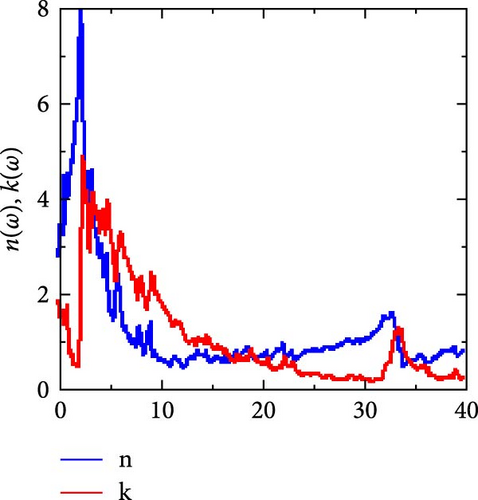
The computed results of n (ω) and k (ω) are shown in Figure 8b. The extinction coefficient quantifies the loss of absorbed electromagnetic energy when a wave propagates in a given medium, whereas the refractive index is a crucial optical parameter for determining the quantity of light that refracted (bent) in a specific material. The obtained static refractive index, n (0) is 2.74, which is in line with the values of popular optoelectronic materials like Ge. This refractive index decreases as photon energy rises after reaching its maximum value at 2.14 eV. In the low energy ranges (0–1.78 eV), the extinction coefficient is very low, indicating very little photon energy absorption, which is advantageous for the material’s transparent qualities in these energy ranges. RhNbSb can be regarded as light absorbent as photon energy increases because it significantly increases after these ranges, peaks at 2.40 eV, and subsequently falls.

The quantity of incident light reflected from a material is measured by reflectivity, or reflection coefficient, R (ω), which is easily computed from a complex dielectric function using the relation [57]

(22)

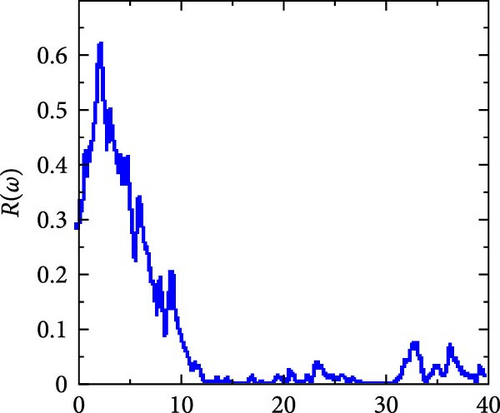
It is displayed in Figure 8c with a static value of 0.28 (the value at which photon energy is zero, or R (0) = 0.28). From this constant value, it rises abruptly to its maximum peak at 2.27 eV, after which it falls as photon energy rises to 23.87 eV.

The most crucial optical parameter in evaluating a material for use in optoelectronic applications is its optical absorption coefficient, or α(ω) [58]. It quantifies the material’s capacity for light absorption. It is one of the optical parameter that determines how well a material interacts with light. This is essential for applications, such as photovoltaic devices, because the energy conversion efficiency of the device is directly affected by effective light absorption. The visible, ultraviolet, and near-infrared energy ranges, for example, correlate to different regions of the solar spectrum. In these regions, materials with high absorption coefficients can optimize collecting of solar energy. Large absorption coefficient materials can make photovoltaic systems thinner, lighter, and more affordable by lowering the thickness needed for efficient light absorption. A substance can increase the efficiency of solar cells by absorbing a larger fraction of the solar spectrum if it shows substantial absorption in the visible or near-infrared regions. The following relation provides it mathematically:

(23)

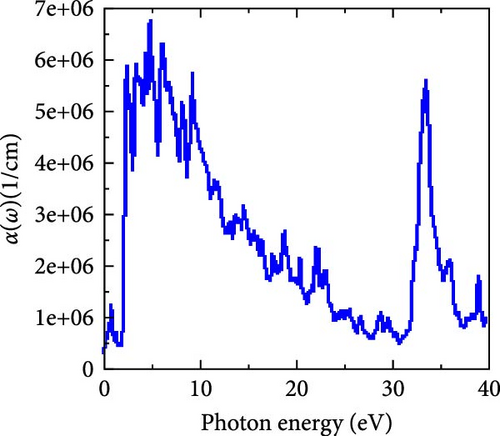
The computed results of α(ω) are displayed in Figure 8d, where the visible and some ultraviolet regions have the highest absorption values, with the visible region having the maximum absorption value. It declines until photon energy reaches 31 eV, at which point it sharply rises to 33.23 eV before eventually declining. Generally speaking, RhNbSb can be regarded as a promising option for optoelectronic applications, for example, for construction of photovoltaic devices that absorbs solar energy efficiently due to its high absorption capacity in the visible energy domain. Absorption coefficient starts increasing from zero photon energy (Figure 8d) indicating that RhNbSb has metallic character as observed by electronic band structure (Figure 4). It should be noted that the calculations for Figure 4 (electronic properties) and optical properties were carried out by GGA approaches.

The energy loss function (L(ω)) is defined as the energy lost by an electron when external radiation strikes a material and some electrons undergo inelastic scattering. It is computed using the following relation [59],

(24)

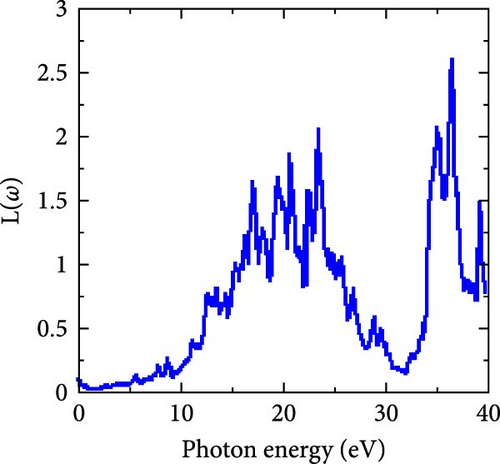
Figure 8e shows the electron energy loss vs photon energy. Its low values at lower photon energies suggest that the RhNbSb compound loses little electron energy at first, increasing to have several peaks around 20 eV. Following numerous oscillations, it reaches its highest peak at 36.39 eV before declining.

The computed results for both real (σ₁) and imaginary (σ₂) parts of optical conductivity is indicated in Figure 8f and they can be obtained from real and imaginary parts of dielectric functions respectively as [60]

(25)

(26)

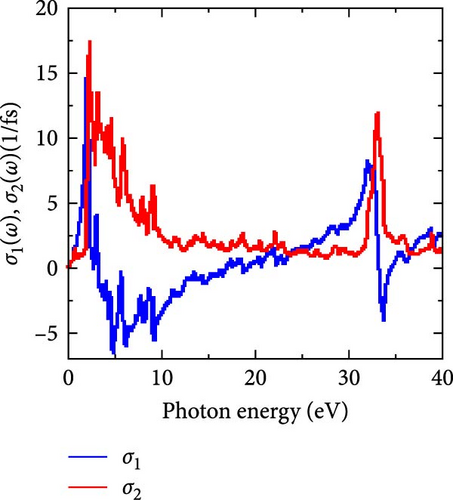
According to the figure, the threshold point for both components of optical conductivity is at 0 eV, indicating that the compound has no band gap (metallic character), which is consistent with the electronic band structure shown in Figure 4 under the sections on electronic properties.

3.6. Magnetic Properties

The magnetic moment of a substance can be used to determine its magnetic properties [61]. Table 6 presents the computed total and partial magnetic moments for the RhNbSb half-Heusler compound in type I of its atomic arrangement. Table 6 shows that Nb atom significantly contributes to the total magnetic moment in both the GGA and GGA+U methods. Under the treatment of GGA+U approach, both Rh and Sb atoms do not favor for magnetism of RhNbSb compound. The estimated total magnetic moment correctly matches with the Slater–Pauling rule of half-metallicity [62], M_t = Z_t − 18, where M_t denoting the total magnetic moment and Z_t the total number of valence electrons in a given half-Heusler compound, in type I under the GGA+U approximation. According to the Slater–Pauling rule, the total valence electron count of the RhNbSb half-Heusler compound is 19, with Rh = 9, Nb = 5, and Sb = 5. This means that M_t = 1, which is precisely equivalent to the total magnetic moment of the RhNbSb compound in type I under the GGA+U method. This suggests that when RhNbSb is treated with GGA+U, it exhibits half-metallic properties, which is consistent with the band structure calculation found in the section on electronic properties (Figure 6).

Table 6. Calculated atomic and total magnetic moments (μ_B of RhNbSb at equilibrium lattice parameters for type I atomic arrangement with both GGA and GGA+U approaches and Slater–Pauling rule.

Type	Method	μ_Rh(μ_B)	μ_Nb(μ_B)	μ_Sb(μ_B)	μ_total (μ_B)
Type I	GGA	0.0444	0.4944	0.0032	0.75
	GGA+U	−0.1684	0.9369	−0.0655	1.00
	Slater–Pauling rule	—	—	—	1.00

By adjusting for the delocalization error in the d-electrons, the U values that were determined by computations guarantee that the magnetic moment of RhNbSb is precisely predicted. Table 6 shows this predicted result by GGA+U comparison with Slater–Pauling rule which exactly matches with this rule. The impact of these values is also reflected in the electronic structure computations, which give a realistic account of the compound’s electronic properties by calculating the band gap and DOS. Using these U values, we were able to get results that were in line with half-Heusler compound trends.

The half-metallic features of type I atomic arrangements for the RhNbSb compound can considerably assist spintronic devices because of their unique electronic and magnetic properties which lead to high percentage of spin polarization at Fermi level. For one spin channel (e.g., spin-up), half-metallic materials, like the RhNbSb half-Heusler compound, behave metallically, while for the other spin channel (e.g., spin-down) they show semiconducting or insulating properties. This leads to 100% spin polarization at the Fermi level, which is a crucial prerequisite for effective spintronic devices. By reducing spin relaxation and scattering, the high spin polarization makes it possible to manipulate spin currents effectively and strongly without suffering a large loss of spin information.

Type I atomic arrangements of RhNbSb compound are perfect for devices, such as spin valves, magnetic tunnel junctions (MTJs), and spin-transfer torque magnetic random-access memory (STT-MRAM) because of this feature, which guarantees maximal spin injection efficiency into nonmagnetic materials. Compared to traditional charge-based logic, devices based on type I RhNbSb half-metal can achieve reduced energy consumption and higher switching speeds in spin-based logic circuits.

Dilute magnetic semiconductors and transition metal oxides are competitors for half-Heusler half-metallic compounds in the construction of spintronic devices; however, these materials frequently have low Curie temperatures or restricted scalability. Half-Heusler half-metallic compounds (e.g., RhNbSb) have high Curie temperature which allows them to work properly even above room temperature. Comparing to their competitor materials, half-Heusler half-metallic compounds have excellent structural, mechanical, and chemical stabilities enabling them incorporation into current semiconductor.

4. Conclusions

The RhNbSb half-Heusler compound’s structural, mechanical, electronic, optical and magnetic properties were calculated using the quantum espresso simulation software, which is based on DFT. The compound is most stable structurally when its atoms are arranged in type I. The compound is mechanically stable in all three forms of its atomic arrangement and ductile in nature. To get good results on the electronic and magnetic properties, the GGA+U technique was applied in addition to the conventional GGA approach. Under the GGA technique, the compound’s type I and type II atomic arrangements were observed to have metallic character. In type I atomic configuration, the compound in GGA+U computations show a half-metallic behavior; however, in type II atomic arrangement, it retains its metallic nature. Under the GGA+U technique, the compound’s total magnetic moment precisely satisfies the Slater–Pauling rule of half-metallic nature in its type I atomic arrangement. This outcome is consistent with the half-metallic attribute derived from the electronic band structure in the type I atomic arrangement under the GGA+U forecast. When the compound is in type I atomic arrangement, it can therefore be viewed as a possible front-runner in the realm of spintronic applications. The compound has a high absorption coefficient and minimal electron energy loss in the visible and certain ultraviolet light areas, according to the results from calculations of optical characteristics, indicating that it can be employed in optoelectronic applications. It should be noted that standard DFT calculations,such as LDA and GGA, approaches have their own limitations in predicting electronic (underestimating band gap), mechanical, optical, and magnetic properties of any compounds including half-Heusler compounds. To minimize these limitations, we used DFT+U approach for electronic and magnetic properties calculations. To further reduce the constraints of standard DFT, we could refine the projected mechanical and magnetic properties of the RhNbSb half-Heusler compound in our next work by incorporating temperature-dependent effects and spin–orbit coupling respectively.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Adem Beriso Bejo, calculations, data analysis, conceptualization, methodology and manuscript writing; Megersa Wodajo Shura, supervising, manuscript review and editing; Kumneger Tadele, supervising, manuscript review and editing; Fekadu Tolessa Maremi, supervising, manuscript review and editing; Mesfin Asfaw Afrassa, manuscript review and editing; Kunsa Haho Habura, manuscript review and editing.

Funding

The authors received no specific funding for this work.

Acknowledgments

Madda Walabu University (MWU) and Adama Science and Technology University (ASTU) are greatly acknowledged for their support during this work.

Open Research

Data Availability Statement

The data that support the findings of this work are available within the article.

References

1 Bainsla L. and Suresh K. G., Equiatomic Quaternary Heusler Alloys: A Material Perspective for Spintronic Applications, Applied Physics Reviews. (2016) 3, no. 3.
10.1063/1.4959093
Web of Science® Google Scholar
2 Rezazadeh H., Hantehzadeh M., and Boochani A., Surface Effect on Electronic, Magnetic and Optical Properties of PtCoBi Half-Heusler: A Dft Study, Archives of Metallurgy and Materials. (2022) 67, no. 1, 155–166.
CAS Web of Science® Google Scholar
3 Kashyap S., Pandey R., and Madan J., Simulated Bending Test Analysis of 23% Efficient Lead-Free Flexible Perovskite Solar Cell with Different Bending States, Physica Scripta. (2023) 98, no. 11.
10.1088/1402-4896/acff28
Web of Science® Google Scholar
4 Jaishi D. R., Sharma N., Karki B., Belbase B. P., Adhikari R. P., and Ghimire M. P., Electronic Structure and Thermoelectric Properties of Half-Heusler Alloys NiTZ, AIP Advances. (2021) 11, no. 2.
10.1063/5.0031512
Web of Science® Google Scholar
5 Abdelakader A., Ahmed B., and Noureddine M., et al.Theoretical Investigations of Electronic, Thermodynamic and Thermoelectric Properties of Filled Skutterudites thfe4p12 and cefe4p12 Using Dft Calculations, Solid State Communications. (2024) 380.
10.1016/j.ssc.2024.115435
Web of Science® Google Scholar
6 Nenuwe N. O. and Yebovi A. S., Predictive Analysis of a New FeVTe Alloy from First Principles: An Excellent Choice for Thermoelectric Applications, Computational Condensed Matter. (2024) 38.
10.1016/j.cocom.2024.e00882
Web of Science® Google Scholar
7 Manna K., Sun Y., Muechler L., Kübler J., and Felser C., Heusler, Weyl and Berry, Nature Reviews Materials. (2018) 3, no. 8, 244–256.
10.1038/s41578-018-0036-5
CAS Web of Science® Google Scholar
8 Ma J., He J., and Mazumdar D., et al.Computational Investigation of Inverse Heusler Compounds for Spintronics Applications, Physical Review B. (2018) 98, no. 9.
10.1103/PhysRevB.98.094410
Web of Science® Google Scholar
9 Gaid F. O., Boufadi F. Z., and Tayebi N., et al.Theoretical Investigation of Structural, Electronic, Elastic, Magnetic, Thermodynamic, and Thermoelectric Properties of Ru₂MnNb Heusler Alloy: Fp-Lmto Method, Emergent Materials. (2022) 5, no. 4, 1065–1073.
10.1007/s42247-021-00229-y
CAS Web of Science® Google Scholar
10 Chernov S., Lidig C., and Fedchenko O., et al.Band Structure Tuning of Heusler Compounds: Spin-and Momentum-Resolved Electronic Structure Analysis of Compounds with Different Band Filling, Physical Review B. (2021) 103, no. 5.
10.1103/PhysRevB.103.054407
Google Scholar
11 Saim A., Belkharroubi F., and Boufadi F. Z., et al.Investigation of the Structural, Elastic, Electronic, and Optical Properties of Half-Heusler CaMgZ (Z = C, Si, Ge, Sn, Pb) Compounds, Journal of Electronic Materials. (2022) 51, no. 7, 4014–4028.
10.1007/s11664-022-09659-8
CAS Web of Science® Google Scholar
12 Samia L., Belkharroubi F., and Ibrahim A., et al.Investigation of Structural, Elastic, Electronic, and Magnetic Proprieties for X₂LuSb (x = Mn and Ir) Full-Heusler Alloys, Emergent Materials. (2022) 5, no. 2, 537–551.
10.1007/s42247-022-00374-y
CAS Web of Science® Google Scholar
13 He J., Shahab Naghavi S., Hegde V. I., Amsler M., and Wolverton C., Designing and Discovering a New Family of Semiconducting Quaternary Heusler Compounds Based on the 18-Electron Rule, Chemistry of Materials. (2018) 30, no. 15, 4978–4985.
10.1021/acs.chemmater.8b01096
CAS Web of Science® Google Scholar
14 Szotek Z., Temmerman W. M., Svane A., Petit L., Stocks G. M., and Winter H., Half-Metallic Transition Metal Oxides, Journal of Magnetism and Magnetic Materials. (2004) 272, 1816–1817.
10.1016/j.jmmm.2003.12.818
Web of Science® Google Scholar
15 Dahmane F., Tadjer A., Doumi B., and Aourag H., First-Principle Calculations of Structural, Electronic, and Magnetic Properties of Cubic Al_1-xTm_xN (Tm = V, Cr, Mn, Fe), Journal of Superconductivity and Novel Magnetism. (2014) 27, 2647–2654.
10.1007/s10948-014-2616-y
CAS Google Scholar
16 Amari D., Mokhtari M., and Dahmane F., et al.A Comparative Study between Hg₂CuTi and Cu₂MnAl Type Structures for Zr₂CoZ (Z = Al, Ga, In) Heusler Alloys, Chinese Journal of Physics. (2019) 60, 450–461.
10.1016/j.cjph.2019.05.024
CAS Web of Science® Google Scholar
17 Mokhtari H., Boumia L., Mokhtari M., Dahmane F., Mansour D., and Khenata R., Mechanical Stability, Electronic, and Magnetic Properties of XZrAs (X = Cr, Mn, V) Half-Heusler Compounds, Journal of Superconductivity and Novel Magnetism. (2023) 36, no. 4, 1217–1224.
10.1007/s10948-023-06560-1
CAS Web of Science® Google Scholar
18 Khandy S. A. and Chai J.-D., Thermoelectric Properties, Phonon, and Mechanical Stability of New Half-Metallic Quaternary Heusler Alloys: FeRhCrZ (Z = Si and Ge), Journal of Applied Physics. (2020) 127, no. 16.
10.1063/1.5139072
Web of Science® Google Scholar
19 Özdemir E. G. and Merdan Ziya, Theoretical Calculations on Half-Metallic Results Properties of FeZrX (X = P, As, Sb and Bi) Half-Heusler Compounds: Density Functional Theory, Materials Research Express. (2019) 6, no. 8.
10.1088/2053-1591/ab19fb
Web of Science® Google Scholar
20 Casper F., Graf T., Chadov S., Balke B., and Felser C., Half-Heusler Compounds: Novel Materials for Energy and Spintronic Applications, Semiconductor Science and Technology. (2012) 27, no. 6.
10.1088/0268-1242/27/6/063001
Web of Science® Google Scholar
21 Nenuwe N. O. and Omugbe E., Electronic Properties of Half-Heusler Compounds XCrSb (X = Fe, Ru, Os): Potential Applications as Spintronics and High-Performance Thermoelectric Materials, Current Applied Physics. (2023) 49, 70–77.
10.1016/j.cap.2023.02.013
Web of Science® Google Scholar
22 Bensaid D., Doumi B., and Mokaddem A., et al.First-Principles Calculation to Investigate Phase Transition and Associated Changes in Electronic, Excitonic, and Optical Behavior of RbMgH₃ Perovskite Polymorphs, International Journal of Hydrogen Energy. (2024) 79, 901–908.
10.1016/j.ijhydene.2024.07.062
CAS Web of Science® Google Scholar
23 Drici L., Belkharroubi F., and Boufadi F. Zohra, et al.First-Principles Calculations of Structural, Elastic, Electronic, and Optical Properties of CaYP (Y = Cu, Ag) Heusler Alloys, Emergent Materials. (2022) 5, 1039–1054.
10.1007/s42247-021-00211-8
CAS Web of Science® Google Scholar
24 Ferjani H., Smida Y. B., and Al-Douri Y., First-Principles Calculations to Investigate the Effect of Van der Waals Interactions on the Crystal and Electronic Structures of Tin-Based 0d Hybrid Perovskites, Inorganics. (2022) 10, no. 10.
10.3390/inorganics10100155
Web of Science® Google Scholar
25 Al-Hawarin J. I., Abu-Yamin A.-A., and Abu-Saleh A. A. A., et al.Synthesis, Characterization, and Dft Calculations of a New Sulfamethoxazole Schiff Base and Its Metal Complexes, Materials. (2023) 16, no. 14, https://doi.org/10.3390/ma16145160.
10.3390/ma16145160
PubMed Web of Science® Google Scholar
26 Rai R. K., Ray R. B., and Niraula O. P., Stability, Electronic, Optical and Thermoelectric Properties of Site-Substituted LaVO₃, Materials Today Communications. (2023) 35.
10.1016/j.mtcomm.2023.105510
Web of Science® Google Scholar
27 Yamusa S. A., Shaari A., and Alsaif N. A. M., et al.Enhanced Dft Predictions of the Structural and Optoelectronic Properties of MoTe₂ for High Performance Photodetection: Application to Gw-Based Functionals and Hubbard U and V Corrections, Chemical Physics. (2023) 573.
10.1016/j.chemphys.2023.112018
Web of Science® Google Scholar
28 Alnujaim S., Bouhemadou A., and Chegaar M., et al.Density Functional Theory Screening of Some Fundamental Physical Properties of Cs₂InSbCl₆ and Cs₂InBiCl₆ Double Perovskites, The European Physical Journal B. (2022) 95, no. 7.
10.1140/epjb/s10051-022-00381-2
Web of Science® Google Scholar
29 Ahmed M., Bakar A., Quader A., Ahmad R. A., and Ramay S. M., First-Principles Calculations to Investigate Structural, Elastic, Mechanical, Electronic and Optical Characteristics of RbSrX₃ (X = Cl, Br), Chemical Physics. (2024) 581.
10.1016/j.chemphys.2024.112260
Web of Science® Google Scholar
30 Hossain M. M. and Mahmud A. A., Structural, Elastic, Electronic and Optical Properties of Lead Free ZnMO₃ (M = Ge, Sn) Perovskites from First Principles Investigation, Computational Condensed Matter. (2022) 32.
10.1016/j.cocom.2022.e00695
Web of Science® Google Scholar
31 Jaishi D. R., Bati S., Sharma N., Karki B., Belbase B. P., and Ghimire M. P., Rhodium Based Half-Heusler Alloys as Possible Optoelectronic and Thermoelectric Materials, arXiv, preprint arXiv: 2105.02177, 2021.
Google Scholar
32 Zahir S., Mehmood N., Ahmad R., Khan S., Rahman A. U., and Dahshan A., Structural, Elastic, Mechanical, Electronic, Magnetic and Optical Properties of Half-Heusler Compounds CoFeZ (Z = P, As, Sb): A GGA+U Approximation, Materials Science in Semiconductor Processing. (2022) 143, https://doi.org/10.1016/j.mssp.2021.106445.
10.1016/j.mssp.2021.106445
Google Scholar
33 Mogulkoc Y. and Ciftci Y., Investigation on Structural, Elastic, Electronic and Vibrational Properties of LiTiAl Half-Heusler Compound Using First Principles Methods, Cumhuriyet University Faculty of Science and Letters Journal of Science. (2017) 38, no. 2, 312–320.
Google Scholar
34 Ma J., Hegde V. I., and Munira K., et al.Computational Investigation of Half-Heusler Compounds for Spintronics Applications, Physical Review B. (2017) 95, no. 2, https://doi.org/10.1103/PhysRevB.95.024411, 2-s2.0-85010303384.
10.1103/PhysRevB.95.024411
Web of Science® Google Scholar
35 Mehmood N., Ahmad R., and Murtaza G., Ab Initio Investigations of Structural, Elastic, Mechanical, Electronic, Magnetic, and Optical Properties of Half-Heusler Compounds RhCrZ (Z = Si, Ge), Journal of Superconductivity and Novel Magnetism. (2017) 30, no. 9, 2481–2488, https://doi.org/10.1007/s10948-017-4051-3, 2-s2.0-85015039459.
10.1007/s10948-017-4051-3
CAS Web of Science® Google Scholar
36 Muhammad I., Zhang J.-M., Ali A., Rehman M. U., and Muhammad S., Structural, Mechanical, Thermal, Magnetic, and Electronic Properties of the RhMnSb Half-Heusler Alloy under Pressure, Materials Chemistry and Physics. (2020) 251, https://doi.org/10.1016/j.matchemphys.2020.123110.
10.1016/j.matchemphys.2020.123110
Web of Science® Google Scholar
37 Bejo A. B., Shura M. W., Tadele K., Afrassa M. A., and Maremi F. T., Structural, Electronic, Mechanical, Optical and Magnetic Properties of RhNbZ (Z = Li, Si, As) Half Heusler Compounds: A First-Principles Study, Materials Research Express. (2025) 12, no. 1, https://doi.org/10.1088/2053-1591/ada5b1.
10.1088/2053-1591/ada5b1
Web of Science® Google Scholar
38 Perdew J. P., Burke K., and Ernzerhof M., Generalized Gradient Approximation Made Simple, Physical Review Letters. (1996) 77, no. 18, 3865–3868, https://doi.org/10.1103/PhysRevLett.77.3865, 2-s2.0-4243943295.
10.1103/PhysRevLett.77.3865
CAS PubMed Web of Science® Google Scholar
39 Kamlesh P. K., Agrawal R., Rani U., and Verma A. S., Comprehensive Ab-Initio Calculations of AlNiX (X = P, As and Sb) Half-Heusler Compounds: Stabilities and Applications as Green Energy Resources, Materials Chemistry and Physics. (2022) 275, https://doi.org/10.1016/j.matchemphys.2021.125233.
10.1016/j.matchemphys.2021.125233
Web of Science® Google Scholar
40 Mokhtari M., Fethallah Dahmane G. B., Zekri L., Benalia S., and Zekri N., Theoretical Study of the Structural Stability, Electronic and Magnetic Properties of XVSb (X = Fe, Ni, and Co) Half-Heusler Compounds, Condensed Matter Physics. (2018) 21, no. 4, arXiv preprint arXiv: 1812.08559, 2018https://doi.org/10.5488/CMP.21.43705, 2-s2.0-85059244547.
10.5488/CMP.21.43705
Web of Science® Google Scholar
41 Uto O. T., Adebambo P. O., Akinlami J. O., Kenmoe S., and Adebayo G. A., Electronic, Structural, Mechanical, and Thermodynamic Properties of CoYSb (Y = Cr, Mo, W) Half-Heusler Compounds as Potential Spintronic Materials, Solids. (2022) 3, no. 1, 22–33.
10.3390/solids3010002
CAS Web of Science® Google Scholar
42 Benichou B., Nabi Z., Bouabdallah B., and Bouchenafa H., Structural, Elastic, Electronic and Magnetic Properties of Quaternary Heusler Alloy Cu2MnSi_{1- x}Al_x (x = 0-1): First-Principles Study, Mexican Journal of Physics. (2018) 64, no. 2, 135–140.
CAS Google Scholar
43 Kaur N. and Srivastava V., First-principles calculations on mechanical properties of Rh₂MnZn Heusler alloy, Journal of Physics: Conference Series. (2022) 2267, IOP Publishing.
10.1088/1742-6596/2267/1/012038
Google Scholar
44 Özdemir E. G., Dogruer S., Özcan A., and Merdan Z., The Effect of Structural Changes on Half-Metallic, Elastic and Magnetic Properties of the FeWGa Half-Heusler Compound via First-Principles Studies, Journal of Magnetism and Magnetic Materials. (2022) 546.
10.1016/j.jmmm.2021.168872
Web of Science® Google Scholar
45 Gao J., Liu Q.-J., and Tang B., Elastic Stability Criteria of Seven Crystal Systems and Their Application under Pressure: Taking Carbon as an Example, Journal of Applied Physics. (2023) 133, no. 13.
10.1063/5.0139232
Web of Science® Google Scholar
46 Cherchab Y. and Gonzalez-Hernandez R., Structural Stability and Thermoelectric Properties of New Discovered Half-Heusler KLaX (X = C, Si, Ge, and Sn) Compounds, Computational and Theoretical Chemistry. (2021) 1200.
10.1016/j.comptc.2021.113231
Web of Science® Google Scholar
47 Zuo L., Humbert M., and Esling C., Elastic Properties of Polycrystals in the Voigt-Reuss-Hill Approximation, Journal of Applied Crystallography. (1992) 25, no. 6, 751–755, https://doi.org/10.1107/S0021889892004874, 2-s2.0-0027001402.
10.1107/S0021889892004874
Web of Science® Google Scholar
48 Wu S.-C., Naghavi S. S., Fecher G. H., and Felser C., A Critical Study of the Elastic Properties and Stability of Heusler Compounds: Phase Change and Tetragonal x_{2}yz Compounds, arXiv preprint arXiv: 1704.01741, 2017.
Google Scholar
49 Zerrouki T., Rached H., Rached D., Caid M., Cheref O., and Rabah M., First-Principles Calculations to Investigate Structural Stabilities, Mechanical and Optoelectronic Properties of NbCoSn and NbFeSb Half-Heusler Compounds, International Journal of Quantum Chemistry. (2021) 121, no. 8, https://doi.org/10.1002/qua.26582.
10.1002/qua.26582
Web of Science® Google Scholar
50 Zitouni A., Benstaali W., Abbad A., Lantri T., Bouadjemi B., and Aziz Z., Structural, Electronic and Elastic Properties of Half-Heusler Alloys CrNiZ (Z = Al, Si, Ge and As), Journal of the Korean Physical Society. (2018) 72, no. 11, 1337–1342, https://doi.org/10.3938/jkps.72.1337, 2-s2.0-85048290052.
10.3938/jkps.72.1337
CAS Web of Science® Google Scholar
51 Ahmed B. S., Anissa B., Radouan D., Bouzieh N. A., Durukan I. K., and Amrane N., Dft Studies on Electronic, Elastic, Thermoelectric and Optical Properties of New Half-Heusler XRhZ (X = V, Nb and Z = Si, Ge) Semiconductors, East European Journal of Physics. (2024) 1, no. 1, 294–307, https://doi.org/10.26565/2312-4334-2024-1-26.
10.26565/2312-4334-2024-1-26
Google Scholar
52 Haleoot R. and Hamad B., Thermodynamic and Thermoelectric Properties of CoFeYGe (Y = Ti, Cr) Quaternary Heusler Alloys: First Principle Calculations, Journal of Physics: Condensed Matter. (2020) 32, no. 7, https://doi.org/10.1088/1361-648X/ab5321.
10.1088/1361-648X/ab5321
PubMed Web of Science® Google Scholar
53 Rani B., Wani A. F., and Sharopov U. B., et al.Electronic Structure-, Phonon Spectrum-, and Effective Mass-Related Thermoelectric Properties of PdXSn (X = Zr, Hf) Half Heuslers, Molecules. (2022) 27, no. 19, https://doi.org/10.3390/molecules27196567.
10.3390/molecules27196567
Web of Science® Google Scholar
54 Meghoufel Z. F., Cherifi F., Boukra A., and Terki F., Ab-Initio Investigation on the Electronic and Thermoelectric Properties of New Half-Heusler Compounds KBiX (X = Ba and Sr), Journal of Physics: Condensed Matter. (2021) 33, no. 39, https://doi.org/10.1088/1361-648X/ac1180.
10.1088/1361-648X/ac1180
PubMed Web of Science® Google Scholar
55 Himanshu Joshi D. P. Rai, Hnamte Lalhriatpuia, Laref Amel, and Thapa R. K., A Theoretical Analysis of Elastic and Optical Properties of Half Heusler MCoSb (M = Ti, Zr and Hf), Heliyon. (2019) 5, no. 3.
PubMed Google Scholar
56 Kamel Hocine G. Youcef, Nabil B., Samir B., Ahmed M., and Ab-delali C., Structural, Electronic and Optical Properties of the Half-Heusler MgYGa Alloy via Dft Calculations, Mexican Journal of Physics. (2024) 70, no. 3 May-Jun, 030502–030501.
Google Scholar
57 Wei J. and Wang G., Thermoelectric and Optical Properties of Half-Heusler Compound TaCoSn: A First-Principle Study, Journal of Alloys and Compounds. (2018) 757, 118–123, https://doi.org/10.1016/j.jallcom.2018.05.037, 2-s2.0-85046817880.
10.1016/j.jallcom.2018.05.037
CAS Web of Science® Google Scholar
58 Bejo A. B., Shura M. W., Afrassa M. A., Tadele K., Marem F. T., and Habura K. H., Structural, Electronic, Mechanical and Optical Properties of RhZrZ (Z = As, Sb) Half-Heusler Compounds: First-Principles Calculations, Advances in Condensed Matter Physics. (2024) 2024, no. 1.
Web of Science® Google Scholar
59 Ciftci Y. O. and Evecen M., First Principle Study of Structural, Electronic, Mechanical, Dynamic and Optical Properties of Half-Heusler Compound LiScSi under Pressure, Phase Transitions. (2018) 91, no. 12, 1206–1222, https://doi.org/10.1080/01411594.2018.1515433, 2-s2.0-85053071662.
10.1080/01411594.2018.1515433
CAS Web of Science® Google Scholar
60 Candan A. and Kushwaha A. K., A First-Principles Study of the Structural, Electronic, Optical, and Vibrational Properties for Paramagnetic Half-Heusler Compound TiIrBi by GGA and GGA+ Mbj Functional, Materials Today Communications. (2021) 27, https://doi.org/10.1016/j.mtcomm.2021.102246.
10.1016/j.mtcomm.2021.102246
PubMed Google Scholar
61 Rahman Nasir, Husain Mudasser, and Yang Juan, et al.First Principle Study of Structural, Electronic, Elastic, and Magnetic Properties of Half-Heusler Compounds ScTiX (X = Si, Ge, Pb, In, Sb, and Tl). Journal of Superconductivity and Novel Magnetism. (2020) 33, no. 12, 3915–3922, https://doi.org/10.1007/s10948-020-05652-6.
10.1007/s10948-020-05652-6
CAS Web of Science® Google Scholar
62 Babalola M. I. and Iyorzor B. E., A Search for Half Metallicity in Half Heusler Alloys, Journal of Magnetism and Magnetic Materials. (2019) 491, https://doi.org/10.1016/j.jmmm.2019.165560, 2-s2.0-85068858873.
10.1016/j.jmmm.2019.165560
Web of Science® Google Scholar

All articles

First-Principles Calculations to Investigate Structural, Electronic, Mechanical, Optical, and Magnetic Properties of RhNbSb Half-Heusler Compound

Abstract

1. Introduction

2. Computational Details