The Role of Generalized Contraction Mappings in Neutrosophic Metric Spaces and Its Applications
Abstract
In this study, we have introduced the neutrosophic generalized contraction as a generalization of the neutrosophic -contraction with admissible mappings. Sufficient conditions for the existence and uniqueness of the fixed points for a neutrosophic generalized contraction are derived in complete strong neutrosophic metric spaces (SNMSs). An application is given to support the main result.
MSC2020 Classification: 47H10, 45D05, 54H25
1. Introduction
Zadeh [1] established the foundation for fuzzy mathematics in 1965. Banach [2] established fixed point theory in 1922 with his famous Banach contraction principle. Mathematicians have generalized it in numerous ways and used it to address issues in a variety of domains [3–5]. Kramosil and Michalek [6] initially introduced the idea of fuzzy metric space and then refitted it by George and Veeramani [7]. Grabiec [8] pioneered the investigation of fixed-point theorems in fuzzy metric space. In 2012, Wardowski [9] proposed an F-contraction as a new kind of contraction in complete metric spaces. Then, other mathematicians [10–16] then extended F-contraction to various spaces; see also [17]. Huang et al. [18] recently published fuzzy F-contraction, an extension of F-contraction in fuzzy metric spaces with simplified conditions, and established various fixed-point theorems for fuzzy F-contraction. Gopal and Vetro [19] extended the notion through the development of α-admissible and β-admissible fuzzy metric spaces. Park [20] proposed the idea of intuitionistic fuzzy metric space using continuous t-norms and continuous t-conorms. In 1998, Smarandache [21] developed the ideas of neutrosophic logic and neutrosophic set. The idea of neutrosophic metric space was established by Kirisci and Simsek [22], which dealt with membership, nonmembership, and neutralness. While fuzzy metric spaces represent uncertainty using a single membership degree, neutrosophic metric spaces (NMSs) expand this framework by incorporating three independent degrees: membership, indeterminacy, and nonmembership. This allows for a more flexible and nuanced representation of uncertainty, making NMSs more suitable for problems involving incomplete or contradictory information. These spaces generalize fuzzy metric spaces, as every fuzzy metric space can be viewed as a special case of an NMS when indeterminacy and nonmembership are appropriately constrained. This richer structure provides a theoretical foundation for addressing complex problems in mathematics and applied sciences. Jeyaraman and Sowndrarajan [23] and Jeyaraman, Hassen, and Manuel [24] demonstrated the applicability of NMSs by establishing fixed-point results for contraction theorems within these spaces.
We have provided generalized neutrosophic contraction with admissible properties in NMSs, inspired by the work of Gopal and Vetro [19], Koon et al. [25], and Huang et al. [18]. By establishing fixed-point theorems for these contractive maps, the theoretical framework is extended, and their practical applications are demonstrated. Our contributions include expanding the understanding of neutrosophic generalized contraction and offering tools for solving integral equations. Additionally, the results have implications for optimization, dynamical systems, and decision-making models under uncertainty.
2. Preliminaries
Definition 1. See [21], let Ξ be a nonempty fixed set. A neutrosophic set ℵ is defined as an object of the form ℵ = {, where
-
: Degree of membership of to the set ℵ;
-
: Degree of indeterminacy;
-
: Degree of nonmembership.
The neutrosophic set ℵ can also be expressed as an ordered triple ℵ = ( in Ξ. In this context, ( are subsets of ] −0, +1[ without further constraints.
Definition 2. See [23], a continuous triangular norm is a binary operation ∗ : [0, 1] × [0, 1] → [0, 1] that satisfies the following conditions:
-
T1. for all ;
-
T2. ∗ is associative and commutative;
-
T3. whenever and , where
-
T4. ∗ is continuous.
Definition 3. See [24], a continuous triangular conorm is a binary operation ⋄:[0, 1] × [0, 1] → [0, 1] that holds the following assertions:
-
TC1. ;
-
TC2. ⋄ is associative and commutative;
-
TC3. whenever and , where ;
-
TC4. ⋄ is continuous;
Definition 4. See [24], the 6-tuple ( is named as a NMS if Ξ is a random set, ∗ is continuous t-norm, ⋄ is a continuous t-conorm, and are neutrosophic sets on Ξ × Ξ × (0, ∞) holds the assertions that are stated below:
-
N1. 0, ; 0, 0, ;
-
N2. , , ,
-
N3. , ;
-
N4. , , ;
-
N5. , , ,
-
N6. .) : (0, ∞) → (0, 1] is continuous, for all
-
N7.
-
N8. , ;
-
N9. , , ;
-
N10. , , ,
-
N11. ,.) : (0, ∞) → (0, 1] is continuous, for all
-
= 0;
-
N13. , ;
-
N14. , , ;
-
N15. , , ,
-
N16. .) : (0, ∞) → (0, 1] is continuous, for all
-
= 0.
If the triangular inequalities are replaced in the definition above, with the condition
N5∗. , , , , , , , , and , , , for all and then is known as a strong NMS (SNMS).
Definition 5. Let be NMS. Let be a sequence in Ξ.
- 1.
is convergent if there exits such that , for every
- 2.
is a Cauchy sequence if for every ε ∈ (0, 1) and there exits such that , and for all ;
- 3.
is complete if every Cauchy sequence is convergent.
For the remaining part of this paper, the class of all mappings such that for every is indicated by ξ.
Definition 6. Let be NMS, and . The function is known to be a neutrosophic -contraction if there exits ι ∈ (0, 1) such that , and for all such that and .
Definition 7. The function is named as a β-admissible mapping if there exists a function β : Ξ × Ξ × (0, ∞) → (0, ∞) such that for every and
3. Main Results
Definition 8. Let be NMS. Let β : Ξ × Ξ × (0, ∞) → (0, ∞) be a mapping, and let A mapping is named as a neutrosophic generalized β--contraction if there exists 0 < ι < 1 such that for every such that and
Definition 9. Let be NMS. Let β : Ξ × Ξ × (0, ∞) → (0, ∞) be a function, and let The function is named to be a neutrosophic β--contraction if there exists 0 <ι < 1 such that for every such that and and
Theorem 1. Let be a complete SNMS, and let be a neutrosophic generalized β--contraction, where If all the conditions stated below are fulfilled:
- 1.
There exists such that for all
- 2.
is β-admissible;
- 3.
For each sequence in Ξ such that for all and there exists such that for all and
- 4.
If is a sequence in Ξ such that for every and and if
as , then for every Then, has an invariant point.
Proof. Let , such that for every We define a sequence by for every If there exists , such that , then is a fixed point of , in which case, there is nothing further to prove. Assume for all
Because for every and is β-admissible mapping, therefore,
By continuing this method, it is concluded that for all .
As is a neutrosophic generalized β--contraction, there exists 0 < ι < 1 fulfilling Equations (1)–(3). It follows that for all and Substituting and we obtain ), for all where ( = min{), ), )} = min {), ), )} = min{)}.
If max {)} = ), then
), for all where ( = max{), ), )} = max {), ), )} = max{)}.
Since is a strictly increasing function, we get , , and for all and .
Hence, for all , the sequence { is bounded above and strictly monotonic increasing in the interval [0,1], the sequence { is strictly monotonic decreasing in the interval [0,1] and bounded below and the sequence { is strictly monotonic decreasing in the interval [0,1] and bounded below.
Therefore, {, {, and { are convergent, that is, for any , there exists , such that , , and
We assert that and for all
Assume that for some . Applying the limit on both sides of Equation (5), we get which is a contradiction.
Suppose on the contrary, is not Cauchy.
By condition (3) there exist two subsequences , of and such that for all with ν ≥ ν0 and and β (
Let be the least integer that fulfills the above inequality.
Then, , , and Since is a SNMS, by (N5∗), (N10∗) and (N15∗), we get , , and .
Letting the limit as ν → ∞, by Equations (8)–(10), (T1) and (TC1), we get
1∗(1 − ε) = 1 − ε, 0 ⋄ε = ε and 0 ⋄ε = ε.
This implies that , , and . Again, by (N5∗), (N10∗), and (N15∗), we get )), and ).
Letting ν → ∞, by Equations (8) and (9), (T1) and (TC1), we have = 1 ∗ (1 − ε) ∗ 1 = 1 − ε, = 0⋄ε⋄0 = ε and = 0 ⋄ε⋄0 = ε.
Therefore, letting ν → ∞ in both sides of Equations (11)–(13), we obtain ( and (.
This implies that and , this contradicts the fact that .
Thus is a Cauchy sequence. Since is complete, there exists such that
= 1, = 0, and = 0 for all , or other words, . Since β ( for all and by condition (4), we have for all Now, we show that is an invariant point of
If , that is, and .
Then, by Equations (5)–(7), we obtain )>ιβ () for all , where min {}.
)<ιβ () for all , where max {}.
)<ιβ () for all , where max {}.
Letting in the above inequalities, we have )>ιβ (){1,1,), )<ιβ (){0,0,) and )<ιβ (){0,0,) this is not possible. Hence, that is, is a fixed point of
Corollary 1. Let be a complete SNMS, and let be a neutrosophic β--contraction, where If the following conditions are fulfilled:
- 1.
There exists such that for all
- 2.
is β-admissible;
- 3.
For each sequence in Ξ such that for all and there exists such that for all and
- 4.
If is a sequence in Ξ such that for all and and
if as , then for every Then, has an invariant point.
Example 1. Let Ξ = [0, ∞), and let ∗ be a minimum continuous t-norm and ⋄ be a maximum continuous t-conorm. The neutrosophic sets , , and are defined by
, , and for all and .
Then, is a complete but not a SNMS. For instance, take and Then, we have and and and and and
Checking with Conditions F5 ∗, F10 ∗, and F15 ∗, it is obvious that on the right side, we obtain = min{, = max { and = max {.
However, 0.287≱0.375. Therefore, is not SNMS.
Define the mapping by for . Let for , and let
Also, define β : Ξ × Ξ × (0, ∞) → (0, ∞) as for every and . It is straightforward to demonstrate that is a neutrosophic generalized -contraction and Conditions 1, 2, 3, and 4 of Theorem 1 are satisfied. Note, however, that the mapping does not have any fixed point.
Example 2. Let Ξ = [0, ∞) and let = min {1, for all We define the neutrosophic sets as follows:
(, 1–, and , for , and
We can easily verify that is a complete SNMS. Let for all , and let for 0 and Also, define for all
First, we establish that is a β-admissible mapping. Let , be such that
It follows that . Thus is a β-admissible mapping.
Next, we check whether the contractive condition of Theorem 1 is fulfilled or not. Let ,
We consider the following cases:
This is seen in Figures 1–3, which depict the behavior of contraction mapping.
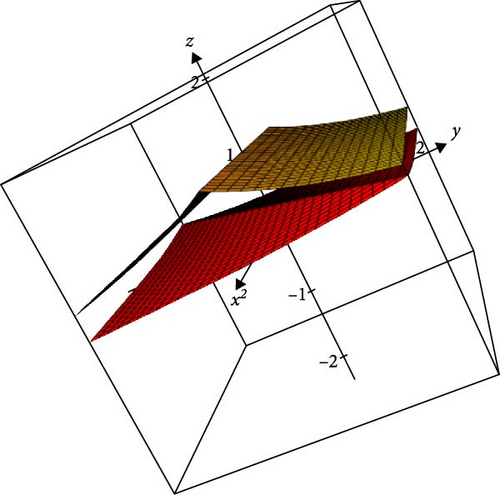
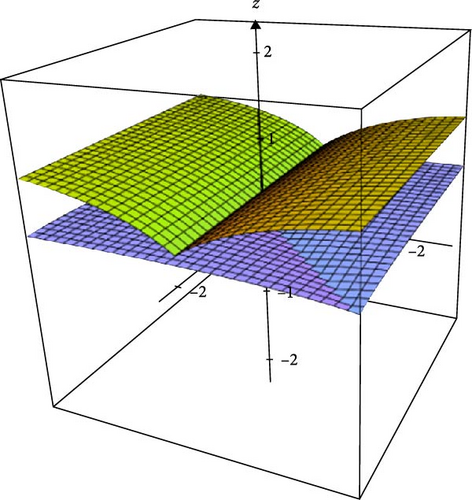
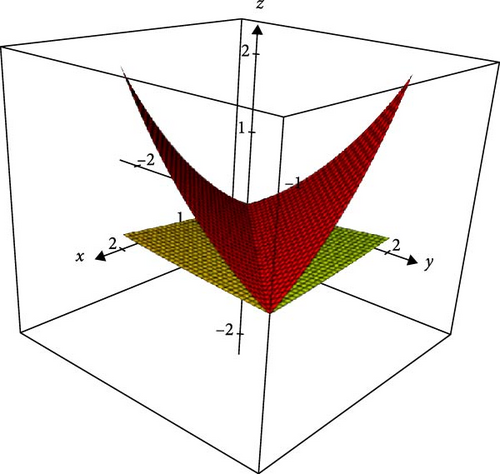
Hence, all the conditions in Theorem 1 are fulfilled. Therefore, has a fixed point.
Theorem 2. Let be a complete SNMS with and
- 1.
There exists such that for all
- 2.
is β-admissible;
- 3.
For each sequence in Ξ such that for all and there exists such that for all and
- 4.
If is a sequence in Ξ such that for all and and if
as →∞, then for every Then, has a fixed point.
Proof. Let be such that forevery Define a sequence by for all If there exists such that , then, is a fixed point of , in which case, there is nothing further to prove.
Assume for every Since for every and is β-admissible mapping, this implies that
By continuing this method, we get for all and .
By the hypothesis there exists ι ∈ (0, 1) satisfying Equations (14)–(16).
It is clear that for all and
), ),}
= min {), ), ),), )}
Since the t-norm is minimum, t-conorm is maximum, by (N5 ∗), (N10 ∗), and (N15 ∗), we get = min {, .
So, we have (), for all and
= max {, .
So, we have (), for all and
= max {, .
So we have (), for all and
If max {)} = ), then, )))), which is a contradiction.
If max {)} = ), then )))), which is a contradiction.
Since is a strictly increasing function, we get , , and for all and the sequence { is bounded above and strictly increasing in the interval [0,1], the sequence { is strictly monotonic decreasing in the interval [0,1] and bounded below and the sequence { is strictly monotonic decreasing in the interval [0,1] and bounded below.
Therefore, {, {, and { are convergent, that is, for any , there exists , such that , , and .
We claim that , , and for all
Suppose is not a Cauchy sequence.
By condition (3) there exist , ε > 0, two sub sequences , of and such that for all with ν ≥ ν0 and (
Let be the least integer that fulfills the above inequality.
Then, , , and
Using (N5∗), (N10∗), and (N15∗) minimum t-norm and maximum t-conorm,
} and } Taking the limit as ν → ∞, by Equations (20)–(22), we get 1, (1 − ε)} = 1 − ε, 0 , ε} = ε and 0 , ε} = ε.
This implies that , , and Again, by (N5∗), (N10∗), and (N15∗) minimum t-norm and maximum t-norm, we get )}, ), and )
Letting ν → ∞, by Equations (20)–(22), we have = min {1, (1 − ε), 1} = 1 − ε,
= max {0, ε, 0} = ε and = max {0 , ε, 0} = ε.
Since , and .
Therefore, letting ν → ∞ in both sides of Equations (23)–(25), we get ( and (.
This implies that and , this is a contradiction to the fact that . Thus, is a Cauchy sequence.
Since is complete, there exists such that = 1, = 0 and = 0 for all , or other words, .
Since β ( for all and by condition (4), we have for every We shall now prove that is a fixed point of
If , i.e., , and
Remark 2. Example 1 demonstrates that the consideration “strong” in Theorem 2 is not redundant. It should be noted that the results above do not ensure that the fixed points are unique.
To determine the uniqueness of the fixed point, apply the following condition:
(I) For any pair of fixed points , β ( for all
Theorem 3. Assume that condition (I) holds in addition to the hypotheses of Theorem 1. Then, has a unique fixed point.
Proof. The existence of a fixed point is established by Theorem 1.
Suppose that and are invariant points of such that , that is, Considering condition (I), we have β (
It follows that , , and this is a contradiction. Hence, we conclude that .
Corollary 2. Assume that condition (I) holds in addition to the hypotheses of Corollary 1. Then, has a unique fixed point.
Theorem 4. Assume that condition (I) holds along with the hypotheses of Theorem 2. Then, has a unique fixed point.
Proof. The existence of a fixed point is demonstrated by Theorem 2. Suppose that and are fixed points of such that , that is, ,
By condition (I), we have
β ( for all By Equations (14)–(16), we obtain ( for all where min{ }, ( for all where max{ } and ( for all where max{ }.
It follows that , , and this is impossible. Hence, we conclude that Therefore, has a unique fixed point.
4. Applications
4.1. Application-I
In this part, it has been demonstrated how the main result is used to solve an integral equation. Define such that is increasing and continuous for every The following theorem is our fixed-point result for the Twardowski-type contraction via β-admissible mappings of the integral type in an NMS.
Theorem 5. Let be a complete SNMS, and let be a neutrosophic generalized β--contraction. Let Ψ be a mapping in Υ such that
- 1.
There exists such that for all
- 2.
is β-admissible;
- 3.
For each sequence in Ξ such that for all and there exists such that for all and if is a sequence in Ξ such that for all and and if as , then for all
- 4.
For any pair of fixed points ( for every
Then, has an invariant point.
Proof. Let Use the Theorem 1 after Theorem 3. The required result is then derived.
4.2. Application-II
Let be the space of all continuous real-valued functions defined on the interval [0,1], for some I > 0. Let = min {1, . Define the neutrosophic sets by , and , where .
Then, (, ⋄) is a complete SNMS.
Theorem 6. Let (, ⋄) be a complete SNMS, as defined above. Let integral operator is defined by
- I.
;
- II.
The integral is bounded, i.e., there exists some θ ∈ (0, 1) such that Furthermore, this holds.
. Then, the integral Equation (26) has a solution.
Proof. Define β : Ξ2 × (0, ∞) → [0, ∞) by and , for .
Since all the requirements of Theorem 1 are fulfilled, hence the operator has a fixed point in , which is a solution of the integral Equation (26).
5. Conclusion
In this article, we have introduced the concept of neutrosophic generalized -contraction, expanding the framework of neutrosophic -contraction in the context of admissible mappings. The sufficient conditions are established for the existence and uniqueness of fixed points in complete SNMSs, advancing the theoretical understanding of this field. The practical application provided demonstrates the potential impact of neutrosophic generalized -contraction in solving integral equations. However, there are several limitations to this work. First, the application of neutrosophic generalized -contraction is primarily focused on integral equations, and future research could expand its use to other domains such as fuzzy control systems or image processing [26]. Since our study is based on NMSs, extending these results to neutrosophic fuzzy metric spaces or Banach spaces could open new avenues for exploration. Furthermore, the theoretical results presented here could be complemented with computational methods to make the theory more accessible for practical applications, similar to the approaches employed in solving nonlinear differential equations [27] or in iterative processes for fractals and dynamical systems [28]. Future work could also explore interdisciplinary applications, such as using neutrosophic logic in medical decision-making and conducting a comparative analysis with other related approaches, such as fuzzy and intuitionistic fuzzy metric spaces, to better understand the unique advantages of NMSs.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
M. Pandiselvi, M. Jeyaraman, and Rahul Shukla: investigation, methodology, writing-original draft. Rahul Shukla: supervision. M. Jeyaraman: writing–review and editing. All authors contributed to various stages of the study’s design and execution and have reviewed and approved the final manuscript for submission.
Funding
No funding was received. Open access funding was enabled and organized by SANLiC Gold.
Open Research
Data Availability Statement
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.




