Abstract and Applied Analysis
Volume 2024, Issue 1 5942773
Research Article
Open Access

On an Euler–Abel Type Transform of Trigonometric Series

N. Sh. Berisha, 

N. Sh. Berisha

Faculty of Economics , University of Prishtina , Agim Ramadani Street, Pristina , 10000 , Kosovo , uni-pr.edu

Search for more papers by this author
F. M. Berisha, 

Corresponding Author

F. M. Berisha

Faculty of Mathematics and Sciences , University of Prishtina , Mother Teresa Street, Pristina , 10000 , Kosovo , uni-pr.edu

Search for more papers by this author
M. Sadiku, 

M. Sadiku

Faculty of Business Administration , South East European University , Tetovo , North Macedonia , seeu.edu.mk

Search for more papers by this author
First published: 19 November 2024
https://doi.org/10.1155/aaa/5942773
Academic Editor: Jaume Giné

Abstract

In the paper, we give several limit case Euler–Abel type transforms for alternating cosine and sine series. Making use of a property of the operator of generalized difference, applied in the transforms, we give transforms for nonalternating series, which are stronger than similar transforms for alternating series given earlier.

MSC2020 Classification: Primary 65B10, Secondary 42A38, 40A25, 40A05

1. Introduction

Let
()
be a convergent real or complex trigonometric series. A method of accelerating the convergence of Equation (1) is given in [1]. It consists of the following.
Let r be a real or complex number such that re±αxi ≠ 1 and a linear operator defined by the following equation:
Then for a positive integer p, we have the following equation:
()
where (m = 0, 1, 2, …).

If the limits and (k = 1, 2, …, p − 1) exist, are finite, and all equal to each other, then by setting the value of the parameter r in transform (Equation 2) equal to the value of these limits, the transformed series converges faster than series (Equation 1).

The acceleration of convergence of series in transform (Equation 2) increases with incrementation of the value of p. Thus, an obvious shortcoming of transform (Equation 2) is the condition that all the p limits from above be equal to each other.

A generalization of transform (Equation 2) overcoming this shortcoming is given in [2]. Applying a generalization of the operator , introduced in [3], a limit case transform for p → ∞ is given there.

For a sequence of real or complex numbers define the operator by the following equation:

In the paper, using this operator of difference, we give a limit case transform for alternating cosine and sine series. The obtained results imply transforms for appropriate nonalternating series, stronger than those given in paper [2] in the sense that the same transforms are obtained under significantly weaker assumptions on the domain of the variable x and the possible choice of the sequence . The conditions guaranteeing a faster convergence of the transformed series are the same as in [2].

2. Auxiliary Statements

In order to establish our results, we use the following lemmas.

Lemma 1. Let the coefficients tnm(0 ≤ m ≤ n) of an infinite triangular matrix (tnm) satisfy the following conditions:

  • 1.

    For every fixed, m holdslimn→∞tnm = 0.

  • 2.

    There exists a positive constant M such that for every non-negative integer, n holds .

Let be a given sequence and let be the sequence defined by (n = 0, 1, 2, …). If , then limn→∞xn = 0.

The proof of the lemma is due to Töplitz [4, p. 325].

Lemma 2. Let and be arbitrary sequences of real or complex numbers. Put D0 = 1, , , , …, Dm = r1r2 … rm (where the summation for Dp is performed over all the combinations of distinct indices between 1 and m taken p at a time). For every positive integers m and n, the following equation holds: 

The statement of the lemma is given in [5].

Lemma 3. Let and be arbitrary sequences of real or complex numbers. For every positive integers m and n, the following equation holds: 

The lemma is proved in [6].

3. Statement of Results

The following theorem gives an Euler–Abel type limit case transform for alternating cosine series.

Theorem 1. Let 

()
be a convergent real cosine series and a sequence of real numbers such that the series converges. Then:
()
where (m = 0, 1, 2, …).

Proof. We put:

where , .

Then, by using the same technique as in [6], it can be proved that:

()
where
()

Since S2(x) = S1(−x), we also have the following equation:

()
where now:
()

We prove that .

Let

be the remainder of the convergent series, whose real part is series (Equation 3). Then, .

Making use of Lemma 2, we get the following equation:

In Lemma 1, we put the following equation:

and we show that the conditions of the lemma are satisfied.

We have the following equation:

()

Notice that since limj→∞|rj| = 0, there exists a positive integer p0 such that for every j > p0 holds the following equation:

()

Further, we notice that for every positive integer p > p0 holds the following equation:

Since , the series converges, implying the convergence of the infinite product [4, p. 355] . Thus, we conclude that the following equation,
()
is also satisfied.

This way, making use of in Equation (10) and the notice to Equation (9) from above, we get the following equation:

where constant C2 does not depend on p.

Hence, for every fixed k holds the following equation:

implying that condition 1 of Lemma 1 is satisfied.

Applying also in Equations (9) and (11), we obtain the following equation:

Since the convergence of series implies the convergence of the infinite product , the last inequation yields that for every fixed p holds the following equation:
meaning that condition 2 of Lemma 1 is also satisfied.

Therefore,

()

On the other hand, since , we have , that is,

()
is also true.

Now setting,

and making use of Lemma 2, we obtain the following equation:
Substituting x≔−x in the last equation, we also get the following equation:
Hence,
Since is a linear operator, we have the following equation:
Thus,

This way, taking into consideration Equations (12) and (13), letting p → ∞ in Equations (5) and (7), and then adding the two equations multiplied by , the last equation implies Equation (4).

The proof of the theorem is completed.

The following theorem gives an analogous transform for sine series.

Theorem 2. Let be a convergent real sine series and a sequence of real numbers such that the series converges. Then: 

where (m = 0, 1, 2, …).

The proof is analogical to the proof of Theorem 1.

We say that a series converges faster than another series , if .

Remark 1. If there exist finite limits (k = 0, 1, 2, …), then for,

the right–hand side series in Theorems 1 and 2 converge faster than the given series on the left–hand side.

We notice that these conditions, allowing a choice of parameters rk which guarantees a faster convergence of the transformed series, are identical to those given in [2]. The proof is analogical. As a result of the subsequent steps in the proof, it follows that the value of p is essential for the acceleration of convergence: the acceleration increases by increasing the value of p.

In order to give an idea about the scope of the class of sequences for which the conditions stated in Remark 1 are satisfied we notice that those conditions are satisfied for every sequence , where by Pk, we denote a polynomial of degree k, l, and m are non-negative integers, and A, B, a, and b are real numbers such that B ≠ 0, |a| < |b|, and Aan + Bbn ≠ 0 for all positive integers n.

We mention that, since the difference operators , , and can be calculated recursively, in practical implementations an appropriate triangular difference scheme could be used for the computations. The triangular scheme for computing the fourth order difference of a sequence is illustrated in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
A triangular scheme for computing the differences.

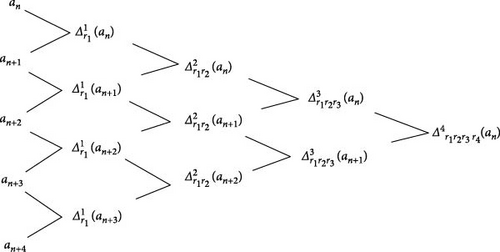
The appropriate algorithm analysis for such an approach is given in [6] (see also [7, pp. 118–120]). Thus the number of operations needed for computing the kth summand for the transformed series could be reduced to O(k2), instead of an algorithm of exponential complexity O(2k) (see also [8, Section 2.3]).

If we put an≔(−1)nan(n = 0, 1, 2, …) and rk≔−rk(k = 1, 2, …) in Theorem 1, and make use of Lemma 3, we obtain the following Euler–Abel type transform for nonalternating cosine series.

Corollary 1. Let Equation (1) be a convergent real cosine series and a sequence of real numbers such that the series converges. Then:

where (m = 0, 1, 2, …).

In an analogous way, with an≔(−1)nan(n = 0, 1, 2, …) and rk≔−rk(k = 1, 2, …) in Theorem 2, we obtain the following transform for nonalternating sine series.

Corollary 2. Let be a convergent real sine series and a sequence of real numbers such that the series converges. Then: 

where (m = 0, 1, 2, …).

Remark 2. Under additional assumptions of and being a sequence of positive real numbers such that for some λ > 1 holds rn = O(n−λ), the transforms of Corollaries 1 and 2 are given in [2].

4. Examples

Example 1. By putting x≔0 in Theorem 1 and making use of Lemma 2 to compute the values , we obtain the following limit case Euler type transform of alternating number series:

Example 2. By putting x≔0 in Corollary 1, in an analogous way, we obtain the following limit case,

of an Euler type transform for number series given in paper [3].

We notice that for rk≔r(k = 1, 2, …) and transform from Example 2 is given in [1].

Example 3. In Theorem 1, we put , α≔1, β≔0, , and for the obtained series , we calculate values of the terms of sequence by the formulae given in Remark 1. It can be shown that , (k = 1, 2, …).

Obviously, the sequence satisfies the conditions of Theorem 1.

Table 1 illustrates the acceleration of convergence of the transformed series by comparing the number of iterations needed for an approximate calculation of the sum of given series. It shows, for instance, that in order to calculate the approximate sum of the given series with an error not greater than 10−16, we must compute the sum of first 52 terms. Applying the transform from Theorem 1, the same accuracy is obtained by computing the sum of the first nine terms.

Table 1. The number of iterations.
ε Given series Transformed series
10−2 4 1
10−4 10 3
10−6 19 4
10−8 25 6
10−10 31 7
10−12 37 7
10−14 43 8
10−16 52 9
10−18 58 9
10−20 64 10
10−22 70 10

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors received no financial support for the research, authorship, and/or publication of this article.

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.