This study introduces a novel extension of the Wright function using the Macdonald function as an extension of the Pochhammer symbol. We establish integral, differential, and generating function formulas for this new function. Furthermore, we apply it to fractional differential equations, providing integral transformations of Cauchy-type problems with graphical representation. The Mellin and Rishi transformations are also derived for the extended Wright function. These results offer new insights and potential applications in fractional calculus (FC), mathematical physics, and engineering.

MSC2020 Classification: 26A33, 33B15, 33C05, 65D20, 33E20, 91B25

1. Introduction and Preliminaries

The different special functions have grown to serve as essential tools in the field of science and technology. The ongoing advancement of engineering, applied mathematics, economics, mathematical physics, and finance gives rise to new classes of special functions as well as their extensions and generalizations. Researchers have been examining generalizations and extensions of a number of special functions in the last several decades, including the Wright, Bessel’s, Beta, Gamma functions, Mittag-Leffler function, and the hypergeometric function [1–5].

These special functions are important in physics, engineering, and mathematics because of their numerous applications, such as solving Schrödinger’s equation, characterizing wave functions, simulating heat and fluid flow, and analyzing signal processing, control systems, and electromagnetics. Extensions to Laplace and Fourier series include links to combinatorics and number theory. Recent advances in the generalization of special functions have led to new developments in fractional calculus (FC) and differential equations. Few works [6–8] have explored the Wright function in continuum physics, mathematical physics, and other complex physical processes. However, existing approaches lack a direct link with integral transformations like Mellin and Rishi transforms. Our work bridges this gap by introducing a more versatile extension of the Wright function, facilitating applications in solving fractional differential equations and related problems.

Some of the extensions of the above-mentioned functions, which are available in the literature, are defined in the following.

1.1. Extension of Gamma Function

Chaudhary and Zubair [9] and Chaudhry and Zubair [10] have introduced and studied generalized Gamma function as follows:

()

where Re(p) > 0, Re(λ) > 0.

If p = 0, then Equation (1) reduces to the classical Gamma functions [11].

1.2. Extension of Pochhammer Symbol

In this section, we revisit a few definitions concerning the classical Pochhammer symbol and its extensions.

The Pochhammer symbol is defined as follows:

()

The generalization of Pochhammer symbols [12] is defined by the following:

()

Another extension of the Pochhammer symbol, defined by Srivastava, Rahman, and Nisar [13], is as follows:

()

where Γ_ν(λ; σ) is defined as follows:

()

The integral representation of (λ; σ, ν)_n is defined by the following:

()

Naturally, applying the knowledge that

and choosing ν = 0 in Equation (6), the following expression can be obtained:

1.3. Extended Wright Function

The classical Wright function is defined by the series representation convergent in the whole complex plane as follows:

()

The generalized Wright function was introduced and examined by El-Shahed and Salem [14] in 2015:

()

The function is an entire function of order .

The Wright function, a lesser-known but highly versatile special function, has gained prominence in addressing fractional-order partial differential equations (FPDEs). Motivated by the prior studies and versatile utility of the Wright function in modeling processes governed by anomalous diffusion and wave propagation, it made it an essential tool in modern applied mathematics and physics. In this paper, we define a new extended Wright function such as the following:

()

2. Main Result

Theorem 1. The following integral formula holds true:

()

where

Proof. By using the integral representation of the extended Pochhammer symbol in the definition of extended Wright function, we get the following:

By changing the order of summation and integration, we obtain the following:

Using Equation (8), we get the required result.

Theorem 2. The following integral formula holds true:

()

Proof. Proof of Equation (11) is trivial for m = 0. If we consider m ≠ 0, then we have the following:

Shift n → n + 1, and using (λ; σ, ν)_n+1 = (λ)(λ + 1; σ, ν)_n and (ρ)_n+1 = (ρ)(ρ + 1)_n in the equation, we have the following:

()

Again differentiating the equation with respect to z, we get the following:

()

The desired theorem assertion is obtained through differentiation up to n times.

3. Families of Generating Function Relation

In this section, we develop certain families of generating function relations for the extended Wright function (9). In order to determine these relationships, we use Δ(N, λ) to represent the following array of N parameters:

()

If N = 0, then the array Δ(N, λ) will be empty [15, 16].

Theorem 3. The following generating function holds:

()

, provided that each member of Equation (15) exists.

Proof. Considering the left-hand side and using the definition of the generalized Wright function, we have the following:

()

which gives the right-hand side of Equation (15).

Theorem 4. The following generating functions hold true:

()

provided that each member of Equation (17) exists.

Proof. Beginning with the left-hand side of the equation and using Equation (9), we have the following:

()

which is written as the right-hand side of Equation (17).

Theorem 5. The following generating functions hold true:

()

for

Proof. Considering the left-hand side of Equation (19), after using Equations (9) and (14), we have the following:

()

in which we get the required result.

Theorem 6. The following generating functions hold true:

()

for

Proof. Using Equation (9) on the left-hand side with some suitable changes, we have the following:

which is the right-hand side of the equation.

4. Integral Transform of

Several significant integral transforms for the extended Wright function have been obtained in this section.

4.1. Mellin Transform

The Mellin transform of a suitably integrable function f(α) with the index s is defined as follows:

()

whenever the improper integral in Equation (22) exists.

Theorem 7. The following Mellin transform representation for the extended Wright function (9) holds true:

()

Proof. Using the definition of Mellin transform and Equation (9), in Equation (23), with the help of Equation (6), we may write the left side as follows:

()

which can also be written as follows:

Now using the definition of K_ν+1/2(−), changing the order of x and p, and using definition of Gamma function, we have the following:

Using the definition of Beta function, we yield the following:

()

4.2. Rishi Transforms

The piecewise continuous function of exponential order, using the Rishi transform f(t), is defined in the interval [0,∞):

Theorem 8. The following Rishi transform representation for the extended Wright function (9) holds true:

()

Proof. Applying the Rishi transform to the extended Wright function, we get the following:

Now switching the integration and summation order, we have the following:

()

which is required result.

5. Generalized Fractional Derivative

An extension of classical calculus, FC applies the ideas of differentiation and integration to noninteger (fractional) orders. This field has drawn a lot of attention because of its strong modeling and simulation skills in a variety of fields, especially physics and engineering. It is frequently more accurate to use differential equations of arbitrary (noninteger) order to describe many physical rules. One prominent use of FC is in fractal systems, where it successfully tackles issues like fractal kinetics. A fundamental concept in FC, many special functions are widely used in fractal mathematics [17–20]. Here, we recall some basic definitions of FC.

The Riemann–Liouville’s fractional integral and differential operator of order ϑ ∈ C, R(ϑ) > 0 is given in Miller and Ross and Samko, Kilbas, and Marichev [18, 20] as follows:

()

where n = [R(ϑ)] + 1, x > 0.

The fractional Hilfer derivative, which is generalized by Dorrego and Cerutti [21] and Hilfer [22], is given in the following.

Let ϑ, β ∈ R⁺ such that 0 < ϑ ≤ 1 and 0 ≤ β ≤ 1:

()

The generalized fractional derivative for (m − 1) < ϑ, β ≤ m, 0 ≤ ς ≤ 1, m ∈ N is as follows:

()

which was given by Garg et al. [23]. If we put ς = 0, m = 1, then it reduces to Riemann–Liouville type fractional derivative of order ϑ. If ς = β, m = 1, then the equation becomes Hilfer’s fractional derivative of order β, ϑ.

The Laplace transform of the Riemann–Liouville fractional integral and derivative is given by the following:

()

For 0 < ϑ < 1 and 0 ≤ β ≤ 1, we have the following:

()

Let f(t) be the piecewise continuous and of exponential order, and then the Laplace transform of generalized fractional derivative is given as follows:

()

Theorem 9. Let f be the sufficiently well-behaved function which has its support in R⁺, (m − 1) < ϑ, β ≤ m, 0 ≤ ς ≤ 1, m ∈ N the Cauchy type problem:

()

where

()

It is solvable for all values of k ∈ R − (0, 1), and its solution is given by the following:

()

Proof. Taking the Laplace transform on both sides of Equation (36) and using Equation (35), with the help of the given condition in Equation (37), then we have the following:

Now taking the inverse Laplace transform, we get the desired result. We can see the graphical representation of Equation (38) in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Graphical representation of Equation (38) for 0.1 ≤ t ≤ 5 with some suitable constants.

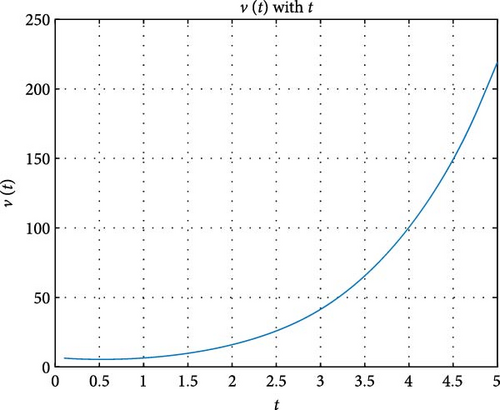
6. Conclusions

In the present investigation, we established an extended Wright function. Also, we presented some families of generating functions for the extended Wright function. We have observed that by letting ν = 0, the result derived in this paper will be reduced to the results of Srivastava, Çetinkaya, and Onur Kıymaz [12]. We have also developed the graphical representation of the Cauchy-type differential equation by using the concept of Laplace transforms. Future research into multidimensional cases or numerical algorithms for its computation may make use of the extension of the Wright function created here. Additionally, it can be used to solve a variety of fractional differential equation-based problems, including modeling anomalous diffusion processes, resolving integro-differential equations in fluid mechanics and thermodynamics, and many more.

Consent

The current study is not based on human or animal study, so no consent is required.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Methodology: E.M. and P.S. Supervision: R.G. and E.M. Writing–original draft: P.S. Formal analysis: D.L.S.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

Data sharing does not apply to this article as no datasets were generated or analyzed during the current study.

References

1 Arshad M., Mubeen S., Nisar K. S., and Rahman G., Extended Wright-Bessel Function and Its Properties, Communications of the Korean Mathematical Society. (2018) 33, no. 1, 143–155.
Google Scholar
2 Özergin E., Özarslan M. A., and Altın A., Extension of Gamma, Beta and Hypergeometric Functions, Journal of Computational and Applied Mathematics. (2011) 235, no. 16, 4601–4610.
10.1016/j.cam.2010.04.019
Web of Science® Google Scholar
3 Suthar D. L., Composition Formulae for the k-Fractional Calculus Operators Associated With k-Wright Function, Journal of Mathematics. (2020) 2020, 9, 5471715.
10.1155/2020/5471715
Google Scholar
4 Suthar D. L., Shimelis B., Ucar F., and Purohit S. D., Caputo Type Fractional Differentiation for the Extended Generalized Mittag-Leffler Function, Progress in Fractional Differentiation and Applications. (2023) 9, no. 1, 135–143, https://doi.org/10.18576/pfda/090110.
10.18576/pfda/090110
Google Scholar
5 Vyas Y., Bhatnagar A. V., Fatawat K., Suthar D. L., and Purohit S. D., Discrete Analogues of the Erdélyi Type Integrals for Hypergeometric Functions, Journal of Mathematics. (2022) 2022, 11, https://doi.org/10.1155/2022/1568632, 1568632.
10.1155/2022/1568632
Web of Science® Google Scholar
6 Luchko Y., The Four-Parameters Wright Function of the Second Kind and Its Applications in FC, Mathematics. (2020) 8, no. 6, https://doi.org/10.3390/math8060970, 970.
10.3390/math8060970
Web of Science® Google Scholar
7 Povstenko Y., Some Applications of the Wright Function in Continuum Physics: A Survey, Mathematics”. (2021) 9, no. 2, https://doi.org/10.3390/math9020198, 198.
10.3390/math9020198
Web of Science® Google Scholar
8 Mainardi F. and Consiglio A., The Wright Functions of the Second Kind in Mathematical Physics, Mathematics. (2020) 8, no. 6, https://doi.org/10.3390/math8060884, 884.
10.3390/math8060884
Web of Science® Google Scholar
9 Chaudhry M. A. and Zubair S. M., Generalized Incomplete Gamma Functions With Applications, Journal of Computational and Applied Mathematics. (1994) 55, no. 1, 99–124, https://doi.org/10.1016/0377-0427(94)90187-2, 2-s2.0-0002352357.
10.1016/0377-0427(94)90187-2
Web of Science® Google Scholar
10 Chaudhry M. A. and Zubair S. M., On a Class of Incomplete Gamma Functions With Applications, 2001, Chapman and Hall/CRC, New York, https://doi.org/10.1201/9781420036046.
10.1201/9781420036046
Google Scholar
11 Srivastava H. M., Chaudhry M. A., and Agarwal R. P., The Incomplete Pochhammer Symbols and Their Applications to Hypergeometric and Related Functions, Integral Transforms and Special Functions. (2012) 23, no. 9, 659–683, https://doi.org/10.1080/10652469.2011.623350, 2-s2.0-84865236200.
10.1080/10652469.2011.623350
Web of Science® Google Scholar
12 Srivastava H. M., Çetinkaya A., and Onur Kıymaz İ, A Certain Generalized Pochhammer Symbol and Its Applications to Hypergeometric Functions, Applied Mathematics and Computation. (2014) 226, 484–491, https://doi.org/10.1016/j.amc.2013.10.032, 2-s2.0-84888270075.
10.1016/j.amc.2013.10.032
Web of Science® Google Scholar
13 Srivastava H. M., Rahman G., and Nisar K. S., Some Extensions of the Pochhammer Symbol and the Associated Hypergeometric Functions, Iranian Journal of Science and Technology, Transactions A: Science. (2019) 43, no. 5, 2601–2606, https://doi.org/10.1007/s40995-019-00756-8, 2-s2.0-85071464547.
10.1007/s40995-019-00756-8
Web of Science® Google Scholar
14 El-Shahed M. and Salem A., An Extension of Wright Function and Its Properties, Journal of Mathematics. (2015) 2015, 11, https://doi.org/10.1155/2015/950728, 2-s2.0-85014297243, 950728.
10.1155/2015/950728
Google Scholar
15 Andrews George E., Askey Richard, and Roy Ranjan, Special Functions, 1999, 71, Cambridge University Press, Cambridge.
10.1017/CBO9781107325937
Google Scholar
16 Olver F. W., Lozier D. W., Boisvert R. F., and Clark C. W., NIST Handbook of Mathematical Functions, 2010, Cambridge University Press, Cambridge.
Google Scholar
17 Araci S., Rahman G., Ghaffar A., Azeema, and Nisar K. S., Fractional Calculus of Extended Mittag-Leffler Function and Its Applications to Statistical Distribution, Mathematics. (2019) 7, no. 3, https://doi.org/10.3390/math7030248, 2-s2.0-85062941320, 248.
10.3390/math7030248
Web of Science® Google Scholar
18 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, John Wiley & Sons, Inc, New York.
Google Scholar
19 Nazir A., Rahman G., and Ali A., et al.On Generalized Fractional Integral With Multivariate Mittag-Leffler Function and Its Applications, Alexandria Engineering Journal. (2022) 61, no. 11, 9187–9201, https://doi.org/10.1016/j.aej.2022.02.044.
10.1016/j.aej.2022.02.044
Web of Science® Google Scholar
20 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Philadelphia, Pa., USA, Switzerland.
Google Scholar
21 Dorrego G. A. and Cerutti R. A., The k-Fractional Hilfer Derivative, International Journal of Mathematical Analysis. (2013) 7, no. 11, 543–550, https://doi.org/10.12988/ijma.2013.13051.
10.12988/ijma.2013.13051
Google Scholar
22 Hilfer R., Applications of Fractional Calculus in Physics, 2000, World Scientific Publishing Co., Inc, River Edge, NJ.
10.1142/3779
Google Scholar
23 Garg M., Manohar P., Chanchalani L., and Alha S., On Generalized Composite Fractional Derivative, Walailak Journal of Science and Technology. (2014) 11, no. 12, 1069–1076.
Google Scholar

All articles

Some New Application of Extended Wright Function

Abstract