International Journal of Aerospace Engineering

Volume 2024, Issue 1 9980746

Research Article

Open Access

Multi-UAV Cooperative Air Combat Target Assignment Method Based on VNS-IBPSO in Complex Dynamic Environment

Yiyuan Li,

Yiyuan Li

orcid.org/0009-0008-3118-6211

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Weiyi Chen,

Corresponding Author

Weiyi Chen

[email protected]

orcid.org/0000-0002-2629-6749

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Shukan Liu,

Shukan Liu

orcid.org/0000-0002-7087-1069

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Guang Yang,

Guang Yang

orcid.org/0000-0002-4206-0736

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Fan He,

Fan He

orcid.org/0000-0002-4970-8435

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Yiyuan Li,

Yiyuan Li

orcid.org/0009-0008-3118-6211

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Weiyi Chen,

Corresponding Author

Weiyi Chen

[email protected]

orcid.org/0000-0002-2629-6749

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Shukan Liu,

Shukan Liu

orcid.org/0000-0002-7087-1069

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Guang Yang,

Guang Yang

orcid.org/0000-0002-4206-0736

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

Fan He,

Fan He

orcid.org/0000-0002-4970-8435

College of Weapon Engineering Naval University of Engineering Wuhan 430033 China hjgcdx.cn

Search for more papers by this author

First published: 24 May 2024

https://doi.org/10.1155/2024/9980746

Academic Editor: Ke Feng

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates the threat assessment method and target assignment algorithm in multi-UAV cooperative air combat decision-making. To address the uncertainty and dynamic changes in multiple threat attributes and attribute information of UAV targets, we propose a UAV target dynamic threat assessment method based on intuitionistic fuzzy multiattribute decision-making. Firstly, we propose a mixed situation information representation method to represent interval-valued fuzzy data appropriately. Secondly, we employ the normal distribution weight assignment method to fuse the multi-time situation information. Then, by incorporating the analytic hierarchy process and entropy method, we determine the normalized threat value of the target considering both objective situation data characteristics and decision-maker preferences. Finally, a simulation example is provided to validate the rationality of our proposed algorithm. For solving the multi-weapon multi-target assignment problem, a target assignment method based on the VNS-IBPSO algorithm is introduced. This method improves upon the limitations of the BPSO algorithm, such as limited local search capability and premature convergence, by combining variable neighborhood search and an improved binary particle swarm optimization algorithm. Simulation results show that the proposed threat assessment method can obtain reasonable threat assessment results under complex dynamic environments. The proposed VNS-IBPSO algorithm can solve the target assignment model quickly and efficiently based on the assessment results, therefore ensuring that the UAV mission planning system makes the correct combat plan.

1. Introduction

Multi-UAV system has attracted increasing attention due to their high robustness, strong adaptivity, flexible scalability, and other advantages. In the military field, multi-UAV cooperative air combat has gradually become an important development trend of future war. It can not only improve combat efficiency and reduce combat losses but also reduce casualties and has broad application prospects. Air combat decision-making is the key for UAVs to win in air combat [1] and is a dynamic process that changes with the battlefield environment, requiring real-time adjustments to maximize the effectiveness of cooperative operations based on external interference and various internal uncertainties [2]. The Observe, Orient, Decide, and Act (OODA) loop combat theory [3] states that multi-UAV cooperative air combat decision-making encompasses several elements, including threat assessment, target assignment, maneuver decision, and motion planning [4, 5]. Among them, threat assessment serves as the basis for target assignment, and its accuracy and timeliness have a decisive impact on the entire decision-making process. Target assignment, on the other hand, is the comprehensive utilization of the threat assessment results, which requires the optimal allocation of various possible targets to ensure the maximization of combat effectiveness. With the continuous improvement of the intelligence level of UAV cluster combat, the future air war will pay more attention to self-organization and self-coordination. Therefore, the study of threat assessment and intelligent target assignment methods in uncertain environments to realize the coupling synergies of multilevel air combat decision-making is a critical research of cooperative air combat decision-making.

In the context of UAV air combat decision-making, it is imperative to base the process on an assessment of the battlefield environment. By obtaining reasonable assessment results, it is possible to ensure that the mission planning system generates the appropriate combat plan. Several threat assessment methods have been developed in the past to address this problem, for example, analytical hierarchy process (AHP) [6], fuzzy set theory [7], Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [8], and multiple attribute decision-making [9]. However, the aforementioned methods fail to account for the impact of changes in air combat situational information. Consequently, several methods for processing situational information under dynamic conditions have been introduced. Qiang et al. [10] proposed an improved group generalized intuitionistic fuzzy soft set (I-GGIFSS) method for dynamic assessment of air target threat. Wang et al. [11] used dynamic Bayesian network inference to estimate the target threat at different time slices. Kun et al. [12] obtained time series weights by a Poisson distribution method based on multiple target posture data. Intelligent optimization methods have a wide range of applications in various fields due to their excellent adaptivity and robustness [13]. For target threat assessment, Yu et al. [14] trained an LSTM neural network for LSS flying target threat assessment. Cao et al. [15] proposed a target threat assessment algorithm based on linear discriminant analysis and improved glowworm swarm optimization algorithm to optimize extreme learning machine. Multi-UAV cooperative air combat typically operates in dynamic and unpredictable environments, requiring real-time threat assessment. In order to better capture the complete dynamics of UAV target behavior and subtle variations indicative of potential threats, short time series data are employed for dynamic threat assessment of UAV targets. Short time series data are susceptible to noise and uncertainties, stemming from environmental factors, sensor inaccuracies, or intermittent communication. Managing and filtering out noise while preserving relevant threat information becomes crucial for effective threat assessment.

Multi-UAV cooperative air combat typically takes place in a formation, and there has even been the emergence of large-scale UAV swarm fighting as a representative mode. Due to the large scale of the problem and the high complexity of the solution, the traditional exact algorithms are difficult to meet the timeliness requirements of the decision-making of air combat [16–18]. With the continuous progress of artificial intelligence technology, solving large-scale target allocation problems based on intelligent optimization algorithms has gradually become the mainstream of research. Intelligent optimization algorithms are able to seek the approximate optimal solution of the problem within a limited time, providing fast and effective support for UAV cooperative air combat decision-making. Zhen et al. [19] proposed an improved cooperative target assignment scheme based on a contract network protocol for target attack mission of heterogeneous UAV swarm. Xing et al. [20] proposed a self-organized offense–defense confrontation decision-making algorithm for a dynamic swarm versus swarm UAV combat problem. Song et al. [21] established a realistic UAV target assignment model and proposed a differential evolution algorithm to solve the problem. Zhao et al. [22] developed an improved hybrid genetic algorithm to solve multi-weapon multi-target assignment (MWMTA) problem in uncertain environment. In addition, considering the issue of cooperative task assignment for heterogeneous UAVs, Gao et al. [23] proposed an improved multiobjective genetic algorithm, which incorporates a natural chromosome encoding format and specially designed genetic operators. The algorithm can effectually tackle the unavoidable deadlock phenomenon while preserving the randomness of the population. It is worth noting that the application of reinforcement learning–based methods in intelligent air combat decision-making is becoming increasingly prevalent and is currently a hot topic of research [24].

In summary, due to the difficulty of accurate modeling of the battlefield environment, the existence of uncertainty, and the measurement information of UAVs being prone to errors, it is necessary to introduce multiple uncertainties into air combat threat assessment to enable the decision-making system to make the most suitable decisions. In addition, traditional intelligent algorithms may fall into the “premature convergence” trap under large-scale complex scenarios. Therefore, designing an improved intelligent optimization algorithm that can effectively solve the problem of collaborative multitarget attack decision-making under uncertain environments is also a key focus of this article.

This study primarily examines the issue of threat assessment and MWMTA in the context of air combat. However, as aircraft stealth continues to improve, along with an increase in interference and sensor measurement error, the uncertainty of acquired information is also on the rise. The primary contributions of this article are summarized as follows:

1.
In terms of threat assessment, a UAV target threat assessment model is constructed, representative threat factors are selected, and interval-valued intuitionistic fuzzy number characterization is used to address the uncertainty and incompleteness in the threat factor information.
2.
An evaluation method based on dynamic interval value intuitionistic fuzzy multiattribute decision-making is presented. For the time-varying nature of the enemy posture, time series weights are generated based on the normal cumulative distribution to fuse multimoment posture information. At the same time, an indicator weight optimization model integrating AHP method and entropy weight method is proposed, and the subjective and objective weight characteristics are comprehensively considered.
3.
A novel target assignment algorithm, Variable Neighborhood Search and Improved Binary Particle Swarm Optimization (VNS-IBPSO), is introduced to address the MWMTA problem. By enhancing the update strategy of Binary Particle Swarm Optimization (BPSO) and incorporating the variable neighborhood search (VNS) operator, it effectively addresses the limitations of local search capability in the initial phase and global search capability in the later phase of particle evolution. Simulation results demonstrate that the VNS-IBPSO algorithm effectively and efficiently identifies the optimal allocation scheme with excellent convergence properties.

The reminder of this article is organized as follows: Section 2 depicts the multi-UAV-coordinated air combat scenario and system model of target threat assessment and MWMTA. Section 3 introduces the target threat assessment method and process in detail. Section 4 analyzes the proposed VNS-IBPSO algorithm for solving MWMTA problem. In Section 5, the performance of the proposed algorithm was tested. Finally, Section 6 summarizes the article and proposes future development directions.

2. Problem Description and Modeling

A brief description of a multi-UAV-coordinated air combat scenario is given. To simplify the problem, it is reasonable to assume that enemy target situational information has been obtained through the search phase. Assume that the number of our UAVs is m and the number of enemy UAVs is n. The total number of weapon resources carried by all UAVs is q and weapon resources carried by each UAV is q_i, i ∈ {1, 2, ⋯, m}. Our UAVs continuously obtain K time slices of situational information; time set is noted as t = {t₁, t₂, ⋯, t_k}.Considering the threat factors of the enemy target and establishing threat assessment model. A list of key symbols used is provided in Table 1.

Table 1. Symbol definitions.

Symbol	Definitions
m	The number of our UAVs
n	The number of enemy UAVs
q	The number of our weapons
s	The number of threat evaluation factors
q_i	The number of weapons carried by each UAV
q_j	The number of weapons assigned to each UAV
t_k	Moment t_k
U_q×n	Weapon target assignment matrix
Q_q×n	Target damage probability matrix
V_q×n	The comprehensive threat assessment matrix of enemy UAVs to our UAVs
	Target situational information matrix obtained by i^th UAV in moment t_k
p_kj	The damage probability of our k^th weapon to the j^thenemy target
S_ij	The threat assessment value of the j^th enemy UAV to our i^th UAV
o_jl	The l^th threat factor value of the j^th enemy UAV

Figure 1 shows the UAV cooperative air combat decision-making flow based on the above parameters. Through the proposed threat assessment method, the dynamic threat assessment of the adversary UAV target is carried out. Next, weapon target assignment scheme is generated after receiving the synthetic threat assessment. Among them, the following key issues need to be addressed.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow of multi-UAV cooperative air combat decision-making.

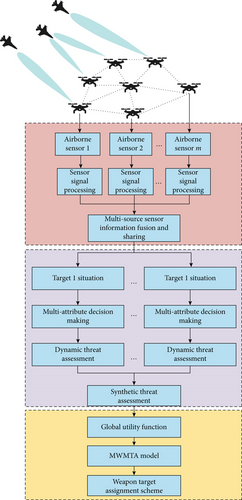
2.1. Selection of Threat Assessment Factor for UAV Targets

Target threat assessment should start with threat assessment factor selection from target situational information. It usually incorporates static and dynamic threat assessment factors. The static threat assessment component, which is usually fixed, represents the adversary UAV’s static features including target mobility, electronic countermeasure capabilities, and battle radius. The dynamic threat assessment element focuses on target motion scenario information, such as relative angle, speed, height, and distance, between the opponent and our UAV. Threat assessment parameters are chosen based on UAV cooperative air combat characteristics, as follows.

2.1.1. Speed Threat Factor

The radial velocity of the enemy UAV target is selected as the speed threat factor, and the near direction is positive and the far direction is negative. The faster the radial velocity of the UAV is, the stronger the maneuverability is and the greater the offensive advantage is. At the same time, the faster the speed can make the UAV get rid of the target or complete the pursuit of the target. It belongs to benefit-oriented factor.

2.1.2. Height Threat Factor

The target height refers to the vertical nearest distance between the target height plane of the enemy UAV and our UAV. The UAV at a higher altitude will occupy a more favorable attack position, and the corresponding weapon load can also obtain higher kinetic energy through the conversion of potential energy. Therefore, the higher target, the greater threat to us. It belongs to benefit-oriented factor.

2.1.3. Distance Threat Factor

The target distance refers to the projection distance on the horizontal plane of the connection between the both sides. Usually, the closer the enemy UAV’s target distance is, the more obvious the attack intention to us, the shorter defense time is, and the greater threat to us is. It belongs to cost-oriented factor.

2.1.4. Angle Threat Factor

The target angle threat can be described by the target entry angle. The target entry angle refers to the angle between the connecting line between the target and our UAV and target UAV speed direction. The smaller the entry angle is, the more obvious the target attack intention is and the greater the threat to us. It belongs to cost-oriented factor.

2.1.5. Radar Cross Section (RCS) Threat Factor

The enemy’s stealth performance is directly related to whether it is detected by airborne sensors. The smaller the RCS, the better the enemy’s stealth performance, the smaller the probability of being detected by airborne radar, and the greater the threat to us. It belongs to cost-oriented factor.

2.1.6. Type Threat Factor

The threat degree of different UAV types is different. In this study, the UAV target types are considered according to the combat function, which can be divided into four categories: attack UAV, interference UAV, scout UAV, and bait UAV.

2.2. Description of Mixed Situational Information in Treat Assessment

Due to data collecting difficulties, target behavior variability, and intelligence information conflict, target situational knowledge is unclear and fragmentary. Threat assessment using set numerical forms to express ambiguous information may provide erroneous, simplistic, and misleading conclusions that may impair decision-making. To define the uncertainty and incompleteness of target situational information, we construct mixed situational information using interval-valued numbers, intuitionistic fuzzy numbers, precise numbers, categorical variables, and other data types. Target situational information matrix obtained by i^th UAV in moment t_k is , j ∈ {1, 2, ⋯, n} and l ∈ {1, 2, ⋯, s}. The l^th threat factor value of the j^th enemy UAV is o_jl, and the representation of o_jl are as follows.

2.2.1. Interval Number Representation

Considering the detection error of the airborne sensor, the error is set to be Δτ. Then, it can be expressed by an interval number , the upper limit of it is and the lower limit of it is . is the initial attribute value detected by the airborne sensor.

2.2.2. Intuitionistic Fuzzy Number Representation

Considering that there are omissions or intelligence conflicts in the collection process of target situational information, then it can be expressed by an intuitionistic fuzzy number ο_jl = 〈μ_jl, ν_jl, π_jl〉, where μ_jl is the membership degree, ν_jl is the nonmembership degree, and π_jl = 1 − μ_jl − ν_jl is the hesitancy degree. They are calculated as follows:

If it belongs to benefit-oriented factor,

()

If it belongs to cost-oriented factor,

()

2.2.3. Classification Variable Representation

When the threat factor value is a categorical variable, it is usually described by linguistic variables such as “very high,” “high,” “general,” and “low” based on domain knowledge. It needs to be transformed into the corresponding intuitionistic fuzzy number. The threat factor values corresponding to different types of UAV targets are shown in Table 2.

Table 2. The threat factor quantification value corresponding to different types of UAV.

Target type	Linguistic variables	Intuitionistic fuzzy number
Attack UAV	Very high	(0.90, 0.05)
Interference UAV	High	(0.75, 0.10)
Scout UAV	General	(0.50, 0.25)
Bait UAV	Low	(0.25, 0.20)

2.2.4. Interval-Valued Intuitionistic Fuzzy Number Representation

Interval-valued number can be regarded as a special fuzzy number. In order to facilitate the subsequent calculation, when threat factor values are described as intuitionistic fuzzy number, it can be transformed into an interval-valued intuitionistic fuzzy number: .

After processing, the uncertain target situational information in complicated dynamic environments can be appropriately represented for target dynamic threat assessment. Section 3 details the threat assessment methodology and procedure.

2.3. Construction of Multiweapon and Multitarget Allocation Model

In this work, we assumed that all missions that were assigned would be finished simultaneously. This assumption could be divided into several assumptions, which are listed below.

Assumption 1. Assume that there is no time consumption for a UAV when conducting assignment. It means that every UAV could start and finish assignment simultaneously.

Assumption 2. Assume that the MWMTA problem would only be solved once and all assign operations would be started right after the allocation solved.

Assumption 3. Each UAV can use any number of weapon resource it carries to attack a target. Every weapon must be assigned to targets, and each weapon can only attack one target.

Assumption 4. The damage probability between the k^th missile to the j^th target is already known and is labeled as p_kj. The threat value of the j^th target against our i^th UAV is also calculated beforehand through the threat assessment.

Denote x_kj as the decision variable of the k^th weapon assigned to the j^th target. When x_kj = 1, it represents the k^th weapon assigned to the j^th target. When x_kj = 0, then means no assign. If the k^th missile is assigned to the target j, the survival probability of target j is 1 − p_kj. After performing a coordinated attack, survival probability of target j becomes

. Moreover, let S_ij be the threat value of the j^th target to our i^th UAV, and the remaining threat can be written as

. Accordingly, the remaining threat of the targets after a round of engagement and the maximum operational efficiency of weapon resources can be derived as the global utility function:

()

where F denotes the minimum threat value of enemy residual targets and E denotes the destruction of enemy UAV target with the greatest probability.

The constraint condition is

()

where constraint 1 denotes that a weapon can only be assigned to a UAV target individually, constraint 2 denotes that up to q_j weapons can be assigned to attack j^th target, and constrains 3 indicates that the max number of weapons can be used is q.

The multiobjective optimization problem is simplified into a single-objective optimization problem by linear weighting method. The penalty function method is used to deal with the constraints. Therefore, the improved objective function model is

()

where M is a penalty factor of the penalty function; it is mainly used to punish the error that one weapon resource attacks more than one target at the same time in the solution space; it is necessary to conduct iterative numerical experiments to determine an appropriate penalty factor.

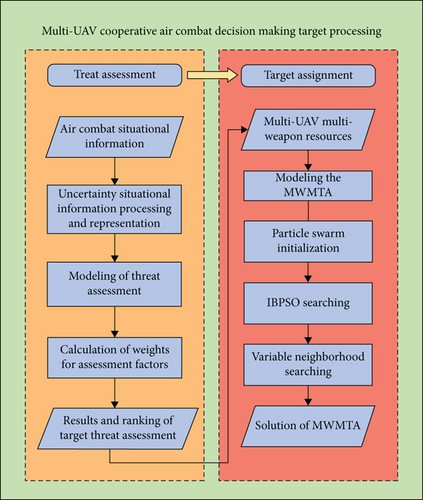
To summarize, Figure 2 illustrates the flowchart for the comprehensive target processing, which includes threat assessment and target assignment. Section 3 and Section 4 provide detailed explanations of the particular techniques and steps involved.

3. Interval-Valued Intuitionistic Fuzzy Multiattribute Decision-Making-Based Dynamic Threat Assessment

3.1. Timing Weighting Model

Time will affect air battle situation information. Current air combat scenario information most affects threat assessment. Situation data closer to the present is more important. However, merely using current data for assessment and neglecting historical knowledge can narrow the assessment results and undermine logic. It is important to study the relationship between air combat situation and threat assessment at multiple times. Refer to [25], for discrete time series data; this paper establishes a time series weight–solving model based on the normal cumulative distribution. It adopts the cumulative distribution function algorithm of the normal distribution to solve the time weight series. The normal cumulative distribution function is expressed as

()

The special function based on the error function is expressed as

()

where K is the number of continuous moments, μ_k denotes the mean value of the set K, and σ_K denotes the std value of the set K; they refer to

()

Based on the cumulative distribution function of normal distribution, the weight of time series is calculated as

()

where η(t_k) is the weight of t_k.

3.2. Threat Factor Weight Optimization Model

AHP [6] and entropy methods [26], based on subjective expert experience and objective data, respectively, reflect the weight of target danger features from many perspectives. Thus, we anticipate to identify a best threat factor weighting approach by combining the two. Assume that the weight obtained by AHP is

, l ∈ {1, 2, ⋯, s}. The weight obtained by entropy method is

, l ∈ {1, 2, ⋯, s}. The objective function of threat factor weight optimization model is

()

The constraint condition is

()

where α is the preference coefficient; when the expert experience is more accurate and reliable, take a larger value; otherwise, take a smaller value. In this article, take α = 0.5.

3.3. Procedure of the Dynamic Threat Assessment

The decision-making process of threat assessment based on dynamic intuitionistic fuzzy multiattribute decision-making is shown in Figure 3.

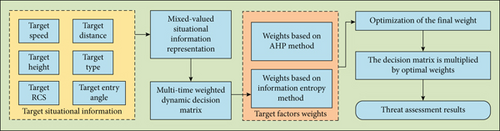
The specific steps are as follows.

Step 1. Based on the mixed situational information processing method in Section 2.2, the threat assessment model is constructed, and the decision matrix of target situational information at the moment is established as .

Step 2. According to Equations (6)–(10), combined with the time series weight model, the multitime weighted dynamic decision matrix is constructed by integrating the multitime target situational information.

()

Step 3. Since the entropy method needs accurate value to calculate the objective weight, the continuous ordered weighted average operator method is used to transform the interval-valued intuitionistic fuzzy number to accurate value according to the following equation:

()

where ρ(y) is a monotone increasing function in [0, 1]. Generally, ρ(y) = y(t), t > 0, so as to

()

where t is inversely proportional to the degree of risk aversion of decision-makers.

Step 4. Calculate the weight of threat factors based on AHP method as . Calculate the weight of threat factors based on entropy method as .

Step 5. According to Equation (11) and Equation (12), calculate the optimal weight of threat factors based on threat factor weight optimization model as .

Step 6. Calculate the threat assessment value of the enemy UAVs to our i^th UAV according to the following equation:

()

Step 7. The above threat assessment process is carried out for all UAVs, and the comprehensive threat assessment matrix of the enemy UAVs to our UAVs can be obtained.

()

where S_ij denotes the threat assessment value of the j^th enemy UAV to i^th our UAV.

4. VNS-BPSO Algorithm for MWMTA Problem

In this section, VBS-IBPSO optimization algorithm is proposed to solve the MWMTA problem under complex dynamic environment.

4.1. Concept of BPSO

BPSO is proposed by Kennedy and Eberhart in the year of 1997, where the PSO algorithm can solve the discrete combinatorial optimization problem [27].

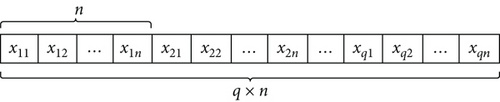
Using the q × n variables in the weapon target assignment matrix as the solution space, the dimension of it is d = q × n. Denote X_id as one origin solution with the initial velocity V_id, and X_id is the binary encoded, as shown in Figure 4.

The update rule for the i^th particle is expressed as follows:

()

where pbest_id denotes individual optimal particle position, gbest_id denotes global optimal particle position, ϕ₁ and ϕ₂ are the coefficient of particle learning from pbest_id and gbest_id, S is the sigmoid function [28], and rand is a random number between 0 and 1.

The rule in Equations (19) and (20) transforms the summation relationship between velocity and position into a mapping relationship. This means the greater the speed, the higher the probability of the position to take 1.

4.2. The Improved BPSO

In the BPSO algorithm, each iteration of the particle is mainly to change its binary sequence. The concept of probability of the bit changing is proposed in Ref. [27], assuming that a bit of binary codes is 0; then, the probability that it changes into 1 is S(V_id). Identically, if it is 1 originally, then the probability that it changes into 0 is 1 − S(V_id). The probability of the bit changing is

()

Substitute Equation (19) into Equation (21):

()

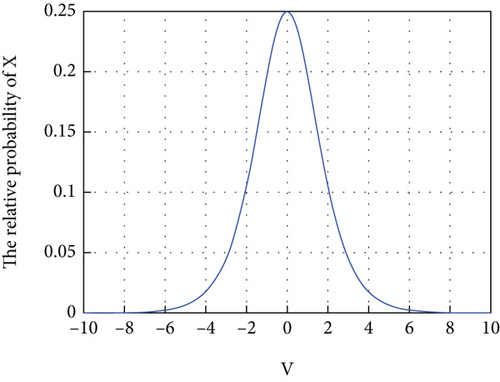
According to Equation (21), the correlation between the particle speed V_id and p(Δ) is shown as Figure 4.

The chart shows that the bit change rate is highest at 0 and lowest at 0.25. In the BPSO method, particle updates depend on individual and global optimal positions. When the particle velocity approaches 0, the likelihood of bit changing is 0.25; therefore, it still has 25% chance of jumping at other point. Thus, while the BPSO algorithm has a great global search ability, it cannot converge to the global optimal position. As the algorithm iterates, its randomness increases and its local search ability decreases. Considering the intrinsic logical relationship of the update rules in the PSO algorithm and drawing on the probability-based mapping rules in BPSO, here, we propose an improved BPSO update strategy:

()

where the Trans function is as follows:

()

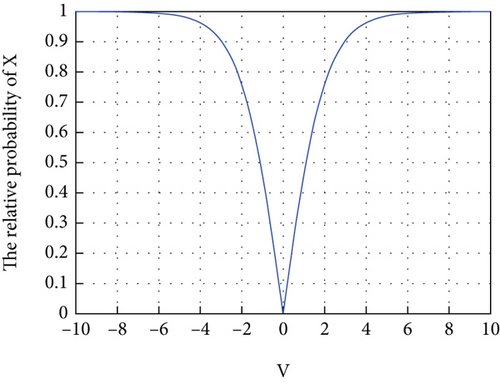
The difference between IBPSO and BPSO is the modification of function Trans and S(V_id). The correlation between the particle speed V_id and p(Δ) after the change of function is shown in Figures 5 and 6. The probability of bit changing tends to 0 when the particle velocity tends to 0. Moreover, when the particle velocity is positive, the binary bit value can only be changed to 1. Otherwise, the binary bit value can only be changed to 0. This method makes it easier for the particle swarm to approach the global optimal particle and improves the local search ability of the BPSO algorithm.

4.3. VNS Operator

The basic principle of the VNS algorithm is to obtain a wider search range by changing the neighborhood structure of multiple historical solutions within a local range [29]. That is, in the case of the same initial solution, the algorithm can expand a wider search space and has a more superior ability to jump out of the “premature trap.” Therefore, on the basis of IBPSO, the VNS operator is introduced to further improve its local search ability. The specific flow is shown in Figure 7.

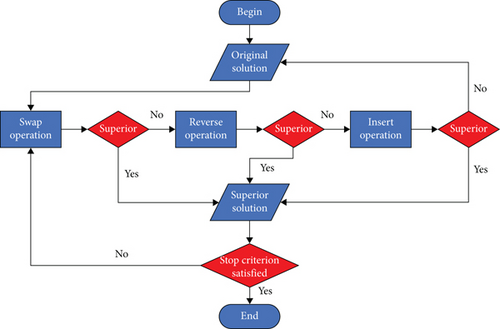
The core of VNS is the design of neighborhood search operation. In this section, three different neighborhood operations are designed for MWMTA, as follows:

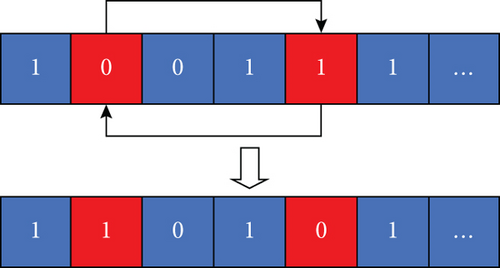
4.3.1. Swap Operation

Suppose that in the MWMTA problem, the individual optimal solution of the current particle has been found by the IBPSO algorithm, and the values of the first and second positions in the solution space are swapped by the swap operation to obtain its neighborhood solution by arbitrarily choosing two positions in the solution space. The specific operation is shown in Figure 8.

4.3.2. Reverse Operation

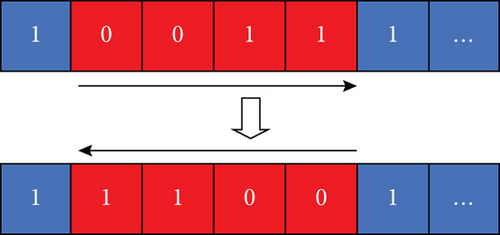
Suppose the current particle individual optimal solution has been obtained, arbitrarily choose two positions in the solution space and reverse all values between the first position and the first position by the reversal operation to reverse the ordering. The specific operation is shown in Figure 9.

4.3.3. Insert Operation

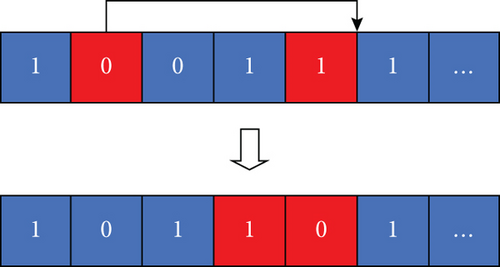
If the value of the former is smaller than the latter, the value of the former is inserted after the latter. Conversely, the value at the latter position is inserted after the former to obtain its neighborhood solution. The specific operation is shown in Figure 10.

4.4. Implementation of VNS-IBPSO

The pseudocode of VNS-IBPSO is shown in Algorithm 1. The hyperparameters that need to be set in advance include particle swarms, popsize, maximum number of IBPSO iterations, maxiter, learning coefficient factors ϕ₁ and ϕ₂, and maximum number of VNS iterations k_max.

Algorithm 1: The pseudocode of VNS-IBPSO.

Procedure VNS-IBPSO
Initialize the hyperparameters
For each particle i
Generate the position X_id and velocity V_id
Calculate its fitness
Set pbest_id = X_id
End for
While iter ≤ Maxiter
For i= 1 to popsize
Update the velocity and position of particle i
Perform constraint processing on particles that do not satisfy the constraint
Calculate its new fitness
The new particle is
If
If
For k = 1 to k_max
Perform VNS operator on pbest_id to get the local optimal value
The new particle is
If
If
iter = iter + 1
End while
Record and print process data
End procedure

The function Fit is the fitness function according to Equation (3). The main steps of IBPSO are explained as follows.

Step 1. Initialize the particle swarms including its population, maximum number of iterations, speed range of particle, and learning coefficient. Then, calculate the fitness value of each particle and record pbest_id and gbest_id.

Step 2. Update the particle swarms according to Equation (23) and Equation (24). Perform constraint processing on particles that do not satisfy the constraint and calculate the fitness value of new particle.

Step 3. Compare the updated fitness value of the particle with the historical optimal fitness value of pbest_id. If the former is better than the latter, update the pbest_id and further compare its value with the value of gbest_id. After comparison, determine whether the current particle has been fully updated; if the update is complete, go to Step 4; otherwise, update the next particle.

Step 4. Denote k = 1, perform VNS operation on pbest_id, and obtain the neighborhood solution . Perform constraint processing on it and calculate updated fitness value.

Step 5. Compare the updated fitness value of the particle with the historical optimal fitness value of pbest_id. If the former is better than the latter, update the pbest_id and further compare its value with the value of gbest_id. After comparison, determine whether the current particle has been fully updated; if the update is complete, then continue to search within the local search range of the next neighborhood solution until k = k_max.

Step 6. If the number of iterations reaches its maximum value, then return gbest_id and exit the algorithm. Otherwise, the iterative process of updating in the next round is started again from the first particle.

4.5. Algorithm Complexity Analysis

4.5.1. Time Complexity Analysis

The time complexity serves as a crucial metric for evaluating the computational efficiency of an algorithm in algorithmic analysis. It characterizes the growth pattern of an algorithm’s running time with respect to increasing input size, which is contingent upon the frequency of executing pivotal steps within the algorithm.

The VNS-IBPSO algorithm mainly contains the following steps: random initialization, fitness evaluation, fitness ranking, neighborhood generation, neighborhood search ranking, and updating the optimal particle position. Assuming that the number of initialized populations is N, the spatial dimension is d, the maximum number of iterations of the IBPSO algorithm is I_max, the number of iterations of the VNS operator is K_max, the complexity of the random initialization algorithm is O(N∗d), the complexity of the fitness evaluation algorithm is O(N), the computational cost of the updating position stage is O(N∗d), the complexity of the fitness sorting stage is O(N∗logN), the complexity of the neighborhood generation stage is O(N²), and the complexity of the neighborhood search sorting stage is O(N²). In summary, the time complexity of the method can be estimated as follows: O(N∗d + I_max∗N(1 + logN + d) + k_max∗(2N²)).

4.5.2. Spatial Complexity Analysis

The spatial complexity of the VNS-IBPSO algorithm consists of four main aspects: the population space, the fitness value space, the neighborhood search space, and the temporary variable space. In population space, it needs to store the position information of each particle in the population. Therefore, the space required for the population is O(N∗d). In fitness value space, it needs to calculate the fitness value of each particle position and record the fitness value of the optimal particle. The extra space required for fitness values is O(N). The space of the set of solutions needed after each operation needs to be considered in neighborhood search space, which is O(N∗d). The extra space required for temporary variables is usually of constant level and negligible. In summary, the spatial complexity of the VNS-IBPSO algorithm is O(2N∗d + N).

5. Simulation Results and Analysis

The simulations are implemented in the MATLAB R2021a software environment, and the main configuration of the hardware environment is Win 10 laptop, Intel Core i9-11900H, 2.50 GHz CPU, and 16 GB RAM.

5.1. Simulation of Target Threat Assessment

Assume that after the target search and tracking identification phase, the adversary UAV cluster consists of six UAVs, marked as T = {T₁, T₂, T₃, T₄, T₅, T₆}. Our is composed of four UAVs, marked as T = {Γ₁, Γ₂, Γ₃, Γ₄}. Take Γ₁ as an example; the target situational information of t₁, t₂, and t₃ moments is obtained as multiattribute decision information for target threat assessment, based on the interval-valued intuitionistic fuzzy number for its representation, as shown in Tables 3 and 4.

Table 3. Target situation index at t₁.

Target	Evaluation indicators
Target	Speed (m·s⁻¹)	Height (m)	Distance (m)	Entry angle (°)	RCS (m²)	Type
1	[0.38, 0.41]	350	3320	[0.43, 0.64]	0.16	[0.90, 0.95]
2	[0.39, 0.42]	344	1720	[0.37, 0.58]	0.15	[0.90, 0.95]
3	[0.38, 0.43]	310	2955	[0.27, 0.50]	0.13	[0.90, 0.95]
4	[0.38, 0.43]	400	3600	[0.16, 0.36]	0.02	[0.25, 0.8]
5	[0.39, 0.43]	305	3200	[0.32, 0.70]	0.05	[0.5, 0.75]
6	[0.39, 0.43]	440	4800	[0.16, 0.64]	0.07	[0.75, 0.90]

Table 4. Target situation index at t₂.

Target	Evaluation indicators
Target	Speed (m·s⁻¹)	Height (m)	Distance (m)	Entry angle (°)	RCS (m²)	Type
1	[0.38, 0.41]	362	3270	[0.43, 0.64]	0.16	[0.90, 0.95]
2	[0.39, 0.42]	355	1805	[0.36, 0.57]	0.15	[0.90, 0.95]
3	[0.38, 0.43]	330	3005	[0.27, 0.50]	0.13	[0.90, 0.95]
4	[0.38, 0.43]	405	3705	[0.16, 0.36]	0.02	[0.25, 0.8]
5	[0.39, 0.43]	295	3200	[0.32, 0.70]	0.05	[0.5, 0.75]
6	[0.39, 0.43]	420	4800	[0.17, 0.63]	0.07	[0.75, 0.90]

According to Equations (6)–(10), the time series weights are calculated:

()

According to Equation (11) and Equation (12), the optimal threat factor weights are obtained:

()

According to Equation (15), multimoment weighted dynamic decision matrix is determined:

()

According to Equation (16), the combined threat value of enemy UAVs to Γ₁ is determined as

()

The above threat assessment process is carried out for each of our UAVs, and the comprehensive threat assessment value of enemy UAVs to our UAVs is obtained. The specific values are shown in Table 5.

Table 5. Target situation index at t₃.

Target	Evaluation indicators
Target	Speed (m·s⁻¹)	Height (m)	Distance (m)	Entry angle (°)	RCS (m²)	Type
1	[0.39, 0.42]	345	3100	[0.43, 0.64]	0.16	[0.90, 0.95]
2	[0.39, 0.42]	350	2000	[0.37, 0.58]	0.15	[0.90, 0.95]
3	[0.38, 0.43]	320	3200	[0.27, 0.50]	0.13	[0.90, 0.95]
4	[0.36, 0.45]	415	3840	[0.15, 0.37]	0.04	[0.25, 0.8]
5	[0.39, 0.43]	305	3210	[0.32, 0.70]	0.08	[0.5, 0.75]
6	[0.37, 0.45]	435	4500	[0.16, 0.64]	0.05	[0.75, 0.90]

5.2. Simulation of MWMTA

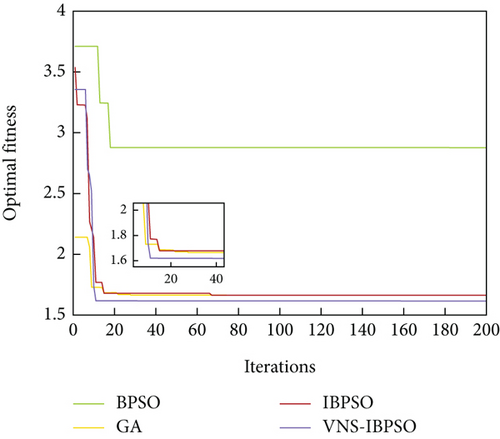
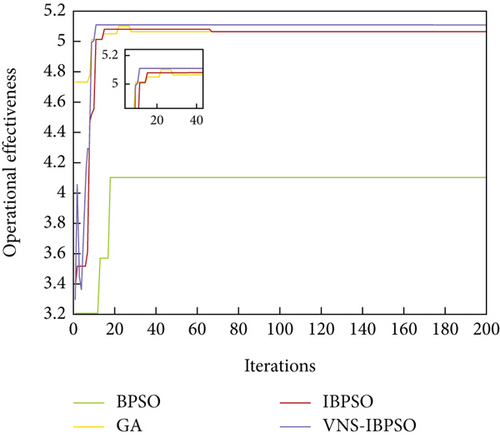
After completing the threat assessment of the enemy UAV targets, the MWMTA phase is entered. Assume that each UAV carries two weapons, and the number of weapon resources to attack the same target is at most two. The target threat of six enemy UAVs to our four UAVs and the damage probability of our eight weapons to six enemy UAVs are given in Tables 6 and 7. To ascertain the efficacy of the VNS-IBPSO algorithm and do a comparative analysis of its performance, three widely used algorithms are also tested. They are BPSO, IBPSO, and hybrid genetic algorithms. The operational parameters used by the above algorithms are given in Table 8. The curve of the optimal fitness value, the expected value of operational effectiveness, and the expected value of residual target threat are given in Figures 11, 12, and 13.

Table 6. The comprehensive threat assessment matrix of enemy UAVs to our UAVs.

Targets	Target threat
Targets	1	2	3	4	5	6
1	0.488	0.426	0.400	0.278	0.342	0.414
2	0.254	0.203	0.252	0.601	0.275	0.482
3	0.195	0.341	0.235	0.371	0.164	0.335
4	0.614	0.109	0.631	0.484	0.292	0.195

Table 7. The damage probability of our weapons to the enemy UAVs.

Weapons	Hit rate
Weapons	1	2	3	4	5	6
1	0.29	0.92	0.23	0.89	0.14	0.72
2	0.49	0.82	0.41	0.10	0.51	0.37
3	0.33	0.46	0.39	0.90	0.43	0.30
4	0.12	0.38	0.52	0.26	0.71	0.41
5	0.22	0.15	0.44	0.29	0.21	0.13
6	0.61	0.95	0.76	0.32	0.24	0.19
7	0.44	0.56	0.16	0.22	0.88	0.17
8	0.81	0.42	0.35	0.43	0.77	0.90

Table 8. Operational parameters of comparing algorithms.

Algorithm	Main reference	Parameters
BPSO	[27]	Population size = 150, iteration times = 200, learning coefficients factors ϕ₁ = ϕ₂ = 2
IBPSO	[30]	Population size = 150, iteration times = 200, learning coefficients factorsϕ₁ = ϕ₂ = 2
Hybrid GA	[22]	Population size = 150, iteration times = 200, the weights ω₁ and ω₂ of target decision model are set to 0.6 and 0.4, penalty factor N = 150
VNS-IBPSO	This paper	Population size = 150, iteration times = 200, learning coefficients ϕ₁=0.8 and ϕ₂=0.9, VNS operations times k_max = 30, penalty factor M = 100

It can be seen that the VNS-IBPSO algorithm is the first to reach convergence among the four algorithms and achieves optimal results on both fronts. After the 11th iterations, the VNS-IBPSO algorithm calculates the optimal fitness value is 1.6186, the optimal value of the residual target threat expectation is 1.2306, and the optimal value of operational effectiveness expectation is 5.1104. The weapon target assignment matrix obtained from the solution is

()

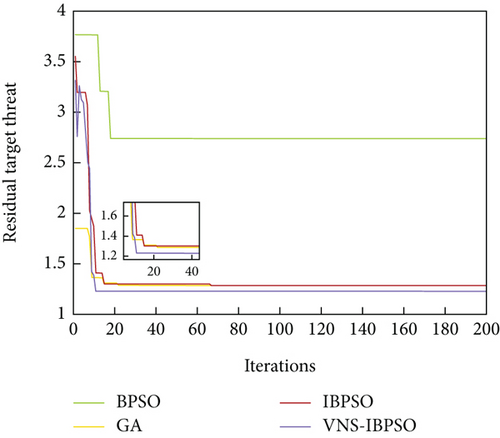
The weapon target assignment scheme is as follows: Weapon 8 attacks Target 1, Weapon 2 attacks Target 2, Weapons 5 and 6 attack Target 3, Weapon 3 attacks Target 4, Weapon 7 attacks Target 5, and Weapons 1 and 4 attack Target 6.

5.3. Comparative Analysis

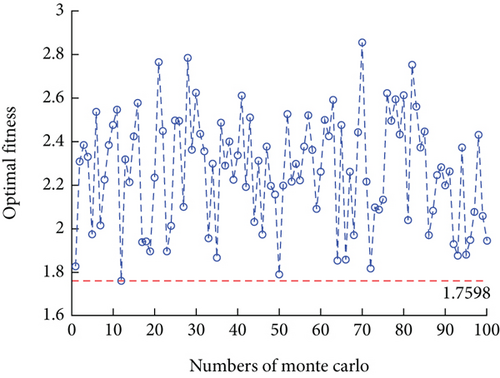
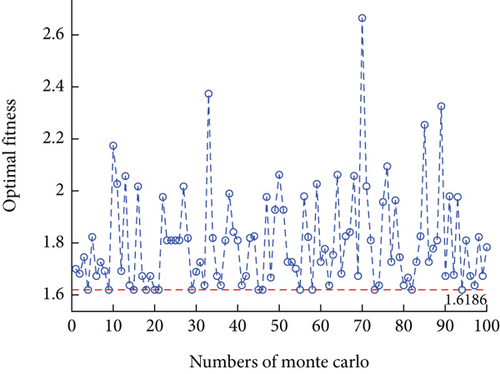
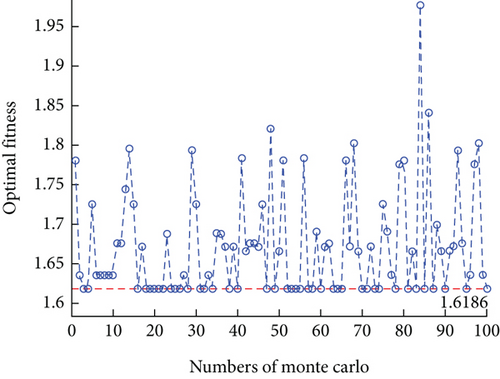
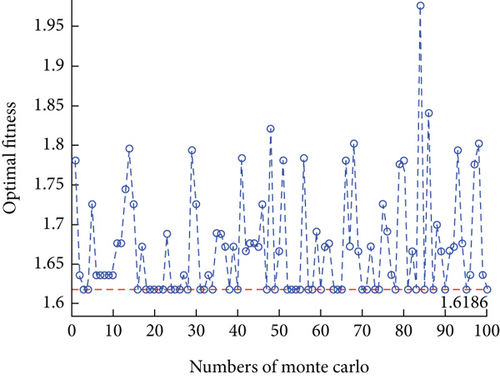
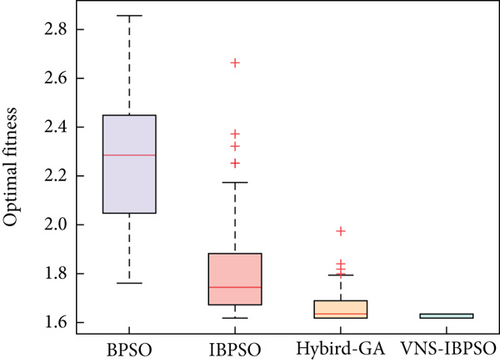
To mitigate the inherent instability and uncertainty of a single experiment, we conducted 100 experiments for each tested algorithm using Monte Carlo simulation. In each experiment, the algorithms were run for a maximum of 200 iterations. The variation curves of the optimal fitness values are shown in Figures 14, 15, 16, and 17. To compare the results of each algorithm more clearly, a boxplot is given as Figure 18. The statistical analysis of the algorithm performance is obtained, as shown in Table 9.

Table 9. Algorithm performance statistics analysis.

	BPSO	IBPSO	Hybrid GA	VNS-IBPSO
Number of iterations of convergence	20	62	22	9
Single iteration time (s)	0.276	0.108	0.212	0.453
Convergence time (s)	5.52	6.86	4.66	4.08
Fitness interval	[1.7598, 2.8563]	[1.6186, 2.6649]	[1.6186, 1.9763]	[1.6186, 1.6316]
Fitness mean	3.0625	1.8025	1.6717	1.6251
Fitness variance	0.0659	0.0363	0.0047	0.0001

The performance comparison of the four algorithms is discussed as follows:

1.
The optimal fitness values achieved by VNS-IBPSO for addressing the MWMTA problem are the same as those obtained by Hybrid GA and IBPSO algorithms, indicating the validity of the solution results. As shown in Table 9, the mean and variance of VNS-IBPSO are substantially smaller than the other three algorithms’, indicating that its solution is the most stable.
2.
Figures 14, 15, 16, 17, and 18 show that the VNS-IBPSO algorithm has a much higher convergence rate than the other three algorithms because it balances global and local search ability during each round of iteration, suppressing immature convergence and improving solution effectiveness.
3.
Because its solution quality and convergence rate are better than the other three algorithms, VNS-IBPSO can identify the optimal feasible solution in the quickest time when solving the same problem.
4.
The VNS-IBPSO increases algorithmic complexity, especially for problems with long calculation and solution times. Within the context of this research, the VNS-IBPSO algorithm has faster convergence, higher solution efficiency, and better quality than the other four algorithms.

6. Conclusion

In the context of multi-UAV cooperative air combat, this paper examines target threat assessment and MWMTA algorithm in complicated dynamic environments. Due to target situational information ambiguity and incompleteness, interval-valued intuitionistic fuzzy number representation is proposed for target threat assessment. Timing weighting and threat factor weight optimization models assess and rank UAV targets. The MWMTA challenge is described as a multiobjective optimization problem to minimize UAV threat and maximize weapon operating effectiveness. To address the BPSO algorithm’s poor local search and premature convergence, VNS operator and V-shaped update scheme are used in a VNS-IBPSO algorithm. Simulation results suggest that the proposed methods are acceptable and effective.

This paper addresses the MWMTA problem in the presence of uncertainties regarding target posture. In practical air combat scenarios, the task of target assignment encounters various uncertainties. Firstly, uncertainty arises from the availability of weapon resources. Secondly, there is uncertainty associated with the characteristics of the target. The interplay between these uncertainties introduces additional complexities to the task of target allocation. Consequently, aligning with combat style characteristics and considering various uncertain factors, researching multi-UAV target assignment methods tailored to actual combat needs is a crucial developmental focus in this field.

Disclosure

This paper was previously published as a preprint version in Authorea. It is available from https://www.authorea.com/users/637597/articles/653825-multi-uav-cooperative-air-combat-target-assignment-method-based-on-vns-ibpso-algorithm-in-complex-dynamic-environment.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (grant no. 11774432).

Open Research

Data Availability Statement

Data will be made available on request to the authors.

References

1 Fu L., Xie F., Wang D., and Meng G., The overview for UAV air-combat decision method, The 26th Chinese Control and Decision Conference (2014 CCDC), 2014, Changsha, China, 3380–3384, https://doi.org/10.1109/CCDC.2014.6852760, 2-s2.0-84905234038.
10.1109/CCDC.2014.6852760
Google Scholar
2 McGrew J. S., How J. P., Williams B., and Roy N., Air-combat strategy using approximate dynamic programming, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 5, 1641–1654, https://doi.org/10.2514/1.46815, 2-s2.0-78149336006.
10.2514/1.46815
Web of Science® Google Scholar
3 Yunming W., Si C., Chengsheng P., and Bo C., Measure of invulnerability for command and control network based on mission link, Information Sciences. (2018) 426, 148–159, https://doi.org/10.1016/j.ins.2017.10.035, 2-s2.0-85032180358.
10.1016/j.ins.2017.10.035
Web of Science® Google Scholar
4 Wang X., Li B., Su X., Peng H., Wang L., Lu C., and Wang C., Autonomous dispatch trajectory planning on flight deck: a search-resampling-optimization framework, Engineering Applications of Artificial Intelligence. (2023) 119, https://doi.org/10.1016/j.engappai.2022.105792.
10.1016/j.engappai.2022.105792
Web of Science® Google Scholar
5 Wang X., Deng Z., Peng H., Wang L., Wang Y., Tao L., Lu C., and Peng Z., Autonomous docking trajectory optimization for unmanned surface vehicle: a hierarchical method, Ocean Engineering. (2023) 279, article 114156, https://doi.org/10.1016/j.oceaneng.2023.114156.
10.1016/j.oceaneng.2023.114156
Web of Science® Google Scholar
6 Luo R., Huang S., Zhao Y., and Song Y., Threat assessment method of low altitude slow small (LSS) targets based on information entropy and AHP, Entropy. (2021) 23, no. 10, https://doi.org/10.3390/e23101292, 34682016.
10.3390/e23101292
PubMed Web of Science® Google Scholar
7 Azimirad E. and Haddadnia J., Target threat assessment using fuzzy sets theory, International Journal of Advances in Intelligent Informatics. (2015) 1, no. 2, 57–74, https://doi.org/10.26555/ijain.v1i2.18, 2-s2.0-85018271765.
10.26555/ijain.v1i2.18
Google Scholar
8 Yin Y., Zhang R., and Su Q., Threat assessment of aerial targets based on improved GRA-TOPSIS method and three-way decisions, Mathematical Biosciences and Engineering. (2023) 20, no. 7, 13250–13266, https://doi.org/10.3934/mbe.2023591, 37501487.
10.3934/mbe.2023591
PubMed Web of Science® Google Scholar
9 Changwen Q. and You H., A method of threat assessment using multiple attribute decision making, 6th International Conference on Signal Processing, 2002, 2002, Beijing, China, IEEE, 1091–1095, https://doi.org/10.1109/ICOSP.2002.1179979, 2-s2.0-33747377218.
10.1109/ICOSP.2002.1179979
Google Scholar
10 Qiang Z., Junhua H., Jinfu F., and An L., Air multi-target threat assessment method based on improved GGIFSS, Journal of Intelligent & Fuzzy Systems. (2019) 36, no. 5, 4127–4139, https://doi.org/10.3233/JIFS-169972, 2-s2.0-85065815415.
10.3233/JIFS-169972
Web of Science® Google Scholar
11 Wang Y., Sun Y., Li J.-Y., and Xia S.-T., Air defense threat assessment based on dynamic Bayesian network, 2012 International Conference on Systems and Informatics (ICSAI2012), 2012, Yantai, China, 721–724, https://doi.org/10.1109/ICSAI.2012.6223112, 2-s2.0-84864223412.
10.1109/ICSAI.2012.6223112
Google Scholar
12 Kun Z., Weiren K., Peipei L., Jiao S., Yu L., and Jie Z., Assessment and sequencing of air target threat based on intuitionistic fuzzy entropy and dynamic VIKOR, Journal of Systems Engineering and Electronics. (2018) 29, no. 2, 305–310, https://doi.org/10.21629/JSEE.2018.02.11, 2-s2.0-85047080521.
10.21629/JSEE.2018.02.11
Web of Science® Google Scholar
13 Zhuang J., Chen Y., Zhao X., Jia M., and Feng K., A graph-embedded subdomain adaptation approach for remaining useful life prediction of industrial IoT systems, IEEE Internet of Things Journal. (2024) 1–1, https://doi.org/10.1109/JIOT.2024.3361533.
10.1109/JIOT.2024.3361533
Google Scholar
14 Yu X., Wei S., Fang Y., Sheng J., and Zhang L., Low-altitude slow small target threat assessment algorithm by exploiting sequential multifeature With long short-term memory, IEEE Sensors Journal. (2023) 23, no. 18, 21524–21533, https://doi.org/10.1109/JSEN.2023.3301090.
10.1109/JSEN.2023.3301090
Web of Science® Google Scholar
15 Cao Y., Kou Y.-X., Xu A., and Xi Z.-F., Target threat assessment in air combat based on improved glowworm swarm optimization and ELM neural network, International Journal of Aerospace Engineering. (2021) 2021, 1–19, https://doi.org/10.1155/2021/4687167, 4687167.
10.1155/2021/4687167
CAS Web of Science® Google Scholar
16 Mills-Tettey G. A., Stentz A., and Dias M. B., The dynamic hungarian algorithm for the assignment problem with changing costs, 2007, Tech. Rep. CMU-RI-TR-07-27, Robotics Institute, Pittsburgh, PA.
Google Scholar
17 Kwon O., Lee K., Kang D., and Park S., A branch-and-price algorithm for a targeting problem, Naval Research Logistics. (2007) 54, no. 7, 732–741, https://doi.org/10.1002/nav.20247, 2-s2.0-34948831568.
10.1002/nav.20247
Web of Science® Google Scholar
18 Kline A. G., Ahner D. K., and Lunday B. J., Real-time heuristic algorithms for the static weapon target assignment problem, Journal of Heuristics. (2019) 25, no. 3, 377–397, https://doi.org/10.1007/s10732-018-9401-1, 2-s2.0-85057784476.
10.1007/s10732-018-9401-1
Web of Science® Google Scholar
19 Zhen Z., Wen L., Wang B., Hu Z., and Zhang D., Improved contract network protocol algorithm based cooperative target allocation of heterogeneous UAV swarm, Aerospace Science and Technology. (2021) 119, article 107054, https://doi.org/10.1016/j.ast.2021.107054.
10.1016/j.ast.2021.107054
Web of Science® Google Scholar
20 Xing D., Zhen Z., and Gong H., Offense–defense confrontation decision making for dynamic UAV swarm versus UAV swarm, Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. (2019) 233, no. 15, 5689–5702, https://doi.org/10.1177/0954410019853982, 2-s2.0-85067808071.
10.1177/0954410019853982
Web of Science® Google Scholar
21 Song Y., Xi Q., Xing X., and Yang B., Multi-UAV cooperative multi-target allocation method based on differential evolutionary algorithm, 2020 39th Chinese Control Conference (CCC),, 2020, Shenyang, China, 1655–1660, https://doi.org/10.23919/CCC50068.2020.9189332.
10.23919/CCC50068.2020.9189332
Google Scholar
22 Zhao Y., Chen Y., Zhen Z., and Jiang J., Multi-weapon multi-target assignment based on hybrid genetic algorithm in uncertain environment, International Journal of Advanced Robotic Systems. (2020) 17, no. 2, article 172988142090592, https://doi.org/10.1177/1729881420905922.
10.1177/1729881420905922
PubMed Web of Science® Google Scholar
23 Gao X., Wang L., Yu X., Su X., Ding Y., Lu C., Peng H., and Wang X., Conditional probability based multi-objective cooperative task assignment for heterogeneous UAVs, Engineering Applications of Artificial Intelligence. (2023) 123, article 106404, https://doi.org/10.1016/j.engappai.2023.106404.
10.1016/j.engappai.2023.106404
Web of Science® Google Scholar
24 Wang X., Wang Y., Su X., Wang L., Lu C., Peng H., and Liu J., Deep reinforcement learning-based air combat maneuver decision-making: literature review, implementation tutorial and future direction, Artificial Intelligence Review. (2024) 57, no. 1, https://doi.org/10.1007/s10462-023-10620-2.
10.1007/s10462-023-10620-2
PubMed Web of Science® Google Scholar
25 Xiao Q., Modeling wind speed time series by Chebyshev polynomial expansion method, Energy Sources, Part A: Recovery, Utilization, and Environmental Effects. (2021) 1–13, https://doi.org/10.1080/15567036.2021.1982074.
10.1080/15567036.2021.1982074
Web of Science® Google Scholar
26 Pourabbas E., Parretti C., Rolli F., and Pecoraro F., Entropy-based assessment of nonfunctional requirements in axiomatic design, IEEE Access. (2021) 9, 156831–156845, https://doi.org/10.1109/ACCESS.2021.3128686.
10.1109/ACCESS.2021.3128686
Web of Science® Google Scholar
27 Kennedy J. and Eberhart R. C., A discrete binary version of the particle swarm algorithm, 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, 1997, Orlando, FL, USA, 4104–4108, https://doi.org/10.1109/ICSMC.1997.637339.
10.1109/ICSMC.1997.637339
Google Scholar
28 Tommiska M. T., Efficient digital implementation of the sigmoid function for reprogrammable logic, IEE Proceedings-Computers and Digital Techniques. (2003) 150, no. 6, 403–411, https://doi.org/10.1049/ip-cdt:20030965, 2-s2.0-0347410661.
10.1049/ip-cdt:20030965
Google Scholar
29 Hansen P., Mladenović N., Todosijević R., and Hanafi S., Variable neighborhood search: basics and variants, EURO Journal on Computational Optimization. (2017) 5, no. 3, 423–454, https://doi.org/10.1007/s13675-016-0075-x, 2-s2.0-85014089422.
10.1007/s13675-016-0075-x
Web of Science® Google Scholar
30 Wu Z., Hu S., Luo Y., and Li X., Optimal distributed cooperative jamming resource allocation for multi-missile threat scenario, IET Radar, Sonar & Navigation. (2022) 16, no. 1, 113–128, https://doi.org/10.1049/rsn2.12168.
10.1049/rsn2.12168
Web of Science® Google Scholar

All articles

Multi-UAV Cooperative Air Combat Target Assignment Method Based on VNS-IBPSO in Complex Dynamic Environment

Abstract

1. Introduction

2. Problem Description and Modeling

2.1. Selection of Threat Assessment Factor for UAV Targets

2.1.1. Speed Threat Factor

2.1.2. Height Threat Factor

2.1.3. Distance Threat Factor

2.1.4. Angle Threat Factor

2.1.5. Radar Cross Section (RCS) Threat Factor

2.1.6. Type Threat Factor

2.2. Description of Mixed Situational Information in Treat Assessment

2.2.1. Interval Number Representation

2.2.2. Intuitionistic Fuzzy Number Representation

2.2.3. Classification Variable Representation

2.2.4. Interval-Valued Intuitionistic Fuzzy Number Representation

2.3. Construction of Multiweapon and Multitarget Allocation Model

3. Interval-Valued Intuitionistic Fuzzy Multiattribute Decision-Making-Based Dynamic Threat Assessment

3.1. Timing Weighting Model

3.2. Threat Factor Weight Optimization Model

3.3. Procedure of the Dynamic Threat Assessment

4. VNS-BPSO Algorithm for MWMTA Problem

4.1. Concept of BPSO

4.2. The Improved BPSO

4.3. VNS Operator

4.3.1. Swap Operation

4.3.2. Reverse Operation

4.3.3. Insert Operation

4.4. Implementation of VNS-IBPSO

4.5. Algorithm Complexity Analysis

4.5.1. Time Complexity Analysis

4.5.2. Spatial Complexity Analysis

5. Simulation Results and Analysis

5.1. Simulation of Target Threat Assessment

5.2. Simulation of MWMTA

5.3. Comparative Analysis

6. Conclusion

Disclosure

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information