In this article, the solutions of Bessel’s differential equations (DEs) by variable change method are formulated. To do so, we have considered the first and second kind of Bessel’s functions which are obtained as solutions of Bessel’s equations and it is used to determine the solutions of the lengthening pendulum (LP). To solve the given equations, we have used Frobenius theorem and the gamma function and hence, apply the obtained results to solve the LP. The finding reveals that Bessel’s functions establish the solutions of LP equations. The solutions obtained for lengthening the pendulum are illustrated graphically using the computer software of MathLab. The graphical results show that the sinusoidal wave natures are compressed or extended based on the chosen parameter k. Finally, it is concluded that the obtained method gives an effective, efficient, and systematic method.

1. Introduction

It has been found many important applications in the real physical world using the second order differential equations (DEs). So, many researchers have found different methods to get their solutions. Among those few of them are: finite element method [1], collocation method [2, 3], fractional differences and derivatives mittag-leffler kernels [4, 5], computational algorithm [6], reproducing kernel hilbert space (rkhs) method [7] and reduced differential transform (RDT) method [8]. Bessel’s equations are second order DEs whose solutions are very important in many applications of science and engineering. The solutions to the Bessel equations are Bessel functions. Bessel’s functions were studied by many researchers [9, 10]. Bessel’s functions are shown by using the function of zero order as a solution to the problem of an oscillating chain hanging at one end and employed Bessel’s functions of both the integral orders and zero orders in an analysis of vibrations of a stretched membrane illustrated by Niedziela [9], Musa [10], and Baricz [11]. It also arises as a result of determining separable solutions to Laplace’s equation and the Helmholtz equation in spherical and cylindrical coordinates [12]. Hence, Bessel’s functions are great important for many problems of mathematics and mathematical physics [13–15].

The first feature to be recognized as unifying the various special functions were that each one can be linked to the solution of a second order DE with none constant coefficients [10, 16]. Lengthening pendulum (LP) is a pendulum whose length increases at its motion and the length is always given as a function of time. The equation of angular motion of a LP in the form of radial is a linear second order ordinary differential equations (ODEs) [17] and it can be solved by changing to Bessel’s DE by using variable change method. The Lagrange’s work on elliptical orbits for the first time applied and noted as J_z,n and further modified to J_n(2z) [18]. Appropriate development of zeros, modified Bessel functions, and the application of boundary conditions has been briefly discussed [19]. The solutions to this equation gives the Bessel functions of first and second kinds, usually denoted by J_n(x) and Y_n(x), respectively.

For our common understanding, the LP involves some change of variables to give a relationship with the Bessel’s equation. The approximation of the first-order Bessel functions (v = 1) of both types along with their zeros are being obtained analytically with a good accuracy as a result of the appropriately chosen associated initial values, and they are extended to the neighboring orders v = 0 and 2 by the recursion relations. The required initial values are also being studied and as a result, the semi classical approximation method which is normally used for the quantum mechanical and optical waveguide systems is applied to the classical LP system successfully [14]. Bessel function is a more difficult interpretation than sinusoidal function [14, 20]. The order of the Bessel equation play a great role on the solutions of the equations and solving such equations using change of variable method with regard to the Bessel’s equation [21]. Now, it can be interesting to use the other convection method named a change of variable method to find solutions of Bessel’s DEs. So in this article, we consider change of variable method and solve the equation of angular motion of a LP using the Bessel’s DE of order k, where k is any positive real number.

2. Mathematical Formations and Preliminaries

2.1. Preliminary Terms

Definition 1. Bessel’s DE of order k is second-order ODE of the form:

()

The singular point occurs in the Bessel’s DE at x = 0. Therefore, the solution to the Bessel’s DE is based on positive values of x.

Definition 2. Bessel’s DE of order zero is the second-order ODE of the form:

()

Remark 3. Frobenius’ Theorem. If t₀ is a regular singular point of the second order DEs of the form:

()

then, there is at least one series solution at t₀ of the form:

()

This equation can be written as:

()

Consider x₀ = 0,

()

where r₁ is the larger of the two roots r₁ and r₂ of the indicial equation. The singular point occurs in the Bessel’s DEs at x₀ = 0. Therefore, our solution to the Bessel’s DE is based on positive values of x. The Frobenius series method is used to solve a second order DEs only for ordinary points or regular singular points.

Definition 4. The Gamma Function. Let z be a complex number such that Re(z) > 0 then, the gamma function (Γ) is:

()

where, z is not an integer [18].

2.2. Solution of Bessel’s DE

By using Frobenius series solution method and the gamma function, we have solutions of Bessel’s DE.

2.2.1. Bessel’s Function J_k(x) of the First Kind of Order k

Bessel’s function J_k(x) of the first kind of order n are the solution of Bessel’s DE which is finite at x = 0, for positive integer k and diverges when x approaches zero for negative noninteger k. By using the series expansion of the Bessel’s function of the first kind J_k(x) around x = 0, we can define J_k(x) in term of the gamma function as [22]:

()

2.2.2. Bessel’s Functions y_k(x) of the Second Kind of Order k

Bessel’s functions of the second kind is a solution of Bessel’s equation when k is nonintegral negative real number and is given by:

()

The series solution Equation (6) is satisfied for −k, because k occurs as square form in the Bessel equation. Then, we can substitute −k in the place of k and we have:

()

•
Asymptotic of Bessel functions

These functions are particular solutions of the Bessel equation derived from the first and the second kind of functions. The asymptotic of Bessel functions are functions of the form:

()

•
General solution of the Bessel’s equation

The general solution of this equation is the linear combination of the two independent functions J_−k and y_k of the form:

()

where c₁ and c₂ are constants and k is the order of the function.

2.3. LP

The equation of angular motion of a LP is a linear second order ODE. This equation with Newtonian mechanics is given by:

()

where a + bt is the length of the pendulum at each time t, a is initial length of the pendulum, b is constant velocity, and g is gravitational acceleration.

Equation (14) is not directly solvable. But, one may realize that it can be transformed, using a change of variables, into a Bessel equation of the form:

()

By using change of variable method, the equation of the pendulum can be changed into a Bessel equation of order one [17].

To determine the solutions of Bessel’s DEs by variable change method, we used the following algorithm of computations:

i.
Bessel’s equation and Bessel functions are defined.
ii.
Equation of angular motion of LP is stated based on physical model of the pendulum.
iii.
Changing equation of angular motion of the pendulum into Bessel’s equation by variable change method.
iv.
The equation of motion of the pendulum is changed to the Bessel’s equations by relating the coefficients of the equations.
v.
The transformed Bessel’s equations are solved by above specific method.
vi.
Finally, the transformed Bessel’s equations solutions are determined and analyzed.

3. Results and Discussion

3.1. Power Series Solution of Bessel’s DE

The power series solution with n as running index and v as an index is given by Equation (6). The only problem here is values of the coefficient a_n. So the aim of this subsection is to find the coefficients of the Bessel equation. This problem can be solved by a formula known as recurrence formula (relation). It is derived from the Bessel equation by substituted derivatives of the series solution.

()

By substituting Equations (6), (16), and (17) into Equation (1), we have:

()

Then, substitute (n − 2) for n in the second summation, it leads:

()

This leads to a recurrence relation. Then, substitute n = 0,

, (v² − k²)a₀ = −a₋₂ = 0, (v² − k²) = 0, v = k or v = −k.

Theorem 5. Bessel’s Function of the First Kind. The first kind of Bessel’s function is a solution of the Bessel equation, when k is positive and considering v = k.

Proof. Equation (20) becomes:

()

Let us see this equation for some values of n:

()

From this tabular structure, we can conclude the following general equations:

()

We can express Equation (6) as:

()

Multiplying Equation (29) by

we get:

()

Multiplying Equation (32) by

we get:

()

Since a₀ is arbitrary, it can be written as:

So Equation (33) can be reduced to:

()

By substituting Equation (34) in Equation (31), we get:

()

This is the desired equation and its asymptotic is given in Equation (11).

Corollary 6. Bessel’s function of the first kind for half integer values of k.

For , Equation (35) becomes:

Proof. Equation (35) can be written as:

()

For

, Equation (36) becomes:

()

From the properties of the gamma function, we get:

()

Then, by using the above equations, Equation (37) can be written as:

()

Then, Equation (41) becomes:

()

With the same way, we can find:

()

to get:

()

Theorem 7. Bessel’s Function of the Second Kind. Bessel’s function of the second kind is a solution of Bessel’s equation when k is nonintegral negative real number (v = −k) and is given by:

()

The series solution:

()

is satisfied for −k, because k occurs as square form in the Bessel’s equation. Then, we can substitute −k in the place of k and we have:

()

This is the second solution of Bessel’s equation of order k and its asymptotic is given by Equation (12). J_−k(x) contains negative powers of x and it is unbounded around the origin; while J_k(x) is finite and does not contain negative powers of x because both m and k are nonnegative. When k is not an integer J_k(x) and J_−k(x) are linearly independent solutions of Bessel’s DE. Therefore, the second solution is:

()

This solution can be written as:

()

which is the second independent solution known as the second kind of Bessel’s function with order k, that is,

()

where

()

Proof. When k is nonintegral:

a.
Since k is not an integer, sin(kπ) ≠ 0. In the above discussion, we have seen that J_k(x) and J_−k(x) are independent solutions and y(x) is the linear combination of J_k(x) and J_−k(x). Therefore, J_k(x) and y(x) are independent solutions of Bessel’s DE.
b.
The second kind of Bessel’s function is defined as solution of the Bessel’s equation with the following asymptotic.
()
Let
()
Equation (53) can be expressed as:
()
Since both π and k are constants, and are also constants. Therefore, Equation (54) can be written as:
()
where
()
Then, substitute Equation (56) into Equation (13) and we have:
()
As we know, the general solution is a linear combination of the first and second kinds of Bessel’s functions, which is given by:
()
where c₁ and c₂ are constants.

3.2. Changing the Equation of Angular Motion of a LP to a Bessel’s Equation

We are going to apply a simple change of variable method to solve the equation.

Theorem 8. The equation of angular motion of a LP can be changed to Bessel’s equation and hence, transformed to the equation of angular motion which has the form of Equation (14), can be changed to a Bessel’s equation of the form:

()

The equation of angular motion of a LP is given by [17]: By changing Equation (14) into a Bessel’s DE of order k as Equation (59), it is possible to express θ in terms of y, x, and t. Let

()

Then, we have:

()

Since, the coefficients of the second and the third terms of the equation of the pendulum are constants, while all the coefficients of the Bessel’s equation contains the variables x and y, it can be expressed as:

()

By using Equation (63) and the chain rule, we get:

()

and

()

Substitute Equation (65) into Equation (64), we get:

Again considering the differentiation of θ with respect to time t, we have:

()

By using the chain rule and rearranging the necessary terms of variables, we get:

()

By substituting Equation (65) into Equation (67), we have:

()

Substituting Equations (68) and (66) into Equation (14), then, we get:

()

Again, Equation (69) can be written as:

()

Since m and b are arbitrary real numbers,

can be the order of Bessel’s DE. Therefore, Equation (69) is the Bessel’s DE of order:

()

The general solution of Equation (69) is given by Equation (13).

3.3. Solution of Equation of Angular Motion of a LP

Theorem 9. Relations between coefficients of Equation (1) and (14) and variables of the equation of angular motion of the pendulum θ can be expressed in terms of y, k, and coefficients of equation of the pendulum. Again, t can be expressed by x and coefficients of the equation of the pendulum.

Proof. Substitute Equation (71) into Equation (60), we have:

()

Then, we can find y^′ at t₀. Since y is given as a function of x, not as a function of t, and applying the chain rule:

()

From Equation (60), we have:

()

Substitute Equation (79) into Equation (78), we get:

()

Therefore,

can be written as:

()

If we release our pendulum from rest, θ^′ = 0, that is,

()

Since y = θx,

()

Theorem 10. Derivatives of the First and Second Kind of Bessel’s Functions. The derivatives of Equations (10) and (11) can be found using the usual method of derivation and properties of the gamma function and is given by:

()

Proof.

()

Then, from the properties of the gamma function, we have:

()

as n → ∞, therefore,

Then, Equation (87) becomes:

()

Substitute Equation (88) into Equation (86), we get:

()

With the same process,

is given by:

()

Values of c₁ and c₂ can be taken from the general solution and its derivative using θ, t, and initial values of the equation of angular motion of a LP.

()

Then by using Equations (13) and (91) and initial values: a = 1 m, b = 0.1 m/s, g = 9.8 m/s²,

rad,

, k = 1, and assuming the pendulum starts from rest, t₀ = 0, we get:

()

where J₁ and y₁ can be calculated from the asymptotic of Bessel’s functions given in Equations (11) and (12), respectively.

()

Then, substituting Equations (95) and (94) into Equation (92), we get:

()

And from

()

we get,

()

Equate Equations (99) and (101), we get: c₁ = −706.54 and c₂ = −43.971. Then, Equation (13) becomes:

()

Again, substitute θ and t into y and x, respectively:

()

which is the required solution.

3.4. Illustrative Examples

This section contains some counter examples of solution of the equation of angular motion of a LP for fixed values of the constants and different values of k.

Example 11. Let k = 0.3 for our general solution:

()

subjected to the initial conditions:

()

By substituting the given values of a, b, and k in Equation (104), we obtain:

()

Its simplified form is:

()

Example 12. Assume k = 0.5 and the initial values are kipping as Example 11, a = 0.5 m, b = 0.1 m/s, and g = 9.8 m/s².

Then, the general solution in its simplified form becomes:

()

Example 13. Let k = 1 and keep the values of initial conditions and gravitational acceleration as Examples 11 and 12. The general solution can be simplified as:

()

Example 14. Let as consider the value of k to be large (k = 2) compared to the above examples, and a = 0.5 m, b = 0.1 m/s, and g = 9.8 m/s². Then, the general solution can be simplified as:

()

3.5. Graphical Results

Graphical results are solutions of the equations of angular motion of a LP for different values of k. These graphs clearly show the effect of k on the solution of equation of a LP, which is given by Equation (103).

Figure 1 shows the graph of the solution given in Example 11 which is the Bessel’s function whose variables y and x are changed to θ and t, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Solution of (a + bt)θ^′′ + 2bθ^′ + gθ = 0, where a = 0.5 m, b = 0.1 m/s, k = 0.3, and g = 9.8 m/s².

This graph shows the solution of:

subjected to the initial values a = 0.5 m and b = 0.1 m/s, by putting k = 0.3 and g = 9.8 m/s² for different values of t ∈ [0, 50].

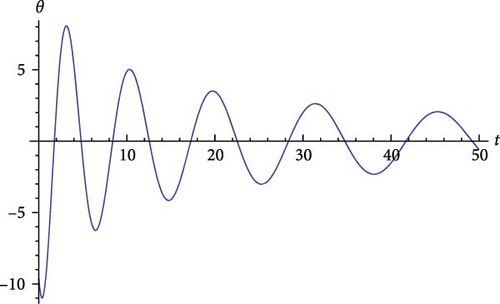
Figure 2 shows the graph of the solution given in Example 12 which is the Bessel’s function whose variables are changed to the variables of equation of a LP.

This graph shows the solution of:

subjected to the initial values a = 0.5 m and b = 0.1 m/s, by putting k = 0.5 and g = 9.8 m/s² for different values of t ∈ [0, 50].

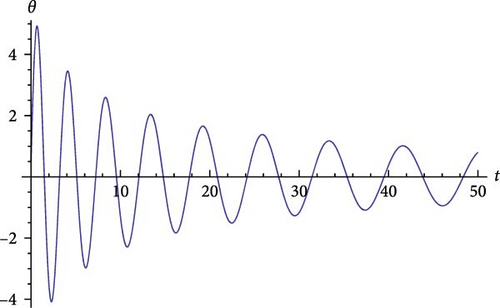
Figure 3 shows the graph of the solution given in Example 13 which is a Bessel’s function describes the motion of a LP for some initial values and a constant k.

This graph shows the solution of:

subjected to the initial values a = 0.5 m and b = 0.1 m/s, by putting k = 1 and g = 9.8 m/s² for different values of t ∈ [0, 50].

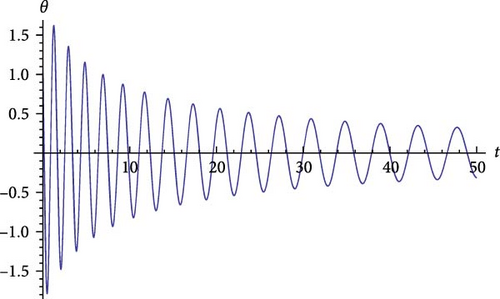
Figure 4 shows the graph of the solution given in Example 14 which is the Bessel’s function describes the motion of a LP for some initial values and the order of the Bessel’s equation.

This graph shows the solution of:

subjected to the initial values a = 0.5 m and b = 0.1 m/s, by putting k = 2 and g = 9.8 m/s² for different values of t ∈ [0, 50].

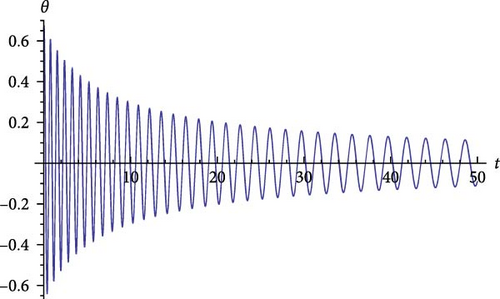
4. Conclusion

In this article, the solution of the equation of angular motion of a LP using the Bessel’s equation has been studied. The change of variable method is used to change the equation of a LP to the Bessel’s equation and the solutions of Bessel’s equation are applied to find the proposed problem. The findings show that a new method to change the equation of the motion of a LP to the Bessel’s equation using a change of variable method is clearly shown. In the results, the obtained solutions reveal that the sinusoidal wave nature type achieved in compressed and extended form. The extended or compressed form of sinusoidal wave nature depends on the parameter k. Moreover, the result of the findings are illustrative by some examples and shown graphically. Hence, the obtained result shows that the Bessel’s equations have a great advantage to find the solution of the angular motion of a LP with an effective method.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Conceptualization, methodology, software, data curation, and writing–original draft preparation: Beyalfew Anley and Daba Meshesha Gusu. Validation: Daba Meshesha Gusu and Tolosa Nigussie. Formal analysis, investigation, writing–review and editing, and visualization: Beyalfew Anley, Daba Meshesha Gusu, and Tolosa Nigussie. Supervision: Daba Meshesha Gusu. All authors have read and agreed to the final version of the manuscript.

Funding

The authors did not receive any funding to do this article.

Open Research

Data Availability Statement

Data availability is not applicable to this article as no new data were created or analyzed in this study.

References

1 Karakoc S. B. G., Numerical Solutions of the Modified KdV Equation With Collocation Method, Malaya Journal of Matematik. (2018) 6, no. 4, 835–842, https://doi.org/10.26637/MJM0604/0020.
10.26637/MJM0604/0020
Google Scholar
2 Zeybek H. and Karakoç S. B. G., Application of the Collocation Method With B-Splines to the GEW Equation, Electronic Transactions on Numerical Analysis. (2017) 46, 71–88.
Google Scholar
3 Karakoc S. B. G., Bhowmik S. K., and Gao F., A Numerical Study Using Finite Element Method for Generalized Rosenau-Kawahara-RLW Equation, Computational Methods for Differential Equations. (2019) 7, no. 3, 1–15.
Google Scholar
4 Abdeljawad T. and Baleanu D., Discrete Fractional Differences With Nonsingular Discrete Mittag-Leffler Kernels, Advances in Difference Equations. (2016) 2016, https://doi.org/10.1186/s13662-016-0949-5, 2-s2.0-84986325930, 232.
10.1186/s13662-016-0949-5
Web of Science® Google Scholar
5 Baleanu D. and Fernandez A., On Some New Properties of Fractional Derivatives With Mittag-Leffler Kernel, Communications in Nonlinear Science and Numerical Simulation. (2018) 59, 444–462, https://doi.org/10.1016/j.cnsns.2017.12.003, 2-s2.0-85037530829.
10.1016/j.cnsns.2017.12.003
Web of Science® Google Scholar
6 Abu Arqub O., Computational Algorithm for Solving Singular Fredholm Time-Fractional Partial Integro Differential Equations With Error Estimates, Journal of Applied Mathematics and Computing. (2019) 59, no. 1-2, 227–243, https://doi.org/10.1007/s12190-018-1176-x, 2-s2.0-85044035451.
10.1007/s12190-018-1176-x
Web of Science® Google Scholar
7 Abu Arqub O. and Rashaideh H., The RKHS Method for Numerical Treatment for Integrodifferential Algebraic Systems of Temporal Two-Point BVPs, Neural Computing and Applications. (2018) 30, no. 8, 2595–2606, https://doi.org/10.1007/s00521-017-2845-7, 2-s2.0-85009752547.
10.1007/s00521-017-2845-7
Web of Science® Google Scholar
8 Gusu D. M., Wegi D., Gemechu G., and Gemechu D., Fractional Order Airy’s Type Differential Equations of Its Models Using RDTM, Mathematical Problems in Engineering. (2021) 2021, 3719206.
10.1155/2021/3719206
Google Scholar
9 Niedziela J., Bessel Functions and Their Applications, 2008, University of Tennessee-Knoxville.
Google Scholar
10 Musa S. S., Unpublished Doctoral Dissertation, 2016, Near East University.
Google Scholar
11 Baricz A., Generalized Bessel Functions of the First Kind, 2010, Springer.
10.1007/978-3-642-12230-9
Google Scholar
12 Marin L. and Karageorghis A., Regularized Mfc-Based Boundary Identification in Two Dimensional Helmholtz-Type Equations, Computers, Materials & Continua (CMC). (2009) 10, no. 3, 259–294.
Google Scholar
13 Ki F. and Abubakar A., Solving Bessel Differential Equation of Collocation Approx, Research Journal of Mathematical and Stat. (2019) 7, no. 2, 21–26.
Google Scholar
14 Deniz C., On the JWKB Solution of the Uniformly Lengthening Pendulum via Change of Independent Variable in the Bessel’s Equation, Pramana—Journal of Physics. (2017) 88, no. 1, 2–18, https://doi.org/10.1007/s12043-016-1319-2, 2-s2.0-85009183819.
10.1007/s12043-016-1319-2
Google Scholar
15 Trench W. F., Elementary Differential Equations With Boundary Value Problems, 2013, Trinity University.
Google Scholar
16 Dattoli G., Giannessi L., Mezi L., and Torre A., Theory of Generalized Bessel Functions, Il Nuovo Cimento B. (1990) 105, no. 3, 327–348, https://doi.org/10.1007/BF02726105, 2-s2.0-51649152123.
10.1007/BF02726105
Google Scholar
17 McMillan M., Blasing D., and Whitney H. M., Radial Forcing and Edgar Allan Poe’s Lengthening Pendulum, American Journal of Physics. (2013) 81, no. 9, 682–687, https://doi.org/10.1119/1.4816241, 2-s2.0-84882615289.
10.1119/1.4816241
Google Scholar
18 Garcia M. E., Bessel Functions and Equations of Mathematical Physics, 2016, The University of the Basque Country.
Google Scholar
19 Karma S. M., A Dissection of Bessel Functions and Application to Solutions of Schroedinger Time Independent Equation in Cylindrical and Spherical Well, 2017, Near East University.
Google Scholar
20 Asadi-Zeydabadi M., Bessel Function and Damped Simple Harmonic Motion, Journal of Applied Mathematics and Physics. (2014) 2, no. 4, 26–34, https://doi.org/10.4236/jamp.2014.24004.
10.4236/jamp.2014.24004
Google Scholar
21 Finot C., Chaussard F., and Boscolo S., Impact of a Temporal Sinusoidal Phase Modulation on the Optical Spectrum, European Journal of Physics. (2018) 39, no. 5, https://doi.org/10.1088/1361-6404/aad61c, 2-s2.0-85053118897, 055303.
10.1088/1361-6404/aad61c
Web of Science® Google Scholar
22 Hoque M. F. and Roshid H. O., Optical Soliton Solutions of the Biswas-Arshed Model by the tan(⊝/2) Expansion Approach, Physica Scripta. (2020) 95, no. 7, 075219.
10.1088/1402-4896/ab97ce
CAS Google Scholar

All articles

Solutions of Bessel’s Differential Equations by Variable Change Method

Abstract

1. Introduction

2. Mathematical Formations and Preliminaries

2.1. Preliminary Terms

2.2. Solution of Bessel’s DE

2.2.1. Bessel’s Function J_k(x) of the First Kind of Order k

2.2.2. Bessel’s Functions y_k(x) of the Second Kind of Order k

2.3. LP

3. Results and Discussion

3.1. Power Series Solution of Bessel’s DE

3.2. Changing the Equation of Angular Motion of a LP to a Bessel’s Equation

3.3. Solution of Equation of Angular Motion of a LP

3.4. Illustrative Examples

3.5. Graphical Results

4. Conclusion

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Solutions of Bessel’s Differential Equations by Variable Change Method

Abstract

1. Introduction

2. Mathematical Formations and Preliminaries

2.1. Preliminary Terms

2.2. Solution of Bessel’s DE

2.2.1. Bessel’s Function Jk(x) of the First Kind of Order k

2.2.2. Bessel’s Functions yk(x) of the Second Kind of Order k

2.3. LP

3. Results and Discussion

3.1. Power Series Solution of Bessel’s DE

3.2. Changing the Equation of Angular Motion of a LP to a Bessel’s Equation

3.3. Solution of Equation of Angular Motion of a LP

3.4. Illustrative Examples

3.5. Graphical Results

4. Conclusion

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information

2.2.1. Bessel’s Function J_k(x) of the First Kind of Order k

2.2.2. Bessel’s Functions y_k(x) of the Second Kind of Order k