Compressive sampling matching pursuit (CoSaMP), as a conventional algorithm requiring system sparsity and sensitive to step size, was improved in this paper by approximating the sparsity with adaptive variable step size. In the proposed algorithm (CoSaMP with variable step size abbreviated as Vss-CoSaMP), the idea of approximating sparsity with adaptive step size was borrowed from the sparsity adaptive matching pursuit (SAMP) algorithm to determine the sparsity for the CoSaMP algorithm. The applicability of the CoSaMP algorithm was therefore expanded considerably. On this basis, a step size reduction was added as the iteration termination condition of an orthogonal frequency division multiplexing (OFDM) system. An adaptive variable step size algorithm was then put forward to address the CoSaMP algorithm’s sensitivity to step size. It could realize the required precision at different initial step sizes. A simulation was carried out to analyze the influence of pilot number and step size in an OFDM system on the algorithm. The algorithms, including SAMP, CoSaMP, and Vss-CoSaMP, were compared with two sparse channels, revealing that the Vss-CoSaMP algorithm overcame the problem of the CoSaMP algorithm, that is, the impossibility to forecast the channel sparsity. With the adaptive step size, the proposed algorithm could reach and achieve better accuracy than the CoSaMP algorithm. Additionally, the proposed algorithm was superior over the SAMP algorithm in terms of reconstruction, mean square error (MSE), and bit error ratio (BER).

1. Introduction

Orthogonal frequency division multiplexing (OFDM), as an underwater acoustic communication technique, has become a hot topic in the underwater acoustic communication field because of its advantages including good resistance to multipath interference, robustness to frequency selective interference, and high bandwidth utilization [1–6]. The design of an OFDM receiver often needs the information of channel status, which is practically difficult to collect. It is therefore very important to explore the channel estimation and equalization technique as the compensation for the underwater acoustic channel distortion in an OFDM system. The underwater data transmission is often troubled by sparse multipath fading channels. Multiple paths are normally identifiable. If channel sparsity is fully utilized, channel estimation will be more accurate. Compressive sensing is one of the main methods taken in sparse channel estimation [7–11]. Greedy algorithm delivers the fastest reconstruction among compressive sensing algorithms [12–16]. As a greedy algorithm, sparsity adaptive matching pursuit (SAMP) [17–20] is most favored since it uses step size to gradually approximate channel sparsity K. Therefore, the sparsity of signals is not needed beforehand for the system. However, the SAMP algorithm may cause underestimation or overestimation. Compressive sampling matching pursuit (CoSaMP) [21–24] is an improved orthogonal matching pursuit (OMP) algorithm, and it is very effective for both sparse and common signals. In channel estimation, it still needs channel sparsity, which is practically impossible to gather. This paper intends to put forward a more effective algorithm by combining the advantages of such two algorithms.

Hence, the structure of this paper is arranged as follows: the first part takes the CoSaMP algorithm as the basis and describes how to address the problem of sparsity for the CoSaMP algorithm by borrowing the idea of approximating sparsity with step size from the SAMP algorithm. On this basis, a step size reduction is added as the iteration termination condition for the algorithm. An adaptive variable step size algorithm is therefore proposed to develop the CoSaMP with variable step size (Vss-CoSaMP) algorithm. It can further resolve the problem of sensitivity to fixed step size for the CoSaMP algorithm.

The second part presents a simulation in three steps. The influence of pilot number is first analyzed. Subsequently, the influence of step size on the convergence of the algorithm is analyzed. The sensing algorithms are compared in terms of performance in the end, so as to verify the superiority of the proposed Vss-CoSaMP algorithm.

2. OFDM System Model With Underwater Acoustic Channel

An underwater acoustic OFDM system is presented in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

An underwater acoustic OFDM system.

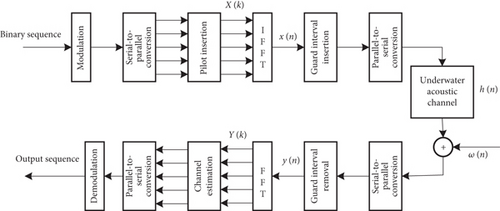
Information bits are modulated and mapped into symbols. The constellation symbols obtained by quadrature amplitude modulation (QAM) are used to convert the serially transmitted signal into the parallel transmitted signal. After pilot insertion, X(k) is obtained. The signal is subsequently treated by inverse fast Fourier transform, guard interval insertion, and parallel-to-serial conversion. The signal received by the receiver is processed in inverse transformations to obtain the frequency domain received signal Y(k).

The frequency domain signal between the receiver and the transmitter is represented by

(1)

where X is the diagonal element matrix of N × N dimensions with the signals obtained after inserting the pilot frequency, F is the fast Fourier transform matrix of N × L dimensions, Y is the frequency domain received signal of N × 1 dimensions, H is the frequency domain channel response of N × 1 dimensions, h is the time domain channel response of L × 1 dimensions, and W is the Gaussian white noise of N × 1 dimensions.

Under normal circumstances, underwater acoustic channels are time-varying sparse multipath channels. Compared with the total length of data frame, each OFDM data block lasts for a short time. Therefore, the time delay of paths is regarded to be linear [2].

For this reason, the sparse underwater acoustic channel impact response can be expressed by

(2)

where K is the number of paths, i.e., the sparsity of the channel; h_k indicates the gain of the k^th path; δ(⋅) is the Kronecker delta function; and τ_k is the delay of the k^th path.

It is assumed that B is a P × N selection matrix used to locate P pilots from the OFDM signal containing N subcarriers. Thus, the pilot signal at the receiver can be expressed by

(3)

where Y_p = BY is the vector of P × 1, X_p = BXB^T is the P × P matrix, F_p = BF is the P × L matrix, and W_p = BW is the vector of P × 1. At the signal receiver, Y_p, X_p, and F_p are all known. In the channel estimation based on the compressive sensing algorithm, such three known values are used to estimate the channel impact response vector h.

3. Principles of the Algorithms

3.1. SAMP Algorithm for Underwater Acoustic Channel Estimation

SAMP keeps the atomic selection principle of the matching pursuit algorithm. It is greatly distinguished from other matching pursuit algorithms by being adaptive.

The procedure of the SAMP core algorithm is as given in Algorithm 1.

Algorithm 1: Procedure of the SAMP core algorithm.

Input: Sensing matrix A (M × N dimensions), sampling vector y, signal-noise ratio i, step size S;
Output: Approximation of K-sparsity to the unknown channel impact response h;
Initialize:
(Initialize the column vector for saving estimations)
F₀ = ∅ (Initialize the support set to save the column serial numbers of the selected sensing matrix)
r₀ = y (Initialize the residual error as the sampling vector)
L = S (Initialize the size of the support set as the step size of initial input)
j = 1 (Initialize the step size expansion counter)
k = 1 (Initialize the subscript)
IterMax = M (Determine the maximum number of iterations)
Repeat
S_k = max(|A^′∗r_k−1|, L) (Select and save the subscripts of L values with the largest inner product)
C_k = F_k−1 ∪ S_k (Expand the candidate set)
(Obtain and save the subscripts of L values with the largest least squares solution)
(Obtain the residual error of this iteration)
if iteration termination condition tol is satisfies,
break the loop
else if
j = j + 1 (The support set is expanded by 1)
L = j × S (Expand the support set)
else
F_k = G (Update the support set)
r_k = r (Update the residual error)
k = k + 1
end
until the iteration termination condition is satisfied or the maximum number of iterations is reached
Output:

The SAMP algorithm utilizes step size to gradually approximate the sparsity K, so that the system does not require the sparsity of signal beforehand. This greatly expands the applicability of the reconstruction algorithm, since it is often impossible to determine the sparsity of system or signal beforehand in practice.

3.2. CoSaMP Algorithm for Underwater Acoustic Channel Estimation

CoSaMP is a classical greedy algorithm put forward by Needell and Tropp in 2008 [21]. As an improved OMP algorithm, it is very effective for both sparse and common signals. However, it still needs channel sparsity beforehand in practical channel estimation. The procedure of the CoSaMP algorithm is presented in Algorithm 2.

Algorithm 2: Procedure of the CoSaMP algorithm.

Input: Sensing matrix A (M × N dimensions), sampling vector y, signal-noise ratio i, sparsity K;
Output: Approximation of K-sparsity to the unknown channel impact response h;
Initialize:
(Initialize the column vector for saving restorations)
F = ∅ (Initialize the support set to save the column serial numbers of the selected sensing matrix)
r = y (Initialize the residual error as the sampling vector)
IterMax = K (Determine the maximum number of iterations)
Repeat
Js = max(|A^′∗r|, 2K) (Select and save the subscripts of 2K values with the largest inner product)
Is = F ∪ Js (Expand the candidate set)
(Take the subscripts of K values with the largest least squares solution, remove the redundant atoms from the candidate set, and update the support set)
(Obtain the residual error of this iteration, and update the residual)
if Iteration termination condition tol is satisfies,
break the loop
end
until the iteration termination condition is satisfied or the maximum number of iterations is reached
Output:

The CoSaMP algorithm borrows the idea of combined algorithms to guarantee its speed. With its strict restriction over error, the signal is very accurately reconstructed. Meanwhile, compressed measurement signal y often exists with noise. In other words, there is noise interference apart from y = Φx, so that we have y = Φx + e, where e is the noise. Compared with other greedy reconstruction algorithms, the CoSaMP algorithm has stronger resistance to noise interference. However, as revealed in the procedure of its core algorithm, the CoSaMP algorithm needs the input of signal sparsity. The number of selected atoms is determined by sparsity K × 2. In practice, it is impossible to obtain the sparsity of system or signal beforehand, so that the applicability of the CoSaMP algorithm is significantly limited.

The SAMP algorithm is adaptive, so that it can reconstruct a signal by gradually approximating the unknown sparsity. Thus, it can effectively resolve the problem of unknown sparsity. Nevertheless, fixed step size plays a significant role in the reconstruction accuracy and efficiency of the SAMP algorithm. When the step size is too small, it may realize high accuracy, but at an unbearable cost of time (underestimation). When the step size is too large, the support set may exceed the sparsity K, resulting in overestimation. Reconstruction is not satisfying in both cases.

3.3. Proposed Algorithm for Underwater Acoustic Channel Estimation

Considering the advantages and disadvantages of the SAMP and CoSaMP algorithms, an improvement is proposed from two approaches:

1.
Improving the CoSaMP algorithm based on the SAMP algorithm

In this approach, the idea of approximating sparsity with step size is borrowed from the SAMP algorithm to address the problem of sparsity for the CoSaMP algorithm, so as to greatly expand the applicability of the CoSaMP algorithm.

2.
Eliminating the influence of fixed step size on the SAMP algorithm by introducing variable step size

The SAMP algorithm is affected by fixed step size; thus, the idea of variable step size is introduced in this paper. In this idea, step size varies adaptively. As for the SAMP algorithm, the step size can be increased by s or s/2 when the candidate set is expanded. In this case, good accuracy of reconstruction can be achieved regardless of different step sizes. After the initial step size is input into the improved algorithm, that is, Vss-CoSaMP, it can be adaptively reduced to achieve gradual approximation.

The Vss-CoSaMP algorithm is compared with the CoSaMP algorithm as shown in Table 1.

Table 1. Differences between the CoSaMP algorithm and the Vss-CoSaMP algorithm.

Step	CoSaMP algorithm	Vss-CoSaMP algorithm
1	Input: Sensing matrix A (M × N dimensions), sampling vector y, signal-noise ratio (SNR) i, step size K	Input: Sensing matrix A (M × N dimensions), sampling vector y, SNR i, step size S;
2	Initialize , F, r, IterMax	Initialize , F₀, r₀, L, k, IterMax
3	Calculate the inner products of sensing matrix and residual error, select the subscripts with the maximum values of 2K term to expand the candidate set (2K term)	No difference (2L term)
4	Calculate the least squares solution for signal approximation, and select the subscripts with the maximum values of K term to remove the redundant atoms from the candidate set	No difference
5	Update the support set for signal approximation	No difference
6	Update the residual error	No difference
7	Judge the iteration termination condition. If satisfied, break the iteration loop. If not, the number of iterations increases by 1, and enter Step 3	Judge the iteration termination condition. If satisfied, break the iteration loop. If not, enter Step 8
8	None	Judge the step size reduction condition. If satisfied, S = S/2
9	None	Judge whether it satisfies . If satisfied, L = L + S/2, or start the next iteration
10	Output	No difference

The Vss-CoSaMP algorithm is compared with the SAMP and CoSaMP algorithms as follows:

1.
Procedure of the Vss-CoSaMP algorithm. As shown in Table 1, the initial step size is first input to start the iteration. A step size reduction condition is then set. If satisfied, the step size is reduced by half, that is, S = S/2. The condition for expanding the support set in the SAMP algorithm is introduced into the algorithm. If satisfied, the support set is expanded to L = L + S/2. If not, it is still L. However, if the condition for step size reduction is not satisfied, L changes as it does in the SAMP algorithm.
2.
Determine the condition for termination of iteration tol. Based on the sparsity of the configured channel, the optimal reconstruction is achieved by constantly changing the number of iterations. With the number of iterations for the optimal reconstruction, the final values of at different signal-noise ratios (SNRs) are obtained. The variation of with the SNR is observed to fit a trend line equation as the condition for termination of iteration for the algorithm. The condition for termination of iteration is adjusted with the simulation curve of the trend line equation.

In this paper, the simulation is conducted under two underwater acoustic channels with a sparsity of 4 and 10, respectively. The trends of the condition for termination of iteration tol in Step 7 of the Vss-CoSaMP algorithm in Table 1 are obtained as shown in Figures 2(a) and 2(b). Based on the trend curves, the constant terms in the polynomial are adjusted. Thus, the condition for termination of iteration tol of the Vss-CoSaMP algorithm with two sparsities is determined to be and , respectively.

Iteration termination condition plays a significant role in the reconstruction performance of the algorithm. If the precision of the condition is set too high, it is impossible to break the loop during each iteration. Therefore, the algorithm is forced to have the maximum number of iterations, which takes much time. More clutter signals are caused to significantly undermine the reconstruction performance of the algorithm. Reconstruction may even fail. In this paper, the iteration termination condition tol of the algorithm is established for the OFDM system model, and it is particularly applicable in this case.

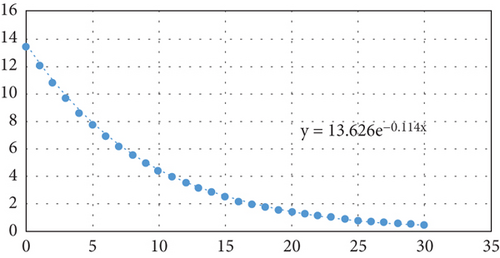
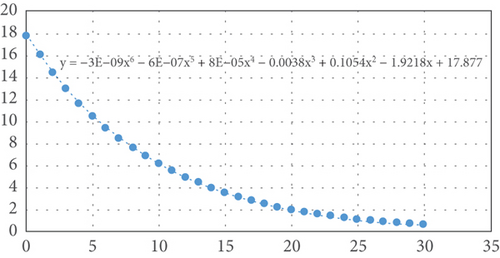
3.
Determine the condition for reduction of step size. As discovered in the simulation, the value of the condition for termination of iteration tol is decreasing within a range. When the condition for reduction of step size is larger, the step size of the Vss-CoSaMP algorithm will be reduced earlier, and it is easier to achieve the reconstruction accuracy as good as the CoSaMP algorithm. When the condition for reduction of step size is smaller, the algorithm will satisfy the condition for reduction of step size later, which may easily cause overestimation and make it difficult to achieve the intended effect. Moreover, the value of the condition for termination of iteration tol is reduced fast in the early stage, but such reduction slows down in the late stage. Considering the influence of time and accuracy, the median value is taken as the value of the condition for reduction of step size for the algorithm. After all, the condition for reduction of step size in the simulation of two underwater acoustic channels with a sparsity of 4 and 10 is set as and , respectively.

4. Experimental Analysis and Comparison

4.1. Influence of System Pilot Number on the Performance of Algorithms

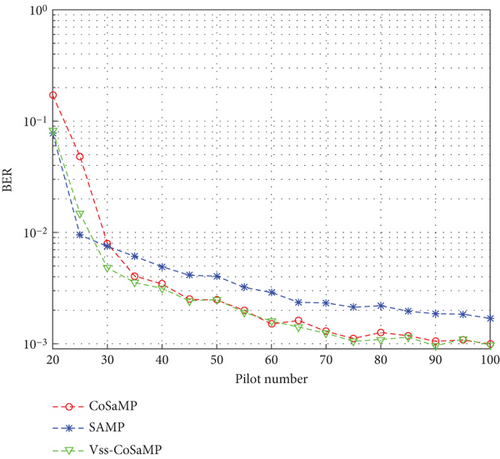
In the simulation, the channel noise of the system was white Gaussian noise with SNR = 18 dB. The pilot interval was 5. There were 256 subcarriers in total. The signal was treated by QAM. The fixed step size of SAMP was S = 4, and the sparsity of simulated channel was K = 4. The input of CoSaMP was K = 4. The initial step size of Vss-CoSaMP was S₀ = 4. The mean square error (MSE) and bit error ratio (BER) curves of three algorithms varied with the pilot number within a value range of [20, 100] as illustrated in Figures 3 and 4, respectively.

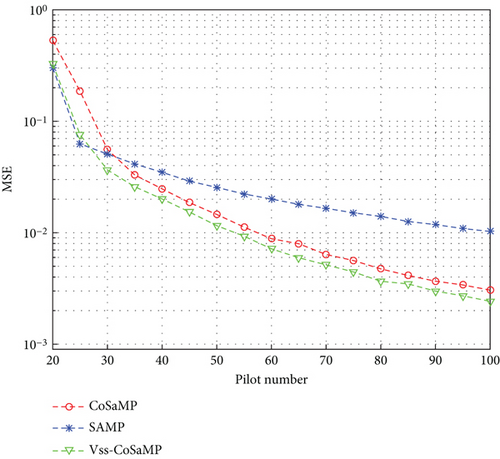
As revealed in Figure 3, the MSE in three algorithms decreases with the increase of the pilot number. This variation is more noticeable in the CoSaMP and Vss-CoSaMP algorithms, revealing their better performance than the SAMP algorithm. It is noted that the SAMP algorithm has better MSE than the CoSaMP algorithm in the beginning. After the pilot number reaches 30, the CoSaMP algorithm clearly surpasses the SAMP algorithm in terms of MSE. During the value range of the pilot number, the Vss-CoSaMP algorithm always has a better MSE than the CoSaMP algorithm.

The comparison of Figures 3 and 4 reveals the similar variation tendency of BER and MSE curves in such three algorithms. The Vss-CoSaMP algorithm has a better BER than the CoSaMP algorithm.

4.2. Influence of Step Size on the Performance of Algorithms

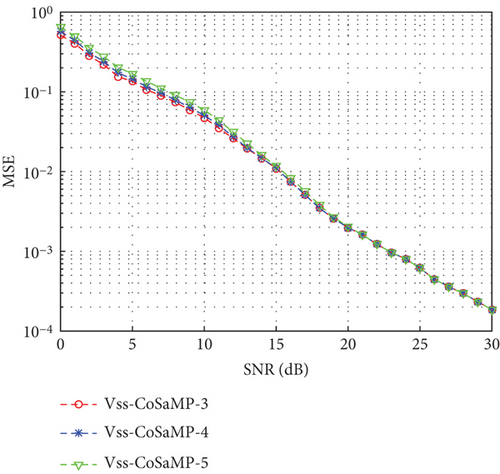
In the simulation, the pilot number was 100 with the other conditions as given in Figure 3. The fixed step size of the SAMP algorithm was S = 3, 4, 5. The initial step size of the Vss-CoSaMP algorithm was S₀ = 3, 4, 5. The performance curves of the SAMP algorithm and the proposed Vss-CoSaMP algorithm are as given in Figures 5 and 6, respectively.

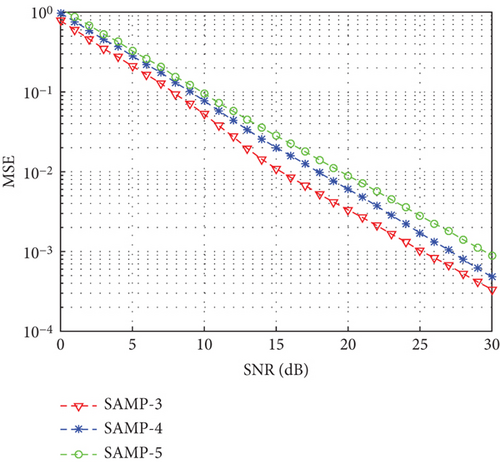
As shown in Figure 5, the MSE curves of the SAMP algorithm with different step sizes differ significantly from each other within the range of SNR. When the SNR does not change, but the step size increases from 3 to 5, the MSE of the algorithm increases gradually. In other words, the increasing step size causes lower reconstruction accuracy of the SAMP algorithm. Hence, overestimation occurs when the step size of the SAMP algorithm increases. This must be attributed to the principles followed by the SAMP algorithm. When the step size is 1, the SAMP algorithm has the highest accuracy, but higher requirements for time. When the step size is too large, the efficiency is great, but the reconstruction accuracy is unacceptable. In practice, the step size must be determined in terms of both time and accuracy.

In Figure 6, the MSE curves of the Vss-CoSaMP algorithm with different initial step sizes basically coincide with each other. It means that the Vss-CoSaMP algorithm can adjust to the variation of step size to some extent. When the step size varies within a certain range, it has very little influence on the reconstruction accuracy.

After comparing such two figures, it is found that the proposed Vss-CoSaMP algorithm resolves the problem of accuracy variation with different fixed step sizes for the SAMP algorithm. In other words, the Vss-CoSaMP algorithm allows a wide range of step size while ensuring the satisfying accuracy.

4.3. Performance Comparison of Sensing Algorithms

The simulation conditions are the same as indicated in Figure 5. When the sparsity of the underwater acoustic channel is K = 4, the fixed step size of the SAMP algorithm is s = 4, the sparsity of the CoSaMP algorithm is K = 4, and the initial step size of the Vss-CoSaMP algorithm is S₀ = 4. The sparsity of underwater acoustic channel is adjusted to K = 10, but other simulation parameters remain unchanged. The sparsity of the CoSaMP algorithm is K = 10, the fixed step size of the SAMP algorithm is s = 8, and the initial step size of the Vss-CoSaMP algorithm is S₀ = 8. The BER variation curves of the OFDM system with the SNR for the three algorithms are illustrated in Figure 7.

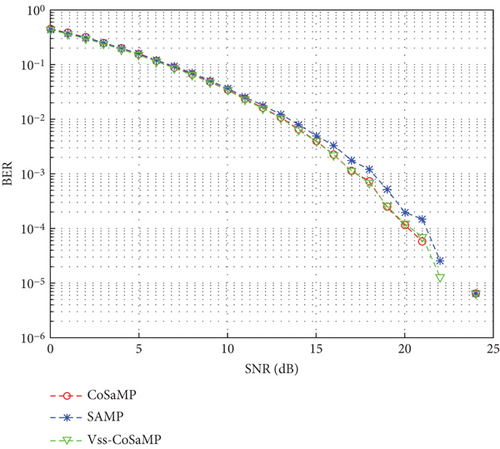
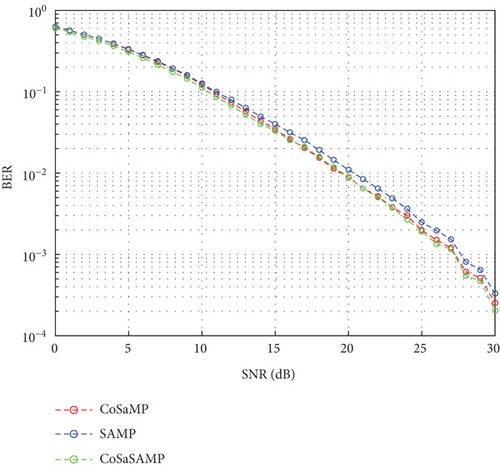
4.3.1. Performance Comparison in Terms of BER

As revealed in Figure 7(a), the BER of the three algorithms is basically consistent within the SNR range of 0–12 dB. Starting from SNR = 13 dB, the CoSaMP algorithm and the Vss-CoSaMP algorithm have better BER than the SAMP algorithm. The curves of the CoSaMP algorithm and the Vss-CoSaMP algorithm basically coincide with each other. As shown in Figure 7(b), starting from SNR = 3 dB, the CoSaMP algorithm and the Vss-CoSaMP algorithm have better BER than the SAMP algorithm. Evidently, the Vss-CoSaMP algorithm and the CoSaMP algorithm have equivalent accuracy when BER is taken as an indicator for measuring the performance of the algorithms.

Meanwhile, the comparison of Figures 7(a) and 7(b) reveals that when the sparsity is K = 4, the BER of the Vss-CoSaMP algorithm is 0.1408, 0.0369, 0.0033, and 1.9231e − 04 for 5 dB, 10 dB, 15 dB, and 20 dB; and the SNR of the Vss-CoSaMP algorithm is 0.3031, 0.1106, 0.0360, and 0.0085 for 5 dB, 10 dB, 15 dB, and 20 dB. It is evident that the BER of the algorithms improves with the increase of the sparsity when the simulation conditions remain unchanged.

4.3.2. Performance Comparison in Terms of MSE

The simulation conditions are the same as given in Figure 7. The performance curve of three algorithms varied with the SNR in terms of MSE as shown in Figure 8.

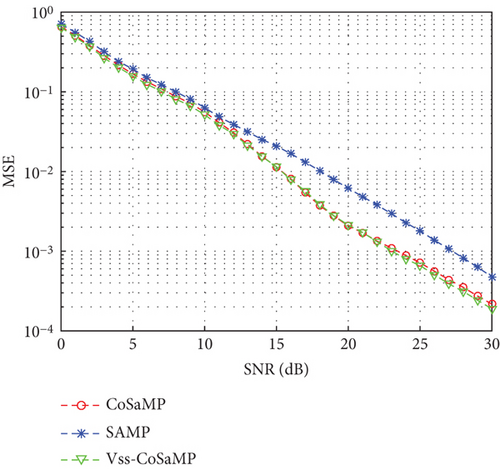
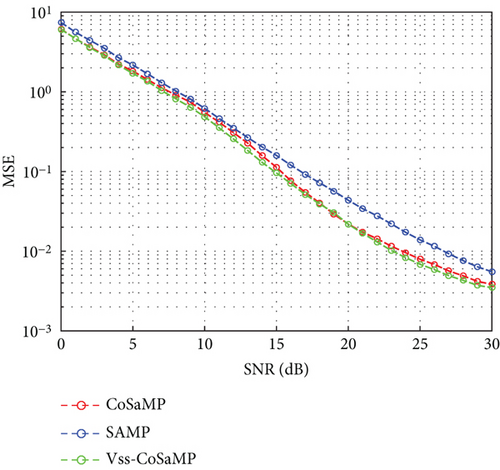
As illustrated in Figure 8, the Vss-CoSaMP and CoSaMP algorithms have a better MSE than the SAMP algorithm within the SNR range of 0–30 dB. When the SNR is 12 dB, the difference between them is more noticeable. The MSE curve of the Vss-CoSaMP algorithm basically coincides with that of the CoSaMP algorithm. The Vss-CoSaMP algorithm has a slightly better MSE than the CoSaMP algorithm.

After analyzing Figures 7 and 8, it is found that the Vss-CoSaMP algorithm can predict channel sparsity beforehand, and adaptive step size enables it to be as accurate as or even more accurate than the CoSaMP algorithm.

4.4. Channel Impact Response Reconstruction Comparison of Three Algorithms

The sparsity of underwater acoustic channel was K = 8. The sparsity of the CoSaMP algorithm was K = 8. The fixed step size of the SAMP algorithm was S = 8. The initial step size of the Vss-CoSaMP algorithm was S₀ = 4. The SNR was 20. The inserted pilot number was 100. The impact response of three algorithms is illustrated in Figure 9.

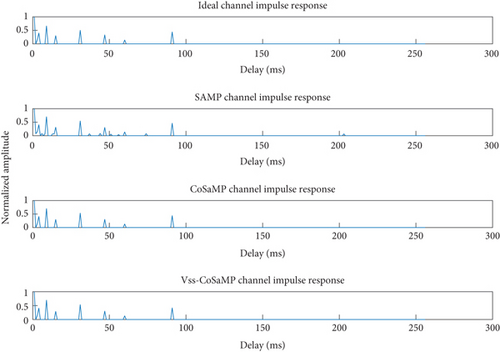
After analyzing Figure 9, it is found that the CoSaMP and Vss-CoSaMP algorithms can more satisfactorily reconstruct a channel than the SAMP algorithm compared with the ideal channel. The impact response of the channel reconstructed by the SAMP algorithm is troubled by lots of interference responses at 0–100 ms. The impact response of the channel reconstructed by the CoSaMP and Vss-CoSaMP algorithms is basically identical to the impact response of the ideal channel. It is evidently concluded that the Vss-CoSaMP algorithm delivers better reconstruction than the SAMP algorithm with the input step size of 4.

5. Conclusion

This paper presents a sparse channel estimation method for an underwater acoustic OFDM system, that is, CoSaMP-based sparse channel estimation algorithm with adaptive variable step size (Vss-CoSaMP). Compared with the CoSaMP algorithm, the proposed Vss-CoSaMP algorithm does not require system sparsity beforehand, so as to expand its practical applicability. Moreover, it borrows the idea of variable step size to overcome the SAMP algorithm’s sensitivity to initial step size, so that it can ensure the satisfying accuracy with different step sizes. Experiments have been carried out to statistically determine the iteration termination condition and variable step size condition suitable for the OFDM system. As proved in the performance comparison in terms of MSE and BER, the Vss-CoSaMP algorithm is superior in resolving the problems of sparsity and sensitivity to step size.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Xiaoling Ning designed the research. Xiaoling Ning and Yangyi Chen processed the data. Xiaoling Ning drafted the manuscript. Yangyi Chen helped in organizing the manuscript. Xiaoling Ning, Yangyi Chen, and Zhang Linsen revised and finalized the paper.

Funding

This study was funded by the National Natural Science Foundation of China (61671461), a project of Naval University of Engineering Independent Research Fund (2022507126).

Open Research

Data Availability Statement

Data will be made available upon request to the corresponding author.

References

1 Tadayon A. and Stojanovic M., Low-complexity superresolution frequency offset estimation for high data rate acoustic OFDM systems, IEEE Journal of Oceanic Engineering. (2019) 44, no. 4, 932–942, https://doi.org/10.1109/JOE.2018.2869657, 2-s2.0-85054651356.
10.1109/JOE.2018.2869657
Web of Science® Google Scholar
2 Zeping S., Shefeng Y., and Guopeng L., Variable step size p-norm-like constraint sparse underwater acoustic channels estimation method, Acta Acustica. (2021) 46, no. 5, 664–676, https://doi.org/10.15949/j.cnki.0371%2D0025.2021.05.003.
10.15949/j.cnki.0371-0025.2021.05.003
Google Scholar
3 Yanling Y. I. N., Gang Q., Songzuo L., and Feng Z., Sparse channel estimation of underwater acoustic orthogonal frequency division multiplexing based on basis pursuit denoising, Acta Physica Sinica. (2015) 64, no. 6, article 064301, https://doi.org/10.7498/aps.64.064301, 2-s2.0-84925865125.
10.7498/aps.64.064301
Web of Science® Google Scholar
4 Tadayon A. and Stojanovic M., Iterative Sparse channel estimation and spatial correlation learning for multichannel acoustic OFDM systems, IEEE Journal of Oceanic Eugineering. (2019) 44, no. 4, 820–836, https://doi.org/10.1109/JOE.2019.2932662, 2-s2.0-85071698073.
10.1109/JOE.2019.2932662
Web of Science® Google Scholar
5 Qing C., Wang L., Dong L., and Wang J., Enhanced ELM-based channel estimation for RIS-assisted OFDM systems with insufficient CP and imperfect hardware, IEEE Communications Letters. (2021) 26, no. 1, 153–157, https://doi.org/10.48550/arXiv.2110.13433.
10.1109/LCOMM.2021.3123736
Web of Science® Google Scholar
6 Qing C., Dong L., and Wang L., Joint model and data-driven receiver design for data-dependent superimposed training scheme with imperfect hardware, IEEE Transactions on Wireless Communications. (2021) 21, no. 6, 3779–3791, https://doi.org/10.1109/TWC.2021.3123948.
10.1109/TWC.2021.3123948
Web of Science® Google Scholar
7 Wang J. J., Yan Z. Q., Shi W., and Yang X., Underwater acoustic sparse channel estimation based on DW-SACoSaMP reconstruction algorithm, IEEE Communications Letters. (2019) 23, no. 11, 1985–1988, https://doi.org/10.1109/LCOMM.2019.2933426.
10.1109/LCOMM.2019.2933426
Web of Science® Google Scholar
8 Jayanthi P. N. and Ravishankar S., Model-based compressed sensing algorithms for MIMO- OFDM channel estimation, Engineering & Technology. (2018) 7, no. 2.4, 5–9, https://doi.org/10.14419/ijet.v7i2.4.10030, 2-s2.0-85043485802.
10.14419/ijet.v7i2.4.10030
Google Scholar
9 Chen Q., Su S. Q., and Lei G. W., Channel estimation based on compressive sensing for multi-user massive MIMO systems, Journal of Physics: Conference Series. (2021) 1865, no. 4, article 042057, https://doi.org/10.1088/1742%2D6596/1865/4/042057.
10.1088/1742-6596/1865/4/042057
Google Scholar
10 Huang Y., HE YG H. E. W., Shi W., Cheng T., and Sui Y., Channel estimation in massive MIMO systems based on generalized block adaptive matching pursuit algorithm, IEEE Wireless Communications Letters. (2020) 9, no. 12, 2098–2101, https://doi.org/10.1109/LWC.2020.3013689.
10.1109/LWC.2020.3013689
CAS Web of Science® Google Scholar
11 Zhiguo L. and Ying L., Compressed sensing-based Bayesian channel estimation algorithm, Journal of Xidian University. (2018) 45, no. 2, https://doi.org/10.3724/SP.J.1004.2011.01413, 2-s2.0-84862941628.
10.3724/SP.J.1004.2011.01413
Google Scholar
12 Hong F. and Yang H., Greedy algorithms and compressed sensing, Acta Automatic Sinica. (2011) 37, no. 12, 1413–1421.
Google Scholar
13 Donoho D. L., Compressed sensing, IEEE Transactions on Information Theory. (2006) 52, no. 4, 1289–1306, https://doi.org/10.1109/TIT.2006.871582, 2-s2.0-33645712892.
10.1109/TIT.2006.871582
Web of Science® Google Scholar
14 Donoho D. L. and Tsaig Y., Extensions of compressed sensing, Signal Processing. (2006) 86, no. 3, 533–548.
Web of Science® Google Scholar
15 Baraniuk R., Compressive sensing [lecture notes], IEEE Signal Processing Magazine. (2007) 24, no. 4, 118–121, https://doi.org/10.1109/MSP.2007.4286571, 2-s2.0-85032751965.
10.1109/MSP.2007.4286571
Web of Science® Google Scholar
16 Blumensath T. and Davies M. E., Iterative hard thresholding for compressed sensing, Applied and Computational Harmonic Analysis. (2009) 27, no. 3, 265–274, https://doi.org/10.1016/j.acha.2009.04.002, 2-s2.0-69949164527.
10.1016/j.acha.2009.04.002
Web of Science® Google Scholar
17 Do T. T., Lu G., Nam N., and Trac D., Sparsity adaptive matching pursuit algorithm for practical compressed sensing, 2008 42nd Asilomar Conference on Signals, Systems and Computers, 2008, Pacific Grove, CA, USA, https://doi.org/10.1186/s13638%2D018%2D1085%2D6, 2-s2.0-85045309788.
10.1186/s13638-018-1085-6
Google Scholar
18 Yao S. H., Guan Q. F., Wang S., and Xie X., Fast sparsity adaptive matching pursuit algorithm for largescale image reconstruction, EURASIP Journal on Wireless Communications and Networking. (2018) 78, no. 1, 1–8, https://doi.org/10.1186/s13638%2D018%2D1085%2D6, 2-s2.0-85045309788.
10.1186/s13638-018-1085-6
Google Scholar
19 Wang Y. H., Peng Y. L., Liu S. G., Li J., and Wang X. L., Sparsity adaptive matching pursuit for face recognition, Journal of Visual Communication and Image Representation. (2020) 67, no. C, article 102764, https://doi.org/10.1016/j.jvcir.2020.102764.
10.1016/j.jvcir.2020.102764
Web of Science® Google Scholar
20 Song S. Z., Zhang X., Hao Q. S., Wang Y., Feng N. Z., and Shen Y., An improved reconstruction method based on auto-adjustable step size sparsity adaptive matching pursuit and adaptive modular dictionary update for acoustic emission signals of rails, Measurement. (2009) 189, https://doi.org/10.1016/j.acha.2008.07.002, 2-s2.0-62749175137.
10.1016/j.acha.2008.07.002
Google Scholar
21 Needell D. and Tropp J. A., CoSaMP: iterative signal recovery from incomplete and inaccurate samples, Applied and Computational Harmonic Analysis. (2019) 26, no. 3, 301–321, https://doi.org/10.1109/LCOMM.2019.2933426.
10.1016/j.acha.2008.07.002
Google Scholar
22 Hemant S. G., Jignesh N. S., and Fahad A., A review on image reconstruction using compressed sensing algorithms: OMP, CoSaMP and NIHT, International Journal of Image, Graphics and Signal Processing. (2019) 9, no. 8, 30–41, https://doi.org/10.4236/jcc.2019.76002.
10.4236/jcc.2019.76002
Google Scholar
23 Lu D. X., Sun G. L., Li Z. Z., and Wang S. J., Improved CoSaMP reconstruction algorithm based on residual update, Journal of Computer and Communications. (2019) 7, no. 6, 6–14, https://doi.org/10.4236/jcc.2019.76002.
10.4236/jcc.2019.76002
Google Scholar
24 Zhang L., Image reconstruction based on compressive sensing via CoSaMP, Applied Mechanics and Materials. (2014) 631-632, 436–440, https://doi.org/10.4028/www.scientific.net/AMM.631%2D632.436, 2-s2.0-84914121218.
10.4028/www.scientific.net/AMM.631-632.436
Google Scholar

All articles

A Sparse CoSaMP Channel Estimation Algorithm With Adaptive Variable Step Size for an OFDM System

Abstract

1. Introduction

2. OFDM System Model With Underwater Acoustic Channel

3. Principles of the Algorithms

3.1. SAMP Algorithm for Underwater Acoustic Channel Estimation

3.2. CoSaMP Algorithm for Underwater Acoustic Channel Estimation

3.3. Proposed Algorithm for Underwater Acoustic Channel Estimation

4. Experimental Analysis and Comparison

4.1. Influence of System Pilot Number on the Performance of Algorithms

4.2. Influence of Step Size on the Performance of Algorithms

4.3. Performance Comparison of Sensing Algorithms

4.3.1. Performance Comparison in Terms of BER

4.3.2. Performance Comparison in Terms of MSE

4.4. Channel Impact Response Reconstruction Comparison of Three Algorithms

5. Conclusion

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Sparse CoSaMP Channel Estimation Algorithm With Adaptive Variable Step Size for an OFDM System

Abstract

1. Introduction

2. OFDM System Model With Underwater Acoustic Channel

3. Principles of the Algorithms

3.1. SAMP Algorithm for Underwater Acoustic Channel Estimation

3.2. CoSaMP Algorithm for Underwater Acoustic Channel Estimation

3.3. Proposed Algorithm for Underwater Acoustic Channel Estimation

4. Experimental Analysis and Comparison

4.1. Influence of System Pilot Number on the Performance of Algorithms

4.2. Influence of Step Size on the Performance of Algorithms

4.3. Performance Comparison of Sensing Algorithms

4.3.1. Performance Comparison in Terms of BER

4.3.2. Performance Comparison in Terms of MSE

4.4. Channel Impact Response Reconstruction Comparison of Three Algorithms

5. Conclusion

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information