Inter-Phase Magnetic Resonance Tech Research Group (IPhy-MRTRG) , 5th Floor Student Centre , @iLabAfrica , Strathmore University , P.O. Box 59857-00200 City Square, Nairobi , Kenya , strathmore.edu

Search for more papers by this author

E. Jobunga,

Corresponding Author

E. Jobunga

[email protected]

orcid.org/0000-0002-2998-7131

Department of Mathematics and Physics , Technical University of Mombasa , P. O. Box 90420-80100, Mombasa , Kenya , tum.ac.ke

Search for more papers by this author

K. Warui,

K. Warui

orcid.org/0009-0006-5911-3298

Department of Mathematics and Physics , Technical University of Mombasa , P. O. Box 90420-80100, Mombasa , Kenya , tum.ac.ke

Search for more papers by this author

B. Menge,

B. Menge

orcid.org/0009-0005-6070-8793

Department of Mathematics and Physics , Technical University of Mombasa , P. O. Box 90420-80100, Mombasa , Kenya , tum.ac.ke

Search for more papers by this author

E. Mugambi,

E. Mugambi

orcid.org/0009-0000-9485-6050

Department of Mathematics and Physics , Technical University of Mombasa , P. O. Box 90420-80100, Mombasa , Kenya , tum.ac.ke

Search for more papers by this author

B. Dillmann,

B. Dillmann

orcid.org/0000-0003-4498-5780

Inter-Phase Magnetic Resonance Tech Research Group (IPhy-MRTRG) , 5th Floor Student Centre , @iLabAfrica , Strathmore University , P.O. Box 59857-00200 City Square, Nairobi , Kenya , strathmore.edu

Search for more papers by this author

First published: 19 September 2024

https://doi.org/10.1155/2024/8881003

Citations: 2

Academic Editor: Mariano Torrisi

Share a link

Email
Wechat
Bluesky

Abstract

Motion of a projectile in the absence of any resistive medium is quite ideal and has an exact analytical solution in classical mechanics. Ordinarily, projectiles move in a resistive medium which modify the acceleration of the body both in the horizontal and vertical directions. So far, the time of flight and the range arising from the solution of the classical problem due to the presence of a linear velocity-dependent resistive force are not exact and can only be determined numerically. In this work, we attempt to solve the problem analytically. We resolve the underlying difficulty in the analytical problem by deriving an analytical function which guides the dynamics of the projectile and by calculating iteratively the falling time as a function of the maximum height reached. We show that the effect of the viscous drag force in the time of flight of the projectile may lead to time asymmetry in the upward and downward motion, reduced maximum height reached, time of flight, and range for any initial launching speed. The downward motion is established to take more time than the upward motion. We obtain excellent agreement between the calculated values and the computed trajectories.

1. Introduction

A projectile can be defined simply as any flying object. Examples of projectiles include a ball kicked at an angle of elevation or a bullet fired in space. Projectile motion has been well studied from antiquity by prominent scientists like Aristotle, Galileo, Euler, Newton, and several others. A historical development of the subject is well discussed in literature [1, 2]. The motion of a projectile in the absence of any resistive medium is quite ideal and has an exact analytical solution in classical mechanics. Ordinarily, projectiles move in a resistive medium which modify the acceleration of the body both in the horizontal and vertical directions, leading to variations in the maximum height reached, time of flight, and the range of the projectile. An accurate description of these dynamical variables in projectile motion in a medium is still a subject of research and pedagogical interest.

The relationship between the drag force and velocity of the object moving in the drag medium is not precisely known [3]. The science of modeling drag in aerodynamics is considered to be more physical and empirical than mathematical, and it relies on the results of the wind tunnel experiments [4]. The linear dependence of the drag force on velocity is universally accepted as the first approximation of the drag force which, under some circumstances, yields results which agree quite well with observations [5]. Empirically, a linear dependent drag force predicts experiments better at relatively low velocities. At very high velocities, however, the linear drag model fails and better results follow the quadratic velocity dependence [6–10]. A gap is therefore created at intermediate velocities which is neither described by the linear or quadratic drag laws. Also, certain aspects of the projectile dynamics remain unclear. For example, calculations derived from both linear and quadratic drag laws predict drag-induced time and space asymmetries which require experimental verification. These uncertainties can be removed if there is a better agreement between theory and experiment.

So far, the time of flight and the range arising from the solution of the classical problem due to the presence of the linear drag are not exact and can only be determined approximately because of the presence of transcendental equations [5, 11–15]. A few semianalytical solutions have been suggested though [14, 16], expressing the time of flight and the range in terms of Lambert functions, or using the method of trajectories in phase space [17], but these still need further numerical techniques to completely solve the related dynamical problems. Timmerman and van der Weele [18] attempted a completely analytical solution for a projectile launched vertically upwards under both linear and quadratic drag. In their solution, the time of flight for the projectile under quadratic drag could be solved exactly, while for linear drag, it could only be estimated approximately. Even within the linear drag model, there are still outstanding questions to be answered in the description of projectile motion. For example, it may be of interest to know if there is a disparity between an exact analytical solution and a numerical solution for the time of flight and the range of the projectile [14].

In this study, we have attempted an analytical approach in the solution of the problem by focussing specifically on the linear drag model. The effects of the quadratic drag, aerodynamic lift, upthrust, and wind drift have been ignored, although we recognize that they may have significant effects at high launching speeds. We resolve the underlying difficulty in the analytical problem by constraining the falling time as a function of the maximum height reached and consequently using the calculated time to determine the terminal speed in the vertical projection. We observe that the time taken to reach the maximum height, the maximum height reached, the time of flight, and the range are reduced as expected. We show that the trajectory is asymmetric both in time and in the horizontal displacement, where the time taken to reach the maximum height is less than the time taken to get back to the same initial vertical position from the maximum height reached; that is, it takes less time to go up than to come down. Conversely, the range is bigger on the upward trajectory than on the downward trajectory. We have also obtained an exact iterative formula for the time of flight which is in excellent agreement with the computational trajectories. The accuracy of the calculated results can be adjusted by increasing the number of iterations in the calculation of the falling time.

2. Theory

From Newton’s second law, the resultant force on a projectile moving in a resistive medium with a linear retarding force can be expressed as

(1)

(2)

(3)

where β is the coefficient of the linear resistive force, assuming that upthrust and lift forces are negligible. These three equations describe different aspects of the projectile motion connected in time. Equation (1) describes the horizontal projection, Equation (2) describes the upward vertical projection, and Equation (3) describes the downward motion. In the upward motion, 0 ≤ t₁ ≤ τ₁ and t = t₁, while on the downward motion, 0 ≤ t₂ ≤ τ₂ and t = τ₁ + t₂. The total time of flight, defined as the time taken by the projectile to return back to the initial vertical position, is given by τ = τ₁ + τ₂. By inspection of Equations (1)–(3), it can be seen that the resistive force introduces a time-dependent acceleration both in the x-direction and y-direction.

Solving the ordinary differential equations given by Equations (1)–(3) yield

(4)

(5)

(6)

as the components of the velocity vector with v₀, α, and k = β/m as the initial speed, the projection angle of the projectile, and the mass-scaled drag coefficient, respectively.

Considering that at the maximum height reached, v_y(t₁ = τ₁) = v_y(t₂ = 0) = 0. We find that

(7)

and the time taken to reach the maximum height can be given by

(8)

Likewise, at the time of flight (τ), using the terminal speed, v_τ(τ₂), reached by the projectile, we obtain

(9)

The displacement of the projectile at any time t, obtained by integrating the components of the velocity vector with respect to time, can be expressed as

(10)

(11)

(12)

By substituting Equation (10) into Equation (11), the vertical displacement at any time can be expressed in terms of x as [16]

(13)

At the maximum displacements, x_max = x(τ) and y_max = y(τ₁) = y(τ₂), Equations (10)–(12) simplify to

(14)

(15)

(16)

where we have substituted Equations (7) and (9), respectively, into Equations (11) and (12) and then simplified. At the time of flight (τ), the vertical displacement

(17)

is zero. This yields the expression of the time of flight

(18)

in terms of v_τ. Starting from the unretarded time of free fall and using the Taylor expansion for v_τ, we have shown in the Appendix that

(19)

and therefore

(20)

must be true for any arbitrary medium.

However, from Equations (14) and (15), respectively, it can be shown that

(21)

(22)

leading to a condition that τ₁ = τ₂ if v_τ = v₀sinα − 2ky_max or if k = 0.

If, on the other hand, τ₁ ≠ τ₂, then

(23)

for the time asymmetric case, where we have used (v₀sinα − v_τ) = ε. If ε < 0, the dynamics contradicts the condition set by Equation (19). This imposes a condition that ε > 0, and hence, 0 ≤ v_τ ≤ v₀sinα − 2ky_max for τ₁ ≥ τ₂ and v₀sinα − 2ky_max ≤ v_τ ≤ v₀sinα for τ₁ ≤ τ₂.

We have observed and shown analytically in Equation (A.6) in the Appendix section that

(24)

is a constraint, connecting the launching speed and the terminal speed. The dimensionless number, 0 ≤ λ ≤ 2, which relates the momentum transferred to the fluid with the drag coefficient, k, is linearly proportional to the Reynolds number. As a first approximation, we established (by taking the statistical average of the momentum loss) that λ ≈ 1 yields physically meaningful results, for which the theoretical range calculations are in fairly good agreement with the computed trajectory. The constraint implies that τ₁ ≤ τ₂. This constraining condition is consistent with the law of conservation of momentum, with the second term of Equation (24) quantifying the velocity lost to the resistive medium.

In a bid to simplify the relations given by Equations (10)–(12) further, the vertical displacement at any time t can alternatively be given by

(25)

where an infinite series expansion and a further simplification of Equation (11) have been used (see the derivation in Equations (A.1) and (A.2) in the Appendix) and with t₁ = t, and

(26)

being a k- and time-dependent parameter. If k = 0, γ = 1/2 as expected in an unretarded case. We have analyzed the infinite series expansion of γ(k, t) and established that it can be represented by the analytical function

(27)

which reduces to 1/2 if k = 0. This function is quite stable at any arbitrary launching speed and for any value of k. The explicit derivation of Equation (27) is shown in Equations (A.1)–(A.4) in Appendix A.

In calculating τ₂, we recognize that for the unresisted projectile,

(28)

and using a mean field approximation of γ(k, τ₂), we get

(29)

for the infinitely resisted projectile, where we have defined

(30)

as the time for the unresisted fall from y_max. Using these as the constraints for any arbitrary value of k, we can determine

(31)

iteratively using

as the initial condition. This iteration ensures that the limiting values for τ₂ are reproduced. In our work, only five iterations have been used to reproduce a reasonably accurate value of τ₂, but smaller values of k or v₀sinα require only fewer iterations. The terminal speed v_τ can consequently be calculated using Equation (9). Equations (29) and (31) have been determined by simplifying Equation (12). Having determined τ₁ using Equation (8) and τ₂ iteratively using Equation (31), the time of flight τ can consequently be obtained as

(32)

and the range using Equation (10).

3. Results

We have analyzed the projectile motion under linear drag forces analytically and compared our results with numerically generated data. The major challenge with the numerical description of projectile motion under linear drag is that the relations for time of flight and the range are functions of the transient time leading to transcendental equations. In our analytical treatment, we solve the ordinary differential equations by accounting for energy dissipation by the drag forces using Equation (24), with λ as the dimensionless number. The time of flight is calculated accurately by determining the falling time τ₂ iteratively using Equation (31). Using the time of flight calculated, the range is consequently determined. Our calculations are then compared with numerical values in the computed trajectory of the projectile. All calculations and computations reported in this work have been done using a Python code.

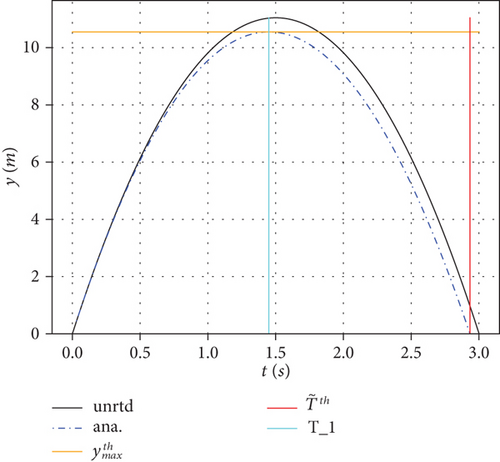
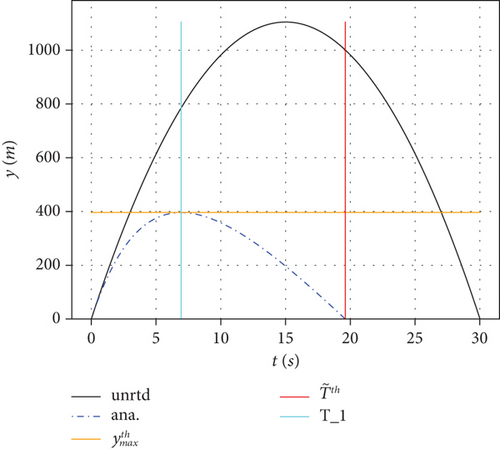
To allow for comparison with works already reported in literature, we chose to use a projectile with an initial velocity of 170 m/s projected at an angle of inclination of 60° to the horizontal axis, and k ≈ 0.047, as reported in ref. [2]. We have also included results for one-tenth of the initial velocity (17 m/s) and results for k = 0.2, corresponding to a projectile whose mass is approximately a twentieth of the original mass in the same medium of propagation. Our results have been calculated theoretically and computationally. The results are summarised in Table 1 and in Figures 1, 2, 3, and 4. The theoretical calculations, based on the formulas outlined in Section 2, are presented in Table 1. τ₀ is the time of flight for the unresisted trajectory, is the drag-free natural time corresponding to the maximum height reached under drag, τ₁ is the time taken to reach the maximum height for the resisted trajectory, τ₂ is the time taken from the maximum height to the range, x₀ is the range for the unresisted motion, τ = τ₁ + τ₂ is a time of flight with τ₁ calculated exactly using Equation (8), and τ₂ is calculated iteratively using Equation (31). The dimensionless number λ has been determined using Equation (24). is the calculated range using Equation (14). x(τ₁) is the horizontal distance covered at the maximum height reached calculated also using Equation(14). Likewise is the maximum height reached calculated using Equation (15). In the table, time is in specified seconds while distance is in metres.

Table 1. Flight data for a projectile launched at 60° for different values of speed under the action of a linear drag force. The drag coefficient is fixed at two values specified in the table. The time taken to reach the maximum height, the time of flight, the range, and the maximum height reached are calculated for both the unretarded and retarded motion. The dimensionless number λ has been determined using Equation (24).

v₀ (m/s)	k(s⁻¹)	τ₀		τ₁	τ₂	τ	λ	x (τ₁)	x₀		y₀
17	0.047	3.00	1.46	1.45	1.48	2.93	1.31	11.91	25.51	23.29	11.04	10.55
170	0.047	30.01	12.46	11.35	13.80	25.16	1.23	748.02	2551.28	1254.34	1104.74	761.96
170	0.2	30.01	8.96	6.93	12.63	19.56	1.15	318.79	2551.28	416.51	1104.74	394.40

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

(Color online) Convergence of the numerical and analytical trajectories for a projectile launched at 170 m per second with an angle of inclination of 60° as the distribution function series γ(k, t) is truncated at different values of n_max as expressed in Equation (26). The corresponding analytical function (in blue dash dot line) is given by Equation (27). The coefficient k = 0.047 has been chosen to match the data given by Figure 2 of ref. [2].

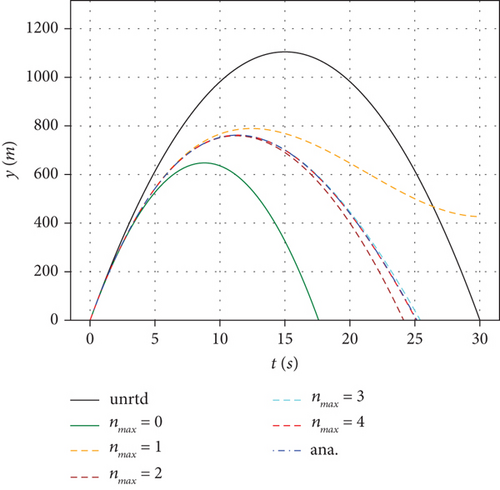
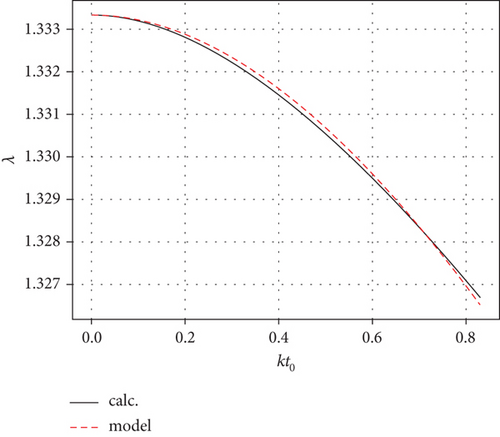
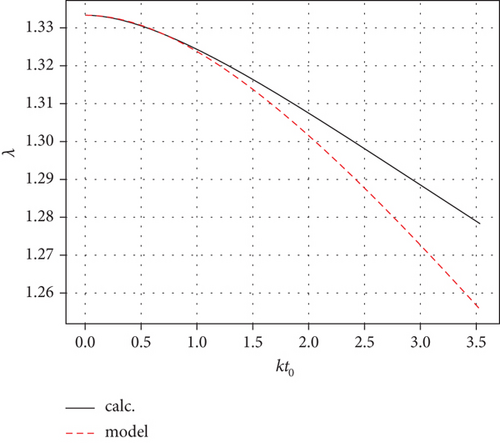
In Figure 1, we show the convergence of the computational trajectory evaluated using a numerical and analytical γ(k, t) distribution functions given by Equations (26) and (27) for different values of n_max. It can be seen that for the chosen projectile parameters, n_max = 4 (as shown in Figure 1) is sufficient for full convergence, and a choice of a smaller n_max may lead to divergence like for the case of n_max = 1 as shown in Figure 1. For higher orders of numerical expansion, it is expected that the numerical and the analytical functions of γ(k, t) be in excellent agreement. This condition has been satisfied in our work for the highest order chosen. We therefore did not find it necessary to go beyond n_max = 5. Also, having verified the performance of the analytical function γ(k, t) in Figure 1, it has consequently been used in all our results.

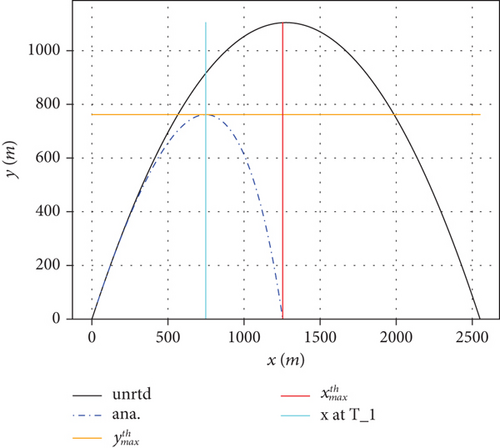
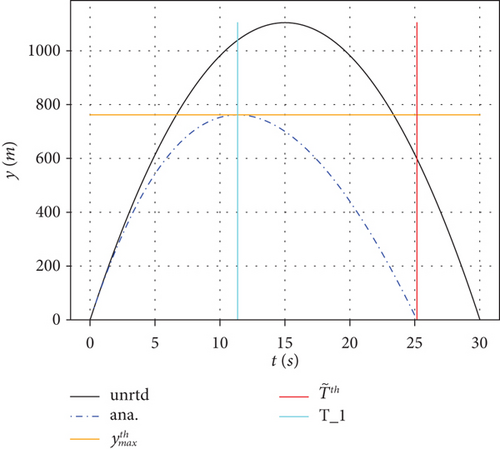
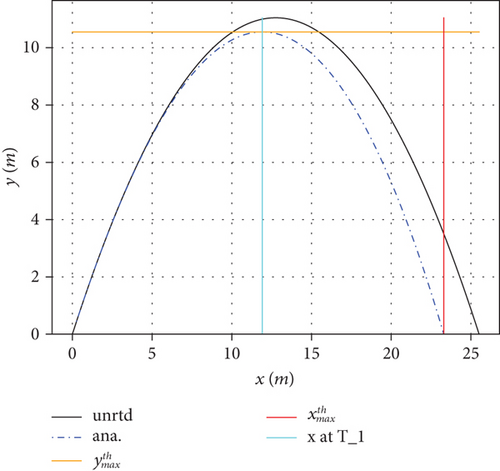
In Figures 2, 3, and 4, we compare the corresponding results with set (a) displaying the trajectories in the y − x plane and set (b) displaying the trajectories in the y − t plane, respectively. In the figures, the black solid line corresponds to the unresisted projectile while the blue dash dot line corresponds to the analytical trajectory (with γ(k, t) given by Equation (27)). The thin solid horizontal and vertical lines correspond to the calculated values for the maximum height reached, (orange); horizontal displacement at maximum height, x at τ₁ (cyan); and range, (red), in Figure 2(a) or time at maximum height, τ₁ (cyan), and time of flight, (red), in Figure 2(b) correspondingly.

As expected, and as observed from the results presented, the linear drag acting on the projectile reduces the time of flight, the maximum height reached, and the range. Equations (8), (31), and (32) have been used to calculate the time of flight. Computationally, the displacements in the x and y directions have been evaluated as functions of time t as shown in the trajectories in Figures 2, 3, and 4. The computations utilize the function γ(k, t) defined analytically using Equation (27). In the figures, we have also plotted our theoretical calculations for the range (x_max), the maximum height reached (y_max), and the time of flight (τ), evaluated using Equations (10), (14), (25), and (32), respectively, for comparison with the values in the trajectories.

It can be seen from the figures that our theoretical and computational results are in excellent agreement with each other for all the dynamical parameters used in this work. The accuracy relies so much on the number of iterations used in Equation (31). In Figures 2 and 3, only two iterations were sufficient to generate an accurate time of flight, but in Figure 4, five iterations were used. This shows that the number of iterations required for accurate results increases with the launching speed v₀ and the drag parameter k.

In general, just as observed in ref. [18], our results show that the time taken to fall down is actually more than the time taken to rise upwards in all the cases that we have considered. This can be phenomenologically explained using the fact that in the upward trajectory, the deceleration is higher than the gravitational value leading to , while on the downward trajectory, the acceleration is less than the gravitational value for the same distance travelled leading to as presented in Table 1. So, the projectile naturally takes more time to fall than to rise up as determined by the linear drag-induced time asymmetry, .

It is observed that the effect of linear drag is diminished at lower launching speeds and also at lower values of k, while at higher launching speeds and at higher values of k, the effect is magnified. Experimental observations, on the other hand, show that even at higher speeds, the deviation of the projectile from the trajectory of the unresisted motion is not very large [2]. This shows that at higher launching speeds, the effects of other forces, which are unaccounted for by the linear drag model, may become significant. A more inclusive model therefore becomes necessary to account for the discrepancy with the experimental observations.

In Figure 5, we have calculated λ parameter iteratively against kt₀, where t₀ = (v₀sinα)/g, using Equations (9), (24), and (31) for different values of k used in this study. We observe that λ decreases monotonically with kt₀. To analyze the functional dependence of λ, we used a fitting function

(33)

where sinc(x) = (sinx)/x and the parameter δ = 1/3 yields a suitable fit. The model function agrees reasonably well with the calculated results within the regime kt₀ ≤ 1.0 as can be seen in Figures 5(a) and 5(b). For kt₀ > 1.0, the model breaks down and is no longer valid, and consequently, an iterative or computational technique must therefore be used to determine the exact value of λ. Within the regime of validity of the model funtion, the terminal speed, the falling time τ₂, the time of flight τ, and the range of the projectile under linear drag force can consequently be estimated accurately without resorting to the iterative treatment used in the calculated results.

4. Conclusion

In this study, we have attempted an analytical approach in the classical solution of the projectile motion problem under a linear velocity-dependent drag force. We show that the time of flight, and consequently the range, can be calculated accurately through iteration. The accuracy obtained in our work rests on the analytically derived distribution function γ(k, t) and the number of iterations used in Equation (31). We observe that the time taken to reach the maximum height, the maximum height reached, the time of flight, and the range are reduced as compared to an unretarded motion. We show that the time of flight and the range are asymmetric. That is, it takes less time to go up than to come down. On the contrary, part of the range covered in the upward trajectory is more than the part covered in the downward trajectory. The y − t graph is therefore peaked to the left while the y − x graph is peaked to the right.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors received no specific funding for this work.

Appendix A

Expanding Equation (11), in terms of t, using the Taylor series expansion of the exponential term and simplifying to get

(A.1)

where we have defined

(A.2)

as an analytic function in an infinite series expansion as expressed in Equation (26).

In deriving the exact analytical form of Equation (A.2), it can be seen that

(A.3)

where we have used x = −kt. Imposing the constraint

(A.4)

From Equation (9), the terminal speed

(A.5)

can be expanded using the Taylor series as

(A.6)

satisfying the inequality v_τ ≤ v₀sinα with equality only for k = 0. Using the definition of γ(k, t) in Equation (A.4), it can be shown that the infinite series expansion converges analytically to

(A.7)

Open Research

Data Availability Statement

All the data generated in the work are embedded as figures in the manuscript.

References

1 Clayton M. E., An investigation of air resistance on projectile motion from Aristotle to Euler, [Ph.D. thesis], 2012, Theses Digitization Project.
Google Scholar
2 Hackborn W. W., On motion in a resisting medium: a historical perspective, American Journal of Physics. (2016) 84, no. 2, 127–134.
10.1119/1.4935896
Google Scholar
3 Symon K. R., Mechanics, 1953, Addison Wesley, Reading, MA.
Web of Science® Google Scholar
4 Long L. N. and Weiss H., The velocity dependence of aerodynamic drag: a primer for mathematicians, The American Mathematical Monthly. (1999) 106, no. 2, 127–135, https://doi.org/10.1080/00029890.1999.12005019.
10.1080/00029890.1999.12005019
Google Scholar
5 Erlichson H., Maximum projectile range with drag and lift, with particular application to golf, American Journal of Physics. (1983) 51, no. 4, 357–362, https://doi.org/10.1119/1.13248, 2-s2.0-0000569710.
10.1119/1.13248
Google Scholar
6 Parker G. W., Projectile motion with air resistance quadratic in the speed, American Journal of Physics. (1977) 45, no. 7, 606–610, https://doi.org/10.1119/1.10812, 2-s2.0-84967802570.
10.1119/1.10812
Web of Science® Google Scholar
7 Hayen J. C., Projectile motion in a resistant medium, International Journal of Non-Linear Mechanics. (2003) 38, no. 3, 357–369, https://doi.org/10.1016/S0020-7462(01)00067-1, 2-s2.0-0037374887.
10.1016/S0020-7462(01)00067-1
Google Scholar
8 Hayen J. C., Projectile motion in a resistant medium part II: approximate solution and estimates, International Journal of Non-Linear Mechanics. (2003) 38, no. 3, 371–380, https://doi.org/10.1016/S0020-7462(01)00068-3, 2-s2.0-0037374880.
10.1016/S0020-7462(01)00068-3
Google Scholar
9 Hackborn W. W., Projectile motion: Resistance is fertile, Canadian Applied Mathematics Quarterly. (2008) 115, no. 9, 813–819, https://doi.org/10.1080/00029890.2008.11920595.
10.1080/00029890.2008.11920595
Google Scholar
10 Hackborn W. W., Projectile motion: resistance is fertile, The American Mathematical Monthly. (2006) 14.
Google Scholar
11 Groetsch C. W., Tartaglia’s inverse problem in a resistive medium, The American Mathematical Monthly. (1996) 103, no. 7, 546–551, https://doi.org/10.1080/00029890.1996.12004784.
10.1080/00029890.1996.12004784
Google Scholar
12 Charles W., Halley′s comment—projectiles with linear resistance, Mathematics Magazine. (1997) 70, no. 4, 273–280, https://doi.org/10.1080/0025570X.1997.11996553.
10.1080/0025570X.1997.11996553
Google Scholar
13 Douglas Gregory R., Classical Mechanics, 2012, Cambridge University Press, New York.
Google Scholar
14 Seán M., An analytic approach to projectile motion in a linear resisting medium, International Journal of Mathematical Education in Science and Technology. (2006) 37, no. 4, 411–431, https://doi.org/10.1080/00207390600594911, 2-s2.0-33751087488.
10.1080/00207390600594911
Google Scholar
15 Pakdemirli M. and Aksoy Y., Determining the velocities and angles for a free kick problem, Canadian Journal of Physics. (2015) 93, no. 11, 1434–1438, https://doi.org/10.1139/cjp-2015-0274, 2-s2.0-84945419501.
10.1139/cjp-2015-0274
CAS Google Scholar
16 Warburton R. D. H. and Wang J., Analysis of asymptotic projectile motion with air resistance using the Lambert W function, American Journal of Physics. (2004) 72, no. 11, 1404–1407, https://doi.org/10.1119/1.1767104, 2-s2.0-8744230858.
10.1119/1.1767104
Web of Science® Google Scholar
17 Morales C. A., Muñoz J. H., and Vera C. E., Some remarks on projectile motion with a linear resistance force, European Journal of Physics. (2023) 44, no. 6, article 065003, https://doi.org/10.1088/1361-6404/acf0a5.
10.1088/1361-6404/acf0a5
Google Scholar
18 Timmerman P. and van der Weele J. P., On the rise and fall of a ball with linear or quadratic drag, American Association of Physics Teachers. (1999) 67, no. 6, 538–546, https://doi.org/10.1119/1.19320, 2-s2.0-0033407885.
10.1119/1.19320
Google Scholar

Citing Literature

All articles

Analytical Solution of the Projectile Motion Under a Linear Drag Force

Abstract

1. Introduction

2. Theory

3. Results

4. Conclusion

Conflicts of Interest

Funding

Appendix A

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analytical Solution of the Projectile Motion Under a Linear Drag Force

Abstract

1. Introduction

2. Theory

3. Results

4. Conclusion

Conflicts of Interest

Funding

Appendix A

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information