Holomorphism and Edge Labeling: An Inner Study of Latin Squares Associated with Antiautomorphic Inverse Property Moufang Quasigroups with Applications
Abstract
Taking into account the most recent improvements in graph theory and algebra, we can associate graphs of some mathematical structures with certifiable, widely known applications. This paper seeks to explore the connections established through edge labeling among Latin squares derived from Moufang quasigroups, which are constructed using additive abelian and multiplicative groups, along with their substructures and complete bipartite graphs. The algebraic characteristics of quasigroups exhibiting the antiautomorphic inverse property have been extensively examined in this study. These characteristics encompass identities associated with fixed element maps. To analyze the behavior of these groups under holomorphism, we utilize similar conditions.
1. Introduction
With the support of weak inverse property quasigroup (see [1, 2]) and conjugacy closed quasigroup (see [3]), Goodaire and Robinson introduced a better understanding of the Wilson quasigroup following the inspirational work about a special Moufang quasigroup done in [4]. Under some limitations put on the elements of the Moufang quasigroup’s Nucleus, Eric L. Wilson demonstrated that the Moufang quasigroup is a subclass of the Wilson quasigroup. Bruck’s idea of a holomorphic quasigroup is presented in [5]. Additionally, holomorphism of a quasigroup extension study was provided in [6]. Inspirable nonassociative generalization, Moufang quasigroup, of the group, was introduced by the German geometer Ruth Moufang in [7]. The minimum cardinality of a unique nonassociative Moufang quasigroup is 12, proved almost fifty years ago by Chein and Pflugfelder (see [8]). O. Chein gave new direction to construct M2n(G, 2), an infinite class of Moufang quasigroups, where commutativity of the group G implies associativity of the Moufang quasigroup (see [9]), and E. G. Goodaire introduced some innovative classes of Moufang quasigroups (see [10]). Modular arithmetic, cyclic construction, dihedral construction, and the pictorial representation of the constructions are discussed in [11] to obtain the classes of nonassociative Moufang quasigroups. The author proved in [7] that the associative part, the nucleus, of the Moufang quasigroup is its normal subgroup. Article [12], written by G. Glauberman in 1968, materialized two important things, odd order Moufang quasigroup is solvable and there are some Moufang quasigroups with a trivial nucleus, while M12(S3, 2) is solvable with a trivial nucleus. If the order of the finite Moufang quasigroup is coprime to 6, then this quasigroup has a nontrivial nucleus, enlightened by Stephen M. Gagola III in [13]. Moufang quasigroups are unquestionably the most contemplated quasigroups. Nonassociative Moufang quasigroups can be observed in the forms of invertible split-octonions, unit norm split-octonions, and projective geometry (Moufang polygons, Moufang planes) (see [14–16]). Mathematicians have discovered attractively all the nonassociative Moufang quasigroups of order less than 64 but for order 64, and there are 4262 nonisomorphic nonassociative Moufang quasigroups (see [9, 10]). Kunen proved in [17] that a quasigroup with Moufang identity forms a Moufang quasigroup, and it is also notable that there is a unique two-sided inverse of each element in the Moufang quasigroup.
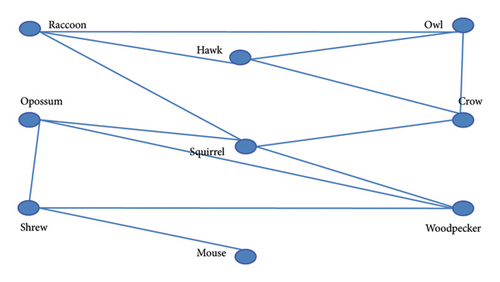
In the ongoing time, analysts are utilizing PCs quickly for the most part utilized applications and the subsequent methodology is graph theory (see [18–20]). In the field of image recognition, algebraic structures and methodologies play a crucial role in the training of machine learning models (see [21–23]). Techniques such as Principal Component Analysis (PCA) are utilized to decrease the dimensionality of data, thereby facilitating the identification of key features within an image, which enhances the efficiency of classification algorithms (see [24, 25]). Additionally, algebraic algorithms are integral to the functioning of neural networks that drive deep learning models, particularly in applications such as object detection and facial recognition (see [26–28]). We can comprehend numerous certifiable applications by relating them with a few graphs. Graph theory came into existence due to the bridge’s problem in 1735, which is the widely utilized bough of mathematics. Simon Antoine Jean L’Huilier, Swiss mathematician, and Augustin-Louis Cauchy, French mathematician, commenced to write some well-known results of topology tremendously to encourage Leonhard Euler’s work. In theoretical chemistry, the first name to associate chemical composition with trees was Arthur Cayley, the British mathematician. James Joseph Sylvester, the English mathematician, introduced the term “graph” and a sound book was written by Frank Harary, an American mathematician, to attach social scientists, computer experts, engineers, chemists, biologists, mathematicians, physicists, geographers, and astronomers (see [29–31]). In an ecosystem, a niche overlap graph can be used to discuss the competition between species (see Figure 1).
Within a network, signal transduction, evolutionary relationships, gene expression, bioentities, metabolic pathways, gene regulation, etc., can be taken as vertices and their relationships as edges of the bipartite graphs. These graphs are very helpful to know expediently about RNA-Seq and microarrays [32, 33], yeast-two-hybrid [34], protein-protein interactions for particular organisms, chemical reaction networks [35–37], personnel assignment problems, query log analysis, advance coding theory, optimal assignment problems, projective geometry, and document/word problems. Graph theory has become a significant, companionable, and prolific tool to examine in various fields extraordinarily like software engineering and chemistry. In the cutting-edge world, it appears to be difficult to talk about the properties of classical random graphs related to the models of certifiable complex networks. Rather than classical random graphs, bipartite graphs can be utilized to defeat this trouble [38].
Quasigroups are characterized by the absence of associativity, and although each element possesses a distinct inverse, the configuration of their inverse graphs is more intricate and less symmetrical than that of groups. This absence of associativity results in irregular relationships between elements and their corresponding inverses. The inverse graph of a quasigroup frequently exhibits a level of irregularity that is not present in groups. The relationships may not establish consistent patterns, resulting in a more complex and possibly chaotic configuration. Quasigroups, characterized by their intricate inverse graphs, are utilized in fields that demand nontraditional symmetries and operations, including cryptography and combinatorial design. The complexity inherent in these graphs can be leveraged to create systems where unpredictability and sophistication are beneficial. A widely recognized method for constructing finite quasigroups involves the use of Latin squares, which are n × n matrices populated with n distinct symbols, ensuring that each symbol appears precisely once in every row and column. The arrangement of symbols within a Latin square determines the operation of the corresponding quasigroup. Additionally, quasigroups can be formed by establishing operations based on permutations of a given set, thereby guaranteeing that each element interacts uniquely with others to fulfil the uniqueness criterion. The formation of groups and quasigroups is governed by different sets of axioms, resulting in unique algebraic structures. Groups possess a higher degree of structure due to the necessity of associativity, which facilitates their analysis and classification. Conversely, quasigroups provide enhanced flexibility by relaxing the requirement for associativity, thus accommodating a wider array of applications, especially in fields that necessitate nonstandard operations.
- (i)
Moufang quasigroups extend the notion of groups while preserving certain group-like characteristics. They provide a more expansive framework for investigating nonassociative structures, potentially yielding new understandings in the fields of algebra and geometry.
- (ii)
In contrast to associative groups, Moufang quasigroups ease this requirement while preserving a degree of structure that facilitates significant algebraic operations. This adaptability proves advantageous when examining systems in which associativity is not inherently present.
- (iii)
The theory of symmetry associated with antiautomorphic inverse property quasigroups is extensive and applicable in numerous fields, including physics, where these structures can represent symmetries that diverge from conventional group frameworks.
- (iv)
Antiautomorphic inverse property quasigroups find applications in the field of cryptography, as their inverse properties are advantageous for developing cryptographic algorithms that necessitate nonassociative operations, thereby enhancing both complexity and security within the system.
2. Preliminaries
Example 1. Table 1 indicates 12 order weak inverse property quasigroup.
We say a loop is a Moufang loop if any one of the following Moufang identities 7, 8, 9, and 10 holds:
∀ ϖ1, ϖ2, and .
| ⋄ | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (e, ϖ1) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) |
| (e, ϖ2) | (e, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (e, ϖ1) |
| (e, ϖ3) | (e, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) |
| (e, ϖ4) | (e, ϖ4) | (i, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (e, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) |
| (e, ϖ5) | (e, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) |
| (e, ϖ6) | (e, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) |
| (i, ϖ1) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) |
| (i, ϖ2) | (i, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) | (i, ϖ1) |
| (i, ϖ3) | (i, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (i, ϖ4) | (i, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) |
| (i, ϖ4) | (i, ϖ4) | (e, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (i, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) |
| (i, ϖ5) | (i, ϖ5) | (e, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (i, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) |
| (i, ϖ6) | (i, ϖ6) | (e, ϖ1) | (e, ϖ2) | (e, ϖ3) | (e, ϖ4) | (e, ϖ5) | (e, ϖ6) | (i, ϖ1) | (i, ϖ2) | (i, ϖ3) | (i, ϖ4) | (i, ϖ5) |
- The diamond sign at the left top of the table indicates the binary operation.
Example 2. Table 2 shows 8 order Moufang quasigroup.
Quasigroup is commutative if and in addition of any one Moufang identity, it can be taken as the commutative Moufang quasigroup. Since loop is the nonassociative structure, so we are interested to see those elements inside the loop which make a group. The intersection of three nuclei, 11, 12, and 13
We present our main findings in the following section. This section includes three parts; in the first one, we give a graphical study of the Moufang quasigroup. Algebraic properties and holomorphic results of the antiautomorphic inverse property quasigroup have been given in the second and third parts, respectively.
| ⋄ | (1, e) | (1, ϖ1) | (1, ϖ2) | (1, ϖ1ϖ2) | (ς, e) | (ς, ϖ1) | (ς, ϖ2) | (ς, ϖ1ϖ2) |
|---|---|---|---|---|---|---|---|---|
| (1, e) | (1, e) | (1, ϖ1) | (1, ϖ2) | (1, ϖ1ϖ2) | (ς, e) | (ς, ϖ1) | (ς, ϖ2) | (ς, ϖ1ϖ2) |
| (1, ϖ1) | (1, ϖ1) | (1, e) | (1, ϖ1ϖ2) | (1, ϖ2) | (ς, ϖ1) | (ς, e) | (ς, ϖ1ϖ2) | (ς, ϖ2) |
| (1, ϖ2) | (1, ϖ2) | (1, ϖ1ϖ2) | (ς, e) | (ς, ϖ1) | (ς, ϖ2) | (ς, ϖ1ϖ2) | (1, e) | (1, ϖ1) |
| (1, ϖ1ϖ2) | (1, ϖ1ϖ2) | (1, ϖ2) | (ς, ϖ1) | (ς, e) | (ς, ϖ1ϖ2) | (ς, ϖ2) | (1, ϖ1) | (1, e) |
| (ς, e) | (ς, e) | (ς, ϖ1) | (ς, ϖ2) | (ς, ϖ1ϖ2) | (1, e) | (1, ϖ1) | (1, ϖ2) | (1, ϖ1ϖ2) |
| (ς, ϖ1) | (ς, ϖ1) | (ς, e) | (ς, ϖ1ϖ2) | (ς, ϖ2) | (1, ϖ1) | (1, e) | (1, ϖ1ϖ2) | (1, ϖ2) |
| (ς, ϖ2) | (ς, ϖ2) | (ς, ϖ1ϖ2) | (1, e) | (1, ϖ1) | (1, ϖ2) | (1, ϖ1ϖ2) | (ς, e) | (ς, ϖ1) |
| (ς, ϖ1ϖ2) | (ς, ϖ1ϖ2) | (ς, ϖ2) | (1, ϖ1) | (1, e) | (1, ϖ1ϖ2) | (1, ϖ2) | (ς, ϖ1) | (ς, e) |
- The diamond sign at the left top of the table indicates the binary operation.
3. Main Results
Definition 1. P-edge labeling. Let Ξ = (Λ, Σ), be the finite simple graph and a Latin square of finite order j associated with quasigroup , respectively. Let T = {T1, T2, …, Tj}, S = {S1, S2, …, Sj} be any two distinct sets of symbols, then the mappings defined by (Ti, Sj)⟼mij, is known as P-edge labeling.
Example 3. In Figure 2, element (β, 1) shows an edge corresponding to two arbitrary vertices M and N. Therefore, K4,4 is the associated graph of Table 3.

| (ϖ, 0) | (ϖ, 1) | (β, 0) | (β, 1) |
| (ϖ, 1) | (ϖ, 0) | (β, 1) | (β, 0) |
| (β, 0) | (β, 1) | (ϖ, 1) | (ϖ, 0) |
| (β, 1) | (β, 0) | (ϖ, 0) | (ϖ, 1) |
Definition 2. V-edge labeling
Now assuming that is any quasigroup of finite order j and that is a Latin square, the map is known as V-edge labeling for the finite simple graph Ξ = (Λ, Σ).
| (b1, 2) | (b1, 1) | (b2, 2) | (b2, 1) |
| (b1, 1) | (b1, 2) | (b2, 1) | (b2, 2) |
| (b2, 2) | (b2, 1) | (b1, 1) | (b1, 2) |
| (b2, 1) | (b2, 2) | (b1, 2) | (b1, 1) |

Definition 3. Left and Right Inverse Graphs. Let Ξ = (Λ, Σ) be the finite simple graph. Through P-edge labeling, we denote an undirected graph of an algebraic structure SA by and similarly for V-edge labeling. In particular, a directed graph is referred to as a left inverse graph (right inverse graph) if and where the edge (ϖ, ϖλ) ((ϖ, ϖρ)) indicates initial vertex ϖ and final vertex ϖλ(ϖρ) in .
Definition 4. Fixed Element Map. Let groups under addition and multiplication, respectively, be Ω2 and Ω1. Ω2 is an abelian group, in addition. A fixed element map is referred to as the function β : Ω1 × Ω1⟶Ω2 that defines as (1, ς)β = (ς, 1)β = 0 ∀ ς ∈ Ω1.
The following binary operation, in the form of β: (ς1, ϖ1)⋄(ς2, ϖ2) = (ς1ς2, ϖ1 + ϖ2 + (ς1, ς2)β).
∀ ς1, ς2 ∈ Ω1 and ∀ ϖ1, ϖ2 ∈ Ω2 can be connected with Ω1 × Ω2. This algebraic structure is denoted by (Ω1, Ω2, β).
3.1. Graphical Representation of Moufang Quasigroup
Theorem 5. With the help of the same notations, the algebraic structure (Ω1, Ω2, β) is a quasigroup and the associated undirected graph through P-edge labeling is .
Proof. Let (ς1, ϖ1) and (ς2, ϖ2) be any two elements of (Ω1, Ω2, β). Obviously, this mathematical structure is closed under the definition of binary operation ⋄. For any arbitrary element (ς, ϖ) of (Ω1, Ω2, β), there exists (1, 0) in (Ω1, Ω2, β) such that (ς, ϖ)⋄(1, 0) = (1, 0)⋄(ς, ϖ) = (ς, ϖ),
Finally, we can say (ς, ϖ)λ = (ς, ϖ)ρ = (ς−1, −ϖ − (ς, ς−1)β).
Therefore, the structure (Ω1, Ω2, β) is a quasigroup with identity (1, 0). Thus, with the help of P-edge labeling, . So, it completes the proof.
Theorem 6. (Ω1, Ω2, β) is a Moufang quasigroup if and only if
Proof. Let (Ω1, Ω2, β) is a Moufang quasigroup, then ∀(ς1, ϖ1), (ς2, ϖ2), (ς3, ϖ3) ∈ (Ω1, Ω2, β)
Remark 7. The previous theorem makes it clear that the left and right inverses of every element of this mathematical structure are equal.
In the following results, we denote the Moufang quasigroup (Ω1, Ω2, β) by .
Theorem 8. .
Theorem 9. is a commutative Moufang quasigroup and .
Proof. Clearly, binary operation ⋄ commutes if Ω1 and Ω2 both hold the commutative law. So, quasigroup is commutative. As a result, the trivial subloop is the set of commutators , and K1,1 is the undirected graph obtained via V-edge labeling.
Theorem 10. . Moreover .
Proof. Since collection of Moufang quasigroups is the subclass of the collection of weak inverse property quasigroups and all the three nuclei in weak inverse property quasigroups are equal. Thus, it can be verified easily that contains only the elements of the quasigroup . The corresponding graph of the Moufang quasigroup is also labelled by the V-edge as . It completes the proof.
Proposition 11. Let be the multiplicative group and |Ω2| = λ > 1, order of the group Ω2, with 0 ≠ σ ∈ Ω2. We define a mapping β : Ω1 × Ω1⟶Ω2 by
Then, (Ω1, Ω2, β) is a Moufang quasigroup.
Example 5. Let be the multiplicative group and be the additive abelian group of residue classes modulo φ. Then, the Moufang quasigroup of even order is in the form of Tables 5 and 6.
| ⋄ | () | (, 1) | (, 2) | (, 3) | … | (-2) | (-1) | () | (eιπ, 1) | (eιπ, 2) | (eιπ, 3) | … | (eιπ, φ-2) | (eιπ, φ-1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | (, 1) | (, 2) | (, 3) | … | (-2) | (-1) | () | (eιπ, 1) | (eιπ, 2) | (eιπ, 3) | … | (eιπ, φ-2) | (eιπ, φ-1) |
| (, 1) | (, 1) | (, 2) | (, 3) | (, 4) | … | (-1) | () | (eιπ, 1) | (eιπ, 2) | (eιπ, 3) | (eιπ, 4) | … | (eιπ, φ-1) | () |
| (, 2) | (, 2) | (, 3) | (, 4) | (, 5) | … | () | (, 1) | (eιπ, 2) | (eιπ, 3) | (eιπ, 4) | (eιπ, 5) | … | () | (eιπ, 1) |
| (, 3) | (, 3) | (, 4) | (, 5) | (, 6) | … | (, 1) | (, 2) | (eιπ, 3) | (eιπ, 4) | (eιπ, 5) | (eιπ, 6) | … | (eιπ, 1) | (eιπ, 2) |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| (-2) | (-2) | (-1) | () | (, 1) | … | (-4) | (-3) | (eιπ, φ-2) | (eιπ, φ-1) | () | (eιπ, 1) | … | (eιπ, φ-4) | (eιπ, φ-3) |
| (-1) | (-1) | () | (, 1) | (, 2) | … | (-3) | (-2) | (eιπ, φ-1) | () | (eιπ, 1) | (eιπ, 2) | … | (eιπ, φ-3) | (eιπ, φ-2) |
- The diamond sign at the left top of the table indicates the binary operation.
| ⋄ | () | (, 1) | (, 2) | (, 3) | … | (-2) | (-1) | () | (eιπ, 1) | (eιπ, 2) | (eιπ, 3) | … | (eιπ, φ-2) | (eιπ, φ-1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | (eιπ, 1) | (eιπ, 2) | (eιπ, 3) | … | (eιπ, φ-2) | (eιπ, φ-1) | (-1) | () | (, 1) | (, 2) | … | (-3) | (, φ-2) |
| (eιπ, 1) | (eιπ, 1) | (eιπ, 2) | (eιπ, 3) | (eιπ, 4) | … | (eιπ, φ-1) | () | () | (, 1) | (, 2) | (, 3) | … | (-2) | (-1) |
| (eιπ, 2) | (eιπ, 2) | (eιπ, 3) | (eιπ, 4) | (eιπ, 5) | … | () | (eιπ, 1) | (, 1) | (, 2) | (, 3) | (, 4) | … | (-1) | () |
| (eιπ, 3) | (eιπ, 3) | (eιπ, 4) | (eιπ, 5) | (eιπ, 6) | … | (eιπ, 1) | (eιπ, 2) | (, 2) | (, 3) | (, 4) | (, 5) | … | () | (, 1) |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| (eιπ, φ-2) | (eιπ, φ-2) | (eιπ, φ-1) | () | (eιπ, 1) | … | (eιπ, φ-4) | (eιπ, φ-3) | (-3) | (-2) | (-1) | () | … | (-5) | (-4) |
| (eιπ, φ-1) | (eιπ, φ-1) | () | (eιπ, 1) | (eιπ, 2) | … | (eιπ, φ-3) | (eιπ, φ-2) | (-2) | (-1) | () | (, 1) | … | (-4) | (-3) |
- The diamond sign at the left top of the table indicates the binary operation.
Example 6. If and , then associated graphs of Moufang quasigroup , and through abovementioned edge labelings are Figures 4, 5, and 6, respectively. Since left and right inverses of each element are same, so Figure 7 indicates the left inverse of this Moufang quasigroup of order 24.
Now, we summarize all the above discussion of this section in the following Table 7.


| Ω1 | Ω2 | Moufang Quasigroup and graph | Graph of nucleus | Graph of commutator subloop |
|---|---|---|---|---|
| , K12,12 | K1,6 | K1,1 | ||
| , K16,16 | K1,8 | K1,1 | ||
| , K20,20 | K1,10 | K1,1 | ||
| , K24,24 | K1,12 | K1,1 | ||
| , K28,28 | K1,14 | K1,1 | ||
| , K32,32 | K1,16 | K1,1 | ||
| , K36,36 | K1,18 | K1,1 | ||
| , K40,40 | K1,20 | K1,1 | ||
| , K44,44 | K1,22 | K1,1 | ||
| , K48,48 | K1,24 | K1,1 | ||
| , K52,52 | K1,26 | K1,1 | ||
| , K56,56 | K1,28 | K1,1 | ||
| , K60,60 | K1,30 | K1,1 | ||
| , K64,64 | K1,32 | K1,1 |
3.2. Algebraic Aspects of Antiautomorphic Inverse Property Quasigroup
Theorem 12. (Ω1, Ω2, β) is an antiautomorphic inverse property quasigroup.
Theorem 13. Let β : Ω1 × Ω1⟶Ω2 be the fixed element map, then (Ω1, Ω2, β) is the antiautomorphic inverse quasigroup iff
Proof. We suppose that (Ω1, Ω2, β) is the antiautomorphic inverse property quasigroup, so it satisfies the identity:
With the help of equation (22), we can write the following:
This is the required identity. It completes the proof.
Remark 14. The fixed element map β : Ω1 × Ω1⟶Ω2 associated with equation (21) is known as the AAIP fixed element map. Also, if |Ω1| = 2w, for w ∈ P where P is the set of positive integers, then equation (21) becomes
Proposition 15. With the availability of the abilian group (Ω2, +) where |Ω2| > 2 and O(δ) > 2 under 0 ≠ δ ∈ Ω2. Let Ω1 = {1, ξ1, ξ2, ξ3} be a Klein 4 group. We define β : Ω1 × Ω1⟶Ω2 by
Then, (Ω1, Ω2, β) is an AAIP quasigroup with nucleus Nnul((Ω1, Ω2, β)) = {(1, ϖ)}∀ ϖ ∈ Ω2 and ∀ξ1, ξ2, ξ3 ∈ Ω1.
Proof. Clearly, the verification of equation (21) indicates that the structure (Ω1, Ω2, β) is the AAIP quasigroup, and Table 8 shows that β is the fixed element map. Moreover, Nnul((Ω1, Ω2, β)) = {(1, ϖ)} implies that (Ω1, Ω2, β) is nonassociative.
| β | 1 | ξ1 | ξ2 | ξ3 |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | o |
| ξ1 | 0 | 0 | −δ | δ |
| ξ2 | 0 | δ | 0 | −δ |
| ξ3 | 0 | −δ | δ | 0 |
Example 7. Let Ω1 = {1, ξ1, ξ2, ξ3} and Ω2 be the Klein four group and group of residue classes of order φ. Following Tables 9, 10, 11, 12, and 13 show the general pattern of the antiautomorphic inverse property loop of order 4φ.
| ⋄ | (1, 0) | (1, 1) | (1, 2) | (1, 3) | … | (1, φ-2) | (1, φ-1) |
|---|---|---|---|---|---|---|---|
| (1, 0) | (1, 0) | (1, 1) | (1, 2) | (1, 3) | … | (1, φ-2) | (1, φ-1) |
| (1, 1) | (1, 1) | (1, 2) | (1, 3) | (1, 4) | … | (1, φ-1) | (1, 0) |
| (1, 2) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | … | (1, 0) | (1, 1) |
| (1, 3) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | … | (1, 1) | (1, 2) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (1, φ-2) | (1, φ-2) | (1, φ-1) | (1, 0) | (1, 1) | … | (1, φ-4) | (1, φ-3) |
| (1, φ-1) | (1, φ-1) | (1, 0) | (1, 1) | (1, 2) | … | (1, φ-3) | (1, φ-2) |
| (ξ1, 0) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | … | (ξ1, φ-2) | (ξ1, φ-1) |
| (ξ1, 1) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | … | (ξ1, φ-1) | (ξ1, 0) |
| (ξ1, 2) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | … | (ξ1, 0) | (ξ1, 1) |
| (ξ1, 3) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | (ξ1, 6) | … | (ξ1, 1) | (ξ1, 2) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (ξ1, φ-2) | (ξ1, φ-2) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | … | (ξ1, φ-4) | (ξ1, φ-3) |
| (ξ1, φ-1) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | … | (ξ1, φ-3) | (ξ1, φ-2) |
| (ξ2, 0) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | … | (ξ2, φ-2) | (ξ2, φ-1) |
| (ξ2, 1) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | … | (ξ2, φ-1) | (ξ2, 0) |
| (ξ2, 2) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | … | (ξ2, 0) | (ξ2, 1) |
| (ξ2, 3) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | (ξ2, 6) | … | (ξ2, 1) | (ξ2, 2) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (ξ2, φ-2) | (ξ2, φ-2) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | … | (ξ2, φ-4) | (ξ2, φ-3) |
| (ξ2, φ-1) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | … | (ξ2, φ-3) | (ξ2, φ-2) |
| (ξ3, 0) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | … | (ξ3, φ-2) | (ξ3, φ-1) |
| (ξ3, 1) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | … | (ξ3, φ-1) | (ξ3, 0) |
| (ξ3, 2) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | … | (ξ3, 0) | (ξ3, 1) |
| (ξ3, 3) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | (ξ3, 6) | … | (ξ3, 1) | (ξ3, 2) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (ξ3, φ-2) | (ξ3, φ-2) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | … | (ξ3, φ-4) | (ξ3, φ-3) |
| (ξ3, φ-1) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | … | (ξ3, φ-3) | (ξ3, φ-2) |
- The diamond sign at the left top of the table indicates the binary operation.
| ⋄ | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | … | (ξ1, φ-2) | (ξ1, φ-1) |
|---|---|---|---|---|---|---|---|
| (1, 0) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | … | (ξ1, φ-2) | (ξ1, φ-1) |
| (1, 1) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | … | (ξ1, φ-1) | (ξ1, 0) |
| (1, 2) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | … | (ξ1, 0) | (ξ1, 1) |
| (1, 3) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | (ξ1, 6) | … | (ξ1, 1) | (ξ1, 2) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (1, φ-2) | (ξ1, φ-2) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | … | (ξ1, φ-4) | (ξ1, φ-3) |
| (1, φ-1) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | … | (ξ1, φ-3) | (ξ1, φ-2) |
| (ξ1, 0) | (1, 0) | (1, 1) | (1, 2) | (1, 3) | … | (1, φ-2) | (1, φ-1) |
| (ξ1, 1) | (1, 1) | (1, 2) | (1, 3) | (1, 4) | … | (1, φ-1) | (1, 0) |
| (ξ1, 2) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | … | (1, 0) | (1, 1) |
| (ξ1, 3) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | … | (1, 1) | (1, 2) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (ξ1, φ-2) | (1, φ-2) | (1, φ-1) | (1, 0) | (1, 1) | … | (1, φ-4) | (1, φ-3) |
| (ξ1, φ-1) | (1, φ-1) | (1, 0) | (1, 1) | (1, 2) | … | (1, φ-3) | (1, φ-2) |
| (ξ2, 0) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | … | (ξ3, φ-3) | (ξ3, φ-2) |
| (ξ2, 1) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | … | (ξ3, φ-2) | (ξ3, φ-1) |
| (ξ2, 2) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | … | (ξ3, φ-1) | (ξ3, 0) |
| (ξ2, 3) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | … | (ξ3, 0) | (ξ3, 1) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (ξ2, φ-2) | (ξ3, φ-3) | (ξ3, φ-2) | (ξ3, φ-1) | (ξ3, 0) | … | (ξ3, φ-5) | (ξ3, φ-4) |
| (ξ2, φ-1) | (ξ3, φ-2) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | … | (ξ3, φ-4) | (ξ3, φ-3) |
| (ξ3, 0) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | … | (ξ2, φ-1) | (ξ2, 0) |
| (ξ3, 1) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | … | (ξ2, 0) | (ξ2, 1) |
| (ξ3, 2) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | (ξ2, 6) | … | (ξ2, 1) | (ξ2, 2) |
| (ξ3, 3) | (ξ2, 4) | (ξ2, 5) | (ξ2, 6) | (ξ2, 7) | … | (ξ2, 2) | (ξ2, 3) |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| (ξ3, φ-2) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | … | (ξ2, φ-3) | (ξ2, φ-2) |
| (ξ3, φ-1) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | … | (ξ2, φ-2) | (ξ2, φ-1) |
- The diamond sign at the left top of the table indicates the binary operation.
| ⋄ | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | … | (ξ2, φ-2) | (ξ2, φ-1) |
|---|---|---|---|---|---|---|---|
| (1, 0) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | … | (ξ2, φ-2) | (ξ2, φ-1) |
| (1, 1) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | … | (ξ2, φ-1) | (ξ2, 0) |
| (1, 2) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | … | (ξ2, 0) | (ξ2, 1) |
| (1, 3) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | (ξ2, 6) | … | (ξ2, 1) | (ξ2, 2) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (1, φ-1) | (ξ2, φ-2) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | … | (ξ2, φ-4) | (ξ2, φ-3) |
| (1, φ-2) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | … | (ξ2, φ-3) | (ξ2, φ-2) |
| (ξ1, 0) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | … | (ξ3, φ-1) | (ξ3, 0) |
| (ξ1, 1) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | … | (ξ3, 0) | (ξ3, 1) |
| (ξ1, 2) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | (ξ3, 6) | … | (ξ3, 1) | (ξ3, 2) |
| (ξ1, 3) | (ξ3, 4) | (ξ3, 5) | (ξ3, 6) | (ξ3, 7) | … | (ξ3, 2) | (ξ3, 3) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (ξ1, φ-2) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | … | (ξ3, φ-3) | (ξ3, φ-2) |
| (ξ1, φ-1) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | … | (ξ3, φ-2) | (ξ3, φ-1) |
| (ξ2, 0) | (1, 0) | (1, 1) | (1, 2) | (1, 3) | … | (1, φ-2) | (1, φ-1) |
| (ξ2, 1) | (1, 1) | (1, 2) | (1, 3) | (1, 4) | … | (1, φ-1) | (1, 0) |
| (ξ2, 2) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | … | (1, 0) | (1, 1) |
| (ξ2, 3) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | … | (1, 1) | (1, 2) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (ξ2, φ-2) | (1, φ-2) | (1 , φ-1) | (1, 0) | (1, 1) | … | (1, φ-4) | (1, φ-3) |
| (ξ2, φ-1) | (1, φ-1) | (1, 0) | (1, 1) | (1, 2) | … | (1, φ-3) | (1 , φ-2) |
| (ξ3, 0) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | … | (ξ1, φ-3) | (ξ1, φ-2) |
| (ξ3, 1) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | … | (ξ1, φ-2) | (ξ1, φ-1) |
| (ξ3, 2) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | … | (ξ1, φ-1) | (ξ1, 0) |
| (ξ3, 3) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | … | (ξ1, 0) | (ξ1, 1) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (ξ3, φ-2) | (ξ1, φ-3) | (ξ1, φ-2) | (ξ1, φ-1) | (ξ1, 0) | … | (ξ1, φ-5) | (ξ1, φ-4) |
| (ξ3, φ-1) | (ξ1, φ-2) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | … | (ξ1, φ-4) | (ξ1, φ-3) |
- The diamond sign at the left top of the table indicates the binary operation.
| ⋄ | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | … | (ξ3, φ-2) | (ξ3, φ-1) |
|---|---|---|---|---|---|---|---|
| (1, 0) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | … | (ξ3, φ-2) | (ξ3, φ-1) |
| (1, 1) | (ξ3, 1) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | … | (ξ3, φ-1) | (ξ3, 0) |
| (1, 2) | (ξ3, 2) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | … | (ξ3, 0) | (ξ3, 1) |
| (1, 3) | (ξ3, 3) | (ξ3, 4) | (ξ3, 5) | (ξ3, 6) | … | (ξ3, 1) | (ξ3, 2) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (1, φ-1) | (ξ3, φ-2) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | … | (ξ3, φ-4) | (ξ3, φ-3) |
| (1, φ-2) | (ξ3, φ-1) | (ξ3, 0) | (ξ3, 1) | (ξ3, 2) | … | (ξ3, φ-3) | (ξ3, φ-2) |
| (ξ1, 0) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | … | (ξ2, φ-3) | (ξ2, φ-2) |
| (ξ1, 1) | (ξ2, 0) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | … | (ξ2, φ-2) | (ξ2, φ-1) |
| (ξ1, 2) | (ξ2, 1) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | … | (ξ2, φ-1) | (ξ2, 0) |
| (ξ1, 3) | (ξ2, 2) | (ξ2, 3) | (ξ2, 4) | (ξ2, 5) | … | (ξ2, 0) | (ξ2, 1) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (ξ1, φ-2) | (ξ2φ-3) | (ξ2, φ-2) | (ξ2, φ-1) | (ξ2, 0) | … | (ξ2, φ-5) | (ξ2, φ-4) |
| (ξ1, φ-1) | (ξ2, φ-2) | (ξ2, φ-1) | (ξ2, 0) | (ξ2, 1) | … | (ξ2, φ-4) | (ξ2, φ-3) |
| (ξ2, 0) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | … | (ξ1, φ-1) | (ξ1, 0) |
| (ξ2, 1) | (ξ1, 2) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | … | (ξ1, 0) | (ξ1, 1) |
| (ξ2, 2) | (ξ1, 3) | (ξ1, 4) | (ξ1, 5) | (ξ1, 6) | … | (ξ1, 1) | (ξ1, 2) |
| (ξ2, 3) | (ξ1, 4) | (ξ1, 5) | (ξ1, 6) | (ξ1, 7) | … | (ξ1, 2) | (ξ1, 3) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (ξ2, φ-2) | (ξ1, φ-1) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | … | (ξ1, φ-3) | (ξ1, φ-2) |
| (ξ2, φ-1) | (ξ1, 0) | (ξ1, 1) | (ξ1, 2) | (ξ1, 3) | … | (ξ1, φ-2) | (ξ1, φ-1) |
| (ξ3, 0) | (1, 0) | (1, 1) | (1, 2) | (1, 3) | … | (1, φ-2) | (1, φ-1) |
| (ξ3, 1) | (1, 1) | (1, 2) | (1, 3) | (1, 4) | … | (1, φ-1) | (1, 0) |
| (ξ3, 2) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | … | (1, 0) | (1, 1) |
| (ξ3, 3) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | … | (1, 1) | (1, 2) |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | |
| (ξ3, φ-2) | (1, φ-2) | (1, φ-1) | (1, 0) | (1, 1) | … | (1, φ-4) | (1, φ-3) |
| (ξ3, φ-1) | (1, φ-1) | (1, 0) | (1, 1) | (1, 2) | … | (1, φ-3) | (1, φ-2) |
- The diamond sign at the left top of the table indicates the binary operation.
| Ω1 | Ω2 | (Ω1, Ω2, β) | Nnul((Ω1, Ω2, β)) |
| C2 | Z2 | (C2, Z2, β) | {(1, 0), (1, 1)} |
| C2 | Z3 | (C2, Z3, β) | {(1, 0), (1, 1), (1, 2)} |
| C2 | Z4 | (C2, Z4, β) | {(1, 0), (1, 1), (1, 2), (1, 3)} |
| C2 | Zφ | (C2, Zφ, β) | {(1, 0), (1, 1), ⋅⋅⋅(1, φ − 1)} |
| V4 | Z3 | (V4, Z3, β) | {(1, 0), (1, 1), (1, 2)} |
| V4 | Z4 | (V4, Z4, β) | {(1, 0), (1, 1), (1, 2), (1, 3)} |
| V4 | Z5 | (V4, Z5, β) | {(1, 0), (1, 1), (1, 2), (1, 3), (1, 4)} |
| V4 | Zφ | (V4, Zφ, β) | {(1, 0), (1, 1), ⋅⋅⋅(1, φ − 1)} |
Example 8. Let Ω1 = {1, ξ1, ξ2, ξ3} and Ω2 be the Klein four group and group of residue classes of order φ. Following Tables 2, 3, 4, and 5 show the general pattern of the antiautomorphic inverse property loop of order 4φ.
Let V4 be the Klein four groups. Following Table 6 gives the recapitulation of all the above discussion of this section.
3.3. Holomorphism of Antiautomorphic Inverse Property Loops
Lemma 16. Inverse property loop is an antiautomorphic inverse property loop if holomorph of loop is AAIPL.
Proof. Given that is a normal subloop of . Additionally, and are isomorphic, making a normal subloop of . The antiautomorphic inverse property of also applies to since is antiautomorphic.
Theorem 17. Let is an antiautomorphic inverse loop, then where and , we have .
Proof.
So, is the antiautomorphic inverse property loop. It completes the proof.
Corollary 18. The holomorph of a loop is an antiautomorphic inverse property loop iff is the antiautomorphic inverse property loop and is the trivial group.
Proof. We suppose that is an AAIPL with and shall prove the following identity: .
Since , so it becomes
Similarly, we can prove the other way. Thus, it completes the proof.
The following example demonstrates how to obtain an automorphism of an antiautomorphic inverse property quasigroup using any arbitrary autotopism.
Example 9. Let (β1, β2, β3) be any autotopism of the antiautomorphic inverse property quasigroup , then provided that all the permutations in the later autotopism are identical.
Lemma 19. If is an antiautomorphic inverse property loop of a commutative loop , then left and right inverse permutations are equal to identity mapping.
Proof. Last two results portray that is commutative AAIPL. Thus, we have done.
Lemma 20. Let , be two AAIP loops under the binary operations, ⋄, ∗ respectively, over the nonempty set . If H(X)≅H(Y), then H(X) = H(Y).
Proof. H(X)≅H(Y) implies ςβ2⋄ϖβ1 = (ςβ3∗ϖ)β2∀ β1, β2 ∈ AUM(Y), , and β3 ∈ AUM(X). Setting β3 = β2 = β1 = I, then we have ςI⋄ϖI = (ςI∗ϖ)I. It implies that . Hence, we have two identical loops X and Y. It completes the proof.
Theorem 21. Let be a loop associated with holomorph . is the antiautomorphic inverse property loop iff , we have and .
Proof. Let us suppose that and we prove that is an antiautomorphic inverse property loop.
Given hypothesis:
So, equation (3) becomes
Reverse inclusion can be proved easily.
The discussion just above can be summed up as follows:
Theorem 22. Taking into account the holomorphism, , of loop , the following statements are equivalent:
- (1)
is antiautomorphic inverse property loop
- (2)
is antiautomorphic inverse property loop with
- (3)
.
Corollary 23. If the holomorph of loop is the antiautomorphic inverse property loop, then .
Proof. Since of loop is the antiautomorphic inverse property loop. Then, by previous theorem and which means β1 = β2 = I by substituting ϖ = ς = e. Then, and so . It completes the proof.
4. Conclusion and Future Directions
This paper deals with the interrelationship between algebraic structures and graph theory. Finding a new mathematical system with the help of old structures is an interesting notion in the study of algebra. The primary objective is to gain insight into specific mathematical structures, namely, nonassociative Moufang quasigroups, as well as the nucleus and commutator subloops, which are intricately associated with bipartite graphs via edge labeling. Our research has focused on the development of antiautomorphic inverse property quasigroups derived from certain abelian 2 groups and additive abelian groups. It is possible to achieve further advancements in the future by establishing connections between these two prominent branches of mathematics through various quasigroups derived from p-groups and additive abelian groups. The exploration of new algebraic structures and their holomorphisms, particularly concerning Sylow p-groups, promises to be particularly intriguing.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
Muhammad Nadeem and Mohammad Mazyad Hazzazi provided conceptualization, formal analysis, and software. Supervision and methodology of this work were given by Ismail Naci and J. Akhter, respectively. Muhammad Kamran prepared the initial draft, and Muhammad Nadeem wrote the final form of this manuscript.
Acknowledgments
The authors extend their gratitude to the deanship of scientific research of King Khalid University, for funding this work through a research project under grant R.G.P.2/5/44.
Open Research
Data Availability
All data required for this research are included within the paper.




