International Journal of Energy Research

Volume 2024, Issue 1 7800284

Research Article

Open Access

Intelligent Collaborative Optimal Scheduling for Water Intake-Supply Pump Groups in Drinking Water Treatment Plants

Dongsheng Wang

orcid.org/0000-0003-4307-0992

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Peng Zhang,

Peng Zhang

orcid.org/0009-0004-3606-6498

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Haixiang Ma,

Haixiang Ma

orcid.org/0009-0009-9969-3372

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Zhixuan Li,

Zhixuan Li

orcid.org/0009-0008-3585-9786

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Suqian Xu,

Corresponding Author

Suqian Xu

[email protected]

orcid.org/0009-0007-0337-0612

Department of Municipal Engineering, Southeast University, Nanjing 210096, China seu.edu.bd

Search for more papers by this author

Chaoqun Tan,

Chaoqun Tan

orcid.org/0000-0001-9064-3234

Department of Municipal Engineering, Southeast University, Nanjing 210096, China seu.edu.bd

Search for more papers by this author

Dongsheng Wang,

Dongsheng Wang

orcid.org/0000-0003-4307-0992

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Peng Zhang,

Peng Zhang

orcid.org/0009-0004-3606-6498

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Haixiang Ma,

Haixiang Ma

orcid.org/0009-0009-9969-3372

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Zhixuan Li,

Zhixuan Li

orcid.org/0009-0008-3585-9786

School of Automation and School of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China njupt.edu.cn

Search for more papers by this author

Suqian Xu,

Corresponding Author

Suqian Xu

[email protected]

orcid.org/0009-0007-0337-0612

Department of Municipal Engineering, Southeast University, Nanjing 210096, China seu.edu.bd

Search for more papers by this author

Chaoqun Tan,

Chaoqun Tan

orcid.org/0000-0001-9064-3234

Department of Municipal Engineering, Southeast University, Nanjing 210096, China seu.edu.bd

Search for more papers by this author

First published: 16 January 2024

https://doi.org/10.1155/2024/7800284

Citations: 2

Academic Editor: Dongdong Yuan

Share a link

Email
Wechat
Bluesky

Abstract

Up to 80% of the electrical energy is consumed by pump groups in water purification plants. Optimizing the scheduling of water intake-supply pump groups is crucial for saving electrical energy and reducing carbon dioxide emissions while ensuring water supply and security requirements are met. Herein, an intelligent collaborative optimal scheduling method is proposed for the water intake pump groups, clean-water reservoirs, and water supply pump groups. A long short-term memory (LSTM) network is applied to predict the flow of the water supply pump group, and a data-driven approach is used to plan the flow of the water intake pump group and model the working characteristics of working pump configurations. Furthermore, based on the dynamic programming (DP) algorithm, the optimal scheduling scheme of the water intake-supply pump groups as well as the working pump configuration at each moment can be obtained. The proposed approach dynamically updates data on an hourly basis to enhance the precision of collaborative optimal scheduling outcomes. The experimental results of long-term operation showed that pump efficiency was increased by 10.68% and 10.70% of electric energy was effectively saved as compared to the results of previous manual scheduling. This study provides a solution for energy conservation and efficiency enhancement of multiple energy-consuming equipment and carbon emission reduction.

1. Introduction

According to data analysis, the world’s energy consumption in 2050 will increase by about 50% compared with that in 2020 [1]. Population growth, urbanization, energy security policies, and growing production and consumption patterns have greatly affected the demand for sustainable energy [2]. To mitigate the energy crisis and climate change, many countries around the world utilize renewable materials and systems to minimize greenhouse gas emissions [3]. The electrical energy consumption of water purification plants accounts for more than 4% of urban electrical energy consumption [4], and up to 80% of this is consumed by the water intake-supply pump groups [5]. Generally, such pump groups are configured based on their maximum flow and head demand under the most unfavorable conditions. Current working pump configurations are generally based on subjective experience, lacking theoretical guidance and relying on potentially arbitrary scheduling judgments of individual engineers. This means that pumps are not necessarily operating at maximum efficiency [6]. The optimization objectives of intelligent cooperative optimal scheduling of water intake and water supply pumping stations are mainly power consumption and pump switching times [7, 8]. Amongst them, the number of pump switching is usually an easy to be ignored optimization goal. If the time interval between the operation and stop of the pump is too small, it could lead to overheating of the motor unit, water hammer phenomenon in the transmission pipeline, pipe explosion accident, and other problems [9], which would shorten the service life of the pump, motor, and transmission pipeline [10]. Therefore, the pump switch number should also be evaluated during optimization. Moreover, these optimizing objectives should be developed under the constraints of the main pipe pressure and the water levels of clean-water reservoirs [11]. The intelligent collaborative optimal scheduling for the water intake-supply pump groups can be divided into four parts, which are the prediction of water demand flow of the water supply pump group, the planning of water demand flow of the water intake pump group, the analysis of pump combination characteristics, and the dispatching decision optimization.

The prediction of the flows in the water supply pump group is the basis of water demand flow planning of the water intake pump group. Moreover, the flow in a supply pump group is mainly determined by the water consumption of residents. In recent years, both domestic and foreign scholars have applied various algorithms to predict residential water demand. Herrera et al. [12] applied support vector regression (SVR), multivariate adaptive regression spline (MARS), projection pursuit regression (PPR), and random forest (RF) algorithms to the field of urban water demand prediction and compared their results. Although the SVR algorithm has a higher prediction accuracy compared to the other three algorithms, it often lags behind in predicting the actual values for most of the time nodes. Antunes et al. [13] applied the artificial neural network (ANN), SVR, RF, k-nearest neighbor (KNN), and autoregressive integrated moving average (ARIMA) algorithms to the field of short-term water demand prediction and compared their results. They concluded that the prediction accuracy of the ARIMA algorithm was better than that of machine learning algorithms. However, certain nodes with significant errors necessitate real-time monitoring and periodic tracking by researchers, rendering the approach challenging to implement in practical settings. Pesantez et al. [14] explored the RF, ANN, and SVR algorithms to predict residential water demand through lag demand, seasonal changes, weather, and household characteristics. The results demonstrated that RF and ANN exhibited higher prediction accuracy compared to SVR. However, the requirements of these methods are high for the type and scale of the training data, making their practical application challenging. Considering engineering practicalities, the long short-term memory (LSTM) network can be employed to learn the historical scheduling data of water purification plants, which affects the flow of the water supply pump groups. An LSTM network can memorize the periodic characteristics of a time series through its gate nodes, resulting in more accurate predictive results [15]. In addition, LSTM algorithm also shows better performance compared with other algorithms in other fields of prediction problems [16, 17].

The optimal operation of an intake pump station can be achieved through water demand flow planning, which determines the energy-saving benefits of intelligent cooperative operation between the intake and supply pump stations. In recent years, both domestic and foreign scholars have predicted the water demand flow of intake pump stations through flow balance and water level control to reduce the electrical energy consumption of intake pump stations during operation [18, 19]. Through data analysis, Shan [20] found that the variation of the daily water consumption of urban residents was presented as peak and trough periods, but such a simple division was insufficiently accurate. Xiang [21] divided a daily water volume into four periods by adjusting the level of a clean-water reservoir. This improved the accuracy of water demand flow planning for the intake pump station, but it neglected the influence of seasonal changes on daily water demand. Therefore, this paper makes full use of the regulation and storage capacity of a clean-water reservoir. The clean-water reservoir is a water treatment structure in the water supply system to regulate the uniform water supply of the water plant and meet the uneven water supply of users. The adjustment and storage capacity of a clean-water reservoir can provide a buffer for the flow changes of the water intake pump group and water supply pump group. The flow of the intake pump group over a 24-hour period is planned along with the water level of the clean-water reservoir [22]. The working conditions of the intake pump group can be divided into three categories—peak water consumption periods, trough water consumption periods, and ordinary water consumption periods—based on seasonal and diurnal flow changes in the supply pump group. The flow of the intake pump group is designed to be as stable as possible to avoid frequent switching of the pumps and to enhance safety.

After determining the flow of the water intake-supply pump groups, it is crucial to model the working characteristics of the pumps. In an intake or supply pump group, the pump station basically increases the pumping flow to meet the needs of daily users by means of multiple pumps in parallel [23, 24]. The dynamics of working pump group configurations are not equivalent to a linear combination of the dynamics of each working pump due to upgrades and repairs over the years. Thus, working pump configurations exhibit different dynamics, which would change with long-term operation. It is necessary to accurately determine the dynamics of the working pump configurations. For configurations that only contain constant frequency pumps, it is necessary to consider the nonlinear relationship between the main pipe pressure and the water flow/electrical energy consumption. For variable frequency drive (VFD) pump configurations, pump frequency is an additional consideration. The data-driven approach is effective in regularly modeling this nonlinear relationship by using the latest operational data from working pump configurations to manage the impact caused by upgrades and repairs over the years. The dispatching decision optimization is based on the existing water supply pump groups’ demand flow prediction results, intake pump groups’ demand flow planning results, and pump combination working characteristic model, considering multiple optimization objectives, through the decision optimization method to obtain the intelligent collaborative optimal scheduling for the water intake-supply pump groups.

In addition, the scheduling decision optimization problem has also attracted the attention of scholars in various fields, such as active distribution network [25], interconnected microgrids [26], smart cities [27], electric vehicles [28, 29], and ship power systems [30]. In recent years, both domestic and foreign scholars have employed genetic algorithms (GAs) [22, 31], deep reinforcement learning [32], model predictive control [33], artificial fish swarms [34], and other algorithms [35] to solve the optimal scheduling problem of water pumping stations. Li Jishan and Weiping [36] obtained a scheduling scheme for optimal operation by using self-optimization simulation technology and dynamic programming theory combined with detailed computer analysis and found this provided economic benefits. Barán et al. [37] proposed the Pareto evolutionary intensity algorithm, which further reduced power costs, maintenance costs, the maximum power peak, and the variation in the liquid level in the reservoir. The aforementioned methods have achieved good results in optimizing the scheduling of pump stations, but the importance of optimizing the switching times of pumps has generally been ignored. As a result, the application of scheduling plans recommended by such optimization methods may cause additional power loss or even affect the operational safety and service life of pumps. Compared to the above-mentioned methods, the dynamic programming (DP) algorithm is easier to implement in practical engineering [38, 39]. Intelligent collaborative optimal scheduling methods based on the DP algorithm can optimize not only electrical energy consumption but also the pump switch number. Additionally, the DP algorithm can more efficiently identify global optimal solutions and is easily applicable to water purification plants with different engineering environments.

Previous scholars usually focus on the single optimization of the water intake pump groups or water supply pump groups and have not fully considered the interaction of each other and lack of thinking about the overall system. This manuscript fully explores the relationship between the clean-water reservoir and the water intake-supply pump groups and designs the intelligent collaborative optimal scheduling for the water intake-supply pump groups. This manuscript proposes an intelligent collaborative optimal scheduling method for the water intake-supply pump groups and compares the experimental results to actual scheduling results. More specifically, an intelligent collaborative optimal scheduling method that buffers the flow changes of the water intake and supply pump groups using a clean-water reservoir is proposed to minimize electrical energy consumption and the number of pump switches. A predictive model based on an LSTM network is proposed to predict the flow of the water supply pump group, and a method is proposed to plan the flow of the water intake pump group. A DP algorithm is then used to obtain an optimal scheduling plan for the water intake-supply pump groups. Finally, the numerical results of the proposed methods are analyzed and discussed.

2. Methods

The flow in a water supply pump group is first predicted using an LSTM network over a period of 24 hours. The flow in the water intake pump group is then planned for 24 hours along with the water level of a clean-water reservoir based on the flow of the water supply pump group and engineering experience. Secondly, nonlinear models of working pump configurations are established according to historical data. Finally, intelligent collaborative optimal scheduling objectives are established to minimize the electrical energy consumption and the pump switch number using the constraints of the flow in the water intake-supply pump groups, the main pipe pressure, and the water level of the clean-water reservoir. An optimal schedule for the water intake-supply pump groups, which specifies the working configurations of pumps at each time, can be obtained using the DP algorithm.

2.1. Flow Prediction of a Water Supply Pump Group

The water temperature and main clean water pipe pressure are important factors affecting the flow in a water supply pump group based on the analysis of historical data. Since an LSTM network can memorize and learn features of long-term data, a predictive model is established to predict the flow in the water supply pump group based on an LSTM network. The input variables include decision variables (the flow in the water supply pump group, the water temperature, and the main clean water pipe pressure in the past 24 hours) and feedback correction. The predicted flow in the supply pump group in the next 24 hours is corrected by the difference between the predicted and actual flow in the supply pump group in the past 24 hours. The output variable is the flow of the supply pump group in the next 24 hours. A schematic diagram of the model is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Predictive model based on LSTM network.

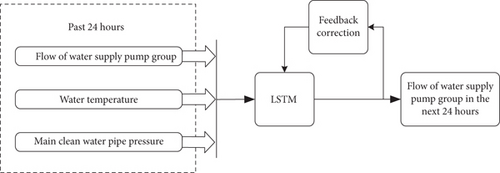
The LSTM network is composed of an input layer, a hidden layer, and an output layer. The LSTM network is different from an RNN because a forget gate f_t, an input gate i_t, an output gate o_t, and a memory cell C_t are added to meet the needs of the time series data. These gates can be opened or closed depending on whether the memory state of the model network (the state of the previous network) in this layer has reached the threshold or not. If it reaches the threshold, it is added to the calculation of the current layer; otherwise, it is ignored. The structure of the LSTM network is shown in Figure A1. x_t is the input at step t, h_t−1 is the output at step t − 1, and h_t is the output at step t [40].

2.1.1. Discarding Information

The first step in the LSTM network is to determine which information will be discarded from the cell state (Eq. (1)). The forget gate reads h(t − 1) and x(t) and returns a value between 0 and 1 and then passes the value to the cell state C(t − 1). 1 means “completely reserved” and 0 means “completely discarded.”

(1)

where W_hf is the weight between the hidden layer and the output layer, W_xf is the weight between the input layer and the hidden layer, b_f is the bias vector, and σ(∙) is the sigmoid activation function.

2.1.2. Storing Information

The second step in the LSTM network is to determine which new information will be stored in the cell state (Eqs. (2)–(4)). i(t) is the selective memory through the sigmoid layer.

is a new candidate value vector computed by the tanh layer.

(2)

(3)

(4)

where W_hi is the weight between the hidden layer at step t − 1 and the hidden layer at step t, W_xi is the weight between the input layer and input gate, W_hC is the weight between the memory cell state at step t and the memory cell state at step t − 1, W_xC is the weight between the memory cell state at step t and the input layer, and b_i and b_C are the bias vectors.

2.1.3. Outputting Information

The last step in the LSTM network is to output the value of h(t).

(5)

(6)

where W_ho is the weight between the memory cell state at step t and the output gate, W_xo is the weight between the input layer and output gate, b_o is the bias vector, and tanh(∙) is the hyperbolic tangent activation function. The predicted flow of the water supply pump group over the next 24 hours can be obtained by using the predictive model, and the predicted results can be utilized as references to schedule the flow of the water supply pump group Q₂ = {q₂(1), q₂(2), ⋯, q₂(t)} (m³/h) over the next 24 hours.

2.2. Flow Planning of the Water Intake Pump Group

The flow of the water supply pump group varies seasonally and daily based on analysis of historical data and engineering experience. The morning and the evening are the peak water consumption periods, the night time is the most significant trough, and the rest of the time is considered the ordinary water consumption period. In different seasons, the change time nodes of the flow of the water supply pump group during the peak water consumption period, trough water consumption period, and ordinary water consumption period will also be different. During the trough water consumption period, the flow of the intake pump group is adjusted to produce a high-water level in the clean-water reservoir, in preparation for high water consumption during the peak consumption period. During the peak consumption period, the flow in the intake pump group is adjusted to replenish the clean-water reservoir. During the ordinary consumption period, the flow of the intake pump group is adjusted to meet the flow of the supply pump group.

It is therefore possible to divide the optimal scheduling plan of the intake pump group in the next 24 hours into three periods according to the seasonal and diurnal flow changes of the supply pump group. May to October can be divided into the peak water consumption period (06:00:00 to 12:59:59, 18:00:00 to 23:59:59), ordinary water consumption period (13:00:00 to 17:59:59), and trough water consumption period (00:00:00 next day to 05:59:59 next day). January to April and November to December are also divided into the peak water consumption period (07:00:00 to 11:59:59, 19:00:00 to 22:59:59), ordinary water consumption period (12:00:00 to 18:59:59), and trough water consumption period (23:00:00 to 06:59:59 the next day). With the water level of the clean-water reservoir kept within the safe range (the minimum safe water level is 0.95 m and the maximum safe water level is 2.95 m), it is ensured as far as possible that the flow of the intake pump group is consistently stable and that the reservoir is at a higher water level. In this study, the flow of the intake pump group Q₁ = {q₁(1), q₁(2), ⋯, q₁(t)} (m³/h) is planned over the next 24 hours:

(7)

(8)

(9)

where

(m³/h) is the flow of the supply pump group at the t-th time in the i-th period, m_i is the number of hours in the i-th period, σ(t) is the feedback adjustment function, Δh(t) is the increment of the water level at the t-th time, and S (m²) is the area of the bottom of the reservoir. If the water level of the reservoir is lower than the minimum or higher than the maximum safe water level, it will be adjusted to meet the safety threshold.

The water adjustment and storage capacity of the reservoir are fully utilized so that the flow required by the intake pump group can be evenly distributed. In each period of time, the required flow levels at each moment are similar. The required flow does not change obviously when the pump switches. This can fundamentally reduce the pump switch number, which can ensure the safety of the pumps.

2.3. Establishment of a Model for the Nonlinear Relationship between the Characteristics of Working Pump Configurations

For working pump configurations containing VFD pumps in the water intake-supply pump groups, nonlinear models between the frequency of the VFD pumps and the water flow/electrical energy consumption/main pipe pressure of the working pump configurations can be directly obtained using the least squares (LS) method. For configurations that contain only constant frequency pumps, nonlinear models between the water flow and the electrical energy consumption/main pipe pressure of the configurations can also be obtained directly using the LS method. Due to uncertain factors such as wear, maintenance, and equipment upgrades, the aforementioned nonlinear models need to be updated regularly.

The LS method can be applied as follows [41]:

(1)
A set of linearly independent functions φ_k(x) and an undetermined coefficient ω_k are selected in advance
(2)
The sum of squares of the distance of each point between f(x) (Eq. (10)) and the fitting function y_i (i = 1, 2, ⋯, n) is compared
(3)
The y_i with the smallest sum of squares of the distance is selected as the fitted result

(10)

For working pump configurations containing VFD pumps, the nonlinear models obtained are as follows:

(11)

(12)

(13)

where

(m³/h) is the water flow of the i_s-th working pump configuration,

(kWh) is its electrical energy consumption,

(MPa) is the main pipe pressure,

(Hz) is the frequency of the VFD pump, and

, and

are the fit coefficients for the nonlinear model. The water intake pump group has 16 working pump configurations containing VFD pumps when s = 1, and the water supply pump group has 16 working pump configurations containing VFD pumps when s = 2.

For the configurations containing only constant frequency pumps, the nonlinear models relating the main pipe pressure and the water flow/electrical energy consumption are as follows:

(14)

(15)

where

, and

are the fit coefficients for the nonlinear models of the i_s-th working pump configuration. The water intake pump group has two configurations containing only constant frequency pumps when s = 1, and the water supply pump group has two configurations containing only constant frequency pumps when s = 2.

2.4. Establishment and Solution of the Intelligent Collaborative Optimal Scheduling Problem

n_s(t)(n_s(t) ∈ [1, 18]) are the serial numbers of the working pump configurations meeting the flow of the water intake pump group or water supply pump group at the t-th time, and M_s(t) is the number set of working pump configurations meeting the flow of the water intake pump group or water supply pump group at the t-th time.

According to the nonlinear fitting functions provided above, an intelligent collaborative optimal scheduling objective for the water intake-supply pump groups that meets the flow of the water intake-supply pump group, the main pipe pressure constraint, and the water level constraint of the clean-water reservoir is established:

(16)

where W₁(t) and W₂(t) (kWh) are the sets of electrical energy consumption (considering the pump switch costs) of each type of working pump configuration meeting the flow of the water intake pump group and the water supply pump group at the t-th time,

and

are the serial numbers of the optimal configurations of the water intake and supply pump groups at the (t − 1)-th time,

are the pump switch costs from

to any working pump configuration of M₁(t), and

are the pump switch costs from

to any working pump configuration of M₂(t).

is given by

(17)

where

is the pump switch cost coefficient from

to any working pump configuration of M_s(t) and K_e (kWh) is the penalty charge when a pump is on or off. The typical pump switch cost coefficient in the water intake-supply pump group is shown in Table A1.

In order to ensure that the VFD pumps in the water intake-supply pump groups run in the high-efficiency range, the variable frequency range of the VFD pump needs to be restricted as in Eq. (18), where f_min and f_max are the minimum and maximum values of the frequency when the VFD pump is operating in the high-efficiency zone. To prevent an excessive pressure difference from causing water hammer and pipe burst accidents, it is necessary to control the difference in the main pipe pressure at adjacent times as in Eq. (19), where P_max is the maximum safe value of the main pipe pressure difference when the pump is switched.

(18)

(19)

The Bellman optimality principle lies at the heart of the DP algorithm, which involves a multistep decision-making process. The DP algorithm solves the original problem by combining the solutions of subproblems. There are two approaches: the top-to-bottom method and the bottom-to-top method. Unlike the divide-and-conquer algorithm or a naive recursion algorithm, the top-to-bottom method memorizes the solution of each subproblem, which greatly reduces the number of repetitive subproblems and the time consumption of the solution process. The current approach, however, does not comprehensively explore all potential subproblems in a recursive manner. Meanwhile, the bottom-to-top method can perfectly fill these loopholes. This method generally needs to properly define the scale of the subproblem so that the solution of any subproblem only depends on the solution of a smaller subproblem. Therefore, we can sort the subproblems by scale and solve them in ascending order. When a certain subproblem is solved, the smaller subproblems it depends on are also solved, and the results are saved. Each subproblem only needs to be solved once, and once solved (the first time we encounter it), all its premise subproblems are solved. These two methods have the same asymptotic running time. The difference is that the bottom-to-top method can find the global optimal solution, while the top-to-bottom method may only find the local optimal solution. Obviously, the bottom-to-top method is more appropriate for finding the optimal solution.

A structural diagram of the intelligent collaborative optimal scheduling decision-making process is shown in Figure 2. For step k + 1 of the scheduling process in the next 24 hours (24 steps in total, T = 24), the decision variable is W_s(k + 1), the state input is M_s(k), and the state output is M_s(k + 1). The relationship between the state input M_s(k) and the state output M_s(k + 1) is determined through the decisions made at step k + 1. When the decision is completed in each step, the recursive relationship can be used to convert the law of the entire objective, so that the strategy constituted by all decisions is the optimal solution of the original optimization objective [42].

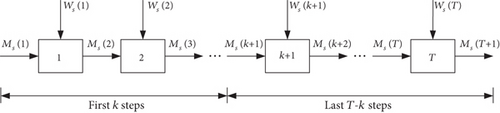
The decision-making process can be transformed into the selection of a pump scheduling plan for the next 24 hours that minimizes the power consumption after considering the pump switch costs. This ensures minimal power consumption by reducing the number of pump switches. As shown in Figure A2, there are n_s(k) choices for W_s(k) at step k and choices for the overall decision-making process.

For a T-step decision-making process, suppose that the performance index function is as given in

(20)

where l(M_s(k), W_s(k)) is the utility function. The goal of the decision-making process is to minimize the performance index function. Suppose the performance index function for all possible steps M_s(k + 1) starting from step k + 1 is

, and all optimal decisions starting from step k + 1 have been determined as

, … . The cost function at step k can then be expressed as

. According to the Bellman optimality principle, the optimal performance index function at step k is as follows:

(21)

The electrical energy consumption considering the pump switch costs (kWh) and the working pump configurations of the optimal scheduling plan is calculated using the recursive method. The electrical energy consumption (kWh) of the optimal scheduling plan can be obtained by subtracting the water pump switch cost from . Then, using Eq. (12), the VFD pump frequency of the working pump configuration of the optimal scheduling plan (Hz) can be obtained (if the working pump configuration contains a VFD pump).

3. Results and Discussion

3.1. Water Supply Pump Group Prediction

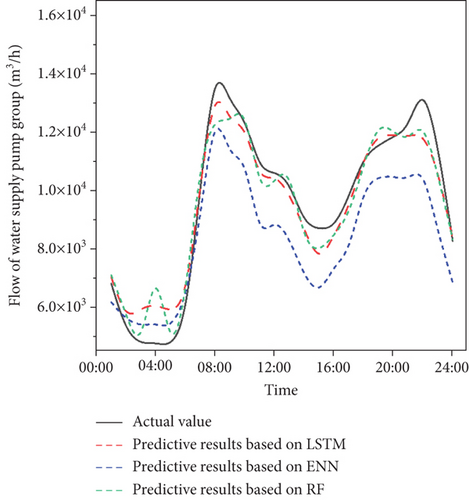
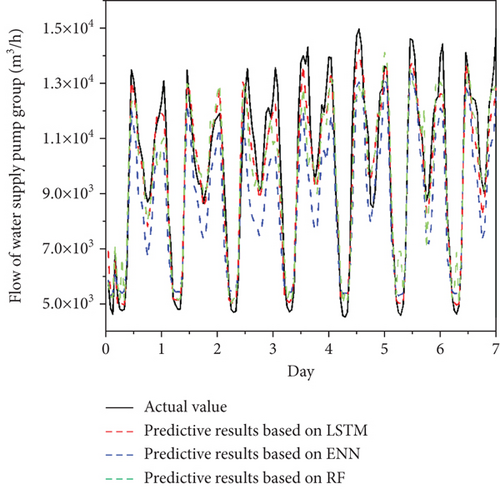
It can be seen from Figure 3 that the actual peak value of peak water consumption period is 13493 m³/h, of which the predictive peak values based on LSTM, ENN, and RF are 13027 m³/h, 11995 m³/h, and 12905 m³/h. The actual trough value of ordinary water consumption period is 8702 m³/h, of which the predictive peak values based on LSTM, ENN, and RF are 7840 m³/h, 6730 m³/h, and 8024 m³/h. The actual trough value of trough water consumption period is 4762 m³/h, of which the predictive peak values based on LSTM, ENN and RF are 5189 m³/h, 5393 m³/h, and 5432 m³/h. Predictive flows of the water supply pump group based on LSTM are closer than flows based on ENN and RF, and the change trend of predictive results based on LSTM is closer to the actual values than the predictive results based on ENN and RF, indicating that the predictive results based on LSTM are more precise. It can be seen from Figure 4 that the values and peak positions of the predictive results based on LSTM are closer to the actual value not only on weekdays but also on weekends. On Sunday, the actual peak values and the predictive peak values of peak water consumption period based on LSTM are 14109 m³/h and 13676 m³/h, while the predictive peak values based on ENN and RF are only 12845 m³/h and 12485 m³/h. The actual trough value and the predictive trough value of ordinary water consumption period based on LSTM are 8743 m³/h and 8266 m³/h, while the predictive peak values based on ENN and RF are only 7224 m³/h and 7005 m³/h. Since the LSTM algorithm realizes long-term learning and retention of key information through the switch control of the gate in the memory block, the prediction accuracy of special time nodes is improved. Compared with the predictive flow of the water supply pump group based on ENN, the predictive flow of the water supply pump group based on LSTM reduces the lag of prediction results and improves the dynamicity of the prediction under the condition of ensuring high prediction accuracy. The average error between the predictive flow based on LSTM and the actual flow of the water supply pump group is about 6.08%. What is more, the average error observed on weekdays and weekends is 5.90% and 6.52%, respectively. Meanwhile, the average error between the predictive flow based on ENN and the actual flow of the water supply pump group is about 13.51%. And the error vales are 11.61% and 18.25%, respectively, for weekdays and weekends. The average error between the predictive flow based on RF and the actual flow of the water supply pump group is about 7.95%. And the error vales are 7.52% and 9.04%, respectively, for weekdays and weekends. It could be concluded that the error of predictive flow based on LSTM of the water supply pump group is smaller than the actual flow of the water supply pump group for all days.

The short-duration memory neural network has the same three layers as the ENN, namely, the input layer, the hidden layer, and the output layer. The weight matrix between these layers and the information from historical moments can be transmitted to the current moment. However, the difference is that when outputting the result for the current moment, the short- and long-term memory neural network also outputs the unit state of the current moment, ensuring that the gradient will not disappear or explode after many time steps. At the same time, it also has three special “gate” structures, namely, the forget gate, the input gate, and the output gate. These structures allow for selective information passage, which can affect the data state at every moment in the neural network model. Each “gate” is controlled by the activation function and will output a value within the interval (0,1) that indicates the extent to which data can be retained and transmitted at the current moment. Therefore, compared with the ENN, the LSTM neural network has better accuracy and stability. Compared with LSTM algorithm, RF algorithm has higher requirements on the type and scale of training data. At the same time, RF algorithm cannot make predictions beyond the range of training set data, which may lead to overfitting when modeling some data with specific noise. Moreover, since the flow rate of the pump at each moment is highly correlated with time, the current state of the moment is related to the historical state of the previous moment to a certain extent. LSTM deep network can well explore and utilize the influence between them.

3.2. Planning for a Clean-Water Reservoir and Water Intake Pump Group

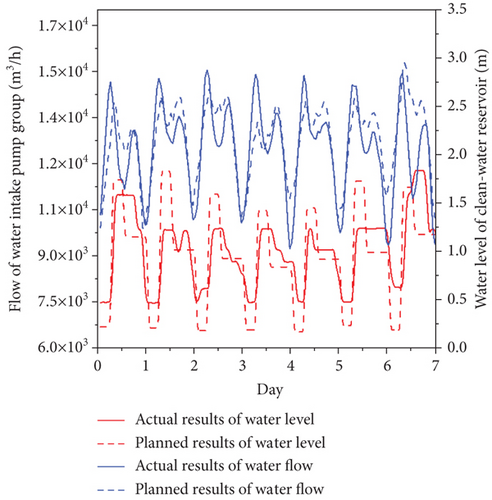
The water level of the clean-water reservoir was planned based on the historical data of changing regulation of water demand of the water supply pump group and the predictive flow of the water supply pump group in the next 24 hours. Figure 5 shows the planned water level of the clean-water reservoir, actual water level of the clean-water reservoir, planned flow of the water intake pump group, and actual flow of the water intake pump group in 24 consecutive hours.

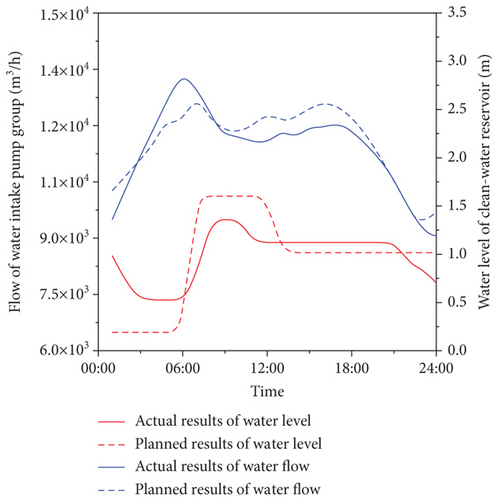
The average planned and actual flow of the water intake pump group are 8721.23 m³/h and 8792.50 m³/h, with an error of 0.81%. The minimum and average planned water level of the clean-water reservoir are 1.35 m and 2.16 m, which is higher than the minimum (1.20 m) and average actual water level (2.10 m) of the clean-water reservoir. Figure 5 displays that the difference between the planned peak and trough is smaller than the difference between the actual peak and trough of the water level of clean-water reservoir. It indicates that the flow of the water intake pump group would stably increase the water level of clean-water reservoir, reduce the pump lift and the main clean water pipe pressure, and then reduce the electric energy consumption of the water supply pump group. Figure 5 also indicates a significant change in the planned flow of water intake pump group around 7:00, with a relatively small deviation from the actual value compared to other times. The planned flow of the water intake pump group is slightly more stable than the actual value, which is mainly manifested in that the number of changes in the planned flow of water intake pump group is less than the actual value. It could reduce the pump switch number and facilitate the acquisition of the subsequent optimal scheduling plan. In combination with Figure 6, it can be seen that the difference between the peak value and the trough value is smaller than the actual value under the premise that the water level of the clean-water reservoir is high at most times, and the planned values of the clean-water reservoir water level is higher than the actual values at weekends. Under the premise of meeting the demand flow of water supply pumping station, the change times of the planned water flow of water intake pumping station can be steadily lower than the actual values, which proves the stability and reliability of the planning method of water intake pumping station demand flow. Under the condition that the water demand of the pumping station and the water level of the clean-water reservoir are met, the planning value of the water demand of the pumping station and the higher water level of the clean-water reservoir can be obtained.

3.3. The Nonlinear Relationship between the Operating Characteristics of Working Pump Configurations

A total of 18 working pump configurations in the water intake pump group were nonlinearly fitted based on the LS method, including 16 working pump configurations containing VFD pumps and two working pump configurations containing only constant frequency pumps. Eighteen working pump configurations in the water supply pump group were also nonlinearly fitted based on the LS method, including 16 working pump configurations containing VFD pumps and two working pump configurations containing only constant frequency pumps. For the working pump configurations containing VFD pumps, , , and represent the goodness of fit between the frequency of the VFD pumps and water flow/electrical energy consumption/main pipe pressure of the working pump configurations, as shown in Table 1. For the working pump configurations containing only constant frequency pumps, and represent the goodness of fit between the main pipe pressure and the water flow/electrical energy consumption of the working pump configurations, which are shown in Table 2.

Table 1. The goodness of fit of working pump configurations containing VFD pump in the water intake-supply pump group.

Working pump configuration in the water intake pump group				Working pump configuration in the water supply pump group
1#, 3#	0.619	0.874	0.898	1#, 3#	0.906	0.851	0.688
2#, 3#	0.471	0.887	0.980	1#, 6#	0.696	0.662	0.770
3#, 4#	0.681	0.896	0.857	1#, 2#, 3#	0.847	0.720	0.936
3#, 5#	0.585	0.874	0.994	1#, 3#, 4#	0.665	0.647	0.768
1#, 6#	0.544	0.877	0.865	1#, 3#, 5#	0.656	0.647	0.734
2#, 6#	0.347	0.894	0.799	1#, 2#, 6#	0.863	0.872	0.941
4#, 6#	0.915	0.919	0.986	1#, 4#, 6#	0.643	0.641	0.852
5#, 6#	0.756	0.879	0.863	1#, 5#, 6#	0.722	0.710	0.909
1#, 3#, 4#	0.999	0.998	0.999	1#, 6#, 7#	0.845	0.876	0.971
1#, 3#, 5#	0.835	0.887	0.887	2#, 4#, 6#	0.953	0.853	0.922
2#, 3#, 5#	0.721	0.868	0.942	1#, 2#, 3#, 4#	0.725	0.648	0.744
1#, 2#, 6#	0.633	0.933	0.879	1#, 3#, 4#, 5#	0.497	0.499	0.775
1#, 5#, 6#	0.796	0.887	0.938	1#, 3#, 4#, 7#	0.515	0.649	0.837
2#, 4#, 6#	0.787	0.868	0.939	1#, 2#, 4#, 6#	0.768	0.895	0.911
2#, 5#, 6#	0.620	0.888	0.720	1#, 4#, 5#, 6#	0.977	0.969	0.992
4#, 5#, 6#	0.973	0.967	0.991	1#, 4#, 6#, 7#	0.999	0.999	0.990

Table 2. The goodness of fit of working pump configurations containing only constant frequency pumps in the water intake-supply pump group.

Working pump configuration in the water intake pump group			Working pump configuration in the water supply pump group
2#, 4#	0.999	0.842	1#, 4#	0.648	0.834
2#, 5#	0.789	0.403	1#, 4#, 5#	0.922	0.795

The formula for the calculation of the goodness of fit is

(22)

where SSR is the regression sum of squares, SST is the sum of squares,

is the regression estimate of y, and

is the average of the actual y. When R² is in the range [0.64, 1], it indicates that the fitting results show a strong correlation with the initial data. When R² is in the range [0.36, 0.64], it indicates that the fitting results show a weak correlation with the initial data. When R² is in the range [0, 0.36], it indicates that the fitting results are not correlated with the initial data. It can be seen from Table 1 that 89.58% of the fitting results showed a strong correlation with the initial data and 9.38% of the fitting results showed a weak correlation with the initial data. As shown in Table 2, 87.50% of the fitting results are strongly correlated with the initial data, and 12.50% of the fitting results are weakly correlated with the initial data. The main reason for the inadequacy of the fitting results of the #2 and #6 working pump configurations in the water intake pump group is that the recorded scheduling data are not accurate enough due to instrumental errors. The results show that the nonlinear function relationships are reliable, which is convenient for solving the objective function later. Due to uncertainties such as wear, maintenance, and equipment upgrades, the above nonlinear models will be updated regularly.

3.4. An Optimal Scheduling Plan for the Water Intake-Supply Pump Groups

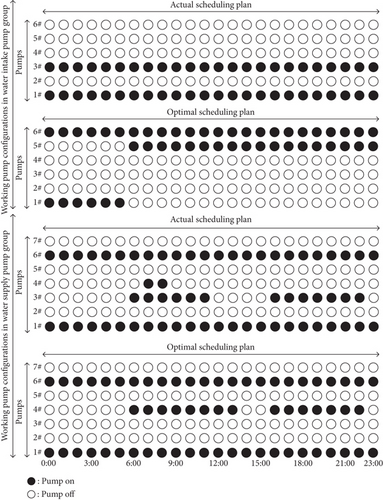
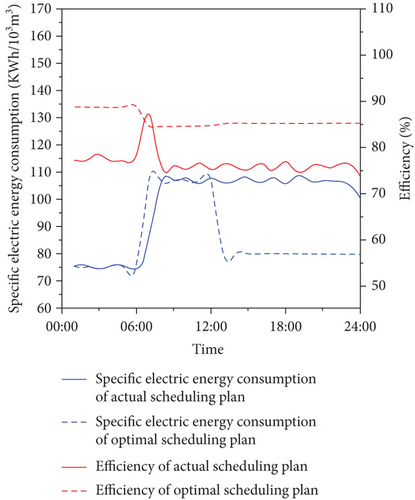
Working pump configurations of actual scheduling plan and optimal scheduling plan in the water intake-supply pump groups in 24 consecutive hours are shown in Figure 7. The main water pipe pressure and VFD pump frequency of actual scheduling plan and optimal scheduling plan in the water intake-supply pump groups in 24 consecutive hours are shown in Figure A3. Specific electric energy consumption and efficiency of actual scheduling plan and optimal scheduling plan in the water intake-supply pump groups in 24 consecutive hours are shown in Figure 8.

It can be seen from Figure 7 that the optimal scheduling plan in the water supply pump group mainly consist of 2~3 pumps, which avoids the increase in electric energy consumption caused by the working pump configurations of 4 pumps. The working pump configurations of actual scheduling plan changed 5 times in the water supply pump group while working pump configurations of optimal scheduling plan changed 4 times in the water supply pump group. Figure A3 indicates that the frequency change of the VFD pumps of the optimal scheduling plan is frequent and that the change in the main pipe pressure is stable. This shows that the optimal scheduling scheme reduces the pump switching frequency. It can be seen from Figures 7 and 8(a) that although the actual scheduling plan in the water intake pump group does not switch the pump while the optimal scheduling plan switches once, the specific electrical energy consumption and efficiency of the optimal scheduling plan are significantly better than the actual scheduling plan. After 12 o’clock at noon, the specific electrical energy consumption of actual scheduling plan in the water intake pump group set is about 105 kWh/10³ m³ for a long time, while the optimal scheduling plan is only 80 kWh/10³ m³. The maximum and minimum efficiency of actual scheduling plan in the water intake pump group are 87.40% and 73.65%, whereas the maximum and minimum efficiency in optimal scheduling plan reach up to 88.89% and 85.32%, respectively. It also can be revealed from Figure 8(b) that the minimum specific electrical energy consumption of actual scheduling plan and optimal scheduling plan in the water supply pump group is 111.05 kWh/10³ m³ and 95.13 kWh/10³ m³, respectively. Meanwhile, the maximum and minimum efficiency of actual scheduling plan in the water supply pump group are 75.37% and 56.66%, and the maximum and minimum efficiency of optimal scheduling plan are 76.70% and 64.60%, respectively. Additionally, most of the time, the specific electrical energy consumption of the optimal scheduling plan is lower than that of the actual scheduling plan, the efficiency of the optimal scheduling plan is higher than that of the actual scheduling plan, and the change in the specific electrical energy consumption of the optimal scheduling plan tends to be more stable. This could not only prolong the pump life but also save electrical energy. The specific electrical energy consumption of working pump configurations Sec_s(t) is calculated as Eq. (23), and the efficiency of working pump configurations η_s(t) is calculated as Eq. (24):

(23)

(24)

where J_s(t) is the electrical energy consumption of working pump configurations at t-th time, q_s(t) is the flow of working pump configurations at t-th time, P_u is the output power of water pump at t-th time, P_a is the shaft power of water pump at t-th time, and P_s(t) is the main water pipe pressure of working pump configurations at t-th time. After calculation, combined with Figure 8, it can be concluded that the specific electrical energy consumption and efficiency of optimal scheduling plan in the water intake pump group in 24 consecutive hours are 85.64 kWh/10³ m³ and 86.10%, of which the actual scheduling plan is 98.01 kWh/10³ m³ and 76.76% and electrical energy saving and efficiency improvement are 12.60% and 12.20%. The specific electrical energy consumption and efficiency of optimal scheduling plan in the water supply pump group in 24 consecutive hours are 115.19 kWh/10³ m³ and 72.92%, of which the actual scheduling plan is 122.40 kWh/10³ m³ and 67.30% and electrical energy saving and efficiency improvement are 5.89% and 8.35%. The total specific electrical energy consumption and total efficiency of optimal scheduling plan in the water intake-supply pump group in 24 consecutive hours are 100.41 kWh/10³ m³ and 79.51%, of which the actual scheduling plan is 110.20 kWh/10³ m³ and 72.03% and electrical energy saving and efficiency improvement are 8.89% and 10.40%.

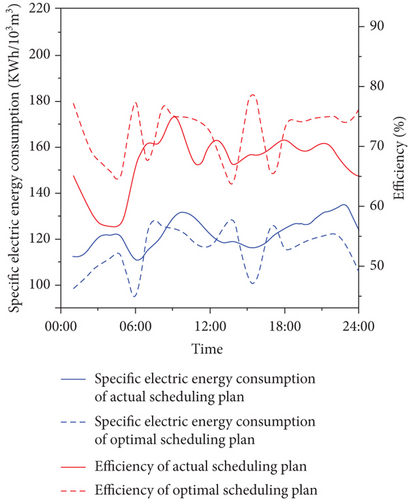
The specific electric energy consumption and efficiency of actual scheduling plan and optimal scheduling plan in the water intake-supply pump groups in 7 consecutive days are shown in Table 3. The operation comparisons of actual scheduling plan and optimal scheduling plan in the water intake-supply pump groups for 7 consecutive days are shown in Table A2.

Table 3. Specific electric energy consumption and efficiency of actual scheduling plan and optimal scheduling plan in the water intake-supply pump groups on 7 consecutive days.

Day	Specific electric energy consumption (kWh/10³ m³)		Average efficiency (%)
Day	Actual	Optimal	Actual	Optimal
Day 1	106.56	97.80	72.24	88.61
Day 2	105.21	99.58	72.54	87.57
Day 3	110.20	100.41	72.03	86.10
Day 4	116.47	102.30	72.87	84.36
Day 5	128.14	104.19	71.50	90.84
Day 6	111.79	101.87	73.18	89.83
Day 7	112.32	100.60	73.59	86.38

The premise to be explained is that the optimal scheduling plan of the water intake-supply pump group meets the following three constraints: the water level of the clean-water reservoir changes within the safe water level, the pressure difference of the main pipe is less than the safe pressure difference, and the VFD pump operates within the high efficiency interval. It can be seen from Table A2 that the pump switch number of the optimal scheduling plan is less than the actual scheduling plan, especially in the water supply pump group. Compared with the actual scheduling plan, which switched 44 times in total, the optimal scheduling plan only switched 26 times. The optimal scheduling plan solved the problem of VFD pumps working out of high-efficiency zone. The VFD pumps of optimal scheduling plan all worked in the range of high-efficiency zone while the numbers of the VFD pumps of actual scheduling plan working out of high-efficiency zone in the water intake pump group and water supply pump group were 34 and 30. The difference was attributed to the intelligent collaborative optimal scheduling method that utilized the frequency modulation effect of the variable frequency pump and replaced switching the pump by adjusting the frequency of the variable frequency pump as much as possible, which could not only prolong the life of the pump but also reduce electrical energy consumption. The specific electrical energy consumption of the optimal scheduling plan and actual scheduling plan in the water intake-supply pump groups during 7 consecutive days is 100.96 and 113.06 kWh/10³ m³ (Table 3), respectively. The electrical energy decreased by 10.70%. The average efficiency of the optimal scheduling plan in the water intake-supply pump groups over seven consecutive days was 80.12%, while that of the actual scheduling plan was 72.39%, and the average efficiency was increased by 10.68%. The above results proved that the optimal scheduling plan obtained from the intelligent collaborative optimal scheduling method in the water intake-supply pump groups was more energy-saving and more stable and relied on a smaller number of pump switches.

4. Conclusion

The intelligent collaborative optimal scheduling method was proposed in this study. LSTM was used to predict the flow of the water supply pump group in the next 24 hours, and the flow of the water intake pump group in the next 24 hours was planned according to the water level of the clear reservoir. The DP algorithm was used to obtain the optimal scheduling plan of the water intake-supply pump group in the next 24 hours. Experimental results showed that the intelligent collaborative optimal scheduling plan reduced the pump switch number by 11 times while decreasing electric energy consumption by 10.70% and increasing efficiency by 10.68% compared to the actual scheduling plan. This method made full use of the VFD pumps under the premise of ensuring the flow of the water intake-supply pump groups and the safe change of the main pipe pressure. The unused working pump configurations can be excavated in the future under the premise of ensuring production safety.

This proposed optimization is aimed at real-time data acquisition of water purification plants to show the optimal scheduling scheme. In the next step, an automatic closed-loop control system can be designed to carry out real-time scheduling control of water intake and water supply pumping stations, and more pump combinations can be studied in the future. Finally, due to the actual production process, it will also involve the operation of the pumping station fault and other problems, which need to carry out fault diagnosis and fault maintenance; the future can consider these special factors and design the pumping station fault diagnosis optimization scheduling system.

Abbreviations

RF:: Random forest
ANN:: Artificial neutral network
MLR:: Multiple linear regression
GA:: Genetic algorithm
SVR:: Support vector regression
MARS:: Multivariate adaptive regression splines
PPR:: Projection pursuit regression
KNN:: k-nearest neighbor
PSO:: Particle swarm optimization
LSTM:: Long short-term memory
ENN:: Elman neural network
RNN:: Recurrent neural network
LS:: Least squares
VFD:: Variable frequency drive.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Authors’ Contributions

Dongsheng Wang contributed to the conceptualization and methodology. Peng Zhang participated in the supervision and visualization and wrote, reviewed, and edited the manuscript. Haixiang Ma contributed to the methodology and wrote, reviewed, and edited the manuscript. Zhixuan Li contributed to the methodology and wrote, reviewed, and edited the manuscript. Suqian Xu was responsible for the software and reviewed the manuscript. Chaoqun Tan wrote, reviewed, and edited the manuscript.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos. 52170001 and 52070041).

Open Research

Data Availability

Data is available upon reasonable request from the corresponding author.

Supporting Information

References

1 Dongdong Yuan W. J., Sha A., Xiao J., Wu W., and Wang T., Technology method and functional characteristics of road thermoelectric generator system based on Seebeck effect, Applied Energy. (2023) 331, article 120459, https://doi.org/10.1016/j.apenergy.2022.120459.
10.1016/j.apenergy.2022.120459
Web of Science® Google Scholar
2 Cihan A., Hacıhafızogˇlu O., and Kahveci K., Energy–exergy analysis and modernization suggestions for a combined–cycle power plant, International Journal of Energy Research. (2006) 30, no. 2, 115–126, https://doi.org/10.1002/er.1133, 2-s2.0-31644436458.
10.1002/er.1133
CAS Web of Science® Google Scholar
3 Wei Jiang D. Y., Shan J., Ye W., Lu H., and Sha A., Experimental study of the performance of porous ultra-thin asphalt overlay, International Journal of Pavement Engineering. (2022) 23, 2049–2061, https://doi.org/10.1080/10298436.2020.1837826.
10.1080/10298436.2020.1837826
Web of Science® Google Scholar
4 Luna T., Ribau J., Figueiredo D., and Alves R., Improving energy efficiency in water supply systems with pump scheduling optimization, Journal of Cleaner Production. (2019) 213, 342–356, https://doi.org/10.1016/j.jclepro.2018.12.190, 2-s2.0-85059560365.
10.1016/j.jclepro.2018.12.190
Web of Science® Google Scholar
5 Zhang Z. and Kusiak A., Models for optimization of energy consumption of pumps in a wastewater processing plant, Journal of Energy Engineering. (2011) 137, no. 4, 159–168, https://doi.org/10.1061/(ASCE)EY.1943-7897.0000051, 2-s2.0-84862956064.
10.1061/(ASCE)EY.1943-7897.0000051
Web of Science® Google Scholar
6 Zhuan X. and Xia X., Development of efficient model predictive control strategy for cost-optimal operation of a water pumping station, IEEE Transactions on Control Systems Technology. (2013) 21, no. 4, 1449–1454, https://doi.org/10.1109/TCST.2012.2205253, 2-s2.0-84879922318.
10.1109/TCST.2012.2205253
Web of Science® Google Scholar
7 Makaremi A. H. Y. and Ghafouri H. R., Optimization of pump scheduling program in water supply systems using a self-adaptive NSGA-II; a review of theory to real application, Water Resources Management. (2017) 31, no. 4, 1283–1304, https://doi.org/10.1007/s11269-017-1577-x, 2-s2.0-85011796777.
10.1007/s11269-017-1577-x
Web of Science® Google Scholar
8 Hong S. P., Kim T., and Lee S., A precision pump schedule optimization for the water supply networks with small buffers, Omega. (2019) 82, 24–37, https://doi.org/10.1016/j.omega.2017.12.001, 2-s2.0-85038857083.
10.1016/j.omega.2017.12.001
Google Scholar
9 Wood D. J., Waterhammer analysis—essential and easy (and efficient), Journal of Environmental Engineering. (2005) 131, no. 8, 1123–1131, https://doi.org/10.1061/(ASCE)0733-9372(2005)131:8(1123), 2-s2.0-23144461506.
10.1061/(ASCE)0733-9372(2005)131:8(1123)
CAS Web of Science® Google Scholar
10 Tang Y., Zheng G., and Zhang S., Optimal control approaches of pumping stations to achieve energy efficiency and load shifting, International Journal of Electrical Power & Energy Systems. (2014) 55, 572–580, https://doi.org/10.1016/j.ijepes.2013.10.023, 2-s2.0-84887297275.
10.1016/j.ijepes.2013.10.023
Web of Science® Google Scholar
11 Wang J. Y., Chang T. P., and Chen J. S., An enhanced genetic algorithm for bi-objective pump scheduling in water supply, Expert Systems with Applications. (2009) 36, no. 7, 10249–10258, https://doi.org/10.1016/j.eswa.2009.01.054, 2-s2.0-67349189815.
10.1016/j.eswa.2009.01.054
Web of Science® Google Scholar
12 Herrera M., Torgo L., Izquierdo J., and Pérez-García R., Predictive models for forecasting hourly urban water demand, Journal of Hydrology. (2010) 387, no. 1-2, 141–150, https://doi.org/10.1016/j.jhydrol.2010.04.005, 2-s2.0-78549256372.
10.1016/j.jhydrol.2010.04.005
Web of Science® Google Scholar
13 Antunes A., Andrade-Campos A., Sardinha-Lourenço A., and Oliveira M. S., Short-term water demand forecasting using machine learning techniques, Journal of Hydroinformatics. (2018) 20, no. 6, 1343–1366, https://doi.org/10.2166/hydro.2018.163, 2-s2.0-85057978717.
10.2166/hydro.2018.163
Web of Science® Google Scholar
14 Pesantez J. E., Berglund E. Z., and Kaza N., Smart meters data for modeling and forecasting water demand at the user-level, Environmental Modelling & Software. (2020) 125, article 104633, https://doi.org/10.1016/j.envsoft.2020.104633.
10.1016/j.envsoft.2020.104633
Web of Science® Google Scholar
15 Abbasimehr H., Shabani M., and Yousefi M., An optimized model using LSTM network for demand forecasting, Computers & Industrial Engineering. (2020) 143, article 106435, https://doi.org/10.1016/j.cie.2020.106435.
10.1016/j.cie.2020.106435
Web of Science® Google Scholar
16 Lei J., Ren C., Li W., Fu L., Li Z., Ni Z., Li Y., Liu C., Zhang H., Chen Z., and Yu T., Prediction of crucial nuclear power plant parameters using long short-term memory neural networks, International Journal of Energy Research. (2022) 46, no. 15, 21467–21479, https://doi.org/10.1002/er.7873.
10.1002/er.7873
Web of Science® Google Scholar
17 Zheng L., Hou Y., Zhang T., and Pan X., Performance prediction of fuel cells using long short-term memory recurrent neural network, International Journal of Energy Research. (2021) 45, no. 6, 9141–9161, https://doi.org/10.1002/er.6443.
10.1002/er.6443
CAS Web of Science® Google Scholar
18 Wanpeng C., Study on operation optimization of water intake and water supply pumping station system, 2020, Huazhong University of Science and Technology, Wuhan.
Google Scholar
19 Denghao Y., Analysis of operation and dispatching management of water intake pumping station, 2021, Technical Supervision in Water Resources.
Google Scholar
20 Shan Z. S. W., An empirical study on the law of urban residents′ water consumption, 2007, City and Town Water Supply.
Google Scholar
21 Xiang H., Water treatment works take the pump set of energy saving optimization scheduling research, 2020, Nanjing university of posts and telecommunications.
Google Scholar
22 Chen W., Tao T., Zhou A., Zhang L., Liao L., Wu X., Yang K., Li C., Zhang T. C., and Li Z., Genetic optimization toward operation of water intake-supply pump stations system, Journal of Cleaner Production. (2021) 279, article 123573, https://doi.org/10.1016/j.jclepro.2020.123573.
10.1016/j.jclepro.2020.123573
Web of Science® Google Scholar
23 Ibarra D. and Arnal J., Parallel programming techniques applied to water pump scheduling problems, Journal of Water Resources Planning and Management. (2014) 140, no. 7, article 06014002, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000439, 2-s2.0-84929074944.
10.1061/(ASCE)WR.1943-5452.0000439
Web of Science® Google Scholar
24 Olszewski P., Genetic optimization and experimental verification of complex parallel pumping station with centrifugal pumps, Applied Energy. (2016) 178, 527–539, https://doi.org/10.1016/j.apenergy.2016.06.084, 2-s2.0-84979917454.
10.1016/j.apenergy.2016.06.084
Web of Science® Google Scholar
25 Ma H., Liu Z., Li M., Wang B., Si Y., Yang Y., and Mohamed M. A., A two-stage optimal scheduling method for active distribution networks considering uncertainty risk, Energy Reports. (2021) 7, 4633–4641, https://doi.org/10.1016/j.egyr.2021.07.023.
10.1016/j.egyr.2021.07.023
Web of Science® Google Scholar
26 Yin F., Hajjiah A., Jermsittiparsert K., Al-Sumaiti A. S., Elsayed S. K., Ghoneim S. S., and Mohamed M. A., A secured social-economic framework based on PEM-blockchain for optimal scheduling of reconfigurable interconnected microgrids, IEEE Access. (2021) 9, 40797–40810, https://doi.org/10.1109/access.2021.3065400.
10.1109/ACCESS.2021.3065400
Web of Science® Google Scholar
27 Duan Q., Quynh N. V., Abdullah H. M., Almalaq A., Do TD A. S. M., and Mohamed M. A., Optimal scheduling and management of a smart city within the safe framework, IEEE Access. (2020) 8, 161847–161861, https://doi.org/10.1109/access.2020.3021196.
10.1109/ACCESS.2020.3021196
Web of Science® Google Scholar
28 Li Ma C. C., Guo J., Shi B., Ding S., and Mei K., Direct yaw-moment control of electric vehicles based on adaptive sliding mode, Mathematical Biosciences and Engineering. (2023) 20, 13334–13355, https://doi.org/10.3934/mbe.2023594.
10.3934/mbe.2023594
PubMed Web of Science® Google Scholar
29 Li Ma K. M., Ding S., and Pan T., Design of adaptive fuzzy fixed-time HOSM controller subject to asymmetric output constraints, IEEE Transactions on Fuzzy Systems. (2023) 31, 2989–2999, https://doi.org/10.1109/TFUZZ.2023.3241147.
10.1109/TFUZZ.2023.3241147
Web of Science® Google Scholar
30 Mohamed M. A., Chabok H., Awwad E. M., El-Sherbeeny A. M., Elmeligy M. A., and Ali Z. M., Stochastic and distributed scheduling of shipboard power systems using MθFOA- ADMM, Energy. (2020) 206, article 118041, https://doi.org/10.1016/j.energy.2020.118041.
10.1016/j.energy.2020.118041
Web of Science® Google Scholar
31 Savic D. A., Walters G. A., and Schwab M., D. Corne and J. L. Shapiro, Multiobjective genetic algorithms for pump scheduling in water supply, Evolutionary Computing, 1997, Springer, Berlin Heidelberg, Berlin, Heidelberg, 227–235, https://doi.org/10.1007/BFb0027177.
10.1007/BFb0027177
Google Scholar
32 Xu J., Wang H., Rao J., and Wang J., Zone scheduling optimization of pumps in water distribution networks with deep reinforcement learning and knowledge-assisted learning, Soft Computing. (2021) 25, no. 23, 14757–14767, https://doi.org/10.1007/s00500-021-06177-3.
10.1007/s00500-021-06177-3
Web of Science® Google Scholar
33 van Staden A. J., Zhang J., and Xia X., A model predictive control strategy for load shifting in a water pumping scheme with maximum demand charges, Applied Energy. (2011) 88, no. 12, 4785–4794, https://doi.org/10.1016/j.apenergy.2011.06.054, 2-s2.0-80052262391.
10.1016/j.apenergy.2011.06.054
Web of Science® Google Scholar
34 Yu H., Zhao T., and Zhang J., Development of a distributed artificial fish swarm algorithm to optimize pumps working in parallel mode, Science and Technology for the Built Environment. (2018) 24, no. 3, 248–258, https://doi.org/10.1080/23744731.2017.1375011, 2-s2.0-85030558863.
10.1080/23744731.2017.1375011
Web of Science® Google Scholar
35 Tian X. Q. D. Y. M. and Li H., Application of genetic algorithm in optimal scheduling of water supply system, China Water & Wastewater. (2001) 17, 63–65, https://doi.org/10.3321/j.issn:1000-4602.2001.12.019.
10.3321/j.issn:1000-4602.2001.12.019
Google Scholar
36 Li Jishan L. L. and Weiping P., Research on optimal operation and economic operation of multi-stage pumping station, Journal of Hydraulic Engineering. (1992) 37, 18–26.
Google Scholar
37 Barán B. N., von Lücken C., and Sotelo A., Multi-objective pump scheduling optimisation using evolutionary strategies, Advances in Engineering Software. (2005) 36, no. 1, 39–47, https://doi.org/10.1016/j.advengsoft.2004.03.012, 2-s2.0-9644278107.
10.1016/j.advengsoft.2004.03.012
Web of Science® Google Scholar
38 Zhuan X. and Xia X., Optimal operation scheduling of a pumping station with multiple pumps, Applied Energy. (2013) 104, 250–257, https://doi.org/10.1016/j.apenergy.2012.10.028, 2-s2.0-84870907218.
10.1016/j.apenergy.2012.10.028
Web of Science® Google Scholar
39 Kim Y. H., Yoo C., and Lee I.-B., Optimization of biological nutrient removal in a SBR using simulation-based iterative dynamic programming, Chemical Engineering Journal. (2008) 139, no. 1, 11–19, https://doi.org/10.1016/j.cej.2007.07.070, 2-s2.0-41949094260.
10.1016/j.cej.2007.07.070
CAS Web of Science® Google Scholar
40 Greff K., Srivastava R. K., Koutnik J., Steunebrink B. R., and Schmidhuber J., LSTM: a search space odyssey, IEEE Transactions on Neural Networks and Learning Systems. (2017) 28, no. 10, 2222–2232, https://doi.org/10.1109/TNNLS.2016.2582924, 2-s2.0-84979010616, 27411231.
10.1109/TNNLS.2016.2582924
PubMed Web of Science® Google Scholar
41 Liu S., Method of Least Squares Problem Calculation, 1989, Beijing University of Technology Press.
Google Scholar
42 Jiang X., Principle and Application of Dynamic Programming, 1988, Xian Jiaotong University Press.
Google Scholar

Citing Literature

All articles

Intelligent Collaborative Optimal Scheduling for Water Intake-Supply Pump Groups in Drinking Water Treatment Plants

Abstract

1. Introduction

2. Methods