International Journal of Energy Research

Volume 2024, Issue 1 7792658

Research Article

Open Access

Multiobjective and Coordinated Reconfiguration and Allocation of Photovoltaic Energy Resources in Distribution Networks Using Improved Clouded Leopard Optimization Algorithm

Mohana Alanazi,

Corresponding Author

Mohana Alanazi

[email protected]

orcid.org/0000-0003-0191-7059

Department of Electrical Engineering, College of Engineering, Jouf University, Sakaka 72388, Saudi Arabia ju.edu.sa

Search for more papers by this author

Abdulmajeed Alanazi,

Abdulmajeed Alanazi

Department of Electrical Engineering, College of Engineering, Jouf University, Sakaka 72388, Saudi Arabia ju.edu.sa

Search for more papers by this author

Kareem M. AboRas,

Kareem M. AboRas

Department of Electrical Power and Machines, Faculty of Engineering, Alexandria University, Alexandria, Egypt alexu.edu.eg

Search for more papers by this author

Yazeed Yasin Ghadi,

Yazeed Yasin Ghadi

orcid.org/0000-0002-7121-495X

Department of Computer Science and Software Engineering, Al Ain University, Abu Dhabi 15322, UAE aau.ac.ae

Search for more papers by this author

Mohana Alanazi,

Corresponding Author

Mohana Alanazi

[email protected]

orcid.org/0000-0003-0191-7059

Department of Electrical Engineering, College of Engineering, Jouf University, Sakaka 72388, Saudi Arabia ju.edu.sa

Search for more papers by this author

Abdulmajeed Alanazi,

Abdulmajeed Alanazi

Department of Electrical Engineering, College of Engineering, Jouf University, Sakaka 72388, Saudi Arabia ju.edu.sa

Search for more papers by this author

Kareem M. AboRas,

Kareem M. AboRas

Department of Electrical Power and Machines, Faculty of Engineering, Alexandria University, Alexandria, Egypt alexu.edu.eg

Search for more papers by this author

Yazeed Yasin Ghadi,

Yazeed Yasin Ghadi

orcid.org/0000-0002-7121-495X

Department of Computer Science and Software Engineering, Al Ain University, Abu Dhabi 15322, UAE aau.ac.ae

Search for more papers by this author

First published: 17 January 2024

https://doi.org/10.1155/2024/7792658

Citations: 9

Academic Editor: Olubayo Babatunde

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, a multiobjective framework for simultaneous reconfiguration and allocation of photovoltaic (PV) energy resources in radial distribution networks is performed for minimizing the power losses, lowering network loading factor, and reducing cost of energy resources as well as increasing the voltage stability index. A novel algorithm called the improved clouded leopard algorithm is used to find the set of optimum decision factors in the combined execution of restructuring and also PV resource distribution. The clouded leopard optimization (CLO) algorithm, which is widely used, takes its cues from the sleeping and foraging habits of the animal, and the improved CLO (ICLO) is formed using adaptive inertia weight to overcome premature convergence. In five cases of base distribution network and different contribution of reconfiguration and PV allocation, single- and multiobjective approach has been applied on 33- and 69-bus distribution networks. According to the findings, the best case includes simultaneous reconfiguration and PV allocation in the radial networks based on the multiobjective approach unlike the single-objective method which obtained the highest network performance with the best compromise between different goals. Also, in the best lowest losses, the decrease in the network loading and cost of energy resources and the better voltage profile and stability are obtained satisfying the constraints. The losses, network loading, voltage profile, and voltage stability are improved by 60.40%, 37.89%, 6.17%, and 27.5% for 33-bus network and also enhanced by 71.77%, 41.23%, 4.76%, and 20.48% for 69-bus network, respectively. Also, the results showed that network reconfiguration only has the weakest performance among other cases based on reconfiguration or photovoltaic sources. Moreover, the superior capability of the ICLO in addressing the aim of the study is proved in comparison with the traditional CLO and well-known particle swarm optimization (PSO) and manta ray foraging optimization (MRFO) to obtain the better objective value and statistical criteria to solve the best case.

1. Introduction

As a result of the radial configuration and high resistance-to-reactance ratio, distribution networks become more susceptible to severe power losses [1]. In conjunction with nonrenewable energy sources, renewable energies are utilized to supplement primary energy requirements and, in particular, to maximize energy efficiency [2]. The energy generated by renewable energy systems has experienced a notable surge in recent years, primarily driven by technological advancements and the heightened global population awareness [3]. The incorporation of renewable energy sources (RES) into the preexisting infrastructure enhances the distribution network’s overall performance. It consists of the economic benefits of energy cost savings as well as the technical benefits of minimizing power losses as well as the voltage condition improvement [4]. In addition, the topology of a reconfigurable network can be altered by actuating and deactivating power line switches. The reconfiguration of the distribution network is noteworthy due to its potential to enhance power grid performance through a modification of the network topology [5]. Consequently, determining the optimal placement and size of renewable resources within the distribution network is crucial for capitalizing on the benefits of reconfiguring the network and utilizing renewable energy resources. Conversely, the optimal network configuration, including the opening and closing status of the network devices, should be determined [6]. Furthermore, the concurrent utilization of network reconfiguration and renewable energy sources in the operation of distribution networks, aiming to maximize the benefits of these approaches, has been formulated as an optimization problem. This framework necessitates the application of optimization algorithms to ascertain the optimal installation locations and capacities of energy sources, along with determining the optimal opening and closing status of network switches [6, 7]. A variety of algorithms are implemented to ensure that distribution networks function optimally. In order to solve the problem using optimization methods, the objective function and problem constraints must be specified [7]. The capabilities of the optimization methods vary depending on the structure that is presented, and each method possesses a distinct capability in achieving the optimal solution [8]. It is important to acknowledge that optimization methods may fail to produce the optimal solution when the problem’s complexity and various objective functions are taken into account. In such cases, alternative strategies are required to enhance their performance [7, 8]. The reset issue can be resolved by employing various objective functions, including but not limited to power losses, voltage variation, voltage stability index, load imbalance, line current unbalance, dependability, and network security [8, 9]. Because there are many network switches, selecting the best switches to access has turned into an optimization issue, necessitating the use of the optimization technique [10, 11]. Due to their pure and cost-free energy, DG sources built on solar energy sources have received a lot of positive attention recently [12, 13]. The distribution grid is immediately linked to renewable photovoltaic energy systems that are tied to the grid, and these systems send their output electricity into the grid to secure and reliable performance [14, 15]. Therefore, they have an impact on network metrics and variables like the voltage, losses, and dependability, just like other producing units and electrical network components [16, 17]. Therefore, in order to benefit from the advantages of photovoltaic energy sources, locating and determining their optimal capacity in the distribution network is very important because the inappropriate selection of the location and capacity of this type of energy sources in the network can weaken the characteristics of the network compared to the previous state. Therefore, it is feasible to mix the methods of reconfiguring and allocating solar energy resources in the distribution networks and profit from each method’s benefits for the functioning of the distribution network. In this way, while determining the optimal configuration of the network, the best installation location and the optimal capacity of photovoltaic energy sources in the network are determined at the same time so that the best value of the objective function is obtained by satisfying the operating constraints and the constraints related to maintaining the radial state of the network and photovoltaic energy sources. However, a technique of optimization with the desired ability to produce the worldwide answer is required to arrive at the optimum solution. Numerous studies have been done recently on the use of restructuring as well as the best dispersal of distributed generation units and green energy sources in peripheral distribution networks. A tangent golden flower fertilization algorithm is used in [18] to reconfigure the distribution network to reduce power losses by choosing the best locations for the DGs and determining the best network reconfiguration. The optimal location and capacity selection of renewable resources, taking into account the maximum allowable capacity constraint, is described in [19]. The objective is to reduce losses and enhance the voltage profile of distribution grids. Particle swarm optimization with the weighted coefficient method is utilized for this purpose. A stochastic-metaheuristic model is implemented in [20] to allocate renewable resources in a distribution network in accordance with multiple criteria, including minimizing power losses, improving voltage profile and stability, and enhancing network reliability while accounting for resource production and demand uncertainty. The reconfiguration of an imbalanced distribution network to reduce losses and voltage instability is proposed in [21] using an enhanced transient search optimization method. In [22], distribution network restructuring is carried out using the jellyfish search method to improve network user dependability metrics. The parallel slime mold method is used in [23] to show a change framework for a peripheral distribution network combined with DGs in order to reduce active loss, increase voltage stability index, and balance load. The authors of [24] suggested stochastic scheduling for a hybrid system consisting of a photovoltaic array, wind turbines, and a battery storage system integrated into the distribution network. The objective was to reduce energy losses, optimize the voltage profile, and decrease system cost. Additionally, the reliability of the system was enhanced through the implementation of the energy-not-provided index, which accounted for uncertainties in energy source generation and network demand via the unscented transformation. A simultaneous two-problem allocation with multiple objectives is suggested in Ref. [25]. This allocation pertains to an unbalanced distribution network and a hybrid distributed generation system consisting of wind turbines, battery storage, and solar panels. The proposed approach is aimed at reducing overall losses and enhancing power quality. To reduce power losses, [26] applies a simulated ecosystem optimization for network restructuring and DG location. To reduce power loss, a novel paradigm for network reconfiguration (NR) is introduced in [27]. It uses an improved binary cuckoo search method. The restructuring of distribution networks to reduce power loss while taking into account issue restrictions is solved in [28] using an acceleration PSO. To reduce power outages, a chaos search group method is used in [29] to simultaneously reconfigure the distribution network and allocate DGs. In order to reduce the processing load placed on the optimization methods while maintaining control over the discontinuous allocation variables, a mathematical procedure for network restructuring based on the positioning of the soft open point is described in [30]. In [31], a multiobjective mixed integer linear programming model is used to create the restructuring of distribution networks, and this model specifically takes into account the effect of automatic changes on the length of interruptions. In [32], the restructuring of distribution networks is carried out using a flexible multicriteria method via an enhanced coronavirus herd immunity optimizer algorithm to reduce power loss and increase power quality. The best network design for reducing the decreased power losses while considering the load balance index is determined by applying a golden flower fertilization method [33]. Using a mixed water cycle algorithm, a soft open point technique is described in [34] with and without system changes to reduce power losses, improve the voltage profile, and reduce the number of soft open points linked to the network. A moth-flame optimization method is used in [35] to create multicriteria restructuring of distribution networks combined with energy resources in order to reduce power loss and improve dependability.

The literature evaluation has revealed that in coordinated and simultaneous methods of reconfiguration and optimal allocation of PV energy resources, several objectives, including minimizing power losses and voltage deviations, as well as improving voltage stability, have been repeatedly defined as a multiobjective function. However, it can be seen that a comprehensive multiobjective function that has various objectives such as minimizing power losses, improving network voltage characteristics and stability, minimizing investment costs, preserving and replacing energy resources, and especially improving the network loading factor is not well addressed. On the other hand, the review of the current literature shows that metaheuristic techniques have played a major role in solving efficiency problems in the energy delivery network. The complex and nonlinear nature of the subject, practical limitations, and the existence of discrete and continuous variables create major problems in the combined and simultaneous method of reconfiguration and distribution of PV energy sources in the electricity delivery network. In addition to this additional difficulty, the high processing cost of the concurrent approach necessitates the use of a robust method with high closure capability and fast access to the ideal global response. A metaheuristic approach may be good at solving some optimization problems but may not be good at many other problems based on the no free lunch (NFL) theorem [36]. The common issue of reorganization and distribution of solar energy resources in environmental distribution networks requires the development of a new metaheuristic method.

Based on the review of previous works, the contributions and novelties of this paper are listed as follows:

(i)
Integration of the multiobjective strategy in the distribution network reconfiguration and photovoltaic energy resource allocation in the networks
(ii)
Formulation of an objective function as minimization of power losses, improvement of network voltage profile and stability, minimization of investment costs, maintenance and replacement of energy sources, and especially the improvement of the network load factor in the presence of the complex and nonlinear nature of the problem, operating constraints and existence discrete and continuous variables
(iii)
Using the improved clouded leopard optimization (ICLO) algorithm to determine the optimal network structure as well as the optimal installation location and size of photovoltaic energy sources and application of the nonlinear inertia weight reduction technique to improve the CLO [37] convergence capability
(iv)
Stablishing the superiority of the ICLO in solving the problem over the traditional CLO, PSO, and MRFO approaches

In this paper, the problem formulation that includes objective function, constraints, and fuzzy multiobjective solution method is presented in Section 2. The proposed improved optimizer and its implementation to solve the simultaneous reconfiguration and photovoltaic resource allocation in distribution networks are formulated in Section 3. The simulation results in different cases of reconfiguration and photovoltaic allocation are presented in Section 4, and the findings are concluded in Section 5.

2. Formulation of the Problem

2.1. Objective Function

In this study, the problem of multiobjective and coordinated allocation of photovoltaic energy resources in radial distribution networks is formulated to minimize power losses, improve the voltage stability index, and improve the network load factor, in addition to reducing the cost of photovoltaic energy resources. The broad goal function is described in the sections that follow.

2.1.1. Power Losses

The reduction of active power losses in the distribution network, which are calculated as the total of losses of all lines as follows [1–8 and [9], is one of the most crucial objectives in the functioning of distribution networks.

(1)

R_ij is the resistance of the k^th line that connects bus i and j, I_ij is the current of the k^th line, P_ij and Q_ij are the active and reactive power that flow flow through k^th line, V_i is the voltage of the i^th bus, and N_branches is the number of network lines.

2.1.2. Voltage Stability

In this research, voltage stability has been incorporated into the formulation of the goal function using the voltage stability index (VSI). According to [16, 38], the voltage stability measure is as follows:

(2)

where P_i and Q_i are the active and reactive power consumption of bus i and X_ij is the reactance of the k^th line. It should be stated here that i ≠ 1.

The proposed method ΔVSI is used as a measure of voltage stability to consider voltage stability. The value ΔVSI should be minimized so that the system has better voltage stability.

(3)

2.1.3. Network Loading

Another goal function for the network reconfiguration and photovoltaic energy source allocation in distribution network is considered minimizing the network loading. The electricity flowing through the lines in proportion to the temperature limit of the lines defines this change. Thus, the below equation [1–8] and [9] is used to determine the loading for each line:

(4)

where Flow_ij is the power passing through the line that connects bus i to bus j, Flow limit_ij is the thermal limit of the line, and LF_ij is the line loading factor. The entire network loading can be defined as follows:

(5)

where LF^tot is the network load.

2.1.4. Cost of PV Energy Resources

For energy resources, there are three types of costs, which includes initial investment and installation of energy sources (IC_DG), operation and power generation costs (OC_DG), and maintenance costs (MC_DG), which are defined [1, 4, 38] as

(6)

(1) Investment Cost. The investment cost of energy resources is the cost that is paid at the beginning of the project, which is related to the purchase and installation of energy resources and is defined based on the kWh produced as follows:

(7)

where

is the purchase and installation cost of i^th DG and N_DG is the number of DGs.

(2) Operation Cost. Another cost related to energy sources is the cost of operation and power generation. This cost can be calculated with the following relationship.

(8)

where

is the annual operating cost of i^th DG.

(3) Annual Operation Cost. The annual operating cost of the i^th DG is defined based on the interest rate and inflation [1] as follows:

(9)

where InfR and IntR refer to the inflation and interest rates and

is the per DG annual operating cost.

(4) Maintenance Cost. Another cost of energy resources is the maintenance cost, which is modeled by the following equation.

(10)

where

is the maintenance cost of the i^th DG and MC_DG is the total maintenance cost of all energy sources.

(5) Annual Maintenance Cost. This annual cost of the i^th DG is defined based on inflation and interest rates as follows [1]:

(11)

where

is the per DG annual maintenance cost.

2.2. Constraints

In the implementation of the proposed method, some limitations must be satisfied. These limitations are presented below [1–8] and [9]:

(i)
The voltage limits

The voltage value of each bus must be within the allowed range.

(12)

where V_min and V_max are the minimum and maximum voltage value of the network buses and N_bus is the number of network buses.

(ii)
The current flow limit

The current value of each line must be within the allowed range.

(13)

where I_min and I_max are the minimum and maximum current value of the network lines.

(iii)
PV power limit

The production power of the photovoltaic source must be within the maximum and minimum permissible limits.

(14)

where P_DGi is the power of i^th DG and

refers to the maximum power size of i^th DG.

(iv)
Network radiality constraint

During the reconfiguration process, the radial state of the network must be observed. The details of these are described in Ref. [1].

2.3. Fuzzy Multiobjective Solution Method

The joint optimization of the objective function and restrictions forms the cornerstone of this approach to tackling the multiobjective optimization issue. A single-objective model of maximizing the lowest degree of satisfaction among the membership functions is created from the multiobjective function. Both the objective functions and the constraints need to be defined as membership functions in order to find the optimal point. The μ_r for the r^th fuzzy objective function is introduced in the simultaneous multiobjective function technique. In other words, a μ is defined for every function and can be defined using Eq. (15). Based on Figure 1, an appropriate membership function for each of the multiobjective functions should be defined.

(15)

where μ_r denotes the fuzzy index of the r^th objective function, f_r,min and f_r,max are the minimum and maximum value of r^th objective function, and f_r is value of r^th objective function in optimization process.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

μ for the r^th objective function.

To determine the minimum value of an objective function, it is thus necessary to solve each individual objective function. The minimum value for μ is determined by which objective function approaches its utmost value, as stated in Eq. (15). The mathematical representation of this correlation is given by

(16)

(17)

where Nr is the number of objective functions. h(x) and g(x) define the equality and equality constraints of the optimization problem. The multiobjective technique permits the optimization of the objective functions and constraints simultaneously. With this in mind, the constraints are examined subsequent to the generation of variables and the objective function calculation. In this study, the network reconfiguration and allocation of the photovoltaic resources in the distribution network is presented considering four objectives mentioned in Section 2.1. Objectives have different dimensions; therefore, they should be solved in a multiobjective framework. In Section 2.3, the structure of multiobjective optimization based on the fuzzy multiobjective method is described, which forms a fuzzy index for each of the objectives based on the provided relations. Therefore, by minimizing the maximum of each index in the overall objective function, the optimization problem is solved using the optimization algorithm, and finally, the optimal variables including the best installation location and the optimal capacity of photovoltaic resources in the distribution network have been determined.

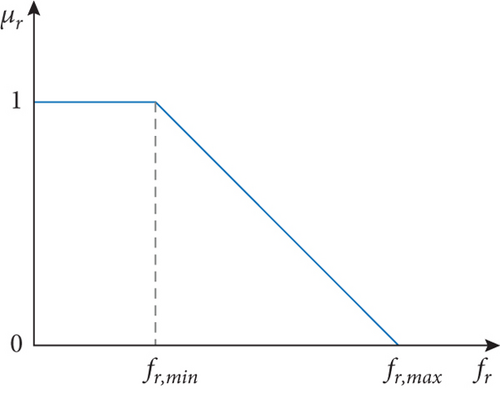
3. Proposed Optimization Method

3.1. Introduction of CLO Algorithm

The clouded leopard is a cat of average stature; and, it is neither large nor tiny. Clouded leopards are reclusive, timid felines. In the observations, two natural behaviors of clouded leopards have been documented as being more important than the rest [26]. Throughout the day, these animals are found relaxing on the trees. Their primary activity occurs when they descend from the trees at night to forage on the ground. These two prominent behaviors exhibited by clouded leopards served as the primary source of motivation for the clouded leopard optimization (CLO) modeling [26].

3.1.1. Initialization of the CLO Positions

Each cloud leopard in the CLO algorithm symbolizes both a member of the community and a potential answer. The choice factors are represented by the clouded leopard’s location in the search area. The components of each vector representing a clouded leopard are comparable to choice factors. Using (18) [26], the location of cloud leopards is initially set at random.

(18)

where X_m represents the m^th clouded leopard, x_m,n is its n^th dimension, N_L is the clouded leopards’ number, N_D represents the decision variable number, rand_m,n are random numbers chosen in the [1, 0], l_n is the minimum limit and u_n is the maximum limit of the variable n. and “• “refers to the symbol of scalar multiplication.

Cloud leopards together constitute the CLO algorithm population, which is shown mathematically using the relation matrix [26].

(19)

where X represents the matrix of the CLO population. Each cloud leopard is a selected solution, for N_L cloud leopards X_m, i = 1, 2, ⋯, N_L (number of algorithm’s population) are the computed fitness values and can be defined using the below vector by

(20)

where F_m denotes the fitness value derived from the m^th cloud leopard and F denotes the array of objective function values.

It introduces the populace with the highest health value. The location of the members of the population in the search space is changed, and new fitness values are computed, revising the best population member in each run. The CLO algorithm’s population located in the search area has been updated using mathematical modeling of two clouded leopard actions.

3.1.2. Exploration Phase

Due to its nighttime foraging habits, the clouded leopard can travel to various locations in pursuit of food. This behavior of the clouded leopard denotes the investigation period, during which the population’s members scour the various parts of the global search area. The new posture of the clouded leopard is established depending on the prey’s location, i.e., (21). The prior cloud leopard [26] is replaced if the freshly formed position has a higher objective function value by (22).

(21)

(22)

where

is the m^th cloud leopard proposed new position according to phase 1 of CLO,

is the n^th dimension and its fitness value is defined by

, rand_m,n is numbers in the [0,1] randomly, p_m,n refers to the position of the chosen prey for the m^th clouded leopard and the fitness value of the prey is

, and I_m,n is selected from the set {1,2}, randomly.

3.1.3. Exploitation Phase

Following a search and feasting on the taken food, clouded leopards take a nap on branches. The period of exploitation and local exploration is indicated by the clouded leopards’ behavior, which leads them to move closer to their spot. A spot is generated at random near each leopard’s location to mimic this behavior. Following (24), the prior location is replaced if a higher fitness value is obtained [26].

(23)

(24)

where

is the proposed new position for the m^th cloud leopard according to phase 2 of CLO,

is its n^th dimension, and

is its fitness value.

The first run of the CLO algorithm is finished by changing the positions of all cloud leopards based on the first and second stages. The CLO algorithm is then run a second time, with each cycle changing the CLO population in equations (21)–(24) until all iterations have been run. The best potential solution saved during the algorithm cycle is selected as the best solution following CLO’s complete implementation. In Pseudocode 1, the CLO pseudocode is displayed.

Pseudocode 1: Pseudocode of the CLO algorithm.

Start CLO.
1. Input: The information of the problem.
2. Adjust the iterations number (T) and the algorithm population number (N_L).
3. Initiate the clouded leopards position using Eqs. (15)-(16) and generation of the objective vector using Eq. (17)
4. For t = 1 : T
5. For m = 1 : N_L
6. Phase 1: Exploration
7. Consider the target prey position randomly for m^th leopard.
8. Compute the new position of the m^th leopard using Eq. (21)
9. Update the m^th leopard considering Eq. (22).
10. Phase 2: Exploitation
11. Compute the new position of the m^th leopard considering Eq. (23).
12. Update the m^th clouded leopard using (24).
13. end for
14. Print the best solution.
15. end for
16. Output: The best variable set achieved via CLO
End CLO.

3.2. The ICLO

To avoid the algorithm from becoming stuck in the local optimal, the adaptive inertia weight (IW) [39] is introduced to the local search and exploitation phase. This weight is adaptively modified based on the current agent’s fitness state. IW is employed in this study’s utilization phase to boost variety and prevent slipping into the local optimal. Using IW, the following information is updated regarding the clouded leopard’s location during the second phase, or the capture phase:

(25)

The operator IW_m(t) (IW_m(t) ∈ [0, 1]), which can be adaptively changed in accordance with the present operator location, determines the convergence modification. This factor is set to the highest value when the fitness of the factor is greater than the average value of the entire population so that they can converge to the best location as quickly as possible. On the other hand, for the present individual, it is given a lesser number when its health is worse than normal. Lower weight values correspond to poorer performance, which lessens the impact of changing the leopards’ location. This operator aids the algorithm’s ability to perform better local searches and avoid early consensus and can be expressed as the following equation [39] using the updated Versoria mapping function:

(26)

where a_m(t) ∈ [0, 1] is the clouded leopard’s ranking in all clouded leopards between the lowest and mean fitness, which is presented as follows:

(27)

and in relation to (15)

(28)

where F_m(t) means the fitness of the m^th clouded leopard at iteration t and F_ave(t) and F_min(t) are the mean value and lowest value of all N_L size populations’ fitness.

Therefore, the proposed optimization algorithm solves the photovoltaic allocation problem by minimizing the objective function and considering the constraints and determines the optimal variables. According to the presentation of the CLO formulation and its improvement strategy, its flowchart is presented in Figure 2.

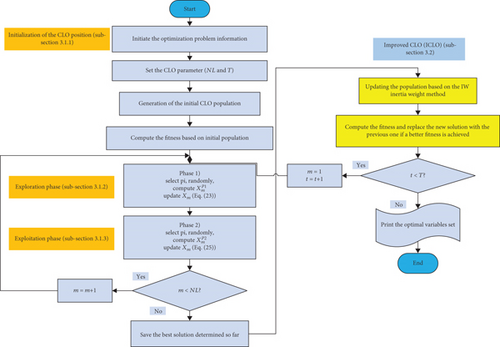
3.3. Implementation of the ICLO

In the proposed method, decision-making variables are represented as X vectors, including tie lines or open lines of the network, as well as the location and capacity of photovoltaic energy sources as shown below.

(29)

The flowchart of ICLO in solving the multiobjective and coordinated reconfiguration and allocation of PV energy resources in the distribution network is shown in Figure 3. Also, the steps of implementing the ICLO to solve the problem are presented as follows:

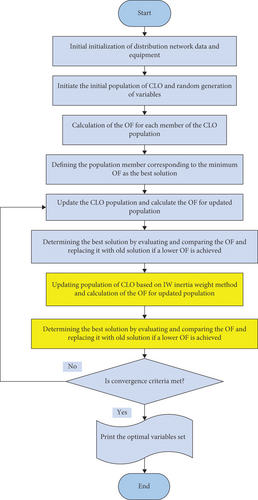
Step 1. Initialization of data for the delivery network and devices. In this stage, the optimization algorithm is updated with power data, network line information, the number of connected lines, solar resource minimal and maximum capacities, and cost data.

Step 2. Initializing the CLO population and creating factors at random. Using trial and error and the writers’ expertise, the algorithm’s maximal repetition and population number are established in this stage. Additionally, each group of factors is decided at random based on the algorithm’s population size, including the equipment’s capability and the equipment’s limitations.

Step 3. Determine the goal function for each CLO community participant. Each collection of factors associated with objective function value is determined.

Step 4. Designating the population member that corresponds to the goal function’s lowest value as the ideal answer. It is decided which individual achieves the greatest goal function.

Step 5. Using CLO to update the algorithm population. The population of the program is changed in this phase to produce new variables.

Step 6. Determine the goal function for the CLO’s revised population from Step 5.

Step 7. Assessing and contrasting the goal function in steps 4 through 6 and then changing the answer to find the best one. The number acquired in Step 4 is changed if the value in Step 6 is higher.

Step 8. The IW inertia weight method-based CLO population update. The population of the program is changed in this phase to produce new variables.

Step 9. Determine the goal function using the revised population from Step 8.

Step 10. Choose the best answer by assessing and contrasting the goal function in Steps 7 and 9 and then changing the answer. If the value acquired in Step 6 is superior to the value of the goal function in Step 9, it is substituted.

Step 11. Have the convergence conditions—achieving the goal function’s lowest value and running the algorithm through its most iterations—been met? Move 5 is the next move to take if the answer is affirmative.

Choosing the factors that best match the objective function as the overall optimum answer, publishing the findings.

Step 12. Stop.

4. Simulation Results

In this section, the simulation results of multiobjective and coordinated reconfiguration and allocation of photovoltaic (PV) energy resource are presented in radial distribution networks to minimize power losses, improve the voltage stability index, enhance the network loading factor, and minimize the cost of energy resource using the ICLO. On bus networks that adhere to IEEE standards 33 and 69, the suggested approach is used. The efficacy of ICLO has been compared with standard CLO, PSO, and MRFO techniques. Each program is said to have a population of 70, a maximum iteration of 300, and a maximum of 25 separate runs. The problem formulation is performed utilizing the MATLAB 2020b program. The proposed methodology includes different cases of application of reconfiguration, and photovoltaic energy resources are presented as follows:

Case 1. Without reconfiguration and photovoltaic energy resource

Case 2. Reconfiguration only

Case 3. Allocation of photovoltaic energy resource

Case 4. Allocation of photovoltaic energy resources after reconfiguration

Case 5. Reconfiguration after the allocation of photovoltaic energy resources

Case 6. Coordinated reconfiguration and allocation of photovoltaic energy resources

4.1. Results of the 33-Bus Test System

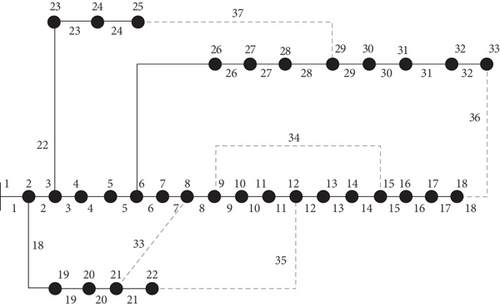
The outcomes of applying the suggested approach to the 33-bus distribution system are shown in this part. Figure 4 displays the 33-bus system’s single-line schematic. This system’s line information is taken from [40]. The overall operating capacity on this network is 3.72 MW and 2.3 MVAr; and it comprises of the 37 lines, including 32 sectionalizing switches and 5 tie switches, on the 33-bus network [40]. The maximum number of PV DG system locations is considered 3 nodes, with each PV system assumed to have a capacity of 2 MW. As a result, the ICLO chooses the best installation location and capacity for PV resources within the distribution network. It also chooses the best situation of the tie lines. Finally, by determining the optimal variables of the problem, the value of different objectives including power losses, minimum VSI, minimum bus voltage of the network, network loading value, and the total cost of photovoltaic energy resources has been determined. According to [1], the investment cost for a PV source per MW in this research is considered $318,000.

4.1.1. Results of Single-Objective Optimization

Table 1 provides a comprehensive overview of the outcomes derived from different optimization scenarios for a 33-bus distribution system. In Case 1, representing the baseline without reconfiguration and PV energy resource allocation, the system exhibits power loss, VSI, and LF values of 202.68 kW, 0.6960 p.u., and 19.61%, respectively. As we delve into subsequent cases, the impact of varying strategies becomes evident.

(i)
Case 2 (reconfiguration only): introducing reconfiguration reduces power losses to 139.55 kW, but the trade-off is a slight increase in LF to 19.77%. This emphasizes the delicate balance required when optimizing for specific objectives
(ii)
Case 3 (allocation of PV energy resources): focusing on PV allocation reduces losses further to 73.71 kW, showcasing the potential of renewable energy integration. However, the challenge is apparent in terms of LF, which increases to 8.88%
(iii)
Case 4 (allocation of PV energy resources after reconfiguration): integrating reconfiguration and PV allocation results in a balance, with power losses at 61.54 kW and LF at 7.97%. This demonstrates the synergy between these strategies
(iv)
Case 5 (reconfiguration after PV allocation): when reconfiguration is performed after PV allocation, the system aims for VSI maximization. This leads to increased losses (228.91 kW) and a higher LF (18.74%). This highlights the need for a coordinated approach
(v)
Case 6 (coordinated reconfiguration and PV allocation): the most comprehensive scenario involves simultaneous reconfiguration and PV allocation. This achieves the lowest losses at 54.20 kW and a reasonable LF of 6.88%, but at the cost of a higher VSI (1.0076). The trade-offs between these objectives are evident, emphasizing the need for a holistic and coordinated optimization approach

Table 1. The results of single-objective optimization of different cases for a 33-bus distribution system.

Scenarios	Function	Optimal configuration	Size and location of DG (MW)	Minimum voltage (p.u.)	Minimum VSI (p.u.)	Losses (kW)	LF (%)	DG cost (M$)
Base case	—	33, 34, 35, 36, 37	—	0.9131	0.6960	202.68	19.61	—

Reconfiguration	Losses	32, 14, 9, 37, 7	—	0.9378	0.7751	139.55	19.77	—
	Voltage stability	14, 7, 9, 27, 32	—	0.9398	0.7816	143.3	18.78	—
	Loading	32, 20, 28, 13, 11	—	0.9294	0.7470	184.74	15.4	—

DG allocation	Losses	33, 34, 35, 36, 37	(10) 0.81 (24) 0.88 (30) 1.04	0.9606	0.8526	73.71	6.39	1.91
	Voltage stability	33, 34, 35, 36, 37	(23) 1.92 (29) 1.72 (17) 1.82	0.9945	0.9806	202.28	23.82	3.67
	Loading	33, 34, 35, 36, 37	(14) 0.85 (30) 0.74 (24) 0.88	0.9583	0.8443	75.80	8.88	1.73

DG allocation after reconfiguration	Losses	32, 14, 9, 37, 7	(25) 0.76 (8) 1.12 (29) 1.18	0.911	0.9765	61.54	7.97	2.14
	Voltage stability	14, 7, 9, 27, 32	(9) 1.77 (31) 1.95 (15) 1.75	0.9968	0.9976	228.91	18.74	3.84
	Loading	32, 20, 28, 13, 11	(8) 1 (15) 0.42 (25) 1.62	0.9732	0.8988	61.85	6.52	2.25

Reconfiguration after DG allocation	Losses	7, 14, 8, 36, 28	(10) 0.81 (24) 0.88 (30) 1.04	0.9736	0.8986	57.76	8.44	1.91
	Voltage stability	13, 22, 31, 19, 8	(23) 1.92 (29) 1.72 (17) 1.82	0.9999	1.0001	318.39	27.7	3.83
	Loading	36, 23, 21, 11, 20	(14) 0.85 (30) 0.74 (24) 0.88	0.9477	0.8075	112.39	7.48	1.73

Simultaneous reconfiguration and WT allocation	Losses	30, 28, 6, 11, 14	(25) 1.08 (32) 0.69 (8) 0.79	0.9698	0.8859	54.2	6.88	1.8
	Voltage stability	9, 17, 21, 4, 18	(29) 2 (9) 2 (30) 2	1	1.0076	286.92	20.44	4.2
	Loading	5, 13, 6, 16, 10	(8) 1.2 (29) 1.55 (32) 0.46	0.9752	0.9049	62.87	5.1	2.26

In summary, the table underscores the complexity of optimizing a distribution system with multiple objectives. The chosen strategy significantly impacts various performance indices, and a trade-off analysis is essential for making informed decisions in designing an efficient and resilient distribution system.

4.1.2. Multiobjective Optimization Results

Table 2 presents the summary of the simulating results of the multiobjective modeling using the ICLO. Numerous instances of network efficiency improvement have been carried out utilizing fuzzy methods and multiobjective optimization. The ICLO is used for all improvements in various situations, and the four-goal functions of power loss mitigation, voltage stability improvement, load factor improvement, and PV cost reduction are taken into account. Table 2 lists the outcomes of the IEEE 33-bus network improvements. According to the multiobjective problem solution, the working point of the network is always in optimum conditions, and all wanted objective functions have appropriate conditions, as can be seen in Table 2. As can be seen, Case 2’s change alone is unable to narrow the gap between the network’s working point and ideal conditions, but in other instances where photovoltaic energy sources are present, the network’s operating conditions are ideal. Except for Case 2, every scenario has losses under 100 kW, a lowest VSI of over 0.83 p.u., and a lowest minimum voltage of over 0.95 p.u. Also, the results showed increasing network loading in Case 2 (reconfiguration only). Therefore, according to Case 6 (simultaneous reconfiguration and DG placement), the network’s working point has improved as a result of multiobjective problem-solving, and the network’s efficiency has improved overall by more increasing the voltage minimum and stability and more reducing the power losses and also DG cost. The minimal voltage value, minimum VSI value, power loss, LF, and cost of PV resources are each 0.9695 p.u., 0.8843 p.u., 80.27 kW, 12.18%, and 0.755 M$ in Case 6, respectively. As a result, the optimization algorithm in Case 6 has obtained the highest performance of the 33-bus distribution network by concurrently using the restructuring and allotment of photovoltaic energy resources.

Table 2. The results of multiobjective optimization of different cases for the 33-bus distribution system.

Case	Definition	Optimal configuration	Location and size of DG (MW)	Minimum voltage	Minimum VSI	Power loss	LF	DG cost (M$)
1	Base case	33, 34, 35, 36, 37	—	0.9131	0.6960	202.68	19.61	—
2	Reconfiguration	32, 14, 9, 37, 7	—	0.9378	0.7751	139.55	19.77	—
3	DG placement	33, 34, 35, 36, 37	(10) 0.34 (16) 0.35 (31) 0.61	0.9549	0.8325	97.08	9.49	0.914
4	DG placement after reconfiguration	32, 14, 9, 37, 7	(31) 0.53 (14) 0.235 (15) 0.32	0.95600	0.8542	82.2	11.55	0.764
5	Reconfiguration after DG placement	6, 9, 14, 30, 37	(31) 0.53 (14) 0.235 (15) 0.32	0.9584	0.8487	81.82	12.15	0.764
6	Simultaneous reconfiguration and DG placement	7, 9, 14, 30, 37	(10) 0.057 (33) 0.77 (30) 0.247	0.9695	0.8843	80.27	12.18	0.755

It can be seen in Table 2 that, in general, the various objectives in all cases have been improved compared to Case 1 (the base case of the network without reconfiguration or photovoltaic sources). Also, the amount of these improvements for Case 6, which is the simultaneous use of reconfiguration and photovoltaic sources, has been better in the set of all objectives. On the other hand, the value of minimum voltage and minimum VSI has been obtained more. However, the total objectives should be considered. Of course, the proposed methodology has improved voltage conditions and also other objectives, i.e., reducing power losses and reducing network loading.

The network voltage profile in different cases are shown in Figure 5. As it is known, different cases have led to the improvement of the voltage profile of the 33-bus distribution network. As can be seen, based on the voltage profile curve and also the numerical results of Table 2, Case 6 has a higher minimum voltage value (0.9695 p.u.) than the rest of the cases. This means that Case 6 has further improved the voltage profile of 33-bus network.

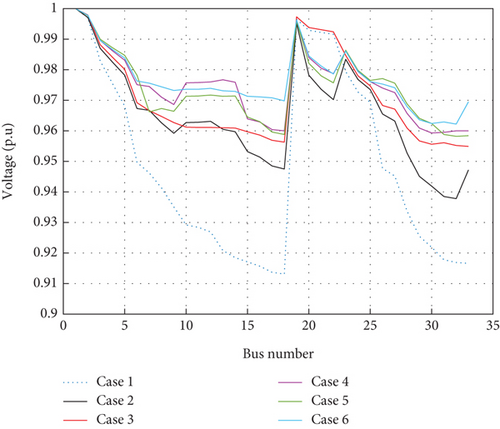
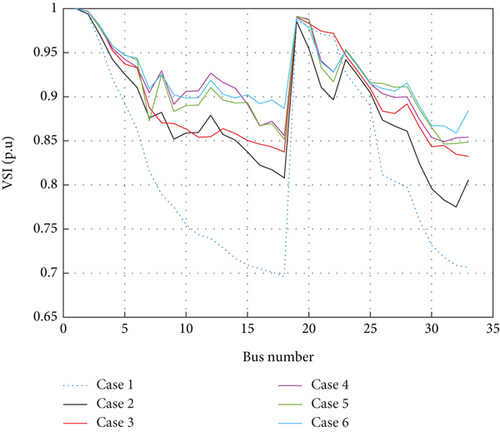
The changes of the VSI for different cases are depicted in Figure 6. As it is clear, the voltage stability index is enhanced for different cases compared to the base 33-bus network. According to Figure 6, it can be seen that Case 6 has obtained a higher value of the minimum VSI (0.8843 p.u.) compared to other cases by simultaneously using the rearrangement and allocation of photovoltaic resources.

4.1.3. ICLO Comparison (33-Bus Network)

The effectiveness of the ICLO in handling Case 6 has been contrasted with traditional CLO, PSO, and MRFO techniques in this part. Figure 7 depicts the convergence of various algorithms and demonstrates the ICLO’s supremacy in reaching a reduced objective function value with a higher convergence speed in fewer convergence iterations. Contrarily, it is evident from the conventional CLO method’s convergence process that enhancing its performance in the form of the ICLO has resulted in the fast accomplishment of the optimum solution and avoided the enhanced algorithm’s early convergence. Therefore, based on the weight of the adaptive inertia, the discovery power of the traditional CLO has increased, and thus it is not trapped in the local optimum like other algorithms and has been able to achieve a lower objective function value, which has resulted in achieving better objectives compared to other algorithms.

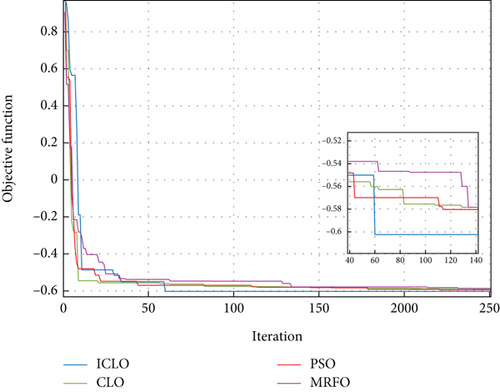
Table 3 provides the exact outcomes of various methods used to solve Case 6. As shown in Table 3, the ICLO achieved the lowest power losses and the greatest VSI and LF values in comparison to other techniques, and it also obtained a superior solution value with a reduced objective function. As shown in Table 4 of the findings, the ICLO is better at achieving statistical analysis metrics than other approaches and is better able to boost the efficiency of the 33-bus network.

Table 3. The results of multiobjective optimization of the different algorithms for the 33-bus distribution system.

Item/method	ICLO	CLO	PSO	MRFO
Optimal configuration	7, 9, 14, 30, 37	7, 9, 13, 32, 37	6, 9, 14, 30, 37	7, 9, 13, 17, 28
Location (bus) and size of DG (MW)	(10) 0.057 (33) 0.77 (30) 0.247	(15) 0.491 (18) 0.009 (31) 0.602	(12) 0.280 (15) 0.199 (31) 0.614	(8) 0.093 (14) 0.229 (31) 0.792
Minimum VSI (p.u.)	0.8843	0.8576	0.8643	0.8441
Power loss (kW)	80.27	82.67	81.88	82.97
LF (%)	12.18	11.62	11.57	11.28
DG cost (M$)	0.755	0.773	0.767	0.781
OF	-0.6024	-0.5921	-0.5960	-0.5906

Table 4. The results of statistical analysis of a different algorithm for the 33-bus distribution system.

Algorithm/index	Best ($)	Worst ($)	Mean ($)	Std ($)
ICLO	-0.6024	-0.5731	-0.5892	-0.0474
CLO	-0.5921	-0.5207	-0.5675	-0.0785
PSO	-0.5960	-0.5631	-0.5822	-0.0503
MRFO	-0.5906	-0.5439	-0.5746	-0.0617

4.2. Results of the 69-Bus Test System

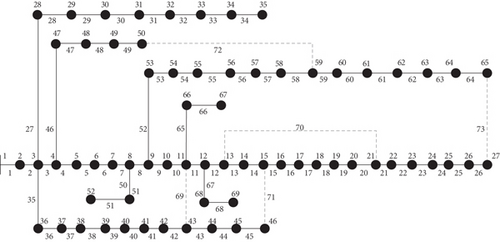
The findings of the suggested approach for the 69-bus dispersal system are given in this part. Figure 8 depicts the 69-bus system’s single-line schematic. This system’s line information is taken from [41]. This network’s overall operating capacity is 3.802 MW and 2.696 MVAr. There are 73 lines total in the 69-base network, including 68 sectionalizing switches and 5 connection lines [41]. Three photovoltaic generators with a combined peak output of 3 MW have been erected for this research. As a result, the ICLO chooses the best position, capacity, and power factor for photovoltaic resources within the distribution network in addition to the best amount of connection lines. The values of each power loss goal, the VSI index, the load factor, the revenue from the selling of resource power, and the cost of resources have all been computed by effectively finding the decision factors. Based on Ref. [1], the funding cost for a photovoltaic source per MW in this research is $318,000.

4.2.1. Results of Multiobjective Optimization

Table 5 lists the outcomes of the various instances using a multiobjective strategy and the ICLO. According to the simulation results in the initial condition, 224.72 kW, 0.6844 p.u., and 20.23%, respectively, are the values for power loss, minimal VSI, and LF. According to the multiobjective problem solution, the working point of the network is always in ideal conditions, and all wanted objective functions are always in appropriate conditions, as shown by the findings of Table 5. As can be seen, network restructuring by itself is unable to operate at a place that is even remotely near ideal circumstances, but in other situations, PV implementation enhances network performance. The lowest VSI is greater than 0.81 p.u., the lowest minimum voltage is greater than 0.95 p.u., and the losses are all less than 81 kW, except the change alone. Therefore, it can be said that the network working aspect has been enhanced by a multiobjective method solution. Case 5 displays the greatest network performance when compared to the other instances, with the lowest voltage, VSI, power loss, LF, and cost of PV resources being equivalent to 0.9525 p.u., 0.8246 p.u., 63.43 kW, 11.89%, and 0.705 M$, respectively. As a result, the optimization program in Case 5 has obtained the highest performance of the 69-bus distribution network through a synchronous and integrated strategy based on restructuring and PV allotment.

Table 5. The results of multiobjective optimization of different cases for the 69-bus distribution system.

Case	Definition	Optimal configuration	Location and size of DG (MW)	Power loss (kW)	Minimum VSI (p.u.)	Minimum voltage (p.u.)	LF (%)	DG cost (M$)
1	Base case	69, 70, 71, 72, 73	—	224.72	0.6844	0.9092	20.23	—
2	Reconfiguration	10, 19, 14, 44, 51	—	107.46	0.7855	0.9414	17.08	—
3	DG placement	69, 70, 71, 72, 73	(3) 1.46 (61) 0.69 (68) 1.23	81.99	0.9054	0.9752	8.766	2.37
4	DG placement after reconfiguration	10, 19, 14, 44, 51	(17) 0.13 (64) 0.36 (61) 0.47	64.48	0.8167	0.9506	10.71	0.667
5	Reconfiguration after DG placement	14, 15, 21, 43, 62	(3) 1.46 (61) 0.69 (68) 1.23	60.77	0.8144	0.9500	6.80	2.37
6	Simultaneous reconfiguration and DG placement	10, 14, 18, 45, 53	(3) 0.055 (4) 0.006 (61) 0.942	63.43	0.8246	0.9525	11.89	0.705

The voltage profile of the 33-bus network in different cases are plotted in Figure 9. According to Figure 9, the voltage profile of the network is improved in different cases in comparison with the base network.

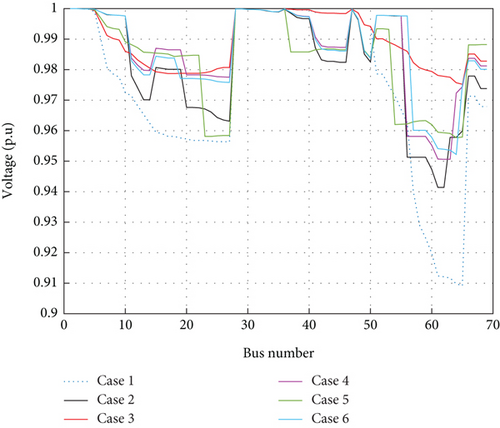
The variations of the VSI for different cases are depicted in Figure 10. As shown as in Figure 10, the voltage stability index is improved for different cases compared to the base 33-bus network.

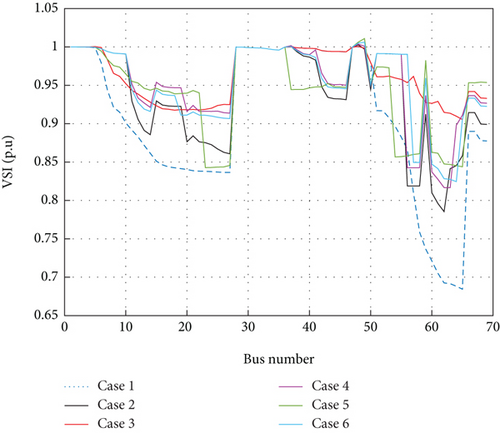
4.2.2. ICLO Comparison (69-Bus Network)

In this section, the performance of ICLO to solve Case 5 for the 69-bus network has been verified with the CLO, PSO, and MRFO algorithms. The convergence curve of different algorithms is shown in Figure 11, which clears the better convergence performance of the ICLO in achieving a lower objective function with higher convergence speed. Based on the convergence process of the conventional CLO, it is clear that enhancing its capability in the form of the ICLO has prevented the premature convergence of the improved algorithm.

The results obtained from different algorithms in solving Case 5 for the 69-bus network are presented in Table 6. As given in Table 6, the ICLO, compared to other methods, obtained a lower objective function and reached the lowest losses and the highest minimum VSI and LS values. Also, the ICLO achieved better statistical analysis indices, according to Table 7, compared to other methods.

Table 6. The results of multiobjective optimization of the different algorithms for the 69-bus distribution system.

Item/method	ICLO	CLO	PSO	MRFO
Optimal configuration	10, 14, 18, 45, 53	10, 14, 19, 46, 53	10, 14, 19, 22, 44	10, 13, 20, 47, 73
Location (bus) and size of DG (MW)	(3) 0.055 (4) 0.006 (61) 0.942	(5) 0.046 (25) 0.139 (61) 0.781	(61) 0.849 (65) 0.107	(22) 0.226 (43) 0.081 (61) 0.671
Minimum VSI (p.u.)	0.8246	0.8119	0.8024	0.7942
Power loss (kW)	63.43	66.28	67.98	73.03
LF (%)	11.89	11.50	11.38	11.19
DG cost (M$)	0.705	0.679	0.671	0.687
OF	-0.6496	-0.6442	-0.6483	-0.6397

Table 7. The results of statistical analysis of the different algorithms for the 69-bus distribution system.

Algorithm/index	Best ($)	Worst ($)	Mean ($)	Std ($)
ICLO	-0.6496	-0.6343	-0.6437	-0.0339
CLO	-0.6442	-0.6215	-0.6394	-0.0617
PSO	-0.6483	-0.6326	-0.6411	-0.0372
MRFO	-0.6397	-0.6204	-0.6355	-0.0643

5. Conclusion

In this paper, a multiobjective framework was proposed for the reconfiguration and allocation of photovoltaic energy sources in distribution networks to minimize the power losses, boost network load factor, improve voltage stability index, and minimize the cost of energy resources. The ICLO was used to identify the network open switches, photovoltaic installation location, and size in distribution networks. In this research, the nonlinear inertia weight reduction technique has been used to overcome the early convergence problem of the traditional CLO. The outcomes of the research are presented as follows:

(i)
The results demonstrated that single-objective optimization did not result in a balance between various objectives and, in some cases, actually diminished some objectives
(ii)
Based on ICLO-based multiobjective strategy, by making compromises between all objectives, the network performance is more improved compared to single-objective optimization. Also, all the targets have been significantly improved compared to their values in the basic state of the network
(iii)
Case 6 including the reconfiguration and allocation of photovoltaic resources in the network has the best performance, and the weakest performance is the case of only network reconfiguration
(iv)
In comparison to the other cases, Case 6 involves the reconfiguration and allocation of PV in distribution networks to achieve the best solution, the least amount of power loss, the greatest possible minimal VSI, and the least amount of LF
(v)
In Case 6, losses and LF dropped for the 33-bus network by 60.40% and 37.89% and for the 69-bus network by 71.77% and 41.23%
(vi)
In comparison to the basic distribution network, the minimum VSI for the 33-bus and 69-bus networks rose by 27.05% and 20.49%, respectively
(vii)
The superiority of the ICLO is proved to solve the Case 6 to obtain the better objective function value (lowest value) as well as better statistical criteria in comparison with the traditional CLO, PSO, and MRFO algorithms
(viii)
To achieve better objectives value, the ICLO’s dominance over traditional CLO, PSO, and MRFO techniques in handling Case 6 was demonstrated

The lack of access to real data and the costs of developing photovoltaic energy sources is one of the limitations of the research. For the future work, integrated multiobjective reorganization with photovoltaic/wind/battery energy microgrid optimization in distribution networks with the aim of improving the reliability and power efficiency indicators of the network is proposed.

Conflicts of Interest

The authors declare no conflicts of interest.

Authors’ Contributions

The authors confirm the final authorship for this manuscript. All the authors have equally contributed to this manuscript.

Acknowledgments

The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia, for funding this research work through project number 223202.

Open Research

Data Availability

Data are available on request.

References

1 Hadidian-Moghaddam M. J., Arabi-Nowdeh S., Bigdeli M., and Azizian D., A multi-objective optimal sizing and siting of distributed generation using ant lion optimization technique, Ain Shams Engineering Journal. (2018) 9, no. 4, 2101–2109, https://doi.org/10.1016/j.asej.2017.03.001, 2-s2.0-85019732035.
10.1016/j.asej.2017.03.001
Web of Science® Google Scholar
2 Chen J., Sun B., Li Y., Jing R., Zeng Y., and Li M., Credible capacity calculation method of distributed generation based on equal power supply reliability criterion, Renewable Energy. (2022) 201, 534–547, https://doi.org/10.1016/j.renene.2022.10.129.
10.1016/j.renene.2022.10.129
Web of Science® Google Scholar
3 Nowdeh S. A., Davoudkhani I. F., Moghaddam M. H., Najmi E. S., Abdelaziz A. Y., Ahmadi A., Razavi S. E., and Gandoman F. H., Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method, Applied Soft Computing. (2019) 77, 761–779, https://doi.org/10.1016/j.asoc.2019.02.003, 2-s2.0-85061623984.
10.1016/j.asoc.2019.02.003
Web of Science® Google Scholar
4 Li S., Efficient algorithms for scheduling equal-length jobs with processing set restrictions on uniform parallel batch machines, Mathematical Biosciences and Engineering. (2022) 19, no. 11, 10731–10740, https://doi.org/10.3934/mbe.2022502, 36124567.
10.3934/mbe.2022502
PubMed Web of Science® Google Scholar
5 Li L. L., Xiong J. L., Tseng M. L., Yan Z., and Lim M. K., Using multi-objective sparrow search algorithm to establish active distribution network dynamic reconfiguration integrated optimization, Expert Systems with Applications. (2022) 193, https://doi.org/10.1016/j.eswa.2021.116445.
10.1016/j.eswa.2021.116445
PubMed Web of Science® Google Scholar
6 Liu M., Gu Q., Yang B., Yin Z., Liu S., Yin L., and Zheng W., Kinematics model optimization algorithm for six degrees of freedom parallel platform, Applied Sciences. (2023) 13, no. 5, https://doi.org/10.3390/app13053082.
10.3390/app13053082
Google Scholar
7 Gu Q., Tian J., Yang B., Liu M., Gu B., Yin Z., Yin L., and Zheng W., A novel architecture of a six degrees of freedom parallel platform, Electronics. (2023) 12, no. 8, https://doi.org/10.3390/electronics12081774.
10.3390/electronics12081774
Web of Science® Google Scholar
8 Shi Q., Li F., Dong J., Olama M., Wang X., Winstead C., and Kuruganti T., Co-optimization of repairs and dynamic network reconfiguration for improved distribution system resilience, Applied Energy. (2022) 318, article 119245, https://doi.org/10.1016/j.apenergy.2022.119245.
10.1016/j.apenergy.2022.119245
Web of Science® Google Scholar
9 Arulprakasam S. and Muthusamy S., Reconfiguration of distribution networks using rain-fall optimization with non-dominated sorting, Applied Soft Computing. (2022) 115, article 108200, https://doi.org/10.1016/j.asoc.2021.108200.
10.1016/j.asoc.2021.108200
Web of Science® Google Scholar
10 Zhang Z., Altalbawy F. M. A., Al-Bahrani M., and Riadi Y., Regret-based multi-objective optimization of carbon capture facility in CHP- based microgrid with carbon dioxide cycling, Journal of Cleaner Production. (2023) 384, article 135632, https://doi.org/10.1016/j.jclepro.2022.135632.
10.1016/j.jclepro.2022.135632
Web of Science® Google Scholar
11 Guo L., Ye C., Ding Y., and Wang P., Allocation of centrally switched fault current limiters enabled by 5G in transmission system, IEEE Transactions on Power Delivery. (2021) 36, no. 5, 3231–3241, https://doi.org/10.1109/TPWRD.2020.3037193.
10.1109/TPWRD.2020.3037193
Web of Science® Google Scholar
12 Li P., Hu J., Qiu L., Zhao Y., and Ghosh B. K., A distributed economic dispatch strategy for power–water networks, IEEE Transactions on Control of Network Systems. (2022) 9, no. 1, 356–366, https://doi.org/10.1109/TCNS.2021.3104103.
10.1109/TCNS.2021.3104103
Web of Science® Google Scholar
13 Lin X., Liu Y., Yu J., Yu R., Zhang J., and Wen H., Stability analysis of three-phase grid-connected inverter under the weak grids with asymmetrical grid impedance by LTP theory in time domain, International Journal of Electrical Power & Energy Systems. (2022) 142, article 108244, https://doi.org/10.1016/j.ijepes.2022.108244.
10.1016/j.ijepes.2022.108244
Web of Science® Google Scholar
14 Yan Z. and Wen H., Electricity theft detection base on extreme gradient boosting in AMI, IEEE Transactions on Instrumentation and Measurement. (2021) 70, 1–9, https://doi.org/10.1109/TIM.2020.3048784.
10.1109/TIM.2020.3048784
PubMed Web of Science® Google Scholar
15 Min C., Pan Y., Dai W., Kawsar I., Li Z., and Wang G., Trajectory optimization of an electric vehicle with minimum energy consumption using inverse dynamics model and servo constraints, Mechanism and Machine Theory. (2023) 181, article 105185, https://doi.org/10.1016/j.mechmachtheory.2022.105185.
10.1016/j.mechmachtheory.2022.105185
Web of Science® Google Scholar
16 Cai T., Dong M., Chen K., and Gong T., Methods of participating power spot market bidding and settlement for renewable energy systems, Energy Reports. (2022) 8, 7764–7772, https://doi.org/10.1016/j.egyr.2022.05.291.
10.1016/j.egyr.2022.05.291
Web of Science® Google Scholar
17 Naderipour A., Nowdeh S. A., Saftjani P. B., Abdul-Malek Z., Mustafa M. W. B., Kamyab H., and Davoudkhani I. F., Deterministic and probabilistic multi-objective placement and sizing of wind renewable energy sources using improved spotted hyena optimizer, Journal of Cleaner Production. (2021) 286, article 124941, https://doi.org/10.1016/j.jclepro.2020.124941.
10.1016/j.jclepro.2020.124941
Web of Science® Google Scholar
18 Swaminathan D. and Rajagopalan A., Optimized network reconfiguration with integrated generation using tangent golden flower algorithm, Energies. (2022) 15, no. 21, https://doi.org/10.3390/en15218158.
10.3390/en15218158
Web of Science® Google Scholar
19 Naderipour A., Abdul-Malek Z., Arabi Nowdeh S., Gandoman F. H., and Hadidian Moghaddam M. J., A multi-objective optimization problem for optimal site selection of wind turbines for reduce losses and improve voltage profile of distribution grids, Energies. (2019) 12, no. 13, https://doi.org/10.3390/en12132621, 2-s2.0-85068821334.
10.3390/en12132621
Web of Science® Google Scholar
20 Alanazi A., Alanazi M., Nowdeh S. A., Abdelaziz A. Y., and Abu-Siada A., Stochastic-metaheuristic model for multi-criteria allocation of wind energy resources in distribution network using improved equilibrium optimization algorithm, Electronics. (2022) 11, no. 20, https://doi.org/10.3390/electronics11203285.
10.3390/electronics11203285
Web of Science® Google Scholar
21 Alanazi M., Alanazi A., Almadhor A., and Memon Z. A., Multiobjective reconfiguration of unbalanced distribution networks using improved transient search optimization algorithm considering power quality and reliability metrics, Scientific Reports. (2022) 12, no. 1, article 13686, https://doi.org/10.1038/s41598-022-17881-x, 35953705.
10.1038/s41598-022-17881-x
PubMed Web of Science® Google Scholar
22 Shaheen A., El-Sehiemy R., Kamel S., and Selim A., Optimal operational reliability and reconfiguration of electrical distribution network based on jellyfish search algorithm, Energies. (2022) 15, no. 19, https://doi.org/10.3390/en15196994.
10.3390/en15196994
Web of Science® Google Scholar
23 Wang H. J., Pan J. S., Nguyen T. T., and Weng S., Distribution network reconfiguration with distributed generation based on parallel slime mould algorithm, Energy. (2022) 244, article 123011, https://doi.org/10.1016/j.energy.2021.123011.
10.1016/j.energy.2021.123011
Web of Science® Google Scholar
24 Hadi Abdulwahid A., Al-Razgan M., Fakhruldeen H. F., Churampi Arellano M. T., Mrzljak V., Arabi Nowdeh S., and Moghaddam M. J. H., Stochastic multi-objective scheduling of a hybrid system in a distribution network using a mathematical optimization algorithm considering generation and demand uncertainties, Mathematics. (2023) 11, no. 18, https://doi.org/10.3390/math11183962.
10.3390/math11183962
Web of Science® Google Scholar
25 Moghaddam M. J. H., Bayat M., Mirzaei A., Nowdeh S. A., and Kalam A., Multiobjective and Simultaneous Two-Problem Allocation of a Hybrid Solar-Wind Energy System Joint with Battery Storage Incorporating Losses and Power Quality Indices, International Journal of Energy Research. (2023) 2023, 24, 6681528, https://doi.org/10.1155/2023/6681528.
10.1155/2023/6681528
Web of Science® Google Scholar
26 Shaheen A., Elsayed A., Ginidi A., El-Sehiemy R., and Elattar E., Reconfiguration of electrical distribution network-based DG and capacitors allocations using artificial ecosystem optimizer: practical case study, Alexandria Engineering Journal. (2022) 61, no. 8, 6105–6118, https://doi.org/10.1016/j.aej.2021.11.035.
10.1016/j.aej.2021.11.035
Web of Science® Google Scholar
27 Nguyen T. T., Nguyen T. T., and Le B., Optimization of electric distribution network configuration for power loss reduction based on enhanced binary cuckoo search algorithm, Computers & Electrical Engineering. (2021) 90, article 106893, https://doi.org/10.1016/j.compeleceng.2020.106893.
10.1016/j.compeleceng.2020.106893
Web of Science® Google Scholar
28 Hizarci H., Demirel O., and Turkay B. E., Distribution network reconfiguration using time-varying acceleration coefficient assisted binary particle swarm optimization, Engineering Science and Technology, an International Journal. (2022) 35, article 101230, https://doi.org/10.1016/j.jestch.2022.101230.
10.1016/j.jestch.2022.101230
Web of Science® Google Scholar
29 Huy T. H. B., Van Tran T., Vo D. N., and Nguyen H. T. T., An improved metaheuristic method for simultaneous network reconfiguration and distributed generation allocation, Alexandria Engineering Journal. (2022) 61, no. 10, 8069–8088, https://doi.org/10.1016/j.aej.2022.01.056.
10.1016/j.aej.2022.01.056
Web of Science® Google Scholar
30 Ali Z. M., Diaaeldin I. M., El-Rafei A., Hasanien H. M., Aleem S. H. A., and Abdelaziz A. Y., A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm, Ain Shams Engineering Journal. (2021) 12, no. 2, 1923–1941, https://doi.org/10.1016/j.asej.2020.12.006.
10.1016/j.asej.2020.12.006
Web of Science® Google Scholar
31 Popović Ž. N. and Kovački N. V., Multi-period reconfiguration planning considering distribution network automation, International Journal of Electrical Power & Energy Systems. (2022) 139, article 107967, https://doi.org/10.1016/j.ijepes.2022.107967.
10.1016/j.ijepes.2022.107967
Web of Science® Google Scholar
32 Naderipour A., Abdullah A., Marzbali M. H., and Nowdeh S. A., An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach, Expert Systems with Applications. (2022) 187, article 115914, https://doi.org/10.1016/j.eswa.2021.115914, 34566274.
10.1016/j.eswa.2021.115914
PubMed Web of Science® Google Scholar
33 Swaminathan D. and Rajagopalan A., Multi-objective golden flower optimization algorithm for sustainable reconfiguration of power distribution network with decentralized generation, Axioms. (2023) 12, no. 1, https://doi.org/10.3390/axioms12010070.
10.3390/axioms12010070
PubMed Web of Science® Google Scholar
34 Alwash S., Ibrahim S., and Abed A. M., Distribution system reconfiguration with soft open point for power loss reduction in distribution systems based on hybrid water cycle algorithm, Energies. (2023) 16, no. 1, https://doi.org/10.3390/en16010199.
10.3390/en16010199
PubMed Web of Science® Google Scholar
35 Jafar-Nowdeh A., Babanezhad M., Arabi-Nowdeh S., Naderipour A., Kamyab H., Abdul-Malek Z., and Ramachandaramurthy V. K., Meta-heuristic matrix moth-flame algorithm for optimal reconfiguration of distribution networks and placement of solar and wind renewable sources considering reliability, Environmental Technology & Innovation. (2020) 20, article 101118, https://doi.org/10.1016/j.eti.2020.101118.
10.1016/j.eti.2020.101118
Web of Science® Google Scholar
36 Adam S. P., Alexandropoulos S. A. N., Pardalos P. M., and Vrahatis M. N., No free lunch theorem: a review, Approximation and Optimization: Algorithms, Complexity and Applications, 2019, Springer, 57–82, https://doi.org/10.1007/978-3-030-12767-1_5, 2-s2.0-85065817298.
10.1007/978-3-030-12767-1_5
Google Scholar
37 Trojovská E. and Dehghani M., Clouded leopard optimization: a new nature-inspired optimization algorithm, IEEE Access. (2022) 10, 102876–102906, https://doi.org/10.1109/ACCESS.2022.3208700.
10.1109/ACCESS.2022.3208700
Web of Science® Google Scholar
38 Dang W., Liao S., Yang B., Yin Z., Liu M., Yin L., and Zheng W., An encoder-decoder fusion battery life prediction method based on Gaussian process regression and improvement, Journal of Energy Storage. (2023) 59, article 106469, https://doi.org/10.1016/j.est.2022.106469.
10.1016/j.est.2022.106469
Web of Science® Google Scholar
39 Cao D., Xu Y., Yang Z., Dong H., and Li X., An enhanced whale optimization algorithm with improved dynamic opposite learning and adaptive inertia weight strategy, Complex & Intelligent Systems. (2022) 9, no. 1, 767–795, https://doi.org/10.1007/s40747-022-00827-1.
10.1007/s40747-022-00827-1
Web of Science® Google Scholar
40 Baran M. E. and Wu F. F., Network reconfiguration in distribution systems for loss reduction and load balancing, IEEE Transactions on Power Delivery. (1989) 4, no. 2, 1401–1407, https://doi.org/10.1109/61.25627, 2-s2.0-84863333614.
10.1109/61.25627
Web of Science® Google Scholar
41 Baran M. E. and Wu F. F., Optimal capacitor placement on radial distribution systems, IEEE Transactions on Power Delivery. (1989) 4, no. 1, 725–734, https://doi.org/10.1109/61.19265, 2-s2.0-0024480765.
10.1109/61.19265
Web of Science® Google Scholar

Citing Literature

All articles

Multiobjective and Coordinated Reconfiguration and Allocation of Photovoltaic Energy Resources in Distribution Networks Using Improved Clouded Leopard Optimization Algorithm

Abstract

1. Introduction

2. Formulation of the Problem

2.1. Objective Function

2.1.1. Power Losses

2.1.2. Voltage Stability

2.1.3. Network Loading

2.1.4. Cost of PV Energy Resources

2.2. Constraints

2.3. Fuzzy Multiobjective Solution Method

3. Proposed Optimization Method

3.1. Introduction of CLO Algorithm

3.1.1. Initialization of the CLO Positions

3.1.2. Exploration Phase

3.1.3. Exploitation Phase

3.2. The ICLO

3.3. Implementation of the ICLO

4. Simulation Results

4.1. Results of the 33-Bus Test System

4.1.1. Results of Single-Objective Optimization

4.1.2. Multiobjective Optimization Results

4.1.3. ICLO Comparison (33-Bus Network)

4.2. Results of the 69-Bus Test System

4.2.1. Results of Multiobjective Optimization

4.2.2. ICLO Comparison (69-Bus Network)

5. Conclusion

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information